Local existence and lower bound of blow-up time to a Cauchy problem of a coupled nonlinear wave equations

1.   Introduction

Thermoelasticity involves the study of materials that experience elastic deformation in response to temperature variations. As a material is heated or cooled, it expands or contracts, leading to the development of thermal stresses. In thermoelastic materials, it is essential to account for the coupling between mechanical deformation and temperature distribution, as these interactions play a critical role in determining the material's overall response to thermal and mechanical loads.

The significance of thermoelasticity has been widely recognized in various engineering and materials science fields. Thermoelasticity is crucial for understanding the behaviour of materials under thermal and mechanical loads, enabling the design and analysis of structures that can effectively withstand these conditions. Thermoelasticity combines concepts from thermodynamics, solid mechanics, and materials science to study the effects of temperature on the mechanical properties of materials. Additionally, the study of thermoelasticity contributes to advancements in nanotechnology, where the behaviour of materials at the nanoscale, under varying temperatures and mechanical loads, is crucial.

Furthermore, integrating thermoelasticity with computational methods and numerical modeling has led to significant developments. Thermoelasticity is of key importance in the development of advanced materials and the design of high-performance engineering structures, particularly in industries such as aerospace, automotive, and civil engineering. Thermoelastic analysis provides critical insights into how materials respond to temperature changes and mechanical stresses, which is essential for ensuring the safety and reliability of engineering components and systems. Many studies have dealt with this topic ^[1], including but not limited to the phenomenon of infinite speed of heat transfer, which is inherent in the theory of thermoelasticity and was addressed by modified generalized theories ^[2,3,4] developed during the past five decades. Green-Naghdi models (Type Ⅱ and Ⅲ) ^[5,6,7] are alternative models of thermoelasticity with or without energy dissipation. The Type Ⅱ model does not allow power dissipation and is a particular case of the Type Ⅲ model, which does. The Moore-Gibson-Thompson equation has garnered significant research interest in recent years, with numerous studies analyzing and investigating its properties ^[8,9,10]. According to the MGT thermoelastic model, Abouelregal et al. ^[11] examined the thermoelastic behavior of an isotropic solid sphere subjected to non-uniform heat flow. The abstract quasi-group approach has been applied to the third-order Moore-Gibson-Thompson partial differential equation ^[12]. The decay rates of the Moore-Gibson-Thompson equation that arise in high-intensity ultrasound are discussed ^[13], as well as the optimal standard products within the Moore-Gibson-Thompson equation ^[14]. Quintanilla ^[15,16,17] analized the Moore-Gibson-Thompson thermoelastic problem and introduced a new heat conduction model described by the Moore-Gibson-Thompson equation by adding a relaxation parameter to the GN-Ⅲ model and employing the modified heat and energy equations. In ^[18,19,20] the Moore-Gibson-Thompson equation is solved in an unbounded medium with a cylindrical orifice. In addition, the effect of variable properties and rotation on an orthotropic viscous and thermally oriented annular cylinder is studied. Marin ^[21] Discussed the domain of influence in the Moore-Gibson-Thompson theory of dipolar bodies. Numerous scientific publications have appeared devoted to studying and interpreting the thermoelasticity under the MGT model ^[22,23,24], and thermoelasticity theory in general ^[25,26].

Voids are small empty spaces or pores within materials that exist either naturally (as in porous rocks and biological tissues) or through intentional engineering (as in foams and lightweight composites). These microscopic cavities modify the material's mechanical properties, specifically reducing stiffness and strength while altering thermal conductivity patterns. The presence of voids creates additional degrees of freedom in material response, generating volume changes and internal pressure variations. These effects require explicit consideration in mathematical models describing the material's mechanical and thermal behavior.

Thermoelastic materials with voids constitute a category of materials where the interplay between thermal and mechanical fields is affected by the presence of voids or pores. These materials hold considerable importance in diverse engineering applications, including porous structures, composites, and foam-like materials, where the voids significantly impact the overall behavior of the material. The presence of voids introduces additional complexity into the mathematical modeling of these materials, as they modify the thermal, mechanical, and thermoelastic properties, necessitating advanced approaches to accurately capture their behaviour under various conditions.

In thermoelastic materials with voids, both the solid matrix and void structure govern the material's response. The void-matrix interactions create complex behaviours, including local stress concentrations, thermal gradients, and material deformation. The void structure facilitates damping and energy dissipation during mechanical and thermal loading, making these materials suitable for applications requiring vibration control and thermal management.

Iesan ^[27] introduced the linear theory for thermoelastic materials with voids. It has applications in various fields, including geology and biology. He used the balance of energy and other tools to obtain the characteristic equations. He established fundamental theorems about uniqueness, the reciprocity theorem, and the variational description of the solution. Cowin and Nunziato ^[28,29] developed the theories of linear and nonlinear elastic materials with voids, which influenced the mechanical behaviour understanding of materials containing voids. Ciarletta and Scarpetta ^[30] conducted a comprehensive study on thermoelasticity operations, focusing on insulation materials with voids to enhance the comprehension of their behaviour under different conditions. Marin's ^[31,32] study delved into the intricacies of thermoelastic bodies with voids, exploring the concept of uniqueness and the sphere of influence. Cicco and Diaco ^[33] have studied and developed thermoelasticity theory with voids and without energy dispersion. Our study aims to extend their model by incorporating energy dispersion effects. Coin and Nunziato ^[34] investigated linear elastic materials with voids, emphasizing the importance of considering voids' volume to understand material behaviour. Othman and Abd-Elaziz ^[35] demonstrated the effectiveness of the DPL model in analysing thermal loading due to laser pulses in a generalized thermoelastic half-space with voids. Creating a theory of linear elastic materials with voids allows for a mathematical study of the mechanical behaviour of solids in the presence of empty spaces or voids. Sharma ^[36,37] investigated the free and three-dimensional vibrations of simply supported, homogeneous transversely isotropic thermoelastic cylindrical panels in the context of linear coupled thermoelasticity, whereas Ponnusamy ^[38] focused on wave propagation in a generalized thermoelastic solid cylinder with arbitrary sampling. ^[39,40] analysed the free vibrations of thermo-diffusive nonlocal elastic solids using LS and DPL models. In ^[41], the vibration of a thermoelastic spherical panel with voids in a three-dimensional model has been studied. Sharma and Prakash ^[42] discussed the vibrations of a nonlocal thermoelastic sphere with voids using a three-phase-lag model. In addition, ^[43] examined the vibration of a non-local isotropic thermoelastic cylinder with voids.

Thermoelastic materials with voids serve critical functions across engineering, materials science, and biomedical applications. Void presence creates complex thermal conduction and mechanical deformation patterns, necessitating sophisticated mathematical modeling approaches. Modern analytical frameworks, including the Moore-Gibson-Thompson model, fractional derivatives, and nonlocal elasticity theory, capture these materials' intricate dynamics. The comprehensive analysis of void-thermal-mechanical field interactions enables the development of materials that combine lightweight properties with thermal stability and mechanical resilience.

This paper introduces a novel mathematical model that analyzes the impact of void volume on variables related to generalized thermoelasticity in an isotropic solid cylinder undergoing free vibrations. By incorporating the Moore-Gibson-Thompson (MGT) thermoelasticity model with voids (MGT.Ⅴ), this study presents a new approach to understanding how the presence of voids affects the behaviour of thermoelastic waves. The model employs Laplace transform techniques and a direct method to derive results in the Laplace transform domain. The findings are compared with existing theories, and the results are illustrated graphically to highlight the influence of phase lags on physical phenomena. This research fills a significant gap in the field by extending the MGT model to account for voids, providing new insights into how void size affects the studied variables. The numerical results demonstrate that the presence of numerous small pores significantly reduces the values of the variables, while wave anisotropy in cylinders containing voids is shown to be minimal. This study's contributions include the first application of the MGT.Ⅴ model to analyze void effects in thermoelastic systems, offering an enhanced understanding of wave propagation and material behaviour in porous structures.

2.   Basic governing equations and formulas

The behaviour of a thermoelastic cylinder with voids is analysed using the governing equations obtained ^[44,45], variations in displacements and stresses along the cylinder's axis at the fixed end provide insights into the behaviour of a thermoelastic cylinder under different conditions.

The constitutive equations

where

The equation of motion

The equation of voids

where ${\sigma }_{ij}$ are the Cauchy stress tensor components, ${e}_{ij}$ are the strain tensor components, ${u}_{i, j}$ are the displacement components, ${\delta }_{ij}$ is the Kronecker delta, $\lambda , \mu$ are Lam's constants, $\theta = T–{T}_{0}$ is change in temperature with reference temperature ${T}_{0}, T$ is the absolute temperature, $\rho$ is the density of the medium, ${\beta }_{} = \left({3\lambda }_{}+2{\mu }_{}\right){\alpha }_{t}$ is coefficients of linear thermal, ${\alpha }_{t}$ is thermal expansion coefficient, $\phi$ is voids volume fraction field, $\alpha , b, \xi$ are voids parameters, $\chi$ is equilibrated inertia.

The conventional theory of heat conductivity, based on the Fourier Law, allows for the physical phenomenon of "infinite velocity of propagation". This is known as the thermal conduction paradox. Experimental evidence shows that thermal signals cannot propagate at infinite speed, which is physically impossible. To address the limitations of classical thermodynamic elasticity, non-classical models called generalized thermoelasticity models have been developed in recent decades. The most well-known of these is the Maxwell and Cattaneo theory, which modifies the Fourier law into a constitutive equation with a relaxation parameter.

The Fourier's law of heat conduction

Green and Naghdi ^[5,6,7] introduced a new concept in thermoelasticity theories and put forward three models known as GN-Ⅰ, Ⅱ and Ⅲ. In the heat conduction law of type Ⅲ proposed by Green and Naghdi, the Fourier law undergoes modification as follows:

where $K$ is the thermal displacement, ${K}^{{*}}$ is the thermal conductivity rate $q$ is heat flux vector, $t$ is the time, ${\tau }_{0}$ is the relaxation time and $\vartheta$ is the thermal displacement ^[7] verifying $\frac{\partial \vartheta }{\partial t} = \theta .$ Fourier's laws governing the thermoelastic cylinder with voids have been reformulated to include additional phase lags for vectors, yielding more comprehensive formulas. These laws are characterized by

Using Eq (8), we can derive a Moore-Gibson-Thompson heat equation model for a thermoelastic cylinder with voids

where ${\delta }_{1}$ is a real parameter with two possible values: either one or zero, ${C}_{e}$ is specific heat, $Q$ is heat source and $M$ is thermos-void coupling parameter.

The Moore-Gibson-Thompson (MGT) equation of thermoelasticity theory, which corresponds to the case ${\delta }_{1} = 1,$ serves as an expansion of both the Lord-Shulman (LS) theory ^[1] and the Green-Naghdi type Ⅲ (GN-Ⅲ) thermoelasticity theory ^[5,6,7]. The Moore-Gibson-Thompson thermo-voids model (MGT.Ⅴ) includes constitutive Eqs (1) and (5), along with thermal conduction Eq (9), and the ensuing equation of motion.

The equation of motion (3) in this theory remains consistent with thermoelasticity theory ^[46,47,48], as the density is assumed constant. However, the governing equations and thermal conductivity equation differ from thermoelastic theory due to the inclusion of a voids volume.

The generalized thermoelastic problem can be considered a specific case of a thermoelastic solid cylinder with voids with radius $a$. We will apply this modified MGT heat conduction model to an infinitely long solid cylinder. Due to the cylindrical symmetry, the displacement components in the cylindrical coordinate system are taken as ${u}_{r} = u\left(r, t\right)$, ${u}_{\theta } = 0$, ${u}_{z} = 0$. The cylinder is assumed to be in an undisturbed state with a uniform initial temperature of ${T}_{0}$. Consequently, the strain components are expressed as follows:

The cubic dilatation $e$ is thus given by

The stress-strain relations may be considered as follow

The motion Eq (3) becomes

Thus from (13) and (14), we obtain

If we take the divergence of Eq (15), we get

where ${\nabla }^{2} = \frac{{\partial }^{2}}{\partial {r}^{2}}+\frac{1}{r}\frac{\partial }{\partial r}$.

The equation of voids (4) becomes

The generalized equation of heat conduction (9) reduces to

Now we introduce the following non-dimensional variables:

In terms of these non-dimensional variables, Eqs (16)–(18) take the following forms, for simplicity, this dash can be ignored.

where ${\alpha }_{1} = \frac{\alpha {{\mathrm{\omega }}_{}^{{*}}}^{2}\rho }{b}, {\alpha }_{2} = \frac{\xi \rho {C}_{1}^{2}}{b}$, ${\alpha }_{3} = \frac{M\rho {C}_{1}^{2}}{\beta }, {\alpha }_{4} = \frac{{\rho }^{2}{C}_{1}^{2}\chi {{\mathrm{\omega }}_{}^{{*}}}^{2}}{b}, {\alpha }_{5} = \frac{KM}{b\beta {C}_{E}}, \epsilon = \frac{{T}_{0}{\beta }_{}^{2}}{{\rho }^{2}{C}_{E}{c}_{1}^{2}}.$

The constitutive Eq (13) is reduced to non-dimensional forms as

where ${\delta }_{}^{2} = \frac{{\lambda }_{}}{{\lambda }_{}+2{\mu }_{}}.$

We initially assume that the surface of the solid cylinder ($r = a$) is subjected to thermal shock, is traction-free, and does not contain voids within the olume fraction field.

In this scenario, the boundary conditions on the surface of the cylinder can be expressed as:

where $H\left(t\right)$ is the Heaviside function, ${\theta }_{0}$ is a constant.

The isotropic thermoelastic hollow cylinder with voids is assumed to be in an undisturbed state and at rest initially, both thermally and mechanically, resulting in the following initial conditions:

3.   Solution in the Laplace transform domain

The Laplace transform is defined by

then Eqs (20)–(23) take the form

Eliminating any one of the variables $\overline {e}, \overline {\theta }$, or $\overline {\phi }$ from Eqs (20)–(22) yields the following differential equation:

where

where

Equation (30) can be factorized as

where ${m}_{1}^{}, {m}_{2}^{}$, and ${m}_{3}^{}$ are the roots with positive real parts of the equation

The solution of (33), which is bounded as $r\to 0$, is given by

where the unknown functions ${A}_{i}^{}, {A}_{i}^{{{'}}}$ and ${A}_{i}^{{{'}}{{'}}}$ are to be determined below by using the boundary conditions (24). The modified Bessel function of the first kind of order zero is denoted by ${I}_{0}(.)$. Substituting Eqs (34) and (35) into (20) and (21), we get the following relations:

We thus have

Thus, by the use of (36)–(38), Eq (29) becomes

In order to evaluate the unknown parameters ${A}_{i}, (i = \mathrm{1, 2}, 3)$, we will use the Laplace transform of the boundary condition (24) to become

Applying these terms in Eqs (34), (35) and (39), we get the following set of linear equations:

4.   Special cases of thermoelasticity and thermoelasticity with voids models

Several situations can be deduced from the modified thermoelastic model incorporating voids, utilizing the Moore-Gibson-Thompson equation.

4.1.   Thermoelasticity without void

Neglecting the effects of voids $(b = \phi = M = 0)$, we get:

● The classical thermoelasticity theory (CTE) is given when ${\delta }_{1} = {\tau }_{0} = K = {K}^{{*}} = 0$.

● Lord-Shulman theory of thermoelasticity (LS) ^[1] is obtained when ${\delta }_{1} = K = {K}^{{*}} = 0$ ${\tau }_{0} > 0$.

● The modified heat equation proposed by Green-Naghdi theory of type Ⅱ (GN-Ⅱ) when ${\delta }_{1} = 1, {\tau }_{0} = 0$.

● The heat equation of Green-Naghdi theory of type Ⅲ (GN-Ⅲ) when ${\delta }_{1} = 1$ and ${\tau }_{0} = 0$.

● The generalized theory based on Moore-Gibson-Thompson thermoelasticity (MGTE) by taking ${\delta }_{1} = 1, K, {K}^{{*}} > 0\;\mathrm{a}\mathrm{n}\mathrm{d}\;{\tau }_{0} > 0.$

4.2.   Thermoelasticity with voids

In case of voids interactions is taken into account, we obtain:

● The coupled theory of thermal void (CTE.Ⅴ) is obtained when $M, b, \phi , {\beta }_{} > 0, {\delta }_{1} = 1$ and ${\tau }_{0} = K = {K}^{{*}} = 0$.

● The theory of thermal void introduced by Lord-Shulman (LS.Ⅴ) ${K}^{{*}} = 0, {\delta }_{1} = 1, {\tau }_{0} > 0$.

● The modified heat equation proposed by Green-Naghdi theory of type Ⅱ (GN-Ⅱ.Ⅴ) when ${\delta }_{1} = 0, {\tau }_{0} = 0, {K}^{{*}} > 0$.

● The heat equation of Green-Naghdi theory of type Ⅲ (GN-Ⅲ.Ⅴ) when ${\delta }_{1} = 1, K, {K}^{{*}} > 0$ and ${\tau }_{0} = 0$.

● The generalized theory based on Moore-Gibson-Thompson voids equation (MGT.Ⅴ) is accessible by taking ${\delta }_{1} = 1, K, {K}^{{*}} > 0\;\mathrm{a}\mathrm{n}\mathrm{d}\;{\tau }_{0} > 0.$

5.   Transformation and numerical results

In this part, the solution to the problem in the physical realm is obtained using the numerical inversion method, and we use the Riemann-sum approximation to obtain the numerical results for the generalized thermoelastic cylinder with voids using Moore-Gibson-Thompson model (MGT.Ⅴ)

5.1.   Inversion of the transforms

According to Honig and Hirdes ^[49], the Laplace transformed function can be inverted in the following manner:

Let $s = v+iw(v, w\in \mathbb{R}),$ the above formulation can be written as

The following approximation formula is obtained by expanding the function $h(r, t) = {e}^{-vt}f(r, t)$ in a Fourier series in the interval [0, 2${t}_{1}$] in accordance with ^[50,51].

where ${F}_{1}\left(r, v, t, {t}_{1}\right)$ is the discretization error. It can be made arbitrarily mini if the free parameter $v{t}_{1}$ is large. The parameter ${t}_{1}$ controls the frequency discretization in the Fourier series expansion. A larger value of t1increases the accuracy of the approximation by reducing the discretization error. The values of $v$ and ${t}_{1}$ are chosen according to the criteria outlined in ^[52,53].

5.2.   Numerical results

This section compares the Moore-Gibson-Thompson model (MGT.Ⅴ) and the CTE.Ⅴ, LS.Ⅴ, GN-Ⅱ.Ⅴ and GN-Ⅲ.Ⅴ models under the thermoelastic cylinders with voids. For this aim, we take $r = a = 5, t = 0.1, {\tau }_{0} = 0.03, {K}_{s} = 0.001.$ The material parameters are given as ^[44,45]:

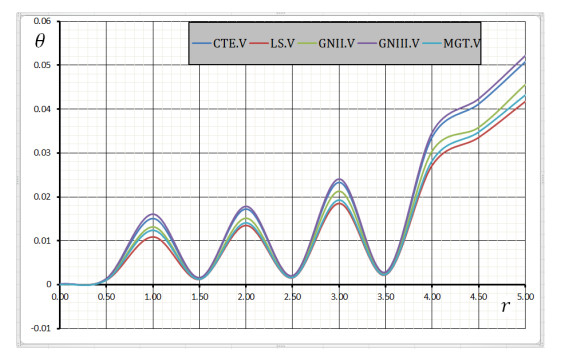
Figure 1 depicts the temperature distribution variations for classical thermal voids (CTE.Ⅴ), Lord-Shulman thermal voids model (LS.Ⅴ), Green-Naghdi models (GN-Ⅱ.Ⅴ and GN-Ⅲ.Ⅴ), as well as the Moore-Gibson-Thompson model of thermoelasticity with voids (MGT.Ⅴ). Primarily, these models exhibit differences in their magnitudes. It is evident that the initial temperature values are higher, gradually decreasing over time intervals across all models, with MGT.Ⅴ and LS.Ⅴ. showing lower temperatures near the cylinder's surface where boundary conditions are dominant. Furthermore, the models CTE.Ⅴ, LS.Ⅴ, GN-Ⅱ.Ⅴ, GN-Ⅲ.Ⅴ, and MGT.Ⅴ exhibit similar distributions before converging to zero within the cylinder interval. This suggests a significant impact of temperature-dependent properties on physical quantity distributions. As such properties increase or decrease in relation to the cylinder's temperature-dependent nature, they move coherently with findings from Abouelregal et al. ^[18,19] and Florea ^[20], substantiating the validity of the MGT.Ⅴ model.

Per Figure 2, the displacement $u$ versus the radial distance $r$ is plotted to compare the different models (CTE.Ⅴ, LS.Ⅴ, GN-Ⅱ.Ⅴ, GN-Ⅲ.Ⅴ, and MGT.Ⅴ).

● The graphic makes it clear that as the radius decreases, the displacement values are increasing.

● The displacement curves in the period $(3.5 < r < 5)$ show higher values in the GN-Ⅲ.Ⅴ and classical theory case than in the other generalised models.

● Additionally, we see that when the five models (CTE.Ⅴ, LS.Ⅴ, GN-Ⅱ.Ⅴ, GN-Ⅲ.Ⅴ, and MGT.Ⅴ) approach zero in the period $(0.0 < r < 1.0),$ they converge with one another. This indicates, in agreement with Abouelregal et al. ^[19,48], that the displacement exhibits oscillatory behaviour for thermoelasticity with voids. The accuracy of the MGT.Ⅴ model is therefore confirmed.

Figure 3 shows the distribution of thermoelastic vibration with voids $\phi$ for different models (CTE.Ⅴ, LST.Ⅴ, GN-Ⅱ.Ⅴ, GN-Ⅲ.Ⅴ, MGT.Ⅴ).

● It is noted that the spatial distribution in the five models starts from zero, where the boundary conditions predominate, and then takes a decreasing oscillatory behaviour, this is in line with Sharma ^[36] and Kumar ^[44].

● We find that the distribution of thermoelastic with voids for GN-Ⅲ.Ⅴ, CT.Ⅴ and GN-Ⅱ.Ⅴ is greater than the distribution of (MGT.Ⅴ).

● All the models attain their largest value at point 4.5 and reach their lowest values at $r = 2.50$. We also note that the five models (CTE.Ⅴ, LST.Ⅴ, GN-Ⅱ.Ⅴ, GN-Ⅲ.Ⅴ and MGT.Ⅴ) present similar curves and very close values but gradually fade inside the solid cylinder until they settle at zero in the period $(0.0 < r < 0.5).$

Figures 4 and 5 depict the thermoelastic stress distribution with voids along the radial direction for various classical thermo-voids theories (CTE.Ⅴ), Lord-Shulman thermo-voids (LS.Ⅴ), Green-Naghdi models (GN-Ⅱ.Ⅴ and GN-Ⅲ.Ⅴ) as well as the Moore-Gibson-Thompson model (MGT.Ⅴ) of thermoelasticity with voids.

● The curves clearly demonstrate significant differences in results near the surface, while showing convergence inside the cylinder.

● It is observed that pressures are minimal initially, gradually increasing and fluctuating over periods before eventually vanishing to zero.

● Additionally, radial stress initiates from zero at the surface, meeting mechanical boundary conditions as described by Quintanilla et al. ^[16], Abouelregal et al. ^[20], and Sharma et al. ^[43].

6.   Conclusions

● A homogeneous thermoelastic cylinder with voids in the radial direction has been studied in reference to the Moore-Gibson-Thompson model (MGTE.Ⅴ) of generalized thermoelasticity.

● In this work, we observed from the graphical results that the effect of the void modulus in the context of different models, such as classical thermoelasticity (CTE.Ⅴ), Lord-Shulman (LS.Ⅴ), Greene-Naghdi (GN-Ⅱ.Ⅴ and GN-Ⅲ.Ⅴ), and Moore-Gibson-Thomson (MGT.Ⅴ) model, played an important role in the field of thermoelasticity.

● Moore-Gibson-Thompson can be used to describe the porous effect on the resulting quantities and their physical characteristics.

● The presence of a large number of small pores decreases the value of thermal conductivity.

● Moore-Gibson-Thompson thermoelasticity with voids (MGT.Ⅴ) describes the behaviour of the particles of the elastic body more realistically than the different models of thermoelasticity that have been studied.

● Several researchers in the field of generalized thermoelasticity have applied the Moore-Gibson-Thompson model (MGT.Ⅴ) to thermoelasticity problems in general form, but very few of them have successfully applied it to the voids thermoelaticity problem.

● In this paper, we conclude that the magnitude of all physical quantities in the (MGT.Ⅴ) model is smaller than the (Coupled Theory and (GN-Ⅱ.Ⅴ and GN-Ⅲ.Ⅴ)) models.

● Moore–Gibson–Thompson can be used to describe the porous effect on the resulting quantities and their physical characteristics.

● It is clear, from the presented study and the discussions above, that the proposed model and numerical results presented in this research are very important to scientists, engineers and researchers, especially those working in the fields of thermodynamics, solid mechanics, and thermoelasticity.

Author contributions

Ahmed Yahya M.H: Drafting and designing the article; formal analysis; data interpretation; critical revision; final approval of the published version. Anouar Saidi: original draft writing, study design, methodology, article revision through critical analysis, and final approval of the published version. Ahmed E. Abouelregal and Ibrahim-Elkhalil: Study design; methodology; data collection and acquisition; writing; initial draft; critical revision; final approval of the published version. Adam Zakria and F. A. Mohammed: Data collection and acquisition, formal analysis, data interpretation, original draft writing, and final approval of the version that will be published. All authors have read and approved the final version of the manuscript for publication.

Acknowledgements

This work was funded by the Deanship of Graduate Studies and Scientific Research at Jouf University under grant No. (DGSSR-2023-02-02317).

Conflict of interest

The authors declare that none of the work reported in this paper could have been influenced by any known competing financial interests or personal relationships.