Contribution of a Ca<sup>2+</sup>-activated K<sup>+</sup> channel to neuronal bursting activities in the Chay model

Danqi Feng; Yu Chen; Quanbao Ji; Danqi Feng; Yu Chen; Quanbao Ji

doi:10.3934/era.2023380

Electronic Research Archive

2023, Volume 31, Issue 12: 7544-7555. doi: 10.3934/era.2023380

Previous Article Next Article

Research article Special Issues

Contribution of a Ca²⁺-activated K⁺ channel to neuronal bursting activities in the Chay model

1.
School of Mathematics and Physics, Guangxi Minzu University, Nanning 530006, China
2.
Center for Applied Mathematics of Guangxi, Guangxi Minzu University, Nanning 530006, China

Received: 27 September 2023 Revised: 21 November 2023 Accepted: 22 November 2023 Published: 28 November 2023

The central nervous system extensively expresses Ca²⁺-stimulated K⁺ channels, which serve to use Ca²⁺ to control their opening and closing. In this study, we explore the numerical computation of Hopf bifurcation in the Chay model based on the equilibrium point's stability and the center manifold theorem to illustrate the emergence of complicated neuronal bursting induced by variation of the conductance of the Ca²⁺-sensitive K⁺ channel. The results show that the formation and removal of various firing activities in this model are due to two subcritical Hopf bifurcations of equilibrium based on theoretical computation. Furthermore, the computational simulations are shown to support the validity of the conceptual approach. Consequently, the conclusion could be helpful to improve and deepen our understanding of the contribution of the Ca²⁺-sensitive K⁺ channel.

Keywords:

bifurcation,
neuron,
computation,
burst

Citation: Danqi Feng, Yu Chen, Quanbao Ji. Contribution of a Ca2+-activated K+ channel to neuronal bursting activities in the Chay model[J]. Electronic Research Archive, 2023, 31(12): 7544-7555. doi: 10.3934/era.2023380

Related Papers:

[1]	Hui Zhou, Bo Lu, Huaguang Gu, Xianjun Wang, Yifan Liu . Complex nonlinear dynamics of bursting of thalamic neurons related to Parkinson's disease. Electronic Research Archive, 2024, 32(1): 109-133. doi: 10.3934/era.2024006
[2]	Yapeng Zhang, Yu Chen, Quanbao Ji . Dynamical analysis of spontaneous Ca²⁺ oscillations in astrocytes. Electronic Research Archive, 2024, 32(1): 405-417. doi: 10.3934/era.2024020
[3]	Xiaofang Jiang, Hui Zhou, Feifei Wang, Bingxin Zheng, Bo Lu . Bifurcation analysis on the reduced dopamine neuronal model. Electronic Research Archive, 2024, 32(7): 4237-4254. doi: 10.3934/era.2024191
[4]	Bo Lu, Xiaofang Jiang . Reduced and bifurcation analysis of intrinsically bursting neuron model. Electronic Research Archive, 2023, 31(10): 5928-5945. doi: 10.3934/era.2023301
[5]	Qixiang Wen, Shenquan Liu, Bo Lu . Firing patterns and bifurcation analysis of neurons under electromagnetic induction. Electronic Research Archive, 2021, 29(5): 3205-3226. doi: 10.3934/era.2021034
[6]	A. M. Elaiw, E. A. Almohaimeed, A. D. Hobiny . Modeling the co-infection of HTLV-2 and HIV-1 in vivo. Electronic Research Archive, 2024, 32(11): 6032-6071. doi: 10.3934/era.2024280
[7]	Fanqi Zeng . Some almost-Schur type inequalities and applications on sub-static manifolds. Electronic Research Archive, 2022, 30(8): 2860-2870. doi: 10.3934/era.2022145
[8]	Ke Yin, Kewei Zhang . Some computable quasiconvex multiwell models in linear subspaces without rank-one matrices. Electronic Research Archive, 2022, 30(5): 1632-1652. doi: 10.3934/era.2022082
[9]	Li Li, Zhiguo Zhao . Inhibitory autapse with time delay induces mixed-mode oscillations related to unstable dynamical behaviors near subcritical Hopf bifurcation. Electronic Research Archive, 2022, 30(5): 1898-1917. doi: 10.3934/era.2022096
[10]	Chengchun Hao, Tao Luo . Some results on free boundary problems of incompressible ideal magnetohydrodynamics equations. Electronic Research Archive, 2022, 30(2): 404-424. doi: 10.3934/era.2022021

Abstract

1. Introduction

It is known that the Chay model, comprising the mixed Na⁺-Ca²⁺ channel current and K⁺ channel current, can be used to simulate and describe various neuronal firings of pancreatic β cells, sensory terminals and cold receptors ^[1,2,3]. Exploring the Chay model is prevalent to understand not only physical-mathematical associations but also physiological due to its simplicity and abundant dynamic behavior consisting of synchronization and oscillations set off by noise. Ca²⁺-sensitive K⁺ channels are significant to the initiation of action potential, contributing substantially to physiological processes and its dysfunction leads to abnormal action potential propagation ^[4,5,6]. Bursting is crucial in the exchange of information between neurons, which is characterized by alternations between resting and repetitive firing states. The most significant messenger in cells is Ca²⁺, which conveys vital information about nearly every action essential to the survival and proper operation of cells. The dynamic modulation of several elements is necessary for Ca²⁺ signaling, and the Na⁺/Ca²⁺ exchanger (NCX) plays a role in maintaining its homeostasis by extracting Ca²⁺ from cells ^[7]. In both healthy and ischemic brains, astrocyte NCX activation may perform various roles. Studies are amassing that demonstrate the importance of one of the major glial ion transporters, NCX, in the regulation of astrocytic, microglial and oligodendrocytic functions. We can conjecture that alterations in NCX activity in distinct brain regions or astrocytic places may be linked to learning, memory and information processing functions in the brain ^[8]. It has become clear that neuronal firing patterns are usually associated with abundant dynamical behaviors since it is affected by intrinsic and extrinsic mediators, for instance, variation of ion path permeability, time delay and noise perturbation, as well as depolarizing current and so on ^[9,10,11]. Although nervous systems are quite different, neurons share many common features, such as action potential as carriers of information, ion channels and rich nonlinear phenomena.

Experimental and theoretical investigations indicate that action potentials generated by Na⁺, Ca²⁺ and K⁺ currents are attributed to Ca²⁺-activated K⁺ channels ^[12,13,14]. Due to the importance of electrical activities associated with Ca²⁺-activated K⁺ channels, the dynamic mechanism underlying bursting in the Chay model should be investigated in detail. This model was studied extensively by Duan et al. ^[15,16,17], Xu et al. ^[18,19], Lu et al. ^[20,21] and Zhu et al. ^[22]. However, most studies are confined to numerical simulation of the Hopf bifurcation with variations in different bifurcation parameters ^{[15,16,17,18]}. Based on these previous works, the mechanisms and contributions involved in firing activities related to various ion channels are not well understood. Hence, we simulate the bursting dynamics associated with Ca²⁺-activated K⁺ ion channels in combination with the use of the Chay model.

2. Stability and bifurcation analysis

We use the two-pool model by Chay ^[23] and develop upon it as a demonstration of stability and bifurcation analysis. This model is formed from three dynamic indexes: The membrane voltage (V), the concentration of Ca²⁺ within the cell (C) and the odds of triggering the voltage-sensitive K⁺ channel (n). The model comprises three equations:

$\left\{ \begin{array}{l} {\text{ }}\frac{{dV}}{{dt}} = g_{_L}^*({V_L} - V) + g_{K, {\text{ }}V}^*{n^4}({V_K} - V) + g_I^*m_\infty ^3{h_\infty }({V_I} - V) + g_{K, {\text{ }}C}^*\frac{C}{{1 + C}}({V_K} - V), \hfill \\ {\text{ }}\frac{{dC}}{{dt}} = \rho \left[ {m_\infty ^3{h_\infty }({V_C} - V) - {k_C}C} \right], \hfill \\ {\text{ }}\frac{{dn}}{{dt}} = \frac{{{n_\infty } - n}}{{{\tau _n}}}, \hfill \\ \end{array} \right.$

(1)

where

$\begin{array}{l} {m_\infty } = \frac{{{\alpha _m}}}{{{\alpha _m} + {\beta _m}}}, \quad {\text{ }}{n_\infty } = \frac{{{\alpha _n}}}{{{\alpha _n} + {\beta _n}}}, {\text{ }}{h_\infty } = \frac{{{\alpha _h}}}{{{\alpha _h} + {\beta _h}}}, \hfill \\ {\alpha _m} = \frac{{0.1(25 + V)}}{{1 - {e^{ - 0.1V - 2.5}}}}, {\text{ }}{\beta _m} = 4{e^{\frac{{ - (V + 50)}}{{18}}}}, {\text{ }}{\alpha _h} = 0.07{e^{ - 0.05V - 2.5}}, \hfill \\ {\beta _h} = \frac{1}{{1 + ({e^{ - 0.1V - 2}})}}, {\text{ }}{\alpha _n} = \frac{{0.01(20 + V)}}{{1 - {e^{ - 0.1V - 2}}}}, {\text{ }}{\beta _n} = 0.125{e^{\frac{{ - (V + 30)}}{{80}}}}, \hfill \\ {\tau _n} = \frac{1}{{{\lambda _n}({\alpha _n} + {\beta _n})}}. \hfill \\ \end{array}$

The details of each parameter can be found in ^[23]. Here, g_kc^* is designated as the bifurcation parameter. It represents the highest conductance of Ca²⁺-sensitive K⁺ channel. Let x = V, y = C, z = n, r = g_kc^*. In order to simplify the calculation process, system (1) is transformed into the subsequent expression:

$\left\{ \begin{array}{l} \dot x = \frac{{126.0{\mkern 1mu} {{\text{e}}^{ - 0.05{\kern 1pt} x - 2.5}}{\mkern 1mu} \left( {x - 100} \right){\mkern 1mu} {{\left( {0.1{\mkern 1mu} x + 2.5} \right)}^3}}}{{{{\left( {{{\text{e}}^{ - 0.1{\kern 1pt} x - 2.5}} - 1} \right)}^3}\left( {0.07{\mkern 1mu} {{\text{e}}^{ - 0.05{\kern 1pt} x - 2.5}} + \frac{1}{{{{\text{e}}^{ - 0.1{\kern 1pt} x - 2}} + 1}}} \right){\mkern 1mu} {\mkern 1mu} {{\left( {4{\mkern 1mu} {{\text{e}}^{ - \frac{x}{{18}} - \frac{{25}}{9}}} - \frac{{0.1{\mkern 1mu} x + 2.5}}{{{{\text{e}}^{ - 0.1{\kern 1pt} x - 2.5}} - 1}}} \right)}^3}}} - 1700{\mkern 1mu} {z^4}{\mkern 1mu} \left( {x + 75} \right) \hfill \\ {\text{ }} - \frac{{r{\mkern 1mu} y{\mkern 1mu} \left( {x + 75} \right)}}{{y + 1}} - 7{\mkern 1mu} x - 280, {\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ \dot y = \frac{{0.0189{\mkern 1mu} {{\text{e}}^{ - 0.05{\kern 1pt} x - 2.5}}{\mkern 1mu} \left( {x - 100} \right){\mkern 1mu} {{\left( {0.1{\mkern 1mu} x + 2.5} \right)}^3}}}{{{{\left( {{{\text{e}}^{ - 0.1{\kern 1pt} x - 2.5}} - 1} \right)}^3}\left( {0.07{\mkern 1mu} {{\text{e}}^{ - 0.05{\kern 1pt} x - 2.5}} + \frac{1}{{{{\text{e}}^{ - 0.1{\kern 1pt} x - 2}} + 1}}} \right){\mkern 1mu} {\mkern 1mu} {{\left( {4{\mkern 1mu} {{\text{e}}^{ - \frac{x}{{18}} - \frac{{25}}{9}}} - \frac{{0.1{\mkern 1mu} x + 2.5}}{{{{\text{e}}^{ - 0.1{\kern 1pt} x - 2.5}} - 1}}} \right)}^3}}} - 0.0495{\mkern 1mu} y, {\kern 1pt} \hfill \\ \dot z = - \left( {28.75{\mkern 1mu} {{\text{e}}^{ - \frac{x}{{80}} - \frac{3}{8}}} - \frac{{230{\mkern 1mu} \left( {0.01{\mkern 1mu} x + 0.2} \right)}}{{{{\text{e}}^{ - 0.1{\kern 1pt} x - 2}} - 1}}} \right){\mkern 1mu} \left( {z + \frac{{0.01{\mkern 1mu} x + 0.2}}{{\left( {{{\text{e}}^{ - 0.1{\kern 1pt} x - 2}} - 1} \right){\mkern 1mu} \left( {0.125{\mkern 1mu} {{\text{e}}^{ - \frac{x}{{80}} - \frac{3}{8}}} - \frac{{0.01{\mkern 1mu} x + 0.2}}{{{{\text{e}}^{ - 0.1{\kern 1pt} x - 2}} - 1}}} \right)}}} \right). \hfill \\ \end{array} \right.$

(2)

The existence of equilibrium points can be determined by analyzing the differential equations of model. Suppose system (2) has three roots x₀, y₀, z_0. Let x₁ = x – x₀, y₁ = y – y₀, z₁ = z – z₀, we get the following representations:

$\left\{ \begin{array}{l} {{\dot x}_1} = \frac{{126.0{\mkern 1mu} {{\text{e}}^{ - 2.5 - 0.05{\kern 1pt} \left( {{x_0} + {x_1}} \right)}}{\mkern 1mu} \left( {\left( {{x_0} + {x_1}} \right) - 100} \right){\mkern 1mu} {{\left( {2.5 + 0.1{\mkern 1mu} \left( {{x_0} + {x_1}} \right)} \right)}^3}}}{{\left( {0.07{\mkern 1mu} {{\text{e}}^{ - 0.05{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2.5}} + \frac{1}{{{{\text{e}}^{ - 0.1{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2}} + 1}}} \right){\mkern 1mu} {{\left( {{{\text{e}}^{ - 0.1{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2.5}} - 1} \right)}^3}{\mkern 1mu} {{\left( {4{\mkern 1mu} {{\text{e}}^{ - \frac{{{x_1} + {x_0}}}{{18}} - \frac{{25}}{9}}} - \frac{{0.1{\mkern 1mu} \left( {{x_1} + {x_0}} \right) + 2.5}}{{{{\text{e}}^{ - 0.1{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2.5}} - 1}}} \right)}^3}}} \hfill \\ {\text{ }} - 1700{\mkern 1mu} {\left( {{z_1} + {z_0}} \right)^4}{\mkern 1mu} \left( {\left( {{x_1} + {x_0}} \right) + 75} \right) - \frac{{{\mkern 1mu} \left( {{y_0} + {y_1}} \right){\mkern 1mu} r\left( {\left( {{x_0} + {x_1}} \right) + 75} \right)}}{{{y_1} + {y_0} + 1}} - 7{\mkern 1mu} \left( {{x_0} + {x_1}} \right) - 280, {\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ {{\dot y}_1} = \frac{{0.0189{\mkern 1mu} {{\text{e}}^{ - 0.05{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2.5}}{\mkern 1mu} \left( {\left( {{x_1} + {x_0}} \right) - 100} \right){\mkern 1mu} {{\left( {0.1{\mkern 1mu} \left( {{x_1} + {x_0}} \right) + 2.5} \right)}^3}}}{{\left( {0.07{\mkern 1mu} {{\text{e}}^{ - 0.05{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2.5}} + \frac{1}{{{{\text{e}}^{ - 0.1{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2}} + 1}}} \right){\mkern 1mu} {{\left( {{{\text{e}}^{ - 0.1{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2.5}} - 1} \right)}^3}{\mkern 1mu} {{\left( {4{\mkern 1mu} {{\text{e}}^{ - \frac{{{x_1} + {x_0}}}{{18}} - \frac{{25}}{9}}} - \frac{{0.1{\mkern 1mu} \left( {{x_1} + {x_0}} \right) + 2.5}}{{{{\text{e}}^{ - 0.1{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2.5}} - 1}}} \right)}^3}}} \hfill \\ {\text{ }} - 0.0495{\mkern 1mu} \left( {{y_1} + {y_0}} \right), {\kern 1pt} \hfill \\ {{\dot z}_1} = - \left( {28.75{\mkern 1mu} {{\text{e}}^{ - \frac{{{x_1} + {x_0}}}{{80}} - \frac{3}{8}}} - \frac{{230{\mkern 1mu} \left( {0.01{\mkern 1mu} \left( {{x_1} + {x_0}} \right) + 0.2} \right)}}{{{{\text{e}}^{ - {\kern 1pt} \left( {{x_0} + {x_1}} \right)0.1 - 2}} - 1}}} \right){\mkern 1mu} \hfill \\ {\text{ }}\left( {{z_1} + {z_0} + \frac{{0.2 + {\mkern 1mu} \left( {{x_0} + {x_1}} \right)0.01}}{{\left( {{{\text{e}}^{ - 0.1{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2}} - 1} \right){\mkern 1mu} \left( {0.125{\mkern 1mu} {{\text{e}}^{ - \frac{{{x_1} + {x_0}}}{{80}} - \frac{3}{8}}} - \frac{{0.01{\mkern 1mu} \left( {{x_1} + {x_0}} \right) + 0.2}}{{{{\text{e}}^{ - 0.1{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2}} - 1}}} \right)}}} \right). \hfill \\ \end{array} \right.$

(3)

Equilibrium is (0, 0, 0) and system (3) has the same properties in system (2). It is clear that the Jacobian matrix (a_ij)_3×3 of system (3) and the characteristic equations satisfy: λ³ + Q₁λ² + Q₂ λ + Q₁ = 0, where Q₃ = a₃₁a₁₃a₂₂ + a₁₂a₂₁a₃₃ + a₃₂a₂₃a₁₁ – a₁₁a₂₂a₃₃ – a₁₂a₂₃a₃₁ – a₁₃a₂₁a₃₂, Q₂ = a₁₁a₂₂ + a₁₁a₃₃ + a₂₂a₃₃ – a₁₃a₃₁ – a₁₂a₂₁ – a₃₂a₂₃, Q₁ = – (a₁₁ + a₂₂ + a₃₃). Examine the Hurwitz matrix in the context of the coefficients Q_i (i = 1, 2, 3) of the characteristic polynomial:

${H_1} = \left[ {{Q_1}} \right], \;{H_2} = \left( {\begin{array}{*{20}{c}} {{Q_1}}&1 \\ {{Q_3}}&{{Q_2}} \end{array}} \right), \;{H_3} = \left[ {\begin{array}{*{20}{c}} {{Q_1}}&1&0 \\ {{Q_3}}&{{Q_2}}&1 \\ 0&0&{{Q_3}} \end{array}} \right] .$

The eigenvalues are negative when the determinant values of Hurwitz matrix are bigger than zero:

$\det \left( {{H_i}} \right) > 0, \;i = 1, 2, 3 .$

The robustness of system (3) is taken into account as varying the values of g_kc^* using the criteria of the Routh's array:

${Q_1} > 0, \;{Q_3} > 0, \;{Q_1}\, {Q_2} > {Q_3} .$

It is easy to see that:

1) r < -41.647, system (3) contains a stable node;

2) r = -41.647, the system possesses a non-hyperbolic stationary state, which is O₁ = (-17.5904, 4.7463, 0.4334);

3) -41.647 < r < 27.25, the system includes a saddle point;

4) r = 27.25, the system contains a non-hyperbolic stationary state, which is O₂ = (24.7680, -0.8969, 0.6095);

5) r > 27.25, the system is stable.

The system (3) reaches equilibrium at (x₀, y₀, z₀) as r = r₀, x₁ = x - x₀, y₁ = y - y₀, z₁ = z - z₀, r₁ = r - r₀. Next, we introduce a new variable denoted as r₁ in the application of center manifold theorem with respect to the parameter g_kc^*. Let dr₁/dt = 0, we obtain:

$\left\{ \begin{array}{l} {{\dot x}_1} = \frac{{126.0{\mkern 1mu} {{\text{e}}^{ - 2.5 - 0.05{\kern 1pt} \left( {{x_0} + {x_1}} \right)}}{\mkern 1mu} \left( {\left( {{x_0} + {x_1}} \right) - 100} \right){\mkern 1mu} {{\left( {2.5 + 0.1{\mkern 1mu} \left( {{x_0} + {x_1}} \right)} \right)}^3}}}{{\left( {0.07{\mkern 1mu} {{\text{e}}^{ - 0.05{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2.5}} + \frac{1}{{{{\text{e}}^{ - 0.1{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2}} + 1}}} \right){\mkern 1mu} {{\left( {{{\text{e}}^{ - 0.1{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2.5}} - 1} \right)}^3}{\mkern 1mu} {{\left( {4{\mkern 1mu} {{\text{e}}^{ - \frac{{{x_1} + {x_0}}}{{18}} - \frac{{25}}{9}}} - \frac{{0.1{\mkern 1mu} \left( {{x_1} + {x_0}} \right) + 2.5}}{{{{\text{e}}^{ - 0.1{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2.5}} - 1}}} \right)}^3}}} \hfill \\ {\text{ }} - 1700{\mkern 1mu} {\left( {{z_0} + {z_1}} \right)^4}{\mkern 1mu} \left( {\left( {{x_0} + {x_1}} \right) + 75} \right) - \frac{{{\mkern 1mu} \left( {{y_0} + {y_1}} \right){\mkern 1mu} \left( {\left( {{x_1} + {x_0}} \right) + 75} \right)\left( {{r_0} + {r_1}} \right)}}{{{y_1} + {y_0} + 1}} - 7{\mkern 1mu} \left( {{x_1} + {x_0}} \right) - 280, {\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ {{\dot y}_1} = \frac{{0.0189{\mkern 1mu} {{\text{e}}^{ - 2.5 - 0.05{\kern 1pt} \left( {{x_0} + {x_1}} \right)}}{\mkern 1mu} \left( {\left( {{x_0} + {x_1}} \right) - 100} \right){\mkern 1mu} {{\left( {2.5 + 0.1{\mkern 1mu} \left( {{x_0} + {x_1}} \right)} \right)}^3}}}{{\left( {0.07{\mkern 1mu} {{\text{e}}^{ - 0.05{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2.5}} + \frac{1}{{{{\text{e}}^{ - 0.1{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2}} + 1}}} \right){\mkern 1mu} {{\left( {{{\text{e}}^{ - 0.1{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2.5}} - 1} \right)}^3}{\mkern 1mu} {{\left( {4{\mkern 1mu} {{\text{e}}^{ - \frac{{{x_1} + {x_0}}}{{18}} - \frac{{25}}{9}}} - \frac{{0.1{\mkern 1mu} \left( {{x_1} + {x_0}} \right) + 2.5}}{{{{\text{e}}^{ - 0.1{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2.5}} - 1}}} \right)}^3}}} \hfill \\ {\text{ }} - 0.0495{\mkern 1mu} \left( {{y_1} + {y_0}} \right), {\kern 1pt} \hfill \\ {{\dot z}_1} = - \left( {28.75{\mkern 1mu} {{\text{e}}^{ - \frac{{{x_1} + {x_0}}}{{80}} - \frac{3}{8}}} - \frac{{230{\mkern 1mu} \left( {0.01{\mkern 1mu} \left( {{x_1} + {x_0}} \right) + 0.2} \right)}}{{{{\text{e}}^{ - 2 - 0.1{\kern 1pt} \left( {{x_0} + {x_1}} \right)}} - 1}}} \right){\mkern 1mu} \hfill \\ {\text{ }}\left( {{z_0} + {z_1} + \frac{{0.01{\mkern 1mu} \left( {{x_0} + {x_1}} \right) + 0.2}}{{\left( {{{\text{e}}^{ - 0.1{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2}} - 1} \right){\mkern 1mu} \left( {0.125{\mkern 1mu} {{\text{e}}^{ - \frac{{{x_1} + {x_0}}}{{80}} - \frac{3}{8}}} - \frac{{0.01{\mkern 1mu} \left( {{x_1} + {x_0}} \right) + 0.2}}{{{{\text{e}}^{ - 0.1{\kern 1pt} \left( {{x_1} + {x_0}} \right) - 2}} - 1}}} \right)}}} \right), \hfill \\ {{\dot r}_1} = 0. \hfill \\ \end{array} \right.$

(4)

As r₁ = 0, system (4) achieves equilibrium O (x₁, y₁, z₁, r₁) = (0, 0, 0, 0), which has the identical property in system (2). When r₀ = -41.647, we consider the characteristic values of balanced state O₁ = (0, 0, 0, 0) in system (4): ξ₁ = -0.0005, ξ₂ = 1.6305i, ξ₃ = -1.6305i, ξ₄ = 0.

Suppose

$\left( {\begin{array}{*{20}{c}} {{x_1}} \\ {{y_1}} \\ {{z_1}} \\ {{r_1}} \end{array}} \right) = U\left( {\begin{array}{*{20}{c}} u \\ v \\ w \\ s \end{array}} \right), {\rm{where}}\;U = \left( {\begin{array}{*{20}{c}} {0.1263}&{1.0000}&0&{ - 0.0829} \\ {0.9920}&0&0&{0.0022} \\ {0.0021}&{0.0001}&{0.0051}&{ - 0.0014} \\ 0&0&0&{0.9966} \end{array}} \right),$

system (4) has the following form

$\left( {\begin{array}{*{20}{c}} {\dot u} \\ {\dot v} \\ {\dot w} \\ {\dot s} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - 0.0005}&0&0&0 \\ 0&0&{ - 1.6305}&0 \\ 0&{1.6305}&0&0 \\ 0&0&0&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} u \\ v \\ w \\ s \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{g_1}} \\ {{g_2}} \\ {{g_3}} \\ {{g_4}} \end{array}} \right) ,$

(5)

where

$\begin{array}{l} {g_1} = 1.008064516{f_2} - 0.002225307983{f_4} + 0.0005u, \hfill \\ {g_2} = {f_1} - 0.1273185484{f_2} + 0.08346387799{f_4} + 1.6305w, \hfill \\ {g_3} = - 0.01960784314{f_1} - 0.4125889469{f_2} + 196.0784314{f_3} + 0.2747260781{f_4} - 1.6305v, \hfill \\ {g_4} = 0, \hfill \\ {f_1} = \frac{{126.0{\mkern 1mu} {{\text{e}}^{ - 0.05{\kern 1pt} {g_{11}} - 2.5}}{\mkern 1mu} \left( {{g_{11}} - 100} \right){\mkern 1mu} {{\left( {0.1{\mkern 1mu} {g_{11}} + 2.5} \right)}^3}}}{{\left( {0.07{\mkern 1mu} {{\text{e}}^{ - 0.05{\kern 1pt} {g_{11}} - 2.5}} + \frac{1}{{{{\text{e}}^{ - 0.1{\kern 1pt} {g_{11}} - 2}} + 1}}} \right){\mkern 1mu} {{\left( {{{\text{e}}^{ - 0.1{\kern 1pt} {g_{11}} - 2.5}} - 1} \right)}^3}{\mkern 1mu} {{\left( {4{\mkern 1mu} {{\text{e}}^{ - \frac{{{g_{11}}}}{{18}} - \frac{{25}}{9}}} - \frac{{0.1{\mkern 1mu} {g_{11}} + 2.5}}{{{{\text{e}}^{ - 0.1{\kern 1pt} {g_{11}} - 2.5}} - 1}}} \right)}^3}}} \hfill \\ {\text{ }} - 1700{\mkern 1mu} {g_{13}}^4{\mkern 1mu} \left( {{g_{11}} + 75} \right) - \frac{{{g_{14}}{\mkern 1mu} {g_{12}}{\mkern 1mu} \left( {{g_{11}} + 75} \right)}}{{{g_{12}} + 1}} - 7{\mkern 1mu} {g_{11}} - 280, \hfill \\ {f_2} = \frac{{0.0189{\mkern 1mu} {{\text{e}}^{ - 0.05{\kern 1pt} {g_{11}} - 2.5}}{\mkern 1mu} \left( {{g_{11}} - 100} \right){\mkern 1mu} {{\left( {0.1{\mkern 1mu} {g_{11}} + 2.5} \right)}^3}}}{{\left( {0.07{\mkern 1mu} {{\text{e}}^{ - 0.05{\kern 1pt} {g_{11}} - 2.5}} + \frac{1}{{{{\text{e}}^{ - 0.1{\kern 1pt} {g_{11}} - 2}} + 1}}} \right){\mkern 1mu} {{\left( {{{\text{e}}^{ - 0.1{\kern 1pt} {g_{11}} - 2.5}} - 1} \right)}^3}{\mkern 1mu} {{\left( {4{\mkern 1mu} {{\text{e}}^{ - \frac{{{g_{11}}}}{{18}} - \frac{{25}}{9}}} - \frac{{0.1{\mkern 1mu} {g_{11}} + 2.5}}{{{{\text{e}}^{ - 0.1{\kern 1pt} {g_{11}} - 2.5}} - 1}}} \right)}^3}}} \hfill \\ {\text{ }} - 0.0495{\mkern 1mu} {g_{12}}, {\kern 1pt} {\kern 1pt} \hfill \\ {f_3} = - \left( {28.75{\mkern 1mu} {{\text{e}}^{ - \frac{{{g_{11}}}}{{80}} - \frac{3}{8}}} - \frac{{230{\mkern 1mu} \left( {0.01{\mkern 1mu} {g_{11}} + 0.2} \right)}}{{{{\text{e}}^{ - 0.1{\kern 1pt} {g_{11}} - 2}} - 1}}} \right){\mkern 1mu} \hfill \\ {\text{ }}\left( {{g_{13}} + \frac{{0.01{\mkern 1mu} {g_{11}} + 0.2}}{{\left( {{{\text{e}}^{ - 0.1{\kern 1pt} {g_{11}} - 2}} - 1} \right){\mkern 1mu} \left( {0.125{\mkern 1mu} {{\text{e}}^{ - \frac{{{g_{11}}}}{{80}} - \frac{3}{8}}} - \frac{{0.01{\mkern 1mu} {g_{11}} + 0.2}}{{{{\text{e}}^{ - 0.1{\kern 1pt} {g_{11}} - 2}} - 1}}} \right)}}} \right), \hfill \\ {f_4} = 0, \hfill \\ {g_{11}} = {x_1} + {x_0} = 0.1263u - 0.0829s + 1.0v - 17.5904, \hfill \\ {g_{12}} = {y_1} + {y_0} = 0.0022s + 0.992u + 4.7463, \hfill \\ {g_{13}} = {z_1} + {z_0} = 0.0021u - 0.0014s + 0.0001v + 0.0051w + 0.4334, \hfill \\ {g_{14}} = 0.9966s - 41.647. \hfill \\ \end{array}$

Based on center manifold theorem, a center manifold exists. The specific form is as follows:

$W_{loc}^c({O_1}) = \{ (u, v, w, s) \in \left. {{R^4}} \right|{\kern 1pt} {\kern 1pt} u = {h^*}(v, w, s), {\kern 1pt} {\kern 1pt} {\kern 1pt} {h^*}(0, 0, 0) = 0, {\kern 1pt} {\kern 1pt} {\kern 1pt} D{h^*}(0, 0, 0) = 0\} ,$

Assume h (v, w, s) = av² + bw² + cs² + dvw + evs + fws +…, the center manifold is

$N(h) = Dh \cdot \left[ {\begin{array}{*{20}{c}} {\dot v} \\ {\dot w} \\ {\dot s} \end{array}} \right] + 0.0005h - {g_1} \equiv 0 .$

(6)

Here a = -0.0000036406, b = -0.000003093017389, c = 0.00008567728077, d = 0.00000180521, e = 0.00000016, f = -0.0000005491. If the system is limited by center manifold, the following conditions are satisfied:

$\left( {\begin{array}{*{20}{c}} {\dot v} \\ {\dot w} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0&{ - 1.6305} \\ {1.6305}&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} v \\ w \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{f^1}\left( {v, w} \right)} \\ {{f^2}\left( {v, w} \right)} \end{array}} \right),$

(7)

where

$\begin{array}{l} {f^1}(v, w) = 0.580313865s - 7.0v + 1.6305w - 0.0000001404922113sv + 0.0000004820211492sw \hfill \\ {\text{ }} - 0.000001584700346vw + \cdots , \hfill \\ {f^2}(v, w) = - 0.01133350044s - 1.493245098v + 0.000000006016773356sv - 0.00000002064322272sw \hfill \\ {\text{ }} + 0.00000006786698519vw + \cdots . \hfill \\ \end{array}$

Then, we have

$\begin{array}{l} a = \frac{1}{{16}}{\left. {[f_{vvv}^1 + f_{vww}^1 + f_{vvw}^2 + f_{www}^2]} \right|_{(0, 0)}} + \frac{1}{{16 \times 0.0204}}[f_{vw}^1(f_{vv}^1 + f_{ww}^1) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left. { - f_{vw}^2(f_{vv}^2 + f_{ww}^2) - f_{vv}^1f_{vv}^2 + f_{ww}^1f_{ww}^2)]} \right|_{(v = 0, w = 0, s = 0)}} = 3.01538319{\text{ > }}0, \hfill \\ d = {\left. {\frac{{d({Re} (\xi (s))}}{{ds}}} \right|_{(v = 0, w = 0, s = 0)}} = - 0.00001623167121 < 0. \hfill \\ \end{array}$

(8)

According to previous numerical computations, we have:

Conclusion 1: At r₀ = -41.647, a supercritical Hopf bifurcation is obtained. When the value of r is less than r₀, the equilibrium O₁ turns to be stable. The equilibrium state loses stability as r > r₀ and a stable periodic solution appears, which causes the oscillation of system (2). As r₀ = 27.25, the characteristic values are ξ₁ = 0.0036, ξ₂ = 3.8251i, ξ₃ = -3.8251i and ξ₄ = 0, respectively.

The simplified form based on the center manifold system (4) is depicted as

$\left( {\begin{array}{*{20}{c}} {\dot v} \\ {\dot w} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0&{ - 3.8251} \\ {3.8251}&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} v \\ w \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{f^1}\left( {v, w} \right)} \\ {{f^2}\left( {v, w} \right)} \end{array}} \right) ,$

(9)

where

$\begin{array}{l} {f^1}(v, w) = 0.62108s - 7.0v + 3.8251w - 0.000007826615347sv + 0.00001148249661sw \hfill \\ {\text{ }} - 0.0001076807683vw + \cdots , \hfill \\ {f^2}(v, w) = - 0.1979232s - 2.9851v + 0.000001122019432sv - 0.000001646124635sw \hfill \\ {\text{ }} + 0.00001543705793vw + \cdots . \hfill \\ \end{array}$

The next conclusion can be obtained as a = 0.32334838 > 0 and d = 0.01462214783 > 0.

Conclusion 2: At r₀ = 27.25, the system exhibits a subcritical Hopf bifurcation transition. As r is less than r₀, the equilibrium O₂ is in an unstable state. As r > r₀, the equilibrium O₂ returns to be stable.

3. Numerical simulations

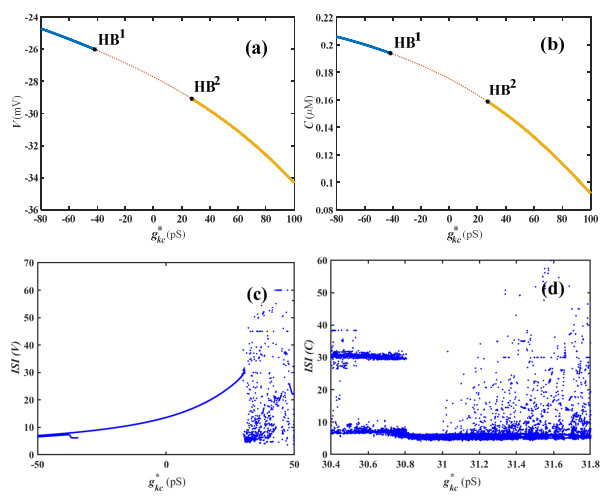
The generation processes of the parameter g_kc^* are presented so as to study the bifurcation phenomenon underlying various firing activities. Figures 1(a), (b) show the bifurcations that illustrate the stationary states of system (2) in the (V, g_kc^*) and (C, g_kc^*) planes, respectively. Each point of the solid line in the curve denotes equilibrium stability, and the dotted curve is an unsteady stationary state. Additionally, g_kc^* passes through two Hopf bifurcations labeled with HB¹ and HB², where g_kc^* ¹ = -41.647 μM/s and g_kc^* ² = 27.25 μM/s. As g_kc^* is increased, the balanced stationary initially loses its steady state at HB¹, only to regain the balanced state at HB².

Figure 1. (Color online) (a) Bifurcation diagram of system (2) in the (g_kc^*, V) plane. (b) Bifurcation diagram of system (2) in the (g_kc^*, C) plane. HB¹ and HB² represent two Hopf bifurcation points. (c) The interspike interval (ISI) bifurcation of equilibrium with V and g_kc^*. (d) Enlargement of the interspike interval (ISI) bifurcation of equilibrium with C and g_kc^* in the selected range.

DownLoad: Full-Size Img PowerPoint

Because of the fluctuation in the parameter g_kc^*, the two Hopf bifurcation points are plainly visible. It can be seen that g_kc^* has a stable equilibrium between g_kc^* = -80 pS and -41.647 pS, as well as between g_kc^* = 27.25 pS and 100 pS. There are two unstable equilibria in the range of g_kc^* = -41.647 pS to 27.25 pS. Firing activities can be obtained from the ISI bifurcation with variation of the parameter g_kc^*. As g_kc^* is increased approximately to 30 pS, simple firing activities occur (Figure 1(c)). Then, in Figure 1(d), a partially enlarged picture of the ISI bifurcation in the (g_kc^*, C) plane is shown. As g_kc^* is increased to 31 pS, bursts are observed.

The corresponding time series of system (2) are presented in Figure 2. Figure 2(a1), (b1), (c1), (d1) shows the time evolution of parameter g_kc^* with different values. Figure 2(a2), (b2), (c2), (d2) represents distinct state trajectories in the three-dimensional phase space under different g_kc^* values.

Figure 2. (Color online) Evolution of the membrane potential (V) in pyramidal neuron emerged in different parts of the curves relative to HB¹ and HB² points in Figure 1(a). (a1), (b1), (c1), (d1) The left column represents the temporal evolution of neuronal membrane potential (V) under different parameters g_kc^*. (a2), (b2), (c2), (d2) The image in the middle column denotes the corresponding V-C-n phase portrait. (a3), (b3), (c3), (d3) The image of the right column is recorded as the spectrum corresponding to Figure (a1)–(d1). (a) g_kc^* = 21 pS, (b) g_kc^* = 11 pS, (c) g_kc^* = 10.9 pS, (d) g_kc^* = 10.4 pS.

DownLoad: Full-Size Img PowerPoint

Figure 2 depicts the time-varying membrane voltage for various values of the parameter g_kc^*. On the left, the time evolution of V is compared with g_kc^*. The state trajectories in the 3D phase portrait V-C-n space are shown in the middle panels, and the right panels are the time-frequency of parameter g_kc^*. For instance, there is a single peak in the oscillation when g_kc^* = 21 pS in Figure 2(a1). The one-to-one correspondence of the three-dimensional phase space is visualized in Figure 2(a2). Moreover, Figure 2(a3) shows a temporal-spectral pattern with the parameter g_kc^* = 21 pS. When the value of the bifurcation parameter g_kc^* drops, the total number of peak counts and magnitudes begins to increase. Similarly, six peaks were produced when g_kc^* = 11 pS, as shown in Figure 2(b1). Then, in Figure 2(c2), chaos appears. Furthermore, the number of peak counts in Figure 2(d1) tends to oscillate in a periodic fashion. Figure 2(a3), (b3), (c3), (d3) illustrates the frequency spectrogram of the temporal evolution pattern, making the change observation more apparent.

The membrane voltage of neurons exhibits spontaneous oscillations in Figure 2(a1). The temporal evolution Figure 2(a1), which corresponds to the 3D phase Figure 2(a2), appears as an inflection point, denoted by a red hollow circle. Figure 2(b1) displays a multi-peak oscillation phenomenon as the parameter g_kc^* lowers continually, in contrast to the single-peak oscillation phenomenon in Figure 2(a1). Among these, Figure 2(a1), (b1), (d1) represents a regular burst of membrane potential (V). Figure 2(c1) depicts chaos. In the third experimental situation, the evolution diagram of time shows significant irregularity, that is, the irregular spike sequence of spontaneous oscillations of membrane voltage (V). These phenomena are plentiful and warrant further investigation.

4. Conclusions

Mathematical modeling and numerical simulation are two effective methods to help us understand the internal workings of the neuronal system. We investigated the properties of primitive hippocampal neurons in the Chay model using the bifurcation parameter g_kc^*. We analyzed the theoretical stability of equilibrium and bifurcation and explored the variations in the conductance of the Ca²⁺-sensitive K⁺ channel. As the parameter g_kc^* varies, two supercritical Hopf critical nodes were found.

The Chay model exhibited a bi-stability phenomenon, namely the coexistence of chaotic attractors and stationary point attractors. This phenomenon was numerically revealed through time evolution, local bifurcation, phase planes and spectrum diagrams. Numerical calculations of Hopf bifurcations confirmed the theoretical analysis. It is concluded that the conductance of Ca²⁺-sensitive K⁺ channels leads to the emergence of complex neuronal bursting. Thus, some dynamic behaviors of system (1) are schematically presented. Measurements corroborated the numerical results, displaying dynamic behaviors. Validation of theoretical results was achieved through the use of numerical methods, which were employed after conducting a thorough theoretical analysis. Other complex dynamical behaviors of the presented Chay model should be further studied. We aim to conduct more comprehensive research on the relationship between the synchronization of oscillatory patterns and bifurcation in our upcoming investigations.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (No. 12062004), the Natural Science Foundation of Guangxi Minzu University (No. 2022KJQD01), the Guangxi Natural Science Foundation (2020GXNSFAA297240), Guangxi Science and Technology Program (Grant No. AD23023001) and Xiangsi Lake Young Scholars Innovation Team of Guangxi Minzu University (No. 2021RSCXSHQN05).

Conflict of interest

The authors declare there is no conflict of interest.

References

[1]	K. Koyama, H. Ando, K. Fujiwara, Functional improvement in β cell models of type 2 diabetes using on-demand feedback control, AIP Adv., 13 (2023), 045317. https://doi.org/10.1063/5.0124625 doi: 10.1063/5.0124625
[2]	Z. Yang, Q. Lu, L. Li, The genesis of period-adding bursting without bursting-chaos in the Chay model, Chaos, Solitons Fractals, 27 (2006), 689–697. https://doi.org/10.1016/j.chaos.2005.04.038 doi: 10.1016/j.chaos.2005.04.038
[3]	Z. Yang, Q. Lu, H. Gu, W. Ren, Integer multiple spiking in the stochastic Chay model and its dynamical generation mechanism, Phys. Lett. A, 299 (2002), 499–506. https://doi.org/10.1016/S0375-9601(02)00746-6 doi: 10.1016/S0375-9601(02)00746-6
[4]	M. Gu, Y. Zhu, X. Yin, D. M. Zhang, Small-conductance Ca²⁺-activated K⁺ channels: insights into their roles in cardiovascular disease, Exp. Mol. Med., 50 (2018), 1–7. https://doi.org/10.1038/s12276-018-0043-z doi: 10.1038/s12276-018-0043-z
[5]	X. Chen, Y. Feng, R. J. Quinn, D. L. Pountney, D. R. Richardson, G. D. Mellick, et al., Potassium channels in parkinson's disease: potential roles in its pathogenesis and innovative molecular targets for treatment, Pharm. Rev., 75 (2023), 758–788. https://doi.org/10.1124/pharmrev.122.000743 doi: 10.1124/pharmrev.122.000743
[6]	J. P. Adelman, J. Maylie, P. Sah, Small-conductance Ca²⁺-activated K⁺ channels: form and function, Annu. Rev. Physiol., 74 (2012), 245–269. https://doi.org/10.1146/annurev-physiol-020911-153336 doi: 10.1146/annurev-physiol-020911-153336
[7]	M. Al-Khannaq, J. Lytton, Regulation of K⁺-Dependent Na⁺/Ca²⁺-Exchangers (NCKX), Int. J. Mol. Sci., 24 (2023), 598. https://doi.org/10.3390/ijms24010598 doi: 10.3390/ijms24010598
[8]	S. Song, L. Luo, B. Sun, D. Sun, Roles of glial ion transporters in brain diseases, Glia, 68 (2020), 472–494. https://doi.org/10.1002/glia.23699 doi: 10.1002/glia.23699
[9]	Y. Li, R. Wang, T. Zhang, Nonlinear computational models of dynamical coding patterns in depression and normal rats: from electrophysiology to energy consumption, Nonlinear Dyn., 107 (2022), 3847–3862. https://doi.org/10.1007/s11071-021-07079-7 doi: 10.1007/s11071-021-07079-7
[10]	L. Li, Z. Zhao, White-noise-induced double coherence resonances in reduced Hodgkin-Huxley neuron model near subcritical Hopf bifurcation, Phys. Rev. E: Stat. Nonlinear Soft Matter Phys., 105 (2022), 034408. https://doi.org/10.1103/PhysRevE.105.034408 doi: 10.1103/PhysRevE.105.034408
[11]	P. Crotty, K. Segall, D. Schult, Biologically realistic behaviors from a superconducting neuron model, IEEE Trans. Appl. Supercond., 33 (2023), 1–6. https://doi.org/10.1109/TASC.2023.3242901 doi: 10.1109/TASC.2023.3242901
[12]	L. Blomer, On the voltage gated ion channels involved in action potential generation and back propagation in layer 5 pyramidal neurons, 2022. Available from: https://theses.hal.science/tel-04077615/file/BLOMER_2022_archivage.pdf.
[13]	M. V. Roshchin, V. N. Ierusalimsky, P. M. Balaban, E. S. Nikitin, Ca²⁺-activated KCa3.1 potassium channels contribute to the slow afterhyperpolarization in L5 neocortical pyramidal neurons, Sci. Rep., 10 (2020), 14484. https://doi.org/10.1038/s41598-020-71415-x doi: 10.1038/s41598-020-71415-x
[14]	R. Orfali, N. Albanyan, Ca²⁺-Sensitive potassium channels, Molecules, 28 (2023), 885. https://doi.org/10.3390/molecules28020885 doi: 10.3390/molecules28020885
[15]	L. Duan, Q. Lu, Q. Wang, Two-parameter bifurcation analysis of firing activities in the Chay neuronal model, Neurocomputing, 72 (2008), 341–351. https://doi.org/10.1016/j.neucom.2008.01.019 doi: 10.1016/j.neucom.2008.01.019
[16]	L. Duan, Q. Lu, Codimension-two bifurcation analysis on firing activities in Chay neuron model, Chaos, Solitons Fractals, 30 (2006), 1172–1179. https://doi.org/10.1016/j.chaos.2005.08.179 doi: 10.1016/j.chaos.2005.08.179
[17]	L. Duan, Q. Lu, Bursting oscillations near codimension-two bifurcations in the Chay Neuron model, Int. J. Nonlinear Sci. Numer. Simul., 7 (2006), 59–64. https://doi.org/10.1515/IJNSNS.2006.7.1.59 doi: 10.1515/IJNSNS.2006.7.1.59
[18]	Q. Xu, X. Tan, D. Zhu, H. Bao, Y. Hu, B. Bao, Bifurcations to bursting and spiking in the Chay neuron and their validation in a digital circuit, Chaos, Solitons Fractals, 141 (2020), 110353. https://doi.org/10.1016/j.chaos.2020.110353 doi: 10.1016/j.chaos.2020.110353
[19]	Q. Xu, X. Tan, D. Zhu, M. Chen, J. Zhou, H. Wu, Synchronous behavior for memristive synapse-connected Chay twin-neuron network and hardware implementation, Math. Probl. Eng., 2020 (2020), 8218740. https://doi.org/10.1155/2020/8218740 doi: 10.1155/2020/8218740
[20]	L. Lu, M. Yi, Z. Gao, Y. Wu, X. Zhao, Critical state of energy-efficient firing patterns with different bursting kinetics in temperature-sensitive Chay neuron, Nonlinear Dyn., 111 (2023), 16557–16567. https://doi.org/10.1007/s11071-023-08700-7 doi: 10.1007/s11071-023-08700-7
[21]	L. L. Lu, M. Yi, X. Q. Liu, Energy-efficient firing modes of chay neuron model in different bursting kinetics, Sci. China Technol. Sci., 65 (2022), 1661–1674. https://doi.org/10.1007/s11431-021-2066-7 doi: 10.1007/s11431-021-2066-7
[22]	F. Zhu, R. Wang, K. Aihara, X. Pan, Energy-efficient firing patterns with sparse bursts in the Chay neuron model, Nonlinear Dyn., 100 (2020), 2657–2672. https://doi.org/10.1007/s11071-020-05593-8 doi: 10.1007/s11071-020-05593-8
[23]	T. R. Chay, Chaos in a three-variable model of an excitable cell, Physica D, 16 (1985), 233–242. https://doi.org/10.1016/0167-2789(85)90060-0 doi: 10.1016/0167-2789(85)90060-0

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

Electronic Research Archive

1 1.3

Metrics

Article views(1201) PDF downloads(79) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Electronic Research Archive

Contribution of a Ca²⁺-activated K⁺ channel to neuronal bursting activities in the Chay model

Related Papers:

Abstract

1. Introduction

2. Stability and bifurcation analysis

3. Numerical simulations

4. Conclusions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

Abstract

1. Introduction

2. Stability and bifurcation analysis

3. Numerical simulations

4. Conclusions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

Electronic Research Archive

Contribution of a Ca2+-activated K+ channel to neuronal bursting activities in the Chay model

Related Papers:

Abstract

1. Introduction

2. Stability and bifurcation analysis

3. Numerical simulations

4. Conclusions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. Stability and bifurcation analysis

3. Numerical simulations

4. Conclusions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

Contribution of a Ca²⁺-activated K⁺ channel to neuronal bursting activities in the Chay model