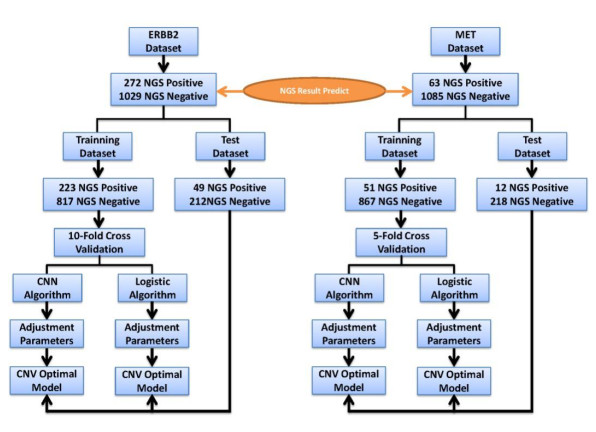
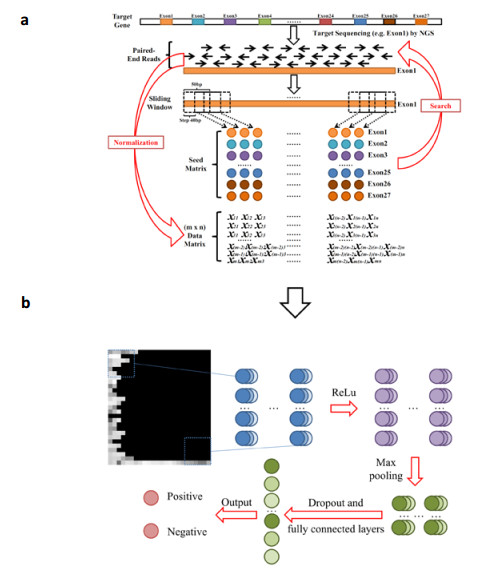
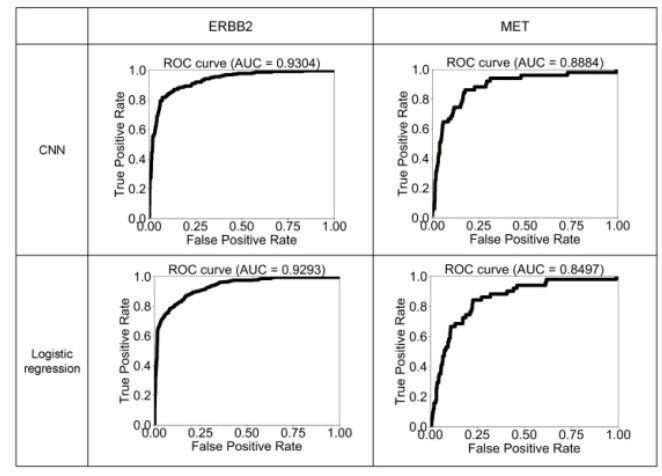
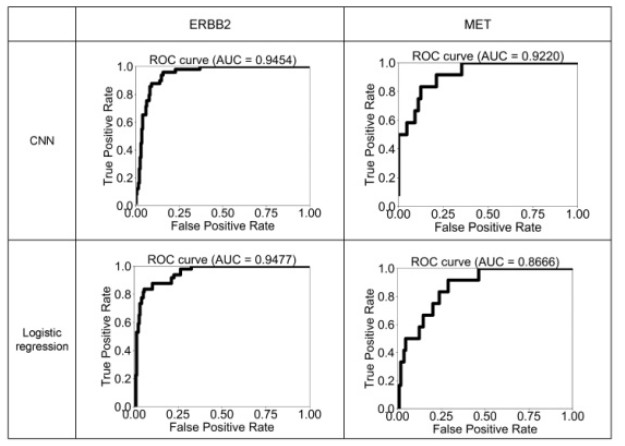
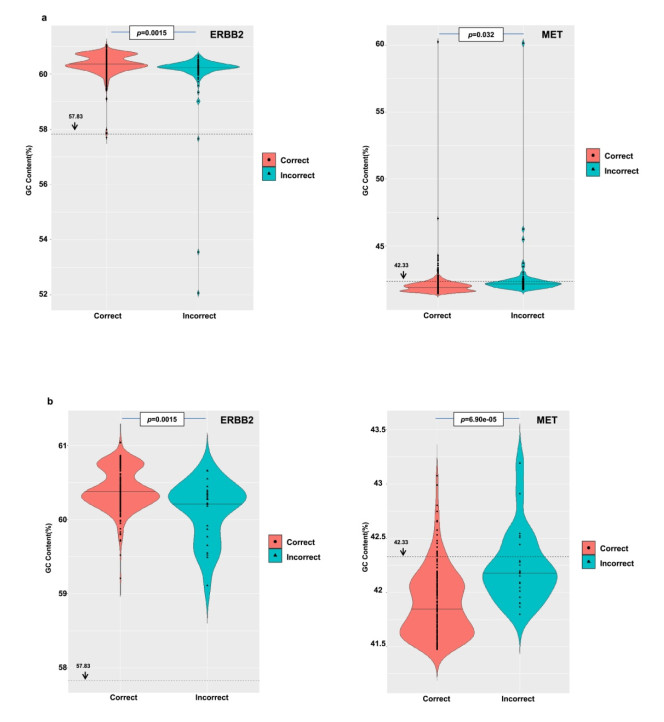
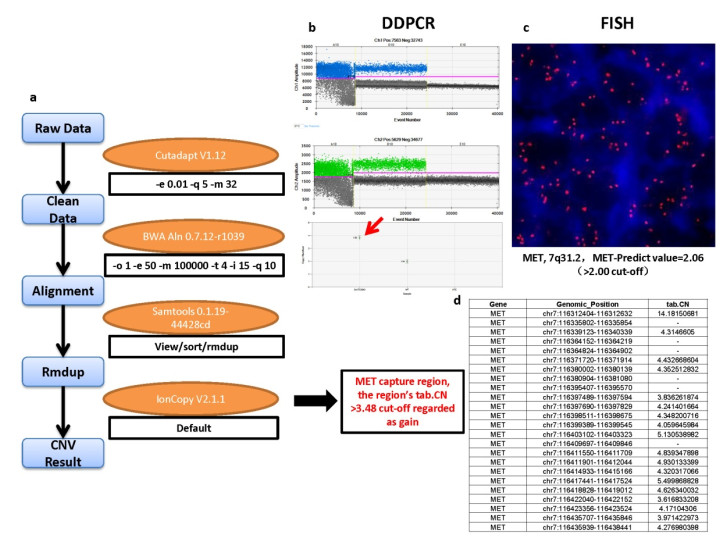
Copy number variations (CNVs) play an important role in many types of cancer. With the rapid development of next generation sequencing (NGS) techniques, many methods for detecting CNVs of a single sample have emerged: (ⅰ) require genome-wide data of both case and control samples, (ⅱ) depend on sequencing depth and GC content correction algorithm, (ⅲ) rely on statistical models built on CNV positive and negative sample datasets. These make them costly in the data analysis and ineffective in the targeted sequencing data. In this study, we developed a novel alignment-free method called DL-CNV to call CNV from the target sequencing data of a single sample. Specifically, we collected two sets of samples. The first set consists of 1301 samples, in which 272 have CNVs in ERBB2 and the second set is composed of 1148 samples with 63 samples containing CNVs in MET. Finally, we found that a testing AUC of 0.9454 for ERBB2 and 0.9220 for MET. Furthermore, we hope to make the CNV detection could be more accurate with clinical pgold standardq (e.g. FISH) information and provide a new research direction, which can be used as the supplement to the existing NGS methods.
1.
Introduction
In nature, human society, engineering technology and other fields, periodic and anti-periodic fluctuations are widespread. Differential equation is an important mathematical model to describe the phenomena and processes in these fields. Therefore, the problem of periodic and anti-periodic solutions of differential equations has always been a focus in the field of qualitative research of differential equations, whether in terms of theoretical research or practical application [1,2,3,4,5]. Since H. Bohr [6] introduced the almost periodic function as a natural extension of periodic function into mathematics, almost periodic solutions to differential equations [7,8,9,10,11] and mathematical models described by differential equations [12,13,14,15] has also become an important problem. Recently, the concepts of Bohr and Stepanov almost anti-periodic functions were proposed in [16]. As we know, Weyl almost periodic function is an extension of Bohr almost periodic function and Stepanov almost periodic function [15,17,18], but unlike them, the space formed by Weyl almost periodic function is incomplete under Weyl seminorm [9,18]. As a result, it is a difficult and interesting problem to investigate Weyl almost periodic solutions to differential equations and has always attracted the interest of many scholars. Therefore, it is also meaningful and challenging to introduce a definition of Weyl almost anti-periodic function and study solutions of such functions to differential equations and dynamical systems.
Inspired by the above analysis and observation, and considering that the semilinear abstract neutral functional differential equation includes many mathematical models as its special cases [19]. The primary purpose of this work is to introduce a definition of Weyl almost anti-periodic function, and then investigate the existence of a unique Weyl almost anti-periodic solution to a semilinear abstract neutral functional differential equation.
The remainder of this work is structured as follows: In Section 2, we propose a notion of Weyl almost anti-periodic function. In Section 3, we discuss the existence of a unique Weyl almost anti-periodic solution for a neutral functional semi-linear differential equation and we provide an example to show the validity of our result. In Section 4, we provide a brief conclusion.
2.
Weyl almost anti-periodic function
Let (B,‖⋅‖) denote a Banach space. For p≥1,f∈Lploc(R,B), the Weyl seminorm of f is defined as:
Definition 2.1. [9] Function f∈Lploc(R,B) is called a p-th Weyl almost periodic function, if for each ϵ>0, it is possible to find a constant l=l(ϵ)>0 such that each interval of length l(ϵ) contains a point τ∈R satisfying
We will denote the collection of such functions by WpAP(R,B).
Remark 2.1. According to [9], for x∈WpAP(R,B), we have ‖x‖Wp<∞.
Definition 2.2. A function f∈Lploc(R,B) is called a p-th Weyl almost anti-periodic function, if for any ϵ>0, it is possible to find an l=l(ϵ)>0 such that each interval with length l(ϵ) contains at least one τ=τ(ϵ)∈R such that
We will use WpANP(R,B) to stand for the space of all such functions.
Definition 2.3. Let f∈Lploc(R×B,B), then it is called p-th Weyl almost anti-periodic in t∈R uniformly in x∈B, if for any ϵ>0 and each compact subset K of B, it is possible to find an l=l(ϵ,K)>0 such that each interval with length l contains at least one τ=τ(ϵ)∈R satisfying
uniformly in x∈K. We will denote the collection of all such functions by WpANP(R×B,B).
Example 2.1. (10) If f1(t)=cos(πt)+cos(√2πt)+1t2+1, then one can easily check that f1(t) is not periodic, not anti-periodic, nor almost anti-periodic but Weyl almost anti-periodic.
(20) Let f2(t)=cos(πt)+cos(√2πt)+1t2+1+3, then one can easily show that f2∈WpAP(R,B), but f2∉WpANP(R,B).
Example 2.2. Take f3(t)=2cos(2t)−11+t2 and f4(t)=−cos(4t)+11+t2, then one can easily show that f3(t) and f4(t) are Weyl almost anti-periodic. Since f3(t)+f4(t)=1 for all t∈R, ‖f3(⋅+τ)+f4(⋅+τ)+f3(⋅)+f4(⋅)‖Wp=2>0 for every τ∈R. Hence, f3(t)+f4(t) is not Weyl almost anti-periodic.
Remark 2.2. Example 2.1 shows that WpANP(R,B) is a proper subset of WpAP(R,B). Example 2.2 shows that WpANP(R,B) does not form a linear space under usual linear operations.
Remark 2.3. Based on Definition 2.1 in [16] and Definition 2.2, one can conclude that an anti-periodic function is an almost anti-periodic function and an almost anti-periodic function is also a Weyl almost anti-periodic function, but the converse is not true.
3.
Weyl almost anti-periodic mild solution
The neutral functional semilinear differential equation we are concerned in this paper is as follow:
in which, A is the infinitesimal generator of a C0-semigroup {T(t):t≥0} on Banach space B, f∈C(B,B), g:R×B→B is a measurable function, θ,ξ>0 are constants.
The initial value imposed on system (3.1) is as follow:
Definition 3.1. Function v:R→B is said to be a mild solution of (3.1) and (3.2) if it satisfies the initial value condition (3.2) and the following equation
for all t∈R with t≥t0.
In order to gain our main result, we assume that:
(H1) There are two positive constants M,ζ satisfying ‖T(t)‖≤Me−ζt.
(H2) The function ϖ→AT(ϖ) defined on [0,∞) is a strongly measurable one and there exists a nonincreasing function J:[0,∞)→[0,∞) with e−ζ⋅J(⋅)∈L1([0,∞),[0,∞)) satisfying
(H3) Function f∈C(B,B),g∈WpANP(R×B,B) and there are constants Lf,Lg>0 such that for all x,y∈B and t∈R,
Moreover, f(0)=g(t,0)=0.
(H4) The constant ˜M:=Lf+K1Lf+MLgζ satisfies 2MLgζ<˜M<1, where M is mentioned in (H1), K1 is mentioned in (H2), ζ is mentioned in (H1) and (H2).
Let L∞(R,B) denote the space of all essentially bounded and measurable functions from R to B. Then, it is a Banach space when endowed with the norm ‖x‖∞=esssupt∈R‖x(t)‖ for x∈L∞(R,B).
Lemma 3.1. If Θ∈Lploc(R,B) with ‖Θ‖Wp<∞, then one has
and
Proof. By Fubini's theorem, we deduce that
and that
The proof is done.
Theorem 3.1. Let assumptions (H1)–(H3) be fulfilled. Then system (3.1) admits one and only one Weyl almost anti-periodic solution in L∞(R,B).
Proof. By Definition 3.1, it is clear that x:R→B is a solution to (3.1) if it meets the equation
Define an operator Λ:L∞(R,B)→B by
where ϕ∈L∞(R,B).
First of all, we will confirm that Λ(L∞(R,B))⊂L∞(R,B). Indeed, for every ϕ∈L∞(R,B), one gets
Hence, Λ is a self-mapping.
Next, we will demonstrate Λ is a contraction mapping. For any x,y∈L∞(R,B), one has
which, by (H4), means that Λ is a contraction mapping. Consequently, we derive that (3.1) admits unique one mild solution x∗∈L∞(R,B).
Lastly, we will demonstrate that the x∗ is Weyl almost anti-periodic. By (3.3), one can infer that
Since g∈WpANP(R×B,B), for every ϵ>0 and each compact subset K of B that contains x∗, there is a constant l=l(ϵ,K)>0 such that in each interval with length l contains at least one τ=τ(ϵ)∈R satisfying
for all x∈K.
On one hand, with the help of (3.4), one can deduce that
Furthermore, by virtue of Lemma 3.1, one can get that
On the other hand, we can derive that
then again by Lemma 3.1, we can get that
Consequently, from (3.5) and (3.6) it follows that
hence, we obtain
which means that x∗ is p-th Weyl almost anti-periodic. The proof is finished.
Example 3.1. Consider the neutral type partial deferential equation
where
and
Take B=L2([0,π]) with ‖⋅‖ and ⟨⋅,⋅⟩ as its norm and inner product, respectively. Let A be an operator defined as Au=u′′ with its domain
According to the statements in Examples' section of [20], the operator A is the generator of an analytic semigroup (T(t))t≥0 on B. Additionally, one gets, for φ∈B,
and for φ∈D(A),
where zn(ξ)=√2πsin(nξ).
Hence, T(t) satisfies (H1) with M=1,ζ=1, and ‖T(t)‖≤e−t, t∈[0,+∞). Take
then (H2) holds with K1=1.
Consequently, (3.7) can be rewritten in a form as (3.1). It is easy to see that assumption (H3) holds with Lf=Lg=0.25 and assumption (H4) holds with ˜M=0.75 and 2MLgζ=0.5<˜M<1. Therefore, according to Theorem 3.1, (3.7) admit one unique Weyl almost anti-periodic mild solution.
4.
Conclusions
In this work, a definition of Weyl almost anti-periodic function has been introduced and the existence of a unique Weyl almost anti-periodic mild solution to a neutral functional semilinear differential equation has been confirmed by using the compressing mapping theorem and some analytical techniques. The concept and the approach developed in this work may be used to study Weyl almost anti-periodic solutions for other kinds of differential equations and may also be used to discuss Weyl almost anti-periodic solutions for neural networks and population models.
Acknowledgments
This work is supported by the National Natural Science Foundation of China under Grant Nos. 12261098 and 11861072.
Conflict of interest
The authors declare that they have no conflicts of interest.













 DownLoad:
DownLoad: