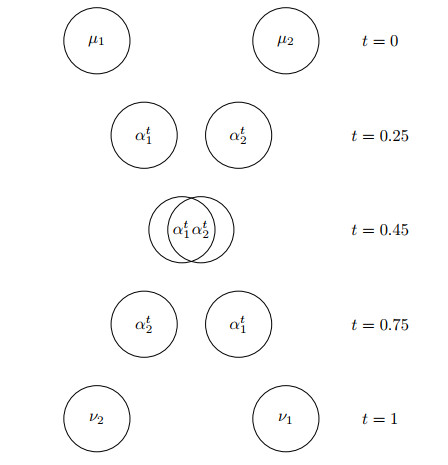
The interpolation between two opposite configurations of spheres along generalized geodesics. In particular, for
We study the extension of the macroscopic crowd motion model with congestion to a population divided into two types. As the set of pairs of density whose sum is bounded is not geodesically convex in the product of Wasserstein spaces, the generic splitting scheme may be ill-posed. We thus analyze precisely the projection operator on the set of admissible densities, and link it to the projection on the set of measures of bounded density in the mono-type case. We then derive a numerical scheme to adapt the one-typed population splitting scheme.
Citation: Félicien BOURDIN. Splitting scheme for a macroscopic crowd motion model with congestion for a two-typed population[J]. Networks and Heterogeneous Media, 2022, 17(5): 783-801. doi: 10.3934/nhm.2022026
| [1] | Bertrand Maury, Aude Roudneff-Chupin, Filippo Santambrogio, Juliette Venel . Handling congestion in crowd motion modeling. Networks and Heterogeneous Media, 2011, 6(3): 485-519. doi: 10.3934/nhm.2011.6.485 |
| [2] | Filippo Santambrogio . A modest proposal for MFG with density constraints. Networks and Heterogeneous Media, 2012, 7(2): 337-347. doi: 10.3934/nhm.2012.7.337 |
| [3] | Matthias Erbar, Dominik Forkert, Jan Maas, Delio Mugnolo . Gradient flow formulation of diffusion equations in the Wasserstein space over a Metric graph. Networks and Heterogeneous Media, 2022, 17(5): 687-717. doi: 10.3934/nhm.2022023 |
| [4] | Michael Fischer, Gaspard Jankowiak, Marie-Therese Wolfram . Micro- and macroscopic modeling of crowding and pushing in corridors. Networks and Heterogeneous Media, 2020, 15(3): 405-426. doi: 10.3934/nhm.2020025 |
| [5] | Raimund Bürger, Christophe Chalons, Rafael Ordoñez, Luis Miguel Villada . A multiclass Lighthill-Whitham-Richards traffic model with a discontinuous velocity function. Networks and Heterogeneous Media, 2021, 16(2): 187-219. doi: 10.3934/nhm.2021004 |
| [6] | Nastassia Pouradier Duteil . Mean-field limit of collective dynamics with time-varying weights. Networks and Heterogeneous Media, 2022, 17(2): 129-161. doi: 10.3934/nhm.2022001 |
| [7] | Daniel Roggen, Martin Wirz, Gerhard Tröster, Dirk Helbing . Recognition of crowd behavior from mobile sensors with pattern analysis and graph clustering methods. Networks and Heterogeneous Media, 2011, 6(3): 521-544. doi: 10.3934/nhm.2011.6.521 |
| [8] | Caterina Balzotti, Simone Göttlich . A two-dimensional multi-class traffic flow model. Networks and Heterogeneous Media, 2021, 16(1): 69-90. doi: 10.3934/nhm.2020034 |
| [9] | Jan Friedrich, Simone Göttlich, Annika Uphoff . Conservation laws with discontinuous flux function on networks: a splitting algorithm. Networks and Heterogeneous Media, 2023, 18(1): 1-28. doi: 10.3934/nhm.2023001 |
| [10] | Felisia Angela Chiarello, Paola Goatin . Non-local multi-class traffic flow models. Networks and Heterogeneous Media, 2019, 14(2): 371-387. doi: 10.3934/nhm.2019015 |
We study the extension of the macroscopic crowd motion model with congestion to a population divided into two types. As the set of pairs of density whose sum is bounded is not geodesically convex in the product of Wasserstein spaces, the generic splitting scheme may be ill-posed. We thus analyze precisely the projection operator on the set of admissible densities, and link it to the projection on the set of measures of bounded density in the mono-type case. We then derive a numerical scheme to adapt the one-typed population splitting scheme.
The modeling of the collective motion of entities - as a human crowd, a population of cells in biology or self-propelled particles in physics - involves a large range of approaches based on the level of description of the particle and its interactions. On the one hand, microscopic models rely on the description of each particle's motion. The population is thus described as a collection of
| dXidt=vi(t,X1,…,Xn)i=1,…,n. | (1) |
It is said as "Lagrangian", since we follow each trajectory in time. It is tractable for a reasonable number of particles, but it becomes unusable when the size of the system increases since it involves the computation of many interactions (roughly increasing as the square of the total population).
On the other hand, in macroscopic models the population is described by its density, that is a number of particles by surface unit. The system is thus a partial differential equation on this very density
| ∂tρ+∇⋅(ρu)=0 | (2) |
where
Congestion. When modeling the collecting motion of particles, one shall often introduce a congestion constraint in the description of the motion. This congestion encodes the impenetrability of the entities at a microscopic scale. Generically, one distinguishes between a desired velocity (or self-propulsion in physics) and an effective velocity, which is the resulting velocity due to the interactions ruled by congestion. There are two main approaches to introduce congestion on a crowd motion model. On the one hand, soft models rely on a relaxation of the constraint that affects the behaviour of the system as some configurations get close of the saturation. In microscopic space-continuous models, a highly repulsive potential of interaction at short-range is usually introduced in the model to prevent any overlapping between particles for instance in the context of pedestrians [11], or collision of solids, see [2], [23]. For discrete-space microscopic models of motion of pedestrians, cellular automaton based models place people on a given grid [3], [5]. In macroscopic models, the porous media equation [8], [13], [19] can be seen as a gradient flow for the functional
| ρ↦∫ρm(x)dx, | (3) |
hence penalizing the high values of the density. A kernel can also be considered [17], by introducing a term of the form
| ∇(G∗ρ), | (4) |
where
In this article, we will be focused on hard models of congestion, that are models that do not allow any overlapping or violation of the constraint. A microscopic hard model of crowd motion is introduced in [15], in which the desired velocities are projected at every time on the set of admissible velocities, that are the velocities that lead to non-overlapping configurations. This complex model (the particles are driven by a velocity that is the projection on a set that evolves in time) is shown to fit into the framework of the sweeping process, introduced by Moreau [18]. The well-posedness of the model is based on a catching-up, or splitting algorithm which has generically two steps:
● Step 1 (prediction): apply the unconstrained velocities during a fixed time step,
● Step 2 (correction): project the obtained positions on the set of admissible configurations.
The macroscopic model of crowd motion introduced in [14] is built on the same approach of projection of the velocities. Given a density on a domain
| Cρ={v∈L2(Ω),∇⋅v≥0 where ρ=1}. | (5) |
The models then reads
| {∂tρ+∇⋅(ρu)=0u∈argminv∈Cρ‖v−U‖22 | (6) |
Macroscopic multi-type models. As the microscopic models allow natively to consider any heterogeneity in the behaviours of the population, there are few extensions of macroscopic congestion models for a population composed by different types. Multiphase flows have been widely studied in physics, see [4] and [9], even under a total density constraint [6], but may not be applied to crowd (or cell) motion since they involve a phase separation and not a total mixture of the types. A separation of phase has been also considered in order to study the motion of cars structured in a multilane traffic [24]. Conversely, in the model we shall consider we assume a mixture between two densities
| p=mm−1(ρ1+ρ2)m−1, | (7) |
that reduces to the classical porous media equation
| ∂tρ−Δρm=0 | (8) |
in the absence of one of the two types.
In what follows, we study the two-species adaptation of the crowd motion model (6), that writes
| {∂tρ1+∇⋅(ρ1u1)=0∂tρ2+∇⋅(ρ2u2)=0(u1,u2)=PCρ1,ρ2(U1,U2) | (9) |
where
Optimal transport, Wasserstein spaces and admissible set of densities. In order to define a splitting scheme that shall be the macroscopic counterpart of the microscopic splitting scheme defined above, we need to introduce the formalism of Wasserstein spaces. Being given a convex compact domain
| W22(μ,ν)=infγ∈Π(μ,ν)∫Ω‖x−y‖2dγ(x,y). | (10) |
It defines a distance on
● Step 1 (prediction): Transport the density by the desired velocity during
| μt=(Id+τU)#ρt, | (11) |
where
● Step 2 (correction): Project the intermediate density on the set of admissible densities
| K1={ρ∈W2(Ω),ρ≤1}. | (12) |
Numerical schemes for hard congestion macroscopic models. We shall end this introduction by saying a few words on schemes developed to approximate the macroscopic crowd motion model (6). In [14], existence of solutions to (6) is proven by considering the limit of a JKO-scheme. This scheme originally introduced in [12] approximates the model by the iterations
| ρk+1=argminρ∈W2(Ω)∫ΩDdρ+1K1(ρ)+12τW22(ρ,ρk), | (13) |
when the desired velocity is of the form
We shall consider in this paper an implementation of the splitting scheme (11) (12) which extends the implementation presented in [15] for a mono-type population. The prediction step (11) is computed by transportation of the cells of the mesh by the desired velocity, in a Lagrangian approach. The correction step (12) is computed by a stochastic algorithm: from each oversaturated cell a random walk starts and dispatches the excess of mass when it reaches a free cell where the density is lower than
The rest of the paper is organized as follows. In section 2, the model is introduced and a splitting algorithm is derived. In section 3, we analyze the projection operator on the set of admissible pairs of densities and state a well-posedness theorem on the scheme. In section 4, we present an implementation of the numerical algorithm and show some simulations.
Let
| Cρ1,ρ2={u1,u2∈L2(Ω,R2),∇⋅(ρ1u1+ρ2u2)≥0 where ρ1+ρ2=1} | (14) |
where "
| ⟨ϕ,q⟩≥0, | (15) |
where
| H1ρ1+ρ2(Ω)={q∈H1(Ω),q≥0 a.e.,q(1−ρ1−ρ2)=0}. | (16) |
We shall thus study the following model:
Problem 1. For
| {∂tρ1+∇⋅(ρ1u1)=0∂tρ2+∇⋅(ρ2u2)=0(u1,u2)=PCρ1,ρ2(U1,U2)ρ1(0,⋅),ρ2(0,⋅)=ρ01,ρ02, | (17) |
where
Let us first recall how the existence is proven in [14] in the case of a single type when the desired velocity is of the form
| ρk+1=argminρ∈W2(Ω)∫ΩDdρ+1K1(ρ)+12τW22(ρ,ρk), | (18) |
with
| K1={ρ∈W2(Ω),ρ≤1 a.e.} | (19) |
the set of admissible densities. The existence of a unique minimizer is obtained by the convexity of
| K2={ρ1,ρ2∈W2(Ω),ρ1+ρ2≤1} | (20) |
is no more convex along a generalized geodesic.
Example 1. Consider for instance
| r1(x,y)=r2(x,y)=(x,y) | (21) |
and the transport plans from
| s1(x,y)=(x+1,y)s2(x,y)=(x−1,y). | (22) |
The generalized geodesic between
| (αt1,αt2)=(1B(t,ϵ),1B(1−t,ϵ)), | (23) |
which is not admissible for
Remark 1. As a matter of fact,
| d((μ1,μ2),(ν1,ν2))2=d(μ1,ν1)2+d(μ2,ν2)2. | (24) |
Indeed, let
Even in the absence of an existence theorem for problem 1, we can write a splitting scheme for Eq. (17).
Definition 2.1. Given
| μk+1j=(Id+τUj)#ρkj (prediction) (ρk+11,ρk+12)∈argmin(ρ1,ρ2)∈K2W22(ρ1,μk+11)+W22(ρ2,μk+12) (correction) | (25) |
From its pushforward structure, the prediction step uniquely defines a pair of intermediate probability measures. It is less straightforward that the projection on
The goal of this section is to show that under tractable assumptions, the splitting scheme (25) is uniquely defined.
Let us start with a lemma that links the projection on
Lemma 3.1. Let
| (ρ1,ρ2)∈argmin(ν1,ν2)∈K2W22(ν1,μ1)+W22(ν2,μ2). | (26) |
Then
| W22(ρ1+ρ2,μ1+μ2)=W22(ρ1,μ1)+W22(ρ2,μ2). | (27) |
Proof. From the definition of
| W22(ρ,μ1+μ2)≤W22(ρ1+ρ2,μ1+μ2). | (28) |
Let
| W22(ρ1+ρ2,μ1+μ2)≤W22(ρ1,μ1)+W22(ρ2,μ2). | (29) |
Let
| dζ1(x,y)=f(x)dζ(x,y)dζ2(x,y)=g(x)dζ(x,y). | (30) |
One has
| W22(ρ,μ1+μ2)=∫Ω2|x−y|2dζ=∫Ω2|x−y|2dζ1+∫Ω2|x−y|2dζ2≥W22(ν1,μ1)+W22(ν2,μ2). | (31) |
By optimality of the pair
| W22(ρ1,μ1)+W22(ρ2,μ2)≤W22(ρ,μ1+μ2). | (32) |
By combining (28), (29), (32), we get
Remark 2. From the previous lemma, we get that the sum of two densities that realize the distance to any pair of densities
| ρ1=fdλρ2=gdλ | (33) |
where
Nevertheless, when every density is absolutely continuous with respect to Lebesgue measure we have uniqueness of the projection.
Proposition 1. Let
Proof. As every measure is absolutely continuous, all the transport plans are transport maps (in the sense of Monge). Let
Let us show that
| ∫Ω|x−y|2dγ=∫Ω|x−T1(x)|2dμ1+∫Ω|x−T2(x)|2dμ2=W22(ρ1,μ1)+W22(ρ2,μ2)=W22(ρ,μ1+μ2). | (34) |
●
●
so
From the previous proof, we get the following corollary that gives the form of the
Corollary 1. Let
Provided that the predicted densities in (25) are absolutely continuous, the correction step is thus uniquely defined. The remaining question is the following: what condition should be assumed to have a pair of predicted densities that are absolutely continuous with respect to Lebesgue measure?
Let us start with a convenient definition.
Definition 3.2. We define the partial order on the set of positive measures on
| μ1≤∗μ2⟺μ1≪μ2 and dμ1dμ2≤1μ2−a.e. | (35) |
In other words,
Lemma 3.3. Let
| (Id+τU)#λ|Ω0≤∗(1+5cτ)λ|Ω0τ‖U‖L∞(Ω0). | (36) |
where
Proof. Let
| f:{Ω0⟶f(Ω0)x⟼x+τU(x). | (37) |
| x−y=τ∫10JacU((1−t)x+ty)⋅(y−x)dt | (38) |
so
Let
| (Id+τU)#λ|Ω0(A)=∫Ω01A((Id+τU)(x))dλ=∫Ω01A(f(x))|det(Jacf(x))||det(Jacf(x))|dλ | (39) |
One has
| (Id+τU)#λ|Ω0(A)≤(1+5cτ)∫Ω01A(f(x))|det(Jacf(x))|dλ=(1+5cτ)∫f(Ω0)1A(x)dλ≤(1+5cτ)λ(A∩Ωτ‖U‖L∞(Ω0)0). | (40) |
We are now able to state a well-posedness result for the splitting scheme at two types (25).
Theorem 3.4. Let
Proof. From lemma 3.3, the first predicted pair of densities is supported in
Lemma 3.4. Let
From this lemma and corollary 1, one gets that the corrected velocities are supported on the ball
| rk=(1+5c2τ)k2(r0+c1τ√1+5c2τ−1)−c1τ√1+c2τ−1. | (41) |
Setting
Let us end this theoretical section with a continuity proposition for the projection on
Proposition 2. Assume that
Proof. Let
| (ρn1,ρn2)=PK2(μn1,μn2)(ρ1,ρ2)=PK2(μ1,μ2). | (42) |
Let
| πy#((Id,Tn)#(μn1+μn2))=Tn#μn1+Tn#μn2. | (43) |
On the one hand,
| lim | (44) |
One thus has, by using twice lemma 3.1:
| (45) |
Since
In this section we detail the numerical scheme used to approximate the splitting scheme (25). It is largely inspired of the methods developed for the mono-type model in [15], [21].
We present here two main methods to implement the prediction step. We consider only one density since the predictions are made independently for the two types.
Finite volume step. In [21], a conservative finite volume scheme in introduced, with an upwind operator to discretize the flux. Given a mesh of size
| (46) |
The prediction step reads
| (47) |
This scheme is conservative, stable under the CFL condition
Example 2. Consider for
Lagrangian transport. In order to have a scheme that can use large time step, we present a Lagrangian version of the prediction step, introduced in [15]. The key idea is to transport the whole cell
| (48) |
on the cells of the mesh, as on figure 3.
Remark 3. This scheme is conservative, stable and preserves the positivity for any time step. The front speed of the density studied in example 2 is now for this scheme
Let us first recall how the projection on
Starting from a density
● Start from a random oversaturated cell and transport the excess of mass
● When an undersaturated cell is reached, deliver as much mass as possible,
● When the total mass has been distributed, restart the process starting from another oversaturated cell.
We then average this random projection on a great number of realizations in order to limit the error introduced in the computation. We refer to [15] or the heuristics used to derive this scheme. Let us illustrate on a toy example that in practical situations, despite the randomness of this projection step, the obtained density does not fluctuate much as we compute it several times with independent replicates.
Example 3. On a 2D squared grid of
| (49) |
For each computation, we run
Whereas the convergence of the previous scheme is far beyond the scope of this paper and could be in itself an interesting research focus, let us recall a partial result of convergence in dimension 1 [21].
Theorem 4.1 (Theorem 5.2.1 in [21]). Let
| (50) |
From this very partial convergence result and the stability of the projection illustrated in example 3, we expect this random method to prescribe a projection close to the actual
The correction step is thus computed with the following scheme :
Remark 4. Let us compute (51) when
| (52) |
so the exact projection
The splitting scheme allows the velocities to be more general than two time-constant velocity fields that are generic when using a JKO scheme. In the implementation we shall consider, we allow a mixture of different terms:
● a constant velocity field
● attraction towards an external potential:
● attraction towards a chemoattractant emitted by the particles:
| (53) |
● attraction/repulsion between the particles:
A full implementation of the previous scheme is available1 with a ready-to-use notebook demo that reproduces every simulation of this section. One can in particular find every parameter and initial condition used to generate these simulations.
1https://gitlab.math.u-psud.fr/bourdin/macroscopic-cell-motion
On figure 5 is depicted the case of two saturated discs of radius
| (54) |
On figure 6, chemoattraction is introduced. After spreading in order to cross, the two densities aggregate back into saturated areas. The desired velocities are taken here of the form
| (55) |
A third example of more complex behavior is illustrated on figure 7. In the absence of external velocities field or potential, the motion is only driven here by chemoattractraction and short-range interactions with the same type. The short range interaction potential has been chosen of the form
| (56) |

Aggregation of a composite crowd driven by chemoattraction and short-range interactions. For
We added a repulsion for the chemoattractant of the other type. One sees that the crowd reaches a compromise to separate into distinct phases.
The desired velocities write here
| (57) |
Proof of lemma 3.4. The proof of the following lemma was suggested by Filippo Santambrogio.
Lemma 3.4. Let
Proof. Let
We consider the following optimization problems
| (58) |
with the convention
| (59) |
where
| (60) |
One can write
| (61) |
| (62) |
Moreover, for
| (63) |
for the transport map from
| (64) |
On the one hand, one has
| (65) |
On the other hand, denote
| (66) |
The derivative of
Let us then show the convergence of the
| (67) |
where
By comparing
| (68) |
Let
| (69) |
Let us show that
| (70) |
Let
| (71) |
One can assume (by extracting)
| (72) |
Let
| (73) |
For any
| (74) |
We get
| (75) |
Let
| (76) |
which is absurd when
The interpolation between two opposite configurations of spheres along generalized geodesics. In particular, for
The cell of the mesh in position
The distribution of the image of the cell
Distribution of the 2-Wasserstein distances between pairs of estimated projections of the density in example 3
The motion of two crossing discs. The first column represents the sum of the two densities, and the other two the separated densities. The total time of the simulation is
The motion of two crossing discs in the presence of chemoattraction. We chose the same parameters that in the previous simulation, with
Aggregation of a composite crowd driven by chemoattraction and short-range interactions. For
In solid line, the function