The supergraph
This paper contains two contributions in the study of optimal transport on metric graphs. Firstly, we prove a Benamou–Brenier formula for the Wasserstein distance, which establishes the equivalence of static and dynamical optimal transport. Secondly, in the spirit of Jordan–Kinderlehrer–Otto, we show that McKean–Vlasov equations can be formulated as gradient flow of the free energy in the Wasserstein space of probability measures. The proofs of these results are based on careful regularisation arguments to circumvent some of the difficulties arising in metric graphs, namely, branching of geodesics and the failure of semi-convexity of entropy functionals in the Wasserstein space.
Citation: Matthias Erbar, Dominik Forkert, Jan Maas, Delio Mugnolo. Gradient flow formulation of diffusion equations in the Wasserstein space over a Metric graph[J]. Networks and Heterogeneous Media, 2022, 17(5): 687-717. doi: 10.3934/nhm.2022023
| [1] | Karoline Disser, Matthias Liero . On gradient structures for Markov chains and the passage to Wasserstein gradient flows. Networks and Heterogeneous Media, 2015, 10(2): 233-253. doi: 10.3934/nhm.2015.10.233 |
| [2] | Steinar Evje, Kenneth H. Karlsen . Hyperbolic-elliptic models for well-reservoir flow. Networks and Heterogeneous Media, 2006, 1(4): 639-673. doi: 10.3934/nhm.2006.1.639 |
| [3] | Fabian Rüffler, Volker Mehrmann, Falk M. Hante . Optimal model switching for gas flow in pipe networks. Networks and Heterogeneous Media, 2018, 13(4): 641-661. doi: 10.3934/nhm.2018029 |
| [4] | Joachim von Below, José A. Lubary . Stability implies constancy for fully autonomous reaction-diffusion-equations on finite metric graphs. Networks and Heterogeneous Media, 2018, 13(4): 691-717. doi: 10.3934/nhm.2018031 |
| [5] | Andrea Corli, Lorenzo di Ruvo, Luisa Malaguti, Massimiliano D. Rosini . Traveling waves for degenerate diffusive equations on networks. Networks and Heterogeneous Media, 2017, 12(3): 339-370. doi: 10.3934/nhm.2017015 |
| [6] | Pedro Aceves-Sanchez, Benjamin Aymard, Diane Peurichard, Pol Kennel, Anne Lorsignol, Franck Plouraboué, Louis Casteilla, Pierre Degond . A new model for the emergence of blood capillary networks. Networks and Heterogeneous Media, 2021, 16(1): 91-138. doi: 10.3934/nhm.2021001 |
| [7] | Michael Helmers, Barbara Niethammer, Xiaofeng Ren . Evolution in off-critical diblock copolymer melts. Networks and Heterogeneous Media, 2008, 3(3): 615-632. doi: 10.3934/nhm.2008.3.615 |
| [8] | Seung-Yeal Ha, Jeongho Kim, Jinyeong Park, Xiongtao Zhang . Uniform stability and mean-field limit for the augmented Kuramoto model. Networks and Heterogeneous Media, 2018, 13(2): 297-322. doi: 10.3934/nhm.2018013 |
| [9] | Dimitra Antonopoulou, Georgia Karali . A nonlinear partial differential equation for the volume preserving mean curvature flow. Networks and Heterogeneous Media, 2013, 8(1): 9-22. doi: 10.3934/nhm.2013.8.9 |
| [10] | Leandro M. Del Pezzo, Nicolás Frevenza, Julio D. Rossi . Convex and quasiconvex functions in metric graphs. Networks and Heterogeneous Media, 2021, 16(4): 591-607. doi: 10.3934/nhm.2021019 |
This paper contains two contributions in the study of optimal transport on metric graphs. Firstly, we prove a Benamou–Brenier formula for the Wasserstein distance, which establishes the equivalence of static and dynamical optimal transport. Secondly, in the spirit of Jordan–Kinderlehrer–Otto, we show that McKean–Vlasov equations can be formulated as gradient flow of the free energy in the Wasserstein space of probability measures. The proofs of these results are based on careful regularisation arguments to circumvent some of the difficulties arising in metric graphs, namely, branching of geodesics and the failure of semi-convexity of entropy functionals in the Wasserstein space.
This article deals with the equivalence of static and dynamical optimal transport on metric graphs, and with a gradient flow formulation of McKean–Vlasov equations in the Wasserstein space of probability measures.
Let
For
| Wp(μ,ν):=minσ∈Π(μ,ν){∫G×Gdp(x,y)dσ(x,y)}1/p, |
where
Metric graphs
The Benamou–Brenier formula. On Euclidean space
| W22(μ,ν)=inf(μt,vt){∫10‖vt‖2L2(μt)dt} | (1) |
where the infimum runs over all 2-absolutely continuous curves
| ddtμt+∇⋅(vtμt)=0 | (2) |
with boundary conditions
Here we are interested in obtaining an analogous result in the setting of metric graphs. However, such an extension is not straightforward, since standard proofs in the Euclidean setting (see [2,26]) make use of the flow map
| ddtT(t,x)=vt(T(t,x)),T(0,x)=x,T(t,⋅)#μ0=μt, |
see, e.g., [2,Proposition 8.1.8]. On a metric graph such a flow map
Circumventing this difficulty, Gigli and Han obtained a version of the Benamou–Brenier formula in very general metric measure spaces [13]. However, this paper requires a strong assumption on the measures (namely, a uniform bound on the density with respect to the reference measure). While this assumption is natural in the general setting of [13], it is unnecessarily restrictive in the particular setting of metric graphs.
In this paper, we prove a Benamou–Brenier formula that applies to arbitrary Borel probability measures on metric graphs. The key ingredient in the proof is a careful regularisation step for solutions to the continuity equation.
Gradient flow structure of diffusion equations. As an application of the Benamou–Brenier formula, we prove another central result from optimal transport: the identification of diffusion equations as gradient flow of the free energy in the Wasserstein space
Here we consider diffusion equations of the form
| ∂tη=Δη+∇⋅(η(∇V+∇W[μ])), | (3) |
for suitable potentials
| F(μ):=∫Gη(x)logη(x)dλ(x)+∫GV(x)η(x)dλ(x)+12∫G×GW(x,y)η(x)η(y)dλ(x)dλ(y), |
if
A key difference compared to the Euclidean setting is that the entropy is not semi-convex along
Interestingly, we do not need to assume continuity of the potential
The Wasserstein distance over metric graphs for
The recent paper [10] deals with dynamical optimal transport metrics on metric graphs. The authors start with the dynamical definition à la Benamou–Brenier and consider links to several other interesting dynamical transport distances. The current paper is complementary, as it shows the equivalence of static and dynamical optimal transport, and a gradient flow formulation for diffusion equations.
Various different research directions involving optimal transport and graphs exist. In particular, dynamical optimal transport on discrete graphs have been intensively studied in recent years following the papers [11,19,21]. The underlying state space in these papers is a discrete set of nodes rather than a gluing of one-dimensional intervals.
Another line of research deals with branched optimal transport, which is used to model phenomena such as road systems, communication networks, river basins, and blood flow. Here one starts with atomic measures in the continuum, and graphs emerge to describe paths of optimal transport [28,7].
Organisation of the paper. In Section 2 we collect preliminaries on optimal transport and metric graphs. Section 3 is devoted to the continuity equation and the Benamou–Brenier formula on metric graphs. In particular, we present a careful regularisation procedure for solutions to the continuity equation. Section 4 contains an example which demonstrates the lack convexity of the entropy along
In this section we collect some basic definitions and results from optimal transport and metric graphs.
In this section we collect some basic facts on the family of
Let
Definition 2.1 (Transport plans and maps).
1. A (transport) plan between probability measures
| (proj1)#σ=μand(proj2)#σ=ν, |
where
2. A transport plan
Definition 2.2 (Kantorovich–Rubinstein–Wasserstein distance). For
| Wp(μ,ν):=inf{(∫X×Xdp(x,y)dσ(x,y))1/p:σ∈Π(μ,ν)}. | (4) |
For any
By compactness of
We conclude this section with a dual formula for the Wasserstein distance (see, e.g., [26,Section 1.6.2]). To this aim, we recall that for
Proposition 2.3 (Kantorovich duality). For any
| Wpp(μ,ν)=supφ,ψ∈C(X){∫Xφdμ+∫Xψdν : φ(x)+ψ(y)≤dp(x,y)∀x,y∈X}. |
Moreover, the supremum is attained by a maximising pair of the form
Any maximiser
In this subsection we state some basic facts on metric graphs; see e.g., [20], [6] or [16] for more details.
Definition 2.4 (Metric graph). Let
| E:=∐e∈E(0,ℓe)and¯E:=∐e∈E[0,ℓe]. |
The metric graph over
| G:=¯E/∼, |
where points in
Note that the orientation of
| ιev:={+1if v=einit,−1if v=eterm,0otherwise. |
As a quotient space, any metric graph naturally inherits the structure of a metric space from the Euclidean distance on its metric edges [9,Chapter 3]: indeed, under our standing assumption that
The distance
| d(x,y):=minn∑i=1ℓei, |
where the minimum is taken over all sequences of vertices
By construction, the distance function
In a metric space
| lip(f)(x):=lim supy→x|f(y)−f(x)|d(x,y), |
whenever
| Lip(f):=supy≠x|f(y)−f(x)|d(x,y). |
If the underlying space
At the risk of being redundant, we explicitly introduce a few relevant function spaces, although they are actually already fully determined by the metric measure structure of the metric graph
(ⅰ)
(ⅱ)
(ⅲ)
(ⅳ) Likewise, we consider the Sobolev spaces
In this section we fix a metric graph
| ∂tμt+∇⋅Jt=0 | (5) |
in this context.
In this work we mainly deal with weak solutions to the continuity equation, which will be introduced in Definition 3.2. To motivate this definition, we first introduce the following notion of strong solution.
Definition 3.1 (Strong solutions to the continuity equation). A pair of measurable functions
Here, we write
To motivate the definition of a weak solution, suppose that we have a strong solution
| ddt∫ℓe0ψρtdx=∫ℓe0∇ψ⋅Utdx+ψUt|ℓe0, |
and summation over
| ddt∫Gψρtdx=∫¯E∇ψ⋅Utdx+∑w∈Vψ(w)∑e∈EwιewUt(we)=∫¯E∇ψ⋅Utdx, |
where we use the continuity of
| ∫Gρsdλ=∫Gρtdλ, |
for all
Definition 3.2 (Weak solution). A pair
| ddt∫Gψdμt=∫¯E∇ψ⋅dJt. | (6) |
Remark 1. Proposition 3.9 below shows that continuous functions on
| ∫T0(∫G∂tφdμt+∫¯E∇φ⋅dJt)dt=0. | (7) |
See Lemma 3.10 below for the weak continuity in
The next result asserts that the momentum field does not give mass to vertices for a.e. time point. Hence, we can equivalently restrict the integrals over
Lemma 3.3. Let
| ∫T0|Jt|(B)dt=0. |
Proof. Fix a metric edge
For instance, we could set
Lemma 3.4 (Weak and strong solutions). The following assertions hold:
(i) If
(ii) If
Proof. Both claims are straightforward consequences of integration by parts on each metric edge in
Let
Definition 3.5. For
| d(γs,γt)≤∫tsgrdr∀s,t∈(0,T):s≤t. | (8) |
The class of
Proposition 3.6. Let
| |˙γ|(t):=lims→td(γs,γt)|s−t| |
exists for a.e.
Proof. See, e.g., [2,Theorem 1.1.2].
The next result relates the metric derivative of
Theorem 3.7 (Absolutely continuity curves). The following statements hold:
(i) If
(ii) Conversely, if
Proof of (ⅰ). We adapt the proof of [2,Theorem 8.3.1] to the setting of metric graphs.
The idea of the proof is as follows: On the space-time domain
| T:=span{(0,T)×G∋(t,x)↦a(t)φ(x) : a∈C1c(0,T),φ∈C1(¯E)∩C(G)},V:={(0,T)ׯE∋(t,x)↦∇xΦ(t,x) : Φ∈T}. |
The strategy is to show that the linear functional
| L(a⊗∇φ):=−∫Q˙a(t)φ(x)dμ(x,t), |
is well-defined and
| −∫T0˙a(t)∫Gφ(x)dμt(x)dt=L(a⊗∇φ)=∫T0a(t)∫¯E∇φ(x)vt(x)d¯μt(x)dt | (9) |
for
Once this is done, we show that the momentum vector field
Step 1. Fix a test function
| H(x,y):={lip(φ)(x)if x=y,|φ(x)−φ(y)|d(x,y)if x≠y, |
for
| |∫Gφdμs−∫Gφdμt|≤∫G×Gd(x,y)H(x,y)dσs→t(x,y)≤W2(μs,μt)(∫G×GH2(x,y)dσs→t(x,y))1/2. | (10) |
As
| |∫Gφdμs−∫Gφdμt|≤Lip(φ)W2(μs,μt) |
and infer that the mapping
Fix
| ∫G×Gd2(x,y)dˆσ(x,y)≤lim infn→∞∫G×Gd2(x,y)dσsn→t(x,y)=lim infn→∞W22(μsn,μt)=0, |
which implies that
Using this result and the upper-semicontinuity of
| lim sups→t|∫Gφdμs−∫Gφdμts−t|≤|˙μ|(t)lim sups→t(∫G×GH2(x,y)dσs→t(x,y))1/2≤|˙μ|(t)⋅‖lip(φ)‖L2(μt). | (11) |
Step 2. Take
| |∫QddtΦ(x,t)dμ(x,t)|=limh↘0|1h∫QΦ(x,t−h)−Φ(x,t)dμ(x,t)|=limh↘0|1h∫T0(∫GΦ(x,t)dμt+h(x)−∫GΦ(x,t)dμt(x))dt|≤∫T0|˙μ|(t)⋅‖lipx(Φ)(⋅,t)‖L2(μt)dt≤(∫T0|˙μ|2(t)dt)1/2(∫Q|lipx(Φ)(x,t)|2dμ(x,t))1/2. | (12) |
Since
In particular, (9) implies that
| ddt∫Gφdμt=∫¯E∇φ⋅vtdμtfor a.e. t∈(0,T). | (13) |
We conclude that
Step 3. It remains to verify (by a standard argument) the inequality relating the
For this purpose, fix a sequence
| ∫Qa(t)|vv(x,t)|2dμ(x,t)=limi→∞∫Qa(t)ϖϖi(x,t)vv(x,t)dμ(x,t)=limi→∞L(aϖϖi)≤(∫T01I|˙μt|2dt)1/2limi→∞(∫Q1I|ϖϖi|2dμ)1/2=(∫T01I|˙μ|2(t)dt)1/2(∫Q1I|v|2dμ)1/2. |
Letting
| ∫I∫E|vt|2dμtdt≤∫I|˙μ|2(t)dt. |
Since
Next we introduce a suitable spatial regularisation procedure for solutions to the continuity equation. This will be crucial in the proof of the second part of Theorem 3.7.
Let
We next define a regularisation procedure for functions based on averaging. The crucial feature here is that non-centred averages are used, to ensure that the regularised function is continuous.
In the definition below, we parametrise each edge
Definition 3.8 (Regularisation of functions). For
| φε(x):=12ε∫αεex+εαεex−εφ(y)dyfor x∈e=[−ℓe2,ℓe2], | (14) |
where
Note that the value of
Proposition 3.9. The following properties hold for every
(i) Regularising effect: For any
| ∇φε(y)=αεe2ε(φ(αεey+ε)−φ(αεey−ε)) | (15) |
for
(ii) If
Proof. (ⅰ) follows by direct computation; (ⅱ) follows using the uniform continuity of
Lemma 3.10 (Weak continuity). Let
Proof. Fix
By duality, we obtain a natural regularisation for measures.
Definition 3.11 (Regularisation of measures). For
| ∫Gextφdμε:=∫Gφεdμ. | (16) |
for all
Analogously, for
It is readily checked that the right-hand side defines a positive linear functional on
Proposition 3.12. The following properties hold for any
(i) Mass preservation:
(ii) Regularising effect:For any
| ρε(x)={12εμ(e∩Ie(x)),for x on e in E, 12ε(1{d(x,w)≤2ε}μ({w})+∑e∈E:w∈eμ(e∩Ie(x))),for x on eextw, w∈V, |
where
| Ie(x):=(x−εaεe∨(−ℓe2),x+εaεe∧ℓe2). |
In particular,
(iii) Kinetic energy bound: For
| ∫Eext|vε|2dμε≤∫E|v|2dμ. | (17) |
(iv) For any
(v) Let
For every absolutely continuous function
| ddt∫Gextφdμεt=∫Eextαε∇φ⋅dJεt, | (18) |
with
In order to prove (ⅲ), we will make use of the so-called Benamou–Brenier functional (see, e.g., [26,Section 5.3.1] for corresponding results in the Euclidean setting).
Define
Definition 3.13. The Benamou–Brenier functional
| B2(μ,J):=sup(a,b)∈C(G,K2){∫Gadμ+∫EbdJ}. |
Some basic properties of this functional are collected in the following lemma.
Lemma 3.14. The following statements hold:
(i) For
| α(z,y):=sup(a,b)∈K2{az+by}={|y|22z if z>0,0 if z=0 and y=0,+∞otherwise. | (19) |
(ii) For
| B2(μ,J)=sup(a,b)∈L∞(G,K2){∫Gadμ+∫EbdJ}. | (20) |
(iii) The functional
(iv) If
| B2(μ,J)=12∫E|v|2dμ. | (21) |
Otherwise, we have
Proof. (ⅰ): see [26,Lemma 5.17].
(ⅱ): Clearly, the right-hand side of (20) is bounded from below by
| μ({a≠aδ})≤δ2,sup|aδ|≤sup|a|and|J|({b≠bδ})≤δ2,sup|bδ|≤sup|b|. |
Define
(ⅲ): This follows from the definition of
(ⅳ): Let
| B2(μ,J)=sup(a,b)∈L∞(G,K2){∫Ga+bvdμ}=12∫E|v|2dμ. |
To prove the converse, suppose first that there exists a Borel set
Proof of Proposition 3.12. (ⅰ): The claim follows readily from the definitions.
(ⅱ): For
| ∫Gextφ(y)dμε(y)=∫Gφε(x)dμ(x)=∑w∈Vφε(w)μ({w})+∑e∈E∫eφε(x)dμ(x). |
For
| φε(w)=12ε∫eextw1{d(w,y)≤2ε}φ(y)dy. |
For
| ∫eφε(x)dμ(x)=12ε∫(−ℓe/2,ℓe/2)(∫αεex+εαεex−εφ(y)dy)dμ(x)=12ε∫(−ℓe/2−2ε,ℓe/2+2ε)φ(y)μ(Iε(y))dy |
Combining these three identities, the desired result follows.
(ⅲ): Take bounded measurable functions
| aε(x)+12|bε(x)|2≤(a+12|b|2)ε(x)≤0∀x∈G, |
i.e.,
| ∫Gextadμε+∫EextbdJε=∫Gaεdμ+∫EbεdJ≤12∫E|v|2dμ. | (22) |
The result follows by taking the supremum over all admissible functions
(ⅳ): This follows from the uniform convergence of
(ⅴ): The function
| ∇φε(x)=αε(x)(∇φ)ε(x)∀x∈E. | (23) |
Since
| ddt∫Gextφdμεt=ddt∫Gφεdμt=∫E∇φε⋅vtdμt=∫E(∇φ)ε⋅αεvtdμt=∫Eext∇φ⋅(αεvεt)dμεt. |
Now we are ready to prove the second part of Theorem 3.7: we adapt the proof of [13], where (much) more general metric measure spaces are treated, but stronger assumptions on the measures are imposed (namely, uniform bounds on the density with respect to the reference measure). Here we consider more general measures using the above regularisation procedure.
In the proof of the second part of Theorem 3.7, we make use of the Hopf–Lax formula in metric spaces and its relation to the dual problem of optimal transport.
Definition 3.15 (Hopf–Lax formula). For a real-valued function
| Qtf(x):=infy∈X{f(y)+12td2(x,y)} |
for all
The operators
Proposition 3.16 (Hopf–Lax semigroup). Let
(i) For every
(ii) For every
| ddtQtf(x)+12lip(Qtf)2(x)≤0 | (24) |
holds for all
(iii) The mapping
Proof. (i): This statement can be derived from [3,Proposition 3.4]. For the convenience of the reader we provide the complete argument here.
Fix
| Qtf(x)=infz∈Xd(x,z)≤2tLF(t,x,z), |
where
| F(t,x,z)=f(z)+12td2(x,z)≥f(x)−Ld(x,z)+12td2(x,z)>f(x)=F(t,x,x), |
which implies the claim.
Fix now
| Qtf(x)−Qtf(y)≤F(t,x,z)−F(t,y,z)+ε=12t(d2(x,z)−d2(y,z))+ε≤d(x,y)2t(d(x,z)+d(y,z))+ε≤d(x,y)2t(d(x,y)+4tL)+ε. |
Reversing the roles of
| lip(Qtf)(x)≤2L. |
Since
(ii): See [3,Theorem 3.5].
(iii): See [3,Propositions 3.2 and 3.6].
We can now conclude the proof of Theorem 3.7 on the characterisation of absolutely continuous curves in the Wasserstein space over a metric graph.
Proof of (ⅱ) in Theorem 3.7. Without loss of generality, we set
| W22(μ0,μ1)≤∫10‖vr‖2L2(μr)dr. | (25) |
From there, a simple reparametrisation argument (see also [2,Lemma 1.1.4 & 8.1.3]) yields
| W22(μt,μs)≤1|s−t|∫ts‖vr‖2L2(μr)dr |
for all
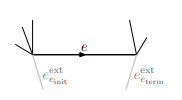
Thus, we have to show (25). To this aim, we will work on the supergraph
By Kantorovich duality (Proposition 2.3), there exists
| 12W22(μ0,μ1)=∫GQ1φdμ1−∫Gφdμ0. | (26) |
Moreover,
Set
| ∫GextQ1φdμε1−∫Gextφdμε0=n−1∑i=0(∫Gext(Q(i+1)/nφ−Qi/nφ)dμε(i+1)/n+∫GextQi/nφd(με(i+1)/n−μεi/n)), | (27) |
and bound the two terms on the right-hand side separately.
Bound 1. To estimate the first term on the right-hand side of (27), we use (24) to obtain
| n−1∑i=0∫Gext(Q(i+1)/nφ−Qi/nφ)dμε(i+1)/n≤−12n−1∑i=0∫Gext∫(i+1)/ni/nlip2(Qtφ)dtdμε(i+1)/n=−12∫Gext×(0,1)lip2(Qtφ)(x)dμμεn(x,t), | (28) |
where the measures
To show weak convergence of the sequence
As
| lim supn→∞n−1∑i=0∫Gext(Q(i+1)/nφ−Qi/nφ)dμε(i+1)/n≤−12∫Gext×(0,1)lip2(Qtφ)(x)dμμε(x,t)=−12∫10∫Eextlip2(Qtφ)dμεtdt, | (29) |
where we use that
Bound 2. We now treat the second term in (27). As
| n−1∑i=0∫GextQi/nφd(με(i+1)/n−μεi/n)=n−1∑i=0∫G(Qi/nφ)εd(μ(i+1)/n−μi/n)=n−1∑i=0∫(i+1)/ni/n(∫E∇(Qi/nφ)εdJt)dt=n−1∑i=0∫(i+1)/ni/n(∑e∈Eαεe∫e(∇Qi/nφ)εdJt)dt=n−1∑i=0∫(i+1)/ni/n(∑e∈Eαεe∫e∇Qi/nφ⋅dJεt)dt≤αεmax2n−1∑i=0∫(i+1)/ni/n∫Eext|∇Qi/nφ|2dμεtdt+αεmax2∫10∫Eext|vεt|2dμεtdt, | (30) |
where
Proposition 3.16.iiiyields the bound
| lim supn→∞n−1∑i=0∫(i+1)/ni/n∫Eext|∇Qi/nφ|2dμεtdt≤∫10∫Eextlip2(Qtφ)dμεtdt. |
Using this estimate together with Proposition 3.12.iii, we obtain
| lim supn→∞n−1∑i=0∫GextQi/nφd(με(i+1)/n−μεi/n)≤αεmax2∫10∫Gextlip2(Qtφ)dμεtdt+αεmax2∫10∫E|vt|2dμtdt. | (31) |
Combination of both bounds. Recalling (27), we use (29) and (31) to obtain
| ∫GextQ1φdμε1−∫Gextφdμε0≤αεmax2∫10∫E|vt|2dμtdt+αεmax−12∫Gext∫10lip2(Qtφ)dμεtdt. |
Using Proposition 3.12.iv, the fact that
| ∫GQ1φdμ1−∫Gφdμ0≤12∫10∫E|vt|2dμtdt. | (32) |
In view of (26), this yields the result.
Corollary 1 (Benamou–Brenier formula).For any
| W22(μ,ν)=min{∫10∫E|vt|2dμtdt}, | (33) |
where the minimum is taken among all weak solutions to the continuity equation
Proof. As
| W22(μ,ν)=min{∫10|˙μ|2(t)dt}, |
where the minimum runs over all absolutely continuous curves
In this section we consider the entropy functional
| Ent(μ):={∫Gρlogρdλif μ=ρλ,+∞otherwise. | (34) |
As is well known, this functional is lower semicontinuous on
A celebrated result by McCann asserts that
Metric graphs are prototypical examples in which such bounds fail to hold. Here we present an explicit example, which shows that the functional
Example 4.1. Consider a metric graph induced by a graph with 3 leaves as shown in Figure 2.
We impose an edge weight
| ρ(x):={12ε1[0,ε](x),x∈e1 or x∈e2,0,x∈f,, η(x):={0,x∈e1 or x∈e2,1ε1[1−ε,1](x),x∈f. |
Lemma 4.2. The unique optimal coupling of
| T(x)=1−ε+x∈f for x∈e1 or x∈e2. |
Proof. Let
Consequently, the constant speed-geodesic from
| Tt(x):={x+(2−ε)t∈ei,if x≤1−(2−ε)t,x+(2−ε)t−1∈f,if x>1−(2−ε)t, |
for
Set
| Ent(μt)={log(12ε),t∈[0,tε0],1ε(1−(2−ε)t)log(12)+log(1ε),t∈[tε0,tε1],log(1ε),if t∈[tε1,1]. |
Thus,
In this section we study gradient flows in the Wasserstein space over a metric graph. Namely, we consider diffusion equations on metric graphs arising as the gradient flow of free energy functionals composed as the sum of entropy, potential, and interaction energies. We give a variational characterisation of these diffusion equations via energy-dissipation identities and we discuss the approximation of solutions via the Jordan–Kinderlehrer–Otto scheme (minimizing movement scheme). This provides natural analogues on metric graphs of the corresponding classical results in Euclidean space. We follow the approach from the Euclidean case; see in particular [2,Section 10.4], and adapt it to the current setting.
Let
| EV(μ):=Ent[μ|m]={∫Gρ(x)logρ(x)dm(x) if μ=ρm,+∞ otherwise. | (35) |
| W(μ):=12∫G×GW(x,y)dμ(x)dμ(y), |
where
Moreover, we define
| F:=EV+W. |
Note that
Further note that for
| EV(μ)=E(μ)+V(μ), |
where
| V(μ):=∫GV(x)dμ(x) |
is the potential energy. The latter is well defined for
We consider the following diffusion equation on the metric graph
| ∂tη=Δη+∇⋅(η(∇V+∇W[μ])). | (36) |
Here
We consider the following notion of weak solution for (36).
Definition 5.1. We say that a curve
| μt=ρtmandJt=−(∇ρt+ρt∇W[μt])m |
is a weak solution to the continuity equation in the sense of Definition 3.2, i.e., we ask that
| ∫T0(∫G∂tφρtdm−∫¯E∇φ⋅(∇ρt+ρt∇W[μt])dm)dt=0. | (37) |
Remark 2. Let us briefly consider the special case where
The dissipation of the free energy along solutions to (36) at
| ddtF(μ)=−∫E|∇ρρ+∇W[μ]|2dμ. |
This motivates the following definition.
Definition 5.2 (Energy dissipation functional). The energy dissipation functional
| I(μ):=∫E|w|2dμ. |
Otherwise, we set
Remark 3. We emphasize that continuity of
We collect the following properties of the dissipation functional.
Lemma 5.3. Let
| supnF(μn)<∞ and supnI(μn)<∞. | (38) |
Then we have
| I(μ)≤lim infnI(μn). | (39) |
Proof. First note that we can rewrite
| I(μ)=Gα(μ,J)=∫Eα(dμdσ,dJdσ)dσ, | (40) |
where
| α(s,u)={|u|2/sif s>0,0if s=0 and u=0,+∞otherwise, | (41) |
and
Now, let
Recall that
| Gα(μ,J)≤lim infnI(μn)<∞. | (42) |
This allows us to write
| −∫Gρn∇sdλ=∫Gs∇ρndλ=∫GseV(∇ρn+ρn∇W[μn])dm−∫GseV∇W[μn]dμn=∫GseVdJn−∫GseV∇W[μn]dμn. | (43) |
The convergence of
| −∫Gρ∇sdλ=∫GseVdJ−∫GseV∇W[μ]dμ=∫Gswwρdλ−∫Gsρ∇W[μ]dλ∀s∈C1c(E). |
We infer that
Let us now show that
Let us denote by
| I0(μ):=∫E|w|2dμ. |
Otherwise, we set
Next, we observe that finiteness of the
Lemma 5.4. For
| ‖ρ‖∞≤A√I0(μ), |
where the constant
Proof. The continuity of
| ∫|∇ρ|dλ≤e‖V‖∞∫|∇ρ|dm≤e‖V‖∞(∫|w|2dμ)12. |
The claim then follows immediately from the Sobolev embedding theorem applied to each of the finitely many edges.
The main result of this section is the following gradient flow characterisation of the diffusion equation (36).
Theorem 5.5. For any 2-absolutely continuous curve
| LT(μ):=F(μT)−F(μ0)+12∫T0|˙μ|2(r)+I(μr)dr≥0. |
Moreover, we have
The main step in proving this result is to establish a chain rule for the free energy
Proposition 5.6 (Chain rule). Let
| ddtF(μt)=∫E⟨wt,dJt⟩for a.e.t∈[0,T]. | (44) |
Proof. We first note that the assumptions ensure that also
| ∫T0∫Eα(ρt,∇ρt)dmdt<∞,∫T0∫Eα(ρt,Ut)dmdt<∞. | (45) |
We proceed by a twofold regularisation. Using a family
| ρδt:=∫δ−δηδ(s)ρt−sds, |
and set
Further, we regularise the logarithm and define for
| Fε(r)=(r+ε)log(r+ε)−εlogε. |
Then we define the regularized free energy
| Fε(μ)=∫GFε(ρ)dm+12∫G×GW(x,y)dμ(x)dμ(y). |
Let us set
| Fε(μδT)−Fε(μδ0)=∫T0∫G⟨∇gε,δt+∇W[μδt],dJδt⟩dt. | (46) |
Then passing to the limit
While establishing (46) we write
| Fε(μδT)−Fε(μδ0)=∫T0∫G(F′ε(ρδ)+W[μδt])∂tρδtdmdt. |
Differentiation under the integral sign is justified by boundedness of
| ∫T0∫Ggαt∂tρδtdmdt=∫T0∫E⟨∇gαt,dJδt⟩. |
Passing to the limit as
| |∫T0∫E⟨∇gαt−∇gt,dJδt⟩dt|≤(∫T0∫E|∇gαt−∇gt|2ρδtdmdt)12×(∫T0∫Eα(ρδt,Uδt)dmdt)12. |
The second factor is finite as noted above. To estimate the first factor, we recall that
| ∫T0∫E|∇gαt−∇gt|2ρδtdmdt≤C∫T0∫E|∇gαt−∇gt|2dλdt |
Using (15) and dominated convergence, the latter term goes to zero as
| ∫T0∫E|∇g|2dλdt<∞. |
But using
| ∫T0∫E|∇g|2dλdt≤e‖V‖∞∫T0I0(μδt)dt<∞. |
Thus, (46) is established.
We will now pass to the limits
For the limit
| ∫T0∫E⟨wwε,δt,Uδt⟩dmdt→∫T0∫E⟨wwεt,Ut⟩dmdt. |
Indeed, we have the majorant
| |⟨wwε,δ,Uδ⟩|≤12|wwε,δ|2(ρδ+ε)+12|Uδ|2ρδ+ε≤α(ρδ,∇ρδ)+C(ρδ+ε)+12α(ρδ,Uδ)≤[α(ρ,∇ρ)]δ+C(ρδ+ε)+12[α(ρ,U)]δ |
for a suitable constant
To further pass to the limit
It remains to pass to the limit on the left-hand side in (46). The weak continuity of
| ∫Fε(ρ)dm=EV(με)−Mεlogε, |
with
| F(μT)−F(μ0)=∫T0∫⟨wwt,dJt⟩dt. |
Hence
We can now prove Theorem 5.5.
Proof of Theorem 5.5. Note that the right-hand side of (44) may be estimated by means of Hölder's and Young's inequality as
| ∫E⟨wt,Ut⟩dm≥−√∫E|wt|2ρtdm√∫E|Ut|2ρtdm≥−12∫E|wt|2ρtdm−12∫E|Ut|2ρtdm. | (47) |
Hence, by integrating both sides of (44) from
Here, we recast the variational characterisation of McKean–Vlasov equations on metric graphs from the previous section in the language of the theory of gradient flows in metric spaces. Let us briefly recall the basic objects. For a detailed account we refer the reader to [2].
Let
The following notion plays the role of the modulus of the gradient in a metric setting.
Definition 5.7 (Strong upper gradient). A function
| |E(xs)−E(xt)|≤∫tsg(xr)|˙x|(r)dr∀a≤s≤t≤b . |
Note that by the definition of strong upper gradient, and Young's inequality
| E(xt)−E(xs)+12∫tsg(xr)2+|˙x|2(r)dr≥0. |
Definition 5.8 (Curve of maximal slope). A locally
| E(xt)−E(xs)+12∫tsg(xr)2+|˙x|2(r)dr≤0∀0<s≤t. | (48) |
We say that a curve of maximal slope starts from
Equivalently, we can require equality in (48). If a strong upper gradient
Finally, we define the (descending) metric slope of
| |∂E|(x)=lim supy→xmax{E(x)−E(y),0}d(x,y). | (49) |
The metric slope is in general only a weak upper gradient for
Corollary 2. The functional
Proof. For a
| |F(μt)−F(μs)|≤∫ts√I(μr)|˙μr|dr∀s,t∈[0,T]:s≤t, | (50) |
i.e.,
The dissipation functional
Lemma 5.9. For any
| I(μ)≤|∂F|2(μ). |
Proof. We assume that
Step 1. We show first that
For this purpose, take any
| limt↘0F((rrt)#μ)−F(μ)t=∫G[−ρ∇ss+ssρ∇W[μ]]dλ. | (51) |
To show this, note that
| ˜ρ(x)=˜ρt(rrt(x))∇rrt(x);. |
Consequently, with
| F((rrt)#μ)−F(μ)=∫GF(˜ρ∇rrt)∇rrt−F(˜ρ)dλ+∫G[V∘rrt−V]dμ+∫G×G[W∘(rrt⊗rrt)−W]dμ⊗μ. |
Note that
For
| W2(μ,(rrt)#μ)≤t‖~ss‖L2(μ). |
This estimate, together with (51), implies
| ∫G[−ρ∇ss+ssρ∇W[μ]]dλ=limt↘0F((rrt)#μ)−F(μ)t≤|∂F|(μ)‖~ss‖L2(μ). |
Hence, the left-hand side defines an
| ∫G[−ρ∇ss+ssρ∇(V+W[μ])]dλ=∫Gww~ssdμ=∫Gwwρsdλ | (52) |
for all
Considering in particular functions
Step 2. Next we show that
Consider a pair of adjacent edges
Combining both steps, we infer that
| I(μ)=‖ww‖2L2(μ)≤|∂F|2(μ). |
From Lemma 5.9 and the lower semicontinuity of
| |∂−F|(μ):=inf{lim infn|∂F|(μn):μn⇀μ}. |
Corollary 3. For all
In this section, we consider the time-discrete variational approximation scheme of Jordan–Kinderlehrer–Otto for the gradient flow [14].
Given a time step
| μτ0=μ0,μτn∈argminν{F(ν)+12τW2(ν,μτn−1)2}. | (53) |
Then we build a discrete gradient flow trajectory as the piecewise constant interpolation
| ˉμτ0=μ0,ˉμτt=μτn if t∈((n−1)τ,nτ]. | (54) |
Then we have the following result.
Theorem 5.10. For any
| ˉμτkt⇀μt∀t∈[0,∞). | (55) |
Moreover, any such limit curve is a gradient flow curve of
Proof of Theorem 5.10. The result basically follows from general results for metric gradient flows, where the scheme is known as the minimizing movement scheme; see [2,Section 2.3]. We consider the metric space
| 12∫t0|˙μ|2(r)+|∂−F(μr)|2dr+F(μt)≤F(μ0). |
Thus, by Corollary 3, it is also a curve of maximal slope for the strong upper gradient
ME acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG), Grant SFB 1283/2 2021 – 317210226. DF and JM were supported by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement No 716117). JM also acknowledges support by the Austrian Science Fund (FWF), Project SFB F65. The work of DM was partially supported by the Deutsche Forschungsgemeinschaft (DFG), Grant 397230547. This article is based upon work from COST Action 18232 MAT-DYN-NET, supported by COST (European Cooperation in Science and Technology), www.cost.eu. We wish to thank Martin Burger and Jan-Frederik Pietschmann for useful discussions. We are grateful to the anonymous referees for their careful reading and useful suggestions.
| 1. | Martin Burger, Antonio Esposito, Porous medium equation and cross-diffusion systems as limit of nonlocal interaction, 2023, 235, 0362546X, 113347, 10.1016/j.na.2023.113347 | |
| 2. | Qiang Du, Amir Sagiv, Minimizing Optimal Transport for Functions with Fixed-Size Nodal Sets, 2023, 33, 0938-8974, 10.1007/s00332-023-09952-8 | |
| 3. | Martin Burger, Ina Humpert, Jan-Frederik Pietschmann, Dynamic Optimal Transport on Networks, 2023, 29, 1292-8119, 54, 10.1051/cocv/2023027 | |
| 4. | Ariane Fazeny, Martin Burger, Jan-F. Pietschmann, Optimal transport on gas networks, 2025, 0956-7925, 1, 10.1017/S0956792525000051 |
The supergraph
The support of probability measures
Plot of the entropy along the geodesic interpolation