We propose a new model for the emergence of blood capillary networks. We assimilate the tissue and extra cellular matrix as a porous medium, using Darcy's law for describing both blood and interstitial fluid flows. Oxygen obeys a convection-diffusion-reaction equation describing advection by the blood, diffusion and consumption by the tissue. Discrete agents named capillary elements and modelling groups of endothelial cells are created or deleted according to different rules involving the oxygen concentration gradient, the blood velocity, the sheer stress or the capillary element density. Once created, a capillary element locally enhances the hydraulic conductivity matrix, contributing to a local increase of the blood velocity and oxygen flow. No connectivity between the capillary elements is imposed. The coupling between blood, oxygen flow and capillary elements provides a positive feedback mechanism which triggers the emergence of a network of channels of high hydraulic conductivity which we identify as new blood capillaries. We provide two different, biologically relevant geometrical settings and numerically analyze the influence of each of the capillary creation mechanism in detail. All mechanisms seem to concur towards a harmonious network but the most important ones are those involving oxygen gradient and sheer stress. A detailed discussion of this model with respect to the literature and its potential future developments concludes the paper.
Citation: Pedro Aceves-Sanchez, Benjamin Aymard, Diane Peurichard, Pol Kennel, Anne Lorsignol, Franck Plouraboué, Louis Casteilla, Pierre Degond. A new model for the emergence of blood capillary networks[J]. Networks and Heterogeneous Media, 2021, 16(1): 91-138. doi: 10.3934/nhm.2021001
| [1] | Abdulwahab Ali Almazroi . Survival prediction among heart patients using machine learning techniques. Mathematical Biosciences and Engineering, 2022, 19(1): 134-145. doi: 10.3934/mbe.2022007 |
| [2] | Weidong Gao, Yibin Xu, Shengshu Li, Yujun Fu, Dongyang Zheng, Yingjia She . Obstructive sleep apnea syndrome detection based on ballistocardiogram via machine learning approach. Mathematical Biosciences and Engineering, 2019, 16(5): 5672-5686. doi: 10.3934/mbe.2019282 |
| [3] | Lili Jiang, Sirong Chen, Yuanhui Wu, Da Zhou, Lihua Duan . Prediction of coronary heart disease in gout patients using machine learning models. Mathematical Biosciences and Engineering, 2023, 20(3): 4574-4591. doi: 10.3934/mbe.2023212 |
| [4] | Jingchi Jiang, Xuehui Yu, Yi Lin, Yi Guan . PercolationDF: A percolation-based medical diagnosis framework. Mathematical Biosciences and Engineering, 2022, 19(6): 5832-5849. doi: 10.3934/mbe.2022273 |
| [5] | Abigail Ferreira, Rui Lapa, Nuno Vale . A retrospective study comparing creatinine clearance estimation using different equations on a population-based cohort. Mathematical Biosciences and Engineering, 2021, 18(5): 5680-5691. doi: 10.3934/mbe.2021287 |
| [6] | Atsushi Kawaguchi . Network-based diagnostic probability estimation from resting-state functional magnetic resonance imaging. Mathematical Biosciences and Engineering, 2023, 20(10): 17702-17725. doi: 10.3934/mbe.2023787 |
| [7] | Michele L. Joyner, Cammey Cole Manning, Whitney Forbes, Valerie Bobola, William Frazier . Modeling Ertapenem: the impact of body mass index on distribution of the antibiotic in the body. Mathematical Biosciences and Engineering, 2019, 16(2): 713-726. doi: 10.3934/mbe.2019034 |
| [8] | Wenzhu Song, Lixia Qiu, Jianbo Qing, Wenqiang Zhi, Zhijian Zha, Xueli Hu, Zhiqi Qin, Hao Gong, Yafeng Li . Using Bayesian network model with MMHC algorithm to detect risk factors for stroke. Mathematical Biosciences and Engineering, 2022, 19(12): 13660-13674. doi: 10.3934/mbe.2022637 |
| [9] | Anastasia-Maria Leventi-Peetz, Kai Weber . Probabilistic machine learning for breast cancer classification. Mathematical Biosciences and Engineering, 2023, 20(1): 624-655. doi: 10.3934/mbe.2023029 |
| [10] | Tingxi Wen, Hanxiao Wu, Yu Du, Chuanbo Huang . Faster R-CNN with improved anchor box for cell recognition. Mathematical Biosciences and Engineering, 2020, 17(6): 7772-7786. doi: 10.3934/mbe.2020395 |
We propose a new model for the emergence of blood capillary networks. We assimilate the tissue and extra cellular matrix as a porous medium, using Darcy's law for describing both blood and interstitial fluid flows. Oxygen obeys a convection-diffusion-reaction equation describing advection by the blood, diffusion and consumption by the tissue. Discrete agents named capillary elements and modelling groups of endothelial cells are created or deleted according to different rules involving the oxygen concentration gradient, the blood velocity, the sheer stress or the capillary element density. Once created, a capillary element locally enhances the hydraulic conductivity matrix, contributing to a local increase of the blood velocity and oxygen flow. No connectivity between the capillary elements is imposed. The coupling between blood, oxygen flow and capillary elements provides a positive feedback mechanism which triggers the emergence of a network of channels of high hydraulic conductivity which we identify as new blood capillaries. We provide two different, biologically relevant geometrical settings and numerically analyze the influence of each of the capillary creation mechanism in detail. All mechanisms seem to concur towards a harmonious network but the most important ones are those involving oxygen gradient and sheer stress. A detailed discussion of this model with respect to the literature and its potential future developments concludes the paper.
Obstructive sleep apnea (OSA) is featured by repeated upper airway narrowing or obstruction, causing a substantial reduction or cessation of airflow during sleep [1,2]. These disruptions in breathing lead to intermittent hypercapnia and hypoxemia, causing metabolic dysregulation, endothelial dysfunction, and systemic inflammatory responses [2,3]. These pathophysiologic changes have contributed to various major comorbidities [2,3,4,5]. OSA is a global health concern and economic burden, with estimates of the incidence of moderate or severe OSA reaching 6%-17% in the general adult population and up to 49% in the elderly population [4,6], with most of the cases being undiagnosed [7].
No single physical examination finding can be used to diagnose or exclusively account for OSA. The gold standard diagnostic test for OSA relies on in-lab all-night polysomnography (PSG) [7,8]. However, this method is costly, and patients require continuous sleep monitoring by medical staff [2]; thus, limited availability of PSG may cause delays in diagnosing OSA and an increased disease burden [7,9].
Several body measurements predispose patients to OSA. Body weight, body mass index (BMI), central body fat distribution, and large neck and waist circumferences are possible risk factors [2,6,10]. In addition, increased age and males are also at risk for OSA [2,6]. Despite the epidemiological reports demonstrating that age, sex, and BMI are associated with OSA severity, an integrated predicting model that uses only these three factors to assess OSA risk has not yet been developed.
Machine learning approaches have expanded the ability to design efficient predictive and diagnostic tools and have gained popularity in many areas of medical research and clinical applications [11,12]. Logistic regression (LR) is one of the computational methods for probing multivariate data to detect the independent effects of a variable after adjusting for the contributions of the others [13]. An artificial neural network (ANN) is a supervised learning algorithm with advantages in analyzing nonlinear data, enhancing data interpretation, and designing effective predictive and diagnostic models to assist different clinical tasks [11,14].
The present study investigated the clinical predictive validity of age, sex, and BMI for sleep apnea and applied LR and ANN algorithms to develop a risk-predicting model using these three parameters as predictors.
This retrospective observational study used clinical data from the medical records of participants who had undergone PSG at the Sleep Center of Shuang Ho Hospital, Taipei Medical University, Taiwan, between January 2015 and January 2020.
The inclusion criteria for this study were: (1) participants aged≥18 years and (2) who had undergone a full-night PSG. Participants were excluded if (1) they had received any OSA treatments or been admitted to the hospital for any invasive surgery for OSA, (2) they had undergone PSG for continuous positive airway pressure (CPAP) titration, (3) the total recording time was < 4 h [8], and (4) the total sleep time was < 3 h [15].
Before the PSG examination, a baseline screening questionnaire was used to assess each participant's basic information, medication, and surgical history. The participants were measured for height, weight, and BMI (kg/m2) at the time of registration.
All the participants underwent a full-night PSG recorded by qualified technicians. All the sleep signals were obtained using an Embla N7000 Recording System (Medcare Flaga, Reykjavik, Iceland) and Sandman Elite sleep diagnostic software (Natus Neurology Inc., Middleton, WI, USA).
Experienced sleep technologists scored all sleep apnea and hypopnea events following the American Academy of Sleep Medicine 2012 updated guideline [8,16]. Each participant's apnea-hypopnea index (AHI) was calculated according to the total number of apnea and hypopnea events divided by the total sleeping time. Hypopnea was defined as a 30-89% reduction in nasal airflow for at least 10s, with arousal or at least a decrease of 3% oxygen saturation. Apnea was defined as a more than 90% reduction in oral airflow for at least 10s with or without arousal or decreased saturation.
The severity of OSA was classified as none (AHI < 5), mild (AHI = 5-15), moderate (AHI = 15-30), and severe (AHI ≥ 30) [2,8]. To develop the predictive models for the risk of moderate-to-severe OSA, we divided the participants into none-and-mild (AHI < 15) and moderate-to-severe (AHI ≥ 15) OSA groups for further analysis.
Taipei Medical University-Joint Institutional Review Board (TMU-JIRB: N201911007) approved the protocol of this study. Waivers of informed consent were approved by the TMU-JIRB (TMU-JIRB: N201911007) for this retrospective study involving the secondary analysis of existing data.
All analyses were performed using STATISTICA software (TIBCO Software, Tulsa, OK, USA). Continuous data are presented as mean and standard deviation, whereas categorical variables are expressed as frequencies and percentages. We used Fisher's exact test to determine associations between two categorical variables and Pearson's chi-squared (X2) test to determine the statistical significance between the means of two continuous variables in the participants with none-to-mild and moderate-to-severe OSA. The one-way analysis of variance (ANOVA) was used to determine the statistical significance between the means of ≥ 3 independent groups. A two-tailed p-value less than 0.05 was considered statistically significant.
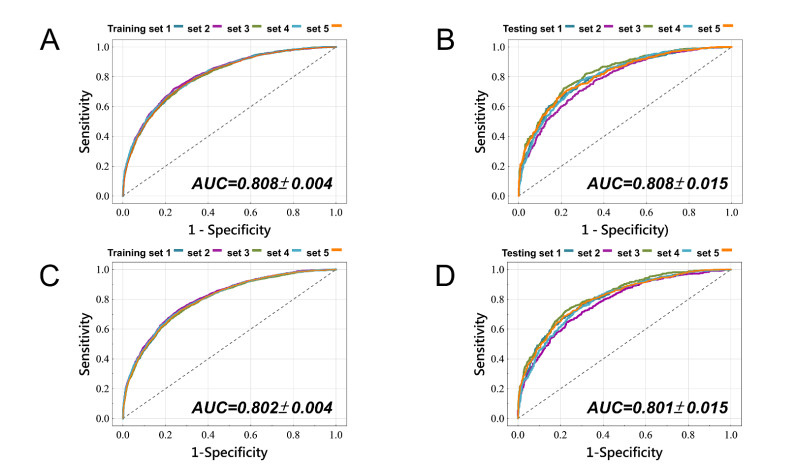
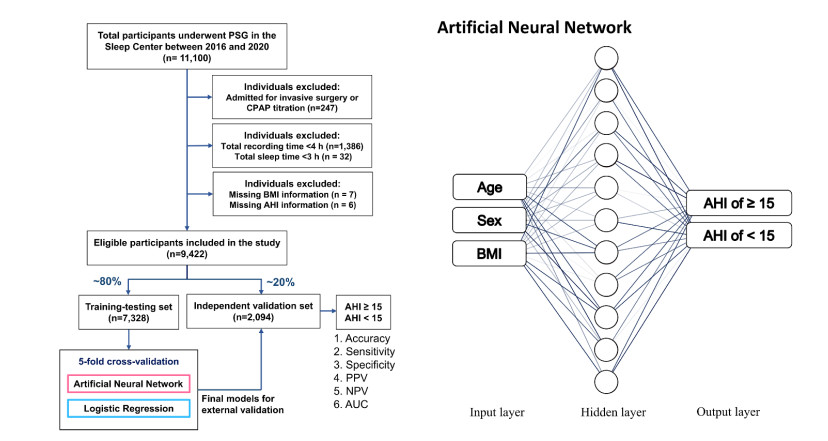
All the LR and ANN models were established and modeled using STATISTICA software. In the models, age and BMI were set as continuous variables, and sex was designated as a categorical variable. For our ANNs, the employed architecture was feed-forward, combined with a back-propagation algorithm with multilayer perceptron (MLP). A bias term was used for each neural layer in the MLP. We set the number of neurons in the hidden layer from 1 to 50. We initially partitioned the eligible PSG data into a training-testing set and an independent validation set, containing ~80% and ~20% of the data, respectively. The data from the training-testing set were used to determine the generalizability of the LR and ANN analyses using five-fold cross-validation (Figure 1A). All participants were stratified by age, sex, BMI, and OSA severity to maintain consistent proportions of demographic data across the training-testing and validation sets. We reported the mean AUCs for the training and testing sets of the LR and ANN models through five-fold cross-validation. The model with the best AUC in the five testing sets was identified to have the best predictive performance and used as the final model. The final models were then applied to the independent validation set, and we calculated the accuracy, sensitivity, specificity, positive predictive value (PPV), negative predictive value (NPV), and AUCs of the validation set derived from the confusion matrix [17] (Figure 1A). The classification threshold was set to 0.5 for all models.
During the study period, 11, 100 participants underwent PSG in the Sleep Center. Of these, 1, 665 participants were excluded from the baseline analyses for the following reasons: they had been admitted to the hospital for invasive surgery or CPAP titration (n = 247), the total recording time < 4h (n = 1, 386), the total sleep time < 3h (n = 32), missing BMI information (n = 7) or missing AHI information (n = 6) (Figure 1A). Overall, 9, 422 participants (2918 women and 6504 men, mean age: 49.2 ± 14.0 years) who had undergone PSG were enrolled in this study. Of these, 5, 920 (62.8%) had an AHI of ≥15, indicating moderate-to-severe OSA, and 3, 502 (37.2%) had an AHI < 15, indicating none-to-mild OSA.
A higher proportion of men have moderate-to-severe OSA than women (Table 1). Compared with participants with none-to-mild OSA, participants with moderate-to-severe OSA were older and had a higher BMI. In addition, participants with moderate-to-severe OSA had a shorter total sleep time, lower sleep efficiency, shorter rapid eye movement duration, and lower oxygen saturation during the PSG recording than those with none-to-mild OSA (Table 1).
| Variables | Moderate-to-severe OSA (AHI ≥ 15) |
None-to-mild OSA (AHI < 15) |
p-value |
| n | 5, 920 | 3, 502 | |
| Age | 50.8 ± 13.5 | 46.6 ± 14.4 | < 0.0001 |
| Female, n (%) | 1266 (21.4) | 1652 (47.2) | < 0.0001 |
| Height (cm) | 167.2 ± 8.5 | 164.4 ± 8.9 | < 0.0001 |
| Weight (kg) | 79.7±16.1 | 66.1 ± 13.1 | < 0.0001 |
| BMI (kg/m2) | 28.4 ± 4.8 | 24.3 ± 3.8 | < 0.0001 |
| Polysomnography | |||
| Total recording time (min) | 366.6±11.9 | 367.8±13.4 | < 0.0001 |
| Total sleep time (min) | 275.8±60.2 | 281.4±61.1 | < 0.0001 |
| Sleep efficiency (%) | 75.2±16.4 | 76.5±16.5 | 0.0002 |
| Non-REM sleep (min) | 240.6±51.7 | 242.2±51.3 | 0.133 |
| REM sleep (min) | 35.2±22.5 | 39.1±23.7 | < 0.0001 |
| AHI | 44.7±23.8 | 6.4±4.5 | < 0.0001 |
| SO2 mean (%) | 94.5±2.6 | 96.6±1.3 | < 0.0001 |
| Data are expressed as mean ± standard deviation. The p-value represents the comparison between the AHI ≥ 15 and AHI < 15 groups. | |||
DownLoad:
CSV
A multivariate analysis was applied to adjust for age, sex, and BMI to determine the independent predictors of moderate-to-severe OSA. Table 2 presents the variables' crude and adjusted odds ratio (OR) values in the LR model. After adjustment for the associated variables, the regression analysis revealed that the female sex was associated with a 0.28-fold reduced risk of moderate-to-severe OSA (95% CI: 0.25-0.32; p < 0.0001), and every unit increase in age or BMI was associated with a 1.04-fold (95%CI: 1.04-1.05; p < 0.0001) or 1.27-fold (95%CI: 1.26-1.29; p < 0.0001) increase in the likelihood of moderate-to-severe OSA, respectively.
| Unadjusted Model | Adjusted Model | |||
| Variables | OR | 95% CI | OR | 95% CI |
| Age | 1.02*† | 1.02-1.03 | 1.04*† | 1.04-1.05 |
| Female | 0.30* | 0.28-0.33 | 0.28* | 0.25-0.32 |
| BMI | 1.27*† | 1.25-1.28 | 1.27*† | 1.26-1.29 |
| The odds ratio (OR) and 95% confidence intervals (CI) represent the association between the variables and the presence of moderate-to-severe OSA (AHI ≥ 15). *p < 0.0001; †Odds ratio of per unit changes. | ||||
DownLoad:
CSV
As mentioned, age, sex, and BMI were used as input parameters for developing the LR and ANN models for predicting moderate-to-severe OSA. As shown in Figure 1A, the 7328 participants in the training-testing group were randomly partitioned into training and testing sets for five-fold cross-validation. Table 3 showed that age, sex, BMI, and OSA severity distribution remained identical across the five testing sets and the independent validation sets.
| Variable | Testing set 1 | Testing set 2 | Testing set 3 | Testing set 4 | Testing set 5 | Independent validation set | p-value |
| n | 1466 | 1465 | 1466 | 1465 | 1466 | 2094 | |
| AHI≥15, n (%) | 920 (62.8) | 919 (62.7) | 920 (62.8) | 919 (62.7) | 920 (62.8) | 1322 (63.1) | 1.000 |
| Age | 49.0 ± 0.4 | 49.0 ± 0.4 | 49.9 ± 0.4 | 49.1 ± 0.4 | 49.0 ± 0.4 | 49.3 ± 0.3 | 0.503 |
| Female, n (%) | 483 (33.0) | 438 (29.9) | 472 (32.2) | 445 (30.4) | 431 (29.4) | 649 (31.0) | 0.266 |
| BMI (kg/m2) | 26.9 ± 4.9 | 26.9 ± 4.9 | 26.9 ± 5.0 | 26.9 ± 5.0 | 26.8 ± 4.8 | 26.9 ± 4.9 | 0.973 |
| The p-value represents the multiple comparisons across the five testing and the independent validation sets. | |||||||
DownLoad:
CSV
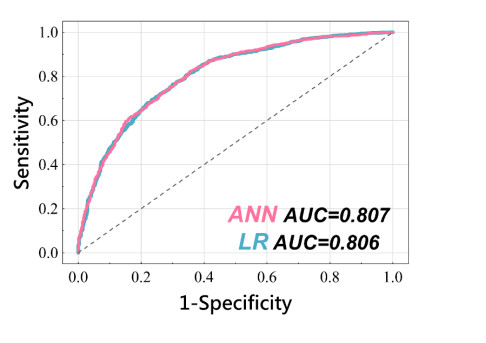
Following adequate training, the five testing sets that achieved the best prediction performance after five-fold cross-validation were ANN models with 3, 14, 25, 27, and 29 hidden neurons, respectively. The mean AUCs of the training sets were 0.808 ± 0.004 (Figure 2A) and 0.808 ± 0.015 for the testing sets (Figure 2B). Among the generated ANN models, the model containing 25 hidden neurons obtained the highest testing AUC and was selected as the final model. After being applied to the independent validation set, the ANN-based model achieved the accuracy, sensitivity, specificity, PPV, and NPV of 76.4%, 87.7%, 56.9%, 77.7%, 73.0%, with the AUC of 0.807, respectively. Results of the LR model revealed a mean AUC of 0.802 ± 0.004 for the training sets (Figure 2C) and 0.801 ± 0.015 for the testing sets (Figure 2D). After being validated to the independent validation set, the accuracy, sensitivity, specificity, PPV, and NPV were 76.3%, 87.5%, 57.0%, 77.7%, and 72. 7% with an AUC of 0.806 for the LR-based model. Figure 3 shows the ROC curve and AUC of the final ANN and LR models applied to the independent validation set.
The present study validated age, sex, and BMI as parameters for use in LR- and ANN models to estimate the risk of OSA in participants who had undergone PSG. The established LR- and ANN-based model integrating the three parameters achieved a notable prediction performance with an AUC of 0.806 and 0.807 for predicting moderate-to-severe OSA in the validation set. The relatively high AUC values indicated that the models could distinguish participants between groups of interest, namely, participants with none-to-mild and those with moderate-to-severe OSA. Patients with OSA are prone to various complications and require interventions [2,7]; our models may contribute to further understanding these three variables' fundamental role in assessing OSA risk.
OSA has been recognized as a global health and economic burden, and early identification and diagnosis of OSA is a crucial issue in preventive medicine [4,6,7]. Since standard diagnostic tests for OSA rely on expensive in-laboratory PSG, which can be challenging to schedule in high-demand situations, identifying crucial factors and developing a simple and reliable tool to estimate the risk of OSA is clinically relevant [7,9].
Anatomical and physiological differences in the oropharynx, larynx and upper respiratory tract, changes in respiratory physiology associated with different sleep structures, and differences in the distribution of adipose tissue have been suggested as reasons for sex differences in developing OSA [18]. Deterioration of the collapsibility of the pharyngeal airway and the sensitivity of the respiratory control system may contribute to the pathogenesis of OSA with aging [2,18]. Hormonal changes in menopausal women have been linked to an increased risk of OSA and a decreased sex difference in OSA with age [19,20]. The prevalence of OSA has been reported to increase 1.4 to 3.2-fold with each 10-year increment in age, and men had a 1.7 to 3.0-fold higher odds of developing OSA than women [2,6]. These findings support the rationale for using age and sex as parameters in a generic prediction model to predict OSA risk.
Obesity is a well-recognized risk factor for developing OSA, and a higher BMI is associated with greater severity of OSA for both sexes [19,21]. As already mentioned, anthropometric profiles, such as body weight, BMI, central body fat distribution, and neck and waist circumference, are predisposed to the risk of OSA [2,6,10]. In patients with OSA, occlusion of the nasal and oro-pharynx may occur during sleep when the tongue and epiglottis move backward and lean together. Individuals with obesity have excess soft tissue around the collapsible pharynx, making the narrow airway more prone to collapse [2,3,21]. In line with the findings of other studies, we observed that the participants with moderate-to-severe OSA had a higher BMI. Although other anthropometric profiles have been associated with OSA, neck and waist circumference were considered surrogates for BMI [4,21,22]. The study by Huxley et al. has also suggested that "measures of central obesity were superior to BMI as discriminators of cardiovascular risk factors, although the differences were small and unlikely to be of clinical relevance" [23]. Furthermore, the same study demonstrated that "combining BMI with any measure of central obesity did not improve the discriminatory capability of the individual measures" [23]. In this study, we proposed BMI as a simple, well-known, and readily available predictor of OSA for the prediction models.
Despite the epidemiological reports indicating that age, sex, and BMI are associated with OSA, an integrated predicting model using only these three attributes to assess OSA risk has not yet been developed. Advances in machine learning techniques have improved the ability of researchers and clinical applications to analyze massive amounts of data and develop appropriate diagnostic and predictive methods [24,25,26,27]. Several studies have applied machine learning algorithms to predict OSA risk. However, most of these studies have incorporated more complex parameters, such as sleep questionnaires [28,29,30], at-home PSG [15], cephalometric images [31], neck and waist circumference measurements [28,29,32,33], and facial-cervical measurements [28,32], into the predictive models.
In this context, our study used a large hospital-based sample of adults, allowing accurate comparison between none-to-mild and moderate-to-severe cases. The generated LR- and ANN-boosted models exhibited relatively high AUCs with adequate accuracy, sensitivity, PPV, and NPV, revealing the ability of these models to distinguish between the groups of interest, namely individuals with moderate-to-severe and none-to-mild OSA. Furthermore, our models used simple and easy-to-obtain parameters (age, sex, and BMI), which may provide a direction for developing predictive models under conditions of limited and constrained information.
Both LR and ANN are widely used models in biomedicine. This study's LR and ANN models achieved similar predictive validity in predicting OSA in patients undergoing PSG, which may be related to our data structure. ANN has the advantage of analyzing complex, multidimensional and nonlinear variables [34,35,36,37]. When the predictor-outcome relationships in the dataset are relatively simple and linear, LR using linear combinations of variables may achieve performance that approximates that of ANN [36,38]. This consideration was contextualized in the conclusion by Dreiseitl and Ohno-Machado [38] that "there is no single algorithm that performs better than all other algorithms on any given data set and application area." and also summarized by Sargent [34] that "both methods should continue to be used and explored in a complementary manner."
The present study has several limitations. First, in our cohort, the incidence of moderate-to-severe OSA was 62.8%, which is higher than the reported prevalence of OSA in the general population [4,19,20,39]. In clinical practice, patients referred for a PSG exam are usually expected to have OSA or another sleep disorder; therefore, the participant population in this study cannot be representative of the general population with a very low prevalence of OSA. Second, the data set used in this study was limited to a single center and included only Asian ethnic groups. Therefore, the trained model may not be generalizable beyond the institution or other ethnic groups [28,29]. Third, this retrospective observational study did not exclude undiagnosed medical conditions associated with OSA, such as neurological, cardiovascular, and pulmonary disorders, which may affect the model's predictive performance. Our model did not contain detailed anthropometric imaging or measurements, which may limit the model's ability to distinguish the disease-specific causes of OSA. Finally, the relatively low specificity for the models (57.0% and 56.9%) suggests a higher rate of false positives, meaning that a healthy person is more likely to receive an incorrect diagnosis of OSA using the proposed tool. As Jonas et al. [30] concluded, "There is uncertainty about the accuracy or clinical utility of all potential screening tools." a PSG to verify OSA severity and confirm the diagnosis is warranted for patients with clinically suspected sleep apnea.
Our study validated the diagnostic relevance of age, sex, and BMI for OSA. The generated LR- and ANN-based model effectively predicted OSA risk using these three simple parameters. Our results, therefore, may improve insights into OSA-related essential risk factors and provide knowledge to facilitate individualized risk stratification and formulate diagnostic decisions for sleep apnea.
This work was funded by the National Science and Technology Council (NSTC 111-2314-B-038-132-MY3) to CC Chung.
The authors declare there is no conflict of interest.
| [1] |
G. Albi, M. Burger, J. Haskovec, P. Markowich and M. Schlottbom, Continuum modeling of biological network formation, in Active Particles, Springer, 1 (2017), 1-48. doi: 10.1007/978-3-319-49996-3_1
|
| [2] |
C. Amitrano, A. Coniglio and F. Di Liberto, Growth probability distribution in kinetic aggregation processes, Phys. Rev. Lett., 57 (1986), 1016. doi: 10.1103/PhysRevLett.57.1016
|
| [3] |
A mathematical model of tumour-induced capillary growth. J. Theoret. Biol. (1985) 114: 53-73.
|
| [4] |
Stability and spectral convergence of fourier method for nonlinear problems: On the shortcomings of the 2/3 de-aliasing method. Numer. Math. (2015) 129: 749-782.
|
| [5] |
A. L. Bauer, T. L. Jackson and Y. Jiang, Topography of extracellular matrix mediates vascular morphogenesis and migration speeds in angiogenesis, PLoS Computational Biology, 5 (2009), e1000445, 18pp. doi: 10.1371/journal.pcbi.1000445
|
| [6] |
Trail formation based on directed pheromone deposition. J. Math. Biol. (2013) 66: 1267-1301.
|
| [7] |
S. C. Brenner and R. L. Scott, The Mathematical Theory of Finite Element Methods, vol. 15, Springer Science & Business Media, 2008. doi: 10.1007/978-0-387-75934-0
|
| [8] |
T. Büscher, A. L. Diez, G. Gompper and J. Elgeti, Instability and fingering of interfaces in growing tissue, New J. Phys., 22 (2020), 083005, 11pp. doi: 10.1088/1367-2630/ab9e88
|
| [9] |
Mathematical models for tumour angiogenesis: Numerical simulations and nonlinear wave solutions. Bull. Math. Biol. (1995) 57: 461-486.
|
| [10] |
Angiogenesis in cancer and other diseases. Nature (2000) 407: 249-257.
|
| [11] |
On the equations of landscape formation. Interfaces Free Bound. (2014) 16: 105-136.
|
| [12] |
Landscape evolution models: A review of their fundamental equations. Geomorphology (2014) 219: 68-86.
|
| [13] |
Kinetics of oxygen uptake by cells potentially used in a tissue engineered trachea. Biomaterials (2014) 35: 6829-6837.
|
| [14] |
G. Dahlquist and Å. Björck, Numerical Methods in Scientific Computing, Volume i, Society for Industrial and Applied Mathematics, 2008. doi: 10.1137/1.9780898717785
|
| [15] |
A cell-based model of extracellular-matrix-guided endothelial cell migration during angiogenesis. Bull. Math. Biol. (2013) 75: 1377-1399.
|
| [16] |
The weighted particle method for convection-diffusion equations, i, the case of an isotropic viscosity. Mathematics of computation (1989) 53: 485-507.
|
| [17] |
A deterministic approximation of diffusion equations using particles. SIAM J. Sci. Stat. Comput. (1990) 11: 293-310.
|
| [18] |
Y. Efendiev and T. Y. Hou, Multiscale finite element methods: Theory and applications, vol. 4, Springer Science & Business Media, 2009. doi: 10.1007/978-0-387-09496-0
|
| [19] |
Angiogenesis in gliomas: Biology and molecular pathophysiology. Brain pathology (2005) 15: 297-310.
|
| [20] |
Angiogenesis in cancer, vascular, rheumatoid and other disease. Nature Medicine (1995) 1: 27-30.
|
| [21] |
(2017) Basic Transport Phenomena in Biomedical Engineering.CRC press.
|
| [22] |
Fluid shear stress threshold regulates angiogenic sprouting. Proc. Natl. Acad. Sci. USA (2014) 111: 7968-7973.
|
| [23] |
B. Garipcan, S. Maenz, T. Pham, U. Settmacher, K. D. Jandt, J. Zanow and J. Bossert, Image analysis of endothelial microstructure and endothelial cell dimensions of human arteries-a preliminary study, Advanced Engineering Materials, 13 (2011), B54-B57. doi: 10.1002/adem.201080076
|
| [24] |
Tumor growth and neovascularization: An experimental model using the rabbit cornea. Journal of the National Cancer Institute (1974) 52: 413-427.
|
| [25] |
M. S. Gockenbach, Understanding and Implementing The Finite Element Method, Vol. 97, SIAM, 2006. doi: 10.1137/1.9780898717846
|
| [26] |
A computational study of the effect of capillary network anastomoses and tortuosity on oxygen transport. J. Theoret. Biol. (2000) 206: 181-194.
|
| [27] |
Spatio-temporal point process statistics: A review. Spat. Stat. (2016) 18: 505-544.
|
| [28] |
J. A. Grogan, A. J. Connor, J. M. Pitt-Francis, P. K. Maini and H. M. Byrne, The importance of geometry in the corneal micropocket angiogenesis assay, PLoS Computational Biology, 14 (2018), e1006049. doi: 10.1371/journal.pcbi.1006049
|
| [29] |
J. Haskovec, L. M. Kreusser and P. Markowich, Rigorous continuum limit for the discrete network formation problem, Comm. Partial Differential Equations, 44 (2019), 1159-1185. doi: 10.1080/03605302.2019.1612909
|
| [30] |
Mathematical analysis of a pde system for biological network formation. Comm. Partial Differential Equations (2015) 40: 918-956.
|
| [31] |
Notes on a pde system for biological network formation. Nonlinear Anal. (2016) 138: 127-155.
|
| [32] |
Laplacian growth as one-dimensional turbulence. Phys. D (1998) 116: 244-252.
|
| [33] |
Geometrical cluster growth models and kinetic gelation. Physics Reports (1986) 136: 153-224.
|
| [34] |
M 5 mesoscopic and macroscopic models for mesenchymal motion. J. Math. Biol. (2006) 53: 585-616.
|
| [35] |
D. Hu and D. Cai, Adaptation and optimization of biological transport networks, Phys. Rev. Lett., 111 (2013), 138701. doi: 10.1103/PhysRevLett.111.138701
|
| [36] |
Effects of shear stress on wound-healing angiogenesis in the rabbit ear chamber. Journal of Surgical Research (1997) 72: 29-35.
|
| [37] |
H. Kang, K. J. Bayless and R. Kaunas, Fluid shear stress modulates endothelial cell invasion into three-dimensional collagen matrices, American Journal of Physiology-Heart and Circulatory Physiology, 295 (2008), H2087-H2097. doi: 10.1152/ajpheart.00281.2008
|
| [38] |
Synergistic regulation of angiogenic sprouting by biochemical factors and wall shear stress. Cellular And Molecular Bioengineering (2011) 4: 547-559.
|
| [39] |
Hypoxia and the hypoxia-inducible-factor pathway in glioma growth and angiogenesis. Neuro-Oncology (2005) 7: 134-153.
|
| [40] |
Direct implicit large time-step particle simulation of plasmas. J. Comput. Phys. (1983) 51: 107-138.
|
| [41] |
Multiscale modelling and nonlinear simulation of vascular tumour growth. Journal of Mathematical Biology (2009) 58: 765-798.
|
| [42] |
Particle approximation of a linear convection-diffusion problem with neumann boundary conditions. SIAM Journal on Numerical Analysis (1995) 32: 1098-1125.
|
| [43] |
Mersenne twister: A 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Transactions on Modeling and Computer Simulation (TOMACS) (1998) 8: 3-30.
|
| [44] |
Mathematical modelling of dynamic adaptive tumour-induced angiogenesis: Clinical implications and therapeutic targeting strategies. J. Theoret. Biol. (2006) 241: 564-589.
|
| [45] |
A model for vein formation in higher plants. Proc. R. Soc. Lond. B (1980) 207: 79-109.
|
| [46] |
The polar transport of auxin and vein patterns in plants. Phil. Trans. R. Soc. Lond. B (1981) 295: 461-471.
|
| [47] |
Smoothed particle hydrodynamics. Annual Review of Astronomy and Astrophysics (1992) 30: 543-574.
|
| [48] | M. Müller, D. Charypar and M. Gross, Particle-based fluid simulation for interactive applications, in Proceedings of The 2003 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Eurographics Association, (2003), 154-159. |
| [49] | W. L. Murfee, Implications of fluid shear stress in capillary sprouting during adult microvascular network remodeling, Mechanobiology of the Endothelium, (2015), 166. |
| [50] |
The physiological principle of minimum work: I. the vascular system and the cost of blood volume. Proc. Natl. Acad. Sci. USA (1926) 12: 207-214.
|
| [51] | Tumor-induced neovascularization in the mouse eye. Journal of the National Cancer Institute (1982) 69: 699-708. |
| [52] |
Viscous fingering: An optimal bound on the growth rate of the mixing zone. SIAM Journal on Applied Mathematics (1997) 57: 982-990.
|
| [53] |
Angiogenesis and vascular remodelling in normal and cancerous tissues. J. Math. Biol. (2009) 58: 689-721.
|
| [54] |
Modelling cell migration strategies in the extracellular matrix. J. Math. Biol. (2009) 58: 511-543.
|
| [55] | First steps of tumor-related angiogenesis, laboratory investigation. A Journal of Technical Methods and Pathology (1991) 65: 334-346. |
| [56] |
J. Y. Park, J. B. White, N. Walker, C.-H. Kuo, W. Cha, M. E. Meyerhoff and S. Takayama, Responses of endothelial cells to extremely slow flows, Biomicrofluidics, 5 (2011), 022211. doi: 10.1063/1.3576932
|
| [57] |
Tumor-related angiogenesis. Critical Reviews in Oncology Hematology (1989) 9: 197-242.
|
| [58] |
Multiscale homogenization for fluid and drug transport in vascularized malignant tissues. Math. Models Methods Appl. Sci. (2015) 25: 79-108.
|
| [59] |
H. Perfahl, H. M. Byrne, T. Chen, V. Estrella, T. Alarcón, A. Lapin, R. A. Gatenby, R. J. Gillies, M. C. Lloyd, P. K. Maini, et al., Multiscale modelling of vascular tumour growth in 3d: The roles of domain size and boundary conditions, PloS One, 6 (2011), e14790. doi: 10.1371/journal.pone.0014790
|
| [60] |
Simple mechanical cues could explain adipose tissue morphology. J. Theoret. Biol. (2017) 429: 61-81.
|
| [61] |
Angiogenesis: A team effort coordinated by notch. Developmental cell (2009) 16: 196-208.
|
| [62] |
Stochastic model for dielectric breakdown. J. Stat. Phys. (1984) 36: 909-916.
|
| [63] |
S. Pillay, H. M. Byrne and P. K. Maini, Modeling angiogenesis: A discrete to continuum description, Phys. Rev. E, 95 (2017), 012410, 12pp. doi: 10.1103/physreve.95.012410
|
| [64] |
A. Pries, T. Secomb and P. Gaehtgens, Structural adaptation and stability of microvascular networks: Theory and simulations, American Journal of Physiology-Heart and Circulatory Physiology, 275 (1998), H349-H360. doi: 10.1152/ajpheart.1998.275.2.H349
|
| [65] |
Resistance to blood flow in microvessels in vivo. Circulation Research (1994) 75: 904-915.
|
| [66] |
P.-A. Raviart, An analysis of particle methods, in Numerical Methods in Fluid Dynamics, Springer, 1127 (1985), 243-324. doi: 10.1007/BFb0074532
|
| [67] |
Mechanisms of angiogenesis. Nature (1997) 386: 671-674.
|
| [68] | Reviewing models of auxin canalization in the context of leaf vein pattern formation in arabidopsis. The Plant Journal (2005) 44: 854-865. |
| [69] |
The penetration of a fluid into a porous medium or hele-shaw cell containing a more viscous liquid. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences (1958) 245: 312-329.
|
| [70] |
Tissue metabolism driven arterial tree generation. Medical Image Analysis (2012) 16: 1397-1414.
|
| [71] |
A review of mathematical models for the formation of vascular networks. J. Theoret. Biol. (2013) 333: 174-209.
|
| [72] |
T. W. Secomb, J. P. Alberding, R. Hsu, M. W. Dewhirst and A. R. Pries, Angiogenesis: An adaptive dynamic biological patterning problem, PLoS Computational Biology, 9 (2013), e1002983, 12pp. doi: 10.1371/journal.pcbi.1002983
|
| [73] |
The role of mechanical stresses in microvascular remodeling. Microcirculation (1996) 3: 143-165.
|
| [74] |
Interstitial flow and its effects in soft tissues. Annu. Rev. Biomed. Eng. (2007) 9: 229-256.
|
| [75] |
Oxygen consumption rate of tissue measured by a micropolarographic method. The Journal of general physiology (1966) 50: 317-335.
|
| [76] |
L. Tang, A. L. van de Ven, D. Guo, V. Andasari, V. Cristini, K. C. Li and X. Zhou, Computational modeling of 3d tumor growth and angiogenesis for chemotherapy evaluation, PloS One, 9 (2014), e83962. doi: 10.1371/journal.pone.0083962
|
| [77] |
R. D. Travasso, E. C. Poiré, M. Castro, J. C. Rodrguez-Manzaneque, and A. Hernández-Machado, Tumor angiogenesis and vascular patterning: A mathematical model, PloS One, 6 (2011), e19989. doi: 10.1371/journal.pone.0019989
|
| [78] |
On particle weighted methods and smooth particle hydrodynamics. Mathematical Models and Methods in Applied Sciences (1999) 9: 161-209.
|
| [79] |
Emergent vascular network inhomogeneities and resulting blood flow patterns in a growing tumor. Journal of Theoretical Biology (2008) 250: 257-280.
|
| [80] |
Vascular remodelling of an arterio-venous blood vessel network during solid tumour growth. Journal of Theoretical Biology (2009) 259: 405-422.
|
| [81] |
Dynamic measurement of human capillary blood pressure. Clinical Science (1988) 74: 507-512.
|
| [82] |
Coupled modeling of blood perfusion in intravascular, interstitial spaces in tumor microvasculature. Journal of Biomechanics (2008) 41: 996-1004.
|
| [83] |
Erythrocyte-derived sphingosine 1-phosphate is essential for vascular development. The Journal of Clinical Investigation (2014) 124: 4823-4828.
|
Figures(14) / Tables(2)
Pedro Aceves-Sanchez, Benjamin Aymard, Diane Peurichard, Pol Kennel, Anne Lorsignol, Franck Plouraboué, Louis Casteilla, Pierre Degond. A new model for the emergence of blood capillary networks[J]. Networks and Heterogeneous Media, 2021, 16(1): 91-138. doi: 10.3934/nhm.2021001
| Variables | Moderate-to-severe OSA (AHI ≥ 15) |
None-to-mild OSA (AHI < 15) |
p-value |
| n | 5, 920 | 3, 502 | |
| Age | 50.8 ± 13.5 | 46.6 ± 14.4 | < 0.0001 |
| Female, n (%) | 1266 (21.4) | 1652 (47.2) | < 0.0001 |
| Height (cm) | 167.2 ± 8.5 | 164.4 ± 8.9 | < 0.0001 |
| Weight (kg) | 79.7±16.1 | 66.1 ± 13.1 | < 0.0001 |
| BMI (kg/m2) | 28.4 ± 4.8 | 24.3 ± 3.8 | < 0.0001 |
| Polysomnography | |||
| Total recording time (min) | 366.6±11.9 | 367.8±13.4 | < 0.0001 |
| Total sleep time (min) | 275.8±60.2 | 281.4±61.1 | < 0.0001 |
| Sleep efficiency (%) | 75.2±16.4 | 76.5±16.5 | 0.0002 |
| Non-REM sleep (min) | 240.6±51.7 | 242.2±51.3 | 0.133 |
| REM sleep (min) | 35.2±22.5 | 39.1±23.7 | < 0.0001 |
| AHI | 44.7±23.8 | 6.4±4.5 | < 0.0001 |
| SO2 mean (%) | 94.5±2.6 | 96.6±1.3 | < 0.0001 |
| Data are expressed as mean ± standard deviation. The p-value represents the comparison between the AHI ≥ 15 and AHI < 15 groups. | |||
DownLoad:
CSV
| Unadjusted Model | Adjusted Model | |||
| Variables | OR | 95% CI | OR | 95% CI |
| Age | 1.02*† | 1.02-1.03 | 1.04*† | 1.04-1.05 |
| Female | 0.30* | 0.28-0.33 | 0.28* | 0.25-0.32 |
| BMI | 1.27*† | 1.25-1.28 | 1.27*† | 1.26-1.29 |
| The odds ratio (OR) and 95% confidence intervals (CI) represent the association between the variables and the presence of moderate-to-severe OSA (AHI ≥ 15). *p < 0.0001; †Odds ratio of per unit changes. | ||||
DownLoad:
CSV
| Variable | Testing set 1 | Testing set 2 | Testing set 3 | Testing set 4 | Testing set 5 | Independent validation set | p-value |
| n | 1466 | 1465 | 1466 | 1465 | 1466 | 2094 | |
| AHI≥15, n (%) | 920 (62.8) | 919 (62.7) | 920 (62.8) | 919 (62.7) | 920 (62.8) | 1322 (63.1) | 1.000 |
| Age | 49.0 ± 0.4 | 49.0 ± 0.4 | 49.9 ± 0.4 | 49.1 ± 0.4 | 49.0 ± 0.4 | 49.3 ± 0.3 | 0.503 |
| Female, n (%) | 483 (33.0) | 438 (29.9) | 472 (32.2) | 445 (30.4) | 431 (29.4) | 649 (31.0) | 0.266 |
| BMI (kg/m2) | 26.9 ± 4.9 | 26.9 ± 4.9 | 26.9 ± 5.0 | 26.9 ± 5.0 | 26.8 ± 4.8 | 26.9 ± 4.9 | 0.973 |
| The p-value represents the multiple comparisons across the five testing and the independent validation sets. | |||||||
DownLoad:
CSV
| Variables | Moderate-to-severe OSA (AHI ≥ 15) |
None-to-mild OSA (AHI < 15) |
p-value |
| n | 5, 920 | 3, 502 | |
| Age | 50.8 ± 13.5 | 46.6 ± 14.4 | < 0.0001 |
| Female, n (%) | 1266 (21.4) | 1652 (47.2) | < 0.0001 |
| Height (cm) | 167.2 ± 8.5 | 164.4 ± 8.9 | < 0.0001 |
| Weight (kg) | 79.7±16.1 | 66.1 ± 13.1 | < 0.0001 |
| BMI (kg/m2) | 28.4 ± 4.8 | 24.3 ± 3.8 | < 0.0001 |
| Polysomnography | |||
| Total recording time (min) | 366.6±11.9 | 367.8±13.4 | < 0.0001 |
| Total sleep time (min) | 275.8±60.2 | 281.4±61.1 | < 0.0001 |
| Sleep efficiency (%) | 75.2±16.4 | 76.5±16.5 | 0.0002 |
| Non-REM sleep (min) | 240.6±51.7 | 242.2±51.3 | 0.133 |
| REM sleep (min) | 35.2±22.5 | 39.1±23.7 | < 0.0001 |
| AHI | 44.7±23.8 | 6.4±4.5 | < 0.0001 |
| SO2 mean (%) | 94.5±2.6 | 96.6±1.3 | < 0.0001 |
| Data are expressed as mean ± standard deviation. The p-value represents the comparison between the AHI ≥ 15 and AHI < 15 groups. | |||
| Unadjusted Model | Adjusted Model | |||
| Variables | OR | 95% CI | OR | 95% CI |
| Age | 1.02*† | 1.02-1.03 | 1.04*† | 1.04-1.05 |
| Female | 0.30* | 0.28-0.33 | 0.28* | 0.25-0.32 |
| BMI | 1.27*† | 1.25-1.28 | 1.27*† | 1.26-1.29 |
| The odds ratio (OR) and 95% confidence intervals (CI) represent the association between the variables and the presence of moderate-to-severe OSA (AHI ≥ 15). *p < 0.0001; †Odds ratio of per unit changes. | ||||
| Variable | Testing set 1 | Testing set 2 | Testing set 3 | Testing set 4 | Testing set 5 | Independent validation set | p-value |
| n | 1466 | 1465 | 1466 | 1465 | 1466 | 2094 | |
| AHI≥15, n (%) | 920 (62.8) | 919 (62.7) | 920 (62.8) | 919 (62.7) | 920 (62.8) | 1322 (63.1) | 1.000 |
| Age | 49.0 ± 0.4 | 49.0 ± 0.4 | 49.9 ± 0.4 | 49.1 ± 0.4 | 49.0 ± 0.4 | 49.3 ± 0.3 | 0.503 |
| Female, n (%) | 483 (33.0) | 438 (29.9) | 472 (32.2) | 445 (30.4) | 431 (29.4) | 649 (31.0) | 0.266 |
| BMI (kg/m2) | 26.9 ± 4.9 | 26.9 ± 4.9 | 26.9 ± 5.0 | 26.9 ± 5.0 | 26.8 ± 4.8 | 26.9 ± 4.9 | 0.973 |
| The p-value represents the multiple comparisons across the five testing and the independent validation sets. | |||||||
