Crystalline evolutions in chessboard-like microstructures

1.   Introduction

We are concerned with the asymptotic behavior of motions of planar curves according to the law

where $v$ is the normal velocity, $\kappa $ is the crystalline curvature, $g\colon\mathbb{R}^2\to \mathbb{R}$ is a periodic forcing term, with average $\bar g$, and $\varepsilon>0$ is a small parameter which takes account the frequency of oscillation.

Crystalline evolutions provide simplified models for describing several phenomena in Materials Science (see [25,27,28] and references therein) and have been significantly studied in recent years (see for instance [1,4,5,16,17,18,21,22]).

The forcing term $g$ models a rapidly oscillating heterogeneous medium and, in the homogenization limit $\varepsilon \to 0$, the oscillations of the medium affect the velocity of the evolving front. The geometric motion (1) corresponds to the gradient flow of the energy

where we identify the evolving curve with the boundary of a set $E$. Since the volume term converges to $\bar g\, \mathcal{L}(E)$ as $\varepsilon \to 0$, the $\Gamma$-limit of the functionals $F_\varepsilon$ (see [7]) is given by

Hence, our analysis can be set in a large class of variational evolution problems dealing with limits of motions driven by functionals $F_\varepsilon$ depending on a small parameter.

For oscillating functionals like $F_\varepsilon$, the energy landscape of the energies can be quite different from that of their $\Gamma$-limit, and the related motions can be influenced by the presence of local minima which may give rise to pinning phenomena, or to effective homogenized velocities (see [26,2,10,8]). In the case of geometric motions, a general understanding of the effects of microstructure is still missing. Recently, some results have been obtained for two-dimensional crystalline energies, for which a simpler description can be given in terms of a system of ODEs (see for instance [9,10,11,12,13]).

Coming back to our specific problem (1), we assume for simplicity that $g$ takes only two values $\alpha <0 <\beta$, its periodicity cell is $[0, 1]^2$, and that $\bar g = \frac{\alpha+\beta}{2}$. We also assume that $g$ has a chessboard structure, as specified in (2) below.

After a careful analysis, it turns out that curves evolving by (1) undergo a microscopic "facet-breaking" phenomenon at a scale $\varepsilon$, with small segments of length proportional to $\varepsilon$ being created and, in some cases, subsequently reabsorbed. The macroscopic effect of this behavior is a "pinning effect" for the limit evolution, corresponding to the possible onset of new edges, with slope of 45 degrees and zero velocity (depending on the initial set and on the values $\alpha, \, \beta$). On the other hand, the horizontal and the vertical edges always travel with the asymptotic velocity $\kappa + \bar g$. We thus obtain a characterization of the limit evolution, which is the main result of this paper, and is stated precisely in Theorems 4.5 and 4.6.

We point out that, due to the possible presence of these new edges with zero velocity, the limit flow does not coincide with the gradient flow of the limit functional $\overline{F}$, which is simply given by $v = \kappa + \bar g$.

We recall that, in a previous paper [11], we considered a similar homogenization problem where the periodic function g depends only on the horizontal variable, so that the medium has a stratified, opposite to a chessboard-like, structure.

It would be very interesting to extend our analysis to the isotropic variant of (1), where the crystalline curvature $\kappa$ is replaced by the usual curvature of the evolving curve, so that (1) becomes a forced curvature flow. However, as such evolution cannot be described in terms of a system of ODEs, different techniques would be needed (partial results in this direction can be found in [15,14]).

The plan of the paper is the following: in Section 2 we introduce the notion of crystalline curvature and the evolution problem we are interested in. In Section 3 we introduce the notion of calibrable edge, that is, an edge which does not break during the evolution, and we state the calibrability conditions. Finally, in Section 4 we characterize explicitly the limit evolution as $\varepsilon \to 0$, for initial data which are squares (Theorem 4.5) and more generally rectangles (Theorem 4.6).

2.   Setting of the problem

Notation.The canonical basis of $\mathbb{R}^2$ will be denoted by $e_1 = (1, 0)$, $e_2 = (0, 1)$.

The 1-dimensional Hausdorff measure and the 2-dimensional Lebesgue measure in $\mathbb{R}^2$ will be denoted by $\mathcal{H}^1$ and $\mathcal{L}$, respectively.

We say that a set $E\subseteq \mathbb{R}^2$ is a Lipschitz set if its boundary $\partial E$ can be written, locally, as the graph of a Lipschitz function (with respect to a suitable orthogonal coordinate system). The outward normal to $\partial E$ at $\xi$, that exists $\mathcal{H}^1$-almost everywhere on $\partial E$, will be denoted by $\ne = (\nu_1^E, \nu_2^E)$.

The Hausdorff distance between two sets $E, \ F\in \mathbb{R}^2$ will be denoted by $d_H(E, F)$.

The crystalline curvature.We briefly recall a notion of curvature $\kappa^E$ on $\partial E$ which is consistent with the requirement that a geometric evolution $E(t)$, reducing as fast as possible the energy

has normal velocity $\kappa^{E(t)}$ $\mathcal{H}^1$-almost everywhere on $\partial E(t)$.

The surface tension $\varphi^\circ(x, y) = |x|+|y|$ is the polar function of the convex norm $\varphi(x, y) = \max\{|x|, |y|\}$, $(x, y)\in\mathbb{R}^2$, so that $P_\varphi(E)$ turns out to be the perimeter associated to the anisotropy $\varphi(x, y)$, that is, the Minkowski content obtained by considering $(\mathbb{R}^2, \varphi)$ as a normed space. The sets $\{\varphi(\xi)\leq 1\}$ and $\{\varphi^\circ(\xi)\leq 1\}$ are the square $K = [-1, 1]^2$, and the square with corners at $(\pm 1, 0)$ and $(0, \pm 1)$, respectively.

Given a nonempty compact set $E\subseteq \mathbb{R}^2$, we denote by $d^E$ the oriented $\varphi$-distance function to $\partial E$, negative inside $E$, that is

The normal cone at $\xi\in\partial E$ is well defined whenever $\xi$ is a differentiability point for $d^E$, and it is given by $T_{\varphi^\circ}\bigl(\nabla d^E(\xi)\bigr)$, where

The notion of intrinsic curvature in $(\mathbb{R}^2, \varphi)$ is based on the existence of regular selections of $T_{\varphi^\circ}\bigl(\nabla d^E\bigr)$ on $\partial E$.

Definition 2.1 ($\varphi$-regular set, Cahn-Hoffmann field, $\varphi$-curvature). We say that a set $E\subseteq \mathbb{R}^2$ is $\varphi$-regular if $\partial E$ is a compact Lipschitz curve, and there exists a vector field $n_\varphi\in {\rm{Lip}}(\partial E;\mathbb{R}^2)$ such that $n_\varphi \in T_{\varphi^\circ}(\nabla d^E)$ $\mathcal{H}^1$-almost everywhere on $\partial E$.

Any selection of the multivalued function $T_{\varphi^\circ}(\nabla d^E)$ on $\partial E$ is called a Cahn-Hoffmann vector field for $\partial E$, and $\kappa = {\rm{div}} n_\varphi$ is the related $\varphi$-curvature (or crystalline curvature) of $\partial E$.

Remark 1 (Edges and vertices). A direct computation gives that $T_{\varphi^\circ}(\xi^\circ)$ is a singleton if $\varphi^\circ(\xi^\circ) = 1$, and $\xi^\circ$ is not a coordinate vector. Moreover one gets

(Here and in the following $\left[\!\left[ {{\xi, \eta}} \right]\!\right]$ is the closed segment joining the vectors $\xi$ and $\eta$). We will deal with $\varphi$-regular sets $E$ whose boundary is the union of a finite number of maximal closed arcs with the property that $T_{\varphi^\circ}(\nabla d^E)$ is a fixed set $T_A$ in the interior of each arc $A$. This set $T_A$ is either a singleton, if the arc $A$ is not a horizontal or vertical segment, or one of the closed convex cones described above. The maximal arcs of $\partial E$ which are straight horizontal or vertical segments will be called edges, and the endpoints of every arc will be called vertices of $\partial E$.

The requirement of Lipschitz continuity keeps the value of every Cahn-Hoffmann vector field fixed at vertices. Hence, in order to exhibit a Cahn-Hoffmann vector field $n_\varphi$ on $\partial E$ it is enough to construct a field $n_A\in {\rm{Lip}}(A;\mathbb{R}^2)$ on each arc $A$, with the correct values at the vertices, and satisfying the constraint $n_A \in T_A$. In what follows, with a little abuse of notation, we shall call $n_A$ the Cahn-Hoffmann vector field on the arc $A$.

Forced crystalline flows. Let $\alpha < 0 < \beta$, and let $g\in L^\infty(\mathbb{R}^2)$ be the function defined almost everywhere in $[0, 1]^2$ by

and extended by periodicity in $\mathbb{R}^2$. For $\varepsilon >0$, let $g_{\varepsilon}(x, y) = g(\frac{x}{\varepsilon }, \frac{y}{\varepsilon })$.

We will denote by $\mathcal{A}_\varepsilon $ (resp. $\mathcal{B}_\varepsilon $) the union of all closed squares $Q$ of side length $\varepsilon /2$ such that $g_\varepsilon = \alpha$ (resp. $g_\varepsilon = \beta$) in the interior of $Q$. The set of discontinuity points of $g_\varepsilon $ will be denoted by $\Xi $. A discontinuity line is a straight line contained in $\Xi $.

We define the multifunction $G_{\varepsilon}$ in $\mathbb{R}^2$, by setting $G_{\varepsilon} = [\alpha, \beta]$ on $\Xi $, and $G_{\varepsilon}(x, y) = \{g_\varepsilon (x, y)\}$ in $\mathbb{R}^2\setminus \Xi $.

We want to introduce our notion of geometric evolution $E(t)$, obeying to the law

where $v$ is the normal velocity, and $\kappa$ is the crystalline curvature on $\partial E(t)$.

In order to give a meaning to (3) it would be enough to require that the evolution is a family of $\varphi$-regular sets. Nevertheless, as underlined in Remark 1, even if $E$ is a $\varphi$-regular set, the crystalline curvature on $\partial E$ may not be uniquely determined, due to the infinitely many choices for the Cahn-Hoffmann vector field on the edges of $\partial E$.

This ambiguity can be overcome introducing an additional postulate, which is consistent with the notion of forced curve shortening flow (see [4], [5], [6], [23], [24]).

Definition 2.2 (Variational Cahn-Hoffmann field). A variational Cahn-Hoffmann vector field for a $\varphi$-regular set $E$ is a Cahn-Hoffmann vector field $n$ on $\partial E$ such that for every edge $L$ of $\partial E$ not lying on a discontinuity line of $g_\varepsilon $, the restriction $n_{L}$ of $n$ on $L$ is the unique minimum of the functional

in the set

where $p$, $q$ are the endpoints of $L$ and $n_0$, $n_1$ are the values at $p$, $q$ assigned to every Cahn-Hoffmann vector field (see Remark 1).

Remark 2. If the minimum $n_{L}$ in $D_L$ of the functional $\mathcal{N}_{L}$ satisfies the strict constraint $n_{L}(\xi)\in {\rm{int}} T_{L}$ for every $\xi\in L$, then the velocity $g_\varepsilon +{\rm{div}} n_{L}$ is constant along the edge, that is the flat arc remains flat under the evolution. This is always the case for non-forced crystalline flows, since the unique minimum is the interpolation of the assigned values at the vertices of $L$, and the constant value of the $\varphi$-curvature is given by

where $\ell$ is the length of the edge $L$ and $\chi_{L}$ is a convexity factor: $\chi_{L} = 1, -1, 0$, depending on whether $E(t)$ is locally convex at $L$, locally concave at $L$, or neither.

Definition 2.3 (Forced crystalline evolution). Given $T>0$, we say that a family $E(t)$, $t\in [0, T[$, is a forced crystalline curvature flow (or forced crystalline evolution) in $[0, T[$ if

(ⅰ) $E(t)\subseteq\mathbb{R}^2$ is a Lipschitz set for every $t\in [0, T[$;

(ⅱ) there exists an open set $A\subseteq \mathbb{R}^2\times [0, T[$ such that $\bigcup_{t\in [0, T[}\partial E(t)\times \{t\}\subseteq A$, and the function $d(\xi, t)\doteq d^{E(t)}(\xi)$ is locally Lipschitz in $A$;

(ⅲ) there exists a function $n \in L^\infty(A, \mathbb{R}^2)$, with ${\rm{div}} n\in L^\infty(A)$, such that the restriction of $n(t, \cdot)$ to $\partial E(t)$ is a variational Cahn-Hoffmann vector field for $\partial E(t)$ for almost every $t\in [0, T[$;

(ⅳ) $\partial_t d-{\rm{div}} n \in G_\varepsilon $ $\mathcal{H}^1$-almost everywhere in $\partial E(t)$ and for almost every $t\in[0, T[$.

3.   Calibrability conditions

In this section we deal with the minimum problem in Definition 2.2 for a given $\varphi$-regular set $E$, and we characterize the edges of $\partial E$ having constant velocity $v_L: = \kappa^L+g_\varepsilon $.

The results concern edges $L\in \partial E$ not lying on a discontinuity line of the forcing term, in such a way that $g_\varepsilon $ is defined $\mathcal{H}^1$-almost everywhere on $L$. We will use the notation $L = [p, q]\times \{y\}$ or $L = \{x\} \times [p, q]$, with $x, y \not\in \frac{\varepsilon}{2}\mathbb{Z}$, so that $\ell = q-p$.

Setting by $n\colon \mathbb{R} \to [-1, 1]$ the unique varying component of the variational Cahn-Hoffmann vector field on $L$ (recall Remark 1), the assigned values of $n$ are the following:

Moreover, we denote by $\gamma_\varepsilon \colon \mathbb{R} \to \mathbb{R}$ the restriction of $g_\varepsilon $ on the straight line containing $L$, and we distinguish two different type of discontinuity points for $\gamma_\varepsilon $:

With this notation, the requirement that $\kappa+g_\varepsilon $ is constant on $L$ can be rephrased in the following 1D problem.

Definition 3.1 (Calibrability conditions). $L$ is a calibrable edge of $\partial E$ if and only if there exists a Lipschitz function $n\colon [p, q]\to \mathbb{R}$ such that the following hold.

(ⅰ) $n$ satisfies (4).

(ⅱ) $|n|\leq 1$ in $[p, q]$.

(ⅲ) $\displaystyle n'+\gamma_\varepsilon = \chi_L\frac{2}{\ell}+ \frac{1}{\ell} \int_p^q \gamma_\varepsilon (s) \, ds$ a.e. in $[p, q]$.

In this case, we say that $v_L = n'+\gamma_\varepsilon $ is the (normal) velocity of the edge $L$.

The calibrability property was studied, in its full generality, in [11]. We collect here the results needed in the rest of the paper, sketching the proofs for sake of completeness.

Denoting by $\ell_{\alpha}$, $\ell_{\beta}\in [0, \varepsilon/2]$ the non-negative lengths given by the conditions

the calibrability condition in Definition 3.1(ⅲ) sets the value of $n'$ outside the jump set of $\gamma_\varepsilon$:

so that $n$ needs to be

where $v_L$ is the feasible velocity of the edge $L$

In conclusion, the calibrability conditions (ⅰ) and (ⅲ) in Definition 3.1 fix a candidate field (7) which is continuous and affine with given slope in each phase of $\gamma_\varepsilon$. This field $n$ is the Cahn-Hoffman field which calibrates $L$ with velocity (8) if and only if it also satisfies the constraint $|n(x)| \leq 1$ for every $x\in [p, q]$.

Remark 3. In what follows we will assume $0 <\varepsilon < \dfrac{8}{\beta-\alpha}$ in such a way that the small perturbation $\chi_L\dfrac{2}{\ell}+ \dfrac{\beta-\alpha}{2\ell}(\ell_\beta -\ell_\alpha)$ has the same sign of the curvature term $\chi_L\dfrac{2}{\ell}$.

Proposition 3.2. Let $L$ be an edge with zero $\varphi$-curvature, and let $n_0\in \{\pm 1\}$ be the given value of the Cahn-Hoffmann vector field at the endpoints of $L$. Then the following hold.

(i) If $\ell = \ell_\alpha+\ell_\beta < \varepsilon$, $L$ is calibrable with velocity $ v_L = \dfrac{\alpha \ell_{\alpha}+\beta \ell_{\beta}}{\ell_\alpha+\ell_\beta} $ if and only if

(ia) $n_0 = 1$, and either $\gamma_\varepsilon(p) = \beta$, $\gamma_\varepsilon(q) = \alpha$, or $L$ has an endpoint on $\mathcal{I}_{\alpha, \beta}$;

(ib) $n_0 = -1$, and either $\gamma_\varepsilon(p) = \alpha$, $\gamma_\varepsilon(q) = \beta$, or $L$ has an endpoint on $\mathcal{I}_{\beta, \alpha}$.

(ii) If $\ell\geq \varepsilon$, $L$ is calibrable with velocity $ v_L = \dfrac{\alpha+\beta}{2} $ if and only if

(iia) $n_0 = 1$, and $p, q \in \mathcal{I}_{\alpha, \beta}$;

(iib) $n_0 = -1$, and $p, q \in \mathcal{I}_{\beta, \alpha}$.

Proof. If $n_0 = 1$ the Cahn-Hoffman vector field $n$ needs to be neither increasing near $p$ nor decreasing near $q$. This occurs only if $L$ is the union of three consecutive segments $L = L_\beta \cup L_c \cup L_\alpha$, with endpoints in $p$, $p+\ell_\beta \in \mathcal{I}_{\beta, \alpha}$, $q-\ell_\alpha \in \mathcal{I}_{ \beta, \alpha}$, and $q$. If $L_c = \emptyset$, then the candidate field (7) always satisfied the constraint in Definition3.1(ⅱ), proving (ⅰ).

If $L_c\neq\emptyset$, from (7) we get

and hence, since $n(p) = n(q) = 1$, the constraint $|n|\leq 1$ is not satisfied if $\ell_\alpha \neq \ell_\beta$. Finally, if $\ell_\alpha = \ell_\beta$, then, by (6)

and a Canh-Hoffmann vector field with this derivative exists only if $\ell_\alpha = \ell_\beta = \varepsilon/2$, otherwise $ n(p+\ell_\beta+\varepsilon/2)>1. $ In conclusion, $L$ is calibrable with velocity $v_L = (\alpha+\beta)/2$ if and only if $p, q\in \mathcal{I}_{\alpha, \beta}$.

The case $n_0 = -1$ follows from similar arguments.

Proposition 3.3. Let $L$ be an edge with positive $\varphi$-curvature. If either

or $p\in \mathcal{I}_{\beta, \alpha}$, $q \in \mathcal{I}_{\alpha, \beta}$, then $L$ is calibrable with velocity $v_L$ given by (8).

Proof. Under the assumption (9), the candidate Cahn-Hoffmann vector field (7) is an increasing function in $[p, q]$. Hence the constraint in Definition 3.1(ⅱ) is fulfilled, and $L$ is calibrable.

Assume now that $p\in \mathcal{I}_{\beta, \alpha}$, and $q \in \mathcal{I}_{\alpha, \beta}$. Then the edge has $n(p) = -1$, $n(q) = 1$, $\ell_\alpha = \varepsilon/2$, and $\ell_\beta = 0$. Then, by (6), the candidate Cahn-Hoffmann field (7) is increasing in $[p, p+\varepsilon/2]$, and, by Remark 3,

Similarly, we obtain that $n$ satisfies the constraint in $[q-\varepsilon, q]$, and hence $|n|\leq 1$ on $L$, so that $L$ is calibrable with velocity $v_L$.

Remark 4. Notice that, if $L$ satisfies the condition (9), then

Proposition 3.4. Let $L$ be an edge with positive $\varphi$-curvature, and such that $\ell+\ell_\alpha-\ell_\beta > 4/(\beta-\alpha)$. Then the following hold.

(i) If either $\gamma_\varepsilon (p) = \beta$, or $\gamma_\varepsilon (q) = \beta$, or $p\in \mathcal{I}_{\alpha, \beta}$, or $q\in \mathcal{I}_{\beta, \alpha}$, then $L$ is not calibrable.

(ii) If $\gamma_\varepsilon (p) = \gamma_\varepsilon (q) = \alpha$, let $\sigma_1$, $\sigma_2\in ]0, \varepsilon/2[$ be such that $p+\varepsilon/2+\sigma_1 \in \mathcal{I}_{\beta, \alpha}$ and $q-\varepsilon/2-\sigma_2 \in \mathcal{I}_{\alpha, \beta}$, and let $\tilde{\ell}$ be the length of the interval $[p+\varepsilon/2+\sigma_1, q-\varepsilon/2-\sigma_2]$. Setting

and

we have $m\in ]0, 1[$, $\Sigma \cap [0, \varepsilon/2]^2 \neq \emptyset$, and $L$ is calibrable with velocity

if and only if $(\sigma_1, \sigma_2)\in \Sigma$.

(iii) if $\gamma_\varepsilon(p)=\alpha$, and $q\in \mathcal{I}_{\alpha, \beta}$ (resp. $p\in \mathcal{I}_{\beta, \alpha}$, and $\gamma_\varepsilon(q)=\alpha$), let $\sigma\in ]0, \varepsilon/2[$ be such that $p+\sigma+\varepsilon/2\in \mathcal{I}_{\beta, \alpha}$ (resp. $q-\sigma-\varepsilon/2\in \mathcal{I}_{\alpha, \beta}$), let $\ell^*$ be the length of the interval $[p+\varepsilon/2+\sigma, q]$ (resp. of $[p, q-\varepsilon/2-\sigma]$), and let

Then $L$ is calibrable if and only if $\sigma \geq \sigma^*$.

Proof. If $\ell+\ell_\alpha-\ell_\beta > 4/(\beta-\alpha)$, by (6) the candidate Cahn-Hoffmann field $n$ is strictly decreasing in the $\beta$ phase. Hence, under the assumptions in (ⅰ), $n$ does not satisfy the constraint $|n|\leq 1$ at least near an endpoint, and $L$ is not calibrable.

If both the endpoints belong to the $\alpha$ phase, then the requirement $(\sigma_1, \sigma_2)\in\Sigma$ is equivalent to the conditions

that guarantee the calibrability of the edge.

Setting

we have that $(\tilde{\sigma}, \tilde{\sigma})\in \Sigma$, and $\tilde{\sigma}\in ]0, \varepsilon/2[$ under the assumption $\ell+\ell_\alpha-\ell_\beta > 4/(\beta-\alpha)$.

The proof of (ⅲ) follows by the same arguments.

Remark 5 (Calibrability threshold). In the special case when $\sigma_1 = \sigma_2 = \sigma>0$, the calibrability condition stated in Proposition 3.4(ⅱ) reduces to the unilateral constraint $\sigma\geq \tilde{\sigma}$, where $\tilde{\sigma}$ is the value defined in (10). Hence $L$ is calibrable if and only if $\sigma\geq \tilde{\sigma}$. Moreover, if $\sigma = \tilde{\sigma}$, the edge $L$ is calibrated by a Cahn-Hoffmann vector field $n$ such that $n(p) = n(p+\varepsilon/2+\tilde{\sigma})$ and $n(q) = n(q-\varepsilon/2-\tilde{\sigma})$. As a consequence, the same field calibrates both the edges $[p, p+\varepsilon/2+\tilde{\sigma}]\times \{y\}$ and $[q-\varepsilon/2-\tilde{\sigma}, q]\times \{y\}$ (as edges with zero $\varphi$-curvature, see Proposition 3.2), and the edge $[p+\varepsilon/2+\tilde{\sigma}, q-\varepsilon/2-\tilde{\sigma}]\times \{y\}$ (as edges with positive $\varphi$-curvature, see Proposition 3.3) with the same velocity.

Similarly, in the case of Proposition 3.4(ⅲ), when $\sigma = \sigma^*$, the edge $L$ is calibrated by a Cahn-Hoffmann vector field $n$ such that $n(p) = n(p+\varepsilon/2+\sigma^*)$, and the same field calibrates both the edge $[p, p+\varepsilon/2+\sigma^*]\times \{y\}$ (as edge with zero $\varphi$-curvature), and the edge $[p+\varepsilon/2+\tilde{\sigma}, q]\times \{y\}$ (as edges with positive $\varphi$-curvature) with the same velocity.

4.   Forced crystalline flows and their effective motion

The results of Section 3 prescribe a velocity to every calibrable edge not lying on a discontinuity line of $g_\varepsilon $, and suggest that the forced crystalline curvature flow starting from a coordinate polyrectangle (that is a set whose boundary is a closed polygonal curve with edges parallel to the coordinate axes) remains a coordinate polyrectangle, whose structure changes when either existing edges disappear by the growth of their neighbors, or new edges are generated by the splitting of no longer calibrable edges.

In every time interval between these events, the motion is determined by a system of ODEs, and hence the behavior of the evolution on the discontinuities can be described using the general theory of differential equations with discontinuous right-hand side [20].

Concerning the changes of geometry, it is clear what is meant by "disappearing edges", that is edges whose length becomes zero in finite time, but the notion of "appearing edges", that is how a no longer calibrable edge breaks, has to be specified.

We focus our attention to coordinate polyrectangles whose edges have non-negative $\varphi$-curvature. In the sequel we will use the abuse of notation $L = [p, q]$ when the edge $L$ is of the form $L = [p, q]\times \{y\}$ or $L = \{x\} \times [p, q]$, and $n(p)$, $n(q)$ will denote the prescribed values of the Cahn-Hoffman vector field at the endpoints of $L$ (see (4)).

Definition 4.1 (Cracking multiplicity and set-up). If $L$ is an edge not lying on a discontinuity line of $g_\varepsilon $, let us define

and let us denote by $L^- = [p, p_b]$, $L^+ = [q_b, q]$, with the convention $L^- = \emptyset$ (resp. $L^+ = \emptyset$) if $p = p_b$ (resp. $q = q_b$). The cracking multiplicity $M(L)$ assigned to $L$ is given by

The points $p_b$, $q_b$, if different from the endpoints of $L$, are said breaking points of $L$, and $\mathcal{C}(L): = \{p, p_b, q_b, q\}$ is the cracking set-up of $L$.

For every edge $L$ lying on a discontinuity line of $g_\varepsilon $, with (inner) normal $\nu(L)$, consider the values

If $v_L^{in}> 0$ and $v_L^{out} <0 $, then we set $M(L)\in \{1, M(L+\frac{\varepsilon }{4}\nu(L)), M(L-\frac{\varepsilon }{4}\nu(L))\}$. Otherwise, the cracking multiplicity $M(L)$ assigned to $L$ is given by

When $M(L) = M(L\pm\frac{\varepsilon }{4}\nu(L))$, the cracking set-up of $L$ is set as $\mathcal{C}(L): = \mathcal{C}(L\pm\frac{\varepsilon }{4}\nu(L))$.

Proposition 4.2. Let $L = [p, q]$ be an edge not lying on a discontinuity line of $g_\varepsilon $, and let $\mathcal{C}(L): = \{p, p_b, q_b, q\}$ the cracking set-up of $L$. Then $L^-$ and $L^+$ are either empty, or calibrable as edges with zero $\varphi$-curvature and prescribed Cahn-Hoffman vector field $n(p) = n(p_b)$, and $n(q_b) = n(q)$, respectively. Moreover, denoting by $v^\pm, v^c$ the velocities of $L^\pm, L^c$ respectively, then

(i) $p_b\in \mathcal{I}_{\beta, \alpha}$, $q_b \in \mathcal{I}_{\alpha, \beta, }$, and $v^\pm>v^c$, if $L$ has positive $\varphi$-curvature;

(ii) $p_b, q_b\in \mathcal{I}_{\beta, \alpha}$, and $v^->v^c>v^+$, if $L$ has zero $\varphi$-curvature, and $n(p) = -1$;

(iii) $p_b, q_b\in \mathcal{I}_{\alpha, \beta}$, and $v^- <v^c <v^+$, if $L$ has zero $\varphi$-curvature, and $n(p) = 1$;

Proof. Let $L = [p, q]$ be an edge with positive $\varphi$-curvature. By Propositions 3.3 and 3.4, if $L^c \neq L$ then $\ell+\ell_\alpha-\ell_\beta > 4/(\beta-\alpha)$, and

Moreover, by Proposition 3.2, $L^- = [p, p_b]\subseteq L$ is either empty or calibrable as edge with zero $\varphi$-curvature and prescribed Cahn-Hoffmann $n_0 = -1$ at the endpoints. Similarly $L^+ = [q_b, q]\subseteq L$ is either empty or calibrable as edge with zero $\varphi$-curvature and prescribed Cahn-Hoffmann $n_0 = -1$ at the endpoints.

Concerning the velocities, assume that $p\neq p_b$. If either $\gamma_\varepsilon (p) = \beta$ or $p\in \mathcal{I}_{\alpha, \beta}$, we have $v^- = \beta > v^c$, by Remark 4. If $\gamma_\varepsilon (p) = \alpha$, then, by Proposition 3.2(ⅰ),

with $0 <\sigma <\sigma_0$, where $\sigma_0$ is such that $v(\sigma_0) = v^c$ (see also Remark 5). The inequality $v^->v^c$ then follows from the fact that the function $v(\sigma)$ is strictly monotone decreasing. The same arguments can be used for $v^+$ in the case $q_b\neq q$.

Recalling Proposition 3.2, we can perform a similar splitting for edges with zero $\varphi$-curvature. If $q-p\geq \varepsilon $, then, if $n(p) = n(q) = 1$, we have

while, if $n(p) = n(q) = -1$, we have

In both cases the remaining parts $L^\pm$ are either empty or calibrable with velocities

for suitable $\sigma_\alpha^\pm, \sigma_\beta^\pm \in [0, \varepsilon /2]$. Since $v^c = \frac{\alpha+\beta}{2}$, the strict inequalities in (ii) and (iii) hold true.

The case of $L$ with zero $\varphi$-curvature and $q-p < \varepsilon $ is similar and is left to the reader. We would like to stress that the edges of this type appearing as $L^\pm$, due to the cracking set-up, are always calibrable.

Definition 4.3 (Breaking configuration). Let $E$ be a coordinate polyrectangle whose edges $\tilde{L}_1, \ldots, \tilde{L}_n$ have non-negative $\varphi$-curvature. For every $i = 1, \ldots, n$, let $\mathcal{C}(L_i) = \{p_i, p_{i, b}, q_{i, b}, q_{i}\}$ be a cracking set-up of the edge $\tilde{L}_i$. The breaking configuration of $\partial E$ associated to $\{\mathcal{C}(\tilde{L}_i)\}_{i = 1}^n$ is given by $L_1, \ldots, L_m$, $m = \sum_{i = 1}^n M(\tilde{L}_i)$, where $L_j$ is either a part of and edge $\tilde{L}_i$ obtained by the splitting procedure in Definition 4.1, or a degenerate segment with legth zero at a cracking point $p_{i, b}$ or $q_{i, b}$.

Remark 6. By Proposition 4.2, a breaking configuration of the boundary of a coordinate polyrectagle $E$, whose edges have non-negative $\varphi$-curvature always exists. Moreover, since the cracking multiplicity and set-up of an edge $L$ is unambiguous except in the case $v_L^{in}> 0$ and $v_L^{out} <0 $, the breaking configuration is unique, provided that no edge $L\subseteq \partial E$ has $v_L^{in}> 0$ and $v_L^{out} <0 $.

The following result shows that, in our setting, the evolution is well posed.

Proposition 4.4. Let $E$ be a coordinate polyrectangle whose edges have non-negative $\varphi$-curvature, and let $L_1, \ldots, L_m$ a breaking configuration of $\partial E$. Then there exists $T>0$ and a family $E(t)$, $t\in [0, T]$ of coordinate polyrectangles with edges $L_1(t), \ldots, L_{m}(t)$ which is a forced crystalline flow starting from $E$. If, in addition, every $L_i$ with positive length and lying on a discontinuity line of $g_\varepsilon $ satisfies one of the following properties

(1) $v^{in}_{L_i} \leq 0$, and $v^{out}_{L_i} \geq 0$,

(2) $v^{in}_{L_i}> 0$ and $v^{out}_{L_i} \geq 0$,

(3) $v^{in}_{L_i}\leq 0$ and $v^{out}_{L_i} < 0$,

then the evolution is unique. Moreover if $L_i$ satisfies condition (1), then $L_i(t)$ is pinned until $v^{in}_{L_i(t)}\leq 0$ and $v^{out}_{L_i(t)}\geq 0$.

Proof. A given coordinate polyrectangle $E$, with edges $\tilde{L}_1, \ldots, \tilde{L}_n$ ordered clockwise, is completely determined by the strings $(\tilde{\nu}_1, \ldots, \tilde{\nu}_n)$ and $(\tilde{s}_1, \ldots, \tilde{s}_n)$, where $\tilde{\nu}_i$ and $\tilde{s}_i$ are the inner normal vector and the distance from the origin of the line containing the edge $L_i$, $i = 1, \ldots, n$, respectively.

Let us denote $e_1 = e_5 = (1, 0)$, $e_2 = (0, 1)$, $e_3 = (-1, 0)$, and $e_4 = e_0 = (0, -1)$, so that if $\tilde{\nu}_i = e_j$, then $\tilde{\nu}_{i+1} \in \{e_{j-1}, e_{j+1}\}$.

We associate to $E$ a breaking configuration $(\nu_1, \ldots, \nu_m)$, $(s_1, \ldots, s_m)$ based on the cracking set-up of its edges in the following way.

If $M(L_1) = 1$, then $\nu_1 = \tilde{\nu}_1$ and $s_1 = \tilde{s}_1$. If $M(L_1) = 3$, $q_{1, b} = q_1$, and $\nu_1 = e_j$ then $(\nu_1, \nu_2, \nu_3) = (e_j, e_{j+1}, e_j)$ and $(s_1, s_2, s_3) = (\tilde{s}_1, p_{1, b}, \tilde{s}_1)$. Similarly, if $M(L_1) = 3$, $p_{1, b} = p_1$, and $\nu_1 = e_j$ then $(\nu_1, \nu_2, \nu_3) = (e_j, e_{j-1}, e_j)$ and $(s_1, s_2, s_3) = (\tilde{s}_1, q_{b, 1}, \tilde{s}_1)$. Finally, if $M(L_1) = 5$, then $(\nu_1, \nu_2, \nu_3, \nu_4, \nu_5) = (e_j, e_{j+1}, e_j, e_{j-1}, e_j)$ and $(s_1, s_2, s_3, s_4, s_5) = (\tilde{s}_1, p_{1, b}, \tilde{s}_1, q_{1, p}, \tilde{s}_1)$. The subsequent elements of the strings are obtained applying the same procedure to $L_2$, and so forth.

By Definition 2.3, a forced crystalline flow $E(t)$, $t\in [0, T]$, given by calibrable coordinate polyrectangles with edges $L_1(t), \ldots, L_m(t)$ and with normal direction $(\nu_1, \ldots, \nu_m)$, is then identified with a solution $s(t) = (s_1(t), \ldots, s_m(t))$ to the system of ODEs

where $V \colon \mathbb{R}^m \to \mathbb{R}^m$ is the field, discontinuous on

and defined outside $\Sigma$ by

Notice that the fictitious edges with zero length, possibly added in the breaking configuration of $E$, are contained on discontinuity lines of $g_\varepsilon $. Then either $E$ is calibrable, or it corresponds to a string $s\in\Sigma$.

System (12) fits therefore into Filippov's theory of discontinuous dynamical systems (see [20], [19]): the field $V$ is extended on $\Sigma$ by the multifunction

(where we denote by $\text{co}(A)$ the convex envelope of a set $A$) and a solution of (12) is, by definition, a solution of the differential inclusion $s'\in F(V)(s)$. Since $V\colon \mathbb{R}^m \to \mathbb{R}^m$ is measurable and essentially bounded, then there exists at least a solution of such a differential inclusion, starting from any initial datum $s$.

In order to deal with the uniqueness of solutions, we need an explicit computation of the multifunction $F(V)$ on $\Sigma$.

For every $s \in \Sigma$, and for every component $s_i$ of $s$ such that $s_i\in \frac{\varepsilon }{2}\mathbb{Z}$, and $s_{i-1}\neq s_{i+1}$, so that $\ell_i(s)>0$, let $V_i^+(s)$ and $V_i^-(s)$ be the values

and let $I(V_i^-(s), V_i^+(s))$ be the interval with endpoints $V_i^-(s)$ and $V_i^+(s)$.

For every $i = 1, \ldots, m$, $V_i(s)$ depends only on $s_{i-1}$, $s_{i}$, and $s_{i+1}$, and it is discontinuous only in the $s_{i}$ variable, then $F(V)(s)$ in (13) is the convex set

where

Assume now that every element of the breaking configuration of $\partial E$ with positive length satisfies one of the conditions (1), (2), (3).

Concerning the edges with zero length, notice that if $L_i(t)$ is an edge starting from $L_i$ with $\ell_i = 0$, then $\ell_i(t)>0$ and $v^{in}_{L_i(t)} = \alpha$, $v^{out}_{L_i(t)} = \beta$ for $t>0$ small enough, so that the edge $L_i(t)$ fulfills (1). Hence we can split the indices $\{1, \ldots, m\} = \mathcal{N}_1\cup\mathcal{N}_2\cup\mathcal{N}_3$ in such a way $L_i(t)$ satisfies (j) for every $i\in \mathcal{N}_j$, locally near $t = 0$.

Let $s^0$ be the string corresponding to the breaking configuration of $\partial E$, let $E(t)$ be any evolution obtained by solving the differential inclusion (12) with initial datum $s(0) = s^0$, and let $\overline{t}\in ]0, T]$ be such that $L_i(t)$ satisfies (j) in $]0, \overline{t}[$ for every $i\in \mathcal{N}_j$, $j = 1, 2, 3$. The family $E(t)$ is then identified with $s(t) = (s_1(t), \ldots, s_m(t))$ solving $s_i'(t)\in I_i(s(t))$ a.e. in $]0, \overline{t}[$, $i = 1, \dots, m$.

Then, for every $i\in \mathcal{N}_1$, we have that $s_i'(s_i-s_i(0)) \leq 0$ for every choice of $s_i'(t)\in I_i(s(t)) = I(V_i^-(s(t)), V_i^+(s(t)))$, and hence $s_i' = 0$ in $]0, \overline{t}[$. (see, e.g., [20] Corollary 2.10.2).

On the other hand, for every $i\in \mathcal{N}_2\cup \mathcal{N}_3$, then either $s_i'>0$ or $s_i' < 0$ in $]0, \overline{t}[$, and hence $s_i'(t) = V_i(s(t))$ a.e. in $]0, \overline{t}[$.

In conclusion, since the function $V$ is Lipschitz continuous outside $\Sigma$, the solution of the differential inclusion is unique in $]0, \overline{t}[$, and it is fully determined by the law

In terms of the breaking configuration of $\partial{E}$, we can conclude that every edge $L_i$, with $i\in \mathcal{N}_2\cup \mathcal{N}_3$ crosses immediately the discontinuity line, moving inward (respectively outward) if $i\in \mathcal{N}_2$ (respectively $i\in \mathcal{N}_3$), while every edge $L_i$ with $i\in \mathcal{N}_1$ is pinned on the discontinuity line.

Remark 7. As a consequence of Proposition 4.4, if $\alpha+\beta <0$, for every $\varepsilon >0$ there are nontrivial equilibria of the forced crystalline curvature flow. For example, a calibrable coordinate polyrectangle $E$ such that

(a) every vertex of $E$ is also a vertex of a square $Q \in \mathcal{A}_\varepsilon $, $Q\subseteq E$,

(b) every edge of $\partial E$ with zero $\varphi$-curvature has length $\ell = \varepsilon /2$,

(c) every edge of $\partial E$ with positive $\varphi$-curvature has length $\ell$ very closed to $-4/(\alpha+\beta)$,

is pinned. Namely, requirement (a) implies that every edge of $\partial E$ lies on a discontinuity line, (b) guarantees that $v^{in}_L = \alpha$ and $v^{out}_L = \beta$ for every edge $L$ with zero $\varphi$-curvature, while (c) guarantees that

for every edge $L$ with positive $\varphi$-curvature.

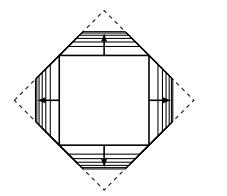
In particular, the symmetric equilibria $O_\varepsilon $ (see Figure 1) converge, as $\varepsilon \to 0$ to an octagon $O$ having horizontal and vertical edges with length $\ell = -4/(\alpha+\beta)$, connected by diagonal edges.

In conclusion, the forced crystalline evolutions defined in Definition 2.3 and starting from a polyrectangle are obtained by the following procedure: we set-up the initial datum and we obtain the evolution $E(t)$ by solving the system of ODEs (12), for $t\in [0, T]$, where $T>0$ is the first time when an edge either disappears or is no more calibrable. The subsequent evolution is obtained by initializing $E(T)$ according to Definition 4.1 as an initial datum for the new system of ODEs of the form (12).

We are interested in stressing the macroscopic effect of the underling periodic structure on the geometric evolutions, depicting clearly the forced crystalline flows and passing to the limit as $\varepsilon \to 0$, and the most of the features are revealed by the evolution starting from the simplest crystals: the coordinate squares.

In what follows $S(\ell)$ will denote a coordinate square with side length $\ell>0$.

Theorem 4.5 (Effective motion of coordinate squares). Let $S(\ell_0)$ be a given coordinate square. For every $\varepsilon >0$, let $S(\ell_0^\varepsilon )$ be a coordinate square such that $ d_H(S(\ell_0), S(\ell_0^\varepsilon )) <\varepsilon. $ Then there exists a forced crystalline curvature flow $E^\varepsilon (t)$, $t\in [0, T[$, starting from $S(\ell_0^\varepsilon )$. Moreover, there exists a family of sets $E(t)$, $t\in [0, T[$, such that $E^\varepsilon (t)$ converges to $E(t)$ in the Hausdorff topology and locally uniformly in time, as $\varepsilon \to 0$. The limit evolution $E(t)$ is independent of the choice of the approximating initial data $S(\ell_0^\varepsilon )$, but its geometry depends on $\ell_0$ in the following way.

(i) If either $\alpha+\beta\geq 0$, or $\alpha+\beta <0$ and $0 <\ell_0\leq -4/(\alpha+\beta)$, then $E(t)$ is a family of coordinate squares $E(t) = S(\ell(t))$, with $\ell(t)$ governed by the ODE

and then shrinking to a point in finite time.

(ii) If $\alpha+\beta <0$ and $\ell_0> -4/(\alpha+\beta)$, then $E(t)$ is a family of octagons $E(t) = S(\ell_0)^\circ \cap S(\tilde{\ell}(t))$, where $S(\ell_0)^\circ$ is the polar square of $S(\ell_0)$, and $\tilde{\ell}(t)$ is the solution to (14). In particular, the moving edges of $E(t)$ have length governed by the ODE

and then $E(t)$ is increasing in $[0, +\infty[$, and converging to a stationary octagon as $t\to +\infty$.

Proof. Given $S(\ell_0)$ and $\varepsilon >0$, let $S(\ell_0^\varepsilon )$ be a square such that $ d_H(S(\ell_0), S(\ell_0^\varepsilon )) <\varepsilon. $

Case (ia): $\ell_0 \leq 4/(\beta-\alpha)$ (self-similar shrinking).

By Proposition 3.3, the breaking configuration of $\partial S(\ell_0^\varepsilon )$ has no breaking points, and, by Remark 4 either $v_L^{in}, v_L^{out}> 0$, if $L\subseteq \partial S(\ell_0^\varepsilon )$ is on a discontinuity line of $g_\varepsilon $, or $v_L> 0$, otherwise. Then, by Remark 6, and Proposition 4.4, there exists a unique forced crystalline flow $E^\varepsilon (t)$ starting from $S(\ell_0)$, and it is given by calibrable squares $S(\ell^\varepsilon (t))$ with side length governed by the ODE

Since $|\ell_\beta^\varepsilon -\ell_\alpha^\varepsilon |\leq \varepsilon /2$, a passage to the limit in (16) as $\varepsilon \to 0$ shows that $E^\varepsilon (t)$ converges in the Hausdorff topology and locally uniformly in time to the family of squares $S(\ell(t))$ with side length governed by the ODE (14).

Case (ib): either $\ell_0> 4/(\beta-\alpha)$ (if $\alpha+\beta\geq 0$), or $4/(\beta-\alpha) < \ell_0 \leq -4/(\alpha+\beta)$ (if $\alpha+\beta < 0$) (shrinking with temporary breaking).

As a first step, we assume, in addition, that every vertex of $S(\ell_0^\varepsilon )$ is also a vertex of a square $Q \in \mathcal{A}_\varepsilon $, $Q\subseteq S(\ell_0^\varepsilon )$ (see Figure 2(Ⅰ)), so that the edges lie on discontinuity lines of $g_\varepsilon $ and they have (the same) velocities $v_{0, \varepsilon }^{in}$, $v_{0, \varepsilon }^{out}\geq 0$. Hence, by Definition 4.1 and Proposition 3.3, we have

and, by Proposition 4.4, there exists a unique forced crystalline flow starting from $S(\ell_0^\varepsilon )$, given by squares $S(\ell^\varepsilon (t))$ with side length governed by the ODE (16), and defined in $]0, t_0[$ where

(see Figure 2(Ⅱ)). By symmetry, the breaking set-up of every edge of $E(t_0) = S(\ell^\varepsilon (t_0))$ is the same, and it is given by Proposition 4.2(ⅰ). More precisely, every edge $L^\varepsilon _i(t_0)$ has cracking multiplicity $M(L^\varepsilon _i(t_0)) = 5$, and set-up $\mathcal{C}(L^\varepsilon _i(t_0)) = \{p_i, p_{i, b}, q_{i, b}, q_i\}$ with

where $\tilde{\sigma}$ is the calibrability threshold defined in (10). Moreover, by Remark 5, using the notation of Proposition 4.2, we have $L^\varepsilon _i(t_0) = L_i^+\cup L_i^c \cup L_i^-$, and $v^+ = v^- = v^c$.

Then, by Proposition 4.4, the evolution admits a unique extension $E^\varepsilon (t)$, given by polyrectangles with 20 edges, and defined for $t\in ]t_0, t_1[$, where $t_1$ is the first time when an edge of $E^\varepsilon (t)$ touches a discontinuity line of $g_\varepsilon $. By symmetry, the evolution in $]t_0, t_1[$ is fully depicted by its behavior near a vertex of $S(\ell^\varepsilon (t_0))$ (see Figure 2(Ⅲ)): pinned edges with zero $\varphi$-curvature are generated in the normal direction of the edges of $S(\ell^\varepsilon (t_0))$ at the breaking points, while the edges parallel to the edges of $S(\ell^\varepsilon (t_0))$ move inward. More precisely, the edges with positive $\varphi$-curvature move inward with constant velocity

while the small edges with zero $\varphi$-curvature move inward with velocity $v_{\pm}^\varepsilon (t)>v_c^\varepsilon$, and reach a discontinuity line at time $t_1$ (see Figure 2(Ⅳ)). Every edge of $S(\ell^\varepsilon (t_1))$ lying on a discontinuity line of $g_\varepsilon $ has zero $\varphi$-curvature, and $v^{in} = \alpha$, $v^{out} = \beta$, and, by Proposition 4.4, there exists a unique extension of the evolution after $t_1$, given by polyrectangles with pinned edges with zero $\varphi$-curvature, and moving edges with positive $\varphi$-curvature. If we denote by $t_2$ the first time when those edges reach the discontinuity lines, in such a way that $E^\varepsilon (t_2)$ becomes again a square $S(\ell_0^\varepsilon -2\varepsilon )$, then we have

where $k$ is a constant independent of $\varepsilon $, and hence the evolution recomposes the square in a time lapse of order $\varepsilon $ (see Figure 2(Ⅴ)).

Since $E^\varepsilon (t_2)$ is a square with every vertex which is also a vertex of a square $Q \in \mathcal{A}_\varepsilon $, $Q\subseteq S(\ell_0^\varepsilon )$, the (unique) evolution then either iterates this "breaking and recomposing" motion, if $\ell^\varepsilon (t_2) = \ell_0^\varepsilon -2\varepsilon > 4/(\beta-\alpha)$, or it is a family of shrinking squares, if $\ell^\varepsilon (t_2)\leq 4/(\beta-\alpha)$. In any case, $E^\varepsilon (t)$ can be approximate, in the Hausdorff topology and locally uniformly in time, by a family of squares with side length satisfying (16), so that the limit motion as $\varepsilon \to 0$ is a family of squares $S(\ell(t))$ governed by the evolution law (14).

Moreover, for every square $S(\ell_0^\varepsilon )$ such that $ d_H(S(\ell_0), S(\ell_0^\varepsilon )) <\varepsilon$, the forced crystalline evolution generates and absorbs the small edges near its corners in slightly different ways, but it can be always approximated by a family of squares with side length satisfying (16). In particular, the limit evolution does not depend on the choice of the approximating data.

Case (ⅱ): $\alpha+\beta <0$, and $\ell_0 > -4/(\alpha+\beta)$ (confinement).

If every vertex of $S(\ell_0^\varepsilon )$ is also a vertex of a square $Q \in \mathcal{A}_\varepsilon $, $Q\subseteq S(\ell_0^\varepsilon )$ (see Figure 3(Ⅰ)), then the edges of the square lie on discontinuity lines of $g_\varepsilon $, and they have the same velocities $v_{0, \varepsilon }^{in}$, $v_{0, \varepsilon }^{out} <0$. Hence, by Definition 4.1 and Proposition 3.3, we have

and, by Proposition 4.2, every edge of $S(\ell_0^\varepsilon )$ is split as $L^\varepsilon _i = L_i^+\cup L_i^c \cup L_i^-$ with $v^{in}_{\pm} = \alpha$, $v^{out}_{\pm} = \beta$, and $v_c^{in}, v_c^{out} <0$. Then, by Proposition 4.4, there exists a unique forced crystalline flow starting from $S(\ell_0^\varepsilon )$ (see Figure 3(Ⅱ)), producing small pinned corners having edges with zero $\varphi$-curvature and length $\varepsilon /2$, while the long edges with positive $\varphi$-curvature move outward with constant velocity $v_c$ given by (17) until they reach, the next discontinuity line (see Figure 3(Ⅲ)).

Then the process iterates, "cutting" the square and reducing the length $\ell^\varepsilon (t)$ of the edges with positive $\varphi$-curvature, so that their (piecewise constant) velocity is given by

until the first time $t_0$ when $|v^\varepsilon (t_0)+4/(\alpha+\beta)| <\varepsilon $. By Proposition 4.4 (see also Remark 7) every edge of $E^\varepsilon (t)$ is pinned for $t>t_0$. In conclusion, if we denote by $E(t)$ the family of octagons $E(t) = S(\ell_0)^\circ \cap S(\tilde{\ell}(t))$, where $S(\ell_0)^\circ$ is the polar square of $S(\ell_0)$, and $\tilde{\ell}(t)$ is the solution to (14), we have $d_H(E^\varepsilon (t), E(t))\leq c \varepsilon $, so that $E^\varepsilon (t)$ converges to $E(t)$ in the Hausdorff topology and locally uniformly in time, as $\varepsilon \to 0$.

Finally, notice that the forced crystalline evolution starting from a general initial datum $S(\ell_0^\varepsilon )$, with $ d_H(S(\ell_0), S(\ell_0^\varepsilon )) <\varepsilon$, reaches a configuration of the type depicted in Figure 3(Ⅲ) in a time span of order $\varepsilon $. Then the macroscopic limit $E(t)$ does not depend on the choice of the approximating initial datum, and it is the effective motion of the square $S(\ell_0)$.

The arguments used in the proof of Theorem 4.5 can be applied to deal with every polyrectangle (and hence, by approximation, to describe the effective evolution of general sets), but a detailed analysis of the forced crystalline flow in these cases requires considerable additional computations. Just to appreciate the application of the previous arguments in a slightly more general setting, we devote the end of this section to a coincise description of the motion starting from coordinate rectangles.

In what follows $R(\ell_1, \ell_2)$ will denote a coordinate rectangle with side lengths $\ell_1, \ell_2>0$. Having already characterized the evolution of a square, without loss of generality we can assume that $\ell_{1, 0}>\ell_{2, 0}$.

Theorem 4.6 (Effective motion of coordinate rectangles). Let $R(\ell_{1, 0}, \ell_{2, 0})$ be a given coordinate rectangle. For every $\varepsilon >0$, let $R(\ell_{1, 0}^\varepsilon , \ell_{2, 0}^\varepsilon )$ be a coordinate rectangle such that $ d_H(R(\ell_{1, 0}, \ell_{2, 0}), R(\ell_{1, 0}^\varepsilon , \ell_{2, 0}^\varepsilon )) <\varepsilon $. Then there exists a forced crystalline curvature flow $E^\varepsilon (t)$, $t\in [0, T[$, starting from $R(\ell_{1, 0}^\varepsilon , \ell_{2, 0}^\varepsilon )$. Moreover, there exists a family of sets $E(t)$, $t\in [0, T[$, such that $E^\varepsilon (t)$ converges to $E(t)$ in the Hausdorff topology and locally uniformly in time, as $\varepsilon \to 0$. The limit evolution $E(t)$ is independent of the choice of the approximating initial data $R(\ell_{1, 0}^\varepsilon , \ell_{2, 0}^\varepsilon )$, but its geometry depends on the values

in the following way.

(i) If $v_{i, 0}\geq 0$, $i = 1, 2$, then $E(t)$ is a family of rectangles $E(t) = R(\ell_{1}(t), \ell_{2}(t))$ with $\ell_i(t)$ governed by the system of ODEs

(ii) If either $v_{i, 0} < 0$, $i = 1, 2$, or $v_{1, 0} < 0$, $v_{2, 0}\geq 0$ and $v_{1, 0}+v_{2, 0}\leq 0$, then $E(t)$ is a family of octagons $E(t) = Q(R(\ell_{1, 0}, \ell_{2, 0})) \cap R(\tilde{\ell}_{1}(t), \tilde{\ell}_{2}(t))$, where $Q(R(\ell_{1, 0}, \ell_{2, 0}))$ is the rotated square touching from outside $R(\ell_{1, 0}, \ell_{2, 0})$ at its vertices, and $(\tilde{\ell}_1, \tilde{\ell}_2)$ is the solution to (18). In particular, the lengths of the moving edges of $E(t)$ are governed by the system of ODEs

(iii) If $v_{1, 0} <0$, $v_{2, 0}\geq 0$ and $v_{1, 0}+v_{2, 0}> 0$, then there exists $T>0$ such that, for $t\in [0, T[$, $E(t)$ is a family of rectangles $E(t) = R(\ell_{1}(t), \ell_{2}(t))$ with $\ell_i(t)$ governed by the system of ODEs (18). If $T = +\infty$, then $E(t)$ converges to an equilibrium (either a point or the square $S(-4/(\alpha+\beta))$) for $t\to +\infty$. If $T <+\infty$, $E(t)$, $t\geq T$, is the family of octagons following the rules of case (ii).

Proof. When either $v_{i, 0}\geq 0$, or $v_{i, 0} < 0$, $i = 1, 2$, the proof is very similar to the one of Theorem 4.5, hence we address our attention to initial data with $v_{1, 0} < 0$ and $v_{2, 0}\geq 0$ (mixed case).

Assume that every vertex of the approximating initial datum $R(\ell_{1, 0}^\varepsilon , \ell_{2, 0}^\varepsilon )$ is also a vertex of a square $Q \in \mathcal{A}_\varepsilon $, $Q\subseteq R(\ell_{1, 0}^\varepsilon , \ell_{2, 0}^\varepsilon )$. By symmetry, it is enough depict the evolution of two contiguous edges $L^\varepsilon _1$ (horizontal) and $L^\varepsilon _2$ (vertical) starting as in Figure 5. We have that $v^{in}_{L^\varepsilon _1}, v^{out}_{L^\varepsilon _1}\leq 0$, so that

while $v^{in}_{L^\varepsilon _2}, v^{out}_{L^\varepsilon _2}\geq 0$, and

Therefore the forced evolution starts breaking the edge $L_1^\varepsilon $, and generating small pinned edges with zero $\varphi$-curvature (see Figure 5(Ⅱ)). The edges with positive curvature move with constant velocities $v_1^\varepsilon $ (outward) and $v_2^\varepsilon $ (inward).

Setting

the subsequent evolution depends on the sign of $U_0 = U(\ell_{1, 0}, \ell_{1, 0})$ (note that $\alpha+\beta <0$ in this case).

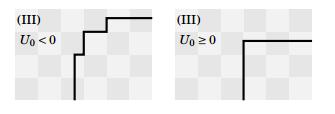
If $U_0 < 0$, so that $v_{2}^\varepsilon < -v_{1}^\varepsilon $, the small pinned edges with zero $\varphi$-curvature and "slope 45 degrees" are not absorbed (see Figure 6, left), and the evolution "cuts the vertices". On the other hand, the edges with positive $\varphi$-curvature move with velocities

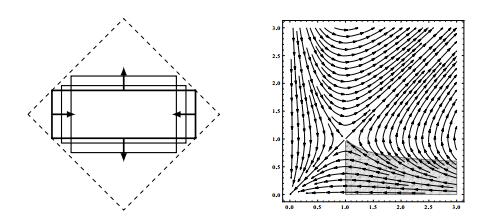
Then, the effective evolution $E(t)$, in the limit $\varepsilon \to 0$, is given by the family of octagons whose moving edges have lengths $(\ell_{1}(t), (\ell_{2}(t))$ solution to (19). Since the level set $\{U\leq 0\}$ is invariant under the flow of the ODEs system (19), $E(t)$ are octagons (not monotonically) converging to a stationary octagon as $t \to +\infty$ (see Figure 7).

If $U_0 = 0$, then in a time-lapse of order $\varepsilon $ the evolution becomes a rectangle with the same features of the initial datum, but with $U_0^\varepsilon <0$. Then the effective evolution is the one depicted above.

If $U_0> 0$, then the effective evolution maintains the rectangular shape for a short time (see Figure 8, left). Namely, the forced crystalline flow becomes a rectangle after a time lapse of order $\varepsilon $ (see Figure 6), and then the geometric motion $E^\varepsilon (t)$ is given by "almost rectangles", that is rectangles with small perturbations of order $\varepsilon$ near the vertices, until the lengths of the edges with positive $\varphi$-curvature have velocities $v_{2}^\varepsilon (t)> -v_{1}^\varepsilon (t)$. Hence there exists $T>0$ such that $E^\varepsilon (t)$ it can be approximated, in the Hausdorff topology and locally uniformly in $[0, T]$, by a family of rectangles $R(\ell_1^\varepsilon (t), \ell_2^\varepsilon (t))$ satisfying

Passing to the limit as $\varepsilon \to 0$, we obtain a family of rectangles $E(t) = R(\ell_1(t), \ell_2(t))$, $t\in [0, T]$ where $(\ell_1, \ell_2)$ is the solution of the system of ODEs (18) with initial datum in the set

Notice that the function

is a constant of motion for system (18). The phase portrait is shown in Figure 8. In particular, $A$ is not a positively invariant set for the system, and the behavior of the trajectories depends on the energy level $J(\ell_{1, 0}, \ell_{2, 0})$ of the initial datum.

The level set $\{J = 0\}$ is positively invariant in $A$, so that, if $J(\ell_{1, 0}, \ell_{2, 0}) = 0$, the effective evolution is given by rectangles converging, as $t\to +\infty$, to the equilibrium square $S(-4/(\alpha+\beta))$.

If $J(\ell_{1, 0}, \ell_{2, 0})<0$, then there exists a unique $t_0>0$ such that $\ell_1'(t_0) = -4/(\alpha+\beta)$, and the effective evolution for $t>t_0$ is the one shown in case (i): rectangles shrinking to a point in finite time.

If $J(\ell_{1, 0}, \ell_{2, 0})>0$, then the solution enters in the region $\{U \leq 0\}$ in finite time, so that the effective evolution becomes a family of octagons, converging to a stationary octagon in infinite time.

5.   Final remarks

The geometric evolution in Definition 2.3 provides a possible mathematical model for the interface motion in a variety of material science problems. Our setting fits, for example, with the description of growth (or dissolution) of a crystal, whose structure manifests itself in the dependency of the interfacial energy density $\varphi^\circ$, evolving in a heterogeneous medium (see for instance [28,25]).

In previous papers [1,3,22] the assumption that every facet of the crystal moves parallely to itself during the evolution facilitates the description of the motion, and leads to a system of ODEs satisfied by the lengths of the facets.

In our model the underlying microstructure is oscillating between two phases $\alpha <0$ (facilitating the growth of the crystal) and $\beta>0$ (facilitating the reduction of the crystal). In Theorems 4.7 and 4.8 we show that this microstructure repeatedly leads to changes of geometry of the interface, even if the evolution starts from very simple crystals (square or rectangular shapes). In particular, during the motion, edges can appear or disappear, and the evolution cannot be described by a system of ODEs.

Our results shows that, in this simple setting, the effective motion of the interface, obtained as a limit as $\varepsilon \to 0$ of the crystalline evolutions with oscillating forcing term, is not in general a forced crystalline evolution.

Acknowledgments

The authors wish to thank Andrea Braides for useful discussions on the topic of this paper. The second author was partially supported by the Italian CNR-GNAMPA and by the University of Pisa via grant PRA-2017 "Problemi di ottimizzazione e di evoluzione in ambito variazionale".