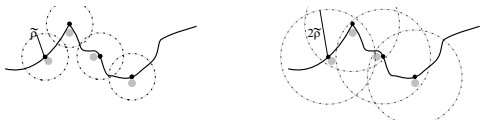Interior regularity to the steady incompressible shear thinning fluids with non-Standard growth

1.   Introduction

Let $ {\bf{p}}(\omega)\subset{\mathbb{R}^{d}} $ be a stationary ergodic connected random open set with random variable $ \omega $ and let $ {\varepsilon} > 0 $ be the smallness parameter. The concept of stationary ergodic random open sets was introduced in detail in Part I ^[5], and we will give a simplified version below, which focuses on the properties used in the present Part III.

For a bounded open domain $ {\bf{Q}} $, we then consider $ {\bf{p}}^{{\varepsilon}}(\omega) = {\varepsilon}{\bf{p}}(\omega) $, $ {\bf{Q}}_{{\bf{p}}}^{{\varepsilon}}(\omega): = {\bf{Q}}\cap{\bf{p}}^{{\varepsilon}}(\omega) $ and $ \Gamma^{{\varepsilon}}(\omega): = {\bf{Q}}\cap\partial{\bf{p}}^{{\varepsilon}}(\omega) $ with outer normal $ \nu_{\Gamma^{{\varepsilon}}(\omega)} $. In order to simplify notation, we keep in mind that $ {\bf{p}} $ and $ {\bf{Q}}_{{\bf{p}}}^{{\varepsilon}} $ are random variables and drop the explicit writing of $ \omega $.

Denoting $ W_{0, \partial{\bf{Q}}}^{1, p}({\bf{Q}}_{{\bf{p}}}^{{\varepsilon}}): = \left\{ u\in W^{1, p}({\bf{Q}}_{{\bf{p}}}^{{\varepsilon}}):\, u|_{\partial{\bf{Q}}}\equiv0\right\} $ one would classically be interested in a family of extension operators $ {\mathcal{U}}_{{\varepsilon}}:\, W_{0, \partial{\bf{Q}}}^{1, p}({\bf{Q}}_{{\bf{p}}}^{{\varepsilon}})\to W^{1, p}({\bf{Q}}) $ such that for some $ C $ independent from $ {\varepsilon} $ it holds

However, estimates of the form Eq (1.1) are known to exist only for (global) John domains but from Part I we know that even random Lipschitz domains are mostly not (globally) John. We recall the definition of a John domain and refer to Figure 1 for an illustration of issues arising in the context of infinite random geometries:

Definition (John domains). A bounded domain $ {\bf{P}}\subset{\mathbb{R}^{d}} $ is a John domain if there exists $ {\varepsilon}, \delta > 0 $ s.t. for every $ x, y\in{\bf{P}} $ with $ \left|x-y\right| < \delta $ there exists a rectifiable path $ \gamma:\, [0, 1]\to{\bf{P}} $ from $ x $ to $ y $ with

On the other hand Part I ^[5] gives rise to the hope that we can find $ 1\leq r < p $ and a family of extension operators $ {\mathcal{U}}_{{\varepsilon}}:\, W_{0, \partial{\bf{Q}}}^{1, p}({\bf{Q}}_{{\bf{p}}}^{{\varepsilon}})\to W^{1, r}({\bf{Q}}) $ for scalar valued functions resp. $ {\mathcal{U}}_{{\varepsilon}}:\, {\bf{W}}_{0, \partial{\bf{Q}}}^{1, p}({\bf{Q}}_{{\bf{p}}}^{{\varepsilon}})\to{\bf{W}}^{1, r}({\mathbb{R}^{d}}) $ for vector valued functions such that

where the full support of $ {\mathcal{U}}_{{\varepsilon}}u $ lies within $ \mathbb{B}_{{{\varepsilon}^{\beta}}}{\left({{\bf{Q}}}\right)} $ for $ {\varepsilon} $ small enough and some fixed $ \beta\in(0, 1) $ depending on $ {\bf{p}} $.

In Part I we have established a general abstract framework for the derivation of uniform bounds on extension operators and except for two special examples, the results in Part I are rather vague, missing a general theory to deal with the connectivity of the domain. The connectivity for general geometries will be the main topic of the present work. We note at this point that connectivity is also the major issue for other former works to restrict to inclusions of an absolutely bounded diameter ^[3,10]. Our method of proof, based on Part I, is different from other proofs in the literature, particularly the literature for periodic ^[7] or John ^[2,8] domains, even though some patterns recur such as the construction of suitable paths along overlapping sets of an open covering. For a further overview over the history and the literature, the reader is referred to Parts I and II ^[6].

Let us finally note that replacing Eq (1.1) by Eq (1.4) also affects the analysis in the homogenization process and we refer to Part II ^[6] where this has been discussed.

1.1.   The setting

Throughout this work, we use $ \left({\bf{e}}_{i}\right)_{i = 1, \dots d} $ for the Euclidean basis of $ {\mathbb{R}^{d}} $. Given a metric space $ \left(M, d\right) $ we denote $ \mathbb{B}_{r}{\left(x\right)} $ the open ball around $ x\in M $ with radius $ r > 0 $. The surface of the unit ball in $ {\mathbb{R}^{d}} $ is $ {\mathbb{S}}^{d-1} $. Furthermore, we denote

A sequence of points will be labeled by $ {\bf{x}}: = \left(x_{i}\right)_{i\in{\mathbb{N}}} $.

In what follows, we will assume that $ {\bf{p}} = {\bf{p}}(\omega) $ is also a random connected domain, that is Lipschitz for almost every realization. We formally introduce the concepts of stationarity and ergodicity of stochastic processes in Section 2.4. If no confusion occurs, we drop $ (\omega) $ in the notation wherever possible in order to improve readability.

According to Part I Chapter 3 for every stationary ergodic random open set $ {\bf{p}} $ the following can be established.

Lemma 1.1. Let $ {\bf{p}} $ be a stationary ergodic random open set. Then there exists $ {\mathfrak{r}} > 0 $ and a positive, monotonically decreasing functions $ f_{{\bf{P}}} $ with $ f_{{\bf{P}}}(R)\to0 $ as $ R\to\infty $ and a random point process $ {\bf{x}}_{{\mathfrak{r}}} = \left(x_{a}\right)_{a\in{\mathbb{N}}} $ jointly stationary with $ {\bf{p}} $ such that

● $ \mathbb{B}_{{\frac{{\mathfrak{r}}}{2}}}{\left({{\bf{x}}_{{\mathfrak{r}}}}\right)}\subset{\bf{p}} $,

● for all $ a, b\in{\mathbb{N}} $, $ a\neq b $, it holds $ \left|x_{a}-x_{b}\right| > 2{\mathfrak{r}} $,

● $ {\mathbb{P}}{\left({\mathbb{B}_{R}{\left(0\right)}\cap{\bf{x}}_{{\mathfrak{r}}} = \emptyset}\right)}\leq f_{{\bf{P}}}(R) $.

Jointly stationary in the sense of Part I means that both of the joint distributions of $ {\bf{x}}_{{\mathfrak{r}}} $ and $ {\bf{p}} $ are invariant over all shifts $ x\in{\mathbb{R}^{d}} $ or over all shifts $ x\in2{\mathfrak{r}}{\mathbb{Z}^{d}} $. Constructing from $ {\bf{x}}_{{\mathfrak{r}}} = \left(x_{a}\right)_{a\in{\mathbb{N}}} $ a Voronoi tessellation of cells $ \left(G_{a}\right)_{a\in{\mathbb{N}}} $ of diameter $ {\mathfrak{d}}_{a} = {\mathfrak{d}}(x_{a}): = \sup_{x, y\in G_{a}}\left|x-y\right| $, then according to Part I for some constant $ C\geq1 $

Furthermore, for any $ x\in{\bf{x}}_{{\mathfrak{r}}} $ and $ y\in{\bf{p}} $ let

denote the set of all continuous paths from $ x $ to $ y $ inside $ {\bf{p}} $. Given $ x\in{\bf{x}}_{{\mathfrak{r}}} $ we further denote

Connectedness ensures $ {\mathscr{R}}(x) < \infty $ for every $ x\in{\bf{x}}_{{\mathfrak{r}}} $. Denoting $ {\mathscr{S}}(x): = {\mathscr{R}}(x)/{\mathfrak{d}}(x) $ we consider monotonically decreasing functions $ f_{{\mathscr{S}}}, f_{{\mathscr{R}}}:\, [0, \infty)\to{\mathbb{R}} $ given through

We call $ {\mathscr{R}} $ the connectivity radius and $ {\mathscr{S}} $ the stretch factor.

Definition 1.2 (Local $ \left(\delta, M\right) $-Regularity). The domain $ {\bf{p}}\subset{\mathbb{R}^{d}} $ is called $ (\delta, M) $-regular in $ p_{0}\in\partial{\bf{p}} $ if there exists an open set $ U\subset{\mathbb{R}}^{d-1} $ and a Lipschitz continuous function $ \phi:\, U\to{\mathbb{R}} $ with Lipschitz constant greater or equal to $ M $ such that $ \partial{\bf{p}}\cap\mathbb{B}_{{\delta}}{\left({p_{0}}\right)} $ is subset of the graph of the function $ \varphi:\, U\to{\mathbb{R}^{d}}\, , \; \tilde{x}\mapsto\left(\tilde{x}, \phi{\left({\tilde{x}}\right)}\right) $ in some suitable coordinate system.

Definition 1.3. For a stationary random Lipschitz domain $ {\bf{p}}\subset{\mathbb{R}^{d}} $ with $ {\mathfrak{r}} $ from Lemma 1.1 and for every $ p\in\partial{\bf{p}} $ and $ n\in{\mathbb{N}}\cup\{0\} $

For every $ p\in\partial{\bf{p}} $ it holds that

Since no confusion occurs, we write $ \delta = \delta_{{\mathfrak{r}}} $ for simplicity.

Definition 1.4 (Extension order). The geometry is of extension order $ n\in{\mathbb{N}}\cup\{0\} $ if there exists $ C > 0 $ such that for almost every $ p\in\partial{\bf{p}} $ there exists a local extension operator

In particular, we assume that $ n\in{\mathbb{N}} $ and $ C > 0 $ in the above definition are deterministic and global. Part I shows that every locally Lipschitz geometry is of extension order $ n = 1 $ and $ C $ is independent from the geometry, though better values (i.e., n = 0) for $ n $ are possible for some geometries. A random distribution of $ n $ among the values $ 0 $ and $ 1 $ could be handled within the theory developped in Part I and in the present paper, but this would lead to additional effort in notation and presentation with no additional insight.

Definition 1.5 (Inner microscopic regularity, see Figure 2). Given $ n\in{\mathbb{N}} $ and $ \tilde{\rho}: = 2^{-5}\rho_{n} $, the inner microscopic regularity $ \alpha\in[0, 1] $ is

As demonstrated in Part I, the values of $ \alpha $ and $ n $ as well as the distribution of $ M $ and $ \rho_{n} $ are crucial for the validity of Eq (1.4) for a given pair $ (r, p) $.

1.2.   Main Result: Uniform extension estimates for stationary ergodic random sets $ {\bf{p}}(\omega) $

We find the following main result.

Theorem 1.6. Let $ {\bf{Q}}\subset{\mathbb{R}^{d}} $ be a bounded Lipschitz domain. Let $ {\bf{p}}(\omega) $ be a stationary ergodic random connected open set in $ {\mathbb{R}^{d}} $ of extension order $ n $ and with inner microscopic regularity $ \alpha $. Furthermore let $ {\bf{x}}_{{\mathfrak{r}}} $ be a jointly stationary point process satisfying Assumption 1.1. Given constants $ 1\leq r < s < p $ and $ q, \tilde{q}\in[1, \infty) $ with $ \frac{s}{p}+\frac{1}{q}+\frac{s}{r\tilde{q}} = 1 $ and writing

let the following hold for $ s_r: = \frac{s(r+1)-r}{r} $:

Alternatively let $ {\mathfrak{d}} $ and $ {\mathscr{S}} $ be independent and writing

replace condition $ Eq\; (1.12) $ with

Then there exists $ \beta_{0}\in(0, 1) $ not depending on $ \omega $ such that for almost every $ \omega $ there exists an extension operator $ {\mathcal{U}}_{\omega}:\, W_{{\mathrm{loc}}}^{1, p}({\bf{p}}(\omega))\to W_{{\mathrm{loc}}}^{1, r}({\mathbb{R}^{d}}) $ and a constant $ C_{\omega} $ and $ N_{0}\geq1 $ such that for every $ N > N_{0} $ it holds

Remark 1.7. Of course it is desireable to get moment estimates on $ C_{\omega} $ but there is a problem involved here: On one hand, $ C_{\omega} $ is clearly related to $ {\mathbb{E}}_{1} $, ... $ {\mathbb{E}}_{4} $. However, for a given fixed $ N $ there arises the following type of inequality in the proofs which is clearly related to $ {\mathbb{E}}_{3} $:

and similar terms appear for $ {\mathbb{E}}_{1} $, $ {\mathbb{E}}_{2} $ and $ {\mathbb{E}}_{4} $. Now the first bracket on the right hand side converges to a positive number by the ergodic theorem. However, for our given $ \omega $ it may become very large with its maximum being not related to $ {\mathbb{E}}_{3} $ or $ \omega $ in a currently quantifyable way. On the other hand, if $ u = u(x, \omega) $ is a random function and we go back to the very begining of Part I, averaging over $ \Omega $ in all calculations, we could get the following:

with $ C $ not depending on $ \omega $ or $ N $.

Remark 1.8. Observe that we do not impose bounds on $ \delta^{-1} $ because the above formula already contains bounds on $ \rho^{-1} $. Through the formula $ \delta^{-1}\propto\rho^{-1}(1+M) $ we can replace the bounds on $ \rho^{-1} $ by bounds on $ \delta^{-1} $ and vice versa.

Remark 1.9. Theorem 1.6 shows that if the distribution of $ \delta $, $ M $, $ {\mathfrak{d}} $, $ {\mathscr{S}} $ is good enough, we can have any $ r < p $. Finally, if $ \delta $ is bounded away from $ 0 $ and $ M $, $ {\mathfrak{d}} $, $ {\mathscr{S}} $ are uniformly bounded from above, we are back in the minimally smooth setting which allows $ r = p $.

1.3.   Discussion

We may apply a rescaling $ N = {\varepsilon}^{-1} $ for some $ {\varepsilon} > 0 $. Writing

inequality (1.16) reads

The important insight is that $ \chi_{\mathbb{B}_{{{\varepsilon}^{1-\beta_{0}}}}{\left({{\bf{Q}}}\right)}}\to\chi_{{\bf{Q}}} $ in $ L^{p}({\mathbb{R}^{d}}) $ for any $ 1\leq p < \infty $ and hence in the limit $ {\mathcal{U}}_{\omega}^{{\varepsilon}}u $ is determined mostly by the values of $ u(x) $ for $ x\in{\bf{Q}} $. Moreover it was shown in Part I that $ u|_{\left({\varepsilon}{\bf{p}}\right)\cap\partial{\bf{Q}}}\equiv0 $ implies that the support of $ {\mathcal{U}}_{\omega}^{{\varepsilon}}u $ will ultimately reduce to $ {\bf{Q}} $ in the limit.

Theorem 1.6 has a rather broad range of geometries it may be applied to. It also gives a hint how probabilistic construction of random geometries might be modified to ensure the existence of extension operators. One particular question that the author was asked frequently on seminar talks and workshops is the applicability of the above result to the boolean model treated in Part I. This is a geometry constructed by assigning to a family of random points balls with radius $ 1 $ around these points. The above result is then applicable if the probability of "touching", i.e., the boundaries of two balls meet in precisely 1 point, has probability zero and the distribution of "small overlap" and "small distance" of two different balls is sufficiently small. We refer to Section 6 of Part I where such a calculation is carried out in detail.

1.4.   Structure of the article

In Section 2 we collect some results from Part I and modify the Voronoi integration lemma from there including a new and shortened proof. In Section 3 we prove Theorem 1.6 based on one of the main results from Part I. An outline of the proof is provided at the beginning of Section 3.

2.   Preliminaries from Part I

The constant $ C $ on the right hand side of Eq (1.16) depends on averaged weights of $ \delta $, $ M $, $ {\mathfrak{d}}_{a} $, $ {\mathscr{S}}_{a} $ and $ {\mathscr{R}}_{a} $ related to Eqs (1.12)–(1.15). In order to judge whether these averages are bounded as $ n\to\infty $, we will rely on the integration theory that is recalled below. In particular, this theory is connected to the ergodic theorems and the Palm measure. We start by briefly explaining how the following results will be applied later on.

In Section 2.1 we recall $ \eta $-regularity introduced in Part I. This concept allows us to cover any closed sets by a suitable family of open balls such that the covering is locally finite and uniformly bounded by a constant. While in Part I this was used to cover only the boundary of $ {\bf{p}} $ in terms of $ \rho_{n} $, we will later in Section 3.3 use this result to extend the covering to the interior full domain.

In Section 2.2 we construct from $ (\delta, M) $ (notably only defined on $ \partial{\bf{p}} $) various integrable functions on $ {\mathbb{R}^{d}} $ which are denoted e.g., $ \rho_{[\dots], {\mathbb{R}^{d}}} $, $ \delta_{[\dots], {\mathbb{R}^{d}}} $, $ M_{[\dots], {\mathbb{R}^{d}}} $. However, we emphasize at this point that the distribution of $ \rho_{n}(x) $, $ \delta(x) $ or $ M(x) $ are w.r.t. the condition that $ x\in\partial{\bf{p}}(\omega) $. Hence, it is necessary to control integrals over the functions $ \rho_{[\dots], {\mathbb{R}^{d}}} $, $ \delta_{[\dots], {\mathbb{R}^{d}}} $, $ M_{[\dots], {\mathbb{R}^{d}}} $ by integrals over the functions $ \rho_{n}(x) $, $ \delta(x) $ or $ M(x) $, which leads to Lemma 2.6.

Section 2.3 provides a frequently used Poincaré inequality and in Section 2.4 we introduce the ergodic theorems on $ {\bf{p}} $ and $ \partial{\bf{p}} $ which will ensure that all the above mentioned averaging integrals converge to their expectation as the support grows infinitely large.

Finally in Section 2.5 we study functions

and provide an estimate on the expectation of $ {\mathfrak{b}}^{q} $, $ q\in[1, \infty) $. This will help us to control integrals that enter the constant $ C $ from the mesoscopic geometric properties.

2.1.   Local $ \eta $-Regularity

We summarize the concept of $ \eta $-regularity and its major consequences from Part I. Note that Lemma 2.2 was proved in Part I only for $ \Gamma = \partial{\bf{p}} $. However, the only property of $ \partial{\bf{p}} $ used for the proof is its closedness.

Definition 2.1 ($ \eta $- regularity). Let $ \Gamma $ be a closed set. For a function $ \eta:\, \Gamma\to(0, r] $ we call $ \Gamma \; \eta $-regular if

Lemma 2.2. Let $ \Gamma $ be a locally $ \eta $-regular set for $ \eta:\Gamma\to(0, {\mathfrak{r}}) $. Then $ \eta:\, {\bf{p}}\to{\mathbb{R}} $ is locally Lipschitz continuous with Lipschitz constant $ 1 $ and for every $ {\varepsilon}\in\left(0, \frac{1}{2}\right) $ and $ \tilde{p}\in\mathbb{B}_{{{\varepsilon}\eta}}{\left(p\right)}\cap\Gamma $ it holds

Theorem 2.3. Let $ \Gamma\subset{\mathbb{R}^{d}} $ be a closed set and let $ \eta{\left({\cdot}\right)}\in C{\left({\Gamma}\right)} $ be bounded and satisfy for every $ {\varepsilon}\in\left(0, \frac{1}{2}\right) $ and for $ \left|p-\tilde{p}\right| < {\varepsilon}\eta{\left(p\right)} $

and define $ \tilde{\eta}{\left(p\right)} = 2^{-K}\eta{\left(p\right)} $, $ K\geq2 $. Then for every $ C\in(0, 1) $ there exists a locally finite covering of $ \Gamma $ with balls $ \mathbb{B}_{{\tilde{\eta}{\left({p_{k}}\right)}}}{\left({p_{k}}\right)} $ for a countable number of points $ {\left({p_{k}}\right)}_{k\in{\mathbb{N}}}\subset\Gamma $ such that for every $ i\neq k $ with $ \mathbb{B}_{{\tilde{\eta}{\left({p_{i}}\right)}}}{\left({p_{i}}\right)}\cap\mathbb{B}_{{\tilde{\eta}{\left({p_{k}}\right)}}}{\left({p_{k}}\right)}\neq\emptyset $ it holds

Remark. The fact that Eq (2.5) can be satisfied for any holds for any given $ C\in(0, 1) $ (even having in mind that the choice of points depends on $ C $) is surprising. In fact, $ \eta{\left(p\right)}-\left|p-\tilde{p}\right| > \left(1-{\varepsilon}\right)\eta{\left(p\right)} $ in Eq (2.4) seems to contradict Eq (2.5). However, we have to keep in mind that Eq (2.5) holds for $ \tilde{\eta} = 2^{-K}\eta $, $ K\geq2 $. Now suppose $ \left|p-\tilde{p}\right| = 2^{-K}\eta{\left(p\right)} $ and $ \eta{\left(p\right)} > \eta{\left({\tilde{p}}\right)} $. Since Eq (2.4) holds for every $ {\varepsilon}\in(0, \frac{1}{2}) $ we find for $ {\varepsilon} = 2^{-K} $ that $ \eta{\left({\tilde{p}}\right)} > (1-2^{-K})\eta{\left(p\right)} $ and hence

So the above calculation shows that the lemma to hold for every $ C < 1 $ is plausible. The major difficulty in the original proof is to provide an algorithm which provides the covering as claimed.

In Part I Theorem 2.3 lead immediately to the following corollary.

Corollary 2.4. Let $ {\mathfrak{r}} > 0 $ and let $ {\bf{p}}\subset{\mathbb{R}^{d}} $ be a locally $ \left(\delta, M\right) $-regular open set, where we restrict $ \delta $ by $ \delta\left(\cdot\right)\leq\frac{{\mathfrak{r}}}{4} $. Given $ n\in{\mathbb{N}} $ there exists a countable number of points $ \left(p_{k}\right)_{k\in{\mathbb{N}}}\subset\partial{\bf{p}} $ such that $ \partial{\bf{p}} $ is completely covered by balls $ \mathbb{B}_{{\tilde{\rho}\left(p_{k}\right)}}{\left({p_{k}}\right)} $ where $ \tilde{\rho}\left(p\right): = \tilde{\rho}_{n}\left(p\right): = 2^{-5}\rho_{n}\left(p\right) $. Writing

for two such balls with $ \mathbb{B}_{{\tilde{\rho}_{k}}}{\left({p_{k}}\right)}\cap\mathbb{B}_{{\tilde{\rho}_{i}}}{\left({p_{i}}\right)}\neq\emptyset $ it holds

Furthermore, depending on the inner microscopic regularity $ \alpha\in[0, 1] $ there exists $ {\mathfrak{r}}_{n, \alpha, k}\geq\frac{\tilde{\rho}_{n, k}}{32\left(1+M_{\tilde{\rho}_{n}(p_{k})}{\left({p_{k}}\right)}^{\alpha}\right)} $ and $ y_{n, \alpha, k} $ such that $ \mathbb{B}_{{{\mathfrak{r}}_{n, \alpha, k}}}{\left({y_{n, \alpha, k}}\right)}\subset\mathbb{B}_{{\tilde{\rho}_{k}/8}}{\left({p_{k}}\right)}\cap{\bf{p}} $ and $ \mathbb{B}_{{2{\mathfrak{r}}_{n, \alpha, k}}}{\left({y_{k}}\right)}\cap\mathbb{B}_{{2{\mathfrak{r}}_{n, \alpha, j}}}{\left({y_{j}}\right)} = \emptyset $ for $ k\neq j $.

Remark 2.5. Given the covering from Corollary 2.4 Lemma 4.4 and Remark 4.5 from Part I imply

2.2.   Integration of $ \delta $ and $ M $

Given $ c\in(0, 1] $ let $ \eta(p) = c\delta(p) $ or $ \eta(p) = c\rho_{n}(p) $, $ n\in{\mathbb{N}} $ and $ r\in C^{0, 1}(\partial{\bf{p}}) $ and define the functions

where $ \inf\emptyset = \sup\emptyset: = 0 $ for notational convenience. We also write $ M_{[\eta], {\mathbb{R}^{d}}}(x): = M_{[\eta, \eta], {\mathbb{R}^{d}}}(x) $ and $ \eta_{{\mathbb{R}^{d}}}{\left(x\right)}: = \eta_{[\eta], {\mathbb{R}^{d}}}{\left(x\right)} $. The relations between $ \eta, M:\partial{\bf{p}}\to{\mathbb{R}} $ and $ \eta_{[r], {\mathbb{R}^{d}}}, M_{[r, \eta], {\mathbb{R}^{d}}}:\, {\mathbb{R}^{d}}\to{\mathbb{R}} $ as well as integrability and measurability are discussed in Part I. Furthermore, we define

Lemma 2.6. Let $ {\mathfrak{r}} > 0 $, let $ {\bf{P}}\subset{\mathbb{R}^{d}} $ be a Lipschitz domain and let $ \eta, r:\, \partial{\bf{P}}\to{\mathbb{R}} $ be continuous such that $ \eta\leq{\mathfrak{r}} $ and $ {\bf{P}} $ is $ \eta $- and $ r $-regular. For $ {\varepsilon}\in(0, 1] $ let $ \eta(p) = {\varepsilon}\delta(p) $ or $ \eta(p) = {\varepsilon}\rho_{n}(p) $, $ n\in{\mathbb{N}} $. For $ \tilde{\eta}: = \eta_{[\frac{\eta}{8}], {\mathbb{R}^{d}}} $ there exists a constant $ C > 0 $ only depending on the dimension $ d $ such that for every bounded open domain $ {\bf{Q}} $ and $ k\in[0, 4) $ it holds

Finally, it holds

2.3.   A fundamental Poincaré inequality

We define for $ a\in{\mathbb{R}^{d}} $ and $ \delta > 0 $ the operator

The following two estimates are special cases of results already proved in Part I.

Lemma 2.7. There exists $ C > 0 $ depending only on the dimension $ d $ such that for $ a, b\in{\mathbb{R}^{d}} $ with $ 0 < \delta_{a}\leq\delta_{b} $ and for either $ i\in\{a, b\} $

Proof. Inequality (2.14) follows from Part I Lemma 2.10 and Corollary 2.11. □

2.4.   Ergodic theorem and Palm measure

In order to make clear what we mean by a random stationary ergodic Lipschitz domain we briefly introduce the technical details which will be used for the averaging property given by the ergodic theorem ^[9,11] below.

Definition 2.8. Throughout this work, $ (\Omega, {\mathscr{F}}, {\mathbb{P}}) $ is a probability space with a dynamical system on $ \Omega $, i.e., a family $ (\tau_{x})_{x\in{\mathbb{R}^{d}}} $ of measurable bijective mappings $ \tau_{x}:\Omega\mapsto\Omega $ satisfying (i)–(iii):

(i) $ \tau_{x}\circ\tau_{y} = \tau_{x+y} $, $ \tau_{0} = id $ (Group property)

(ii) $ {\mathbb{P}}(\tau_{-x}B) = {\mathbb{P}}(B)\quad\forall x\in{\mathbb{R}^{d}}, \, \, B\in{\mathscr{F}} $ (Measure preserving)

(iii) $ A:\, \, {\mathbb{R}^{d}}\times\Omega\rightarrow \Omega\qquad(x, \omega)\mapsto\tau_{x}\omega $ is measurable (Measurability of evaluation)

We further assume that $ \left(\tau_{x}\right)_{x\in{\mathbb{R}^{d}}} $ is ergodic, i.e., a $ {\mathbb{P}} $-measurable function satisfies $ f(\tau_{x}\cdot\, ) = f(\, \cdot\, ) $ if and only if $ f $ is constant.

Definition 2.9 (Stationary). Let $ X $ be a measurable space and let $ f:\Omega\times{\mathbb{R}^{d}}\to X $. Then $ f $ is called (weakly) stationary if $ f(\omega, x) = f(\tau_{x}\omega, 0) $ for (almost) every $ x $.

Although the original definition is different, it is sufficient for this work (see ^[4] Section 2) to say that a random Lipschitz domain $ {\bf{p}}(\omega) $ is stationary if $ \chi_{{\bf{p}}(\omega)}(x) $ is stationary and there exists $ {\bf{P}}\subset\Omega $ such that

A random measure is a measurable mapping

which is equivalent to either one of the following two conditions

1. For every bounded Borel set $ A\subset{\mathbb{R}^{d}} $ the map $ \omega\mapsto\mu_{\omega}(A) $ is measurable

2. For every $ f\in C_{c}({\mathbb{R}^{d}}) $ the map $ \omega\mapsto\int f\, {\mathrm{d}}\mu_{\omega} $ is measurable.

A random measure is stationary if the distribution of $ \mu_{\omega}(A) $ is invariant under translations of $ A $ that is $ \mu_{\omega}(A) $ and $ \mu_{\omega}(A+x) $ share the same distribution. The Palm measure is defined as

on the measurable space $ \Omega $ and in case $ \mu_{\omega} = {\mathcal{L}} $ we find $ {\mu_{\mathcal{P}}} = {\mathbb{P}} $. By a deep theorem due to Mecke (see ^[1,9]) every $ {\mathcal{B}}({\mathbb{R}^{d}})\times{\mathcal{B}}(\Omega) $-measurable non negative or $ {\mu_{\mathcal{P}}}\times{\mathcal{L}} $- integrable functions $ f $ satisfies the Campbell formula

We denote by

For random measures we find the following.

Theorem 2.10 (Ergodic Theorem ^[1] 12.2.VIII). Let $ \left(\Omega, {\mathscr{F}}, {\mathbb{P}}\right) $ be a probability space, $ {\bf{Q}} $ be a bounded open domain with Lipschitz boundary and let $ f:\, \Omega\to{\mathbb{R}} $ be measurable with $ \int_{\Omega}\left|f\right|{\mathrm{d}}{\mu_{\mathcal{P}}} < \infty $. Then for $ {\mathbb{P}} $-almost all $ \omega\in\Omega $

In our setting, the above implies in total for any differentiable function $ f:\, {\mathbb{R}}^{3}\to{\mathbb{R}} $ that almost surely

Since the essential property of $ f $ in Eq (2.16) is its stationarity, we infer that Eq (2.18) also holds for "non-local" functions such as $ {\mathfrak{b}} $ in Eq (2.19) in the following Lemma 2.11.

2.5.   A Voronoi-integration lemma

We state and prove a variant of a Voronoi integration lemma that was proved in Section 4 of Part I.

Lemma 2.11. Let $ {\mathbb{X}}_{{\mathfrak{r}}} $ be a stationary and ergodic random point process with minimal mutual distance $ 2{\mathfrak{r}} $ for $ {\mathfrak{r}} > 0 $. Given fixed constants $ \eta, \xi > 0 $ let

and write $ {\mathbb{P}}_{k, R}: = {\mathbb{P}}({\mathfrak{d}}(x)\in[k, k+1), \, {\mathscr{R}}(x)\in[R, R+1)) $. Then there exists $ C > 0 $ depending only on $ d $ and $ {\mathfrak{r}} $ such that for any $ r > 1 $ it holds

Proof. In what follows $ C $ is a varying constant depending only on $ d $ and $ {\mathfrak{r}} $. W.l.o.g let $ {\mathfrak{r}} = 1 $. We write $ {\mathfrak{d}}_{i} = {\mathfrak{d}}(x_{i}) $, $ R_{i} = {\mathscr{R}}(x_{i}) $, $ {\mathbb{B}}_{i}: = \mathbb{B}_{{R_{i}}}{\left({x_{i}}\right)} $. Let

We observe that the mutual minimal distance of points in $ {\bf{x}}_{{\mathfrak{r}}} $ implies

which follows from the uniform boundedness of the $ {\mathbb{B}}_{i} $ for $ x_{i}\in X_{k, R} $ and the minimal distance of $ \left|x_{i}-x_{j}\right| > 2{\mathfrak{r}} $. Then for every $ y\in{\mathbb{R}^{d}} $, $ M > 0 $ it holds by stationarity and the ergodic theorem for every $ y\in{\mathbb{R}^{d}} $

In the last inequality we made use of the fact that every ball $ \mathbb{B}_{{R_{i}}}{\left({x_{i}}\right)} $, $ x_{i}\in X_{k, N} $, has volume smaller than $ C\left(R+1\right)^{d}\left(k+1\right)^{d} $ and $ \#\left\{ x_{i}\in{\bf{x}}_{{\mathfrak{r}}}\cap\mathbb{B}_{N}{\left(0\right)}\right\} < C\left|\mathbb{B}_{N}{\left(0\right)}\right| $. We note that for $ \frac{1}{p}+\frac{1}{q} = 1 $

Due to Eq (2.21) we find

and obtain for $ q = \frac{p}{p-1} $ and $ C_{q}: = \left(\sum_{k, R = 1}^{\infty}\alpha_{k, R}^{q}\right)^{\frac{p}{q}}\left|{\mathbb{S}}^{d-1}\right|^{p} $ due to Eq (2.22):

For the sum $ \sum_{k, R = 1}^{\infty}\alpha_{k, R}^{q} $ to converge, it is sufficient that $ \alpha_{k, R}^{q} = \left(k+1\right)^{-r}\left(R+1\right)^{-r} $ for some $ r > 1 $. Hence, for such $ r $ it holds $ \alpha_{k, R} = \left(k+1\right)^{-r/q}\left(R+1\right)^{-r/q} $ and thus Eq (2.20). □

3.   Proof of Theorem 1.6

In this section, we will prove Theorem 1.6. The proof consists of 5 sections: In Section 3.1 we quote one of the main results from Part I. This is a an estimate of the extended gradient field by the original gradient field and the difference of local averages. This makes it clear that one has to estimate differences of local averages by the gradient field "connecting" the two averaging regions. Since the geometry $ {\bf{p}} $ is connected, we identify in Section 3.2 a constant $ \beta\in(0, 1) $ such that for $ M\in{\mathbb{N}} $ large enough the set $ {\bf{Q}}_{M}: = M{\bf{Q}} $ is connected through paths inside $ \mathbb{B}_{{M^{\beta}}}{\left({{\bf{Q}}_{M}}\right)} $. In Section 3.3 we extend the covering Corollary 2.4 of $ \partial{\bf{p}} $ to a full covering of $ {\bf{p}} $ using also the seeds $ {\bf{x}}_{r} $. This covering will provide a basis to suitably integrate the gradient along paths connecting the averaging regions. In Section 3.5 we will finally prove the main theorem.

3.1.   The Main Result from Part I

Based on the notation from Section 1.1 we use the Voronoi tessellation $ \left(G_{a}\right)_{a\in{\mathbb{N}}} $ with seeds $ \left(x_{a}\right)_{a\in{\mathbb{N}}} = {\bf{x}}_{{\mathfrak{r}}} $ and a partition of unity $ \left(\Phi_{a}\right)_{a\in{\mathbb{N}}} $ with support $ \mathbb{B}_{{\frac{{\mathfrak{r}}}{2}}}{\left({G_{a}}\right)} $. The gradient of $ \Phi_{a} $ is locally bounded by the number of sets $ \mathbb{B}_{{\frac{{\mathfrak{r}}}{2}}}{\left({G_{a}}\right)} $ interacting. Since the number of cells $ G_{a} $ interacting with $ \mathbb{B}_{{{\mathfrak{r}}}}{\left({G_{a}}\right)} $ is bounded by (Part I, Lemma 2.19) $ \left(4{\mathfrak{d}}(x_{a}){\mathfrak{r}}^{-1}\right)^{d} $ we obtain

Furthermore, there exists by Corollary 2.4 (cited from Part I) a complete covering of $ \partial{\bf{p}} $ by balls $ A_{i}: = \mathbb{B}_{{\tilde{\rho}_{n}\left(p_{i}^{n}\right)}}{\left({p_{i}^{n}}\right)} $, $ \left(p_{i}^{n}\right)_{i\in{\mathbb{N}}}\subset\partial{\bf{p}} $, where $ \tilde{\rho}_{n}{\left(p\right)}: = 2^{-5}\rho_{n}{\left(p\right)} $ and where Eq (2.6) holds for any two points $ p_{i}, p_{k} $ with $ A_{i}\cap A_{k}\neq\emptyset $. Finally there exists a partition of unity $ \left(\phi_{i}\right)_{i\in{\mathbb{N}}\backslash\{0\}} $ with support of $ \phi_{i} $ in $ A_{i} $ and $ \phi_{0} $ with support in $ {\mathbb{R}^{d}}\backslash\partial{\bf{p}} $ such that $ \sum_{i\in{\mathbb{N}}}\phi_{i} = 1 $.

Given $ n\in\{0, 1\} $ and $ \alpha\in[0, 1] $ from Definitions 1.4 and 1.5 we chose

and some $ y_{n, \alpha, i} $ such that

and for every $ p_{i}\in\partial{\bf{p}} $ and $ x_{a}\in{\bf{x}}_{{\mathfrak{r}}} $, we define

local averages close to $ \partial{\bf{p}} $ and in $ x_{a} $. We finally have to recall from Lemma 4.4 of Part I that

Theorem 3.1. Let $ {\bf{p}}\subset{\mathbb{R}^{d}} $ be a stationary ergodic Lipschitz domain of extension order $ n $ with $ {\mathfrak{r}} > 0 $ from Lemma 1.1 and inner regularity $ \alpha\in[0, 1] $ (Definitions 1.4 and 1.5). Then for every $ 1\leq r < p $ there exists a linear extension operator

and $ C > 0 $ such that with

for every bounded Lipschitz domain $ {\bf{Q}} $ the operator $ {\mathcal{U}}_{n, \alpha} $ satisfies

where

Remark. We recall in this context Remark 1.8 on the lack of a dependence on $ \delta $ for the above Theorem.

3.2.   The support lemma

Definition 3.2. Given a domain $ {\bf{Q}}\subset{\mathbb{R}^{d}} $ and a stationary random domain $ {\bf{p}} $ with the jointly stationary point process $ {\bf{x}}_{{\mathfrak{r}}} $ we define the sets

Remark 3.3. Since $ \mathbb{B}_{{{\mathfrak{r}}}}{\left({x_{a}}\right)}\subset G_{a} $ the last definition implies $ x_{a}\in{\bf{x}}_{{\mathfrak{r}}}({\bf{Q}}) $ for every $ x_{a}\in{\bf{x}}_{{\mathfrak{r}}} $ with $ \chi_{{\bf{Q}}}\chi_{\mathbb{B}_{{{\mathfrak{r}}}}{\left({G_{a}}\right)}}\not\equiv0 $.

In order to estimate the terms $ \left(\tau_{n, \alpha, i}^{{\mathfrak{s}}}u-{\mathcal{M}}_{a}^{{\mathfrak{s}}}u\right) $ and $ \left({\mathcal{M}}_{a}^{{\mathfrak{s}}}u-{\mathcal{M}}_{b}^{{\mathfrak{s}}}u\right) $ in Eq (3.6) we integrate the gradient along paths connecting the centers of the balls underlying the definition of $ \tau_{n, \alpha, i}^{{\mathfrak{s}}} $ and $ {\mathcal{M}}_{a}^{{\mathfrak{s}}} $ in Eq (3.4). However, in doing so we cannot possibly avoid quitting the domain $ {\bf{Q}} $ but we can avoid quitting the domain $ {\mathbb{C}}{\left({{\bf{Q}}, {\bf{x}}_{{\mathfrak{r}}}}\right)} $. In homogenization, we start with a given domain $ {\bf{Q}} $ and scale $ {\bf{p}} $ by $ {\varepsilon} $ and study the intersection $ {\bf{Q}}\cap{\varepsilon}{\bf{p}} $. Alternatively, we can study the intersection $ {\bf{p}}\cap N{\bf{Q}} $, $ N = {\varepsilon}^{-1} $. The follwoing lemma now states that if the distribution of $ {\mathscr{R}} $ is lucky, i.e., it decreases fast enough for large $ {\mathscr{R}} $, the probability to find $ x_{a}\in{\bf{x}}_{{\mathfrak{r}}}(N{\bf{Q}}) $ with $ \mathbb{B}_{{{\mathscr{R}}(x_{a})}}{\left({x_{a}}\right)}\not\subset\mathbb{B}_{{N^{\beta_{0}}}}{\left({N{\bf{Q}}}\right)} $ tends to $ 0 $ for some $ \beta_{0}\in(0, 1) $ and almost surely there exists $ N_{0} $ such that for $ N > N_{0} $ the maximal support of paths lies in $ {\mathbb{C}}{\left({N{\bf{Q}}, {\bf{x}}_{{\mathfrak{r}}}}\right)}\subset\mathbb{B}_{{N^{\beta_{0}}}}{\left({N{\bf{Q}}}\right)} $. The fact $ \beta_{0}\in(0, 1) $ then causes that $ {\mathbb{C}}{\left({{\bf{Q}}, {\varepsilon}{\bf{x}}_{{\mathfrak{r}}}}\right)}\subset\mathbb{B}_{{{\varepsilon}^{1-\beta_{0}}}}{\left({{\bf{Q}}}\right)} $, i.e. the paths leaving $ {\bf{Q}} $ lie in a comparatively thin strip around $ {\bf{Q}} $. We finally note that in the periodic case we can assume that $ \beta_{0} = 0 $ and hence $ {\mathbb{C}}{\left({{\bf{Q}}, {\varepsilon}{\bf{x}}_{{\mathfrak{r}}}}\right)}\subset\mathbb{B}_{{{\varepsilon}}}{\left({{\bf{Q}}}\right)} $.

Lemma 3.4. Recalling (1.5) and (1.7) assume that

1. either there exist $ C > 0 $ and $ \beta_{{\mathfrak{d}}}, \beta_{{\mathscr{R}}} > d+1 $ such that for every $ D > {\mathfrak{r}} $, $ r > 1 $ it holds $ f_{{\mathfrak{d}}}(D)\leq CD^{-\beta_{{\mathfrak{d}}}} $ and $ f_{{\mathscr{R}}}(r)\leq Cr^{-\beta_{{\mathscr{R}}}} $

2. or $ {\mathfrak{d}} $ and $ {\mathscr{S}} $ are independent and there exist $ C > 0 $ and $ \beta_{{\mathfrak{d}}} > d+2 $, $ \beta_{{\mathscr{S}}} > 1 $ such that for every $ D > {\mathfrak{r}} $, $ S > 1 $ it holds $ f_{{\mathfrak{d}}}(D)\leq CD^{-\beta_{{\mathfrak{d}}}} $ and $ f_{{\mathscr{S}}}(S)\leq CS^{-\beta_{{\mathscr{S}}}} $.

Then there exists $ \beta_{0}\in(0, 1) $ such that the following holds: For every bounded open set $ {\bf{Q}} $ with $ 0\in{\bf{Q}} $ there almost surely exists a constant $ N_{0} > 0 $ such that for every $ N > N_{0} $

Remark 3.5. The scaling $ N^{\beta_{0}} $of the radius of $ \mathbb{B}_{{N^{\beta_{0}}}}{\left({N{\bf{Q}}}\right)} $ implies that the additional mass of $ {\mathbb{C}}{\left({N{\bf{Q}}, {\bf{x}}_{{\mathfrak{r}}}}\right)}\setminus N{\bf{Q}} $ becomes asymptotically negligible.

Proof. We consider two balls $ \mathbb{B}_{r}{\left(0\right)}\subset{\bf{Q}}\subset\mathbb{B}_{R}{\left(0\right)} $ with $ r > 0 $. We write $ {\bf{Q}}_{N}: = N{\bf{Q}} $ and $ {\mathbb{B}}_{N, \beta_{0}}^{k, {\bf{Q}}}: = \mathbb{B}_{{N^{\beta_{0}}+k}}{\left({{\bf{Q}}}\right)} $ and $ {\mathbb{S}}_{N, \beta_{0}}^{k, {\bf{Q}}}: = {\mathbb{B}}_{N, \beta_{0}}^{k, {\bf{Q}}}\backslash{\mathbb{B}}_{N, \beta_{0}}^{k-1, {\bf{Q}}} $ for $ \beta_{0}\in(0, 1) $. Our aim is to show that for the events $ B_{N}: = \left({\mathbb{C}}{\left({{\bf{Q}}, {\bf{x}}_{{\mathfrak{r}}}}\right)}\subset{\mathbb{B}}_{2^{\frac{1}{\beta_{0}}}N, \beta_{0}}^{0, {\bf{Q}}_{N}}\right) $ it holds $ {\mathbb{P}}(B_{N})\to1 $ as $ N\to\infty $, provided $ \beta_{0} $ is chosen properly. For this we use

Step 1: It holds $ {\bf{x}}_{{\mathfrak{r}}}(N{\bf{Q}})\subset\tilde{{\bf{Q}}}_{N} $ and we find

We use the very rough estimate $ \#\left({\mathbb{S}}_{N, \beta_{0}}^{k+1, {\bf{Q}}_{N}}\right)\cap{\bf{x}}_{r}\leq\left(NR+N^{\beta_{0}}+k+1\right)^{d} $ to find

where in the last inequality we used $ (d-1) $-times integration by parts and $ C $ depends on $ d $, $ \beta_{{\mathfrak{d}}} $ and $ R $.

Step 2: We now assume that $ A_{N} $ holds true. Since

and since $ {\bf{x}}_{{\mathfrak{r}}}(N{\bf{Q}})\subset\tilde{{\bf{Q}}}_{N}\subset{\mathbb{B}}_{N, \beta_{0}, 0, {\bf{Q}}_{N}} $ it holds

If $ \beta_{{\mathscr{R}}} > d+1 $ and $ \beta_{{\mathfrak{d}}} > d+1 $ it holds

and the first statement of the lemma almost surely holds due to Eq (3.10).

Step 3: Alternatively we can assume that $ d_{a} $ and $ S_{a} $ are independent with $ R_{a}\leq d_{a}S_{a} $. Then

From here we conclude from the first part.

□

3.3.   An extended covering lemma

For $ x\in{\bf{p}} $ let

Then we find the following:

Lemma 3.6. Let $ {\bf{p}} $ be a connected open set which is locally $ \left(\delta, M\right) $-regular and has inner regularity $ \alpha\in[0, 1] $. For $ {\mathfrak{r}} > 0 $ let $ {\bf{x}}_{{\mathfrak{r}}} = \left(x_{k}\right)_{k\in{\mathbb{N}}} $ be a family of points with a mutual distance of at least $ 2{\mathfrak{r}} $ satisfying $ {\mathrm{dist}}{\left({x_{k}, \partial{\bf{p}}}\right)} > \frac{1}{2}{\mathfrak{r}} $ and let $ n\in{\mathbb{N}} $ and $ \partial{\bf{x}}: = \left(p_{k}\right)_{k\in{\mathbb{N}}}\subset\partial{\bf{p}} $ with corresponding $ \left(\tilde{\rho}_{k}\right)_{k\in{\mathbb{N}}}: = \left(\tilde{\rho}_{n, k}\right)_{k\in{\mathbb{N}}} $, $ \left({\mathfrak{r}}_{n, \alpha, k}\right)_{k\in{\mathbb{N}}}: = \left({\mathfrak{r}}_{n, \alpha, k}\right)_{k\in{\mathbb{N}}} $ and $ {\bf{y}}_{\partial{\bf{x}}}: = \left(y_{k}\right)_{k\in{\mathbb{N}}}: = \left(y_{n, \alpha, k}\right)_{k\in{\mathbb{N}}} $ like in Corollary 2.4. Then there exists a family of points $ \mathring{{\bf{x}}} = \left(\hat{p}_{j}\right)_{j\in{\mathbb{N}}}\subset{\bf{p}} $ with $ {\bf{x}}_{{\mathfrak{r}}}\subset\mathring{{\bf{x}}} $ such that with $ \tilde{\eta}_{k}: = \tilde{\eta}{\left({\hat{p}_{k}}\right)} $, $ \hat{B}_{k}: = \mathbb{B}_{{\tilde{\eta}_{k}}}{\left({\hat{p}_{k}}\right)} $ and $ B_{k}: = \mathbb{B}_{{\tilde{\rho}_{k}}}{\left({p_{k}}\right)} $ the family $ \left(B_{k}\right)_{k\in{\mathbb{N}}}\cup\left(\hat{B}_{k}\right)_{k\in{\mathbb{N}}} $ covers $ {\bf{p}} $ and

Furthermore, $ B_{k}\cap\hat{B}_{j}\neq\emptyset $ implies

i.e. $ \mathbb{B}_{{{\mathfrak{r}}_{k}}}{\left({y_{k}}\right)}\cap\mathbb{B}_{{\frac{1}{8}\tilde{\eta}_{j}}}{\left({\hat{p}_{j}}\right)} = \emptyset $ and $ x\in\hat{B}_{i} $ for some $ i $ implies

Finally, there exists $ C > 0 $ such that for every $ x\in{\bf{p}} $

Proof of Lemma 3.6. We recall $ \tilde{\rho}_{k}: = \tilde{\rho}\left(p_{k}\right): = 2^{-5}\rho\left(p_{k}\right) $ and $ {\mathfrak{r}}_{k} = \frac{\tilde{\rho}_{k}}{32\left(1+M_{k}\right)} $ and that Eq (2.6) holds. Furthermore, $ \mathbb{B}_{{{\mathfrak{r}}_{k}}}{\left({y_{k}}\right)}\subset\mathbb{B}_{{\tilde{\rho}_{k}/8}}{\left({p_{k}}\right)}\cap{\bf{p}} $ and hence we also find $ \mathbb{B}_{{{\mathfrak{r}}_{k}}}{\left({y_{k}}\right)}\cap\mathbb{B}_{{{\mathfrak{r}}_{j}}}{\left({y_{j}}\right)} = \emptyset $ for $ k\neq j $.

If we define $ {\bf{p}}_{B}: = \overline{{\bf{p}}\backslash\bigcup_{k}B_{k}} $ and observe that $ {\bf{p}}_{B} $ is $ \eta $-regular (for $ \eta $ defined in Eq (3.11)). Then Lemma 2.2 and Theorem 2.3 yield a cover of $ {\bf{p}}_{B} $ by a locally finite family of balls $ \hat{B}_{k} = \mathbb{B}_{{\tilde{\eta}_{k}}}{\left({\hat{p}_{k}}\right)} $, where $ \left(\hat{p}_{k}\right)_{k\in{\mathbb{N}}}\subset{\bf{p}}_{B} $, and where Eq (3.12) holds. Looking into the proof of Theorem 2.3 we can assume w.l.o.g. that $ \left(x_{k}\right)_{k\in{\mathbb{N}}}\subset\left(\hat{p}_{k}\right)_{k\in{\mathbb{N}}} $ by suitably bounding $ \eta $.

Furthermore, we find for $ B_{k}\cap\hat{B}_{j}\neq\emptyset $ that on one hand

On the other hand $ \hat{p}_{j}\not\in B_{k} $ by construction of $ \left(\hat{{\mathbb{B}}}_{i}\right)_{i\in{\mathbb{N}}} $. Hence $ \tilde{\eta}_{j}\geq\frac{1}{4}\tilde{\rho}_{k}\, . $ Finally, $ \mathbb{B}_{{{\mathfrak{r}}_{k}}}{\left({y_{k}}\right)}\cap\mathbb{B}_{{\frac{1}{8}\tilde{\eta}_{j}}}{\left({\hat{p}_{j}}\right)} = \emptyset $ follows from $ \tilde{\rho}_{k}\leq4\tilde{\eta}_{j}\leq\left|\hat{p}_{j}-p_{k}\right| $.

If $ x\in\hat{B}_{i} $ let $ p_{x}\in\partial{\bf{p}} $ with $ \left|p_{x}-x\right| = {\mathrm{dist}}(x, \partial{\bf{p}}) $ and chose some $ p_{k} $ with $ p_{x}\in B_{k} $. Then the above implies

To see Eq (3.15) let $ x\in{\bf{p}} $ and let $ \hat{p_{j}} $ such that $ \tilde{\eta}_{j} $ is maximal among all $ \hat{B}_{j} $ with $ x\in\hat{B}_{j} $. Let $ \hat{p}_{i} $ with $ x\in\hat{B}_{i}\cap\hat{B}_{j} $ and observe that both $ \left|\hat{p}_{i}-\hat{p}_{j}\right| $ and $ \tilde{\eta}_{i} $ are bounded from below and above by a multiple of $ \tilde{\eta}_{j} $. If $ x\in\hat{B}_{i}\cap\hat{B}_{k}\cap\hat{B}_{j} $, $ \left|\hat{p}_{i}-\hat{p}_{k}\right| $ is bounded from above and below by $ \tilde{\eta}_{i} $, hence by $ \tilde{\eta}_{j} $. This provides a uniform bound on $ \#\left\{ j\in{\mathbb{N}}:\; x\in\mathbb{B}_{{\tilde{\eta}_{j}}}{\left({\hat{p}_{j}}\right)}\right\} $. The second part of Eq (3.15) follows in an analogue way. □

3.4.   Set-paths

We recall the notations given in Eqs (2.7) and (2.8). In the below formula (3.17) we furthermore highlight that with the text following Eqs (2.7) and (2.8) we could also provide the following upper estimate:

Here we make use of the notation (2.9) modified as $ {\bf{p}}_{r} = {\bf{p}}_{[r], {\mathbb{R}^{d}}} $ for notational convenience.

Lemma 3.7. There exists a constant $ C > 0 $ such that the following holds:

Let $ {\bf{p}} $ be a connected open set which is locally Lipschitz regular and has inner regularity $ \alpha\in[0, 1] $ and extension order $ n\in{\mathbb{N}}\cup\{0\} $. For $ {\mathfrak{r}} > 0 $ let $ {\bf{x}}_{{\mathfrak{r}}} = \left(x_{k}\right)_{k\in{\mathbb{N}}} $ be a family of points with a mutual distance of at least $ 2{\mathfrak{r}} $ satisfying $ {\mathrm{dist}}{\left({x_{k}, \partial{\bf{p}}}\right)} > \frac{1}{2}{\mathfrak{r}} $ and $ \partial{\bf{x}}: = \left(p_{k}\right)_{k\in{\mathbb{N}}}\subset\partial{\bf{p}} $ with corresponding $ \left(\tilde{\rho}_{k}\right)_{k\in{\mathbb{N}}}: = \left(\tilde{\rho}_{n, k}\right)_{k\in{\mathbb{N}}} $, $ \left({\mathfrak{r}}_{n, \alpha, k}\right)_{k\in{\mathbb{N}}}: = \left({\mathfrak{r}}_{n, \alpha, k}\right)_{k\in{\mathbb{N}}} $ and $ {\bf{y}}_{\partial{\bf{x}}}: = \left(y_{k}\right)_{k\in{\mathbb{N}}}: = \left(y_{n, \alpha, k}\right)_{k\in{\mathbb{N}}} $ like in Corollary 2.4.

If $ x\in{\bf{x}}_{{\mathfrak{r}}} $ with $ b_{x}: = \mathbb{B}_{{\frac{{\mathfrak{r}}}{64}}}{\left(x\right)} $ and either $ y\in{\bf{y}}_{\partial{\bf{x}}}\cap\mathbb{B}_{{4{\mathfrak{d}}(x)}}{\left(x\right)} $ with $ b_{y} = \mathbb{B}_{{\frac{1}{8}\tilde{\eta}(y)}}{\left(y\right)} $ or $ y\in{\bf{x}}_{{\mathfrak{r}}}\cap\mathbb{B}_{{4{\mathfrak{d}}(x)}}{\left(x\right)} $ with $ b_{y} = \mathbb{B}_{{\frac{1}{64}{\mathfrak{r}}}}{\left(y\right)} $ then there exists an open set $ {\bf{ \pmb{\mathsf{ γ}}}}(x, y)\subset\left({\bf{p}}\cap\mathbb{B}_{{{\mathscr{R}}(x)}}{\left(x\right)}\right) $ with $ b_{x}\cup b_{y}\subset{\bf{ \pmb{\mathsf{ γ}}}}(x, y) $ and such that for $ C $ independent of $ u\in L_{{\mathrm{loc}}}^{1}({\bf{p}}) $, $ x $, $ y $ and $ {\bf{p}} $

where

Proof. We cover $ {\bf{p}} $ by a set of balls given by Lemma 3.6 and write for simplicity $ \tilde{\rho} = \tilde{\rho}_{n} $. Given $ x\in{\bf{x}}_{{\mathfrak{r}}} $ and $ y\in{\bf{y}}_{\partial{\bf{x}}}\cup{\bf{x}}_{{\mathfrak{r}}}\cap\mathbb{B}_{{4{\mathfrak{d}}(x)}}{\left(x\right)} $ let then $ \gamma:\, [0, 1]\to{\bf{p}}\cap\mathbb{B}_{{{\mathscr{R}}(x)-\frac{{\mathfrak{r}}}{2}}}{\left(x\right)} $ be a continuous path with $ \gamma(0) = x $ and $ \gamma(1) = y $. Such $ \gamma $ exists because of the definition of $ {\mathscr{R}} $ in Eq (1.6).

Step 1: We chose a finite sequence of points $ \left(Y_{i}\right)_{i} $ as a discrete equivalent of $ \gamma $ using the following algorithm:

1. Set $ Y_{0}: = x $ and $ b_{0}: = \mathbb{B}_{{\frac{1}{4}\eta(x)}}{\left(x\right)} = \mathbb{B}_{{\frac{{\mathfrak{r}}}{8}}}{\left(x\right)} $, $ t_{0} = 0 $.

2. For $ i\in{\mathbb{N}}\cup\{0\} $: If $ \gamma(t)\in b_{i} $ for every $ t > t_{i} $ cancel loop. Otherwise define $ t_{i+1}: = \sup\left\{ T > t_{0}:\, \forall t\in(t_{0}, T):\, \gamma(t)\in b_{i}\right\} $ and chose $ {\varepsilon} > 0 $ and

$ \bullet $ either $ Y_{i+1}\in\partial{\bf{x}} $ with $ b_{i+1} = \mathbb{B}_{{\tilde{\rho}(Y_{i+1})}}{\left({Y_{i+1}}\right)} $

$ \bullet $ or $ Y_{i+1}\in\mathring{{\bf{x}}} $ with $ b_{i+1} = \mathbb{B}_{{\tilde{\eta}(Y_{i+1})}}{\left({Y_{i+1}}\right)} $

such that it holds $ \gamma(t_{i+1})\in b_{i+1} $.

We have thus constructed a sequence of points $ \left(Y_{i}\right)_{i = 0, \dots, I} $ with $ Y_{0} = x $ and $ y\in b_{I} $. Furthermore, it holds $ b_{i}\cap b_{i+1}\neq\emptyset $ for every $ i\in\left\{ 0, \dots, I-1\right\} $ and $ \gamma([0, 1])\subset\bigcup_{i}b_{i} $.

Step 2: For two points $ \hat{p}_{1}, \hat{p}_{2}\in\mathring{{\bf{x}}} $ with $ \tilde{\eta}_{i}: = \tilde{\eta}(p_{i}) $ and $ \mathbb{B}_{{\tilde{\eta}_{2}}}{\left({\hat{p}_{2}}\right)}\cap\mathbb{B}_{{\tilde{\eta}_{1}}}{\left({\hat{p}_{1}}\right)}\neq\emptyset $ and $ \eta_{1} > \eta_{2} $ we find due to Eq (3.12) that $ \mathbb{B}_{{\frac{1}{8}\tilde{\eta}_{2}}}{\left({\hat{p}_{2}}\right)}\subset\mathbb{B}_{{\tilde{\eta}_{1}}}{\left({\hat{p}_{1}}\right)} $. Hence for the convex hull holds $ {\mathrm{conv}}{\left({\mathbb{B}_{{\frac{1}{8}\tilde{\eta}_{2}}}{\left({\hat{p}_{2}}\right)}\cup\mathbb{B}_{{\frac{1}{8}\tilde{\eta}_{1}}}{\left({\hat{p}_{1}}\right)}}\right)}\subset\mathbb{B}_{{\tilde{\eta}_{1}}}{\left({\hat{p}_{1}}\right)} $ and according to Eq (3.12) together with Lemma 2.7 we find

We define $ \tilde{{\bf{ \pmb{\mathsf{ γ}}}}}(\hat{p}_{1}, \hat{p}_{2}) = \tilde{{\bf{ \pmb{\mathsf{ γ}}}}}(\hat{p}_{2}, \hat{p}_{1}): = \mathbb{B}_{{\tilde{\eta}_{1}}}{\left({\hat{p}_{1}}\right)} $.

Let $ p_{1}, p_{2}\in{\bf{x}}_{\partial} $, with $ \tilde{\rho}_{i}: = \tilde{\rho}(p_{i}) $ and $ \mathbb{B}_{{\tilde{\rho}_{2}}}{\left({p_{2}}\right)}\cap\mathbb{B}_{{\tilde{\rho}_{1}}}{\left({p_{1}}\right)}\neq\emptyset $. We find for $ {\mathfrak{r}}_{i} $ and $ y_{i} $ given by Corollary 2.4 w.l.o.g. $ \mathbb{B}_{{{\mathfrak{r}}_{2}}}{\left({y_{2}}\right)}\subset\mathbb{B}_{{3\tilde{\rho}_{1}}}{\left({p_{1}}\right)} $ and $ {\mathfrak{r}}_{1} < {\mathfrak{r}}_{2} $. Furthermore, there exists a connected set $ \tilde{{\bf{ \pmb{\mathsf{ γ}}}}}(y_{1}, y_{2}) $ consisting of $ \mathbb{B}_{{{\mathfrak{r}}_{2}}}{\left({y_{2}}\right)} $ and of two cylinders inside $ {\bf{p}}\cap\mathbb{B}_{{\frac{1}{8}\delta(p_{1})}}{\left({p_{1}}\right)} $ of radius $ {\mathfrak{r}}_{1} $ and length smaller than $ \tilde{\rho}(p_{1})\left(1+M\right)^{n}(p_{1}) $ such that $ \mathbb{B}_{{{\mathfrak{r}}_{1}}}{\left({y_{1}}\right)}\subset\tilde{{\bf{ \pmb{\mathsf{ γ}}}}}(y_{1}, y_{2}) $ and $ \mathbb{B}_{{{\mathfrak{r}}_{2}}}{\left({y_{2}}\right)}\subset\tilde{{\bf{ \pmb{\mathsf{ γ}}}}}(y_{1}, y_{2}) $. Together this implies with Lemma 2.7

We define $ \tilde{{\bf{ \pmb{\mathsf{ γ}}}}}(p_{1}, p_{2}) = \tilde{{\bf{ \pmb{\mathsf{ γ}}}}}(p_{2}, p_{1}): = {\bf{p}}\cap\mathbb{B}_{{\frac{1}{8}\delta(p_{1})}}{\left({p_{1}}\right)} $.

Let $ p_{1}\in{\bf{x}}_{\partial} $, $ \hat{p}_{2}\in\mathring{{\bf{x}}} $ with $ \tilde{\rho}_{1}: = \tilde{\rho}(p_{1}) $, $ \tilde{\eta}_{2}: = \tilde{\eta}(p_{2}) $ and $ \mathbb{B}_{{\tilde{\eta}_{2}}}{\left({\hat{p}_{2}}\right)}\cap\mathbb{B}_{{\tilde{\rho}_{1}}}{\left({p_{1}}\right)}\neq\emptyset $. According to (3.13) we find $ \mathbb{B}_{{\frac{1}{8}\tilde{\eta}_{2}}}{\left({\hat{p}_{2}}\right)}\subset\mathbb{B}_{{2\tilde{\rho}_{1}}}{\left({p_{1}}\right)} $ and from here we conclude similar to the previous case

We define $ \tilde{{\bf{ \pmb{\mathsf{ γ}}}}}(p_{1}, \hat{p}_{2}) = \tilde{{\bf{ \pmb{\mathsf{ γ}}}}}(\hat{p}_{2}, p_{1}): = {\bf{p}}\cap\mathbb{B}_{{\frac{1}{8}\delta(p_{1})}}{\left({p_{1}}\right)} $.

Step 3: Let $ \left(Y_{i}\right)_{i = 0, \dots, I} $ be the sequence of points constructed in Step 1 and we assume w.l.o.g that every point appears only once in the sequence (otherwise the path may be shortened). Let $ {\bf{ \pmb{\mathsf{ γ}}}}(x, y): = \bigcup_{i = 0}^{i-1}\tilde{\gamma}(Y_{i}, Y_{i+1}) $. Then $ \gamma([0, 1])\subset{\bf{ \pmb{\mathsf{ γ}}}}(x, y) $ and by Step 2, the total bound on the number of local overlaps (3.15) of $ {\mathbb{B}}_{\eta_{i}} $ and estimate (3.5) on the local bound on the number of overlapping $ \mathbb{B}_{{\delta_{i}}}{\left({p_{i}}\right)} $, the condition (3.14), Remark 2.5 and the triangle inequality we find $ C > 0 $ such that Eqs (3.16) and (3.17) holds. □

3.5.   Proof of Theorem 1.6

Proof. Throughout the proof, $ C > 0 $ is a varying constant depending on $ s, r, q, \tilde{q}, {\mathfrak{r}} $, $ d, {\bf{Q}} $ but not on $ {\bf{p}} $ or $ N $.

Step 1: For simplicity of notation, set $ N = 1 $ during Steps 1 and 2 but keep in mind that the constant $ C $ below does not depend on $ {\bf{Q}} $ unless this is state explicitly. In view of Theorem 3.1 it remains to derive estimates on the terms

in terms of $ C({\bf{Q}}, {\bf{p}})\left(\frac{1}{\left|{\bf{Q}}\right|}\int_{{\bf{p}}(\omega)\cap{\mathbb{C}}{\left({{\bf{Q}}, {\bf{x}}_{{\mathfrak{r}}}}\right)}}\left|\nabla u\right|^{p}\right)^{\frac{r}{p}} $.

Denoting $ c_{i}: = \rho_{n, i}^{-1} $ and $ \tilde{c} = \rho_{n, [\tilde{\rho}_{n}]}^{-1} $ observe $ c_{i}\leq\tilde{c} $ and apply Lemma 3.7 and Jensens inequality:

We write $ {\mathbb{B}}_{a}: = \mathbb{B}_{{{\mathscr{R}}(x_{a})}}{\left({x_{a}}\right)} $ and make use of $ \Phi_{a}\phi_{i}\left|{\bf{ \pmb{\mathsf{ γ}}}}(x_{a}, y_{i})\right|^{r-1}\leq\Phi_{a}\phi_{i}\left|{\mathbb{B}}_{a}\right|^{r-1} $, $ {\bf{ \pmb{\mathsf{ γ}}}}(x_{a}, y_{i})\subset{\mathbb{B}}_{a} $ and $ \sum_{i\neq0}\phi_{i}\leq1 $ to find for $ s\in(r, p) $ from Hölder's inequality

From Jensen's inequality and the fact that $ \left|{\mathrm{supp}}\Phi_{a}\right|\leq{\mathfrak{d}}_{a}^{d} $ and $ \sum\Phi_{a}^{\frac{s}{s-r}}\leq1 $ we find

Next, we simplify the notation and write $ \mathit{{\rlap{-} \smallint }}_{{\mathbb{C}}}f: = \frac{1}{\left|{\bf{Q}}\right|}\int_{{\mathbb{C}}{\left({{\bf{Q}}, {\bf{x}}_{{\mathfrak{r}}}}\right)}}f $. For $ q $ and $ \tilde{q} $ with $ \frac{s}{p}+\frac{1}{q}+\frac{s}{r\tilde{q}} = 1 $ it then holds

Now define $ \tilde{\Phi}_{a, l}: = \frac{\partial_{l}\Phi_{a}}{D_{l+}^{\Phi}} $. Since the number of cells interacting with the support of $ \Phi_{a} $ is limited by $ \left(4{\mathfrak{d}}(x_{a}){\mathfrak{r}}^{-1}\right)^{2} $ and with Eq (3.1) we observe $ D_{l+}^{\Phi}\leq\sum_{a}{\mathfrak{d}}(x_{a})^{2d}\, \chi_{G_{a}}(x) $. Hence by a similar calculation to the estimate of $ I_{1} $

We make use of $ \Phi_{a}\tilde{\Phi}_{b, l}\left|{\bf{ \pmb{\mathsf{ γ}}}}(x_{a}, x_{b})\right|^{r}\leq\Phi_{a}\tilde{\Phi}_{b, l}\left|{\mathbb{B}}_{a}\right|^{r} $, $ {\bf{ \pmb{\mathsf{ γ}}}}(x_{a}, x_{b})\subset{\mathbb{B}}_{a} $ and $ \sum_{b}\tilde{\Phi}_{b, l}\leq1 $ as well as the definition of $ {\mathbb{C}}{\left({{\bf{Q}}, {\bf{x}}_{{\mathfrak{r}}}}\right)} $ to find that

Step 2: We continue deriving an estimate on $ \frac{1}{\left|{\bf{Q}}\right|}\int_{{\mathbb{C}}{\left({{\bf{Q}}, {\bf{x}}_{{\mathfrak{r}}}}\right)}}{\mathfrak{z}}^{r\tilde{q}} $ in terms of $ (\delta, M) $.

We first observe that

Since the first integral on the right hand side can be estimated using Lemma 2.6, we focus on the second integral. Because of Lemma 2.2 it holds for the support

for the family of points $ p_{k} $ given by Corollary 2.4 resp. Lemma 3.6. Using that the covering with $ {\mathbb{B}}_{k} $ is absolutely locally bounded it holds

and using

we find

Step 3: Let now $ N > 1 $, i.e., replace $ {\bf{Q}} $ by $ N{\bf{Q}} $ in the above calculations. We observe from Lemma 3.4 for sufficiently large $ N_{0} $ and every $ N > N_{0} $ that

Given Theorem 3.1, the definition of $ I_{1} $ and $ I_{2, l} $ as well as Eqs (3.20)–(3.25) we find

where the finite positive constants $ C_{0}, C_{00} $ depend only on $ r, s, p $ and $ q, \tilde{q} $ as well as $ d $, $ {\mathfrak{r}} $ and $ {\bf{Q}} $ but not on $ N $ and where

with $ f_{\alpha, n} $ given by Theorem 3.1 and

It remains to show that $ C_{i, N} $, $ i = 1, 2, 3 $, are bounded independently from $ N $. Due to the ergodic theorem, this is guarantied if

Step 4: Using Lemma 2.6 and $ M_{[\frac{3\delta}{8}, \frac{\delta}{8}], {\mathbb{R}^{d}}} > M_{[\frac{1}{8}\delta], {\mathbb{R}^{d}}} > M_{[\tilde{\rho}_{n}], {\mathbb{R}^{d}}} $ as well as $ M_{\frac{3\delta}{4}} > M_{[\frac{3\delta}{8}, \frac{\delta}{8}], {\mathbb{R}^{d}}} $ on $ \partial{\bf{p}} $ we infer

Taking the limit $ N\to\infty $ and using the ergodic theorem in its form Eq (2.17) we obtain the condition

Similarly we can show that

Step 5: We observe from the lower bound on $ {\mathfrak{d}} $ and $ {\mathscr{R}} $ that

Lemma 2.11 now shows that

Step 6: Steps 4 and 5 imply (3.27) and the theorem is thus proved in the first case. In the second case, if $ {\mathscr{S}} $ and $ {\mathfrak{d}} $ are independent, we can proceed in a similar way except that $ {\mathbb{B}}_{a}: = \mathbb{B}_{{{\mathscr{S}}(x_{a}){\mathfrak{d}}(x_{a})}}{\left({x_{a}}\right)} $ and we use Part I Lemma 3.18 and thus

□

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The work was financed by DFG through the SPP2256 Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials, project HE 8716/1-1 project ID:441154659.

Conflict of interest

The authors declare that there is no conflict of interest.