Traveling wave profiles for a Follow-the-Leader model for traffic flow with rough road condition

1.   Introduction

We consider an ODE model for traffic flow with rough road condition. Given an index $i\in\mathbb{Z}$ and a time $t\ge0$, let $z_i(t)$ be the position of car number $i$ at time $t$. Let $\ell$ be the length of all cars, so that

one defines a discrete local density $\rho_i(t)$ for each car with index $i$:

By this normalized definition, the maximum car density is $\rho = 1$ where cars are bumper-to-bumper.

The road condition includes many factors, for example the number of lanes, quality of the road surface, surrounding situation, among other things. For simplicity of the discussion, we let $k(x)$ be the speed limit which reflects the various road conditions. We are particularly interested in the case where $k(x)$ is discontinuous.

At time $t$, given a distribution of car positions $\{z_i(t)\}$, the speed of each car is determined by its discrete local density and the road condition:

Here $\phi(\rho)$ is a decreasing function, with

For example, the popular Lighthill-Whitham model [18] uses,

The system of ODEs (1.2) describes the Follow-the-Leader behavior, and is referred to as the FtL model. By simple computation we obtain an equivalent system of ODEs for the local densities $\rho_i$:

Note that given the set $\{\rho_i\}$, one can recover the set for the car positions $\{z_i\}$ by $z_{i+1} = z_i + \ell/\rho_i$. The car position distribution $\{z_i\}$ is unique if we fix any car, say $z_0 = 0$.

Let $\{z_i(t), \rho_i(t)\}$ denote the solution of the FtL model. We seek stationary profiles $Q(x)$ such that the points $\{z_i(t), \rho_i(t)\}$ trace along the graph of $Q(x)$. To be specific, we require

Differentiating (1.6) in $t$, and using (1.2) and (1.5), we obtain

Using

and writing $x$ for $z_i$ (since it is arbitrary), we get

Here $x^\sharp$ is the location of the "leader" for the car located at $x$. In the literature, (1.7) belongs to a type of equations which is called a delay differential equation (DDE), or a differential equation with retarded argument. We refer to [11,12] for general treatments of DDEs.

When the road condition is uniform so that $k(x)\equiv V$ is constant, it is known that the solutions of the FtL model (1.5) converge to the scalar conservation law (cf. [10,7,16,17] and references there in)

as $\ell\to 0+$, under suitable assumptions on the initial data. In the literature it is customary to consider the flux $f$ a concave function with

This leads to the following reasonable assumption on $\phi$:

In this simpler case where $k(x) = V$, equation (1.7) takes a simpler form. Let $W(x)$ denote this stationary profile. We have

Equation (1.11) is studied by the author and collaborator in [22], where we establish the existence and uniqueness (up to horizontal shifte) of the profile $W(x)$, connecting two "boundary" conditions at the infinities

where

We show that the profile $W(x)$ is monotone and approaches $\rho_\pm$ at an exponential rate. Furthermore, we prove that the profile $W(x)$ is a local attractor for nearby solutions of the FtL model.

In this paper we consider rough road condition, and analyze the behavior of solutions in the neighborhood of a discontinuity in $k(x)$. To fix the idea, we consider the case where $k(x)$ is piecewise constant and has a jump at $x = 0$, i.e.,

The ODEs for $\rho_i$ in (1.5) take the following form

The system of ODEs in (1.13) has discontinuous right hand side. The discontinuity occurs twice for each $\rho_i$, as the car position $z_i$ crosses $x = 0$, and as its leader $z_{i+1}$ crosses $x = 0$.

The corresponding profile $Q(x)$ satisfies the following discontinuous delay differential equation (DDDE):

where

is the position for the leader of the car at $x$. Note that for the first case in (1.14) the equation is the same as (1.11). For the second case, where the car is behind the jump in $k(x)$ but the leader is ahead of the jump, the equation is different from (1.14).

Formally, as $\ell\to 0$, the car density function $\rho$ satisfies the following conservation law:

Here $k(x)$ is discontinuous at $x = 0$. Two types of jumps occur in the solution, namely the $k$-jump at $x = 0$ and the $\rho$-shock where $k$ is constant. The $\rho$-shock and its corresponding traveling wave profiles of the FtL model is studied in [22], where existence, uniqueness and local stability are proved. In this paper we consider the $k$-jump at $x = 0$, and analyze the stationary profile $Q(x)$ that connects the two constant states $\rho_\pm$ as $x\to\pm\infty$.

There are various cases, with different relations between $(V_-, V_+)$ and $(\rho_-, \rho_+)$. For each of these cases, we study the initial value problem for (1.14), with initial data given on $x\ge 0$. Due to the discontinuity in the coefficient $k(x)$, the analysis is non-trivial. The initial value problem of the DDDE (1.14) can be solved by method of steps, solving backwards in $x$ over a suitable interval in each step. At some steps, as $x$ or $x^\sharp$ cross 0, one needs to solve a discontinuous ODE. The existence and well posedness of the solutions can be established under the transversality condition, i.e., at every point where the right hand side of the ODE has a jump, the vector field for ODE crosses the curve of jump transversally. For literature on discontinuous ODEs and transversality condition, we refer to [4,5,6,13] and the references therein.

We also show that the solution of the initial value problem with suitable initial data gives the desired stationary profile $Q(x)$ with the given boundary conditions at the infinities. For different cases we prove that: (ⅰ) there exist infinitely many profiles, (ⅱ) there exists exactly one profile, or (ⅲ) no profile exists. Depending on the case, some of the profiles attract nearby solutions for the FtL model, while others are unstable.

We compare our result to the classical vanishing viscosity approach. The conservation law (1.15) can be approximated by a viscous equation

where $\varepsilon>0$ is a small parameter representing the viscosity. When $k(x)$ has a jump as in (1.12), the $k$-jump at $x = 0$ has a corresponding stationary viscous profile $\rho^\varepsilon(x)$, satisfying the ODE

where

Monotone viscous profiles exist if one of the followings holds:

● We have $\rho_- < \rho_+$ and there exists a $\hat\rho \in[\rho_-, \rho_+]$ such that

● We have $\rho_->\rho_+$ and there exists a $\hat\rho \in[\rho_+, \rho_-]$ such that

See [14,20,15] for more details. For other general references on scalar conservation law with discontinuous coefficient, we refer to a survey paper [1] and the references therein. Other related references on micro-macro models for traffic flow and their analysis include [2,3,9,19]. We would like to mention a recent work [8] (and the references therein), which considers the traveling waves for degenerate diffusive equations on network, where a necessary and sufficient algebraic condition is established for the existence of traveling waves.

The rest of the paper is organized as follows. In section 2 we present various technical Lemmas, on specific properties for the solutions of (1.14) and (1.11). Section 3 is dedicated to the case with $V_->V_+$, where 4 sub-cases are analyzed in detail. The analytical result is also confirmed by numerical simulations. For one sub-case, we also show that the profiles $Q(x)$ are attractor for the solutions of the FtL model. The case with $V_- <V_+$ is studied in section 4, following a similar line of approach as in section 3. The analysis for the main sub case here is much more involving due to the lack of monotonicity. In section 5 we present a numerical simulation with "Riemann initial data". Finally, concluding remarks are given in section 6.

2.   Technique lemmas

For the rest of the paper, we denote the flux functions

Since the jump is stationary, the Rankine-Hugoniot condition requires

We note that the cases with $\bar f = 0$ are trivial, since they represent the cases where the road is either empty or completely bumper-to-bumper. Indeed, we have:

● If $\rho_- = \rho_+ = 0$ then there is no car on the road;

● If $\rho_- = \rho_+ = 1$ then the road is completely bumper-to-bumper with cars and no one moves;

● If $\rho_- = 0, \rho_+ = 1$, then there is no car on $x <0$ but completely bumper-to-bumper on $x>0$, therefore no one moves.

For the rest of the discussion, we assume

We start with some definitions.

Definition 2.1. Let $Q(x)$ be a continuous function defined on $x\in\mathbb{R}$ with $0 < Q(x) <1$. We call a sequence of car positions $\{z_i\}$ a distribution of car positions generated by $Q(x)$, if

Note that if one imposes $z_0 = 0$, then the distribution $\{z_i\}$ is unique.

Definition 2.2. Given a profile $Q(x)$ and a distribution of car positions $\{z_i(t)\}$. Let $\{\rho_i(t)\}$ be the corresponding discrete densities for the cars, computed as (1.1). We say that $\{z_i(t), \rho_i(t)\}$ traces along $Q(x)$, if

The following Lemma is immediate.

Lemma 2.3. Let $Q(x)$ be a given profile and $\{z_i(0)\}$ be a distribution generated by $Q(x)$. Let $\{z_i(t)\}$ be the solution of (1.2) with initial data $\{z_i(0)\}$, and let $\{\rho_i(t)\}$ be the corresponding discrete density. Then, $Q(x)$ satisfies (1.7) if and only if $\{z_i(t), \rho_i(t)\}$ traces along $Q(x)$.

Solutions of (1.7) exhibit a periodical behavior.

Lemma 2.4. (Periodicity) Let a continuous function $Q(x)$ be given on $x\in\mathbb{R}$ with $0 <Q(x) <1$. Let $\{z_i(0)\}$ be a distribution of car positions generated by $Q(x)$, and let $\{z_i(t)\}$ be the solution of the FtL model (1.2) with this initial data. Then the followings are equivalent.

(a) $Q(x)$ satisfies the equation (1.7);

(b) There exist a constant period $t_p$ such that

Proof. We first prove that (b) implies (a). Writing

and using

the time it takes for car no $i$ to reach the position of its leader is

Differentiating the above equation in $x$ on both sides, one gets

which easily leads to (1.7). The proof for (a) implies (b) can be obtained by reversing the order of the above arguments.

The next lemma connects the period $t_p$ with the flux $\bar f$ at the infinities.

Lemma 2.5. (i) In the setting of Lemma 2.4, if we have

then the period is determined as

(ii) On the other hand, if the period $t_p$ is given and the solution approach some asymptotic limits such that

then the limits must satisfy

The proof is for Lemma 2.5 is the same as the proof of Lemma 2.7 in [22]. We skip the details.

Next Lemma shows that the solution $Q(x)$ is monotone in some sense of "average".

Lemma 2.6. Let $Q(x)$ be a profile that satisfies (1.7). Given $x$, we let

be the position of the leader for the car at $x$. Then, for any $x$, we have

When $k(x)\equiv V$ is constant on $[x, x^\sharp]$, (2.7) is simplified to

Proof. The Lemma follows immediately from the periodicity property in Lemma 2.4

and subtracting from it the identity

Remark 2.1. Since $\phi' <0$, the mapping $\rho\mapsto (1/\phi(\rho))$ is monotone increasing. Then, (2.8) roughly says that if $f(V, Q(x)) > \bar f$ at some $x$, then some "averaged-value" of $Q$ on $[x, x^\sharp]$ is larger than $Q(x)$, so in "average" $Q(x)$ is increasing. Similarly, if $f(V, Q(x)) < \bar f$ at some $x$, then in "average" $Q(x)$ is decreasing.

Lemma 2.7. Let $Q(x)$ be a profile that satisfies (1.7). Let $\{z_i\}$ be a distribution of car positions generated by $Q(x)$. Then, for any $y$ with

we have

Proof. We prove by contradiction. We first assume that

By the periodic property in Lemma 2.4, we have

a contradiction. We now assume

But again, the periodic property in Lemma 2.4 implies

again a contradiction. Thus, we conclude (2.9), completing the proof.

We now establish the invariant regions $Q(x)>\rho_-$ and $Q(x) <\rho_-$, on $x <0$.

Lemma 2.8. Let $k(x)$ be the step function in (1.12), and let $Q(x)$ be a profile that satisfies (1.14) with

Let $\rho^*$ be the unique stagnation point where $f_-'(\rho^*) = 0$, and $\rho_- <\rho^*$ be the value that satisfies $f_-(\rho_-) = \bar f$. Denote the interval

Then, the followings hold.

(a) If $f_-(Q(x)) > \bar f$ and $Q(x)>\rho_-$ for $x\in I$, then the same holds for all $x\le y$.

(b) If $f_-(Q(x)) <\bar f$ and $Q(x) <\rho_-$ for $x\in I$, then the same holds for all $x\le y$.

In both cases, we have

Proof. We only prove (a), while the proof for (b) is similar. The proof is achieved by contradiction. Suppose that $f_-(Q(x)) > \bar f$ and $Q(x) > \rho_-$ on $x\in I$. First, we assume that $Q(x)$ can be less than $\rho_-$ for $x\le y$. Let $\bar y$ be the right most point where $Q(x)$ crosses $\rho_-$, such that

Now (2.8) implies that the "average" value of $Q(x)$ on the interval $[\bar y, \bar y+\ell/Q(\bar y)]$ is $\rho_-$. Clearly, this contradicts (2.10). On the other hand, we assume that $Q(x)$ can be bigger than $\hat \rho$ where $f_-(\hat \rho) = \bar f$ and $\hat \rho >\rho^*$. Let $\hat y$ be the right most point where $Q(x)$ crosses $\hat\rho$, such that

Again, this contradicts (2.8), proving (a).

To prove the asymptotic limit as $x\to-\infty$, let $\{z_i\}$ be a distribution of car position generated by $Q(x)$ with $z_0 = y^\sharp$, and denote the interval $I_k = [z_k, z_{k+1}]$. Let

and let $\{y_k\}$ be the points where these maxima are attained:

We claim that

which implies that

Indeed, if $Q(x)$ is monotone on $I_k$ for some $k\le -2$, then $Q(x)$ must be monotone increasing on $I_k$ due to (2.8). An induction argument shows that $Q(x)$ is monotone on $x\le z_k$. Then

Now, (2.8) gives

which implies

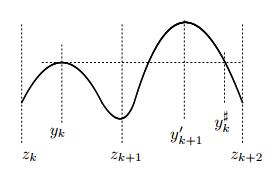
Now consider the case where $Q(x)$ is not monotone on any interval $I_k$, such that $x\mapsto 1/\phi(Q(x))$ is oscillatory with at least one local minimum or local maximum on any $I_k$ for $k\le -2$. Then, generically for some index $k <-2$, $M_k$ is attained at a local maximum of $1/\phi(Q(x))$, say $y_k\in I_k$. Then $y_k$ is the local maximum of $Q(x)$ on $I_k$, with $Q'(y_k) = 0$. Denoting its leader as $y^\sharp_k$, we have $y^\sharp_k \in I_{k+1}$ by Lemma 2.7. Also, $Q'(y_k) = 0$ implies that $Q(y_k) = Q(y_k^\sharp)$. Then (2.8) implies that there exists a local maximum $y'_{k+1} \in ( z_{k+1}, y^\sharp_k)$ with $Q(y'_{k+1})>Q(y_k)$. See Figure 1 for an illustration.

Furthermore, applying (2.8) on $[y_k, y_k^\sharp]$ we get

Since $M_{k+1} \ge \frac{1}{\phi(Q(y'_{k+1}))} $, this gives

completing the proof.

Lemma 2.9. (Ordering of the profiles) Assume that there exist multiple profiles that solve the equation (1.14) with asymptotes $\rho_\pm$ that satisfies (2.2). Then the graphs of these profiles never intersect.

Proof. We prove by contradiction. Assume that there exist two profiles $Q_1(x), Q_2(x)$ which intersect at a point $y$, such that

Let

be the position of the leader for the car at $y$ for both profiles, and let $t_{p, 1}$ and $t_{p, 2}$ be the times for the car at $y$ to reach its leader's position at $y^\sharp$, tracing along $Q_1(x)$ and $ Q_2(x)$, respectively. Then

Since both profiles $Q_1, Q_2$ approach the same asymptotic limits, by Lemma 2.5 one must have $t_{p, 1} = t_{p, 2}$, a contradiction.

3.   Case 1: $V_->V_+$

In this section we consider the case where the speed limit has a downward jump at $x = 0$. Recall the Rankine-Hugoniot jump condition (2.2). Fix a $\bar f$, with

and let $\rho_1^-, \rho_2^-, \rho_1^+, \rho_2^+$ be the unique values that satisfy

See Figure 2 for an illustration. Note that we may have $\rho_1^+ = \rho^* = \rho_2^+$ when $\bar f = f_+(\rho^*)$.

There are 4 possible combinations of $(\rho_-, \rho_+)$ which satisfy (3.1):

1A. $(\rho_-, \rho_+) = (\rho_1^-, \rho_2^+)$, i.e., $0 <\rho_- < \rho^* < \rho_+ <1$;

1B. $(\rho_-, \rho_+) = (\rho_1^-, \rho_1^+)$, i.e., $0<\rho_- < \rho_+ \le \rho^*$;

1C. $(\rho_-, \rho_+) = (\rho_2^-, \rho_2^+)$, i.e., $ \rho^* < \rho_+<\rho_-<1$;

1D. $(\rho_-, \rho_+) = (\rho_2^-, \rho_1^+)$, i.e., $ 0<\rho_+\le\rho^* < \rho_-<1$.

We denote by $W(x)$ the unique stationary profile that satisfies (1.11), with

Note that any horizontal shifts of $W(x)$ is again a solution of (1.11). The existence and uniqueness of such a profile is proved in [22].

We also recall Lemma 2.5 in [22], where the following is proved:

● As $x\to\infty$, $Q(x)$ can approach $\rho_+$ asymptotically with exponential rate only if $\rho_+ > \rho^*$. This means, if $\rho_+ \le \rho^*$, the asymptote is unstable.

● As $x\to-\infty$, $Q(x)$ can approach $\rho_-$ asymptotically with exponential rate only if $\rho_- < \rho^*$. This means, if $\rho_- \ge \rho^*$, the asymptote is unstable.

We discuss each sub-case in detail in the rest of this section.

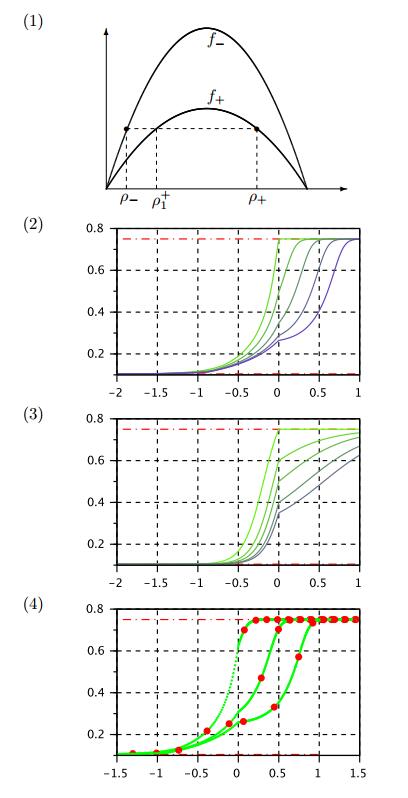
3.1.   Case 1A: $0 <\rho_- < \rho^* < \rho_+ <1$

Since here $\rho_+>\rho^*$ is a stable asymptote, on $x>0$ the solution for $Q(x)$ must be either some horizontal shift of $W(x)$ or the trivial solution $Q(x) \equiv \rho_+$. For different horizontal shifts, these profiles take different values of $Q(0)$. In all cases, we have

3.1.1.   The initial value problems

Once $Q(x)$ is given for $x\ge 0$, one can solve (1.14) backward in $x$ as an "initial value problem". It is understood that the derivative in (1.14) is the left derivative, as one solves the equations backward in $x$. The profile $Q(x)$, if exists, can have kinks, but remains continuous. Next Theorem provides well posedness of this initial value problem.

Theorem 3.1. (Well posedness of the initial value problems) Let $V_->V_+$. Given $\rho_+$ such that $\rho^* <\rho_+ <1$. Consider the initial value problem for (1.14), where an initial data is given on $x\ge0$, as either a horizontal shift of $W(x)$ or the constant function $\rho_+$. Then, the initial value problem has a unique monotone solution $Q(x)$ on $x <0$.

Proof. The proof takes a couple of steps.

Step 1. In the $(x, Q)$ plane, let $\mathcal{C}_0$ be the vertical line where $x = 0$, and let $\mathcal{C}_1$ be the graph of the function $h(x) = -\ell/x$, for $x <-\ell$. The curve $\mathcal{C}_1$ indicates the position and local density of the cars whose leader is at $x = 0$. Since the car length is $\ell$, the position of these car must be less than $-\ell$, so $h(x)$ is only defined on $x <-\ell$. The discontinuities in (1.14) occur along $\mathcal{C}_0$ and $\mathcal{C}_1$. To ensure the existence and uniqueness of solutions, we must verify that the vector field of the DDDE (1.14) must cross the curves of discontinuity transversally, see [4].

Along $\mathcal{C}_0$, the discontinuity line is vertical, with infinite tangent. Thus, we need that

This is easily verified from (1.14), since $Q(0)\le \rho_+ <1$ so $\phi(Q(0)) >0$.

Along the curve $\mathcal{C}_1$, the tangent at a point $(x, h(x))$ is

Let $Q(x)$ be a profile that solves (1.14), and let $y <0 $ be its intersection point with $\mathcal{C}_1$ such that $Q(y) = h(y)$. It suffices to show that

Indeed, from (1.14) we have

Thus (3.4) holds since $Q(0) <1$ and $\phi(Q(0))>0$.

Step 2. Once the transversality properties (3.3)-(3.4) are established, the existence and uniqueness of the solution for $Q(x)$ is achieved by method of steps. Denote

Consider $I_1$. If $x\in I_1$, then its leader $x^\sharp$ is located at

We have an ODE with discontinuous right hand side, with

where $Q(x^\sharp)$ is given by the initial data on $x\ge0$. Standard theory for discontinuous ODEs (see [4]) gives a uniqueness solution on $I_1$, provided that $Q(x)$ satisfies $ 0 < Q(x) < 1$ on $I_1$. Indeed, the lower bound $Q(x)> 0$ is a consequence of the fact that $0$ is a critical point. Assuming that $Q(x)$ becomes negative on some subset of $I_1$, then there exists a point $\hat x \in I_1$ such that $Q(\hat x) = 0$ and $Q'(\hat x)>0$. But this is not possible because by (1.14) we have

To prove the upper bound, we claim that $Q'(x) >0$ on $I_1$. We argue with contradiction. Assuming that $Q(x)$ is not monotone on $I_1$, then there exists a point $y \in I_1$ such that

Since $Q'(0-)>0$, then $y <0$, and we have

Now (3.5) and $Q'(y) = 0$ imply

Since $V_->V_+$ and $\phi' <0$, we get

a contradiction to (3.6).

Step 3. We iterate the argument in Step 2 for $k = 2, 3, \cdots$, until $I_k$ crosses the curve $\mathcal{C}_1$. After that, (3.5) is replaced by

The same argument follows. This proves the existence and uniqueness of a monotone solution $Q(x)$ on $x <0$, for the initial value problem.

3.1.2.   The boundary value problems

Next Corollary establishes the existence of infinitely many monotone profiles $Q(x)$ for the boundary value problem, with given boundary conditions $\rho_-$ and $\rho_+$ at $ \pm\infty$.

Corollary 3.2. Let

There exist infinitely many monotone profiles $Q(x)$ which satisfy the DDDE (1.14), and the boundary conditions

Moreover, these profiles never intersect with each other, and

Proof. In Theorem 3.1 we show that there exist many profiles $Q(x)$ that satisfy (1.14), (3.9), and the second boundary condition in (3.8). Let $Q(x)$ be such a profile. It remains to show that the first boundary condition in (3.8) holds. Since $Q(x)$ is monotone and bounded below by $0$, then there exists an asymptotic limit as $x\to-\infty$. Since $\lim_{x\to\infty} Q(x) = \rho_+$, by part (ⅰ) of Lemma 2.5 the period must be

By part (ⅱ) of Lemma 2.5 the limit at $x\to-\infty$ must be $\rho_-$ which satisfies $f^-(\rho_-) = \bar f$. Since $\rho_-$ must a stable asymptote, we have $\rho_- \le\rho^*$.

The non-intersecting property of the profiles follows from Lemma 2.9.

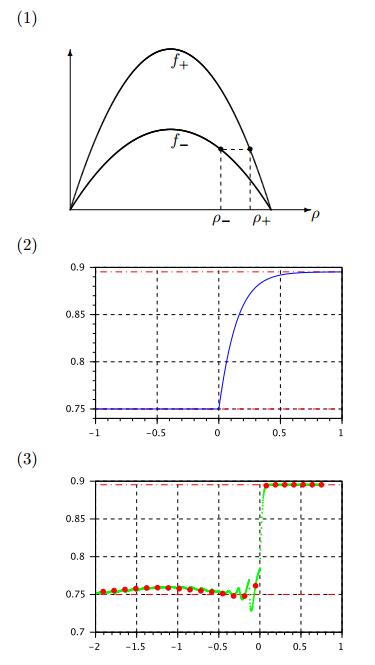
Sample profiles of $Q(x)$ with various $Q(0)$ values are illustrated in Figure 3 plot (2), using

As comparison, we also illustrate the stationary viscous profiles. For this sub-case there exist infinitely many stationary monotone viscous profiles that satisfy the ODE (1.17). For each value of $\rho^\varepsilon(0) \in (\rho_1^+, \rho_+]$, there exists a unique viscous profile. Sample viscous profiles $\rho^\varepsilon(x)$ with $\varepsilon = 0.2$ and with various $\rho^\varepsilon(0)$ values are given in Figure 3 plot (3).

3.1.3.   Local stability of the profiles

We have shown that for each given $Q(0)\in(\rho_1^+, \rho_+]$, there exists a unique stationary profile $Q(x)$. Let $Q^\sharp(x)$ be the profile with $ Q^\sharp(0) = \rho_+$, and let $Q^\flat(x)$ be the limit profile as $Q(0) \to \rho_1^+$. We define the domain

Clearly all profiles of $Q(x)$ lie in $D$. We now show that $D$ is a basin of attraction of the solution of the FtL, in the sense described below.

Since all the profiles in $D$ never cross each other, we can parametrize the family of profiles, say by the value $Q(0)$. By continuity, any point $( x, y)\in D$ belong to a unique profile, call it $Q_{( x, y)}$ such that

For any point $(x, y)\in D$, we define the function

Theorem 3.3. Consider the setting of Corollary 3.2 and let $D$ be defined as in (3.10). Let $\{z_i(0)\}$ be a set of initial car positions and $\{\rho_i(0)\}$ be the corresponding discrete density defined as (1.1), and assume that

Let $\{z_i(t)\}$ be the solution of the FtL model with this initial data, and let $\{\rho_i(t)\}$ be the corresponding discrete density. Then

Denote

and define the total variation

Then, we have

Thus, asymptotically the points $\{z_i(t), \rho_i(t)\}$ trace along the profile $Q(x)$ with $Q(0) = \tilde\Psi$ as $t\to\infty$.

Proof. We first assume (3.13) and prove (3.14). Fix a time $\tau\ge0$. It suffices to show the followings:

(ⅰ) If $\Psi_m(\tau) > \Psi_{m+1}(\tau)$ at time $\tau$ for some $m$, then $ \frac{d}{dt} \Psi_m(\tau) <0 $; and

(ⅱ) If $\Psi_n(\tau) < \Psi_{n+1}(\tau)$ at time $\tau$ for some $n$, then $ \frac{d}{dt} \Psi_n(\tau) >0 $.

We prove (ⅰ) while (ⅱ) can be proved in an entirely similar way. Let $\hat Q(x)$ be the profile that passes through the point $\{z_m(\tau), \rho_m(\tau)\}$. By the assumption $\Psi_m(\tau) > \Psi_{m+1}(\tau)$, and the point $\{z_{m+1}(\tau), \rho_{m+1}(\tau)\}$ lies below the profile $\hat Q(x)$, i.e.,

It suffices to show that

indicating that the point $(z_m(\tau), \rho_m(\tau))$ moves below the profile $\hat Q(x)$ as $t$ increases from $\tau$. Indeed, equation (1.7) gives

On the other hand, (1.2) and (1.5) give

Since $\rho_m = \hat Q(z_m)$, together with (3.15), we conclude (3.16).

We now prove (3.13). We consider the upper bound $Q^\sharp$, while the lower bound is entirely similar. Given a time $\tau\ge0$, we assume that $(z_i(\tau), \rho_i(\tau))\in D$ for all $i$, such that

It suffices to show that, if there exist an index $m$ such that,

then

The proof for (3.19) is entirely similar to that of (3.16), replacing $Q^\sharp$ with $\hat Q$.

Numerical approximations are computed for the solutions of the FtL model with the following "Riemann initial data",

The simulations are carried out for $0\le t \le 2$. In Figure 3 plot (4), we plot the trajectory of $z_i(t)$ (in green) for the last period

together with the car positions at $t = 2$ as thick dots (in red). The 3 profiles in the plot are for

Even though the initial data points $\{z_i(0), \rho_i(0)\}$ are not entirely in $D$, nevertheless we observe that the solutions of FtL model converge quickly to certain profiles of $Q(x)$, suggesting that Theorem 3.3 probably applies to a larger domain.

All numerical simulations in this paper are carried out using SciLab. The source codes are available from the author's web-site, see [21].

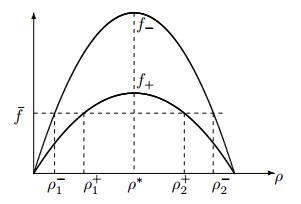
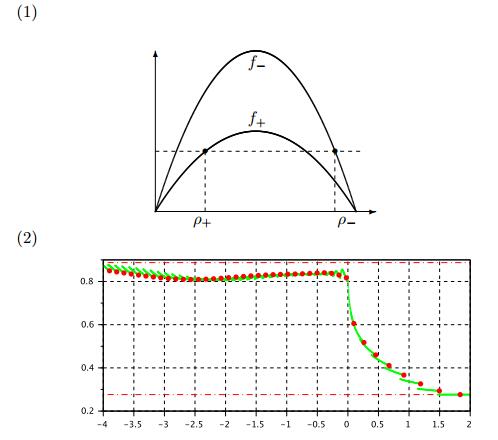
3.2.   Case 1B: $0 <\rho_- < \rho_+ \le \rho^*$

Since $\rho^+\le \rho^*$ is an unstable asymptote for $x\to+\infty$, the only solution on $x\ge 0$ is the constant solution $Q(x) \equiv \rho_+$. Once $Q(x)$ is given on $x>0$, the rest can be solved backward in $x$ using (1.14), as an initial value problem. The existence and uniqueness of the profile follows from the same arguments as those for Theorem 3.1 and Corollary 3.2. We summarize the result in next Theorem.

Theorem 3.4. Let $V_->V_+$ and $0 <\rho_- < \rho_+ \le \rho^*$ with $f_-(\rho_-) = f_+(\rho_+)$. There exists a unique monotone profile $Q(x)$ which satisfies the equation (1.14) with

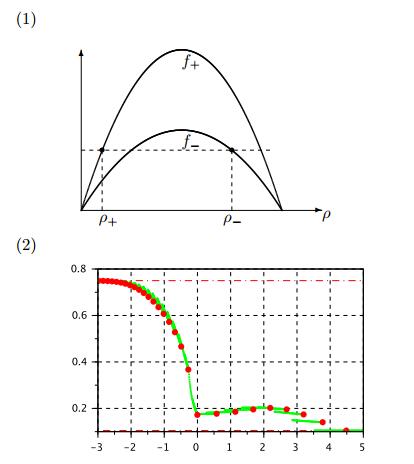
A typical plot of $Q(x)$ is given in Figure 4 plot (2). As comparison, we also plot the viscous profile $\rho^\varepsilon(x)$ in Figure 4 plot (3), with $\rho^\varepsilon(x) = \rho_+$ on $x\ge 0$. This is the only viscous profile that connects the two limit values $\rho_\pm$ at $x\to\pm\infty$.

Instability. Since $\rho_+$ is an unstable asymptote, the profile is unstable with respect to perturbations on $x>0$, and the solution of the FtL model can not converge to the profile in the sense of Theorem 3.3. Even if one starts with "Riemann" initial data with $\rho_i(0) = \rho_+$ for all $z_i(0)\ge 0$, the perturbation, initially on $x <0$, will propagate into the region $x>0$. Numerical simulation verifies this fact, see Figure 4 plot (4), where a perturbation is formed and moves into $x>0$. Although on $x <0$ the FtL solution gets very close to the profile $Q$, the stability can not be achieved on $x>0$. This forward propagating wave is caused by the fact that the characteristic speed satisfies

therefore information travels to the right.

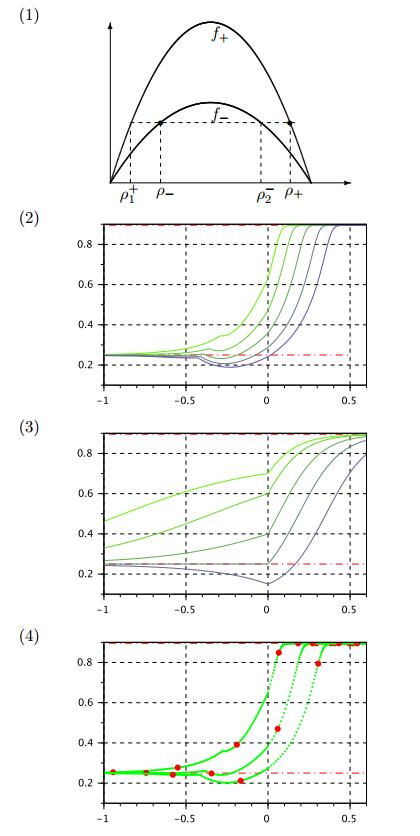
3.3.   Case 1C: $\rho^* < \rho_+ < \rho_- <1$

Since $\rho_->\rho^*$ is an unstable asymptote as $x\to-\infty$, one must have

Now consider the value $Q(0+)$. Since $Q'(-\ell/\rho_-) = 0$, equation (1.14) implies

This implies that $Q(x)$ is discontinuous at $x = 0$, which is not possible for the solution of (1.14). We have the following Theorem.

Theorem 3.5. Let $V_->V_+$ and $\rho^* < \rho_+ <\rho_- <1$ with $f_-(\rho_-) = f_+(\rho_+)$. There exists no profile $Q(x)$ that satisfies (1.14) and the boundary conditions (3.8).

We remark that for this sub-case there exists a unique viscous profile for this case, see Figure 5 plot (2). We also plot the solution of the FtL model with this "Riemann data", see Figure 5 plot (3). Observe that the solution is highly oscillatory on $x <0$, and it never settles, indicating no convergence as $t$ grows.

3.4.   Case 1D: $0 < \rho_+ \le \rho^* < \rho_- <1$

Since both $\rho_->\rho^*$ and $\rho_+ \le\rho^*$ are unstable asymptotes, one must have $Q(x) = \rho_-$ on $x <0$ and $Q(x) = \rho_+$ on $x>0$, which is not possible.

Theorem 3.6. Let $V_->V_+$ and $0 <\rho^+ < \rho^* <\rho_- <1$ with $f_-(\rho_-) = f_+(\rho_+)$. There exists no profile $Q(x)$ that satisfies (1.14) and the boundary conditions (3.8).

For this sub-case there are no monotone viscous profiles either. In Figure 6 we plot numerical simulation result for the FtL model, with "Riemann initial data". We observe oscillatory behavior on $x <0$, and a rarefaction wave behavior on $x>0$. The solution does not settle into any profile as $t$ grows.

4.   Case 2: $V_- < V_+$

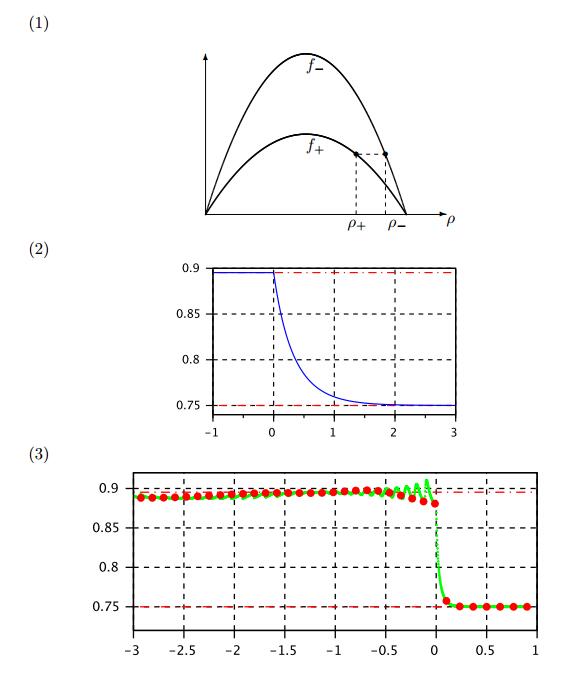
In this section we study the case where the speed limit has an upward jump at $x = 0$. The discussion for this case follows a similar path as for Case 1, but with rather different details. Given $\bar f$, which is in the range of both $f_\pm$, the candidates for $\rho_\pm$ are illustrated in Figure 7, with

We have the following 4 sub-cases:

● Case 2A: $\rho_- = \rho_1^-$ and $\rho_+ = \rho^+_2$, such that $0 <\rho_- < \rho^* < \rho_+ <1$;

● Case 2B: $\rho_- = \rho_1^-$ and $\rho_+ = \rho^+_1$, such that $ 0 <\rho_+ <\rho_- <\rho^*$;

● Case 2C: $\rho_- = \rho_2^-$ and $\rho_+ = \rho^+_2$, such that $ \rho^* \le \rho_- <\rho_+ <1$;

● Case 2D: $\rho_- = \rho_2^-$ and $\rho_+ = \rho^+_1$, such that $ 0 <\rho_+ < \rho^* \le \rho_- <1$.

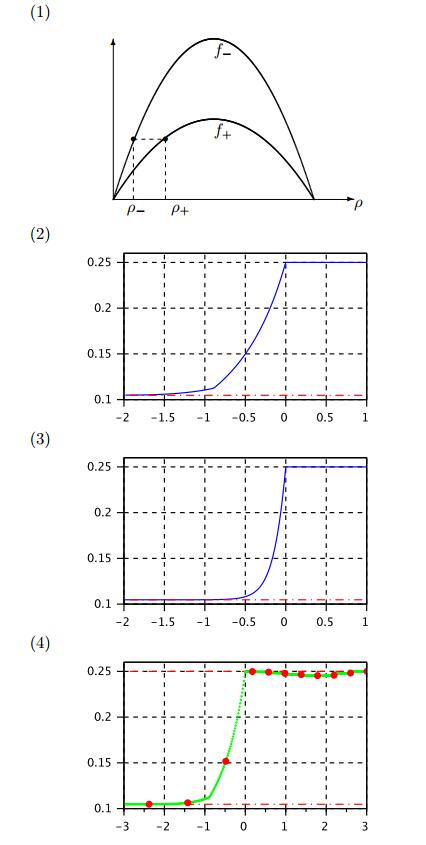
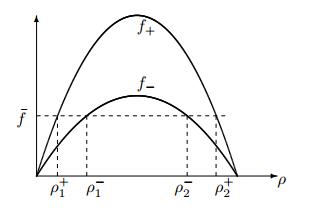
4.1.   Case 2A: $0 <\rho_- \le\rho^*< \rho_+ <1$

Here both $\rho_- < \rho^* $ and $\rho_+>\rho^*$ are stable asymptotic limits as $x \to -\infty$ and $x\to +\infty$, respectively. Then, on $x>0$, the profile $Q(x)$ must be some horizontal shift of $W(x)$. Using some horizontal shift of $W(x)$ as "initial condition", one can solve (1.7) backward in $x$ on $x <0$. In next Theorem we establish unique solution of the initial value problem for (1.14), which in turn gives us the infinitely many profiles $Q(x)$ that satisfy the proper boundary conditions at the limit $x\to\pm\infty$.

Theorem 4.1. Let $V_- <V_+$. Given $\rho_+$ such that $\rho^* <\rho_+ <1$. Consider the initial value problem of (1.14) with initial data given on $x\ge 0$ as some horizontal shift of $W(x)$, with

Then the initial value problem has a unique solution $Q(x)$ on $x <0$.

Furthermore, such a solution satisfies also

Piecing together $Q(x)$ on $x <0$ and $Q(x) = W(x)$ on $x\ge 0$, we obtain a solution to (1.14) with boundary conditions

Varying the $Q(0)$ value, always satisfying $\rho_1^+ \le Q(0) \le \rho_2^-$, one obtains infinitely many stationary wave profiles with the boundary conditions (4.3).

Proof. This Theorem is the counter part of Theorem 3.1 and Corollary 3.2 for Case 1A, but the proof here is much more involving due to the lack of monotonicity. See Figure 8.

Let the initial data be given on $x\ge0$ as some horizontal shift of $W(x)$ such that (4.1) holds. Denote by $Q(x)$ the solution for this initial value problem, solved backward in $x$ for $x <0$. Then $Q(x)$ is monotone on $x\ge 0$ with $Q'(x) > 0$. Let $\{z_i\}$ be a car position distribution generated by $Q(x)$ with $z_0 = 0$ and

We also denote the intervals

Throughout the rest of the proof, we use the simplified notations, for any index $k$,

The proof takes several steps.

Step 1. Assume that $Q(x)$ is a solution of the initial value problem, with the additional condition

We claim that

Indeed, since $Q'(x)>0$ for $x>0$, by (2.8) we have

By using $\bar f \le V_- Q_0 \phi_0$ and (4.7), we get

Equation (1.14) leads to

proving (4.6).

Step 2. We claim that on the interval $I_{-1}$ there doesn't exist any local maximum. Indeed, assume local maxima exist on $I_{-1}$, and let $y_1$ be the right most local maximum, with $Q'(y_1) = 0$. Let $y_1^\sharp >0$ be its leader. By (1.14) and $Q'(y_1) = 0$, we get

Moreover, there exists a point $y_2$, such that

Let $y_2^\sharp >0$ be its leader, where $ y_2^\sharp > y_1^\sharp >0$. Since $Q'(x)>0$ on $x>0$, we must have

On the other hand, by (1.14) and $Q'(y_2) <0$, we get

a contradiction to (4.10).

Step 3. We now show that, if (4.5) holds, then

Indeed, we know that there are no local maxima on $I_{-1}$ and $Q'(0-)>0$. If $Q(x)$ is monotone increasing on $I_{-1}$, then (4.11) trivially holds. Now consider the case where $Q(x)$ has a local minimum. We prove by contradiction. Assume that there exist a point $y \in(z_{-1}, 0)$ where

Let $y^\sharp$ be its leader, where $0<y^\sharp<z_1$. Recall (2.7), we have

which gives

Since the first integrand on the right hand side is strictly negative, we get

But (4.12) is not possible. Indeed, since $Q'(x)>0$ on $x>0$, the mapping $x\mapsto (1/\phi(Q(x)))$ is increasing. Using that

one reaches

a contradiction to (4.12).

Step 4. We now have that, for the initial value problem with initial data $W(x)$ on $x\ge 0$ satisfying (4.5), the solution $Q(x)$, defined on $x <0$, satisfies

We now claim that there exists a unique solution $Q(x)$ for the initial value problem, which satisfies

Indeed, if $Q(x)$ stays on one side of $\rho_-$ on an interval $I_k$ for some index $k\le -2$, then Lemma 2.8 provides the results. Now consider the case the $Q(x)$ is oscillatory and crosses $\rho_-$ at least once on each interval $I_k$, for $k\le -2$. We apply a similar argument as the proof for Lemma 2.8. Let

Then, we have, for some index $k\le 2$,

Let $y_k^\sharp = y_k + \ell/Q(y_k)$ denote the position of the leader for the car at $y_k$. By Lemma 2.7 we have $y_k^\sharp\in I_{k+1}$. Then $Q'(y_k) = 0$ implies that $Q(y_k) = Q(y_k^\sharp)$, and (2.8) implies

Thus, we conclude that

Therefore on $x\le 0$ there exists an upper envelope $E^\sharp (x)$ for $Q(x)$, such that

A symmetrical argument for the local minima below $\rho_-$ leads to a lower envelope $E^\flat(x)$ on $x <0$ for $Q(x)$, with

The result (4.14) follows from a squeezing argument. Finally, the uniqueness of the solution follows from the transversality properties (3.3)-(3.4), see [4].

Piecing together the solution $Q(x)$ on $x <0$ with the initial data $Q(x) = W(x)$ on $x\ge 0$, we obtain a stationary profile, calling it again by $Q(x)$ for $x\in\mathbb{R}$, that satisfies the DDDE (1.14) and the boundary conditions (4.3). Thus, we obtain infinitely many profiles for $Q(x)$, one for each $Q(0)$ value satisfying (4.5).

Step 5. Denote by $Q^\sharp(x)$ the unique profile with $Q^\sharp(0) = \rho_2^-$. By Step 3, we have

We now relax the condition (4.5) on $Q(0)$ to (4.1), i.e, $ \rho_1^+ < Q(0) < \rho_2^-$. Indeed, any profile $Q(x)$ with $ \rho_1^+ < Q(0) < \rho_2^-$ will lie below $Q^\sharp(x)$, with

By Step 4, such a profile satisfies the boundary condition (4.14), completing the proof.

Remark 4.1. We remark on the bound (4.1), in particular the upper bound $Q_0 \le \rho_2^-$, which is different from Case 1A in section 3.1. First, we show that the constant solution $Q(x)\equiv \rho_+$ on $x\ge 0$ is not valid. Indeed, with $Q_0 = Q_1 = \rho_+$, we have

Then, on the interval $I_{-1} = [z_{-1}, z_0]$, $V_- \phi(Q(x)) < V_+\phi(\rho_+)$, so $Q'(x)<0$. By induction argument one concludes that $Q'(x) <0$ for $x <0$. In fact, numerical simulation shows that $Q(x)$ blows up to $\infty$ at finite $\bar x <0$ as $x$ goes backwards.

With the upper bound $Q_0 \le \rho_2^-$ we have (4.6), and we ensure that $Q(x) < \rho_2^-$ on $x <0$, and consequently the asymptotic limit of $\rho_-$ as $x\to-\infty$. It is possible that this upper bound could be somewhat relaxed, but a sharp bound is difficult to find.

Sample profiles of $Q(x)$ are plotted in Figure 8 plot (2), where we observe that the profiles are not monotone. We also plot multiple viscous profiles $\rho^\varepsilon(x)$ in Figure 8 plot (3), as a comparison. Note that if $\rho^\varepsilon(0) \in(\rho_-, \rho_+)$, the viscous profiles are monotone, a property not preserved by $Q(x)$.

Local Stability of the Profiles. Let $Q^\sharp(x)$ be the profile with $Q^\sharp(0) = \rho_2^-$, and let $Q^\flat(x)$ be the limit profile as $Q(0) \to \rho_1^+$. Similar to Case 1A, we define a basin of attraction $D$ as (3.10). All profiles lie in $D$, and they do not intersect with each other. Parametrizing the region with these profiles, as in Theorem 3.3, we get the same local stability property. We skip the details.

Again, numerical simulations are performed for the FtL model for Case 2A, and we plot the solutions with "Riemann initial data" (3.20). See Figure 8 plot (4). We see the clear convergence to a certain profile for each choice of initial data.

4.2.   Case 2B: $ 0 <\rho_+ <\rho_- <\rho^*$

This is similar to Case 1B. Since $\rho_+$ is an unstable asymptote for $x\to\infty$, we must have $Q(x)\equiv \rho_+$ on $x\ge 0$. Using this as the initial data, one can solve $Q(x)$ backward in $x$. Since $\rho_-$ is a stable asymptote, we have $Q(x)\to \rho_-$ as $x\to-\infty$. Thus there exists a unique monotone profile $Q(x)$. For the same reason as for case 1B, this profile is not a local attractor for the solutions of the FtL model.

In Figure 9 we plot the profile $Q(x)$ in plot (2), the viscous profile $\rho^\varepsilon(x)$ in plot (3), and the solution of the FtL model with "Riemann initial data" in plot (4). Note that a perturbation enters the region $x>0$, even with initial Riemann data, indicating the instability of the profile $Q(x)$.

4.3.   Case 2C: $\rho^* \le \rho_- < \rho_+ <1$

This is the corresponding sub-case as for Case 1C. With the same argument, one concludes that there doesn't exist any profile $Q(x)$, although a viscous profile $\rho^\varepsilon(x)$ does exist. See Figure 10 plot (2). The solution of the FtL model in Figure 10 plot (3) demonstrates severe oscillation on $x <0$ which never settles as $t$ grows.

4.4.   Case 2D: $ 0 < \rho_+ <\rho^*\le \rho_- <1$

For this case, we have neither the profile $Q(x)$ nor the viscous profile $\rho^\varepsilon(x)$. We plot a solution of the FtL model in Figure 11, with "Riemann initial data". We see that the solution of the FtL model doesn't converge to any limit as time grows.

5.   A numerical simulation

We perform numerical simulation to obtain approximate solution for the FtL model, with "Riemann" initial data $(\rho^L, \rho^R)$ such that

We choose values of $(\rho^L, \rho^R)$ such that

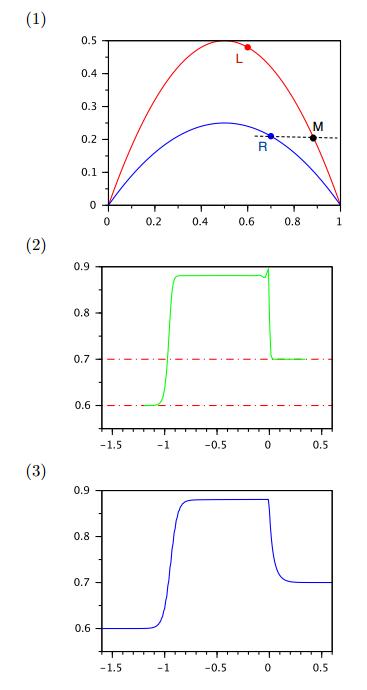
We use

The flux functions $f_-, f_+$ and the locations of $\rho^{L, R}$ are illustrated in Figure 12 plot (1), while the solution $\{z_i(T), \rho_i(T), \}$ of the FtL model is shown in plot (2). As a comparison, we also simulate the viscous conservation law

using the same Riemann data, with $\varepsilon = 0.02$ and $k(x)$ the jump function (1.12). The result is shown in plot (3).

The vanishing viscosity limit solution for the conservation law (1.15) consists of a shock with negative speed from L to M, and a stationary jump from M to R. The solution of the FtL model captures this main feature. However, due to the instability of the path M-R (where the left state is unstable), we observe oscillations behind the stationary jump at $x = 0$. We remark that the solution of the viscous conservation law with the same initial data does not contain oscillation behind $x = 0$.

6.   Concluding remarks

In this paper we derive a discontinuous delay differential equation for the stationary traveling wave profile for an ODE model of traffic flow, where the road condition is discontinuous. For various cases, we obtain results on the existence, uniqueness and local stability of the profiles.

These results offer alternative approximate solutions to the scalar conservation law with discontinuous flux, as a counter part to the classical vanishing viscosity approach. The stabilizing effect of the viscosity is not entirely present in the FtL model, where oscillations are observed behind the discontinuity in the road condition. This is caused by the "directional" influence in real life traffic, where the drivers adjust their behavior only according to situations ahead of them, not what is behind. Heuristically, this fact contributes to the "lack of viscosity" behind the jump at $x = 0$, and thus the oscillations.

The natural followup work is to investigate the convergence of solutions of the FtL model, under suitable assumptions, to some entropy admissible solution of the scalar conservation law with discontinuous flux. We expect this to be a challenging task, due to the non-monotone profiles and oscillations behind the jump in the road condition.

One may criticize the FtL model used here of being too simple, especially around the jump in the road condition, where the drivers change their speeds suddenly as they cross $x = 0$. The model is a first order approximation where one assumes instant acceleration. A high order model, where the acceleration is finite, might smooth out the behavior near $x = 0$ and remove the oscillations. However, such model would take the velocities of the cars as unknowns, and thus become much more complex.

Acknowledgments

The author is grateful to an anonymous referee for careful reading of the first manuscript and detailed comments, which led to the improvement of the manuscript.