1.
Introduction
It is clear that there is a degree of compartmental specialization in terms of dendritic cells (DC) and their roles in induction of T cell responses, including activation of effector (e.g., Th1, Th2, etc) or regulatory T cells (Tregs). Thus, hepatic, intestinal, cutaneous and pulmonary DC that present innocuous antigens to naive T cells each have distinct mechanisms to ensure that compartment-specific immune tolerance is established [1]. For example, DC that develop in association with the healthy intestine do so while exposed to epithelium-derived retinoic acid (RA) and TGFβ, such that they can induce Treg that express the lamina propria-targeting α4β7 integrin and CCR9. Indeed, such RA-induced DC can foster the differentiation of Treg that home exclusively to the lamina propria of the gut to maintain tolerance to gut-associated symbiotic bacteria and food allergens [2]. As such, when we targeted food allergies for experimental regulatory DC (DCreg) immunotherapy we utilized RA-induced DCreg (termed DC-RA), which expressed high levels of the RA metabolism-associated enzyme Aldh1A2, as well as TGFβ and IL-27. These DC-RA effectively induce allergen tolerance in mouse models of OVA and peanut oral allergies [3], reinforcing the notion that RA-induced DCreg have a natural affinity for the intestinal environment. We know from numerous studies that IL-10-differentiated DC (DC10) induce tolerance in mouse models of asthma in an IL-10-dependent manner [4]–[7].
In some respects, the observations that experimental DC10 and DC-RA induce tolerance in the context of lung and intestinal allergies respectively would seem to fit with the natural biology of the tolerogenic DC populations found in these compartments. IL-10 is important to the induction of tolerance to innocuous environmental challenges by lung DC [8]. We know that our treatment DC10 naturally track to the lungs and lung-draining lymph nodes following intraperitoneal (i.p.) injection in asthmatic mice [4] and that this coincides with an upregulation of activated allergen-specific CD25+Foxp3+ Treg in the lungs [9] and the dampening of the asthma phenotype [5],[7]. As noted, gut-associated RA and TGFβ are important to the induction of regulatory DC (DCreg) in that compartment [10]. Our DC-RA express CD103, Aldh1A2 and TGFβ [3], just as do steady-state gut-associated DC and, like these gut DC [2], they induce the differentiation of Treg that suppress the food allergic phenotype in treated mice [3]. This seeming compartment-specificity in regulatory activities could be thought of as precluding potential roles for DC10 in food allergy tolerance and, reciprocally, DC-RA in asthma tolerance. Therefore, we asked whether DC-RA could induce asthma tolerance equally as well as DC10, and reciprocally whether DC10 would be effective in inducing tolerance in the context of food allergies, in both cases as assessed in our mouse models [3],[7].
2.
Materials and methods
2.1. Animals and reagents
Six- to eight-week-old female BALB/c mice were purchased from our institutional Animal Resources Center, while DO11.10 OVA-specific TCR-transgenic mice were from the Jackson Laboratory (Bar Harbor, ME). The mice were housed in groups of 5–10 in our institutional animal facility, and allowed food and water ad libitum.
The following reagents were purchased: Lymphocyte separation medium (LSM) (Valeant Pharmaceuticals, CA); RPMI-1640 medium, fetal bovine serum (FBS), 2, 2′-azinobis (3-ethylbenthiazoline-sulfonic acid) (ABTS) peroxidase substrate solution (Gibco, Grand Island, NY); penicillin, streptomycin, L-glutamine, and 2-mercaptoethanol, OVA, all-trans retinoic acid and Tween 20 (polyoxyethylene-sorbitan monolaurate) (Sigma Chemical Co, Mississauga, ON); recombinant murine granulocyte-macrophage colony-stimulating factor (rmGM-CSF) and rmIL-10 (R&D Systems, Minneapolis, MN); rmIL-2 (Peprotech, Rocky Hill, NJ); 6-well tissue culture plates (VWR, Mississauga, ON); E.coli serotype 0127:B8 lipopolysaccharide (LPS) (MD Biosciences, St Paul, MN); rmIL-4, FITC-labeled anti-mouse CD40 (clone HM 40-3) and MHC II (clone M5/114.15.2) and isotype control antibodies, PE-Cy5-labeled anti-mouse Foxp3 antibody (clone FJK-16s) and PE anti-mouse CD4 antibody (clone GK1.5; eBioscience/ThermoFisher Scientific, Waltham, MA); FITC-labeled antibodies specific for CD86 (clone GL1), CCR5 (clone C34-3448), CCR7 (clone 4B12), CCR9 (clone CW1.2), CD103 (clone M290), α4β7 (clone DAK32), and biotinylated anti-IgG1 and -IgE antibodies (Becton-Dickenson, Mississauga, ON); type 4 collagenase and hyaluronidase (Worthington Biochemical Corp, Freehold, NJ); CD4-specific paramagnetic microbeads (Miltenyi Biotec, Auburn, CA); Immunolon-4 96-well flat-bottom ELISA plates (Dynatech Laboratories, Chantilly, VA); streptavidin-conjugated horseradish peroxidase (Vector Laboratories, Burlingame, CA); RNA extraction kits (RNeasy Mini Kits; Qiagen, Mississauga, ON); Brilliant II SYBR Green qRT-PCR Master Mix Kits (Stratagene, La Jolla, CA).
2.2. Generation and characterization of dendritic cells
Single cell suspensions of murine bone marrow cells were cultured in complete RPMI (RPMI-1640 with 100 U/mL of penicillin and streptomycin, 2 mM L-glutamine, 50 µM 2-mercaptoethanol, and 10% heat-inactivated FBS) supplemented with 20 ng/mL rmGM-CSF in 6-well plates [11]. On day 10 the levels of rmGM-CSF were reduced to 7.5 ng/mL and either IL-10 (50 ng/mL; tolerogenic DC10) [12] or E.coli serotype 0127:B8 LPS (immunostimulatory DC-LPS) [9] was added to the cells for an additional 3 days, after which the cells were pulsed overnight with 50 µg/mL OVA, and then washed 2 times before use. To generate DC-RA, the bone marrow cells were cultured in the presence of 20 ng/mL rmGM-CSF, 10 ng/mL rmIL-4, and 1 µM retinoic acid for 8 days; during the final day of culture the cells were exposed overnight to 1 µg/mL LPS and 50 µg/mL OVA, then washed 2 times before use [3]. Characterization of DCs. DCs were collected and stained with marker (CD40, CD86, MHC II, CCR5, CCR7, CCR9, CD103, α4β7)-specific or appropriate isotype control antibodies and then analyzed using an EPICS XL Flow Cytometer (Beckman-Coulter, Mississauga, ON) and Flow-Jo software (Tree Star, Ashland, Ore).
2.3. ELISA
Our ELISA protocol has been reported previously [13]. The purified capture antibody in coating buffer (1M NaHCO3, 1M Na2CO3; pH 9.6) was incubated overnight at 4 °C in Immunolon-4 plates, then blocked at room temperature for 2 h with PBS-10% FBS. For the allergen-specific IgE assays, anti-IgE was used as the capture reagent, while OVA itself was used as the capture reagent for the OVA-specific IgG1 assays. Recombinant cytokine standards, DC culture supernatants or bronchoalveolar lavage fluids (BALF) for detection of IL-4, IL-5, IL-9, IL-13, IL-27 or TGF-β levels were not diluted for the ELISAs, while serum samples for IgG1 or IgE assays were diluted 1:10 in PBST; all samples were incubated overnight at 4 °C. Biotinylated detection antibodies or biotinylated OVA (IgE ELISA only) were added to the wells, followed by streptavidin-conjugated horseradish peroxidase (each for 1 h), and then the plates were developed using ABTS peroxidase substrate solution, and the colorimetric products detected using a NOVOSTAR plate reader (BMG Labtech/Mandel Scientific, Guelph, ON). The cytokine data are presented as picograms per milliliter, according to the recombinant protein standard curves, while the IgG1 and IgE levels were presented as OD values; all cytokine assays were sensitive to 5–10 pg/mL.
2.4. Tracking of DC-RA in vivo
Allergen-loaded CFSE-stained BALB/c mouse DC-RA were injected i.p. into asthmatic mice (5 × 106 cells/mouse). After 3, 7, 10, or 14 d, we collected the indicated organs from each animal and generated single cell suspensions either by mechanical (spleens, lymph nodes) or enzymatic (lungs) dispersal of the tissues [14]. Each cell population was quantified by flow cytometry (Beckman Coulter Epics XL) and the data analyzed using Flow-Jo v.8 software (Three Star, Ashland, OR).
2.5. Models of allergic disease
2.5.1. Mouse model of asthma
Mice were sensitized as noted previously [13],[14]. Briefly, they were given two i.p. injections of OVA-alum (2 µg of OVA/mg alum) on days 0 and 14, and exposed to 1% (w/v) nebulized OVA in saline aerosols on days 30, 32, and 34 (20 min/day). Mice used as asthmatic CD4+ T cell donors were sacrificed at 2–4 wk after asthma induction, but mice used for DCreg immunotherapy were treated i.p. with 1 × 106 DCreg at 2 wk after delivery of the last sensitizing dose of OVA aerosol. Four weeks later they were assessed for airway hyperresponsiveness (AHR) to methacholine by head-out, whole-body plethysmography, as noted [7]. Briefly, we monitored the changes in the airflow in response to doubling doses of nebulized methacholine (0.75–25 mg/mL), measured as running 1s means of the airflow at the 50% point in the expiratory cycle (Flow@50%TVe1)—this data accurately reflects bronchiolar constriction as determined by invasive measures [15],[16]. After assessing AHR the animals were challenged for 20 min with 1% OVA in saline aerosols, then sacrificed 48 h later and bronchoalveolar lavage (BAL) was performed to obtain airway cells and fluids (BALF). Cytocentrifuge slides of the BALF cells were stained with Giemsa–Wright solution and differential cell counts were performed [7],[13] while ELISA assays were used to quantify the airway levels of Th2 cytokines.
2.5.2. Mouse model of food allergy
We used the previously noted BALB/c mouse model of OVA oral allergy [3]. Briefly, mice were given two i.p. injections of OVA-alum (2 µg of OVA/mg alum on days 0 and 14) and then, beginning 2 wk later they were gavaged every second day with 2 mg OVA (with 3 h fasting before each gavage), until they displayed anaphylactic responses to the oral challenge (usually 6–9 such serial gavages). We found that once signs of anaphylaxis were first observed during the sensitization phase, ≥3 additional challenges would most often lead to lethal outcomes. Since our purpose was to evaluate the positive or negative impact of the DC treatments on the anaphylaxis phenotype, we titrated our OVA model by adjusting the numbers of pre-experiment challenges to yield half-maximal mean scores (i.e., 2.5) at the time of DCreg therapy. We employed a standard 5-point scoring system for anaphylactic responses wherein: 0 = no clinical symptoms; 1 = repetitive vigorous nose/ear scratching; 2 = lethargy, puffy eyes/mouth; 3 = periods of motionless for >1 m, lying prone; 4 = no response to whisker stimuli, reduced or no response to prodding; and 5 = tremor, convulsion, death; for humane reasons, animals that attained a clinical score of 4 were euthanized immediately. The mice were treated with DCreg at 2 wk after their last allergen gavage and re-challenged by gavage with allergen 4 wk later; at 30 min post-challenge the clinical scores and incidence of diarrhea were assessed, while at 50 min serum was collected for analysis of mouse mast cell protease-1 (mMCP-1), as a surrogate marker of intestinal mast cell activation. The mice were sacrificed 48 h after recall allergen challenge, when serum and peritoneal lavage fluids were collected for analysis of OVA-specific IgG1 and IgE and Th2 cytokines, respectively [3].
2.6. Preparation of T cells, lung single cell suspensions, and splenocytes
2.6.1. Lung single cell suspensions
Asthmatic or healthy control mice were sacrificed and their lung tissues were finely diced and then digested for 30 min at 37 °C in RPMI-1640/10% FBS, containing 0.75 mg/mL Type 4 collagenase and 2 mg/mL hyaluronidase. The dispersed tissues were filtered through sterile gauze and washed with RPMI-1640-10% FBS medium [14].
2.6.2. Splenocyte single cell suspensions
Spleens were mechanically dispersed and the cells passed through 70 µm-mesh cell strainers, after which contaminating red blood cells were lysed with hypotonic tris-ammonium chloride. The single cell suspensions were washed and resuspended in fresh medium and counted.
2.6.3. Lung CD4+ T cells
Lung single cell suspensions from asthmatic mice were centrifuged at 400× g for 15 min on LSM density gradients and the mononuclear cells harvested from the top of the gradients, washed and processed for magnetic purification of CD4+ T cells, according to the kit supplier's protocol, as noted [6].
2.7. Characterization of Treg
We used in vitro T cell suppression assays to assess the function of Treg induced by our DCreg, as noted [9],[17]. Briefly, OVA-pulsed, 3000 rad-irradiated DC10 or DC-RA (5 × 104 cells/well) were cultured in round-bottom 96-well tissue culture plates with optimized numbers of irradiated OVA-presenting DC-LPS (4 × 103 cells/well) and CD4+CD25− Th2 cells (1 × 105 cells/well) harvested from the lungs of asthmatic mice at 4 wk after their last allergen exposure; we previously reported that our “asthmatic lung T” cells secrete higher levels the Th2 cytokines IL-4, -5, -9 and -13, with modest levels of IFNγ relative to normal mouse T cells, and that they are CD44hiCD69+CD62Llo [4]. In some experiments, we used 3H-thymidine uptake assays to assess T cell proliferation, measuring 3H incorporation by liquid scintillation counting. In other experiments, we labeled the starter T cells with 2 µM CFSE and cultured them for 5 days with OVA-pulsed DC10 or DC-RA in the presence of 10 U/mL rmIL-2 as a growth factor. In these assays we used CFSE dilution as a measure of proliferation and intracellular Foxp3 staining as a marker for Foxp3+ Treg.
2.8. RNA isolation and quantitative real-time PCR (qRT-PCR)
Total RNA was isolated from our DCreg using RNeasy Mini Kits, according to the supplier's instructions, and reverse-transcribed to DNA. qRT-PCR analysis was carried out using Brilliant II SYBR Green qRT-PCR Master Mix Kits and a Mx3005P Instrument (Stratagene, La Jolla, CA). The primers for mouse IL-10 were: forward, AAGCCTTATCGGAAATGATCCA; reverse, GCTCCACTGCCTTGCTCTTATT. The reactions were carried out according to the following parameters: 50 °C for 30 min and 95 °C for 10 min (1 cycle); 95 °C for 30 sec (denaturation); 63 °C for 30 sec (annealing); and 72 °C for 30 sec (extension) (40 cycles); readings were taken at 72 °C during the 30-sec plateau. IL-10 mRNA levels were normalized to mouse β-actin mRNA levels.
2.9. Statistical analyses
All data were expressed as the mean ± SEM. Most group differences were analyzed by ANOVA with Bonferroni post-hoc testing, although ELISA data was assessed by ANOVA with LSD post-hoc testing, and AHR by two-way ANOVA. The diarrhea data was assessed using a N-1 Chi-Square test [18]. Differences were considered statistically significant when P-values were less than 0.05.
2.10. Ethics approval of research
All experiments were approved by the Animal Research Ethics Board of the University of Saskatchewan (Protocol 19960112), in accord with the standards of the Canadian Council on Animal Care.
3.
Results
3.1. In Vitro characterization of regulatory dendritic cells
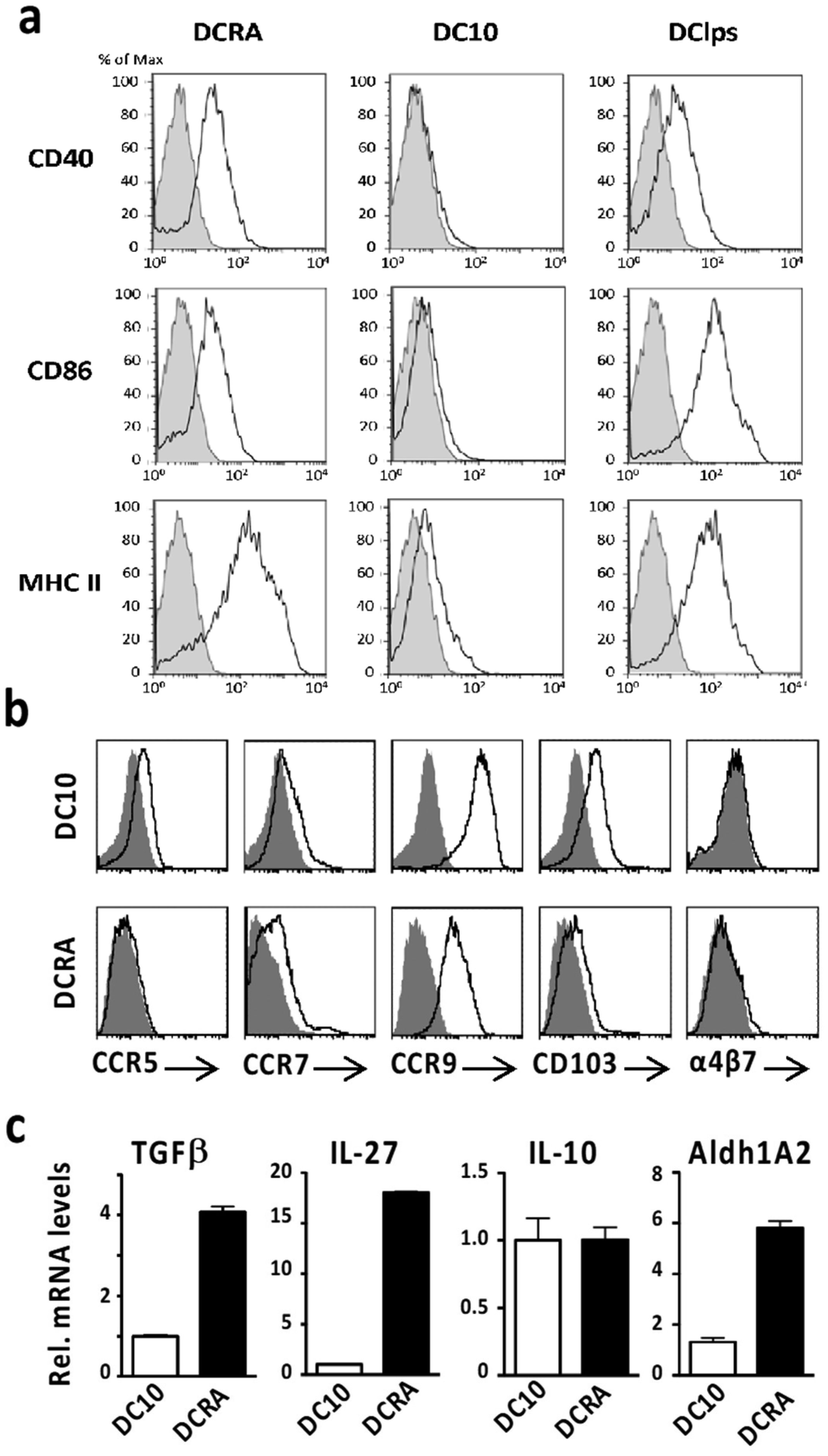
We used FACS to assess the expression levels of the antigen-presentation markers CD86 and MHC II as well as CD40 on DC10 and DC-RA, comparing these cells with mature immunostimulatory dendritic cells (i.e., DC-LPS). DC10 expressed lower levels of CD40, CD86 and MHC II than DC-LPS, while the LPS-exposed DC-RA displayed substantially higher levels of each marker than the DC10. The DC-LPS expressed levels of CD40 and MHCII equivalent to those of DC-RA, but higher levels of CD86 (Figure 1a). We also examined the expression of cell surface markers associated with cellular chemotaxis or positioning and found that DC-RA expressed lower levels of CCR5, CCR7, CCR9, and CD103 than DC10, while neither cell expressed appreciable levels of the mucosal addressin α4β7 (Figure 1b); DC-RA also expressed substantially higher levels of mRNA for TGF-β1, IL-27, and the retinoic acid-metabolism-related enzyme retinaldehyde 1A2 (Aldh1A2), but equivalent levels of IL-10 (Figure 1c).
We next compared the abilities of DC-RA and DC10 to suppress Th2 cell proliferative responses in vitro. We titrated irradiated OVA-presenting DC-RA or DC10 into co-cultures of irradiated OVA-presenting DC-LPS and magnetically-sorted CD4+ T cells from the lungs of OVA-asthmatic mice and assessed T cell proliferation 3 days later (Figure 2). We had previously reported that both DC10 and DC-RA suppress T cell responses in an allergen-specific fashion [3],[7]. We also found herein that OVA-presenting DC-RA and DC10 both suppressed Teff cell proliferative responses to DC-LPS activation in a cell number-dependent fashion, although overall the DC-RA were better at this than the DC10 (p < 0.05). In conclusion, while both DC-RA and DC10 were tolerogenic and capable of suppressing T cell proliferation in vitro, DC-RA were somewhat more effective in this regard.
3.2. Assessment of regulatory T cell induction by DC-RA and DC10
We had previously reported that DC10 foster peripheral tolerance in asthmatic mice by inducing asthmatic Foxp3− Teff cells to transdifferentiate into CD25+Foxp3+ Treg [6],[9], and that human DC10 similarly convert autologous T cells from atopic asthmatics into CD25+Foxp3+ Treg [17]. We have also reported that DC-RA induce T cells from food-allergic mice to differentiate into CD25+LAG3+CD49−Foxp3− Treg [3]. Given that distinct types of Treg can possess different regulatory activities [19],[20], we next asked whether DC10- and DC-RA-induced Treg were equally tolerogenic. To this end, we co-cultured DC10 or DC-RA for 5 days with naïve CFSE-labeled DO11.10 CD4+ T cells and used FACS to assess T cell proliferation (CFSE dilution) and expression of Foxp3 (Figure 3a). As expected, there was low-level expression of Foxp3 among the input T cells that were not exposed to any DC while, as reported previously, DC10 promoted the proliferation of CD4+ T cells and a marked upregulation of Foxp3 expression among the proliferating and, to some extent, non-proliferating T cells. OVA-presenting DC-RA had no such effect on T cell proliferation, although there was modest expression of Foxp3+ among the non-proliferating CFSE-stained T cells in the DC-RA co-cultures. Unstimulated negative control DO11.10 CD4+ T cells did not discernibly proliferate (Figure 3a), while positive control OVA-presenting DC-LPS induced very robust DO11.10 T cell proliferation with no discernible induction of Foxp3 expression (data not shown), as noted previously [9].
We next assessed the regulatory activities of the T cells from these DCreg-T cell cultures (Figure 3b). CD4+ T cells were isolated from 5 day DC10- or DC-RA-Teff cell co-cultures by magnetic sorting, irradiated, and titrated into fresh cultures of OVA-presenting DC-LPS and DO11.10 CD4+ T cells. After 72 h we assessed the DO11.10 T cell proliferative responses using a standard 3H-thymidine uptake assay. The sorted CD4+ T cells from the DC-RA-Th2 cell co-cultures did not inhibit DO11.10 responses in a statistically significant way when used at T cell:DCreg ratios of 4:1 or 2:1, but did suppress proliferation when used at a ratio of 1:1 (p ≤ 0.05). The DC10-induced Treg were seemingly more effective in this assay, reducing DO11.10 T cell proliferation at both lower (p ≤ 0.05) and higher (p ≤ 0.01) numbers of input DCreg. When used as limiting numbers (i.e., T cell:DCreg ratios of 2:1 or 4:1) the DC10-induced Treg were better able to suppress T cell activation than were the DC-RA-induced Treg (p ≤ 0.05). Taken together, our data indicates that both DC10 and DC-RA were able to suppress in vitro proliferative responses of asthmatic lung CD4+ T cells and induce differentiation of Treg that differentially express Foxp3, although the DC10-induced Treg carried modestly more regulatory activities than the DC-RA-induced cells.
3.3. Tracking of DC-RA in vivo after intraperitoneal delivery
We previously reported that within 2 days of i.p. injection into asthmatic mice, DC10 can be found in the airways, lung tissues and lung-draining (mediastinal; Med) LN. While significant numbers of DC10 eventually localize to the spleen, few are found at any time in the blood, bone marrow, mesenteric LN or liver [4]. As noted, steady-state intestinal DC develop under the influence of retinoic acid and TGFβ, which drives the development of gut-homing Treg [10]. Indeed, this association between retinoic acid and gut-associated tolerance was our initial rationale for exploring the use of DC-RA as a therapeutic approach to food allergies [3]. An important question to ask when assessing their therapeutic potential in the context of asthma was whether DC-RA that are given i.p. to asthmatic mice become positioned to interact directly with lung or lung-draining lymph node-associated T cells. We treated asthmatic mice with CFSE-labeled DC-RA given i.p. and then at various times thereafter harvested the indicated organs from the recipients and used FACS to assess the numbers of CFSE-labeled cells in each compartment (Figure 4). Within 3 days we found a significant accumulation of DC-RA in the lung tissues, followed by their appearance in increasing numbers in the lung-draining LN (peak, 7 days). Large numbers of DC-RA could be found within the spleens at 7 & 10 day, when they also achieved peak accumulation in the mesenteric LN. While we also examined single cell suspensions from the intestinal lamina propria we did not detect discernible numbers of labeled cells in that compartment (data not shown).
3.4. Comparison of the therapeutic effectiveness of allergen-presenting DC10 and DC-RA in a mouse model of asthma
We next asked whether both DC10 and DC-RA would be effective therapeutically in our OVA-alum model of asthma [7]. We previously reported that neither immature (i.e., DC-GM-CSF) or mature (i.e., immunostimulatory) specific allergen-presenting DC [4],[6],[7], or irrelevant allergen-presenting DC10 [6] induce tolerance in this model. Herein we treated the mice with 1 × 106 OVA-pulsed DC10 or DC-RA, or an equal volume of saline (i.p.) and then 4 weeks later assessed the animals' AHR to methacholine. We then challenged the mice with nebulized aerosols of 1% OVA and sacrificed them 48 h later to assess airway inflammation (bronchoalveolar lavage (BAL) eosinophils, Th2 cytokines) and serum OVA-specific IgE and IgG1 antibody levels. Both DC-RA and DC10 equally inhibited AHR in our asthmatic mice (p < 0.001 versus saline-treated asthmatic mice), such that there were no differences in AHR between the DC-RA- and DC10-treated mice (p > 0.05; Figure 5a). Similarly, both DC10 and DC-RA therapies significantly reduced the airway eosinophil response to allergen challenge, and there were no significant differences in their efficacy (p > 0.05, Figure 5b). When we analyzed BAL fluid levels of IL-4, -5, -9 and -13 we found that there were also no statistically significant differences between the levels of any of these cytokines in the DC10- versus DC-RA-treated mice (for each, p > 0.05 versus one another). The DC-RA treatments reduced the levels of IL-4, IL-9 and IL-13, but the levels of IL-5 were above the cut-off for statistical significance (p = 0.09, Figure 5c). We also found that the circulating levels of OVA-specific IgG1 and IgE antibodies were significantly reduced in the DC10- and DC-RA-treated mice (p ≤ 0.001, relative to the saline-treated animals, Figure 5d). Overall, despite the observation that our DC10 treatments did not statistically significantly reduce the airway levels of all four Th2 cytokines assessed, there were no statistically significant differences in the impact of the DC10 and DC-RA on the asthma phenotype in these experiments.
3.5. DC-RA and DC10 immunotherapy are equally effective in reversing oral egg allergy
We next assessed the relative efficacy of both types of DCreg in our mouse model of OVA food allergy [3]. As noted previously, we titrated the model such that the clinical scores at the time of DCreg treatment were half-maximal (≈2.5). Over the following 4 weeks post-treatment (during which the mice did not receive any OVA challenges) the mean clinical responses of the saline-treated animals to subsequent OVA challenge declined to 1.71 ± 0.21 (Figure 6a). The DC-RA and DC10 therapies both reduced the clinical scores following oral allergen challenge to background or near background (p < 0.001 versus the saline-treated mice), such that there was no significant difference between the two groups (p ≥ 0.05; Figure 6). Allergen challenge-induced mast cell activation, as determined by the serum levels of mouse mast cell protease-1 (mMCP-1), was reduced ≈50% by both the DC10 and DC-RA treatments, and that outcome was consistent with the observed reductions in circulating OVA-specific IgE and IgG1. Oral allergen challenge elicited an explosive diarrhea response in 80% of the saline-treated mice; the DC-RA and DC10 treatments reduced the incidence of diarrhea by ≈37 and 75%, respectively (p ≤ 0.05 and 0.01, respectively versus saline-treated mice). There was no significant difference in the diarrhea responses in the DC10- and DC-RA-treatment groups of mice (p ≥ 0.05). Peritoneal Th2 cytokine (IL-4, -5, -9 and -13) levels were also more or less equally reduced by the DC10 and DC-RA treatments (Figure 6b). Taken together, this data indicates that specific allergen-presenting DC10 and DC-RA were both effective in reducing the anaphylaxis phenotype in OVA-allergic mice.
4.
Discussion
We had previously shown that IL-10-differentiated DC (DC10) can reverse the asthma phenotype [6],[7],[9], while LPS-matured, retinoic acid-induced DC (DC-RA) can suppress anaphylactic responses to food allergen challenge [3] in mouse models. We have reported that IL-10 production by DC10 drives their suppression of Th2 cells and induces Th2 cells to transdifferentiate into CD25+Foxp3+ Treg [4],[9]. We found herein that DC-RA produced approximately four-fold more TGFβ than DC10. We have also reported previously that suppression of Th2 responses by DC-RA is attributable to their secretion of both IL-10 and TGFβ, while it is their production of IL-27 (but not IL-10 or TGFβ) that drives the transdifferentiation of Th2 cells into CD25+LAG3+CD49b−Foxp3− Treg [3]. We suggest that the differences we observed herein in DC10 versus DC-RA suppression of Th2 cell proliferation may well have been due to the differential effects of TGFβ production by these DCreg. Thus, DC10 and DC-RA both carry marked regulatory activities, although they display substantially distinct phenotypes and mechanisms of action.
We have previously tracked DC10 following i.p. delivery to asthmatic mice [4]. It was reported by others that leukocytes that adventitiously find themselves within the peritoneal cavity are evacuated from that compartment through the diaphragmatic lymphatics. They then traffic via the thoracic duct into the jugular vein, just proximal to the vena cava and the heart [21]. As such, our DCreg would have tracked through the thoracic duct, and from there through the vascular bed of the lungs before reaching any other compartment. This fits with our having shown that both DC10 [4] and the DC-RA herein were first found in large numbers in the lungs, but the DC-RA were also found in large numbers in the lung-draining mediastinal lymph nodes. This might be expected to position them to impact allergen-specific Teff cells in the lungs, inasmuch as we showed herein that DC-RA do engage with and suppress the responses of pulmonary Teff cells. Soon after the DC-RA passed through these compartments they achieved peak accumulation in the spleen and gut-draining mesenteric lymph nodes, which could have positioned them to engage Teff cells found in the intestinal compartment. We have reported previously that DCreg-induced tolerance is a progressive process, with full tolerance not being realized until 3–4 wk after treatment [7], after the treatment DCreg are no longer detectable in treated animals [4]. We know that DCreg-induced Treg are substantially more potent as regulatory cells than natural Treg [19]. We also showed herein that both DC10- and DC-RA-induced Treg can suppress allergen-specific Teff cells. We did not track the DCreg-induced Treg in either of our models, but the timing of tolerance induction would suggest that DCreg-induced Treg are the ultimate tolerance-effector cells in these models. This suggested to us that the Treg induced by DC10 in the lungs [9] may well subsequently home to other compartments, including the gastrointestinal tract [22] and that that could well be the mechanism by which DC10 induce food allergen tolerance. Reciprocally, specific allergen-presenting DC-RA were tolerogenic in our asthma model. Nevertheless, it is broadly considered that the induction of CCR9 on mesenteric lymph node T cells by retinoic acid-induced intestinal DC renders these T cells to be selectively gut-homing, and that that is the immunologic basis for gut-specific immune responses [2]. By extension then, DC-RA could potentially be thought of as uniquely suited to induction of gut-related tolerance, but the recent report of CCR9 and its CCL25 ligand mediating eosinophil and T cell recruitment into the lungs in asthmatic mice [23] indicates that CCR9 expression, such as we saw on our DC-RA, is relevant in the context of both pulmonary and intestinal inflammation.
Our observation that DC-RA express higher levels of TGFβ and Aldh1A2 than DC10 could explain the increased in vitro regulatory activities of DC-RA that we observed herein. We reported previously that DC-RA suppression of effector T cell responses was dependent on their secretion of IL-10 and TGFβ, but independent of their IL-27 secretion, with the latter being the driving force for their induction of Treg and suppression of the food anaphylaxis phenotype in vivo [3]. Interestingly, in contrast to the abilities of these DCreg to differentially suppress effector T cell responses in vitro, there were no statistically significant differences in the suppressive activities of the Treg induced by DC10 versus DC-RA. The therapeutic equivalence of these two populations of DCreg in the asthma and food allergy models raises questions regarding precisely how they suppress the disease phenotype (i.e., whether they act directly as the operational regulatory cells, or also indirectly via induced Treg). Our data suggests that the impact of DC10 and DC-RA on the allergic disease phenotype is attributable in no small part to their abilities to activate Treg responses. Either way, however, it is clear that DCreg that use quite different mechanisms to induce tolerance can equally well accomplish this in different contexts (e.g., food allergies versus asthma). This opens up questions regarding just how critical the phenotype of the DCreg to be employed in immunotherapeutics is to the therapeutic outcome. Specifically, while unlikely, could DCreg induced by a variety of means (e.g., IL-10, retinoic acid, dexamethasone) be equally efficacious across an array of diseases, or do they express a degree of specialization, such that some DCreg would be better suited therapeutically for disease conditions that affect a specific organ (e.g., gut versus lung). Important questions to address in considering this are how do the different DCreg operate, and do they display distinct characteristics that make them better suited to any particular application. Thus, for example, given that Foxp3+ Treg can lose expression of Foxp3 and convert into Th17-phenotype cells [24], would it be important in some therapeutic contexts to use DCreg that act via induction of Foxp3−, versus Foxp3+ Treg.
There have been many pre-clinical studies of the efficacy of murine DCreg in an array of models, and many ex vivo studies relating to human DCreg [1],[25], but increasingly we pursue the clinical applications of these cells. Phase I clinical trials have been undertaken with DCreg of different types in Type 1 diabetes [26] rheumatoid arthritis [27], Crohn's disease [28], multiple sclerosis [29] and liver transplantation [30] each of which has proven these cells as well tolerated and safe, while other trials are still under way [25]. Some of these Phase I trials, particularly when taken together with non-human primate trials [31], have yielded tantalizing preliminary evidence that, in the not-too-distant future, DCreg will provide a viable alternate approach to long-term use of pharmacologic agents for the treatment immune-based diseases.
5.
Conclusions
IL-10-differentiated DC (DC10) induce T cells to differentiate into Foxp3+ Treg, while retinoic acid-induced DC (DC-RA) induce differentiation of Foxp3− Treg in an IL-27-dependent fashion. Given that colitis inflammation has been reported to suppress Foxp3 in Foxp3+ Treg, and to convert these cells into pathogenic Th17 cells, we queried whether the success of DC-RA in reversing gut-associated food allergies was attributable to their induction of Foxp3−, rather than Foxp3+ Treg. Thus, although DC10 and DC-RA display distinct phenotypes, mechanisms of action and can induce tolerance in distinct organ systems, we found that both DCreg populations were able to reverse the disease phenotype in both models, equally suppressing effector T cell responses to allergen challenge and equally efficiently inducing Treg responses, albeit distinct types of Treg. This suggests that, at least in some circumstances, there is sufficient plasticity in the system to allow different types of DCreg to be used for similar purposes.









 DownLoad:
DownLoad: