A novel numerical method for solution of fractional partial differential equations involving the $ \psi $-Caputo fractional derivative

Amjid Ali; Teruya Minamoto; Rasool Shah; Kamsing Nonlaopon; Amjid Ali; Teruya Minamoto; Rasool Shah; Kamsing Nonlaopon

doi:10.3934/math.2023110

AIMS Mathematics

2023, Volume 8, Issue 1: 2137-2153. doi: 10.3934/math.2023110

Previous Article Next Article

Research article

A novel numerical method for solution of fractional partial differential equations involving the $\psi$ -Caputo fractional derivative

1.
Faculty of Science and Engineering, Saga University, Saga 840-8502, Japan
2.
Department of Mathematics, Abdul Wali Khan University Mardan, Pakistan
3.
Department of Mathematics, Faculty of Science, Khon Kaen University, Khon Kaen 40002, Thailand

Received: 23 August 2022 Revised: 03 October 2022 Accepted: 06 October 2022 Published: 28 October 2022
MSC : 26A33, 35A20, 35A35, 33B15, 33F05

In this study, the $\psi$ -Haar wavelets operational matrix of integration is derived and used to solve linear $\psi$ -fractional partial differential equations ( $\psi$ -FPDEs) with the fractional derivative defined in terms of the $\psi$ -Caputo operator. We approximate the highest order fractional partial derivative of the solution of linear $\psi$ -FPDE using Haar wavelets. By combining the operational matrix and $\psi$ -fractional integration, we approximate the solution and its other $\psi$ -fractional partial derivatives. Then substituting these approximations in the given $\psi$ -FPDEs, we obtained a system of linear algebraic equations. Finally, the approximate solution is obtained by solving this system. The simplicity and effectiveness of the proposed method as a mathematical tool for solving $\psi$ -Fractional partial differential equations is one of its main advantages. The sparse nature of the operational matrices improves the ability of the proposed method to execute with less computation complexity. Numerical examples are provided to show the efficiency and effectiveness of the method.

Keywords:

Citation: Amjid Ali, Teruya Minamoto, Rasool Shah, Kamsing Nonlaopon. A novel numerical method for solution of fractional partial differential equations involving the $\psi$ -Caputo fractional derivative[J]. AIMS Mathematics, 2023, 8(1): 2137-2153. doi: 10.3934/math.2023110

Related Papers:

[1]	Iyad Suwan, Mohammed S. Abdo, Thabet Abdeljawad, Mohammed M. Matar, Abdellatif Boutiara, Mohammed A. Almalahi . Existence theorems for $\Psi$ -fractional hybrid systems with periodic boundary conditions. AIMS Mathematics, 2022, 7(1): 171-186. doi: 10.3934/math.2022010
[2]	Ibtisam Aldawish, Mohamed Jleli, Bessem Samet . Blow-up of solutions to fractional differential inequalities involving $\psi$ -Caputo fractional derivatives of different orders. AIMS Mathematics, 2022, 7(5): 9189-9205. doi: 10.3934/math.2022509
[3]	Dinghong Jiang, Chuanzhi Bai . On coupled Gronwall inequalities involving a $\psi$ -fractional integral operator with its applications. AIMS Mathematics, 2022, 7(5): 7728-7741. doi: 10.3934/math.2022434
[4]	Choukri Derbazi, Zidane Baitiche, Mohammed S. Abdo, Thabet Abdeljawad . Qualitative analysis of fractional relaxation equation and coupled system with Ψ-Caputo fractional derivative in Banach spaces. AIMS Mathematics, 2021, 6(3): 2486-2509. doi: 10.3934/math.2021151
[5]	Ridha Dida, Hamid Boulares, Bahaaeldin Abdalla, Manar A. Alqudah, Thabet Abdeljawad . On positive solutions of fractional pantograph equations within function-dependent kernel Caputo derivatives. AIMS Mathematics, 2023, 8(10): 23032-23045. doi: 10.3934/math.20231172
[6]	Arjumand Seemab, Mujeeb ur Rehman, Jehad Alzabut, Yassine Adjabi, Mohammed S. Abdo . Langevin equation with nonlocal boundary conditions involving a $\psi$ -Caputo fractional operators of different orders. AIMS Mathematics, 2021, 6(7): 6749-6780. doi: 10.3934/math.2021397
[7]	Deepak B. Pachpatte . On some ψ Caputo fractional Čebyšev like inequalities for functions of two and three variables. AIMS Mathematics, 2020, 5(3): 2244-2260. doi: 10.3934/math.2020148
[8]	Shazia Sadiq, Mujeeb ur Rehman . Solution of fractional boundary value problems by $\psi$ -shifted operational matrices. AIMS Mathematics, 2022, 7(4): 6669-6693. doi: 10.3934/math.2022372
[9]	Ishfaq Mallah, Idris Ahmed, Ali Akgul, Fahd Jarad, Subhash Alha . On $\psi$ -Hilfer generalized proportional fractional operators. AIMS Mathematics, 2022, 7(1): 82-103. doi: 10.3934/math.2022005
[10]	Reny George, Fahad Al-shammari, Mehran Ghaderi, Shahram Rezapour . On the boundedness of the solution set for the $\psi$ -Caputo fractional pantograph equation with a measure of non-compactness via simulation analysis. AIMS Mathematics, 2023, 8(9): 20125-20142. doi: 10.3934/math.20231025

Abstract

1. Introduction

Fractional calculus is considered the generalization of classical calculus. Fractional differential equations have been widely employed in various science and engineering fields ^[1,2,3]. Many researchers have defined fractional order derivatives and integrals in various forms. New definitions of fractional differential operators and $\psi$ -fractional derivatives and integrals have been considered by several researchers, such as the Riemann-Liouville, Caputo, Hilfer, Erdelyi-Kober, Hadamard ^[4,5,6,7]. Additionally, studies by Sousa et al. contain fascinating details concerning the $\psi$ -Riemann-Liouville fractional partial integral, and the $\psi$ -Caputo fractional partial derivative ^[8]. Furthermore, many interesting results from the qualitative analysis of fractional ordinary and partial differential equations involving different fractional derivatives have been recorded ^{[9,10,11,12,13,14,15,16]}. However, numerical solutions for fractional partial differential equations (FPDEs) involving the $\psi$ -Caputo fractional partial derivatives have not been performed using the $\psi$ -Haar wavelet operational matrix method. Thus, this study establishes a numerical technique for solving $\psi$ -Caputo FPDEs.

The rest of the paper is organized as follows: Section 2 presents some fundamental definitions and results from $\psi$ -Fractional calculus. Section 3 reviews Haar wavelets and their applications in function approximation. Furthermore, we derive the operational matrix of $\psi$ -fractional integration of Haar wavelets. Section 4 presents a detailed numerical procedure for solving $\psi$ -FPDEs using constant and variable coefficients. Finally, Section 5 presents the conclusion.

2. Basics of $\psi$ -fractional calculus

This section highlights concepts, definitions, and basic conclusions from the $\psi$ -fractional calculus that are important in later sections.

Let the function $f:[a, b]\rightarrow \mathbb{R}$ be integrable, $\alpha$ a positive real number, $n$ a natural number and $\psi \in C^1([a, b])$ be an increasing function such that ${\psi}^{\prime}(\varkappa)\neq 0$ for all $\varkappa\in [a, b]$ .

Definition 1. ^[4,5,17] The $\psi$ -Riemann-Liouvile ( $\psi$ -RL) fractional integral operator of order $\alpha$ is defined by

$\begin{equation} \mathcal{J}_{a}^{\alpha,\psi} f(\varkappa) = \dfrac{1}{ \Gamma(\alpha)} \int_{a}^{\varkappa}{\psi}^{\prime}(\Im){\left(\psi(\varkappa)-\psi(\Im)\right)}^{\alpha-1}f(\Im)d\Im. \end{equation}$

(2.1)

The $\psi$ -RL fractional differential operator is given by

$\begin{align*}& {D_{a}^{\alpha,\psi}} f(\varkappa) = \left(\dfrac{1}{\psi^{'}(\varkappa)} \dfrac{d}{d\varkappa} \right)^n \mathcal{J}_{a}^{n-\alpha,\psi}f(\varkappa) =\\& \dfrac{1}{\Gamma(n-\alpha)} \left(\dfrac{1}{\psi^{'}(\varkappa)} \dfrac{d}{d\varkappa} \right)^n \int_{a}^{\varkappa}\psi^{'}(\Im){\left(\psi(\varkappa)-\psi(\Im)\right)}^{n-\alpha-1}f(\Im)d\Im, \end{align*}$

where $n = \lfloor \alpha \rfloor+1$ .

Definition 2. ^[6] Let $\alpha$ be a positive real number, $n$ a natural number and $f, \psi \in C^n([a, b])$ such that $\psi$ is increasing and ${\psi}^{\prime}(\varkappa)\neq 0$ for all $\varkappa\in[a, b]$ . The $\psi$ -Caputo differential operator of fractional order $\alpha$ is defined by

$\begin{equation*} {^C}{D_{a}^{\alpha,\psi}} f(\varkappa) = \dfrac{1}{\Gamma (n-\alpha)}\int_{a}^{\varkappa}\psi^{'}(\Im){\left(\psi(\varkappa)-\psi(\Im)\right)}^{n-\alpha-1}f^{[n]}_{\psi}(\Im)d\Im, \end{equation*}$

where $f^{[n]}_{\psi}(\varkappa) = \left(\dfrac{1}{\psi^{'}(\varkappa)} \dfrac{d}{d\varkappa} \right)^n f(\varkappa)$ , here $n = \left\lfloor{\alpha}\right\rfloor+1$ for $\alpha \notin \mathbb{N}$ , or

$\begin{equation*} ^{C}D_{a}^{\alpha,\psi} f({\varkappa}) = \mathcal{J}_{a}^{n-\alpha,\psi} f^{[n]}_{\psi}({\varkappa}). \end{equation*}$

Also, the $\psi$ -Caputo derivative can be defined as

$\begin{equation*} ^{C}D_{a}^{\alpha,\psi} f({\varkappa}) = D_{a}^{\alpha,\psi}\left[f({\varkappa}) - \sum\limits_{k = 0}^{n-1} \frac{f^{[k]}_{\psi}(a)}{k!}(\psi({\varkappa})- \psi(a))^{k}\right], \end{equation*}$

where $n = \lceil \alpha \rceil$ , whenever $\alpha \notin \mathbb{N}$ and for $\alpha \in \mathbb{N}, n = \alpha$ .

Definition 3. The two-parameter Mittag–Leffler function $E_{\alpha, \beta}({\Im})$ is defined as

$\begin{equation} E_{\alpha,\beta}({\Im}) = \sum\limits_{k = 0}^{\infty}\frac{{\Im}^{k}}{\Gamma(\alpha k+\beta)},\quad {\Im}\in \mathbb{R},\; \; \alpha,\; \beta > 0. \end{equation}$

(2.2)

The Mittag-Leffler function can also be given for these exceptional cases:

(ⅰ) $E_{0, 1}({\Im}) = \frac{1}{1+{\Im}};$

(ⅱ) $E_{1, 1}({\Im}) = e^{\Im};$

(ⅲ) $E_{2, 1}(-{\Im}^2) = \cos({\Im});$

(ⅳ) $E_{2, 2}(-{\Im}^2) = \frac{\sin({\Im})}{\Im}.$

Properties of the $\psi$ -fractional operators include:

Property 2.1. The following property holds:

$\begin{equation*} \mathcal{J}_{a}^{\alpha,\psi}\mathcal{J}_{a}^{\beta,\psi}f({\Im}) = \mathcal{J}_{a}^{\alpha + \beta,\psi}f({\Im}). \end{equation*}$

Property 2.2. If $f({\Im}) = \big(\psi({\Im})-\psi(a)\big)^{\beta}$ , where $\beta > n$ and $\alpha > 0$ , then

$\begin{equation*} ^{C}D_{a}^{\alpha,\psi} f({\Im}) = \frac{\Gamma(\beta+1)}{\Gamma(\beta-\alpha +1)}\left(\psi({\Im})-\psi(a)\right)^{ \beta-\alpha}. \end{equation*}$

Property 2.3. The following property holds:

$\begin{equation*} ^{C}D_{a}^{\alpha,\psi}\mathcal{J}_{a}^{\alpha,\psi} f({\Im}) = f({\Im}). \end{equation*}$

Proof. By definition, we have

$\begin{equation} ^{C}D_{a}^{\alpha,\psi}\mathcal{J}_{a}^{\alpha,\psi} f({\Im}) = D_{a}^{\alpha,\psi}\left[\mathcal{J}_{a}^{\alpha,\psi} f({\Im}) - \sum\limits_{k = 0}^{n-1} \frac{\left[\mathcal{J}_{a}^{\alpha,\psi} f\right]^{[k]}_{\psi}(a)}{k!}(\psi({\Im})- \psi(a))^{k}\right]. \end{equation}$

(2.3)

Note that

$\begin{align*} [\mathcal{J}_{a}^{\alpha,\psi} f]^{[k]}_{\psi}({\Im}) & = \left(\dfrac{1}{\psi^{'}({\Im})} \dfrac{d}{d{\Im}} \right)^{k}\mathcal{J}_{a}^{\alpha,\psi} f({\Im})\\ & = \left(\dfrac{1}{\psi^{'}({\Im})} \dfrac{d}{d{\Im}} \right)^{k-1} \dfrac{1}{\psi^{'}({\Im})} \dfrac{d}{d{\Im}} \int_{a}^{\Im}\dfrac{{\left(\psi({\Im})-\psi({s})\right)}^{\alpha-1}}{ \Gamma(\alpha)}{\psi}^{\prime}({s})f({s})ds\\ & = \left(\dfrac{1}{\psi^{'}({\Im})}\dfrac{d}{d{\Im}} \right)^{k-1}\dfrac{1}{\psi^{'}({\Im})} \int_{a}^{\Im}\dfrac{{(\alpha-1)\left(\psi({\Im})-\psi({s})\right)}^{\alpha-2}}{ \Gamma(\alpha)}{\psi}^{\prime}({\Im}){\psi}^{\prime}({s})f({s})ds\\ & = \left(\dfrac{1}{\psi^{'}({\Im})}\dfrac{d}{d{\Im}} \right)^{k-1} \int_{a}^{\Im}\dfrac{{\left(\psi({\Im})-\psi({s})\right)}^{\alpha-2}}{ \Gamma(\alpha-1)}{\psi}^{\prime}({s})f({s})ds\\ & = \left(\dfrac{1}{\psi^{'}({\Im})}\dfrac{d}{d{\Im}} \right)^{k-1}\mathcal{J}_{a}^{\alpha-1} f({\Im}). \end{align*}$

Then, we have

$\begin{equation*} \left[\mathcal{J}_{a}^{\alpha,\psi} f\right]^{[k]}_{\psi}({\Im}) = [\mathcal{J}_a^{\alpha-1,\psi}f]_{\psi}^{[k-1]}({\Im}). \end{equation*}$

Repeating the process $k$ -times, we have

$\begin{equation} \left[\mathcal{J}_{a}^{\alpha,\psi} f\right]^{[k]}_{\psi}({\Im}) = \mathcal{J}_{a}^{\alpha-k, \psi}f({\Im}). \end{equation}$

(2.4)

Now, substituting (2.4) into (2.3), we have

$\begin{equation} ^{C}D_{a}^{\alpha,\psi}\mathcal{J}_{a}^{\alpha,\psi} f({\Im}) = D_{a}^{\alpha,\psi}\left[\mathcal{J}_{a}^{\alpha,\psi} f({\Im}) - \sum\limits_{k = 0}^{n-1} \frac{\mathcal{J}_{a}^{\alpha-k, \psi} f(a)}{k!}(\psi({\Im})- \psi(a))^{k}\right]. \end{equation}$

(2.5)

Next, we show that $\mathcal{J}_{a}^{\alpha-k, \psi} f(a) = 0$ . That is, we prove that $\lim_{\Im \rightarrow a} \mathcal{J}_{a}^{\alpha-k, \psi} f({\Im}) = 0$ . Now, we have

$\begin{align*} \left\Vert\mathcal{J}_{a}^{\alpha,\psi} f({\Im}) \right\Vert & = \left\Vert \dfrac{1}{ \Gamma(\alpha)} \int_{a}^{\Im}{\left(\psi({\Im})-\psi({s})\right)}^{\alpha-1}{\psi}^{\prime}({s})f({s})ds \right\Vert\\ &\leq \dfrac{1}{ \Gamma(\alpha)}\int_{a}^{\Im} \left\Vert {\left(\psi({\Im})-\psi({s})\right)}^{\alpha-1}{\psi}^{\prime}({s})f({s})\right\Vert\,ds \\ &\leq \dfrac{\Vert f \Vert}{ \Gamma(\alpha)}\int_{a}^{\Im}{\left(\psi({\Im})-\psi({s})\right)}^{\alpha-1}{\psi}^{\prime}({s})ds\\ &\leq \Vert f \Vert \frac{{\left(\psi({\Im})-\psi(a)\right)}^{\alpha}}{\Gamma(\alpha +1)}, \end{align*}$

since $\psi^{'}({\Im}) > 0$ and $\Gamma(\alpha +1) = (\alpha)\Gamma(\alpha)$ . Hence, $\mathcal{J}_{a}^{\alpha, \psi} f({\Im})$ tends to $0$ as $\Im$ tends to $a.$ Thus, from (2.5), we have

$\begin{align*} ^{C}D_{a}^{\alpha,\psi}\mathcal{J}_{a}^{\alpha,\psi} f({\Im})& = D_{a}^{\alpha,\psi} \mathcal{J}_{a}^{\alpha,\psi} f({\Im})\\ & = \left(\dfrac{1}{\psi^{'}({\Im})}\dfrac{d}{d{\Im}} \right)^{n}\mathcal{J}_{a}^{n-\alpha, \psi}\mathcal{J}_{a}^{\alpha, \psi} f({\Im})\\ & = \left(\dfrac{1}{\psi^{'}({\Im})}\dfrac{d}{d{\Im}} \right)^{n}\mathcal{J}_{a}^{n-\alpha + \alpha, \psi}f({\Im})\\ & = \left(\dfrac{1}{\psi^{'}({\Im})}\dfrac{d}{d{\Im}} \right)^{n}\mathcal{J}_{a}^{n, \psi}f({\Im}). \end{align*}$

Consequently, we have $^{C}D_{a}^{\alpha, \psi}\mathcal{J}_{a}^{\alpha, \psi} f({\Im}) = f({\Im}).$ This complete the proof.

By Leibnitz rule, we have

$\begin{align*} \dfrac{1}{\psi^{'}({\Im})}\dfrac{d}{d{\Im}}\mathcal{J}_{a}^{1, \psi}f({\Im})& = \dfrac{1}{\psi^{'}({\Im})}\dfrac{d}{d{\Im}}\int_{a}^{\Im}{\left(\psi({\Im})-\psi({s})\right)}^{1-1}{\psi}^{\prime}({s})f({s})ds\\ & = \dfrac{1}{\psi^{'}({\Im})}\psi^{'}({\Im})f({\Im})\\ & = f({\Im}). \end{align*}$

Repeating the above process $n$ -times we have

$\begin{equation*} \left(\dfrac{1}{\psi^{'}({\Im})}\dfrac{d}{d{\Im}}\right)^{n}\mathcal{J}_{a}^{n, \psi}f({\Im}) = f({\Im}). \end{equation*}$

Lemma 1. The following property holds:

$\begin{equation*} \mathcal{J}_{a}^{n, \psi}f^{[n]}_{\psi}({\Im}) = f({\Im})-\sum\limits_{k = 0}^{n-1}\frac{f^{[n]}_{\psi}(a)}{k!}\left( \psi({\Im})-\psi(a)\right)^{k}. \end{equation*}$

Proof. For $n = 1$ , we have

$\begin{align} \mathcal{J}_{a}^{1, \psi}f^{[1]}_{\psi}({\Im})& = \int_{a}^{\Im}\frac{{\left(\psi({\Im})-\psi({s})\right)}^{1-1}}{\Gamma(1)}{\psi}^{\prime}({s})\frac{1}{{\psi}^{\prime}({s})}\frac{d}{ds}f({s})ds\\ & = \int_{a}^{\Im}\frac{d}{ds}f({s})ds = f({\Im})-f(a). \end{align}$

(2.6)

For $n = 2$ , we have

$\begin{align} \mathcal{J}_{a}^{2, \psi}f^{[2]}_{\psi}({\Im})& = \mathcal{J}_{a}^{1,\psi}\mathcal{J}_{a}^{1,\psi}\left[f^{[1]}_{\psi}\right]^{1}_{\psi}({\Im}) = \mathcal{J}_{a}^{1,\psi}\left[f^{[1]}_{\psi}-f^{[1]}_{\psi}\right]\\ & = \mathcal{J}_{a}^{1,\psi}f^{[1]}_{\psi}({\Im})-\mathcal{J}_{a}^{1,\psi}f^{[1]}_{\psi}(a)\\ & = f({\Im})-f(a) - f^{[1]}_{\psi}(a)\int_{a}^{\Im}(\psi({\Im})-\psi(a))^{1-1}{\psi}^{\prime}({s})ds\\ & = f({\Im})-f(a) - f^{[1]}_{\psi}(a)(\psi({\Im})-\psi(a)). \end{align}$

(2.7)

Repeating the above process $n$ -times, we have

$\begin{equation*} \mathcal{J}_{a}^{n, \psi}f^{[n]}_{\psi}({\Im}) = f({\Im})-\sum\limits_{k = 0}^{n-1}\frac{f^{[k]}_{\psi}(a)}{k!}\left( \psi({\Im})-\psi(a)\right)^{k}. \end{equation*}$

This completes the proof.

Lemma 2. The following property holds:

$\begin{equation*} \mathcal{J}_{a}^{\alpha, \psi} {}^{\; \; C}D_{a}^{\alpha,\psi} f({\Im}) = f({\Im}) - \sum\limits_{k = 0}^{n-1} \frac{f^{[k]}_{\psi}(a)}{k!}(\psi({\Im})- \psi(a))^{k}. \end{equation*}$

Proof. Since

$\begin{equation*} ^{C}D_{a}^{\alpha,\psi} f({\Im}) = \mathcal{J}_{a}^{n-\alpha, \psi}f^{[n]}_{\psi}({\Im}), \end{equation*}$

thus

$\begin{align*} \mathcal{J}_{a}^{\alpha, \psi}{}^{C}D_{a}^{\alpha,\psi} f({\Im})& = \mathcal{J}_{a}^{\alpha, \psi}\mathcal{J}_{a}^{n-\alpha, \psi}f^{[n]}_{\psi}({\Im})\\ & = \mathcal{J}_{a}^{\alpha + n-\alpha, \psi}f^{[n]}_{\psi}({\Im})\\ & = \mathcal{J}_{a}^{n, \psi}f^{[n]}_{\psi}({\Im}). \end{align*}$

Therefore, we have

$\begin{equation*} \mathcal{J}_{a}^{\alpha, \psi}{}^{C}D_{a}^{\alpha,\psi} f({\Im}) = f({\Im})-\sum\limits_{k = 0}^{n-1}\frac{f^{[k]}_{\psi}(a)}{k!}\left( \psi({\Im})-\psi(a)\right)^{k}. \end{equation*}$

The proof is completed.

3. Haar wavelets and function approximation

The Haar wavelet, invented by Hungarian mathematician Alfred Haar in 1909, is the most basic example of an orthogonal wavelet. The Haar mother wavelet is defined by a two-scale relation for the scaling function $\varphi({\Im}) = \chi_{[0, 1)}$ as:

$\begin{equation} h({\Im}) = \varphi(2{\Im}) - \varphi(2\Im - 1) = \chi_{\left[0,\frac{1}{2}\right)}({\Im}) - \chi_{\left[\frac{1}{2}, 1\right)}({\Im}). \end{equation}$

(3.1)

Define

$\begin{equation} h_{j, k}({\Im}) = 2^{\frac{j}{2}}h(2^{j}({\Im}) - k),\quad 0\le k < 2^j,\;\; j = 0, 1, 2, \ldots\; . \end{equation}$

(3.2)

Then, the Haar system ${\varphi, h_{j, k}: j\ge 0, 0\le k < 2^j}$ forms an orthonormal basis for the Hilbert space $L_2(0, 1)$ . Thus, for some fixed $j$ , the inner product expansion of $f \in L_2[0, 1]$ is given as

$\begin{equation} f({\Im}) \approx \langle f,\varphi \rangle \varphi({\Im}) \sum\limits_{j = 0}^{j-1} \sum\limits_{k = 0}^{2^j - 1} \langle f,h_{j,k} \rangle h_{j,k}({\Im}) = C^{T} H({\Im}), \end{equation}$

(3.3)

where $C$ , determined by the inner product $c_{i} = \langle f(\Im){, }h_{j, k}(\Im)\rangle, \langle\cdot\rangle$ is a $1 \times 2^j$ coefficient matrix and $H({\Im}) = \left[\varphi, h, h_{1, 0}, h_{1, 1}, h_{2, 0}, \ldots, h_{2, 3}, \ldots, h_{j-1, 0}, \ldots, h_{j-1, 2^j - 1}\right]$ represents the vector of the Haar functions. For simplicity, consider $\phi = h_0, h_{0, 0} = h = h_1$ and $h_i = h_{j, k}$ , where $i = 0, 1, 2, \ldots, m-1, m: 2^j$ , then, equation (3.3) becomes

$\begin{equation} f({\Im}) \approx \sum\limits_{i = 0}^{m-1}k_ih_i({\Im}) = C^{T}H({\Im}). \end{equation}$

(3.4)

Also, a function of two variables, ${y({\varkappa}, {\Im})} \in L^2([0, 1]\times [0, 1])$ can be approximated using Haar wavelets as:

$\begin{equation} {y({\varkappa},{\Im})} \approx \sum\limits_{i = 0}^{m-1} \sum\limits_{j = 0}^{m-1} c_{i,j}h_i({\varkappa})h_j({\Im}) = H^T({\varkappa})CH({\Im}), \end{equation}$

(3.5)

where $C$ , a $2^j \times 2^j$ coefficient matrix, is computed using the inner product

$c_{i,j} = \langle h_i({\varkappa}), \langle {y({\varkappa},{\Im})} h_j({\Im})\rangle \rangle.$

$\psi$ -Haar wavelets operational matrix:

The operational matrix of $\psi$ -fractional integration of Haar wavelet is defined as

$\begin{equation} P^{\alpha,\psi} _{i}(\varkappa) = \dfrac{1}{ \Gamma(\alpha)} \int_{a}^{\varkappa}\psi^{'}(\Im){\left(\psi(\varkappa)-\psi(\Im)\right)}^{\alpha-1}h_i(\Im)d\Im. \end{equation}$

(3.6)

Furthermore, the $\psi$ -fractional integral can be generalized and approximated analytically as:

$\begin{equation} P^{\alpha,\psi}_{i} (\varkappa) =\\ \begin{cases} 0, &\; \text{if}\; \; \varkappa < \zeta_1(i);\\ \frac{1}{\Gamma(\alpha+1)}\left[\psi(\varkappa)-\psi(\zeta_1(i))\right]^\alpha, &\; \text{if}\; \; \varkappa \in [\zeta_1(i),\zeta_2(i));\\ \frac{1}{\Gamma(\alpha+1)}\left[\left(\psi(\varkappa)-\psi(\zeta_1(i))\right)^\alpha-2\left(\psi(\varkappa)-\psi(\zeta_2(i))\right)^\alpha\right], &\; \text{if}\; \; \varkappa \in (\zeta_2(i),\zeta_3(i)];\\ \frac{1}{\Gamma(\alpha+1)}\left[\left(\psi(\varkappa)-\psi(\zeta_1(i))\right)^\alpha-2\left(\psi(\varkappa)-\psi(\zeta_2(i))\right)^\alpha\right. & \\+\left.\left(\psi(\varkappa)-\psi(\zeta_3(i))\right)^\alpha\right], &\; \text{if}\; \; \varkappa > \zeta_3(i). \end{cases} \end{equation}$

(3.7)

Equation (3.7) is true for $i > 1$ and for $i = 1$ , we have

$\begin{equation} P^{\alpha,\psi} (\varkappa) = \frac{1} {\Gamma(\alpha+1)}\left[\psi(\varkappa)-\psi(a)\right]^\alpha. \end{equation}$

(3.8)

Below is the operational matrix $P^{\alpha, \psi}$ of $\psi$ -Haar wavelets computed for $\psi(\varkappa) = \sin(\varkappa)$ and $\alpha = 0.8$ .

$\begin{equation} P^{\alpha,\psi} = \\\left[ \begin{array}{cccccccc} 0.5606 & -0.2219 & -0.1403 & -0.0847 & -0.08164 & -0.0611 & -0.0484 & -0.0362 \\ 0.2769 & 0.0617 & -0.1403 & 0.1369 & -0.08164 & -0.0611 & 0.0896 & 0.0521 \\ 0.0656 & 0.0826 & 0.05017 & -0.0093 & -0.08164 & 0.0935 & -0.0092 & -0.0020 \\ 0.0689 & -0.0689 & 0 & 0.03492 & 0 & 0 & -0.0690 & 0.0696 \\ 0.0150 & 0.0188 & 0.04881 & -0.0011 & 0.03404 & -0.0054 & -0.0008 & -0.0003 \\ 0.0175 & 0.0231 & -0.04066 & -0.0044 & 0 & 0.0318 & -0.0048 & -0.0007 \\ 0.0178 & -0.0178 & 0 & 0.0401 & 0 & 0 & 0.0279 & -0.0041 \\ 0.0166 & -0.0166 & 0 & -0.0332 & 0 & 0 & 0 & 0.0224 \end{array} \right]. \end{equation}$

(3.9)

4. Numerical solution to $\psi$ -FPDEs

This section discusses numerical solutions for linear $\psi$ -FPDEs using a technique based on two-dimensional $\psi$ -Haar wavelets.

4.1. $\psi$ -FPDEs with constant coefficients

This section considers linear FPDEs with constant coefficients involving $\psi$ -Caputo fractional derivative

$\begin{equation} \frac{\partial^{\alpha,\psi} {y({\varkappa},{\Im})}}{\partial {\Im}^{\alpha,\psi}} + \lambda \frac{\partial^{\beta,\psi} {y({\varkappa},{\Im})}}{\partial {\Im}^{\beta, \psi}} + \mu {y({\varkappa},{\Im})} = \eta \frac{\partial^{\gamma, \psi} {y({\varkappa},{\Im})}}{\partial {\varkappa}^{\gamma, \psi}}+f({\varkappa},{\Im}), \end{equation}$

(4.1)

for $0 < \alpha\leq2, 0\le \beta\leq1, 1\le \gamma\leq2$ and have non-homogeneous boundary and initial conditions given by

$\begin{equation} {y({\varkappa},{0})} = \rho({\varkappa}), \; \; \; \frac{\partial {y({\varkappa},{\Im})}}{\partial \Im}\bigg\vert _{\Im = 0} = \sigma ({\varkappa}), \; \; \; {y({0},{\Im})} = \xi({\Im}), \; \; \; {y({1},{\Im})} = \zeta({\Im}). \end{equation}$

(4.2)

For $1 < \alpha\leq2$ and $\lambda, \mu, \eta > 0$ , then (4.1) reduces to the fractional telegraph equation. For special cases, it includes the heat, wave, and Poisson equations. The $\psi$ -Haar wavelets technique provides numerical solutions. By approximating $\frac{\partial^{\alpha, \psi} {y({\varkappa}, {\Im})}}{\partial {\Im}^{\alpha, \psi}}$ using two-dimensional Haar wavelets, we have

$\begin{equation} \frac{\partial^{\alpha, \psi} {y({\varkappa},{\Im})}}{\partial {\Im}^{\alpha, \psi}} = H_{m}^{T}({\varkappa})C_{m \times m}H_{m}({\Im}). \end{equation}$

(4.3)

Operating both sides of (4.3) by $\mathcal{J}^{\alpha, \psi}_{\Im}$ , we get

$\begin{equation} {y({\varkappa},{\Im})} = H_{m}^{T}({\varkappa})C_{m \times m}\left( \int_{0}^{\Im}\psi^{\prime}(\Im)\frac{(\psi({\Im})-\psi(s))^{\alpha-1}}{\Gamma(\alpha)}H_{m}({s})ds \right) + p({\varkappa}){\Im} + q({\varkappa}). \end{equation}$

(4.4)

Applying the initial conditions ${y({\varkappa}, {0})} = \rho({\varkappa})$ and $\frac{\partial {y({\varkappa}, {\Im})}}{\partial t}\left\vert _{\Im = 0} = \sigma ({\varkappa})\right.$ , from (4.2), we have $q({\varkappa}) = \rho({\varkappa})$ and $p({\varkappa}) = \sigma({\varkappa})$ . Therefore, (4.4) becomes

$\begin{equation} {y({\varkappa},{\Im})} = H_{m}^{T}({\varkappa})C_{m \times m}P^{\alpha, \psi}_{m\times m}H_{m}({\Im}) + \sigma({\varkappa}){\Im} + \rho({\varkappa}). \end{equation}$

(4.5)

Applying $\frac{\partial^{\beta, \psi}}{\partial {\Im}^{\beta, \psi}}$ to (4.5), we obtain

$\begin{equation} \frac{\partial^{\beta, \psi} {y({\varkappa},{\Im})}}{\partial {\Im}^{\beta, \psi}} = H_{m}^{T}({\varkappa})C_{m \times m}P^{\alpha-\beta, \psi}_{m\times m}H_{m}({\Im}) + \sigma({\varkappa}) \frac{{\Im}^{1-\beta}}{\Gamma(2-\beta)}. \end{equation}$

(4.6)

By substituting (4.3), (4.5) and (4.6) in (4.1), we have

$\begin{align} \eta \frac{\partial^{\gamma, \psi} {y({\varkappa},{\Im})}}{\partial {\varkappa}^{\gamma, \psi}}& = H_{m}^{T}({\varkappa})C_{m \times m}H_{m}({\Im}) + \lambda H_{m}^{T}({\varkappa})C_{m \times m}P^{\alpha-\beta, \psi}_{m\times m}H_{m}({\Im})\\ &\quad+ \mu H_{m}^{T}({\varkappa})C_{m \times m}P^{\alpha, \psi}_{m\times m}H_{m}({\Im})+ g({\varkappa},{\Im})\\ & = H_{m}^{T}({\varkappa}) \left(C_{m \times m}( I + \lambda P^{\alpha-\beta, \psi}_{m\times m} + \mu P^{\alpha, \psi}_{m\times m} + G_{m\times m})\right)H_{m}({\Im}), \end{align}$

(4.7)

where

$\begin{equation*} g({\varkappa},{\Im}) = \sigma({\varkappa}) \left( \frac{\lambda {\Im}^{1-\beta}}{\Gamma(2-\beta)} + \mu {\Im}\right) + \mu \rho({\varkappa})-f({\varkappa},{\Im}) = H_{m}^{T}({\varkappa})G_{m\times m}H_{m}({\Im}). \end{equation*}$

Applying $\mathcal{J}^{\gamma, \psi}_{\varkappa}$ on both sides of (4.7), we have

$\begin{equation} \eta {y({\varkappa},{\Im})} = \mathcal{J}^{\gamma, \psi}_{\varkappa}H_{m}^{T}({\varkappa}) \left(C_{m \times m}( I + \lambda P^{\alpha-\beta, \psi}_{m\times m} + \mu P^{\alpha, \psi}_{m\times m} + G_{m\times m})\right)\\H_{m}({\Im})+ x\phi_{1}({\Im}) + \phi_{2}. \end{equation}$

(4.8)

Implementing the condition ${y({0}, {\Im})} = \xi({\Im})$ , we get $\phi_{2}({\Im}) = \xi({\Im})$ and ${y({1}, {\Im})} = \zeta({\Im})$ gives

$\begin{equation} \phi_{1}({\Im}) = \mathcal{J}^{\gamma, \psi}_{\varkappa}H_{m}^{T}(1) \left(C_{m \times m}( I + \lambda P^{\alpha-\beta, \psi}_{m\times m} + \mu P^{\alpha, \psi}_{m\times m} + G_{m\times m})\right)\\H_{m}({\Im})+ \zeta({\Im}) - \xi({\Im}). \end{equation}$

(4.9)

Substituting (4.9) in (4.8), we have

$\begin{align} \eta {y({\varkappa},{\Im})}& = H_{m}^{T}({\varkappa}) \left( (P^{\gamma, \psi}_{m \times m})^{T}-(Q^{\gamma, \psi}_{m \times m})^{T} \right)\\ &\quad\times\left(C_{m \times m}( I + \lambda P^{\alpha-\beta, \psi}_{m\times m} + \mu P^{\alpha, \psi}_{m\times m} + G_{m\times m})\right)\\ &H_{m}({\Im}) + x(\zeta({\Im}) - \xi({\Im})) + \xi({\Im}), \end{align}$

(4.10)

where

$\begin{equation*} \mathcal{J}^{\gamma, \psi}_{\varkappa}H_{m}({\varkappa}) = P^{\gamma, \psi}_{m \times m}H_{m}({\varkappa}) = H_{m}^{T}({\varkappa})(P^{\gamma, \psi}_{m \times m})^{T} \end{equation*}$

and

$\begin{equation*} x\mathcal{J}^{\gamma, \psi}_{\varkappa}H_{m}(1) = Q^{\gamma, \psi}_{m \times m}H_{m}({\varkappa}). \end{equation*}$

From (4.5) and (4.10), we get the Sylvester equation

$\begin{align} &\left( (P^{\gamma, \psi}_{m \times m})^{T}-(Q^{\gamma, \psi}_{m \times m})^{T} \right)\left(C_{m \times m}( I + \lambda P^{\alpha-\beta, \psi}_{m\times m} + \mu P^{\alpha, \psi}_{m\times m}\right) - \eta C_{m \times m}P^{\alpha, \psi}_{m \times m}\\ & = S_{m \times m} - \left( (P^{\gamma, \psi}_{m \times m})^{T}-(Q^{\gamma, \psi}_{m \times m})^{T} \right)G_{m\times m}, \end{align}$

(4.11)

where

$s({\varkappa},{\Im}) = {\varkappa}(\zeta({\Im})-\xi({\Im})) + \xi({\Im}) - \eta(\sigma({\varkappa}){\Im}+\varrho({\Im})) = H_{m}^{T}({\varkappa})S_{m \times m}H_{m}({\Im}).$

Solving (4.11) for $C_{m \times m}$ and using (4.5) or (4.6), we can get the solution of the problem (4.1).

4.2. $\psi$ -FPDEs with variable coefficients

This section discusses the procedure for numerical solutions of the following class of $\psi$ -FPDEs.

$\begin{equation} \begin{split} \frac{\partial^{\gamma, \psi}{y}({\varkappa},{\Im})}{{\partial{\Im}^{\gamma, \psi}}}-{a}{({\varkappa})}\frac{\partial^{\alpha, \psi}{y}({\varkappa},{\Im})}{\partial{{\varkappa}^{\alpha, \psi}}}+{b}{({\varkappa})}\frac{\partial^{\beta, \psi}{y}({\varkappa},{\Im})}{\partial{{\varkappa}^{\beta, \psi}}}+\\{d}({\varkappa}){y}({\varkappa},{\Im}) = {f}({\varkappa},{\Im}), \; 1 < \alpha\leq2, \ \ 1 < \beta\leq2, \ \ 0 < \gamma\leq2, \end{split} \end{equation}$

(4.12)

with the initial conditions

$\begin{equation} {y}({\varkappa},{0}) = \phi_1({\varkappa}),\;\;\frac{{y}({\varkappa},{\Im})}{\partial{\Im}}\bigg|_{{\Im} = 0} = \psi_1({\varkappa}), \; \text{or }\; {y}({\varkappa},{0}) = \phi_1({\varkappa}), \; \; \; {y}({\varkappa},{1}) = \psi_2({\varkappa}), \end{equation}$

(4.13)

and boundary conditions:

$\begin{equation} {y}({0},{\Im}) = \mu({\Im}), \; \; \; {y}({1},{\Im}) = \nu({\Im}). \end{equation}$

(4.14)

Here, we present a numerical technique based on $\psi$ -Haar wavelets operational matrices for $\psi$ -fractional integration. We approximate $\frac{\partial^{\alpha, \psi}{y}({\varkappa}, {\Im})}{\partial{{\varkappa}^{\alpha, \psi}}}$ with Haar wavelets as

$\begin{equation} \frac{\partial^{\alpha, \psi}{y}({\varkappa},{\Im})}{\partial{{\varkappa}^{\alpha, \psi}}} = H^{T}_{m}({\varkappa})C_{{m}\times{m}}H_{m}({\Im}). \end{equation}$

(4.15)

Operating $\mathcal{J}^{\alpha, \psi}_{\varkappa}$ on (4.15), we get

$\begin{equation} {y}({\varkappa},{\Im}) = \mathcal{J}^{\alpha, \psi}_{\varkappa}H^{T}_{m}({\varkappa})C_{{m}\times{m}}H_{m}({\Im})+{p}({\Im}){\varkappa}+q({\Im}). \end{equation}$

(4.16)

Applying boundary conditions in (4.14) to (4.16), we have

$\begin{equation} q({\Im}) = \mu({\Im}), \ \ p({\Im}) = -\mathcal{J}^{\alpha, \psi}_{\varkappa}H^{T}_{m}({\varkappa})C_{{m}\times{m}}H_{m}({\Im})+\nu({\Im})-\mu({\Im}). \end{equation}$

(4.17)

Therefore, (4.16) can be written as

$\begin{align} {y}({\varkappa},{\Im})& = \mathcal{J}^{\alpha, \psi}_{\varkappa}H^{T}_{m}({\varkappa})C_{{m}\times{m}}H_{m}({\Im})-{\varkappa}\mathcal{J}^{\alpha, \psi}_{\varkappa}H^{T}_{m}({\varkappa})C_{{m}\times{m}}H_{m}({\Im})\\ &\quad+{\varkappa}({nu}({\Im})-\mu({\Im}))+\mu({\Im}). \end{align}$

(4.18)

Since $\mathcal{J}^{\alpha, \psi}_{\varkappa}H_{m}({\varkappa}) = P^{\alpha, \psi}_{{m}\times{m}}H_{m}({\varkappa})$ and $\phi^1({\varkappa})\mathcal{J}^{\alpha, \psi}_{\varkappa}H_m({\varkappa}) = Q^{\alpha, 1}_{{m}\times{m}}$ , where $\phi^1({\varkappa}) = {\varkappa}$ . Therefore, (4.18) takes the form

$\begin{align} {y}({\varkappa},{\Im})& = H^{T}_{m}({\varkappa})(P^{\alpha, \psi}_{{m}\times{m}})^{T}C_{{m}\times{m}}H_{m}({\Im})-H^{T}_{m}({\varkappa})(Q^{\alpha,1}_{{m}\times{m}})^TC_{{m}\times{m}}H_{m}({\Im})\\ &\quad+{\varkappa}(\nu({\Im})-\mu({\Im}))+\mu({\Im}). \end{align}$

(4.19)

Applying the $\psi$ -Caputo operator $\frac{\partial^{\beta, \psi}}{\partial{\varkappa}^\beta}$ on (4.18), we have

$\begin{align} \frac{\partial^{\beta, \psi}{y}({\varkappa},{\Im})}{\partial{\varkappa}^\beta}& = \mathcal{J}^{\alpha, \psi}_{\varkappa}H^{T}_{m}({\varkappa})C_{{m}\times{m}}H_{m}({\Im})-\frac{{\varkappa}^{1-\beta}}{\Gamma(2-\beta)}\mathcal{J}^{\alpha, \psi}_{\varkappa}H^{T}_{m}({\varkappa})C_{{m}\times{m}}H_{m}({\Im})\\ &\quad+\frac{{\varkappa}^{1-\beta}}{\Gamma(2-\beta)}({nu}({\Im})-\mu({\Im}))+\mu({\Im}). \end{align}$

(4.20)

For simplicity, we introduced some convenient notations.

$\begin{align*} \phi_2& = \frac{{b}({\varkappa}){\varkappa}^{1-\beta}}{\Gamma(2-\beta)}, \; \phi_3 = {\varkappa}d({\varkappa}), \\ {r}({\varkappa},{\Im})& = \frac{{\varkappa}^{1-\beta}}{\Gamma(2-\beta)}({nu}({\Im})-\mu({\Im}))+ d({\varkappa})q({\Im}) + (\nu({\Im})-\mu({\Im})){\varkappa}d({\varkappa}),\\ s({\varkappa},{\Im})& = {\varkappa}(\nu({\Im})-\mu({\Im}))+\mu({\Im})+\psi_1({\varkappa}){\Im}+\phi_1({\varkappa}),\\ {g}({\varkappa},{\Im})& = {\varkappa}(\nu({\Im})-\mu({\Im}))-\mu({\Im})+(\psi_2({\varkappa})-\phi_1({\varkappa})){\Im}+\phi_1({\varkappa})\\ d({\varkappa})\mathcal{J}^{\alpha, \psi}_{\varkappa}H_{m}({\varkappa})& = \bar{P}^{\alpha, \psi}_{{m}\times{m}}H_{m}({\varkappa}), \\ b({\varkappa})\mathcal{J}^{\alpha, \psi}_{\varkappa}H_{m}({\varkappa})& = {\bar{P}}^{\alpha, \psi}_{{m}\times{m}}H_{m}({\varkappa}). \end{align*}$

Substituting (4.15), (4.18) and (4.20) in (4.12), we have

$\begin{align*} \frac{\partial^{\gamma, \psi} {y({\varkappa},{\Im})}}{\partial {\Im}^{\gamma, \psi}}& = \left(a({\varkappa})H^{T}_{m}({\varkappa})-H_{m}^{T}({\varkappa})(\bar{P}^{\alpha-\beta}_{m\times m})^{T} + \right.\\ &\left.H_{m}^{T}({\varkappa})(Q^{2,\alpha}_{m\times m})^{T} - H_{m}^{T}({\varkappa})(\bar{P}^{\alpha}_{m\times m})^{T}+ H_{m}^{T}({\varkappa})(Q^{\alpha, 3}_{m\times m})^{T} \right)\\ &\quad \times C_{m\times m}H_{m}({\Im})+ H_{m}^{T}({\varkappa})R_{m\times m}H_{m}({\Im}). \end{align*}$

Applying $\mathcal{J}^{\gamma, \psi}_{\varkappa}$ on previous equation, we get

$\begin{align*} {y({\varkappa},{\Im})}& = \left(a({\varkappa})H^{T}_{m}({\varkappa})-H_{m}^{T}({\varkappa})(P^{\alpha-\beta}_{m\times m})^{T} + \right.\\ &\left.H_{m}^{T}({\varkappa})(Q^{2,\alpha}_{m\times m})^{T} - H_{m}^{T}({\varkappa})(\bar{P}^{\alpha}_{m\times m})^{T}+ H_{m}^{T}({\varkappa})(Q^{\alpha, 3}_{m\times m})^{T} \right)\\ &\quad \times C_{m\times m}\mathcal{J}^{\gamma, \psi}_{\varkappa}H_{m}({\Im}) + H_{m}^{T}({\varkappa})R_{m\times m}\mathcal{J}^{\gamma, \psi}_{\varkappa}H_{m}({\Im})+ w({\varkappa}){\Im} + \omega({\varkappa}). \end{align*}$

Using the initial conditions, we get $\omega({\varkappa}) = \phi_{1}({\varkappa})$ and $w({\varkappa}) = \psi_{1}({\varkappa})$ . Therefore,

$\begin{align} {y({\varkappa},{\Im})}& = \left(a({\varkappa})H^{T}_{m}({\varkappa})-H_{m}^{T}({\varkappa})(\bar{P}^{\alpha-\beta}_{m\times m})^{T} + H_{m}^{T}({\varkappa})(Q^{2,\alpha}_{m\times m})^{T} - \right.\\ &\left.H_{m}^{T}({\varkappa})(\bar{P}^{\alpha}_{m\times m})^{T}+ H_{m}^{T}({\varkappa})(Q^{\alpha, 3}_{m\times m})^{T} \right)\\ &\quad \times C_{m\times m}\mathcal{J}^{\gamma, \psi}_{\varkappa}H_{m}({\Im})+ H_{m}^{T}({\varkappa})R_{m\times m}\mathcal{J}^{\gamma, \psi}_{\varkappa}H_{m}({\Im})+ \psi_{1}({\varkappa}){\Im} + \phi_{1}({\varkappa}). \end{align}$

(4.21)

Now, we employ the boundary conditions to get $w({\varkappa}) = \phi_1({\varkappa})$ and

$\begin{align} v({\varkappa}) & = \left[\left(a({\varkappa})H_{m}^{T}{\varkappa} - H_{m}^{T}{\varkappa}(\hat{P}^{\alpha - \beta, \psi}_{m\times m })^T + H_{m}^{T}{\varkappa} (Q^{\alpha, \psi , 2}_{m\times m})^T - H_{m}^{T}{\varkappa}(\bar{P}^{\alpha, \psi}_{m\times m })^T \right.\right.\\ &\left.\left. \quad+ H_{m}^{T}{\varkappa} (Q^{\alpha, \psi , 3}_{m\times m})^T \right)C_{m \times m} + H_{m}^{T}{\varkappa}R_{m\times m} \right]\mathcal{J}^{\gamma}_t H_{m} (1) + \psi_2{\varkappa} - \phi_1({\varkappa}). \end{align}$

(4.22)

Therefore, (4.21) becomes

$\begin{align} {y({\varkappa},{\Im})} & = \left[\left(a({\varkappa})\Psi^T_M ({\varkappa}) - H_{m}^{T}({\varkappa})(\hat{P}^{\alpha - \beta, \psi}_{m\times m })^T + H_{m}^{T}({\varkappa}) (Q^{\alpha, \psi , 2}_{m\times m})^T - H_{m}^{T}({\varkappa})(\bar{P}^{\alpha, \psi}_{m\times m })^T \right.\right.\\ &\left.\left.\quad+ H_{m}^{T}({\varkappa}) (Q^{\alpha, \psi , 3}_{m\times m})^T \right)C_{m \times m} + H_{m}^{T}({\varkappa})R_{m\times m}\right] \left(P^{\gamma}_{m\times m} - Q^{\gamma}_{m\times m}\right)\Psi_{m}({\Im})\\ &\quad+ (\psi_2({\varkappa}) - \phi({\varkappa})){\Im} + \phi_1({\varkappa}). \end{align}$

(4.23)

Combining (4.19) and (4.21) gives the Sylvester equation

$\begin{align} &\left((P^{\alpha, \psi}_{m\times m})^T - (Q^{\alpha, \psi,1}_{m\times m})^T\right)C_{m\times m}\\ &-\left(\frac{\eta}{m} \Psi_{m\times m}A_{m\times m}H^{T}_{m\times m}-(\hat{P}^{\alpha - \beta, \psi}_{m\times m}) - (\bar{P}^{\alpha, \psi}_{m\times m })^T + (Q^{\alpha, \psi ,2}_{m\times m})^T+ (Q^{\alpha, \psi , 3}_{m\times m})^T\right)C_{m \times m}P^{\gamma}_{m\times m}\\ & = R_{m\times m} P^{\gamma}_{m\times m} + S_{m\times m}, \end{align}$

(4.24)

where $A_{m\times m} : = diag[(a({\varkappa}_i))], x_i = \frac{2i - 1}{2m}, i = 1, 2, 3, \dots, m$ . Also, using (4.19) and (4.23), we obtain the following matrix form:

$\begin{align} &\left((P^{\alpha, \psi}_{m\times m})^T - (Q^{\alpha, \psi,1}_{m\times m})^T\right)C_{m \times m}\\ &\quad-\left(\frac{\eta}{m} \Psi_{m\times m}A_{m\times m}H^{T}_{m\times m} - \right.\\ &\left. (\hat{P}^{\alpha - \beta, \psi}_{m\times m}) - (\bar{P}^{\alpha, \psi}_{m\times m })^T + (Q^{\alpha, \psi ,2}_{m\times m})^T + (Q^{\alpha, \psi , 3}_{m\times m})^T\right) C_{m \times m}\left(P^{\gamma}_{m\times m} - Q^{\gamma}_{m\times m}\right)\\ &\quad = R_{m\times m} \left(P^{\gamma}_{m\times m} - Q^{\gamma}_{m\times m}\right) + G_{m\times m}. \end{align}$

(4.25)

By solving (4.25) for $G_{m\times m}$ and substituting it into (4.19), we get the approximate solution of problem (4.12).

To solve various $\psi$ -FPDEs, we use the $\psi$ -Haar wavelets technique. Additionally, we compared the graphical results obtained using the proposed method with the exact solutions. For the first two examples, we use the technique discussed in subsection 4.1 and for the other two examples, we follow the procedure discussed in subsection 4.2.

Example 1. Consider the time-fractional telegraph equation with $\psi$ -Caputo fractional derivative

$\begin{align} &\frac{\partial^{\alpha, \psi} {y({\varkappa},{\Im})}}{\partial {\Im}^{\alpha, \psi}} + \frac{\partial^{\alpha -1, \psi} {y({\varkappa},{\Im})}}{\partial {\Im}^{\alpha -1, \psi}} + {y({\varkappa},{\Im})}\\ & = \frac{\partial^{2} {y({\varkappa},{\Im})}}{\partial {\varkappa}^{2}} + \frac{\Gamma(2\alpha + 1)}{\Gamma(\alpha + 1)}\left( 1+ \frac{\psi({\Im})}{\alpha + 1}\right) (\psi({\Im}))^{\alpha, \psi}\cos(7{\varkappa})+50 (\psi({\Im}))^{2\alpha}\cos(7{\varkappa}) \end{align}$

(4.26)

satisfying the initial and boundary conditions

${y({\varkappa},{0})} = 0,\;\;\frac{\partial {y({\varkappa},{\Im})}}{\partial \Im}\bigg\vert _{\Im = 0} = 0,\;\; {y({0},{\Im})} = (\psi({\Im}))^{2\alpha}, \;\;{y({1},{\Im})} = 0.7539022(\psi({\Im}))^{2\alpha}.$

The exact solution for the problem (4.26) is given by

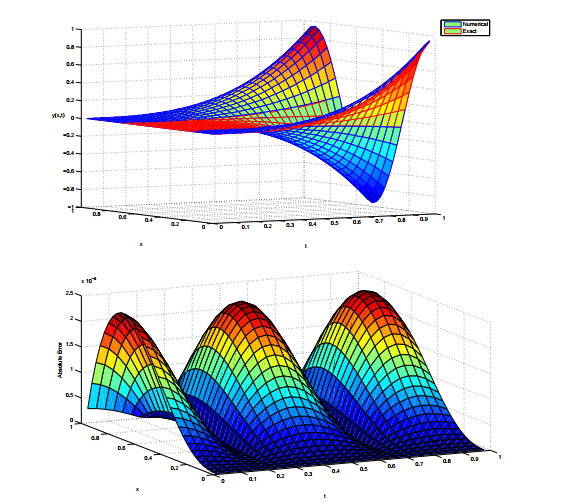
${y({\varkappa},{\Im})} = (\psi({\Im}))^{2\alpha}\cos(7{\varkappa}).$

Exact and approximate solutions of the problem (4.26) and their absolute error are plotted in Figure 1.

Figure 1. Approximate and exact solutions of (4.26) and their absolute error.

DownLoad: Full-Size Img PowerPoint

Also absolute error for problem (4.26) is given in for various choices of the parameters $\alpha, J, \Im$ and $\varkappa.$

Table 1. Absolute error for

$\psi(\varkappa) = \sin(\varkappa)$ .

$\Im$	$\varkappa$	$\alpha$	$J=3$	$J=4$	$J=5$	$J=6$	$J=7$
0.25	0.20	$1.5$	$3.3780\times 10^{-3}$	$7.4702\times 10^{-4}$	$2.4498\times 10^{-5}$	$8.0425\times 10^{-6}$	$2.6428\times 10^{-6}$
	0.50	$1.6$	$2.1513\times 10^{-3}$	$6.5313\times 10^{-4}$	$1.9862\times 10^{-5}$	$6.0507\times 10^{-6}$	$1.8462\times 10^{-6}$
	0.80	$1.7$	$2.0818\times 10^{-3}$	$5.8754\times 10^{-4}$	$1.6603\times 10^{-5}$	$4.6985\times 10^{-6}$	$1.3317\times 10^{-6}$
0.50	0.20	$1.8$	$2.0718\times 10^{-3}$	$5.4730\times 10^{-4}$	$1.4458\times 10^{-5}$	$3.8213\times 10^{-6}$	$1.0106\times 10^{-6}$
	0.50	$1.9$	$2.0363\times 10^{-3}$	$5.3432\times 10^{-4}$	$1.3359\times 10^{-5}$	$3.3400\times 10^{-6}$	$8.3502\times 10^{-7}$
	0.80	$2.0$	$2.0363\times 10^{-4}$	$5.3432\times 10^{-4}$	$1.3359\times 10^{-5}$	$3.3400\times 10^{-6}$	$8.3502\times 10^{-7}$

| Show Table

DownLoad: CSV

Example 2. Consider the $\psi$ -FPDE given by

$\begin{align} &\frac{\partial^{\alpha,\psi} {y({\varkappa},{\Im})}}{\partial {\Im}^{\alpha, \psi}}-\lambda\frac{\partial^{2} {y({\varkappa},{\Im})}}{\partial {\varkappa}^{2}}\\ & = \left( \frac{(\psi({\Im}))^{1-\alpha}}{\Gamma(2-\alpha)} - \frac{\Gamma(3\alpha+1)}{\Gamma(2\alpha+1)}(\psi({\Im}))^{2\alpha}\right) \\ & +144\lambda \psi({\Im})\left[1-(\psi({\Im}))^{3\alpha-1}\right]\sin(12{\varkappa}),\quad 0\leq \alpha \leq 1 \end{align}$

(4.27)

with the initial and boundary conditions

${y({\varkappa},{0})} = y(0,{\Im}) = 0,\;\; {y({1},{\Im})} = -0.536573\psi({\Im})\left[1-(\psi({\Im}))^{3\alpha-1}\right].$

The exact solution of problem (4.27) is given by

${y({\varkappa},{\Im})} = \sin(12{\varkappa}) \psi({\Im})\left[1-(\psi({\Im}))^{3\alpha-1}\right].$

Approximate and exact solution of the problem (4.27) and their absolute error are plotted in Figure 2.

Figure 2. Approximate and exact solutions of (4.27) and their absolute error.

DownLoad: Full-Size Img PowerPoint

Also the maximum absolute error is presented in the Table 2.

Table 2. Maximum absolute error for

$\psi(\varkappa) = \varkappa^2$ and different values of

$J$ and

$\alpha$ .

$\Im$	$\varkappa$	$\alpha$	$J=3$	$J=4$	$J=5$	$J=6$	$J=7$
0.25	0.20	$0.5$	$4.3007\times 10^{-2}$	$4.1167\times 10^{-4}$	$4.5672\times 10^{-5}$	$3.2361\times 10^{-5}$	$3.4349\times 10^{-6}$
	0.50	$0.6$	$6.3553\times 10^{-3}$	$6.2332\times 10^{-4}$	$5.4130\times 10^{-5}$	$4.2321\times 10^{-6}$	$2.6340\times 10^{-7}$
	0.80	$0.7$	$4.6571\times 10^{-3}$	$2.7212\times 10^{-5}$	$4.2014\times 10^{-6}$	$3.1478\times 10^{-6}$	$4.3216\times 10^{-7}$
0.50	0.20	$0.8$	$6.5786\times 10^{-4}$	$6.7634\times 10^{-5}$	$6.3132\times 10^{-6}$	$4.7324\times 10^{-7}$	$3.6210\times 10^{-7}$
	0.50	$0.9$	$2.1714\times 10^{-4}$	$5.3452\times 10^{-6}$	$3.0884\times 10^{-6}$	$4.2703\times 10^{-7}$	$5.7381\times 10^{-8}$
	0.80	$1.0$	$3.2738\times 10^{-5}$	$1.2753\times 10^{-6}$	$2.8801\times 10^{-7}$	$4.6721\times 10^{-8}$	$8.5382\times 10^{-9}$

| Show Table

DownLoad: CSV

Example 3. Consider the linear fractional diffusion equation with $\psi$ -Caputo derivative

$\begin{equation} \frac{\partial {y({\varkappa},{\Im})}}{\partial \Im} = a({\varkappa})\frac{\partial^{1.8,\psi} {y({\varkappa},{\Im})}}{\partial {\varkappa}^{1.8,\psi}}+f({\varkappa},{\Im}) \end{equation}$

(4.28)

with initial and boundary conditions

${y({\varkappa},{0})} = (\psi({\varkappa}))^{2}(1-\psi({\varkappa}))\;\;\text{and}\;\; y(0,{\Im}) = 0,\;\; {y({1},{\Im})} = 0.$

For $a({\varkappa}) = \Gamma(1.2)(\psi({\varkappa}))^{1.8}$ and $f({\varkappa}, {\Im}) = (6\psi({\varkappa})-3)(\psi({\varkappa}))^{2}e^{-\Im}$ , the problem (4.28) has the exact solution as

${y({\varkappa},{\Im})} = ((\psi({\varkappa}))^{2}-(\psi({\varkappa}))^{3})e^{-\Im}.$

Numerical and exact solutions using $\psi$ -Haar wavelets technique and their absolute error for $\alpha = 1.8$ and $J = 5$ are shown in . Also absolute error for problem (4.28) is given in for various choices of the parameters $\alpha, J, \Im$ and $\varkappa.$

Figure 3. Approximate and exact solutions of (4.28) and their absolute error.

DownLoad: Full-Size Img PowerPoint

Table 3. Absolute error for

${\varkappa} = 0.25, {\varkappa} = 0.5$ , different values of

$J, \alpha$ and

$\psi(\varkappa) = \varkappa^3$ .

$\Im$	$\varkappa$	$\alpha$	$J=3$	$J=4$	$J=5$	$J=6$	$J=7$
0.25	0.20	$1.5$	$1.2733\times 10^{-3}$	$6.2471\times 10^{-4}$	$3.0934\times 10^{-4}$	$1.5391\times 10^{-4}$	$7.6766\times 10^{-5}$
	0.50	$1.6$	$1.2910\times 10^{-3}$	$6.3216\times 10^{-4}$	$3.1273\times 10^{-4}$	$1.5552\times 10^{-4}$	$7.7551\times 10^{-5}$
	0.80	$1.7$	$1.1161\times 10^{-3}$	$5.4369\times 10^{-4}$	$2.6824\times 10^{-4}$	$1.3321\times 10^{-4}$	$6.6382\times 10^{-5}$
0.50	0.20	$1.8$	$7.1349\times 10^{-4}$	$3.4173\times 10^{-4}$	$1.6710\times 10^{-4}$	$8.2612\times 10^{-5}$	$4.1071\times 10^{-5}$
	0.50	$2.0$	$6.1030\times 10^{-5}$	$1.5258\times 10^{-5}$	$3.8146\times 10^{-6}$	$9.5367\times 10^{-7}$	$2.3841\times 10^{-7}$

| Show Table

DownLoad: CSV

Example 4. Consider the convection-diffusion equation with $\psi$ -Caputo fractional derivative:

$\begin{equation} \begin{split} \frac{\partial^{\gamma, \psi}{y}({\varkappa},{\Im})}{{\partial{\Im}^{\gamma, \psi}}}& = -{a}{\varkappa}\frac{\partial^{\alpha, \psi}{y}({\varkappa},{\Im})}{\partial{{\varkappa}^{\alpha, \psi}}}+{b}{\varkappa}\frac{\partial^{\beta, \psi}{y}({\varkappa},{\Im})}{\partial{{\varkappa}^{\beta, \psi}}}\\&+{f}({\varkappa},{\Im}),\; 1 < \alpha\leq2,\; 0 < \beta\leq1,\; 0 < \gamma \leq2 \end{split} \end{equation}$

(4.29)

with initial and boundary conditions

$\begin{equation*} {y({\varkappa},{0})} = {y({\varkappa},{1})} = 0,\; {y({0},{\Im})} = 0,\; {y({1},{\Im})} = 0. \end{equation*}$

We solve this problem with

$\begin{align*} a({\varkappa})& = \Gamma(\beta+2)\Gamma(5-\{\alpha+\beta\})\psi({\varkappa})^{\beta},\; \; b({\varkappa}) = \Gamma(2\beta+2-\alpha)\Gamma(5-2\alpha)\psi({\varkappa})^{\alpha},\\ f({\varkappa},{\Im})& = (2\pi \psi({\varkappa})^{2\beta+1}-\psi({\varkappa})^{4-\alpha})\psi({\Im})^{1-\gamma}E_{2,2-\gamma(-(2\pi \psi({\Im}))^2)} \\ &\quad+\left(\Gamma(2\beta+2)\Gamma(5-\{\alpha+\beta\})-\Gamma(5-2\alpha)\psi({\varkappa})^{2\beta+1}\right.\\ &\left.\quad+\Gamma(5-2\alpha)(\Gamma(2\beta+2-\alpha)-\Gamma(\beta+2))\psi({\varkappa})^{4-\alpha}\right)\sin(2\pi \psi({\Im})). \end{align*}$

The exact solution of the problem (4.29) is

${y({\varkappa},{\Im})} = (\psi({\varkappa})^{2\beta+1}-\psi({\varkappa})^{4-\alpha})\sin(2\pi \psi({\Im})).$

Exact and approximate solutions of problem 4.29 and their absolute error is plotted in Figure 4.

Figure 4. Approximate and exact solutions of (4.29) and their absolute error.

DownLoad: Full-Size Img PowerPoint

Also absolute error is given in for various values of $\alpha, \varkappa$ and $J$ at $\Im = 0.25$ and $\Im = 0.50$ .

Table 4. Absolute error for

$\psi(\varkappa) = \varkappa^2$ .

$\Im$	$\varkappa$	$\alpha$	$J=3$	$J=4$	$J=5$	$J=6$	$J=7$
0.25	0.20	$1.5$	$4.3854\times 10^{-4}$	$1.4252\times 10^{-4}$	$4.6203\times 10^{-5}$	$1.4996\times 10^{-5}$	$4.8789\times 10^{-6}$
	0.50	$1.6$	$3.3031\times 10^{-4}$	$1.0001\times 10^{-4}$	$3.0183\times 10^{-5}$	$9.1122\times 10^{-6}$	$2.7562\times 10^{-6}$
	0.80	$1.7$	$2.4252\times 10^{-4}$	$6.8593\times 10^{-5}$	$1.9314\times 10^{-5}$	$5.4339\times 10^{-6}$	$1.5301\times 10^{-6}$
0.50	0.20	$1.8$	$1.7673\times 10^{-4}$	$4.6930\times 10^{-5}$	$1.2396\times 10^{-5}$	$3.2674\times 10^{-6}$	$8.6081\times 10^{-7}$
	0.50	$2.0$	$1.3575\times 10^{-4}$	$3.4133\times 10^{-5}$	$8.5580\times 10^{-6}$	$2.1426\times 10^{-6}$	$5.3605\times 10^{-7}$

| Show Table

DownLoad: CSV

5. Conclusions

We developed and used the $\psi$ -Haar wavelets operational matrix of integration of fractional order for the first time for the numerical solution of $\psi$ -FPDEs. The numerical results of the proposed method are compared to the exact solutions and illustrated along with their absolute error in the figures. Furthermore, the absolute errors are presented in tables, indicating that our method agrees well with the exact solutions. The proposed method can also be applied to other wavelet bases, such as Legendre, Chebyshev, and Gegenbauer wavelets, and can also be applied to nonlinear $\psi$ -FPDEs.

Conflict of interest

The authors declare no conflicts of interest.

References

[1]	V. E. Tarasov, Handbook of fractional calculus with applications, Boston, Berlin: de Gruyter, 5 (2019).
[2]	L. Debnath, Recent applications of fractional calculus to science and engineering, Int. J. Math. Math. Sci., 2003 (2003), 753601. https://doi.org/10.1155/S0161171203301486 doi: 10.1155/S0161171203301486
[3]	H. G. Sun, Y. Zhang, D. Baleanu, W. Chen, Y. Q. Chen, A new collection of real world applications of fractional calculus in science and engineering, Commun. Nonlinear Sci., 64 (2018), 213–231. https://doi.org/10.1016/j.cnsns.2018.04.019 doi: 10.1016/j.cnsns.2018.04.019
[4]	R. Almeida, A. B. Malinowska, T. Odzijewicz, An extension of the fractional Gronwall inequality, In: Advances in non-tnteger order calculus and its applications, Springer, 2018, 20–28.
[5]	R. Almeida, Fractional differential equations with mixed boundary conditions, B. Malays. Math. Sciences So., 42 (2019), 1687–1697.
[6]	R. Almeida, A Caputo fractional derivative of a function with respect to another function, Commun. Nonlinear Sci., 44 (2017), 460–481. https://doi.org/10.1016/j.cnsns.2016.09.006 doi: 10.1016/j.cnsns.2016.09.006
[7]	C. Derbazi, Z. Baitiche, M. S. Abdo, T. Abdeljawad, Qualitative analysis of fractional relaxation equation and coupled system with $\psi$ -Caputo fractional derivative in Banach spaces, AIMS Mathematics, 6 (2021), 2486–2509. https://doi.org/10.3934/math.2021151 doi: 10.3934/math.2021151
[8]	J. V. da C. Sousa, E. C. de Oliveira, On the stability of a hyperbolic fractional partial differential equation, Differ. Equat. Dyn. Sys., 2019, 1–22. https://doi.org/10.48550/arXiv.1805.05546 doi: 10.48550/arXiv.1805.05546
[9]	N. Adjimi, A. Boutiara, M. S. Abdo, M. Benbachir, Existence results for nonlinear neutral generalized Caputo fractional differential equations, J. Pseudo-Differ. Oper., 12 (2021), 1–17. https://doi.org/10.1007/s11868-021-00400-3 doi: 10.1007/s11868-021-00400-3
[10]	S. Abbas, M. Benchohra, N. Hamidi, J. Henderson, Caputo-Hadamard fractional differential equations in Banach spaces, Fract. Calc. Appl. Anal., 21 (2018), 1027–1045. https://doi.org/10.1515/fca-2018-0056 doi: 10.1515/fca-2018-0056
[11]	D. Vivek, E. M. Elsayed, K. Kanagarajan, Theory and analysis of partial differential equations with a $\psi$ -Caputo fractional derivative, Rocky Mt. J. Math., 49 (2019), 1355–1370. https://doi.org/10.1216/RMJ-2019-49-4-1355 doi: 10.1216/RMJ-2019-49-4-1355
[12]	A. Suechoei, P. S. Ngiamsunthorn, Existence uniqueness and stability of mild solutions for semilinear $\psi$ -Caputo fractional evolution equations, Adv. Differ. Equ., 2020 (2020), 114. https://doi.org/10.1186/s13662-020-02570-8 doi: 10.1186/s13662-020-02570-8
[13]	Y. Yang, M. H. Heydari, Z. Avazzadeh, A. Atangana, Chebyshev wavelets operational matrices for solving nonlinear variable-order fractional integral equations, Adv. Differ. Equ., 2020 (2020), 611. https://doi.org/10.1186/s13662-020-03047-4 doi: 10.1186/s13662-020-03047-4
[14]	M. Bilal, A. R. Seadawy, M. Younis, S. T. R. Rizvi, H. Zahed, Dispersive of propagation wave solutions to unidirectional shallow water wave Dullin-Gottwald-Holm system and modulation instability analysis, Math. Method. Appl. Sci., 44 (2021), 4094–4104. https://doi.org/10.1002/mma.7013 doi: 10.1002/mma.7013
[15]	A. R. Seadawy, A. Ali, W. A. Albarakati, Analytical wave solutions of the (2+1)-dimensional first integro-differential Kadomtsev-Petviashivili hierarchy equation by using modified mathematical methods, Results. Phys., 15 (2019), 102775. https://doi.org/10.1016/j.rinp.2019.102775 doi: 10.1016/j.rinp.2019.102775
[16]	A. R. Seadawy, M. Arshad, D. Lu, The weakly nonlinear wave propagation of the generalized third-order nonlinear Schrodinger equation and its applications, Wave. Random. Complex., 32 (2022), 819–831. https://doi.org/10.1080/17455030.2020.1802085 doi: 10.1080/17455030.2020.1802085
[17]	A. A. Kilbas, H. M. Srivastava, J. J. Trujillo, Theory and applications of fractional differential equations, Elsevier Sci. Limited., 204 (2006), 1–523.

This article has been cited by:

1.	Parisa Rahimkhani, A numerical method for Ψ-fractional integro-differential equations by Bell polynomials, 2025, 207, 01689274, 244, 10.1016/j.apnum.2024.09.011
2.	Parisa Rahimkhani, Mohammad Hossein Heydari, Numerical investigation of $\Psi$ -fractional differential equations using wavelets neural networks, 2025, 44, 2238-3603, 10.1007/s40314-024-02965-3
3.	Majida H. Majeed, 2025, 3264, 0094-243X, 050133, 10.1063/5.0265328

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(1726) PDF downloads(117) Cited by(3)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(4) / Tables(4)

AIMS Mathematics

A novel numerical method for solution of fractional partial differential equations involving the $\psi$ -Caputo fractional derivative

Related Papers:

Abstract

1. Introduction

2. Basics of $\psi$ -fractional calculus

3. Haar wavelets and function approximation

4. Numerical solution to $\psi$ -FPDEs

4.1. $\psi$ -FPDEs with constant coefficients

4.2. $\psi$ -FPDEs with variable coefficients

5. Conclusions

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Mathematics

A novel numerical method for solution of fractional partial differential equations involving the ψ \psi -Caputo fractional derivative

Related Papers:

Abstract

1. Introduction

2. Basics of ψ \psi -fractional calculus

3. Haar wavelets and function approximation

4. Numerical solution to ψ \psi -FPDEs

4.1. ψ \psi -FPDEs with constant coefficients

4.2. ψ \psi -FPDEs with variable coefficients

5. Conclusions

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

A novel numerical method for solution of fractional partial differential equations involving the $\psi$ -Caputo fractional derivative

2. Basics of $\psi$ -fractional calculus

4. Numerical solution to $\psi$ -FPDEs

4.1. $\psi$ -FPDEs with constant coefficients

4.2. $\psi$ -FPDEs with variable coefficients