Computational analysis of COVID-19 model outbreak with singular and nonlocal operator

1.   Introduction

In the 21st century, due to several applications of mathematical biology, researchers have shown exceptional interest in this sector. So, in the case of mathematical modeling, their vital concern is to express contagious diseases and control them. Brownlee ^[1] arranged a solid foundation of mathematical biology. For the spread of infection ^[2], he suggested a law with the help of probabilistic techniques. The implementation of fractional derivatives is helpful in the modeling of several problems of mathematical biology, like hepatitis, glucose, Ebola, HIV, etc. ^{[3,4,5,6,7,8,9,10,11]}.

Within a few years, several techniques were used to investigate the dynamics of COVID-19. Among these, Caputo ^[12], Caputo-Fabrizio ^[13] and Atangana-Baleanu-Caputo (ABC) ^[14] are the focus of attention around the world. ^{[15,16,17,18,19]} Some applications of these were helpful in several issues. Also, over the last few months, numerous infection models have been constructed and discussed based on various fractional-order operators to study the dynamic behavior and control of new COVID-19 cases. In ^[20], with the help of the famous Caputo Fabrizio derivative, a new transmission model for COVID-19 dynamics was established. In ^[21], the authors developed a fractional-order model with the ABC operator. In ^[22], to see the effect of lockdown, Atangana presented a model with the assistance of the fractal fractional operator. Vaccines play a vital role in decreasing the growth of COVID-19, and their effects can be seen in ^[23]. In ^[24], Akgül et al. analyzed the differential equation model in the context of COVID-19. Further, they determined its stability with fractal-fraction derivative. Din et al. ^[25] proceed Akgül's work to solve the problems of Hepatitis B. In ^[26], the authors qualitatively used the stability theory of DEs and the basic reproduction number, which represents an epidemic index obtained from the so-called maximum eigenvalues of the next-generation matrix. They presented a mathematical model that calculates the results, and it turns out to be beneficial to public health initiatives. ^[27,28,29] Various fractional operators associated with the infection COVID-19 have been proposed to work the dynamics of fractional epidemic models. ^[30] Atangana et al. suggested a model and extended it to the scope of nonlocal operators. Moreover, simulations were performed for different non-integer numbers. In ^[31], the authors initially considered the classical integer model and then generalized it by introducing the Caputo fractional derivative. Further, for the case of simulation, they used the generalized Adams-Bashforth-Moulton scheme.

An inverse problem for the heat equation in two dimensional space with the Robin boundary condition that involves a new fractional derivative, namely, the Atangana-Baleanu approach with non-local and non-singular kernel was considered in ^[37]. Futher, a numerical algorithm in the reproducing kernel Hilbert space (RKHS) approach was applied to the inverse source problem for the diffusion equation in a time-space fractional sense, where determinations of state variables and source parameters subject to initial boundary and over-determination conditions are the main goal. ^[38] dealt with two types of inverse problems for diffusion equations involving Caputo fractional derivatives in time and the fractional Sturm-Liouville operator for space. An inverse source problem for fractional diffusion equation that containing fractional derivative with non-singular and non-local kernel, namely, the Atangana-Baleanu-Caputo fractional derivative, was studied in ^[39].

The manuscript is arranged as follows: In Section 2, some basic notions related to the Caputo derivative are described. In Section 3, we formulated COVID-19 model. We analyze the positivity and local stability of the system in Section 4. Moving on, in Section 5, we proved some useful results related to existence and uniqueness of the model. We develop numerical schemes in Section 6. Further, we discuss simulations in Section 7. The last segment consists of a conclusion.

2.   Basic definitions

In this section, some primary notions are described that are helpful for analyzing the system.

Definition 2.1. ^[32] A Caputo derivative of fractional order $\varrho \in (0, 1)$, for the function $Z$ can be defined as

Definition 2.2. ^[32] The integral operator of fractional order $\varrho \in (0, 1)$ corresponding to the Caputo fractional derivative is defined as

Lemma 2.3. ^[12] Suppose $\mathscr{S}(\curlywedge) \in \mathscr{C}(0, T)$, the result of the fractional differential equation

is given by

where $L_{m} \in R, \; m = 0, 1, 2, ..., p$.

Lemma 2.4. ^[14,25,33] For any arbitrary $a_{m} \in R, \; m = 0, 1, 2, ..., p-1$, the following result holds:

where $p = [\varrho]+1$, and $[\varrho]$ represents the integer part of $\varrho$.

Lemma 2.5. ^[25] Suppose $\curlywedge \in \mathscr{A}C^{l}[0, T], \; \varrho > 0$, and $l = [\varrho]$. Then, the following condition is satisfied:

Lemma 2.6. ^[14,25] From the above Lemma, 2.5, the outcome $\mathscr{D}^{\varrho} \curlywedge(\wedge) = x(t), \; l-1 < \varrho < l$, is

where $b_m \in R$.

Definition 2.7. ^[14] If

then

Here, $R_{m} ^{\varrho}(t)$ is the remainder.

Theorem 2.1. ^[32,33] Let $\mathscr{B}:Y\rightarrow \mathscr{G}$ be compact and continuous, where $\mathscr{G}$ is a Banach space. If the set

is bounded, then we can say that $\mathscr{B}$ has a unique fixed point.

3.   Model formation

The epidemiological compartment concept is one that we support ^[34] that takes into consideration the distinction among people with extreme symptoms, mild symptoms, and without symptoms. We can split the model into nine parts at time t: Susceptible $Z_{S}(t)$, exposed $Z_{E}(t)$, severe symptoms of infectious individuals, $Z_{I_{ss}}(t)$, mild symptoms infectious individuals $Z_{I_{ms}}(t)$, infectious but asymptomatic individuals $Z_{I_{a}}(t)$, hospitalized $Z_{H}(t)$, intensive care unit class $Z_{I_{cu}}(t)$, recovery with immunity $Z_{R}(t)$ and the class of death $Z_{D}(t)$.

with initial condition

The human-to-human transmission coefficient per unit time per person is $\overline {\beta}$ in this case. The rate at which an individual departs the exposed clan by becoming contagious is represented by $\overline{k}$. An incubation period is defined as a time of $1 /\overline{k}$. The parameter $\overline{p_{1}}$ represents the likelihood that an individual will leave an exposed compartment $Z_{E}$ and become infected with severe symptoms $Z_{I_{ss}}$. $\overline{p_{2}}$ is the probability that an exposed person will become infected with moderate symptoms is called $Z_{I_{ms}}$ and $1 - \overline{p_{1}} - \overline{p_{2}}$ is the likelihood that exposed people joined an asymptomatic clan. $Z_{I_a}$. $\overline{h}$ represents the pace at which a person exits the compartment $Z_{I_{ss}}$ while $\overline{q_1}$ is the probability at which a person in $Z_{I_{ss}}$ went to the compartment H of hospitalized individuals. The recovery rate of persons with minor symptoms and asymptomatic people who are not hospitalized is $\overline{\gamma_3}$. The death rate of hospitalized patients $H$ who do not receive intensive care is $\overline{\delta_1}$. $\overline{\gamma_1}$ is the death rate of hospitalized patients with intensive care $Z_{I_{cu}}$.

We apply the Caputo derivative to the COVID-19 model

with initial condition

4.   Analysis of the system

Theorem 4.1. The solution of the proposed model (3.2) along initial conditions is unique and bounded in $R_+^9$.

Proof. In system (3.2), we can get its existence and uniqueness on the time interval $(0, \infty)$. Afterwards, we need to show that the non-negative region $R_+^9$ is a positively invariant region. From model (3.2), we find

If $Z_{S}(0), \; Z_{E}(0), \; Z_{I_{ss}}(0)\, \; Z_{I_{ms}}, \; Z_{I_{a}}(0), \; Z_{H}(0), \; Z_{I_{cu}}(0), \; Z_{R}(0), \; Z_{D}(0) \in R_+^9$, then according to Eq (4.1), the solution cannot escape from the hyperplanes. Also, on each hyperplane bounding the non-negative orthant, the vector field points into $R_+^9$, i.e., the domain $R_+^9$ is a positively invariant set.

4.1.   The basic reproduction number

For the system (3.2), the disease-free equilibrium is given by $Z_{S} = N, \; Z_{E} = Z_{I_{ss}} = Z_{I_{ms}} = Z_{I_{a}} = Z_{H} = Z_{I_{cu}} = Z_{R} = Z_{D} = 0$). Further, to figure out the reproduction number $R_0$ of the proposed system, we use the next-generation approach defined in ^[35,36]. Thus,

and

Hence,

We investigate the sensitivity of $R_0$ by taking the partial derivatives of $R_{0}$ for the involved parameters as follows:

We see that change in parameter $R_0$ is very sensitive. Here, $\overline{\beta}, \; \overline{p_{1}}, \; \overline{\gamma_{3}}$ are growing while $\overline{h}$ is decreasing. Hence, from the above analysis, we can say that prevention is better to control the disease.

4.2.   Stability analysis

Theorem 4.2. If $R_{0} < 1$, the disease-free equilibrium $(E^*)$ of the system (3.2) is locally stable, and it is unstable if $R_{0} > 1$.

Proof. For (3.2), we have

The total population $N$ is constant, so we have

Thus, for the system (3.2), we can find the local stability through the variables $Z_{E}, \; Z_{I_{ss}}, \; Z_{I_{ms}}, \; Z_{I_{a}}, \; Z_{H}$ and $Z_{I_{cu}}$. Therefore, the system is:

The Jacobian matrix $J(E^*)$ for the above system is:

The two eigenvalues are $\lambda_{1} ^* = \lambda_{2} ^* = -1$. For the remaining, we have

where

If $R_{0} < 1$, then all the states are fulfilled, which shows system (3.2) is locally stable and disease will decrease. If $R_{0} > 1$, the last state is not fulfilled, which shows system (3.2) is unstable, and disease can be increase.

5.   Existence and uniqueness of the model

For the sake of the required goal, here we set up the states for the existence and uniqueness of the system. Consider the functions:

Consider the Banach space, $\mathscr{C}[0, T] = \mathscr{B}$, having norm

where

From (5.2), we can represent the system (3.2) as

From Lemma 1, Eq (5.3) can be written as:

We assume the following hypothesis.

$\bullet (h_{1})\; There \; exists \; constants\; Z_K, \; Z_M\; > 0$

$\bullet \; (h_{2})\; For\; each\; \curlywedge, \; \overline{\curlywedge}, \; exists\; a \; constant\; Z_L\; > 0$

For an operator $\diamond :\mathscr{B}\longrightarrow \mathscr{B}$,

Theorem 5.1. or the authentication of Eq (5.3), suppose our hypotheses are true. Then, it has at least one solution $h_{1}, \; h_{2}$ are true. Then, it has at least one solution.

Proof. We validate it in the following four steps:

S1.Initially, we show that operator, $\diamond$ is continuous. For that, consider an operator $\wp$ is a continuous, so that $\wp(\rho, \curlywedge(\rho))$ is continuous as well. Further, if for $\curlywedge, \; \curlywedge_{m} \in \mathscr{G}$ there exist $\curlywedge_{n} \longrightarrow \curlywedge$ then we have $\diamond \curlywedge_{n} \longrightarrow \diamond \curlywedge$. Suppose

Thus, $\wp$ is continuous, so $\diamond$ is continuous.

S2.In this step, we show that $\diamond$ is bounded. For this, we consider that $\diamond$ fulfills the growth condition:

Hence, $\diamond$ is bounded.

S3.Furthermore, we show that $\diamond$ is equi-continuous. For this, consider $t_{2}\leq t_{1} = [0, T]$. Then,

Thus, by using the theorem of Arzela-Ascoli, it is compact

S4.At the final stage, we show that set $\mathscr{E}$ is bounded. For this, consider that for all $t\in [0, T]$, we have $\curlywedge \in \mathscr{E}$ and then

So, it is bounded, and by following the outcomes of Schauder's fixed point theorem, $\diamond$ has at least one solution.

Theorem 5.2. If $\frac{T^{\varrho} Z_{K}}{\Gamma(\varrho+1)} < 1$, then Eq (5.3) has a distinct solution.

Proof. Suppose $\curlywedge, \overline{\curlywedge} \in \mathscr{G}$ and then

Therefore, the fixed point is distinct and has a single outcome.

6.   Advanced numerical technique

In this part, our focus is to implement the operators on the proposed model. Further, we restore the classical operators with the power-law kernel and implement the variable version. For the power-law kernel

For clarification, we represent the model as;

where

For the Caputo fractal fractional derivative, consider

By applying the fractional integral with power law kernel, we can write the above expression as:

At $t_{\sigma +1} = (\sigma+1)\Delta t$, we get

For clarity, we take

We also have

Replacing them in the above equation and substituting $Q(t, \curlywedge(t)) = \wp(t, \curlywedge(t))t^{\tau-1}$, we get the numerical scheme

7.   Simulation and discussion

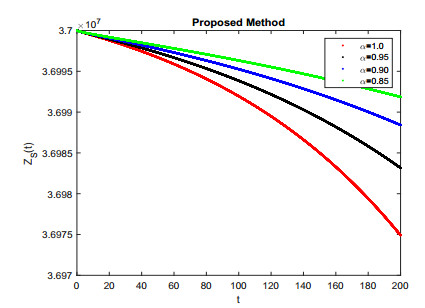
The plot plays a dominant role in realizing the behavior of the simulation of the model with the Caputo operator. We plot, for different values of $\alpha = 0.85, 0.9, 0.95, 1.0$, all nine compartments of the model in Figures 1–9. In Figures 1 and 6, we can see that the plot of susceptible and hospitalized people are decreasing with the passage of time. We see that the number of exposed ones and population having no symptoms both are increasing as shown in Figure 2. In the cases of people with severe and mild symptoms, their numbers initially go down rapidly and then rise. Similarly, the number of people in the intensive care unit also goes down rapidly. At certain value, plot moves smoothly, which means minor patients are in severe condition, as shown in Figures 3–7. Lastly, computational results of recovers and death populations are shown in Figures 8 and 9. The results of the nonlinear system memory were also detected with the help of fractional value results. Results provides a better way in case you want to control the disease without defining other parameters.

8.   Conclusions

The spread of COVID-19 infections is not only for both human health, but also a serious threat to the economy. Although the amount of exercise and the number of reports on the possibility of this new pandemic possibility control are published in recent years. In this study, we have formulated a new mathematical model to analyze the complex transfer dynamics of COVID-19 under the Caputo operator. The model has been studied qualitatively as well as quantitatively. For the suggested system, positivity, uniqueness, and boundedness for solution are proven. The proposed compartment model is prescribed by a classic differential equation first with an integer order. Treatment classes are suitable for model construction. We determined that our obtained results are effective for the proposed model. Some theoretical results were also discussed for the model.

Conflict of interest

The authors declare no conflict of interest.