Fractional modeling of COVID-19 pandemic model with real data from Pakistan under the ABC operator

1.   Introduction

COVID-19 which is an infectious respiratory illness spreads in China in 2019 and affects the whole world in the shape of human and economic loss. It is known that 11 to 14 days are its latency period while old age people and comorbid patient are their favorite prey. Similar to the symptoms of common flu and cold it is advisable to do the test at a first glance. It is also reported that people have no symptoms even though they are infected. The basic reproduction number for COVID-19 stays between 2.2 and 3.58, which shows that the disease transmission rate is very high. Hence, it disperse throughout the world in the blink of an eye and disturbed 213 nations. Keeping this in mind, the World Health Organization (WHO) officially announced that COVID-19 is one of the global pandemics. At first, there were no proper vaccine/antiviral strategies to control the COVID-19 disease hence most the countries have adopted non-pharmaceutical interventions (NPIs), which are quarantining of exposed individuals, travel restrictions, closure of educational institutes, avoiding mass gatherings, and isolation of infected individuals.

Daily a lot of people die due to Infectious diseases and hence it is considered to be the 2nd biggest reason for death throughout the world. In Mathematics, modeling is considered to be the best tool to elaborate on the dynamic phenomena of infectious diseases. In this regard, researchers and mathematician try their best to explore infectious diseases by using mathematical modeling. The stability analysis of an SVEIR model with continuous age structure in the exposed and infection classes is discussed in ^[1]. The dynamics of covid-19 via the stochastic epidemic model are explained in ^[2]. The dynamics of dengue infection through fractal-fractional operator with real statistical data is shown in ^[3]. The stability analysis and optimal vaccination of a SIR epidemic model are proven in ^[4]. The global stability of the COVID-19 model involving the quarantine strategy and media coverage effects are depicted in ^[5]. Fractional COVID-19 transmission is formulated by using the Caputo fractional derivative in ^[6].

Fractional derivatives received much applause during the last few years as their involvement in science and engineering is much more than expected. Fractional derivatives split into Local and nonlocal theories in which the nonlocal definitions received much more attraction due to their interesting applications ^{[7,8,9,10,11,12,13,14]}. According to singularity, fractional derivatives have two kinds i.e singular and nonsingular kernel. The Caputo, the Grünwald, and the Riemann–Liouville belong to the first kind while the Atangana–Baleanu and the Caputo–Fabrizio belong to the second kind. The Atangana-Baleanu which is based upon the Mittag-Leffler function answered the queries raised by the Caputo-Fabrizio definition. The classical queries of complex analysis have been easily addressed by the Mittag-Leffler function as can be seen from the power-law series analytic continuation which is convergent outside the disc. A dynamical process based on fractional-order derivatives carries its past and present state information ^{[15,16,17,18,19]}. Thus, in epidemiological compartmental models, utilizing a fractional-order system is more reasonable to work the transmission dynamics of infectious diseases.

Section 2 is devoted to some basic definitions regarding fractal fractional operators. In Section 3 the model is reformulated with the help of the Atangana-Baleanu-Caputo fractional derivative. The real data comparison is shown in Section 4. Section 5 deals with the equilibrium points and basic reproduction number and local stability. Existence and uniqueness are carried out in Section 6. Section 7 deals with the Ulam-Hyers stability of the proposed model. The sensitivity of different parameters corresponding to basic reproduction is discussed in Section 8. Some plots are given to conclude the simplicity and reliability of the algorithm in Section 9. Section 10 deals with the conclusion of our work.

2.   Preliminaries

The study presents basic definitions to set the tone for the mathematical derivation of the model.

Definition 2.1. The Riemann-Liouville integral as ^[20]:

Definition 2.2. The definition of Caputo derivative as ^[21]:

where $n-1 < \alpha \leq n, n \in \mathbb{N}$. Note that if $\alpha \rightarrow 1$ then ${ }^{C} D_{0, \vartheta}^{\alpha} f(\vartheta)$ approaches to $f^{\prime}(\vartheta)$.

Definition 2.3. The Caputo-Fabrizio operator of order $\zeta > 0$ is defined as follows ^[22]:

Definition 2.4. Suppose that $f(\vartheta) \in \mathbb{H}^{1}(0, T), T > 0$, and $\left.\lambda \in\right] 0$, 1[; then, the Atangana-Baleanu operator of order $\lambda$ in the Caputo sense can be represented by ^[23]:

Definition 2.5. The integral operator under the Atangana-Baleanu-Caputo sense is defined by the following expression ^[24]:

3.   The model with the classical derivative

In this section, we consider the highly nonlinear epidemiological model for the transmission of the newly raised COVID-19 infection. In this model the total population is categorized into six time dependent classes namely: Recovered R; Hospitalized infected J, infected I; Quarantine Q, Exposed E, and Susceptible S. The model is expressed as ^[25]:

with

The description of the parameters are as stated in Table 1.

In addition, $W(S, E)$ is a feature known as the uptake function. The incidence of susceptible with exposed class is related to this feature. In this article, we provide the susceptible and exposed interaction, as in ^[26], which has the form:

In addition, the function described in (3.2) displays the susceptible and exposed harmonic mean. For several studies, the $W(S, E)$ uptake function is considered to be the product of susceptible and exposed, known as the ^[25] bi-linear incidence rate. The dynamics of the COVID-19 model were addressed by the writers of ^[25] when considering the uptake feature to be the product of $S$ and $E$. Apart from these, it is very interesting to consider $W(S, E): = \frac{2 S E}{S+E}$ as the uptake function. Since it is understood that if there are two quantities $S$ and $E$ in the sense that $S, E \geq 0$, then the following relation is true:

In fact, the average of two values is a measure of the centrality of a data set. In addition, the geometric mean is mainly used to reach average data change ratios or rates. As far as harmonic means are concerned, as opposed to arithmetic or geometric means, it is less susceptible to a few broad values. It is used for highly skewed variables often^[27]. The readers are referred to ^[28] for the biological interpretation to the harmonic mean.

Remark 3.1. The system (3.1) satisfies

where $N(\varphi) = S(\varphi)+ E(\varphi)+ Q(\varphi)+I(\varphi)+J(\varphi)+ R(\varphi)$ at any time with $t$. Eq. (3.3) has the exact solution as:

with

We have

Therefore, we get

Remark 3.2. It should be noticed that $V(S): = \frac{S}{S+E}$ where $V:[0, \infty) \rightarrow [0, \infty)$ is referred as the uptake function and satisfies some of the features defined as ^[27]:

1) $V(0) = 0, \quad V(S) > 0, \quad$ for $S > 0$,

2) $\lim _{P \rightarrow \infty} \frac{S(\varphi)}{S(\varphi)+E(\varphi)} = L_{1}, \quad 0 < L_{1} < \infty;$ where $L_{1} = 1$,

3) $V(S)$ is continuously differentiable,

4) $\frac{d V}{d t} = \frac{E}{(S+E)^{2}} > 0.$

3.1.   Model with the Atangana-Baleanu derivative

In this subsection, We reformulate the fractional variant of the model (3.1), as:

with

4.   Real data comparison

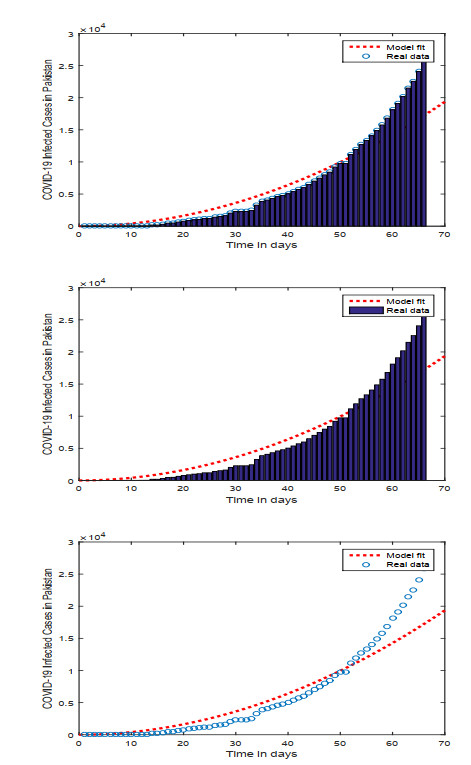
The key and significant step for the problem validity is the comparison of real statistics which is helpful for achieving numerical values for the model validation. We consider here to obtain the nonlinear least square fitting method to fit the data to proposed model (3.4), we have thirteen parameters in which nine will be fitted, while the rest of the parameters must be assumed. Estimated parameters value given in Table 1. The parameters assumption techniques under the least-square fit via MATLAB software were used. We use the data of infected cases of COVID-19 in Pakistan from 04 March to May 10, 2020, the result is given in Figure 1. The associated mean relative error of the fitted data are obtained by formula $\frac{1}{6} \sum_{k = 1}^{6}\left|\frac{x_{k}^{\rm {real }}-x_{k}^{\rm {approximate }}}{x_{k}^{\rm {real }}} \ \ \ \ \ \right|$.

5.   Equilibrium points and Basic reproductive number

5.1.   Steady States

The disease free equilibrium (DFE) of the model system (3.4) can be computed by putting $^{\mathrm{ABC}} \mathbb{D}_{0, \varphi}^{\lambda}[E(\varphi)] = 0, ^{\mathrm{ABC}} \mathbb{D}_{0, \varphi}^{\lambda}[Q(\varphi)] = 0, ^{\mathrm{ABC}} \mathbb{D}_{0, \varphi}^{\lambda}[I(\varphi)] = 0, ^{\mathrm{ABC}} \mathbb{D}_{0, \varphi}^{\lambda}[J(\varphi)] = 0$ and denoted by $E^{0} = \left(S^{0}, 0, 0, 0, 0, R^{0}\right)$, where $S^{0} = \frac{\Gamma^{\lambda}}{u^{\lambda}}$ and $R^{0} = 0$.

5.2.   Basic Reproductive Number $R_0$

By using the next generation method ^[28], we have

where the elements in matrix $F$ constitute the new infection terms, and

Also,

Now, $\mathcal{R}_0$ is dominant eigenvalue of $\rho(FV^{-1})$, and is given by;

5.2.1.   Existence of endemic equilibrium

The existence of endemic equilibrium (EE) of (3.4) is established in terms of $R_0$ herein. $B_{1} = \gamma^{\lambda}_{1}+\gamma^{\lambda}_{2}+\mu^{\lambda}, B_{2} = q^{\lambda}_1+r^{\lambda}_1+\mu^{\lambda}, B_{3} = d^{\lambda}_{1}+r^{\lambda}_{2}+\alpha^{\lambda}+\mu^{\lambda},$ and $B_{4} = d^{\lambda}_{2}+r^{\lambda}_{3}+\mu^{\lambda}$.

Let an arbitrary EE point of (3.4) be depicted by $E_{1}^{*} = \left(S^{*}, E^{*}, Q^{*}, I^{*}, J^{*}, R^{*}\right)$. Then, we get

Solving (5.5), one reaches

since $B_{1} B_{2}-\gamma^{\lambda}_{1} r^{\lambda}_{1} = \left(\gamma^{\lambda}_{2}+\mu^{\lambda}\right)\left(q^{\lambda}_{1}+r^{\lambda}_{1}+\mu^{\lambda}\right)+\gamma^{\lambda}_{1}\left(q^{\lambda}_{1}+\mu^{\lambda}\right) > 0$, it is clear that the model system (3.4) has a unique endemic equilibrium when $R_{0} > 1$ and no endemic equilibrium when $R_{0} < 1$.

5.3.   Local stability of DFE

Theorem 5.1. Let $m > 0$ and $n > 0$ are the integers such that $\operatorname{gcd}(m, n) =$ 1 for $\lambda = \frac{m}{n}$ and $M = n$, then the DFE $E^0$ of the model in fractional derivative is locally asymptotically stable if $|\arg (\vartheta)| > \frac{\pi}{2 M}$ for all roots $\vartheta$ of the associated characteristic equation,

Proof. The Jacobian matrix of model (3.4) at $E^{0}$ is given by

where $a_{22} = 2\beta^{\lambda} (1-\kappa)-(\gamma^{\lambda}_{1}-\gamma^{\lambda}_{2}-\mu^{\lambda})$ and $a_{44} = \left(d^{\lambda}_{1}+r^{\lambda}_{2}-\alpha^{\lambda}-\mu^{\lambda}\right)$. The three eigenvalues of the matrix (5.8) have negatine real part, i.e., $\vartheta^{a}_1 = -\mu^{\lambda}$, $\vartheta^{a}_2 = -\left(d^{\lambda}_{2}+r^{\lambda}_{3}+\mu^{\lambda}\right)$, $\vartheta^{a}_3 = -\left(d^{\lambda}_{1}+r^{\lambda}_{2}+\alpha^{\lambda}+\mu^{\lambda}\right)$. Moreover, for last three eigenvalues we use the following reduce matrix.

The characteristic equation of $RJ_{E^{0}}$ (5.9) is given by

where

Clearly, $a_{2}, a_{1}$ and $a_{0}$ are all positive, if $\mathcal{R}_{0} < 1$. The argument of the root of equations

and

are similar, that is:

where $k = 0, 1, 2, 3, ..., (m-1).$ Then, we get

are all greater than ${\pi \over 2 M}$ if $\mathcal{R}_{0} < 1$, having an argument less than ${\pi \over 2 M}$ for $\mathcal{R}_{0} > 1$. Thus the DFE is locally asymptotically stable for $\mathcal{R}_{0} < 1$.

6.   Existence and uniqueness

Assume that a continuous real-valued function denoted by $B(J)$ containing the sup norm property is a Banach space on $J = [0, b]$ and $P = B(J) \times B(J) \times B(J)$ $\times B(J) \times B(J) \times B(J)$ with norm $\left\|\left(S, E, Q, I, J, R \right)\right\|$ $= \|S\|+\|E\|$ $+\left\|Q\right\|+\left\|I\right\|$ $+\left\|J\right\|+\|R\|$, where $\|S\| = \sup _{\varphi \in J}|S(\varphi)|, \|E\|$ $= \sup _{t \in J}|E(\varphi)|, \left\|Q\right\|$ $= \sup _{\varphi \in J}|Q(\varphi)|, \left\|I\right\|$ $= \sup _{\varphi \in J}|I(\varphi)|, \left\|J\right\| =$ $\sup_{\varphi \in J}|J(\varphi)|, \left\|R\right\|$ $= \sup _{\varphi \in J}|R(\varphi)|.$ We get

Now using the Definition 2.5 on each of the above equations, one obtains

where

Thus, we reach

Taking into account

one reaches

Then, we acquire

Where

Then, we reach

together with $S_{0}(\varphi) = S(0), E_{0}(\varphi) = E(0), Q_{0}(\varphi) = Q(0), I_{0}(\varphi) = I(0), J_{0}(\varphi) = J(0), R_{0}(\varphi) = R(0)$. Thus, we get

Additionally, by using Eqs (6.4) and (6.5) and considering that

we reach

Now, we are in position to prove the following theorem.

Theorem 6.1. If

Then, (3.4) has a unique solution for $t \in [0, b]$.

Proof. It is observed $S, E, Q, I, J, R$ are bounded functions. In Addition, as can be seen from Eqs (6.4) and (6.5), the symbols $K_{1}, K_{2}, K_{3}, K_{4}, K_5$, and $K_{6}$ hold for Lipchitz condition. Therefore, utilizing Eq (6.8) together with a recursive hypothesis, we arrive at

Then, we get

$\left\|\Xi_{S, n}(\varphi)\right\| \rightarrow 0,$ $\left\|\Xi_{E, n}(\varphi)\right\| \rightarrow 0,$ $\left\|\Xi_{Q, n}(\varphi)\right\| \rightarrow 0,$ $\left\|\Xi_{I, n}(\varphi)\right\| \rightarrow 0,$ $\left\|\Xi_{J, n}(\varphi)\right\| \rightarrow 0,$ $\left\|\Xi_{R, n}(\varphi)\right\| \rightarrow 0$

as $n \rightarrow \infty$. Thus, we reach

with $Z_{i} = \frac{1-\lambda}{B(\lambda)}\Omega_{i} + \frac{\lambda}{B(\lambda) \Gamma(\lambda)} b^{\lambda}\Omega_{i} < 1$ by hypothesis.

7.   Hyers-Ulam stability

Definition 7.1. ^[23] The model (3.4) is Hyers-Ulam stable if there exist a real number $\gamma \geq 0$, such that for every $\epsilon > 0$ and for any solution $\mathcal{Y} \in C^{1}(\mathcal{G}, \mathbb{R})$ of the following inequality:

there is a unique solution $\mathfrak{W} \in C^{1}(\mathcal{G}, \mathbb{R})$ of the model (3.4), such that

Definition 7.2. The ABC fractional integral system given by Eq (6.2) is said to be Hyers-Ulam stable if exist constants $\Delta_i > 0, i \in \textbf{N}^6$ fulfilling: For every $\gamma_i > 0, i \in \textbf{N}^6$, for

there exist $(\dot{S}(\varphi), \dot{E}(\varphi), \dot{Q}(\varphi), \dot{I}(\varphi), \dot{J}(\varphi), \dot{R}(\varphi))$ which are satisfying

Such that

Theorem 7.1. With assumption $J$, the suggested model of fractional order (3.4) is Hyers-Ulam stable.

Proof. With the help of theorem (6.1), the given ABC fractional model (3.4) has a unique solution $({S}(\varphi), {E}(\varphi), {Q}(\varphi), {I}(\varphi), {J}(\varphi), {R}(\varphi))$ satisfying equations of system (6.2). Then, we acquire

Taking, $\gamma_i = \Omega_i, \Delta_i = \frac{1-\lambda}{B(\lambda)}+\frac{\lambda}{B(\lambda) \Gamma(\lambda)},$ this implies

Thus, we get

With the help of Eqs (7.10) and (7.11), the ABC fractional integral system (6.2) is Hyers-Ulam and consequently the ABC-fractional order model (3.4) is Hyers-Ulam stable.

8.   Sensitivity analysis

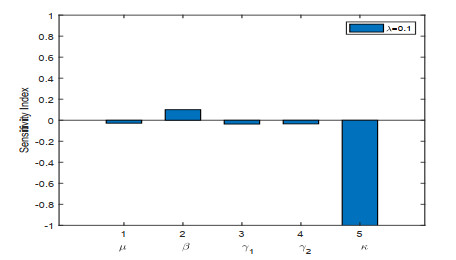
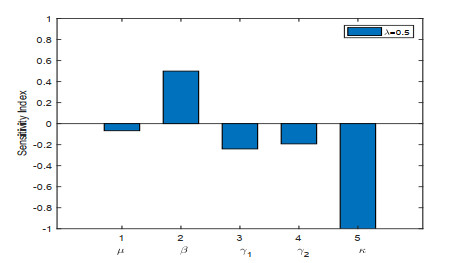
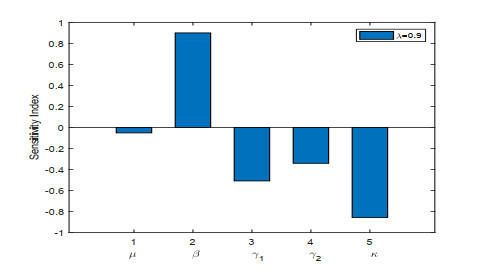
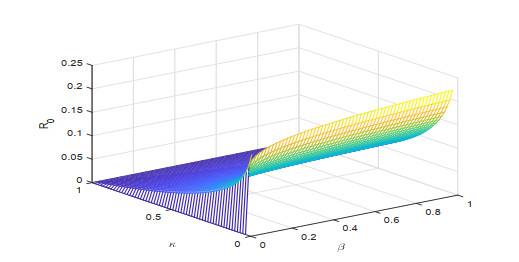
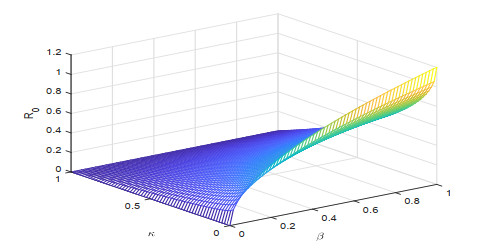
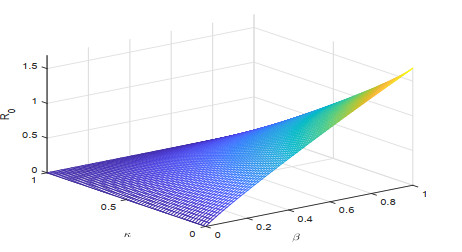
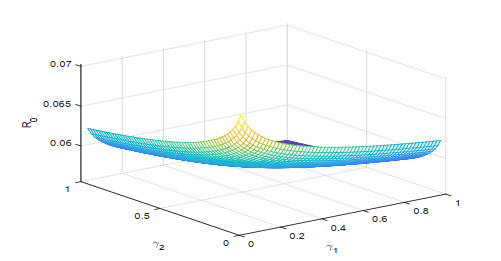
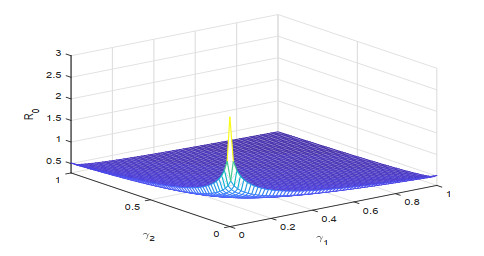
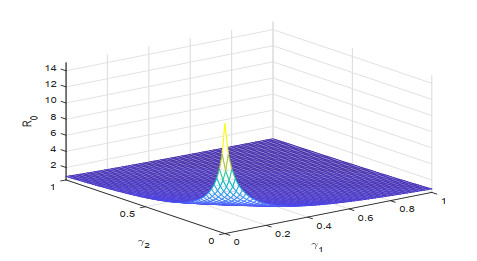
To know the influence of various parameters upon the basic reproduction number, we use sensitivity analysis. To calculate the sensitivity index we used the direct differentiation method. The sensitivity index $\Upsilon^{R_0}_\tau$ of a parameter $\tau$ is calculated by $\Upsilon^{R_0}_\tau = \frac{dR_0}{d\tau}\frac{\tau}{R_0}$. Sensitivity indices of different parameters for our proposed model are given in Figures 1–3. The effect of different parameters over basic reproduction number are shown grap hically in Figures 4–9.

9.   Numerical dynamics

In the present section, we have simulated the proposed scholastic epidemiological system for the ABC. While simulating the system, convergent iterative scheme is employed. Fractional-order chaotic system via bifurcation is studied in ^[30] and through Caputo operator is discussed in ^[31]. Consider a general Cauchy problem of fractional order having autonomous nature

where $y = (a, b, c, w) \in \mathbb{R}^{4}_{+}$ being a continuous function (real-valued) fulfills the Lipchitz condition as:

where $M > 0$ is said to be Lipchitz constant.

where $J^{\lambda}_{0, \varphi}$ denotes the fractional integral operator. Consider an equispaced integration intervals over [0, T] with the fixed step size $h( = 10^{-2}$ for simulation) $= \frac{T}{n}$, $n \in N$. Suppose that $y_q$ is the approximation of $y(\varphi)$ at $t = t_q$ for $q = 0, 1, … n.$ Consequently, our model becomes

10.   Discussions

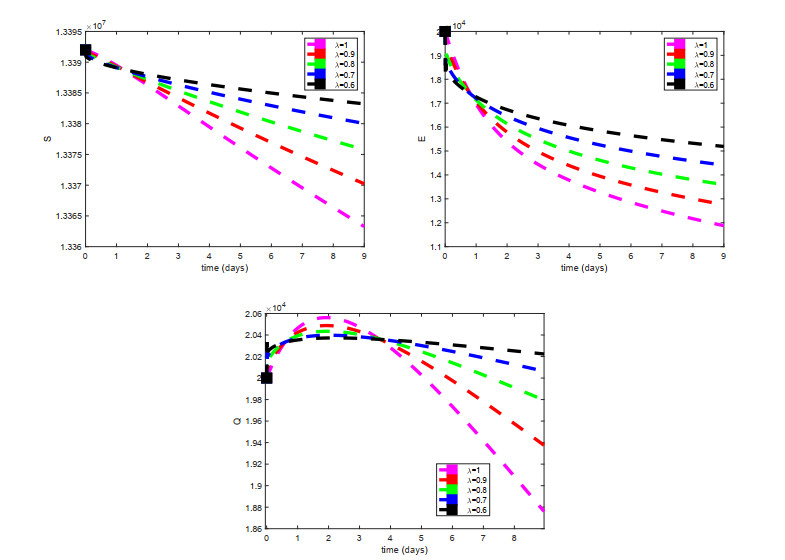
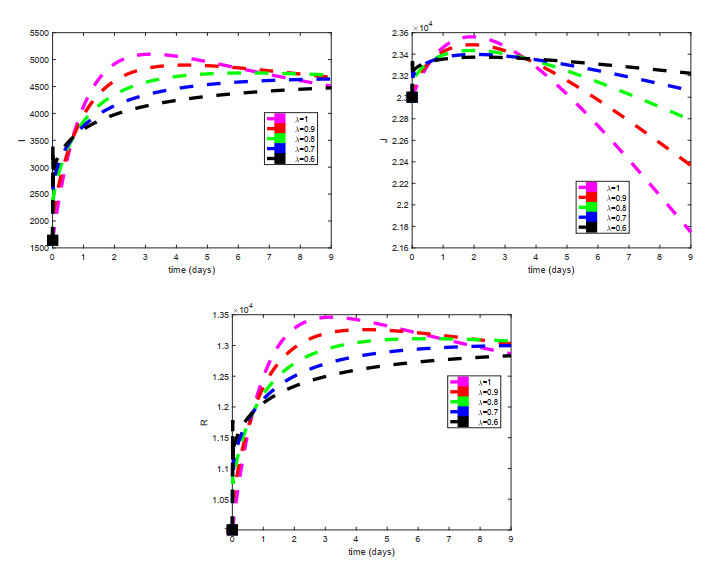
Figures 2–4 shows the sensitivity indices of all the parameters corresponding to different values of fractional parameter $\lambda$. From Figures 2–4 it is noted that the largest positive parameter is $\beta$ which means that by increasing the transmission rate $\beta$, the basic reproduction number will increase and hence $\beta$ is the most sensitivity parameter upon $R_0$. While on the other hand, the smallest negative parameter is $\mu$ which means that by increasing the natural death rate $\mu$, the basic reproduction number will decrease and hence $\mu$ is most senseless parameter upon $R_0$. From Figures 2–4, it is obtained that by increasing the fractional parameter $\lambda$ the positive sensitive parameter is increasing while the negative sensitive parameters are decreasing. Figures 5–7 depicts the sensitivity analysis of $R_0$ vs $\kappa$ and $\beta$ for different values of $\lambda = 0.1, 0.5, 0.9$. It is depicted that transmission rate $\beta$ is directly proportional to $R_0$ while the lockdown parameter $\kappa$ is inversely proportional to $R_0$. Figures 8–10 shows the sensitivity analysis of $R_0$ vs $\gamma_1$ and $\gamma_2$ for different values of $\lambda = 0.1, 0.5, 0.9$. It is shown that the transmission rate from exposed class to quarantined class $\gamma_1$ and the transmission rate from exposed class to infected class $\gamma_2$ both are inversely proportional to $R_0$. Figure 11 shows the impact of fractional parameter $\lambda$ on the first three classes $S, E,$ and $Q$, while Figure 12 shows the impact of fractional parameter $\lambda$ on the other three classes $I, J$, and $R$.

11.   Conclusions

The fractional operator is convenient in the literature for working the transmission dynamics of COVID-19 disease. Many valuable properties of the given fractional version of the model have been presented, such as the model formation, the existence and uniqueness of the solution through the fixed point theorem, invariant region, stability analysis, the sensitivity analysis and, most importantly, the basic number of reproductions. It should be noted that the most sensitive variable to the basic reproduction number is $\beta$ which is the disease transmission rate from infected to susceptible people. Also, the least sensitive parameters are $\mu$ and $\gamma_2$, which are the natural mortality rate and Recovery rate of isolated individuals. Also, the effect of fractional parameter on the sensitivity indices is very high, as the fractional parameter increasing the indices of all the parameters also increases.

Acknowledgments

This research project was supported by Thailand Science Research and Innovation (TSRI). Basic Research Fund: Fiscal year 2022 under project number FRB650048/0164.

Conflict of interest

The authors declare no conflict of interest.