Fractional-order coronavirus models with vaccination strategies impacted on Saudi Arabia's infections

1.   Introduction

Throughout the ages, the world has witnessed the spread of various diseases. It claimed the lives of many, but soon faded by finding an effective and rapid vaccine. Recently, specifically March 11, 2020, the World Health Organization (WHO) announced the outbreak of the Corona pandemic globally ^[1]. During that period till now, the number of deaths has exceeded the barrier of 2 million deaths. The world was forced to follow a lot of precautionary laws such as imposing quarantine and using masks and sanitizers. Eventually, several vaccines of different efficacy were reached.

From the point of view of mathematicians, it was necessary to take slightly different approach and to have a mathematical model describing the development of COVID-19 disease and the effect of different vaccinations to ensure complete immunity, (see ^{[2,3,4,5,6,7]}). In fact, the Susceptible-Exposed-Infectious-Removed model (or simply SEIR model) is considered one of the most popular mathematical models that used to describe the pandemic dynamics and to estimate feasible infection scenarios. The SEIR model might be very helpful to evaluate the efficiency of several actions, such as lock-down, since the infectious disease outbreak. This model relies typically on a set of ordinary differential equations that take the population's amount into account subject to infection, the direction of persons who recover after infection over a given time, and the persons who unfortunately die.

The extended SEIR model that considered here involves seven classes: Susceptible, exposed, infectious, quarantined, recovered, deaths, and vaccinated classes. As a matter of fact, this model has been more recently established by Ghostine et al. in their paper ^[23]. All parameters' values are already estimated based on a real data collected for forecasting the COVID-19 pandemic in Saudi Arabia. However, this research focuses mainly on studying the effect of this model when converting its ordinary derivatives to its fractional-order case. In particular, the expanded SEIR models established in ^[23] will be fractionalized using two fractional-order differential operators; Caputo and Caputo-Fabrizio operators. The Generalized Euler Method (GEM) and Adams-Bashforth Method (ABM) are then implemented, respectively, to deal with the Caputo fractional-order COVID-19 model and the Caputo-Fabrizio fractional-order COVID-19 model, and consequently to clarify the interaction of the targeted vaccine with the disease and its immunological aspect. In summary, the role of fractional calculus in describing the growth of COVID-19 dynamics on Saudi Arabia's society from 17 Dec 2020 to 31 March 2021 will be clearly revealed, where the Saudi Minister of Health (Tawfiq Al-Rabiah) received the first dose of the available coronavirus vaccine at the beginning of that period. Besides, the equilibrium of the fractional-order models, the basic reproductive number $R_0$ with its elasticity indices of the COVID-19 model will be also determined and documented in view of some mathematical analysis.

The main contribution that can be gained from performing this study is to provide an insight into the influence of fractional calculus in describing the growth of COVID-19 dynamics implemented on Saudi Arabia's society over 107 days; from 17 Dec 2020 to 31 March 2021. In particular, it will be revealed via certain numerical comparisons that the fractional-order COVID-19 models will be better than that of traditional one when such comparisons are performed between them and some real data collected from Saudi Arabia's society. This conclusion will undoubtedly enable mathematicians to predict the number of infected cases that may be correctly detected in the whole of society, and hence allow decision makers and influencers to set the right plans and logic strategies that should be followed to face this pandemic.

The rest of this paper is structured as follows: In the closest section, some of essential definitions, concepts and notions related to fractional calculus are inserted. Whereas in Section 3, an overview of the model configuration is given, as it reported in reference ^[23]. The fractional-order COVID-19 models are established in Section 4. Whereas some stability analysis related to the proposed models are discussed in Section 5. Finally, some comments and concluding remarks on what have been implemented in this research can be found in the conclusion section.

2.   Preliminaries

A set of essential definitions and basic facts related to the fractional calculus are addressed in this section for full explanation.

Definition 2.1. ^[8] (Riemann-Liouville integrator) Suppose $f\in\;$$L_1 [a, b]$, the Riemann-Liouville fractional-order integral operator is defined by:

where $q\in\mathbb{R^+}$, $a\leq t \leq b$.

Definition 2.2. ^[9] (Caputo Differentiator) Suppose $0\leq n-1 < q < n \in \mathbb{Z}^+$, the Caputo fractional-order derivative operator is defined by:

Definition 2.3. ^[10] (Caputo-Fabrizio Differentiator) Suppose $0 < q < 1$ and $L(q)$ is the normalized function in which $L(0) = L(1) = 1$. The Caputo-Fabrizio fractional-order differential operator $D_*^q$ of a function $f\in$$H^1(a, b)$ is defined by:

If $f\notin$$H^1(a, b)$, then such operator is defined by:

Remark 2.1. ^[11] If $\mu$$= \frac{1-q}{q}$$\in [0, \infty)$, (i.e. $q$$= \frac{1}{1+\mu}$$\in [0, 1])$, then (2.3) could be rewritten in the following form:

where $L(0)$ = $L(\infty) = 1$ and

Definition 2.4. ^[12,13] (Caputo-Fabrizio integrator) The corresponding Caputo-Fabrizio fractional-order integral operator $J_* ^q$ of the operator $D_* ^q$ for a function $f$ can be expressed as follows:

where $0 < q < 1$ and $t\ge 0$.

Remark 2.2. ^[12,13] From Definition 2.4, we can get the following confirmation:

Based on Remark 2.2, modern version of the parameter has been created as:

where $0 < q < 1$.

3.   An overview of the model configuration

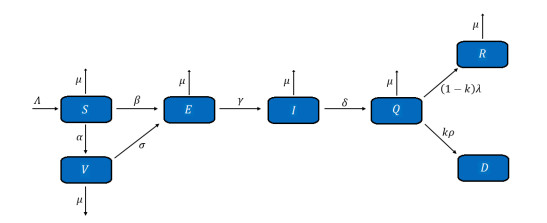
When studying and analyzing the spread out of infectious diseases and the ability to control them, mathematical modeling come as an effective tool that could be employed to provide better support of control strategies development which should be followed to face these diseases. Several studies of SEIR epidemiological models, which are commonly used for the COVID-19 pandemic, have made minor or major changes to the classical SEIR model. Extremely significant mathematical models have been developed to study the dynamics transmission of the COVID-19 pandemic, and to illustrate their relations by structuring them into inputs and outputs, which, in their role, can show the pandemic's impact on the whole population. The compartment diagram of the expanded SEIR model established in ^[23] can be shown in Figure 1. It exhibits the growth of COVID-19 dynamics on Saudi Arabia's society from 17 Dec 2020 to 31 March 2021, where the population has been divided into the following classes: Susceptible (S), vaccinated (V), exposed (E), infected (I), recovered (R), quarantined (Q), and dead (D).

Figure 1.  Disease transmission flow of the proposed model.

DownLoad: Full-Size Img PowerPoint

In order to gain more depth in understanding these model and their impact on reality, it is useful to set the initial values of the model's states ($S_0, V_0, E_0, I_0, R_0, D_0$) as well as all the parameters' values. In particular, the initial values of the model's states can be listed, as reported in ^[14,15,18], in Table 1, where $S_0 = \aleph-V_0-E_0-I_0-R_0-D_0$, so that $\aleph$ represents the size of population. On the other hand, the parameters' values of the model at hand can be shown in Table 2 ^[23].

Table 1.  Initial values of the extended SEIR model ^[14,15,18].

Variable of compartment	Value
$\aleph$	$\text{ 3.4218}\times 10^{7}$
$\text{ E(0)}$	$\text{ 0}$
$\text{ V(0)}$	$\text{ 1}$
$\text{ I(0)}$	$\text{ 174}$
$\text{ R(0)}$	$\text{ 208}$
$\text{ Q(0)}$	$\text{ 10}$
$\text{ D(0)}$	$\text{ 10}$

---

 | Show Table

DownLoad: CSV

Table 2.  Description of the model's parameters ^[23].

Parameters	Description	Initial Value	References
${ \Lambda }$	New births and new residents	${ 2300}$	[14]
${ \beta_1 }$	Transmission rate before intervention	${ 8.58}\times 10^{-9}$	assumed
${ \beta_2 }$	Transmission rate during and after intervention	${ 3.43}\times 10^{-9}$	assumed
${ \alpha }$	Vaccination rate	${ 3.5}\times 10^{-4}$	[15]
${ \mu }$	Natural death rate	${ 3}\times 10^{-5}$	[14]
${1/ \gamma }$	Incubation period	5.5 days	[16]
${ \sigma }$	Vaccine inefficacy	${ 0.05}$	[17]
${ 1/ \delta }$	Infection time	3.8 days	[16]
${ \kappa }$	Case fatality rate	${ 0.014}$	[18]
${1/ \lambda }$	Recovery time	10 days	[16]
${1/ \rho }$	Time until death	15 days	[16]

---

 | Show Table

DownLoad: CSV

Generally, the Ordinary Differential Equations (ODEs) applied to expound the extended SEIR model with the vaccination impact can be given by the following system ^[23]:

where $t\ge 0$, and the initial conditions $S(0) = S_0$, $V(0) = V_0$, $I(0) = I_0$, $Q(0) = Q_0$, $D(0) = D_0$, $E(0) = E_0$ and $R(T) = R_0$.

4.   Fractional-order COVID-19 models

In this section, we aim to propose two new versions of the extended SEIR model given in ^[23]. These two versions will be established by operating the Caputo and the Caputo-Fabrizio fractional-order operators instead of the ordinary operator applied to the model at hand. Below, these two versions are clearly listed.

● COVID-19 model in Caputo sense

● COVID-19 model in Caputo-Fabrizio sense

Of course, the above two fractional-order models are established subject to the initial conditions given in Table 1. It is worth noting that the GEM has been successfully employed to solve the fractional-order system (4.1), while the ABM has confirmed its ability in providing an efficient numerical solution of system (4.2). The reader may understand the merits of these two methods and the modality to use them in various researches by referring to the references ^[19,20]. However, in order to see the numerical solutions of system (4.1) and system (4.2), the GEM and ABM are respectively implemented to produce Figures 2 and 3 according to different values of $\alpha$. Actually, these two simulations represent the size of all classes over the time for system (4.1) and system (4.2) in view of different values of $\alpha$.

Figure 2.  Size of all classes over the time $t$ (in days) for system (4.1) in view of different values of $\alpha$ using GEM via Caputo operator.

DownLoad: Full-Size Img PowerPoint

Figure 3.  Size of all classes over the time $t$ (in days) for system (4.2) in view of different values of $\alpha$ ABM via Caputo-Fabrizio operator.

DownLoad: Full-Size Img PowerPoint

For the purpose of investigating the fractional-order COVID-19 models, certain numerical comparisons are carried out between the two vector-valued solutions of systems (4.1) and (4.2). Such comparisons are performed by considering the initial values provided in Table 1, and the same values of parameters provided in Table 2. The whole numerical simulations of these comparisons are exhibited in Figure 4. The executed graphs compare the number of each class of the whole compartments' classes based on simulating all dynamics of the two proposed systems (system (4.1) and system (4.2)) from 0 to 500 day. It should be mentioned that the behaviour of the two proposed systems' dynamics are likewise and close in terms of results. Overall, there is a steadily increase of the recovered and vaccinated people over the period given. On contrary, there is a steadily decrease of susceptible people over the same period. For quarantined, infectious and exposed cases, it can be observed that such cases began with a few persons and then climbed dramatically to the top in the middle of the period. From that point, they have fluctuated in gradual downward trends to same of beginning at the end of period.

Figure 4.  Comparison results between the dynamics of system (4.1) via GEM and the dynamics of system (4.2) via ABM.

DownLoad: Full-Size Img PowerPoint

5.   Stability analysis

This section is devoted to exploring some mathematical aspects related to fractional-order of the COVID-19 model with its two types Caputo operator (4.1) and Caputo-Fabrizio operator (4.2) and deducing results of the stability analysis. Which is represented in discussing the equilibrium points and the non-negative solution such system, calculating the basic reproductive of and its elasticity indices.

5.1.   The equilibrium points

In order to obtain epidemiological stability of the COVID-19 model, it is necessary to determine its equilibrium points. In fact, there are generally two types of equilibrium points of the epidemiological models. The first one is the Disease-Free Equilibrium ($T_{DFE}$) point that typically occurs when assuming $I = 0$, and equating the left-hand side of the considered system to zero. For instance, one can deduce the following point:

On the other hand, the second type of equilibrium points is the Endemic Equilibrium ($T_{EE}$) point. Such point can be yielded by setting $I\neq0$, and then equating the left-hand side of the system to zero too. In particular, the $T_{EE}$ point of the system at hand can be expressed as follows:

where

and where

In light of obtaining equilibrium points of the system at hand, we can find that the so-called basic reproductive number $R_0$, which can be commonly fruitful in guiding various monitor strategies to face the pandemic in all. This is, actually, what we will discuss and present in the upcoming subsection.

5.2.   Basic reproductive number $R_0$

Epidemiology defines the basic reproductive number $R_0$ as the number of infections caused by the first disease case, that appeared in an appointed population where assume everyone is susceptible to infection. The importance of $R_0$ lies in knowing the rapidity of the spread of the emerging disease among the inhabitants and the proportion of the population to be immunized. To be precise, the population spread of the epidemic will occur when $R_0 > 1$, where it is difficult to control. The method to numerate the basic reproductive ratio by finding the spectral radius of the next generation matrix $Y$ (i.e. $R_0 = \rho (Y)$). The matrix $Y$ is a multiplication of $F$ by $W^{-1}$, where:

where $F_i$ refers to the stream of freshly infected cases into compartment $t_j$, and $W_i$ refers to the entering/leaving streams connected with $t_j$, for $i, j = 1, 2, 3, ..., m$ such that $m$ is the total of compartments demonstrated in the model. Based on the aforesaid argument, one might calculate $R_0$ for any the fractional-order models ((4.1) or (4.2)) by first obtaining the two primary matrices $F$ and $W$. These matrices have the following forms:

In this regard, the basic reproductive number $R_0$ can be then calculated to be as follows:

With the help of the above resultant relation, it is possible to estimate the epidemiological situation in the community as a whole ^[21,22], where the value of $R_0$ is deemed very important in medical sense. In particular, an epidemic is predictable climb up if $R_0 > 1$, and to end if $R_0 < 1$ ^[21]. Along the same lines, the aforementioned discussion lays the foundation to explore further result connected with the local stability analysis of the $T_{DFE}$ point. This result is stated and derived below.

Theorem 5.1. The disease-free equilibrium point $T_{DFE}$ of the systems (4.1) and (4.2) is locally stable if $R_0 < 1$, and unstable if $R_0 > 1$.

Proof. It is possible to express systems (4.1) and (4.2) more clearly with the Jacobin matrix by deleting the equation expressing the death compartment ($D$) where its importance appears only in the following differential equation:

The Jacobian matrix of the reduced model at $T_{DFE}$ point is then given by:

The eigenvalues of the above matrix will be then as:

Obviously, we have $\lambda_i < 0, \ \forall i = 1, 2, 3, 4$. At the same time, if one assumes $R_0 < 1$, then $\lambda_5 < 0$, and $\lambda_6 < 0$. Thus, due to all eigenvalues of the matrix are negative, then the $T_{DFE}$ point is locally asymptotically stable. On the contrary, if one assumes $R_0 > 1$, then we have $\lambda_5 < 0$ and $\lambda_6 > 0$, which leads to assert that the $T_{DFE}$ point is locally asymptotically unstable.

5.3.   Impact of vaccination

In order to evaluate the performance of the two fractional-order systems (systems (4.1) and (4.2)) and their impacts, we will make certain predictions through using such proposed systems based on some numerical comparisons that have been performed between their dynamics and some real data collected from Saudi Arabia's society over 107 days; from 17 Dec 2020 to 31 March 2021 ^[14,15,18]. Actually, these numerical comparisons are deemed one of the main focuses of this research, as they clearly show the agreement of the numbers of people recovering from the COVID-19 disease with the results of the two fractional-order epidemiological models proposed previously. In other words, Figure 5 reveals that the fractional-order COVID-19 models given in systems (4.1) and (4.2) are better than the traditional system (3.1) especially when we make a comparison between their dynamics and certain real data collected throughout the aforesaid period. In particular, we note that those data aggregate and come closer to the recovering cases curve for systems (4.1) and (4.2) more than they aggregate and come closer to the recovering cases curve for system (3.1). It means that the fractional-order systems (4.1) and (4.2) formulated at $\alpha = 0.9$ have proved their efficiency in describing the dynamics of the recovery cases against the integer-order system (3.1). This outcome will undoubtedly enable specialists to predict the number of infected cases that may be correctly detected in the whole of society, and hence allow decision makers and influencers to set the right plans and logic strategies that should be followed to face this pandemic.

Figure 5.  Comparison results between the dynamics of the recovery cases and certain real data collected from Saudi Arabia's society. (a) Between the integer-order system (3.1) and the real data. (b) Between the fractional-order systems (4.1) and (4.2) and the real data when $\alpha = 0.9$.

DownLoad: Full-Size Img PowerPoint

5.4.   Elasticity indices of $R_0$

Among the measures of control that have an effect on the transmission of the disease are the so-called sensitivity and elasticity indices. The sensitivity index of $R_0$ with respect to a parameter $\tau$ is $\frac{\partial R_0}{\partial \sigma}$, whereas the elasticity index of $R_0$, which measures the relative change of $R_0$ with respect to $\tau$, denoted by $\chi_\tau^{R_0}$, and defined as:

As a result of an explanation, the sign of the elasticity indicator shows a decrease or increase in $R_0$. By knowing the value of $R_0$, it is easy to infer and accurately calculate the elasticity index of each parameter. The magnitude of the elasticity indices depends generally on the parameter values found in the expression of $R_0$. These values can be mostly determined by adopting certain methods of estimation. According to the parameters' values presented in Table 2, the baseline parameters' values and their corresponding elasticity indices of $R_0$, which are calculated based on the relation (5.11), are reported in Table 3. For further illustration, these indices can be shown, at the same time, in the bar graph given in Figure 6.

Table 3.  Baseline parameters' values and elasticity indices of $R_0$.

Parameter	Elasticity index	Numerical value
${ \Lambda }$	${ \chi_{\Lambda}^{R_0} }$	${1}$
${ \beta }$	${ \chi_{\beta}^{R_0} }$	${ 1}$
${ \alpha }$	${ \chi_{\alpha}^{R_0} }$	${-0.552632}$
${ \mu }$	${ \chi_{\mu}^{R_0} }$	${ -0.447647}$
${ \gamma }$	${ \chi_{\gamma}^{R_0} }$	${ 1.64973}\times 10^{-4}$
${ \delta }$	${ \chi_{\delta}^{R_0} }$	${ -0.999886}$
${ \sigma }$	${ \chi_{\sigma}^{R_0} }$	${ -0.368421}$

---

 | Show Table

DownLoad: CSV

Figure 6.  Bar graph illustrating the elasticity indices for each parameter of $R_0$.

DownLoad: Full-Size Img PowerPoint

In light of the above drawings and results, it appears notably that the two parameters $\Lambda$ and $\beta$ are the most influential in calculating $R_0$. That is, the higher the values of these two parameters, the higher the number of people infected with COVID-19. In contrast, the parameter $\delta$ is appeared as the least influential. To see how such three parameters impact on $R_0$, we plot Figure 7. In particular, based on Figure 7(a, b), we can observe that when the two parameter's values of $\lambda$ and $\beta$ are increased, the value of $R_0$ will be so, indicating that the ratios of the new births and new resident as well as the ratio of the transmission before intervention are the most impactful on the society in terms of they have an ability to yield an pandemic in all. On the contrary, when the value of the parameter $\delta$ is decreased, the value of $R_0$ will be so, as exhibited in Figure 7(c). This, actually, indicates that the ratio of infection time is the slightest impactful on the society.

Figure 7.  Effect of the most and least impactful parameter on $R_0$.

DownLoad: Full-Size Img PowerPoint

6.   Conclusions

In this work, two newly nonlinear fractional-order COVID-19 models have been proposed and investigated to describe the growth of COVID-19 dynamics implemented on Saudi Arabia's society over 107 days; from 17 Dec 2020 to 31 March 2021. In particular, these two models have been proposed in view of the Caputo and the Caputo-Fabrizio operators. The Generalized Euler Method (GEM) and the Adams-Bashforth Method (ABM) have been successfully implemented to simulate the dynamics of the established models, where the stability analysis of the such models has been discussed and exmined in light of finding the equilibrium points, determining the reproductive number ($R_0$) and computing the elasticity indices of $R_0$. It has been demonstrated, through some numerical comparisons, that the fractional-order COVID-19 models are better than the classical one due to what these models have presented in comparison with some real data collected from Saudi Arabia's society. In summary, the proposed fractional-order models allow specialists to predict the growth of the COVID-19 dynamics more efficiency than the integer-order one allows. This conclusion can enable primary decision makers and influencers to set the right plans and logic strategies that should be followed to face this pandemic.

Conflict of interest

All authors declare that they have no conflicts of interest.