Monotonicity, convexity properties and inequalities involving Gaussian hypergeometric functions with applications

1.   Introduction

For $a, b, c\in \mathbb{R}$ with $c\neq 0, -1, -2, \cdots$, the Gaussian hypergeometric function is defined by ^[1,3]

where $(a, n)$ is the shifted fractional function, namely $(a, n) = a(a+1)(a+2)\dots(a+n-1)$ for $n = 1, 2, 3, \dots$, and $(a, 0) = 1$ for $a\neq 0$. The function $F(a, b; c;x)$ is called zero-balanced when $c = a+b$.

Firstly, we introduce the following properties of the function $F(a, b; c;x)$ at $x = 1$:

$(1)$ For $a+b < c$ (See ^[13]),

$(2)$ For $a+b = c$ (See ^[1,6]),

The above asymptotical formula was raised by Ramanujan, where

is the classical beta function and

$\psi(z) = \Gamma^{'}(z)/\Gamma(z), \ Re(z) > 0$ is the digamma function and $\gamma$ is called Euler-Mascheroni constant defined by

For $a+b < c$, we have (See ^[2], Theorem 1.19(10)]),

From the uniform convergence of the termwise first derivative of $(1, 1)$ in ^[1], it follows that

It is well known that $F(a, b; c;x)$ has been widely applied in many fields of mathematics and physics. Many special functions in mathematical physics and even some common elementary functions are particular or limiting cases of $F(a, b; c;x)$ in ^[1,10]. For example, Legendre's complete elliptic integrals of the first kind, are defined by

Here and hereafter we always let $r^{'} = \sqrt{1-r^2}$ for $r\in(0, 1)$.

For $a\in(0, 1)$, we can use zero-balanced Gaussian hypergeometric function to define generalized elliptic integrals $\mathscr{K}_{a}(r)$ and $\mathscr{K}^{'}_{a}(r)$ of the first kind on $(0, 1)$ as follow ^[7]:

If $a = 1/2$, then we get complete elliptic integrals $\mathscr{K}(r)$ and $\mathscr{K}^{'}(r)$.

During the past decades, many properties are revealed for $F(a, b; c;x)$ (See ^{[5,17,18,21,22,28,30]}), $\mathscr{K}(r)$ and $\mathscr{K}_{a}(r)$ (See ^{[4,8,9,15,16,19,20,23,24,25,26,27,29]}) by showing the monotonicity and cancavity properties of certain combinations defined in terms of these special functions and other elementary functions. From these analytic properties, we can get some inequalities of $F(a, b; c;x)$ and $\mathscr{K}_{a}(r)$.

For $r\in(0, 1)$, one kind of known elegant functional inequalities for $\mathscr{K}_{a}(r)$ are of the following form

where $R(a) = R(a, 1-a) = -2\gamma-\psi(a)-\psi(1-a)$, with constants $c_{1}, c_{2} \in (0, 1)$. For example, Wang and Chu ^[19] proved that

for $r\in(0, 1)$, where $A_{1} = R(a)/B(a)$ and $A_{2} = 1-a(1-a)$.

In present paper, we try to generalize the above inequality (1.9) to zero-balanced hypergeometric function.

In 1999, Qiu and Vuorinen ^[12] considered the ratio function $x \mapsto F(a, b; a+b; x)/\log[e^{R}/(1-x)]$, and obtained the following theorem:

Theorem 1.1. $($^[12], Theorem 2.1]$)$Let $a, b \in (0, \infty)$ with $R(a, b)\geq0$. Then the function

is strictly decreasing from $(0, 1)$ onto $(1/B(a, b), 1/R(a, b))$. In particular, $\mathscr{K}(\sqrt(1-r^{2}))/\log(4/r)$ is strictly decreasing from $(0, 1)$ onto $(1, \pi/\log16)$.

It is natural to think about the monotonicity of the reciprocal of $F(x)$, that is

and the relationship between the monotonicity of the function $f(x)$ and the value of $R(a, b)$. Thus we consider the following questions:

Question 1.2. For $a, b > 0$, is the function $f(x)$ stictly increasing or decreasing on $(0, 1)$? What's the relationship between the monotonicity of the function $f(x)$ and the value of $R(a, b)$?

Let $f(x)$ be in (1.11) and

In ^[7], Huang, Qiu and Ma considered the above functions for the particular case of $a+b = 1$ and obtained the following theorems:

Theorem 1.3. $($^[7], Theorem 1.1]$)$Let $f(x)$ be as in $(1.11)$, $f_{1}(x)$ be as in $(1.12)$, and $f_{2}(x)$ be as in $(1.13)$.If $a+b = 1$, then we have the following conclusions:

$(1)$ $f(x)$ is convex on $(0, 1)$.

$(2)$ $f_{1}(x)$ is strictly increasing from (0, 1) onto $(1-abR(a, b), B(a, b)-R(a, b))$.

$(3)$ $f_{2}(x)$ is strictly increasing from (0, 1) onto $(B(a, b)-R(a, b), abB(a, b))$.

Theorem 1.4. $($^[7], Theorem 1.2]$)$Let $f(x)$ be as in $(1.11)$ and $f_{3}(x)$ be as in $(1.14)$. If $a+b = 1$, then we have the following conclusions:

$(1)$ $f_{3}(x)$ is strictly decreasing from $(0, 1)$ onto $((c+1)/B(a, b), c/R(a, b))$ if and only if $c\geq R(a, b)/(1-abR(a, b))$.

$(2)$ $f_{3}(x)$ is strictly increasing form $(0, 1)$ onto $(c/R(a, b), (c+1)/B(a, b))$ if and only if $0 < c\leq 1/(ab)-1$. Moreover $f_{3}(x)$ is concave on $(0, 1)$ provided that $0 < c\leq 1/(ab)-1$.

$(3)$ If $1/(ab)-1 < c < R(a, b)/(1-abR(a, b)$, then there exists a unique number $x_{0} = x_{0}(a, c)\in (0, 1)$, depending on $a$ and $c$, such that $f_{3}(x)$ is strictly increasing on $(0, x_{0})$, and decreasing on $(x_{0}, 1)$.

For the particular case of $a+b = 1$, Theorem 1.3 and 1.4 actually obtain the conclusions of generalized elliptical integral $\mathscr{K}_{a}(r)$. In light of the above results, we are trying to extend the above theorem to the zero-balanced hypergeometric function and it is natural to consider the following questions:

Question 1.5. Whether Theorem 1.3 and 1.4 can be extended to zero-balanced hypergeometric function?

The purpose of this paper is to give complete answers to Question 1.2 and 1.5. This paper is organized as follows. The preliminaries we needed are listed in Section 2, and the main results and their complete proofs of this paper are listed in Section 3. As applications, inequalities of hypergeometric function are displayed in Section 4.

2.   Preliminaries

Before proving our main results, we firstly introduce the following important lemmas, which will be used in the proofs of main results.

Lemma 2.1. $($See ^[11], Lemma 2.1]$)$ Let $-\infty < a < b < \infty$, $f, g:[a, b]\rightarrow {\mathbb{R}}$ becontinuous on $[a, b]$ and differentiable on $(a, b)$, and$g'(x)\neq 0$ on $(a, b)$. If $f^{\prime}(x)/g^{\prime}(x)$ isincreasing (decreasing) on $(a, b)$, then so are the functions

If $f^{\prime}(x)/g^{\prime}(x)$ is strictly monotone, then themonotonicity in the conclusion is also strict.

Lemma 2.2. $($See ^[14], Lemma 1.1]$)$ Suppose that the power series $f(x) = \sum\limits_{n = 0}^{\infty}a_{n}x^{n}$ and $g(x) = \sum\limits_{n = 0}^{\infty}b_{n}x^{n}$ have the radius of convergence $r > 0$ and that $b_{n} > 0$ for all $n\in\{0, 1, 2, \cdots\}$. Let $h(x) = f(x)/g(x)$.If the sequence $\{a_{n}/b_{n}\}$ is (strictly) increasing (decreasing), then $h(x)$ is also (strictly) increasing (decreasing) on $(0, r)$.

Lemma 2.3. For $a\in (0, \infty)$, the following function

is decreasing from $(0, 1]$ onto $[0, \infty)$, and increasing from $(1, \infty)$ onto $(0, \infty)$.

Proof. Firstly, we consider the monotonicity of $\phi(x) = x \psi^{'}(x)$, $x\in(0, +\infty)$. From the formula

we have

Differentiating $\phi(x)$ gives

Let $y = v/x$, it is not difficult to find $e^{y}-y-1 > 0$ for $y > 0$. It implies $(v/x+1)/e^{v/x}-1 < 0$ and $\phi^{'}(x) < 0$. Hence $\phi(x)$ is a decreasing function on $(0, +\infty)$.

Next by the monotonicity of $\phi(x) = x \psi^{'}(x)$ and

we have

The proof of this lemma is completed.

Lemma 2.4. For $a, b > 0$ and $ab\leq1$, we have $R(a, b)\geq0$.

Proof. Firstly, we let $b = 1/a$, then $R(a, 1/a) = -2\gamma-\psi(a)-\psi(1/a)$. By Lemma 2.3, we obtain $R(a, 1/a)$ is decreasing from $(0, 1]$ onto $[0, \infty)$, and increasing from $(1, \infty)$ onto $(0, \infty)$. Hence the equation $R(a, 1/a) = 0$ has only one zero point $a = 1$, that is $ab = 1$ and $R(a, b) = 0$ have only one intersection point $(a, b) = (1, 1)$.

Next, we can easily find some special points $(a, b)$ such that $ab > 1$ and $R(a, b)\leq0$, such as $(3, 0.4)$ and $(4, 0.4)$. Since the symmetry of the two regions, $ab\leq1$ and $R(a, b)\geq0$, we obtain that if $ab\leq1$, then $R(a, b)\geq0$.

Lemma 2.5. For $a, b > 0$ and $ab\leq1$. If $0\leq c\leq 1/(ab)-1$, then the function

is a decreasing function and $f_{4}(x) < 0$ on $(0, 1)$.

Proof. According to (1.1)

Since $0\leq c\leq 1/(ab)-1$, we have $ab(c+1)-1\leq 0$. Hence

and

Since

there is a extremal point $(1/3, 1/3)$ of $u(a, b)$, and $u(1/3, 1/3) = -4/3 < 0$. Since

we have $u(a, b)\leq 0$. Hence $ab(c+1)(a+b)+3ab-2a-2b-1\leq 0$.

Similarly, since

we have that $(a-b)[2(a+b)-2ab+3] = 0$. Since $2(a+b)-2ab+3 > 0$, $a = b$, there is an extremal point $(a, b) = (a_{0}, a_{0})$, where $a_{0}$ is the solution of equation $-2a^3+6a^2-a-1 = 0$ and $v(a_{0}, a_{0}) < 0$. Since

we have $v(a, b)\leq 0$. Hence $a^2b^2c+2ab(a+b)-(a^2+b^2)-(a+b)\leq 0$. Therefore, $f_{4}(x)$ is a decreasing function on $(0, 1)$, and

Hence $f_{4}(x) < 0$ on $(0, 1)$.

3.   Main results and proofs

In the following statement, we always let $R = R(a, b), B = B(a, b)$ for $(a, b)\in (0, \infty)$.

Theorem 3.1. Let $a, b \in (0, \infty)$. The function

is strictly increasing from $(0, 1)$ onto $(R, B)$.

Proof. Differentiating $f(x)$ gives

where $g_{1}(x) = F(a, b; a+b; x)-[ab/(a+b)]F(a, b; a+b+1;x)\log[e^{R}/(1-x)]$, $g_{2}(x) = (1-x)F(a, b; a+b; x)^{2}$.

For $x\in(0, 1)$, $g_{2}(x) > 0$. If $g_{1}(x) > 0$, then $f^{'}(x)$ is a ratio of two positive functions, and $f(x)$ is strictly increasing on $(0, 1)$.

By (1.1) and (1.3), $g_{1}(0) = 1-abR/(a+b)$ and

By $(1.5)$, we obtain

Case 1. If $R\geq 0$, then $\log[e^{R}/(1-x)]\geq0$, $g_{1}^{'}(x)\leq0$ on $(0, 1)$. Therefore, $g_{1}(x)$ is decreasing and positive and $f^{'}(x) = g_{1}(x)/g_{2}(x) > 0$.

Case 2. If $R < 0$, then $\log[e^{R}/(1-x)]$ is increasing on $(0, 1)$, $\log[e^{R}/(1-x)] < 0$ on $(0, 1-e^{R})$ and $\log[e^{R}/(1-x)] > 0$ on $[1-e^{R}, 1)$. Therefore, $g_{1}^{'}(x) > 0$ on $(0, 1-e^{R})$ and $g_{1}^{'}(x) < 0$ on $[1-e^{R}, 1)$. Moreover, $g_{1}(x)$ is increasing on $(0, 1-e^{R})$ and decreasing on $[1-e^{R}, 1)$. Meanwhile, $g_{1}(0) = 1-abR/(a+b) > 0$ and $g_{1}(1^{-}) = 0$. Hence $g_{1}(x) > 0$ and $f^{'}(x) = g_{1}(x)/g_{2}(x) > 0$ on $(0, 1)$.

In summary, no matter what value $R$ takes, $f^{'}(x) > 0$ on $(0, 1)$. By $(1.1)$ and $(1.3)$, we obtain $f(0) = R/F(a, b; a+b; 0) = R$ and

Hence $f(x)$ is strictly increasing from $(0, 1)$ onto $(R, B)$.

Remark 3.2. From the above proof, it can be known that no matter what value $R$ takes, $f(x)$ is an increasing function. Hence Theorem 3.1 answers Question 1.2.

Remark 3.3. $(1)$ For $R\geq0$, $R-\log(1-x) > 0$ and $f(x) > 0$ for $x\in(0, 1)$. Acorrding to Theorem 3.1, it is easy to know that $F(x) = 1/f(x)$ in Theorem 1.1 is strictly decresing on $(0, 1)$.

$(2)$ For $R < 0$, there exists unique point $x_{0}\in(0, 1)$ such that $R-\log(1-x) = 0$, that is $x_{0} = 1-e^{R}$. Acorrding to Theorem 3.1, we can know that $F(x) = 1/f(x)$ is strictly decreasing from $(0, x_{0})$ onto $(-\infty, 1/R)$ and strictly decreasing from $(x_{0}, 1)$ onto $(1/B, +\infty)$.

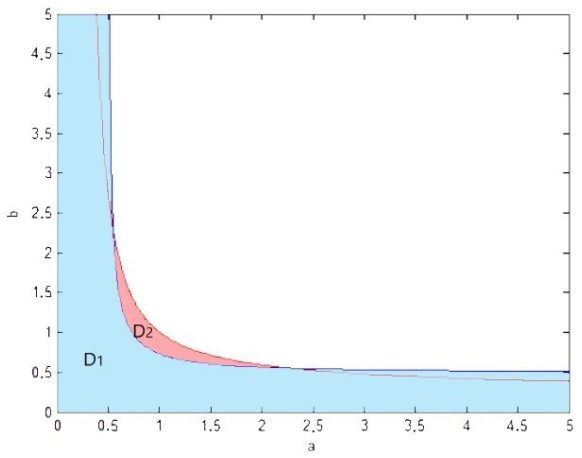
Theorem 3.4. For $(a, b)\in D_{1} = \{(a, b)|a, b > 0, (a+b)(a+b+1)-ab(2a+2b+3) > 0\}$ as shown in the Figure 1, the function $f(x)$is convex on $(0, 1)$.

Proof. By $(1.1)-(1.5)$, we obtain $g_{1}(1^{-}) = 0$ and

and

where

By $(1.1)$, $h(x)$ can be written as

where

Let

where $p(n) = (1+a+b-2ab)n+(a+b)(a+b+1)-ab(2a+2b+3)$, $q(n) = n^{2}+(1+2a+2b-2ab)n+(a+b+1)(a+b-2ab)$.

We can easily obtain $a+b-2ab > 0$ by $(a+b)(a+b+1)-ab(2a+2b+3) > 0$. Hence $C_{n} > 0$, $q(n)$ is positive and increasing and $p(n)$ is positive and increasing for $n\in \mathbb{N}$. Meanwhile, $q(n)-p(n) = n^2+(a+b)n+ab$ is positive and increasing for $n\in \mathbb{N}$. It implies $0 < p(n)/q(n) < 1$ and $p(n)/q(n)$ is decreasing for $n\in \mathbb{N}$. Hence $h(x)$ is positive and increasing on $(0, 1)$ by Lemma 2.2

Case 1. For $R\geq0$, we have $g_{1}^{'}(x)/g_{2}^{'}(x) = abf(x)h(x)$ is positive and increasing on $(0, 1)$. According to Lemma 2.1, $f^{'}(x) = g_{1}(x)/g_{2}(x)$ is increasing and $f(x)$ is convex on $(0, 1)$.

Case 2. For $R < 0$, we have

Hence $g_{1}(x)$ is positive and increasing on $(0, 1-e^{R})$.

Differentiating $g_{2}(x)$ gives

Hence $g_{2}(x)$ is positive and decreasing on $(0, 1)$. Moreover, $f^{'}(x) = g_{1}(x)/g_{2}(x)$ is positive and increasing on $(0, 1-e^{R})$. For $x\in [1-e^{R}, 1)$, $f(x)\geq 0$ and $g_{1}^{'}(x)/g_{2}^{'}(x) = abf(x)h(x)$ is non-negative and increasing. Hence $f^{'}(x)$ is increasing on $[1-e^{R}, 1)$. Therefore, $f^{'}(x)$ is increasing and $f(x)$ is convex on $(0, 1)$.

Remark 3.5. Theorem 3.4 is a generalization of Theorem 1.3(1) for $a\in(0, 1)$ and $a+b = 1$.

Theorem 3.6. Let $f_{1}(x)$ be as in $(1.12)$ and $f_{2}(x)$ be in (1.13). If $(a, b)\in D_{1}$, then we have the following conclusions:

$(1)$ $f_{1}(x)$ is strictly increasing from $(0, 1)$ onto $(1-abR/(a+b), B-R)$.

$(2)$ $f_{2}(x)$ is strictly increasing from $(0, 1)$ onto $(B-R, abB)$.

Proof. (1) By (1.3) and (1.5), we obtain

and

By Lemma 2.1, we obtain

and

If $(a, b)\in D_{1}$, then $f^{''}(x) > 0$ and $xf^{'}(x)-f(x)+R$ is strictly increasing on $(0, 1)$. Since $xf^{'}(x)-f(x)+R\to 0$ as $x \to 0$. Hence $xf^{'}(x)-f(x)+R > 0$ on $(0, 1)$, and $f_{1}(x)$ is strictly increasing from $(0, 1)$ onto $(1-ab/(a+b)R, B-R)$.

(2) By (1.3) and l'Hopital's Rule, we obtain

and

Since $B-f(x)\to 0$ and $1-x\to 0$ as $x\to 1^{-}$ and

the monotonicity of $f_{2}(x)$ follows from Lemma 3.1 and the convexity of $f(x)$ when $(a, b)\in D_{1}$. Hence $f_{2}(x)$ is strictly increasing from $(0, 1)$ onto $(B-R, abB)$.

Remark 3.7. If $(a, b)\in D_{1}$, then we have a general conclusion of Theorem 1.3.

Theorem 3.8. If $c\geq0$ and $(a, b)\in D_{1}\cap D_{2}$, where $D_{2} = \{(a, b)|a, b > 0, R(a, b) > 0\}$ as shown in the Figure 1, the function

is strictly decreasing from $(0, 1)$ onto $((c+1)/B, c/R)$ if and only if $c\geq R/(1-abR/(a+b)) > 0$.

Proof. If $(a, b)\in D_{2}$, then $R > 0$ and $f_{3}(x) = (c+x)/f(x) > 0$ on $(0, 1)$, Next by Theorem 3.1, we obtain

and

Let $g_{3}(x) = f(x)-(c+x)f^{'}(x)$. Then $f^{'}_{3}(x) = g_{3}(x)/[f(x)]^{2}$ and $g^{'}_{3}(x) = -(c+x)f^{''}(x)$. By Theorem 2.2, if $(a, b)\in D_{1}$, then $f^{''}(x) > 0$ and $g_{3}(x) < 0$ for $x\in (0, 1)$. $f^{'}(0) = 1-abR/(a+b)$ and $f^{'}(1^{-}) = abB$. It follows from the above that $g_{3}(x)$ is strictly decreasing from $(0, 1)$ onto $(B-(c+1)abB, R-c(1-abR/(a+b)))$. Hence $g_{3}(x) < 0$ if and only if $R-c(1-abR/(a+b))\leq0$. Therefore, $f_{3}(x)$ is strictly decreasing on $(0, 1)$ if and only if $R-c(1-abR/(a+b))\leq0$.

Theorem 3.9. If $c\geq0$ and $(a, b)\in D_{3}$, where $D_{3} = \{(a, b)| a, b > 0, ab < 1\}$ as shown in the Figure 2, the function

is strictly increasing from $(0, 1)$ onto $(c/R, (c+1)/B)$ if and only if $c\leq 1/(ab)-1$.

Proof. By Lemma 2.4, if $(a, b)\in D_{3}$, then $(a, b)\in D_{2}$.

$\Leftarrow$ Differentiating $f_{3}(x)$ gives

where

Next, differentiating $f_{5}(x)$ gives

where

By Lemma 2.4 and 2.5,

hence $f_{5}(x)$ is a decreasing function on $(0, 1)$

By (1.2),

Hence we have $f_{5}(x) > 0$ and $f^{'}_{3}(x) > 0$ on $(0, 1)$. It implies $f_{3}(x)$ is strictly increasing from $(0, 1)$ onto $(c/R, (c+1)/B)$.

$\Rightarrow$ Suppose $c > 1/(ab)-1$,

For the function

we have $\lim\limits_{x \to 1^{-}} f_{4}(x) = +\infty$. It implies there is a $\delta > 0$ such that $f^{'}_{5}(x) = \log[e^{R}/(1-x)] f_{4}(x) > 0$ on $(1-\delta, 1)$. So $f_{5}(x)$ is increasing on $(1-\delta, 1)$. Since $f_{5}(1^{-}) = 0$, $f_{5}(x) < 0$ and $f^{'}_{3}(x) = f_{5}(x)/[(1-x)\log[e^{R}/(1-x)]]^2 < 0$ on $(1-\delta, 1)$. Hence $f_{3}(x)$ is decreasing on $(1-\delta, 1)$. This is a contradiction, since $f(x)$ is an increasing function on $(0, 1)$. Hence $c\leq1/(ab)-1$.

Remark 3.10. Theorem 3.8 is a general conclusion of Theorem 1.4 (1) in region $D_{1}\cap D_{2}$ and Theorem 3.9 is a general conclusion of Theorem 1.4 (2) in region $D_{3}$.

4.   Applications for inequalities

From our main Theorems, we can easily obtain several asymptotically sharp inequalities for $F(a, b; a+b; x)$. Let $x = r^2$, we can get the inequalities of generalized elliptic integral $\mathscr{K}_{a}(r)$.

Corollary 4.1. Let $(a, b)\in D_{1}\cap D_{2}$ and $c > 0$. Then for the inequalities

we have the following conclusions:

$(1)$ $(4.1)$ holds if and only if $c\leq R/(B-R)$.

$(2)$ $(4.2)$ holds if and only if $c\geq R/(1-abR/(a+b))$.

Proof. Since

By Theorem 3.1, $f(x)$ is strictly increasing from $(0, 1)$ onto $(R, B)$. Hence $f_{1}(x) = (f(x)-R)/x > 0$ on $(0, 1)$.

For $(a, b)\in D_{1}\cap D_{2}$, $R > 0$,

Corollary 4.2. Let $(a, b)\in D_{1}$ and $c > 0$. Then for the inequalities

we have the following conclusions:

$(1)$ $(4.3)$ holds if and only if $c\geq R/(B-R)$.

$(2)$ $(4.4)$ holds if and only if $c\leq 1/(ab)-1$.

Proof. Since

By Theorem 3.1, $f(x)$ is strictly increasing from $(0, 1)$ onto $(R, B)$. Hence $f_{2}(x) = (B-f(x))/(1-x) > 0$ on $(0, 1)$.

Similary,

Corollary 4.3. Let $(a, b)\in D_{1}$ and $c > 0$. Then

for $x\in(0, 1)$, with equality in each instance if and only if $x\to 0$.

Proof. It follows from the monotonicity properties of $f_{1}(x)$ and $f_{2}(x)$ given in Theorem 3.5 that

Hence we have (4.5) for $x\in(0, 1)$, with equality in each instance if and only if $x\to 0$.

Corollary 4.4. Let $(a, b)\in D_{1}\cap D_{2}$ and $C_{1} = R/(1-abR/(a+b))$. Then

for $x\in(0, 1)$.

Proof. It follows from the monotonicity properties of $f_{3}(x)$ of Theorem 3.7 that

for $c\geq R/(1-abR/(a+b))$ and $x\in(0, 1)$. Let $c = C_{1}$, we have (4.6).

Corollary 4.5. Let $(a, b)\in D_{3}$ and $C_{2} = 1/(ab)-1$. Then

for $r\in(0, 1)$. In particular, if $(a, b)\in D_{1}\cap D_{3}$, then

for $x\in (0, 1)$, with equality in each instance if and only if $x\to 0$.

Proof. The proof is similar to the proof of Corollary 4.4. Using the monotonicity properties of $f_{3}(x)$ of Theorem 3.8 that

for $c\leq 1/(ab)-1$ and $x\in(0, 1)$. And let $c = C_{2}$, we have (4.7).

If $(a, b)\in D_{1}\cap D_{3}$, then (4.6) and (4.7) both holds. Hence we have (4.8) for $x\in (0, 1)$, with equality in each instance if and only if $x\to 0$.

Remark 4.6. Acorrding to the above Corollaries, let $a+b = 1$ and $x = r^2$, we can obtain the conculsions of genelized ellptic integral $\mathscr{K}_{a}(r)$ in ^[7].

Acknowledgments

The authors would like to thank the anonymous referees for their valuable comments and suggestions, which led to considerable improvement of the article. This research was supported by the China Scholarship Council and the Natural Science Foundation of China (Grant No. 11401531, 11671360).

Conflict of interest

The authors declare that they have no competing interests.