Singularities and regularity of stationary Stokes and Navier-Stokes equations on polygonal domains and their treatments

1.   Introduction

The mathematical modeling of natural or real-world phenomena, the partial differential equations (PDE's) theory is the core topic of modern mathematics in the past as well as in recent years. Partial differential equations (PDE's) provide a quantitative description of various problems arise in engineering, physical, biological, and social sciences, etc. The understanding of the theoretical analysis of partial differential equations mainly focuses on the well-posedness and regularity (smoothness) of the solution in suitable function spaces.

The elliptic type partial differential equations have been considered as the starting point to study a class of linear partial differential equations. They arise in every field of science and have been used in mathematics to understand the solutions of the problems. They have attracted various fields such as potential theory, functional analysis, variational calculus, differential geometry, algebraic topology, and so forth. They have a long history and their treatment goes back to the 18th century. In two or three-dimensional bounded domains, the analysis of elliptic boundary value problems may have a singular solution. It depends on: the non-smoothness of the domain (domain has corners, edges, etc. on the boundary), change of the boundary conditions at some points like Dirichlet boundary conditions to Neumann or vice versa, discontinuities of the solutions (transmission problems), and singularities of the coefficients.

The corner singularity functions provide an appropriate mathematical structure to understand the physical trajectories of the fluid particles. The singularities may be associated with the singular behavior of the motion of boundaries and the geometry of the fluid body. These arise suddenly at free surfaces due to the viscous stresses. Many researchers have paid attention to the highest order terms occurs in the elliptic operator which help to determine the singularities in the solutions that come from a corner of the boundary. Besides, the lowest order terms also have an effect on the singularity expansion of the solution to the problem.

The discontinuity in a solution of the fluid dynamics problems is a very important issue, where it arises in fluid flow variables. Particularly, the thermodynamics theory for non-equilibrium states and the study of cavity flow problems in a singular domain with corners or edges have faced this issue. Different techniques of mathematical analysis have been used to address this issue ^{[14,15,26,49,68]}. Generally, it depends on a type of flow which is compressible or incompressible, the domain is bounded or unbounded and the smooth or singular boundaries have corners or edges, etc. Normally, the bounded domains are considered for solving physical and engineering problems but it requires technical and complicated calculations. Furthermore, in fluid mechanics, very simple geometry of cavity flows yield interesting phenomena. The compressible flows display the acoustic instabilities, wave interactions, and resonant tones ^{[8,11,15,18,36,49,50,55,58,64,73,80,94]}. The incompressible flows also show the flow separations, eddies, internal recirculation, transition, turbulence and discontinuities. These technical and mathematical important issues are resolved in ^{[16,26,28,30,32,39,59,86,91,92]}.

Currently, the theory has been constructed for compressible viscous Stokes and Navier-Stokes systems for the polygonal domain in 2-dimension and the polyhedral domain in 3-dimension. The mathematical techniques to analyze the singular structure of the solutions near corners, edges and cusp have discussed in ^{[2,7,9,12,17,18,29,33,36,38,44,61,63,87]}. The key point of this theory is the decomposition of the solution of the given problem into a singular and regular part. In corner singularities, the unknown constant coefficients in the decomposition of the solution at a corner of the boundary are called the stress intensity factors. In 3-dimensional domains, these coefficients are functions and are called the edge flux intensity factors. In most of the engineering applications to derive the rigorous formulas for the computation of these coefficients are still of constant interest and a challenging task. The singular part of the solution is the significant part that does not satisfy the shift theorem which is obtained near corners or edges in two or three-dimensional non-smooth domains. It has the lower regularity result that does not belong to $H^2$ for any elliptic boundary value problem for a given datum ${{\bf f}}\in L^2$. The remainder part that satisfies the shift theorem is known as the regular part and is obtained after removing the singular part from the solution of the given problem. It has the $H^2$-regularity for any datum ${{\bf f}}\in L^2$. It is an important aspect for elliptic boundary value problems that the regularity of the solution depends on the geometry of the problem, the given conditions, and the regularity of the data.

In singularity expansion theory for the Stokes problem, the spectral problems related to corner singularities of solutions to elliptic equations are discussed in ^{[18,19,20,21]}. The regularity issues of the solution for stationary Stokes system on a polygonal domain with weighted Sobolev spaces are addressed by ^[51,55]. The velocity, vorticity and pressure formulations of the Stokes problem on smooth domains are discussed in ^[4,31,32], but ^[77] has modeled this formulation for stationary Navier-Stokes equations. He has considered a bounded plane polygonal domain with a non-convex corner. The existence and regularity results are obtained by constructing corner singularity functions for the Stokes operator in an infinite sector with zero normal velocity and zero vorticity boundary conditions. The remaining part has increased regularity by removing the leading singularities from the solution. Finally, the obtained solution is the sum of the coefficients of the singularities and the remaining smoother part.

^[56,66] have considered the zero Dirichlet boundary conditions to investigate the regularity results of the incompressible Navier-Stokes equations in a non-convex polygonal domain. ^[67,79] have extended these results for a non-convex polyhedral cylinder in $\mathbb{R}^{3}$ with inflow boundary conditions for compressible Navier-Stokes equations. They found the existence and regularity results for smooth and non-smooth domains. The interior discontinuities and piecewise regularities of the solutions in a bounded plane domain with a grazing or non-grazing corners are given in ^{[47,69,70,78]}. ^[71] has used the suitable Helmholtz decomposition to obtain the regularity results of the compressible Stokes system in a non-convex polygonal domain with no-slip boundary conditions. In ^[5,31,32,77], the authors have used the non-standard or Navier type boundary conditions to find the existence and regularity results of the compressible Stokes and Navier-Stokes systems in a bounded plane domain.

Hence, the mathematical analysis like well-posedness and regularity results of such type of elliptic boundary value problems in non-smooth domains have attracted many mathematicians and scientists to examine the singular behavior of the solution structure near the singular points as discussed earlier.

The organization of this paper is as follows: Section 2 is dedicated to the analytic preliminaries, functional framework, and the treatment of corner singularities in the Poisson equation. The obtained results of the corner singularity theory for the Stokes problem on polygonal domains are given in Section 3. The existence and regularity results of stationary compressible Stokes and Navier-Stokes systems on polygonal domains are discussed in Section 4. Section 5 addresses the existence and regularity results related to the stationary incompressible Stokes and Navier-Stokes systems. Some concluding remarks and future works are given in the last Section.

2.   Analytical preliminaries

In what follows, some basic preliminary results, domain description, and the functional frameworks regarding the corner singularities of the stationary Stokes and Navier-Stokes systems on a bounded plane polygonal domains are presented. Moreover, the solution operators to construct the solution structure of the elliptic boundary value problems and to find the regularity results of the solution which will be used later in the upcoming sections are defined. Furthermore, the problems in plane polygonal domains with smooth boundary and the treatment of singularities in Laplace's equation and the Poisson equation are discussed.

Many authors have used sufficiently smooth domains for compressible or incompressible Navier-Stoke equations to find the existence and regularity results. However, a lot of problems exists in practice whose geometries are simple but not smooth. Some of them are dealing with non-smooth domains having corners or edges ^{[2,3,6,10,11,33,45,59,94]}. For two dimensional problems, we consider the following definition.

Definition 1. A bounded domain $\Omega\subset \mathbb{R}^2$ is called polygonal if its boundary $\Gamma$ consists of finitely many straight edges (possibly of infinite length) said sides meeting each other at a point where the angle is greater than zero and less than $2\pi$.

Additionally, we denote

● $\Gamma_i, \: i\in X$ the set of edges, enumerated in counter-clockwise, where $X = \big\{1, ..., n\big\}$ is the analogous index set,

● $x_i, \: i\in X$ the set of corner points where $x_i$ is the intersection of $\Gamma_i$ and $\Gamma_{i+1}$ such that $\Gamma_{n+1} = \Gamma_{1}$.

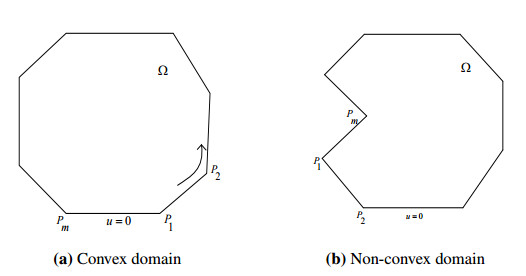
Let $\Omega$ be an open bounded plane domain with polygonal boundary $\partial\Omega$ (see Figure 1) and $P_m = (x_{m}, y_{m}):m = 1, 2, ...n$, where $n$ denote the number of vertices of the domain $\Omega$. Let $r_{m}$ is the distance of a point to $P_{m}$ and is defined as $r_{m} = \sqrt{(x-x_m)^2 +(y-y_m)^2}$. The vertex $P_{m}$ associate two numbers $\omega _{m, \, 1}$ and $\omega _{m, \, 2}$ with the property $\omega _{m, \, 1} < \omega _{m, \, 2} < \omega _{m, \, 1} +2\pi$. Let $\Gamma _{m, \, 1}$ and $\Gamma _{m, \, 2}$ denote the two sides with $\Gamma _{m} = \Gamma _{m, \, 1} \cup \Gamma _{m, \, 2}$, and $\partial\Omega = \cup _{m}\Gamma _{m}$ is the boundary of $\Omega$. The two sides of the domain $\Omega$ at point $P_{m}$ lie along the rays $(x_{m}+t\, cos\, \omega _{m, \, 1}, \, y_{m}+t \, sin\, \omega _{m, \, 1})$ and $(x_{m}+t\, cos\, \omega _{m, \, 2}, \, y_{m}+t\, sin\, \omega _{m, \, 2})$ where $t\geq 0$. The vector $\textbf{n}_{m, \, p}, \: p = 1, \, 2$ is the outward unit normal vectors to the sides $\Gamma _{m, \, p}$ and is defined as $\textbf{n}_{m, \, p} = (-1)^{p}[-sin\, \omega _{m, \, p}+cos\, \omega _{m, \, p}]^t$. The interior angle of the domain $\Omega$ at the point $P_{m}$ is written as $\omega _{m} = \omega _{m, \, 2}-\omega _{m, \, 1}$, and taken $\alpha = \frac{\pi}{\omega_{m}}$. The geometry of the convex and the non-convex bounded domains are shown in (Figure 2).

Now, let we considered the function spaces and their norms from ^[1,35,38]. For any $1\leq p < \infty$, the space of all measurable functions ${\bf v}$ defined on $\Omega$ is denoted by ${L}^{p}(\Omega)$ and equipped the norm $\big\Vert\textbf{v}\big\Vert_{p, \, \Omega} = \big(\int_{\Omega} \vert \textbf{v}(x)\vert^{p}dx\big)^{\frac{1}{p}} < \infty$. If $p = 2$, then $\Vert \textbf{v} \Vert_{o, \, \Omega}$ is the norm of ${L}^{2}(\Omega)$ and for $p = \infty$, the norm of ${L}^{\infty}(\Omega)$ is defined by $\big\Vert\textbf{v}\big\Vert_{\infty} = ess\, sup \big\{\vert\textbf{v}(x)\vert: x\in \Omega\}$. In particular, one can write ${L}^{2}(\Omega) = {H}^{0}(\Omega)$. Let $\alpha$ be a multi-index of order $\vert\alpha\vert = \alpha_1+\alpha_2+...+\alpha_n,$ and $D^\alpha\, v$ be the $\alpha^{th}$ order weak derivative of ${v}$. Let $H^{s}(\Omega)$ for any $s\geq 0$ denote the Sobolev spaces of fractional order and is equipped with the norm $\Vert v \Vert_{s, \, \Omega}$. Generally, one can take $H^{s} = H^{s}(\Omega),$ $L_{0}^{2} = \big\{q\in L^2 :\int_\Omega q\, dx = 0\big\}$ and $H_{0}^{1}$ denote the function in $H^{1}$ with zero boundary values. For $s\in (0, \, 1)$, $H_{0}^{s}$ denote the closure of $C_{0}^{\infty}$ in the topology of $H^{s}$ where $C_{0}^{\infty} (\Omega)$ is the space of all $C_{0}^{\infty}$ functions with compact support in $\Omega.$ When $s \geq 1,$ $H_{0}^{s} = H^{s} \cap H_{0}^{1}$. The dual space of $H_{0}^{s}$ is denoted by $H^{-s}$ and is endowed the norm $\Vert { f}\Vert_{-s} = \sup\limits_{0\neq v\in H_{0}^{s}} \frac{\big\langle{f}, \, v\big\rangle}{\Vert v\Vert_s}$, where the notation $\big\langle, \big\rangle$ denotes the duality pairing. For the vector spaces, we can write ${\bf H}^{s} = H^{s} \times H^{s}$, ${\bf L}^{s} = L^{s} \times L^{s}$, etc. Let ${C}$ represent a generic constant which can have different values in different places and depends on certain quantities.

2.1.   The problems of polygonal domains

It is recognized from the regularity theory of elliptic boundary value problems that the regularity of the solution depends on the geometry of the problem, regularity of the boundary data, and the assign boundary conditions. Let $\Omega$ be a plane bounded domain with smooth boundary $\varGamma$ or $\partial\Omega$ and ${\bf{L}}$ is a second-order elliptic operator of the domain $\Omega$. Moreover, if the coefficients of $\textbf{L}$ are sufficiently smooth, then the solution $\textbf{v}$ of the following boundary value problem

satisfies the inequality

Therefore, the norm $\lVert \textbf{v} \rVert_{k}$ measure the size of the $k^{th}$ order derivatives of $\textbf{v}$ in different ways (Hölder, ${L}^{p}$) and $C$ is a constant that has different values. Sometimes, the smoothness properties are not satisfied then the inequality $(2.2)$ does not hold and it provides important information about the behavior of the solution structure of the problem. For example, if the boundary $\partial\Omega$ of the domain $\Omega$ is not more smooth, then one cannot attain as much as possible regularity of the solution ${\bf v}$. There are different conditions which are reasons for the failure of the inequality $(2.2)$ but in this article, we will address some of them. Each of these types of failure gives distinctive features of the solution to the problem that has been comprehensively studied by ^[56]. The principal purpose of this paper is to investigate those types of problems that present this type of failure.

2.2.   Singularities in Laplace equation

This subsection defines the singularities in Laplace's equation near the vicinity of corners. It has been observed that the problems of corner singularities are very interesting in their lot of applications in practice and in research fields. Usually, three types of singularities arise in elliptic type problems: ⅰ. the angular type singularity, ⅱ. the interface, ⅲ. the infinity type singularities in unbounded solution domains.

Many researchers have discussed them in ^{[10,34,37,81,82,83,84,95]}. There are several approaches to find and describe the characteristics of the corner singularities in Laplace's equation based on the requirement of the knowledge about the subject. Some of them are discussed here:

Singular elements, local refinements and infinite elements. They used when the origin is the singular point, for known location and the asymptotic behavior of the singular point. Usually, use to analyze the singular structure of the solution of the polygonal domains ^[22,29,39].

Singular function methods and the Dual singular function. In these methods, the known leading singular solution can be defined as

where the unknown constant coefficients $c_{i}$ are called the expansion coefficients or the stress intensity factors, the functions $\phi_{i}$ are the singularity functions for the elliptic operator. The singular functions of the Laplace's equation can be found in ^[13,46].

Combine methods. In these methods, the total solution depends on the analytic solution and the local singular solution. It defined as

where $u_{a}$ is the analytic part and $u_{s}$ is the singular part of the solution $u$. The analytic functions are denoted by $\psi_{i}$, and $d_{i}$ are known as the expansion coefficients. For the applications of these methods, we refer ^{[23,38,52,53,61,62,65,68,76]}. The corner singularity functions for the Laplace operator with a different type of boundary conditions are discussed in ^{[40,41,42,43,45,48,54,96]}.

2.3.   The Poisson equation

Let us consider the boundary value problem for the Poisson equation with the mixed homogeneous boundary conditions

where $\textbf{f}\in L^2(\Omega)$. Let $\Omega\subset \mathbb{R}^2$ is a bounded domain with boundary $\Gamma = \bar{\Gamma}_{\mathcal{D}}\cup\bar{\Gamma}_{\mathcal{N}}$ and $\Gamma_{\mathcal{D}}\cap\Gamma_{\mathcal{N}} = \emptyset$ with meas$(\Gamma_{\mathcal{D}}) > 0$ (Lebesgue measure), and $\nu$ is the unit outward normal on $\Gamma$.

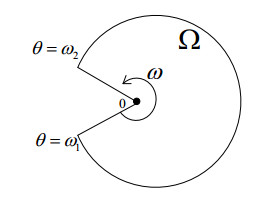
Henceforth, we suppose that $\Omega$ is a bounded plane polygonal domain with sides $\Gamma_i: i = 1, 2, ..., N$ and has only one corner point $O$ with the interior angle $\omega \in (0\, , 2\pi]$, where $\omega = 2\pi$ is used for the case of a crack. In some neighborhood of the corner point $O$, the boundary $\Gamma$ is a straight line and outside of $O$ it is sufficiently smooth. Let $\widetilde{S}\subset \Omega$ is a small circular sector neighborhood of $O$ with angle $\omega$ and radius $\acute{r_0}$, i.e.,

where $(r, \, \theta)$ are the local polar coordinates with respect to the corner point $O$. Let $\partial {\widetilde{S}}$ is the boundary of $\widetilde{S}$ and is denoted as $\partial {\widetilde{S}} = {\overline{\Gamma}_{\widetilde{S}}}_0\, \cup{\overline{\Gamma}_{\widetilde{S}}}_i\, \cup{\overline{\Gamma}_{\widetilde{S}}}_{i+1},$ where

Let ${\Gamma_\mathcal{D}}$ denote the Dirichlet boundary condition and ${\Gamma_\mathcal{N}}$ the Neumann boundary condition of the boundary $\partial {\widetilde{S}}$, such that $\partial {\widetilde{S}} = {\overline{\Gamma}_\mathcal{D}}\cup{\overline{\Gamma}_\mathcal{N}}$ with ${\Gamma}_\mathcal{D}\cup{\Gamma}_\mathcal{N} = \emptyset$. Let $\chi\in C^{\infty}[0, \infty)$ is a smooth truncation function as defined under

it depends only on the distance $r$ with respect to $O$ and $\mbox{supp}(\chi)\subset{\widetilde{S}}$. Suppose that $\textbf{v}\in V_{0}(\Omega) = \big\{\textbf{v}\in H^1(\Omega): \textbf{v} = 0\quad \mbox{on}\quad \Gamma_{\mathcal{D}}\big\}$ is the unique weak solution of (2.5). Now, multiplying the truncation function $\chi$ on both-sides of (2.5), we get the function $\textbf{v}_\chi = \chi\textbf{v}$. The function $\textbf{v}_\chi$ is nonzero only in the circular sector neighborhood ${\widetilde{S}}$. Therefore, the functions $\textbf{v}$ and $\textbf{v}_\chi$ have the same singular structure near the vertex $O$. It is recognized for elliptic boundary value problems that the regularity of the solutions is a local problem. So that, the characteristics of the solution $\textbf{v}$ can be obtained to study the regularity properties of the function $\textbf{v}_\chi$. The subsequent lemma is helpful to understand this argument.

Lemma 1. Let ${\bf v}\in V_{0}(\Omega)$ is the uniquely determine weak solution of (2.5) for any ${{\bf f}}\in L^2(\Omega)$. Then the function ${\bf v}_\chi\in V_{0}(\widetilde{S})$ is the uniquely determined weak solution of the subsequent problem

where ${{\bf f}}_{\chi}\in L^2(\widetilde{S})$ is described as

and satisfies the following inequality

2.3.1.   The singular decomposition of the solution

To determine the solution of the problem (2.5), the Fourier method of separation of variables is used. The eigenvalues $\big\{\alpha_l, \: l\in\mathbb{N}\big\}$ and the corresponding eigenfunctions are depends on the boundary conditions.

A system of an orthogonal and complete set of basis functions in $L^2(0, \omega)$ is introduced as

Consequently, the functions ${{\bf f}}_{\chi}$ and ${\bf v}_\chi$ introduced in (2.7) can be signified in the form of Fourier series

with the fourier coefficients $\big\{{\bf v}_l :l\in\mathbb{N}\big\}$ and $\big\{{{\bf f}}_l:l\in\mathbb{N}\big\}$ are usually defined as

The most important consideration of this section is the condition when the eigenvalues $\alpha_l$ are $0 < \alpha_l < 1$ for some $l\in\mathbb{N}$. This situation is addressed in the subsequent theorem.

Theorem 1. Let ${\bf v}\in V_{0}(\Omega)$ be the uniquely determine weak solution of the problem (2.5) for any ${{\bf f}}\in L^2(\Omega)$, and the domain $\Omega$ has only one vertex $O$ with an angle $\omega$. Let the real numbers $\big\{\alpha_l: l\in\mathbb{N}\big\}$ and the functions $\big\{\Phi_l :l\in\mathbb{N}\big\}$ are defined in (2.8). If $0 < \alpha_l < 1$ for some $l\in\mathbb{N}$, then the weak solution ${\bf v}\in V_{0}(\Omega)$ of the problem (2.5). Additionally, the solution ${\bf v}$ can be decomposed into a regular part ${\bf w}(x, \, y)\in H^2(\Omega)$ and a singular part $s(x, y)$ with lower regularity

and the stress intensity factors $c_l$ are defined as

where

Moreover, there exists a constant $C > 0$ independent of ${{\bf f}}$ and the following estimate holds

Proof. The main strategy used to get the proof of Theorem 1 is summarized in ^[10,89,90]. The Poisson equation with the nonhomogeneous boundary conditions is discussed by ^[88].

Remark 1. It is noted that the stress intensity factors formula (2.13) are agreed with the formula given in ^[10] for Dirichlet boundary condition, and it is independent of the precise form of the smooth cutoff function $\chi$.

3.   The theory of corner singularity for the Stokes system on polygonal domains

In this section, some basic results related to the corner singularity theory of the Stokes system on a bounded plane polygonal domains are described. The results of corner singularities and regularity for the stationary Stokes system on polygonal domains have been developed by ^{[24,25,40,62,65,66]}. A particular type of singular function is introduced to describe the singular solution structure of the considered problem near the singular points of the boundary. The obtained results for the singular behavior of the solution are important for numerical schemes. It is observed that the obtained lowest order corner singularity results for the compressible stationary Stokes system on a polygonal domain with inflow boundary conditions are the same as Laplacian near each non-convex vertices.

The velocity and pressure formulation of the stationary Stokes system on a domain $\Omega$ with zero Dirichlet boundary condition is described as

where ${{\bf f}}$, $g$ are given data functions and the constant $\mu$ is known as the viscosity of the fluid flow. For Stokes operator, a formula for the corner singularity is defined as $\textbf{L}[{\bf v}, \, p] = [\textbf f, \, g]$, where the operator $\textbf{L}$ is written as

The singular functions of the Stokes operator $\textbf{L}$ are obtained by solving the eigenvalue problem in an infinite sector domain having a corner by considering zero Dirichlet boundary condition. The more detail about the eigenvalues and the corresponding eigenfunctions can be seen in ^[62].

To describe the formulas and to give the eigenvalues and the corresponding eigenvectors, the following algebraic equation is considered from ^[39,60]

Let $\lambda _{m, \, j}: j = 1, 2, ...$ be a nondecreasing sequence of numbers and ordering these solutions in a non-decreasing real part, as follows

The number $s_{m, \, j}$ are given by

which is sometimes known as the order of the regularity of the solution space and depends on the corner singularity. Let $[\Phi_{m, \, j}, \, \phi_{m, \, j}]$ be the singular functions relative to the velocity and pressure with the singular exponents $\lambda _{m, \, j},$ and defined as

The functions $\xi_{m, \, j}(\theta)$ and $\tau_{m, \, j}(\theta)$ are the definite trigonometric eigenfunctions for the pressure and velocity relative to the eigenvalues $\lambda _{m, \, j}, \, j = 1, 2, ...$ and $\chi_{m}$ is a smooth cutoff function. Further information about the number $\lambda _{m, \, j}$ can be found in ^[60,62].

(1) For the non-convex case that is $\omega_{m} \in (\pi, \, 2\pi)$, the first 3 leading eigenvalues $\lambda _{m, \, j}, \, j = 1, 2, 3$ are real and holds the property

In particular, $\omega^{*}\approx 1.4303\pi$ is the unique solution of the equation $\tan \omega- \omega = 0$ for an angle $\omega \in [0, 2\pi)$.

(2) For a convex case $\omega_{m} \in (0, \, \pi),$ then $\lambda _{m, \, 1}$ is a simple and unique eigenvalue that lie in the strip $0 < \mathcal{R}_{e} \lambda_{m, \, 1} < \frac{\pi}{\omega_m}$. For this, the relative pressure eigenfunction $\xi_{m, \: j}(\theta)$ has a constant value and the velocity eigenfunction $\tau_{m, \: j}(\theta)$ is zero.

Similarly, the dual singular functions for the velocity vector and the pressure function are $\Big\{\big(\Phi^{-}_{m, \, j}, \, \phi^{-}_{m, \, j}\big), \, \mbox{for}\, j\geq1\Big\}$ and defined by

Hence, the functions $\big\{\tau^{-}_{m, \, j}(\theta), \: \xi^{-}_{m, \, j}(\theta)\big\}$ can be attained by replacing $\lambda = -\lambda_{m, \, j}$ into the eigenfunctions $\big\{\tau_{m, \, j}(\theta), \: \xi_{m, \, j}(\theta)\big\}$.

4.   Compressible Stokes and Navier-Stokes problems on polygonal domains

This section is devoted to stationary compressible Stokes and Navier-Stokes systems on a bounded plane polygonal domains that have convex or non-convex corners.

A complete mathematical analysis of the solution of the boundary value problems for compressible Stokes and Navier-Stokes equations have not been achieved yet. Various questions are still open for domains with singular boundaries like a complete existence and the regularity analysis for the 3-dimensional compressible Stokes and Navier-Stokes equations in polyhedral domains. To solve the 3-dimensional problem for the polyhedral domain, the solution has both the edge and vertex singularities. The edges of the domain generate edge singularities and where these edges meet vertex singularities are generated. A limited number of known results exist in the literature to find the corner singularities of the solutions of the compressible Stokes system and the Navier-Stokes system in polygonal or polyhedral domains. Maybe one of the reasons is the mixed type equations.

In high-speed flow problems, like hypersonic or supersonic, the flow properties change their behavior significantly near the corners or edges. The shift theorem holds for general elliptic equations for a smooth domain. For example, we consider the Poisson problem in a bounded domain $\Omega$ with the homogeneous Dirichlet boundary condition

Suppose that if the given right-hand side function ${\bf f}\in H^{s-2}, \, \forall s\geq 0,$ then the solution ${\bf v}\in {\bf H}^{s}$, which shows that $\Omega$ is the sufficiently smooth domain. Thus, the non-smooth domains do not satisfy the shift theorem.

For a bounded domain with non-convex corner positioned at the origin, it is recognized from ^{[26,45,60,61,62]} that the solution $\textbf{v}\in H_0^1({\Omega})$ of the problem (4.1). Let us considered if ${\bf f}\in H^{s-2}$ and $\Lambda$ is known as the continuous linear functional on $H^{s-2}, \, s > 1+ \alpha,$ then

and also satisfy the following regularity estimate

where $C$ is a constant. In ^[73,74], the authors have extended these results for stationary barotropic compressible viscous Navier-Stokes system by considering inflow boundary conditions for pressure and also generalized it for whole compressible Navier-Stokes system. The consider boundary value problem is described as

After linearizing (4.4) around the ambient flow and dropping the convective term yield the compressible Stokes system

The vector $\textbf{V} = [1, \, 0]^t$ is known as a convective vector or the horizontal vector. Let $\Gamma_{in}$ and $\Gamma_{out}$ denote the inflow and the outflow boundary and defined as

and $\textbf{n} = \big[n_1, \, n_2\big]$ is known as the unit outward pointing normal to the boundary. The boundary condition for pressure function occurs due to the hyperbolic behavior of the continuity equation. The ambient flow field $\textbf{V}\neq \textbf{0}$ on the boundary $\partial\Omega.$ The system (4.5) is a combination of three equations, the first two represent the momentum equations and the third one is the continuity equation. The derivative of the term $\textbf{V}\cdot \nabla p$ in the continuity equation represents the convection and the system is not permitted from being elliptic. Consequently, the theory of corner singularities cannot be applied directly. In the Stokes system, the singularities in the solution can occur only at the vertices of the domain. But in a compressible Stokes system, the singularities in the pressure and the density are resultant from the streamlines that emanating from the corners of the domain.

Some existence and regularity results of the system (4.5) in smooth and in a polygonal domain with corners are defined as follows. For a smooth domain $\Omega$, the subsequent result can be seen in ^[72,73].

Theorem 2. Let $q\in (2, \, 3)$ and suppose that the boundary $\partial\Omega$ is sufficiently smooth, if $\textbf{f}\in L^{q}(\Omega)$ and $g\in H^{1, \, q}(\Omega)$, then a pair $\big[{\bf v}, \, p\big] \in H_{0}^{1}(\Omega)^2 \times L^{2}(\Omega)$ is the unique weak solution of problem (4.5). Furthermore, if the viscosity $\mu$ is adequately large then the following estimate holds

and the constant $C_1 = C_1(\mu, \, \Omega)$.

Several mathematicians have studied the singular structure of the solutions of the boundary value problems in domains having piecewise smooth boundaries. The following theorems defined the results regarding the corner singularity and the regularity issues for a plane bounded domains with convex and non-convex corners.

Theorem 3. Let $\Omega$ be a plane polygonal domain with non-convex corner and suppose that the viscosity $\mu$ is adequately large. If $\big[\mathit{{\bf{f}}}, \mathit{\mbox{g}}\big]\in L^{2}(\Omega)^2\times H^{1}(\Omega)$, then (4.5) has a unique weak solution $\big[{\bf v}, p\big]$. Thus the velocity vector ${\bf v}$ can be split near the vertex into a singular part ${\bf v}_{s}$ and a regular part ${\bf v}_{r}$, that is, ${\bf v} = {\bf v}_{r}+ {\bf v}_{s},$ with the property $\big[{\bf v}_{r}, \, p] \in H^{2}(\Omega)^2\times H^{1}(\Omega)$ and the singular solution near the each non-convex vertex with interior angle $\omega > \pi$ is ${\bf v}_{s} = {\bf C}\, r^{\alpha}\, \sin\big[\alpha\, (\theta- \omega_{1})\big],$ where $r$ is the distance to the vertex, ${\bf C}$ is an unknown constant vector and $\alpha = \frac{\pi}{\omega} < 1.$ Furthermore, if $\mu$ is sufficiently large then a constant $C_1 = C_1(\mu, \, \Omega)$ exists and the following inequality is satisfied

Remark 2. The main idea and the strategy used to obtain the proof of Theorem 3 is summarized by ^[73]. Firstly, split the solution into a regular and a singular part, then apply the known results of a Poisson problem for polygonal domains to problem (4.5). To construct the singular part ${\bf v}_{s}$ of the solution, choose a suitable vector function whose each component is a multiple of the harmonic function near the corner points which belongs to $H^{1}$ but not $H^{2}.$ Hence, the two solution operators are defined as follows. Let ${B}: H^{-1}\, (or\, L^{2})\rightarrow H^{1}$ be given as ${B}{\bf G} = z$, where $z$ is the solution of the following boundary value problem

The second operator is $A: L^{2}\rightarrow L^{2},$ where $q = {A}\, \mbox{F}$, and $q$ is the solution of the following equation

where

The solution of (4.9) can be obtained by integrating it in the $x$-direction and described as

The solution operator ${A}$ gives the solution of the continuity equation, and some manipulations yield the reformulation form of (4.5). The required form can also be obtained by applying the basic theory of corner singularity for Laplacian and splitting the velocity vector into a regular and a singular part.

The next theorem describes the regularity result of the system (4.5) for a convex polygon.

Theorem 4. Let $\Omega$ be a convex polygon and assume that the viscosity $\mu$ is adequately large. If ${\bf f}\in L^{2}(\Omega)^2$, ${g}\in H^{1}(\Omega)$ and a pair $\big[{\bf v}, \, p\big]$ be a unique weak solution of (4.5), then $\big[{\bf v}, \, p\big] \in H^{2}(\Omega)^2\times H^{1}(\Omega)$. Moreover, a constant $C_1 = C_1(\mu, \, \Omega)$ exists such that the subsequent estimate holds

Proof. For the proof, we refer ^[45,59].

Recently, the system (4.5) is considered for a rectangular domain $\Omega$ in ^[47]. The interior jump discontinuity of the solution, piecewise regularity, and Rankine-Hugoniot conditions with inflow jump datum have shown. The interface curve preserved a discontinuity along the ambient vector field. The main difficulty is to find the solution and its regularity to handle the gradient of pressure function at the jump point. To resolve this issue, a vector function is constructed for an interior jump of the pressure function. Splitting this vector function from the velocity vector and the remainder formulate a boundary value problem. The subsequent theorem states the main result.

Theorem 5. Let $\Omega$ be a rectangular domain and $q\geq 2$ be any number. Let $p_0$ be an inflow datum that has jump across $y = 0$, and also satisfies the conditions $p_0\neq 0$ for $y > 0$ and is $0$ for $y < 0.$ Suppose that the viscosity $\mu$ is adequately large and there exists a constant $C_1 = C_1(\mu, q)$ such that if the pair $\big[{{\bf f}}, \, g\big]\in {\bf H}^{s-2} \times {H}^{s-1}$ for $s\in\big[1, \, 1+\frac{2}{q}\big)$ and $p_{0} \in {H}^{s-1, \, q}(0, 1)$, then $\big[{\bf v}, \, p\big]$ the solution of the problem (4.5) belongs to the space $\textbf{H}^{s, \, q}({\Omega_j}) \times {H}^{s-1, \, q}({\Omega_j})$ and the subsequent inequality is satisfied

In fact, if $s < 1+\frac{1}{q}$, then one has the following inequality

On the other hand, let ${\bf K}$ and ${\bf J}$ be the vector functions formulated as

where ${\bf K}^{\ast}$ is the extension by zero to $\Omega_1$ of ${\bf K}.$ Let we set $p_{{\bf K}^{\ast}} = -B\, {\mathit{\mbox{div}}}\, {\bf K}^{\ast}$ and $p_{\bf J} = -B{\mathit{\mbox{div}}}\, {\bf J}.$ Suppose $\big[{{\bf f}}, g\big]\in {\bf L}^{q} \times {H}^{1, \, q}$ and $p_0 \in {H}^{1, \, q}(0, \, 1)$, then there exists a unique vector ${\mathit{{\bf{v}}}}_{R}\in {\bf H}^{2, \, q}$ and a scalar function ${p}_{R} = B\big(g- {\mathit{\mbox{div}}} \, {\bf v}_{R}\big)\in {H}^{1, \, q}$. Such that the velocity vector $\mathit{{\bf{v}}}$ and pressure function $p$ can be represented as

where ${\bf K}^{\ast}\in \textbf{H}^{2, \, q}({\Omega_j})$, ${\bf J}\in \textbf{H}^{s, \, q}$ for $s < 1+\frac{2}{q}$, ${p}_{{\bf K}^{\ast}}\in {H}^{1, \, q}({\Omega_j})$ and ${p}_{\bf J}\in {H}^{1, \, q}.$ Furthermore, for a constant $C_1 = C_1(\mu, \, q)$ the following estimate holds

Proof. The proof can be found in ^[47].

In ^[71], a new idea has been used to demonstrate the best regularity results of the compressible Stokes system on a polygonal domain. An appropriate Helmholtz decomposition ${\bf v} = {\bf u}+\nabla\varphi_{r}$ has been considered to find the best regularity result without subtracting the corner singularities from the solution, and the vector ${\bf u}$ be the solution of the incompressible Stoke system with ${\mbox{div}} \, {\bf u} = 0$ and a potential function $\varphi_{r}$. The potential $\varphi_{r}$ is attained by subtracting the two leading corner singularities of the solution at non-convex vertices of the domain from the obtained solution of the Neumann boundary value problem. So that the direct Helmholtz decomposition cannot be apply because one has to consider ${\bf v} = {\bf u}+\nabla\, \varphi$ with $\nabla\cdot{\bf u} = 0$. So, the potential $\varphi$ solve the problem $\Delta \varphi = {\mbox{div}}\, {\bf u} \in {L}^{2}$ with boundary condition $\frac{\partial\varphi}{\partial {\bf n}} = 0$ and its corner singularities are denoted by $r^{j\, \alpha}\, \cos\big(j\, \alpha\, \theta\big), \: j = 1, \, 2, ...$ where $\alpha = \frac{\pi}{\omega}.$ That are not in ${\bf H}^{2}$ for $j = 1, \, 2, ...$ and so $\nabla\varphi\notin\, {\bf H}^{1}.$ But for a convex polygon domain $r^{\alpha}\, \cos\big[\alpha\, \theta\big]\in{\bf H}^{2}$ for an interior angle $\omega < \pi.$

The system to be considered is

with $\int_{\Omega}\rho\, d{\bf x} = 0.$ Let $\Omega$ be a bounded plane polygon with a non-convex corner on the boundary $\partial\Omega$ and the pressure $P$ is a strictly increasing function in $\rho.$ Therefore, $\nu$ and $\mu$ are the viscous coefficients having the property $\mu > 0$, $\mu_{1} = \mu +\nu > 0$, and $\mu_{2} = \mu +|\nu|.$ The derivation of the system (4.17) can be seen in ^[94]. The subsequent theorem states the main result of (4.17) and shows the best regularity result.

Theorem 6. Let ${\bf V}$ be a vector field which belongs to ${\bf V}\in {\bf H}^{1}_{0}(\Omega) \cap{L}^{\infty}(\Omega)$ and assume that $|\nabla\, {\bf V}|_{\infty, \, \Omega}$ is small enough. Let a pair $\big[{{\bf f}}, \, g\big]\in {\bf H}^{-1}(\Omega)\times {L}^{2}_{0}(\Omega)$, then a unique weak solution $\big[{\bf v}, \, \rho\big]\in {\bf H}^{1}_{0}(\Omega)\times {L}^{2}_{0}(\Omega)$ of system (4.17) exists that satisfies the inequality

and the constant $C = C(\Omega, \mu_{1}).$ On contrary, let ${\bf L}$ be a Stoke operator and $\lambda_ {1, \, m}$ be its leading singular eigenvalues, that is, $\frac{1}{2} < \lambda _{1, \: m} < \frac{\pi}{\omega_{m}} < 1.$ Let there exist a vector ${\bf u}\in {\bf H}^{s}$ with

for a real number $s$ with $1 < s < \min_m\big\{3\alpha_{m}, \, \lambda_ {1, \, m}+1\big\}$ and a potential $\varphi_{r}\in {H}^{s+1}$ with $\frac{\partial \varphi_{r}}{\partial {\bf n}}\big|_{\partial\Omega} = 0$. Therefore, the Helmholtz decomposition ${\bf v} = {\bf u}+\nabla\varphi_{r}$ holds and the potential $\varphi_{r}$ can be described as $\varphi_{r} = -\Phi+\varphi,$ where the function $\varphi$ is the solution of the Neumann boundary value problem and $\Phi = \sum\limits_{n\in\tau}\big(\mathcal{C}_{1, \, m}\, \phi_{1, \, m}+\mathcal{C}_{2, \, m}\, \phi_{2, \, m}\big)$ for some numbers $\mathcal{C}_{j, \, m} = \mu_1^{-1}\Lambda_{j}(\sigma-\rho)$, where $\Lambda_{j}$ is defined by

for some ${u}_{j}\in {H}^{2-s}.$ Also ${\bf u}$ is the solution of the subsequent stationary incompressible Stokes system

with $\int_{\Omega}\sigma\, d{\bf x} = 0.$ Finally, if $\big[{{\bf f}}, \, g\big]\in {H}^{s-2}(\Omega)\times {H}^{s-1}_{0}(\Omega)$ and the viscosity $\mu$ is sufficiently large, then $\big[{\bf v}, \, \rho\big]$ the solution of (4.17) holds the subsequent inequality

and the constant $C_1 = C_1(\mu, \, |\nabla\, {\bf V}|_{\infty, \, \Omega}).$

Proof. The proof has shown by ^[71].

5.   Incompressible Stokes and Navier-Stokes systems on polygonal domains

This section contains some known results relating to the existence and regularity of the solutions of the stationary incompressible Stokes and Navier-Stokes systems on polygonal domains with corners.

Let the domain $\Omega$ be bounded in $\mathbb{R}^2$ with polygonal boundary $\partial\Omega$. The stationary Navier-Sokes equations of incompressible flow with no-slip boundary condition are defined as

where ${\bf v}$ and $p$ are known as the unknown velocity vector and unknown pressure function; $\mu > 0$ is known as the viscous coefficient. Let ${{\bf f}}$ and $g$ are given functions with the property $\int_{\Omega} g\, d\, {\bf x} = 0.$ Generally, for incompressible flows to satisfy the incompressibility condition the function $g$ is set equal to zero. If $g$ is non-zero then a particular regularity of $g$ is required for arising a regularity of the pressure function or to handle non-zero boundary data.

In ^[57], a convex polygon is considered to obtain the ${\bf H}^{2}\times {\bf H}^{1}$ regularity of the problem (5.1). The $\textbf{H}^{s}$ regularity of the stationary Stokes problem on a convex polygon and also for a convex polyhedron has been discussed by ^[27]. The corner singularities and regularity results of the Stoke system for corner domains with the applications of weighted Sobolev spaces have constructed in ^[62]. The 3-dimensional stationary Navier-Stokes equations with arbitrary boundary conditions have considered by ^[85]. The non-stationary Navier-Stokes equations for polygonal domains have been discussed by ^[75].

In the subsequent theorems, we state some known results relating to the existence and regularity of the problem (5.1) in a bounded plane polygonal domains.

Theorem 7. $(i)$ Let the domain $\Omega$ be a plane bounded Lipschitz domain. Suppose that if $\big[{{\bf f}}, \, g\big]\in {\bf H}^{-1}_{0}(\Omega) \times {L}^{2}_{0}(\Omega),$ then the pair $\big[{\bf v}, \, p\big]$ is the unique weak solution of (5.1) which belongs to the space ${\bf H}^{1}_{0}(\Omega) \times {L}^{2}_{0}(\Omega)$.

$(ii)$ Let $\Omega$ be a plane bounded domain with smooth boundary $\partial\Omega$ belong to $\mathcal{C}^2$. If the pair $[{{\bf f}}, \, g]\in{\bf L}^{2}(\Omega)\times \bar{H}^{1}(\Omega)$, then their exists a unique weak solution $\big[{\bf v}, \, p\big]\in {\bf H}^{2}_{0}(\Omega)\times \bar{H}^{1}(\Omega)$.

$(iii)$ If the domain $\Omega$ is a convex polygon and $[{{\bf f}}, g]\in{\bf L}^{2}(\Omega)\times\bar{H}^{1}(\Omega)$, then $[{\bf v}, p]\in {\bf H}^{2}_{0}(\Omega)\times\bar{H}^{1}(\Omega)$.

Proof. The assertions $(i)$-$(ii)$ have been proved in ^[93] and $(iii)$ has proved by ^[57].

The extended regularity results of assertions $(ii)$-$(iii)$ of Theorem 7 for generalized polygonal domains with non-convex corners have proved by ^[19].

Let $\lambda_{m, \: 1}$ and $\lambda_{m, \: 2}$ be less than $1$ are two eigenvalues of the Stokes problem for angle $\omega_{m}\in (\omega^{\ast}, 2\pi)$. Let $\tau = \tau_{1}\cup \tau_{2}$ where $\tau_{1} = \big\{m: \frac{1}{2} < \lambda_{m, \, 1} < \lambda_{m, \, 2} = 1\big\}$ and $\tau_{2} = \big\{m: \frac{1}{2} < \lambda_{m, \, 1} < \lambda_{m, \, 2} < 1\big\}.$ The number $s_{m, \, i}$ be define by $s_{m, \, i} = \mathcal{R}{e} \lambda_{m, \, i}+1$ for all integers $m, i$. Let $s_1 = \max _{m\in\tau_1}s_{m, \, 1}$ and $s_2 = \max _{m\in\tau_2}s_{m, \, 2}.$ Set $s_{\star} = \max \{s_1, \, s_2\}.$

Theorem 8. Let the domain $\Omega$ be a planar polygonal domain and $P_{m}: m\in \tau$ are its non-convex vertices. If ${{\bf f}}\in {\bf H}^{-1}(\Omega)$, $g\in{L}^{2}_{0}(\Omega),$ then a unique weak solution ${\bf v}\in {\bf H}^{1}_{0}(\Omega)$ and $p\in{L}^{2}_{0}(\Omega)$ of the problem (5.1) exists and satisfies the inequality for a positive constant $C_1$

On contrary, for any number $s$ with $s_{\star} < s\leq 2,$ if we presume that ${{\bf f}}\in{\bf H}^{s-2}(\Omega)$ and $g\in \bar{H}^{s-1}(\Omega)$ with the property that $g$ is zero at the non-convex vertex $g(P_{m} = 0)$ for $m\in\tau$, then there exists some constants $\mathcal{C}_{m, \, j}$ for $j = 1, 2:\, m\in\tau$, and a regular part $[{\bf v}_{r}, \, p_{r}]\in {\bf H}^{s}_{0}(\Omega) \times{H}^{s-1}(\Omega)$. Therefore, the solution $[{\bf v}, p]$ can be written as

where the pair $[{\bf v}_{r}, \, p_{r}]$ solves the generalized Stokes system and satisfies the following inequality for any $s\in(s_{\star}, \, 2]$

such that the constant $C_1 = C_1(\Omega).$

Finally, if ${{\bf f}}\in{\bf H}^{s-2}(\Omega),$ and $g\in\bar{H}^{s-1}(\Omega)$ for $1 < s < \min_{m\in\tau} s_{m, \, 1},$ then for some constant $C_1$ the solution $[{\bf v}, \, p]$ of the problem (5.1) holds the following regularity result

Proof. For the proof, we refer ^[19]. But some clues are discussed here. First, one has to display the regularity results of the stationary Stokes problem on a particular domain $\Omega$, then have to extend these results to generalized polygonal domains. Lastly, use the fixed point theory to obtain the regularity of the problem (5.1). As an application of Theorem 8, ^[20] has used the decomposition (5.3) to formulate the discrete form of the Stokes system. ^[39] has developed the error estimates for the stress intensity factors (unknown coefficients) and for the regular part, which based on the regularity result of (5.4). The numerical examples for the convergence rates can be found in ^[20].

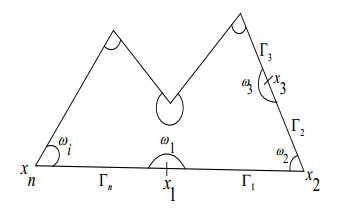
The next theorem represents the regular and singular decomposition of the solution and also the ${\bf H}^{2}\times{H}^{1}$ regularity of the stationary Stokes system. A specific bounded domain $\Omega$ (see Figure 3) is considered whose boundary $\partial\Omega$ has only one non-convex vertex at the point $O = (0, 0)$. Assume that the opening angle $\omega\in (\omega^{\star}, 2\pi)$ and analogous for the case of $\omega\in (\pi, \omega^{\star}]$.

Theorem 9. Let $\Omega$ be a bounded domain as shown in (Figure 3). Let ${{\bf f}}\in {\bf H}^{-1}(\Omega), \, g\in {L}^{2}_{0}(\Omega)$ are given functions and the pair $[{\bf v}, \, p]\in {\bf H}^{1}_{0}(\Omega)\times {L}^{2}_{0}(\Omega)$ be the unique weak solution of the generalized Stokes equation ${\bf L}[{\bf v}, \, p] = [{{\bf f}}, \, g]$ in $\Omega.$ Let $[{\bf v}, \, p]$ belongs to $({\bf H}^{1}_{0}\cap {\bf H}^{2}_{loc})\times ({L}^{2}_{0}\cap {H}^{1}_{loc})$ for the pair $[{{\bf f}}, \, g]\in {\bf L}^{2}\times ({L}^{2}_{0}\cap {H}^{1}_{loc}).$ Suppose that for a number $r_{0}$ for $0 < r_{0} < r$, the pair $[{\bf v}, \, p] = [0, \, 0]$ and the solution can be defined as follows. Let $s^{\star}_{4} = \min \{s_{4}, \, 3\}$. For any $s\in (s_{2}, \, s^{\star}_{4}]$, there exists two numbers $\mathcal{C}_{01}, \, \mathcal{C}_{02}$ and a pair $[{\bf v}_{r}, \, p_{r}]\in{\bf H}^{s}_{0}\times {H}^{s-1}$ for $[{{\bf f}}, \, g]\in {\bf H}^{s-2}\times \bar{H}^{s-1}$ with $g(O) = 0,$ then the solution can be decomposed near the non-convex vertex $O$ as

Let for angle $\omega\in (\pi, \, \omega^{\star}]$, we can set $\mathcal{C}_{02} = 0$. The coefficients $\mathcal{C}_{0j}: j = 1, 2,$ and the regular part $[{\bf v}_{r}, \, p_{r}]$ in (5.6) are estimated by $\forall\, s\in(s_{2}, \, s^{\star}_{4})$, and for a constant $C_1$

In specifically, we can set ${{\bf f}}_{0} = {{\bf f}}, \, {g}_{0} = g$ and for $i\geq 1,$

where ${{\bf f}}_{j}^{s} = \mu\Delta\Phi_{j}-\nabla\phi_{j}$ and ${g}_{j}^{s} = {\mathrm{div}}\, \Phi_{j}.$ For $j = 1, 2$ the coefficients $\mathcal{C}_{0j}$ are written as

Moreover, ${q}_{j}\in{\bf H}^{1-s}$ and ${\bf u}_{j}\in{\bf H}^{2-s}$, and are expressed as ${q}_{j} = \gamma_{j}\, (\phi^{-}_{j}+\psi_{j})$ and ${\bf u}_{j} = \gamma_{j}\, (\Phi^{-}_{j}+\Psi_{j})$. Thus the number $\gamma_{j}$ is defined as

The functions $\psi_{j}$ and ${\Psi}_{j}$ satisfies the equations

excepting the origin point $O$ where $[{{\bf f}}^{-}_{j}, \, {g}^{-}_{j}] = -{\bf L}[\Phi_{j}^{-}, \, \phi_{j}^{-}].$ From (5.6)–(5.7), it is recognized that if ${{\bf f}}\in {\bf H}^{s-2}$ and $g\in\bar{H}^{s-1}$ for $1\leq s < s_{1},$ then the subsequent estimate holds for a some constant $C_1$

Proof. This theorem has been proved in five steps for $s\in (s_{2}, s^{\star}_{4}]$ when the opening angle $\omega$ have values $\omega\in (\omega^{\star}, 2\pi)$ and the analogous for the case of opening angle $\omega\in (\pi, \omega^{\star}]$. The complete proof can be seen in ^[19].

Remark 3. The mapping $\Lambda_{j}$ defined by equation (5.8) is a continuous linear functional on ${\bf H}^{s-2}\times {H}^{s-1}, \, s\geq s_{j}$ and the following approximation holds

In the next theorem, the stationary Navier-Stokes equations with the formulation of fluid variables vorticity, velocity, and pressure are considered and the existence and regularity results have shown. The construction of these fluid variables can be found in ^[4,31,32]. The results have been found in a bounded plane polygonal domain and the non-standard or Stokes type boundary conditions have been considered with convex and concave corners. To construct the corner singularity functions, Stokes operator has considered in an infinite sector domain with zero normal velocity and zero vorticity boundary conditions. The solution is obtained by splitting the leading singularities and has increased the regularity of the remainder.

The velocity, vorticity, and pressure formulation of the Navier-Stokes equations with non-standard boundary conditions are considered as

where $\omega$, ${\bf v}$ and $p$ is known as scalar vorticity, velocity vector and pressure function. Let ${\bf v}^{\perp} = [v, \, -u]^{t}$ is the perpendicular velocity. The number $\nu$ is known as viscosity, i.e., $\nu > 0$, ${\bf n}$ is the unit normal vector and ${\bf t}$ is the unit tangential vectors on the boundary. Let ${\bf v}_{0}, \, p_{0}, \, \omega_{0}$ are given functions and $\Omega$ be a bounded domain whose boundary has non-convex and convex vertices. The boundary $\Gamma = \partial\Omega$ is formed by disjoint and open subsets $\Gamma = \Gamma_{a}\cup\Gamma_{b}\cup\Gamma_{c}.$ The physical meaning of the boundary conditions can be seen in ^[5,8,59,77].

The main goal is to examine the singular behavior of the solution structure near the non-convex vertex. Before going to describe the main results of this problem, some information about the corner singularity theory is given for the later use.

Let $\Phi_{i}$ be define the corner singularity functions, $m$ is the number of corner singularities, and $s_{i}$ be the order of the regularity. Let the number $m^{\star}$ be defined via $m^{\star} = \max\{i: {\bf d}_{1}\in {\bf H}^{s-2}, \, s > s_{i}\}$ where ${\bf d}_{1} = \Phi^{\perp}_{1}\, \mbox{curl}\, \Phi_{2}$ for $\beta \in (\pi, \, \frac{3\pi}{2}]$ and ${\bf d}_{1} = \Phi^{\perp}_{1}\, \mbox{curl}\, \Phi_{3}$ for $\beta \in (\frac{3\pi}{2}, 2\pi).$ Let $m^{\star} = 2$ for $\beta = \frac{3\pi}{2}$ and $m = m^{\star}$ when $\beta\neq\frac{3\pi}{2}$. Let us consider the following Hilbert spaces

and

where $\prime$ means the dual space and the norm is defined as

Theorem 10. Suppose that if ${{\bf f}}\in {\bf L}^{2}(\Omega)$, $[{\bf v}_{0}, \, p_{0}]\in{\bf H}^{2}\times{H}^{1},$ then there exists a unique weak solution $[\omega, \, {\bf v}, \, p]\in{L}^{2}\times \mathbb{M}_{b}\times{L}^{2}$ of problem (5.12). For any constant $K_{1} > 0$, a constant $K_{2} > 0$ exists such that the following estimates holds

and

Then there exists a pair $[{\bf v}_{r}, \, p_{r}]\in ({\bf H}^2\cap \mathbb{M})\times{H}^{1}$ and a pair $[\Psi, \, \psi]\in({\bf H}^{s}\cap\mathbb{M})\times{H}^{s-1}$ for $s\in (s_{m_{\star}}, \, 2)$ and a constant $C_{i}\in \mathbb{R}^m, \, i = 1, 2, ...m,$ such that

where the coefficients $\mathcal{C}_{1} = \Lambda_{1}\, [{{\bf f}}({\bf v}, \, {\bf v}), \, \nabla\cdot{\bf v}_{0}]$ and $\mathcal{C}_{2}, ..., \mathcal{C}_{m}$ are defined by

and the auxiliary singular functions $[\Psi, \, \psi]$ are defined as

Thus, the following regularity result holds

where the constant $k_{3} = C(K_{1}, K_{2})$. The vorticity $\omega = \mathrm{curl}\, {\bf v}$ can be defined by the vector function ${\bf v}$ given in (5.15).

Proof. For the proof, we refer to the readers ^[77].

6.   Conclusion and future work

It is known from the theory of elliptic boundary value problems in domains with boundary irregularities, like corners, conic vertices, edges, and cracks, etc., the solution may exhibit singularities. Generally, the flows over corners usually change their behaviors and properties as a result of an abrupt geometrical change in the shape. In this article, we have provided a historical review of the treatment of corner singularity expansion and regularity of the solution of the stationary Stokes and Navier-Stokes equations on polygonal domains with non-convex or convex corners. It covers the recent developments in this field and also presents some future directions which can be explored.

Several interesting results about the regularity of the solution of the boundary value problems cannot be extended if one of the following situations appears: Domain has corners or edges on the boundary, change of the boundary conditions at some points, discontinuity of the solution and singularities of the coefficients. The general theory on $H^2$-regularity for linear elliptic boundary value problems states that the generalized solution of the stationary Stokes problem for the velocity field and pressure for two or three-dimensional domain $\Omega$ with corner or edge singularities and for any right-hand side function ${{\bf f}}\in L^2(\Omega)$ can be decomposed into sum of a singular and a regular part. The corners or edges in the domain $\Omega$ do not affect the behavior of the regular part, where the singular part is expressed by a linear combination of explicit model singular solutions $s_m$ for the Stokes operator and the unknown coefficients ${c}_{m}$. The special singular functions $s_m$ rely on the geometry of the model problem, the differential operator and the characteristic boundary conditions. The derivation of the rigorous formulas for the estimation of the unknown coefficients ${c}_{m}$ is of constant interest and a challenging task. In two-dimensional domains with corners or the polyhedral vertices and the case with conical points, the space of the singularity solutions is finite-dimensional. The asymptotic expansion of the solution of the boundary value problems on a (non-convex) polygon plays an important role to describe the regularity behavior of the solution accurately. The information about the singularity functions in non-smooth domains can help to improve the rate of convergence of the numerical methods for approximations.

At present, the Navier-Stokes equations with the Navier-slip boundary conditions and the free-boundary problems in domains with corners have very interesting phenomena. The issues regarding their existence and regularity are considered for smooth domains but the theoretical results for the corner singularity decomposition are still not achieved. Therefore, these issues are numerically interesting and important in future works to show the unique existence of the approximations for the regular parts and the coefficients, and derive their error estimates.

On the other hand, it is also observed that a complete mathematical analysis of the existence and regularity results of the compressible Stokes and Navier-Stokes equations on polygonal or polyhedral domains with corners or edges have not been given yet. Various questions are still open for domains with singular boundaries like a complete existence and the regularity analysis for the 3D compressible Stokes and Navier-Stokes equations in polyhedral domains. The solution of the 3D problem for the polyhedral domain has both the edge and vertex singularities. The edges of the domain generate edge singularities and where these edges meet vertex singularities are generated. Likewise, the non-stationary compressible Stokes and Navier-Stokes equations on polygonal domains could be considered. In this case, the corner singularity corresponds to each time, and so the corner singularity involved space is infinite-dimensional. Further, as the distance to the vertices increases, the coefficients of the singularities at corners decay exponentially. As a result, the derivatives of the flow variables can blow up along the trajectory curves starting near each non-convex vertices. Therefore, the dynamical behaviors will be abruptly changed there.

Additionally, the jump discontinuities and its piecewise regularity in the initial jump data for linear problems have been constructed in rectangular domains. The major difficulty is to find the solution and its regularity to controlling the gradient of pressure function around the interior curve starting at the jump point that the inflow datum has. To resolve this issue, a vector function is constructed for an interior jump of the pressure function. Splitting this vector function from the velocity vector and the remainder formulates a boundary value problem. However, the issues regarding the jump discontinuities and piecewise regularity for nonlinear problems with the domains such as rectangular domain containing an interior cut, cavity region (T-shaped cavity), and a vertex (cone-like) circulation, etc., are challenging tasks for future works. As the driven cavity flows display all phenomena that can probably arise in compressible or incompressible flows. The most important trigger of them is the corner. Moreover, the important mathematical issues for handling the flow behaviors mainly depends on the corner singularity behaviors at the front and rear corners, the differences (jump discontinuities) between the exterior and interior flows of the domain. These issues can be resolved by determining the singular behaviors at the corners and establishing the piecewise regularities for the continuity and momentum equations.

Acknowledgments

The author would like to extend his sincere appreciation to Prof. Chunjing Xie from the school of Mathematical science, Shanghai Jiao Tong University, China for his prolific discussion and valuable suggestions to improve the quality of the paper.

Conflict of interest

The author declares that no conflict of interest.