Analysis of superquadratic fuzzy interval valued function and its integral inequalities

1.   Introduction

The theory of convexity is a dynamic and fascinating area of research, with numerous scholars contributing innovative approaches to extend and generalize its different forms. This framework enables the creation of highly efficient numerical algorithms that can address challenges in both pure and applied sciences. Recently, convexity has seen significant advancements and generalizations, particularly in its interaction with inequality theories. For example, Dragomir et al. ^[1] explored novel inequalities of the H.H type, laying a foundation for subsequent developments. Butt et al. ^[2] extended Popoviciu-type inequalities using Fink's identity, which opened new avenues in generalizing inequality frameworks. Qin ^[3] provided an extensive treatment of integral and discrete inequalities, highlighting their practical applications in various mathematical domains. Agarwal et al. ^[4] further advanced mathematical inequalities with a focus on their applications in real-world problems. Bakula et al. ^[5] applied Jensen-Grüss inequalities to analyze the Zipf-Mandelbrot law, demonstrating its utility in statistical modeling. Butt ^[6] introduced Mercer-type inequalities for generalized strongly convex functions on fractal sets, emphasizing their relevance to complex systems. Meanwhile, Valdés et al. ^[7] and Vivas-Cortez et al. ^[8] investigated H.H type inequalities, presenting generalized forms and applications that significantly enriched the field.

Decision-making entails determining the best choice in contradictory scenarios that arise in several aspects of our everyday lives. It is also necessary to study several subjects, such as optimization theory, operational research, and management science. A choice is made based on a variety of considerations, including future uncertainty and risk. Decision-making is characterized using a certainty scale that spans from complete certainty to full uncertainty; this scale is known as the degree of certainty. There are numerous kinds of decisions, such as, decisions under conflicting situations, decisions under certainty, decisions under uncertain conditions, decisions under risk, and others. Additionally, a decision made under uncertainty is classified into numerous sorts. Two of them make optimistic decisions, while the other makes pessimistic ones. When someone makes an optimistic decision, they select the best alternative despite some doubt, although occasionally they select the most advantageous option despite uncertainty. Real numbers often represent deterministic parameters in mathematical models. Mathematical models may explain specific problems traditionally. However, many uncertain real-life circumstances exist, particularly in the engineering field or various disciplines of management science and operations research, where it is extremely difficult to make assumptions about the inputs which are assumed as real numbers. Certain inaccurate or inexact features are automatically included into the models since the decision maker must make judgements in the face of ambiguity in these circumstances. Experts of management sciences and operations research typically employ fuzzy or stochastic methodologies to deal with imprecise or uncertain parameters. The stochastic technique treats imprecise parameters as random variables with known probability distributions. In contrast, fuzzy techniques treat uncertainty as either a fuzzy set with a suitable membership function or a fuzzy number. In some circumstances, both procedures are used to address imprecise results. In these approaches, there is a concern about which probability distributions or membership functions to use. In actuality, it might be difficult to make judgements in an unpredictable setting. To get around this issue, several researchers have recently defined inaccurate parameters using intervals. The sequence of intervals plays a crucial role in identifying the best option in decision-making situations. In recent decades, scholars have presented various mathematical ways to define order relations of intervals. These approaches were primarily designed to reformulate or address various interval-oriented optimization problems. Because their major goal was to develop improved solution approaches, there were often no detailed discussions regarding the corresponding interval ordering definition. The researchers concluded the discussions after achieving their goal.

It was Moore in 1969 who established the foundations of interval analysis, and who is considered to be the first mathematician to have formally used this approach in the automatic analysis of errors ^[9]. His work was of great pioneering value in giving a systematic method for dealing with uncertainties and computational inaccuracies, thereby significantly improving the accuracy of numerical computations. By systematically accounting for errors, Moore's interval analysis provided a reliable framework for numerical problem-solving, which sparked great interest among researchers and practitioners in various scientific disciplines. Interval analysis simply replaces traditional numerical values as variables with interval numbers which recognize that in most real-world applications, exact values would not always be available or accessible due to either inaccuracies in measurement, some rounding approximations, and intrinsic uncertainties. Interval arithmetic is used instead of using standard arithmetic operations. This approach enables the derivation of tight error bounds and ensures that all possible results are included, which makes it especially useful in scenarios where accuracy and reliability are paramount.

Researchers have developed strong relations between convex functions and inequalities in the frame of interval analysis, resulting in some impressive results. Scholars like Chalco-Cano et al. ^[10], Flores-Franulič et al. ^[11], Costa et al. ^[12], and others have extended traditional integral inequalities to fuzzy-valued functions ($F_{V.Fs}$) and interval-valued functions ($I_{V.Fs}$). Such efforts have enriched the area by making classical mathematical outcomes applicable in a wider sense. For instance, Zhao et al. ^[13] employed the interval inclusion relation to introduce $h$-convex $I_{V.F}$ and obtained the related inequalities which gave new information on the connection between convexity and integral analysis. Likewise, in 2021, Khan et al. ^[14] further developed this field with the help of an $h$-convex $I_{V.F}$ using the Kulisch-Miranker order and some related inequalities that were valid only for this class of convex functions. Further in this direction, Zhang et al. ^[15] extended their line of research; they explored fuzzy set-valued functions and derived Jensen's inequalities, which showed the various flexibility of convexity ideas in more generalized settings. The collective studies indicate vivid interplay between interval and fuzzy-valued analysis toward the development of a better platform for further research activities in mathematical inequalities and related applications.

One should consult the material listed in the sources ^{[16,17,18,19]} to gain a thorough understanding of convex $F_{I.V.Fs}$, their types, and related inequalities, including fractional extensions utilizing various fuzzy fractional integral operators.

The refinement brought forth by superquadraticity results in more substantial or improved accuracy when working with integral inequalities. For instance, the extra formula makes it possible to compare the integral of a function and the function of the integral more precisely when using Jensen-type inequalities on superquadratic functions. This refinement is particularly helpful in applied mathematics, where more accurate estimates enhance models, and in domains such as optimization, where exact limits are required to get optimum solutions. For the derivation and implementation of integral inequalities, superquadraticity provides a more reliable framework than convexity, allowing for more precise and in-depth conclusions that are beneficial for both theoretical study and real-world applications.

As explained in ^[20], Abramovich and associates first proposed the idea of a one-variable superquadratic function as a modification of a certain class of convex functions. A function $\mathfrak{f}:[0, \infty)\longrightarrow\mathfrak{R}$, is said to exhbit superquadraticity if it fulfills the below mentioned inequality, $\forall \varkappa\geq 0$,

where ${\mathfrak{C}}_{\varkappa}\in\mathfrak{R}$, is a constant. $\mathfrak{f}$ exhibits subquadraticity provided "$\leq$" in (1.1) flips. When $\mathfrak{f}$ is subquadratic, it suggests that $-\mathfrak{f}$ is superquadratic.

The function $\mathfrak{f}(\mathfrak{\varkappa}) = \mathfrak{\varkappa}^\mathfrak{k}$ might be used as an example. Therefore, the aforementioned function is referred to as superquadratic for $\mathfrak{\varkappa}\geq0$ and $\mathfrak{k} \geq 2$, but it is regarded as subquadratic for $0\leq\mathfrak{k} < 2$. The constant $\mathfrak{C}_\mathfrak{\varkappa}$ may be expressed for this function as $\mathfrak{C}_\mathfrak{\varkappa} = \mathfrak{f}^{'}(\mathfrak{\varkappa})$. Furthermore, equality in (1.1) is maintained at $\mathfrak{k} = 2$, which is the point at which subquadratic and superquadratic behavior diverge.

Abramovich et al. have contributed significantly to the definition and advancement of a basic understanding of superquadratic functions, as documented in ^[20] and ^[21]. Equation (1.1), the condition they created in their work, is a powerful criterion for identifying superquadratic functions. In fact, this criterion is stronger than the usual convexity requirement and provides a more stringent test for identifying whether a function is superquadratic. Nevertheless, the superquadratic function in question needs to be non-negative for (1.1) to hold. In ^[21], the researchers provided a detailed explanation of this necessity. Lemma 1.1 further characterizes superquadratic functions by stating that every randomly selected superquadratic function will inherently satisfy three certain qualities, or axioms. These premises reinforce the unique behavior of superquadratic functions with respect to convex functions and a part of the fundamental requirements that they must meet.

Lemma 1.1. If $\mathfrak{f}:[0, \infty)\longrightarrow\Re$ exhibits superquadraticity, then:

(i) $\mathfrak{f}(0)\leq0$.

(ii) $\mathfrak{f}(0) = \mathfrak{f}'(0) = 0 \Rightarrow \mathfrak{f}^{'}(\mathfrak{\varkappa}) = {\mathfrak{C}}_{\mathfrak{\varkappa}}$ provided $\mathfrak{f}$ is differentiable at $\mathfrak{\varkappa} > 0$.

(iii) If $\mathfrak{f}$ is positive and $\mathfrak{f}(0) = \mathfrak{f}'(0) = 0$, then $\mathfrak{f}$ is convex.

Abramovich et al. earlier created a lemma in ^[20], which we explore in the following. It explains how convexity and superquadraticity are related.

Lemma 1.2. If $\mathfrak{f}'(0) = \mathfrak{f}(0) = 0$, and $\mathfrak{f}'$ is convex, then $\mathfrak{f}$ is said to exhibit superquadraticity.

Jensen and H.H integral inequalities are the two significant inequalities that develop and expand this idea. These inequalities are crucial to understanding superquadratic functions since they not only capture the essence of superquadraticity but also have numerous applications in other mathematical studies. Specifically, the classical version of Jensen's inequality, which is covered below, provides a crucial understanding of the properties of a superquadratic function. It helps identify these functions' distinct characteristics and behaviors by offering a criteria that sets them apart.

Theorem 1.1. ^[21] If a function $\mathfrak{f}$ exhibits superquadraticity, let $\varkappa_i \geq 0$, $0\leq {\lambda_{o}}_i\leq1$, and $\overline{\varkappa}$ = $\Sigma^{\mathfrak{n}}_{i = 1}{{\lambda_{o}}}_{i}\varkappa_{i}$, where $\Sigma^{\mathfrak{n}}_{i = 1}$${{\lambda_{o}}}_{i} = 1$, then

According to their study, Banić and associates created H.H type inequalities especially for superquadratic functions ^[22].

Theorem 1.2. If a function $\mathfrak{f}\colon I\subset[0, \infty[\longrightarrow\mathfrak{R}$ exhibits superquadraticity on I = $[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}]$, where $0\leq{\mathfrak{a}_{o}} < {\mathfrak{b}_{o}}$, then

A fundamental definition of superquadratic functions comes from an extended form of Jensen's inequality, provided here in its simplest form. This extended inequality serves as a key criterion for identifying superquadratic functions, so the following definition directly applies to any function that is superquadratic.

Definition 1.1. If a function $\mathfrak{f}$ exhibits superquadraticity, then it holds the inequality (1.4).

where $\forall 0 < {{\lambda_{o}}} < 1$ and $\varkappa_1, \varkappa_2 \geq 0$.

For a nonnegative superquadratic function $\mathfrak{f}$, the inequality (1.4) clearly represents an extension of Jensen's inequality. In this inequality, $\mathfrak{f}$ is categorized as a subquadratic function if the "$\leq$" sign is reversed. This reversal separates subquadratic behavior from superquadratic behavior by altering the function's development characteristics.

Remarkably, the fractional perspective of H.H's inequality via Riemann-Liouville fractional integrals provided by the following theorem was developed by Li and his colleague in ^[23].

Theorem 1.3. If a function $\mathfrak{f}\colon I\subset[0, \infty[\longrightarrow\mathfrak{R}$ exhibits superquadraticity and integrability on I = $[\mathfrak{a}_{o}, \mathfrak{b}_{o}]$, with $0\leq\mathfrak{a}_{o} < \mathfrak{b}_{o}$, then

In (1.5), the symbols $\mathfrak{I}^{{ß}}_\mathfrak{{\mathfrak{a}_{o}}^+}\mathfrak{f}(\varkappa)$ and $\mathfrak{I}^{{ß}}_\mathfrak{{\mathfrak{b}_{o}}^-}\mathfrak{f}(\varkappa)$ denote the right and left Riemann-Liouville fractional operators, respectively, with $\mathfrak{a}_{o}\geq0$, which are outlined below:

where $\Gamma({{\lambda_{o}}}) = \int_{0}^{\mathfrak{\infty}}{\mathrm{y}}^{{{\lambda_{o}}}-1}e^{-{\mathrm{y}}}d{\mathrm{y}}$ is a gamma function.

Alomari and Chesneau in ^[24] developed a new category of superquadratic functions known as $h$-superquadratic functions in an attempt to expand and generalize the idea of superquadratic functions. They looked into and explained some of its fundamental characteristics. In ^[25], Krnić and his collaborators presented the idea of a multiplicatively or logarithmically superquadratic function and developed the required characteristics for it. According to ^[26], Khan and Butt further investigated the idea of a center-radius cr-order interval valued superquadratic function, including its fractional variant. By creating basic and fractional versions of H.H and Fejér type inequalities, Butt and Khan have further developed the idea of $h$-superquadraticity (see ^[27]). These extended inequalities offer a foundation for a more thorough analysis of $h$-superquadratic functions, and their applications show how useful these functions are in real-world situations. Readers interested in superquadratic functions can learn more about the functions, instances and their uses in the framework of inequality theory by consulting ^[28,29,30] and the sources referenced therein.

Expanding upon earlier studies on convexity, convex $F_{I.V.F}$, and superquadraticity, we discovered that there are still no proven characteristics and inequalities pertaining to superquadratic $F_{I.V.F}$. This disparity inspired us to concentrate on these areas and create a brand-new idea of superquadraticity, known as superquadratic $F_{I.V.F}$. Since the superquadratic function and its associated inequalities are the refinement of the convex function and its associated inequalities, as was previously stated, our generated idea is the refinement of the convex $F_{I.V.F}$ notion and its associated findings.

Over the past few years, there has been a significant increase in the use of fractional calculus to integral inequalities. To proceed in this direction and arrive at new findings in the theory of inequalities, superquadratic $F_{I.V.F}$ must incorporate fractional calculus concepts. The superquadratic $F_{I.V.F}$ and its inequalities, as well as its fractional version, have not been studied before. To bridge this gap in the literature, we aim to refine and improve H.H's type inequalities using fractional calculus, time-scale calculus, and quantum calculus. We will start the research by combining fractional calculus with the superquadratic $F_{I.V.F}$ in order to demonstrate our main findings. These concepts will be covered in the aforementioned areas in later publications. We advise the reader to go to ^{[31,32,33,34,35]} and the references therein for further findings about the fractional integral operators.

2.   Preliminaries

We first develop the concept of superquadratic $F_{I.V.Fs}$ by taking into consideration the following fundamental mathematics related to fuzzy order relations.

Let $\mathbb{K}_{c}$ be designated as the space of intervals of ${\Re}$ which are closed as well as bounded, and any ${\omega_{o}}\in\mathbb{K}_{c}$ can be defined as follows:

with width $({\omega_{o}^{\ast}}-{\omega_{{o}_{\ast}}})$. If $({\omega_{o}^{\ast}}-{\omega_{{o}_{\ast}}}) = 0$, then ${\omega_{o}}$ is termed as degenerate. Here, ${\omega_{o}^{\ast}}, {\omega_{{o}_{\ast}}}\in\Re$ are the upper and lower limits of ${\omega_{o}}$, correspondingly. Any $\mathfrak{\varkappa}\in\Re$ can be pointed out as an interval $[\mathfrak{\varkappa}, \mathfrak{\varkappa}]$ with no gape. If $({\omega_{o}^{\ast}}-{\omega_{{o}_{\ast}}}) > 0$, then ${\omega_{o}}$ is considered as positive. The space of positive intervals is represented by $\mathbb{K}^{+}_{c}$ and given by

For each $\mathfrak{{{\lambda_{o}}}}\in \Re$, we attain

Addition and multiplication operations on intervals are defined as follows:

where ${\omega_{o}} = [{\omega_{{o}_{\ast}}}, {\omega_{o}^{\ast}}]$ and ${\mathrm{v}_{o}} = [{\mathrm{v}_{{o}_{\ast}}}, {\mathrm{v}_{o}^{\ast}}]$.

Remark 2.1. ^[15] One can assert that $[{\omega_{{o}_{\ast}}}, {\omega_{o}^{\ast}}]\leq_{I}[{\mathrm{v}_{{o}_{\ast}}}, {\mathrm{v}_{o}^{\ast}}] \Leftrightarrow {\omega_{{o}_{\ast}}}\leq{\mathrm{v}_{{o}_{\ast}}}, {\omega_{o}^{\ast}}\leq{\mathrm{v}_{o}^{\ast}}$; in this scenario, the relation $\leq_{I}$ is called partial order.

Remark 2.2. ^[36] Let $d_{H_s}$ represent the Hausdorff-Pompeiu distance between $[{\omega_{{o}_{\ast}}}, {\omega_{o}^{\ast}}]$ and $[{\mathrm{v}_{{o}_{\ast}}}, {\mathrm{v}_{o}^{\ast}}]$ listed below.

The pair $(\mathbb{K}_{c}, d_{H_s})$ obviously fulfills the criteria for complete metric space.

Definition 2.1. ^[37] Let $\mathrm{K}_{\overline{{\mathfrak{f}}}}$ be designated as the space of all fuzzy subsets of $\Re$. Then, the mapping $\overline{{\mathfrak{f}}}:\Re\rightarrow [0, 1]$ is termed as a fuzzy interval or number if it fulfills the subsequent features.

(i) $\overline{{\mathfrak{f}}}$ should be normal, which means that there must be the existence of some $\varkappa\in \Re$ such that $\overline{{\mathfrak{f}}}(\varkappa) = 1.$

(ii) $\overline{{\mathfrak{f}}}$ should possess the upper semi-continuity on $\Re$, which means that for any given $\varkappa\in\Re$ and $\epsilon > 0$, $\exists$ $\delta > 0$ such that $\overline{{\mathfrak{f}}}(\varkappa)-\overline{{\mathfrak{f}}}({\mathrm{y}}) < \epsilon$, $\forall {\mathrm{y}}\in\Re$, with $|\varkappa-{\mathrm{y}}| < \delta.$

(iii) $\overline{{\mathfrak{f}}}$ should possess fuzzy convexity such that $\overline{{\mathfrak{f}}}((1 - {{{\lambda_{o}}}}){\varkappa_{1}} + {{{\lambda_{o}}}} {\varkappa_{2}}) \geq min(\overline{{\mathfrak{f}}}(\varkappa_{1}), \overline{{\mathfrak{f}}}(\varkappa_{2})), \; \forall \varkappa_{1}, \varkappa_{2} \in \Re$, and ${{{\lambda_{o}}}} \in [0, 1]$.

(iv) $cl\{\varkappa \in \Re / \mathfrak{f}(\varkappa) > 0\}$ is compact which implies that $\overline{{\mathfrak{f}}}$ is compactly supported.

Here, we introduce a notation $\mathbb{F}_{c}(\Re)$, which is designated as the set of all fuzzy intervals of $\Re$.

Definition 2.2. ^[37] For any given $\overline{{\mathfrak{f}}}\in \mathbb{F}_{c}(\Re)$, the level or cut sets are provided by $[\; \overline{{\mathfrak{f}}}\; ]^{{ß}} = \{\varkappa\in\Re:\overline{{\mathfrak{f}}}(\varkappa) > {{ß}}\}, \; \forall{{ß}}\in[0, 1].$ In case ${{ß}} = 0,$ then we attain $[\; \overline{{\mathfrak{f}}}\; ]^{0} = \{\varkappa\in\Re:\overline{{\mathfrak{f}}}(\varkappa) > 0\}.$ These sets are termed as ${{ß}}$-cut or ${{ß}}$-level for $\overline{{\mathfrak{f}}}$.

Definition 2.3. ^[38] Let $\overline{{\mathfrak{f}}}, \overline{{\mathfrak{g}}}\in \mathbb{F}_{c}(\Re)$, and $"\preceq"$ is a relation on $\mathbb{F}_{c}(\Re)$, then $\overline{{\mathfrak{f}}}\preceq \overline{{\mathfrak{g}}}$ $\Leftrightarrow$ $\big[\overline{{\mathfrak{f}}}\big]^{{ß}}\leq_{I} \big[\overline{{\mathfrak{g}}}\big]^{{ß}}$, $\forall{{ß}}\in[0, 1].$

Note that the relation "$\preceq$" is partial ordering.

We will now talk about a few characteristics related to basic arithmetic operations of real fuzzy intervals. For $\overline{{\mathfrak{g}}}, \overline{\mathfrak{f}} \in \mathbb{F}_{c}(\Re)$, $\mathfrak{p}\in \Re$, and ${{ß}}\in[0, 1]$, these operations are provided by

Theorem 2.1. ^[37] If the set $\mathbb{F}_{c}(\Re)$ is associated to supremum metric, then, $\forall \overline{{\mathfrak{g}}}, \overline{\mathfrak{f}} \in \mathbb{F}_{c}(\Re)$,

is a complete metric space. In the above expression $d_{H}$ represents the Hausdorff metric on $\mathbb{F}_{c}(\Re)$.

Theorem 2.2. ^[37] Let us have an interval-valued function (I.V.F), i.e., $\overline{\mathfrak{f}}: [{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}]\rightarrow \mathbb{K}_{c}$, which is provided in the form of $\overline{\mathfrak{f}} = [\mathfrak{f}_{\ast}, \mathfrak{f}^{\ast}]$, then $\overline{\mathfrak{f}}$ is said to possess interval Aumann integrability on $[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}]$ $\Leftrightarrow$ ${\mathfrak{f}_{\ast}}$, and $\mathfrak{f}^{\ast}$ are both possessing Aumann integrability on $[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}]$, i.e.,

Definition 2.4. ^[39] A function $\overline{\mathfrak{f}}:\mathrm{I}\subset\Re\rightarrow \mathbb{F}_{c}(\Re)$ is termed as F-I-V, $\; \forall {{{ß}}}\in[0, 1]$, the ${{{ß}}}$-levels or cuts define the family of I.V.Fs, $\overline{\mathfrak{f}}_{{{ß}}}:\mathrm{I}\subset\Re\rightarrow \mathbb{F}_{c}(\Re)$, which is provided by $\overline{\mathfrak{f}}_{{{{ß}}}}(\varkappa) = [\mathfrak{f}_{\ast}(\varkappa, {{{{ß}}}}), \mathfrak{f}^{\ast}(\varkappa, {{{{ß}}}})], \; \forall \varkappa \in \mathrm{I}$. Here, $\forall {{{ß}}} \in [0, 1]$, the functions $\mathfrak{f}^{\ast}(\cdot, {{{{ß}}}}), \mathfrak{f}_{\ast}(\cdot, {{{{ß}}}}):\mathrm{I}\rightarrow \Re$ are real functions of $\overline{\mathfrak{f}}_{{{{ß}}}}(\varkappa)$, and are known as upper and lower functions of $\overline{\mathfrak{f}}$.

Definition 2.5. ^[39] Let the function $\overline{\mathfrak{f}}:\mathrm{I}\subset\Re\rightarrow \mathbb{F}_{c}(\Re)$ be an F.I.V, then $\overline{\mathfrak{f}}$ is said to possess continuity at $\varkappa\in\mathrm{I}$, if $\; \forall {{{ß}}}\in[0, 1]$, $\overline{\mathfrak{f}}_{{{{ß}}}}(\varkappa)$ is continuous $\Leftrightarrow$ upper and lower functions $\mathfrak{f}^{\ast}(\varkappa, {{{{ß}}}})$ and $\mathfrak{f}_{\ast}(\varkappa, {{{{ß}}}})$, respectively, are both continuous at the same point.

Definition 2.6. ^[39] A function $\overline{\mathfrak{f}}:\mathrm{I}\subset\Re\rightarrow \mathbb{F}_{c}(\Re)$ is assumed to be the F.I.V. The fuzzy integral of $\mathfrak{f}$ on $[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}]$, designated by $(FR)\int_{{\mathfrak{a}_{o}}}^{{\mathfrak{b}_{o}}}\overline{\mathfrak{f}}(\varkappa)d\varkappa$, which is defined level wise as

$\forall {{{ß}}}\in[0, 1]$. Here, ${\mathbf{R}}_{[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}]}$ is considered as the set of the functions that lie at the end of the $F_{I.V.F}$. $\mathfrak{f}$ is fuzzy Riemann $(FR)$-integrable on $[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}]$, if $(FR)\int_{{\mathfrak{a}_{o}}}^{{\mathfrak{b}_{o}}}\mathfrak{f}(\varkappa)d\varkappa\in \mathfrak{f}_{c}(\Re)$.

Definition 2.7. ^[39] A function $\mathfrak{f}:\mathrm{I}\subset\Re\rightarrow \mathbb{F}_{c}(\Re)$ is assumed to be the $F_{I.V.F}$ as well as ${{ß}}$-cuts or levels define the family of I.V.Fs, $\mathfrak{f}_{{{ß}}}:[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}]\subset\Re\rightarrow \mathbb{K}_{c}$ such that $\mathfrak{f}_{{{ß}}}(\varkappa) = [\mathfrak{f}_{\ast}(\varkappa, {{ß}}), \mathfrak{f}^{\ast}(\varkappa, {{ß}})]$, $\forall {{ß}}\in[0, 1]$ and $\varkappa\in[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}]$. Then, $\mathfrak{f}$ is (FR)-integrable on $[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}]$ $\Longleftrightarrow$, both $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$ and $\mathfrak{f}^{\ast}(\varkappa, {{ß}})$ are integrable on $[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}]$, then

$\forall {{{ß}}}\in[0, 1]$.

It is to be noted that if both functions lying at the ends of the interval are Lebesgue-integrable, then $\mathfrak{f}$ is stated as a fuzzy Annum integrable function.

In the subsequent, we mention fuzzy Riemann-Liouville fractional integral operators which were established by Allahviranloo et al. ^[40].

Definition 2.8. Let ${{\lambda_{o}}} > 0$ and $L([{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}], \mathbb{F}_{c}(\Re))$ be the space of all Lebesgue measurable $F_{I.V.Fs}$ on $[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}]$, then the fuzzy right and left Riemann-Liouville fractional integral of $\overline{\mathfrak{f}}\in L([{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}], \mathbb{F}_{c}(\Re))$ of order ${{\lambda_{o}}} > 0$ are given by

and

respectively, where $\Gamma({{\lambda_{o}}}) = \int_{0}^{\mathfrak{\infty}}{{\mathrm{y}}}^{{{{\lambda_{o}}}}-1}e^{-{{\mathrm{y}}}}d{{\mathrm{y}}}$ is termed as the gamma function.

While the fuzzy right and left Riemann-Liouville fractional integrals for the upper and lower functions of the interval can be stated as follows:

where

and

in a similar fashion we can state left Riemann-Liouville fractional integral for the upper and lower end point functions of the interval.

The structure of the paper is organized as follows: After reviewing the essential background information and pertinent details regarding fuzzy theory, fractional theory, superquadraticity and its associated inequalities in Section 1, we briefly discuss the ideas of $F_{I.V.Fs}$ and $I.V.Fs$, as well as fuzzy interval Riemann-Liouville fractional integral operators, in Section 2. We come up with the concept of superquadratic $F_{I.V.Fs}$ in Section 3 and more significantly, we develop new inequalities of H.H's and Jensen's types for superquadratic $F_{I.V.Fs}$ in the same section. Then, using fuzzy interval Riemann-Liouville fractional integral operators, the fractional form of inequalities of H.H's type are obtained for superquadratic $F_{I.V.F}$ in Section 4. Graphical behavior, numerical estimates and examples of the results are also taken into consideration in order to assess if the results are beneficial. Section 5, the last part, looks at a brief conclusion and potential directions for future study based on the work's findings.

3.   Superquadratic $F_{I.V.F}$ and its integral inequalities

This section develops the definition of superquadratic $F_{I.V.F}$ and discusses its features as well as establishes novel inequalities of H.H's and Jensen's types for such a sort of function.

Definition 3.1. A function $\mathfrak{f}: \mathrm{I}\subset \Re \rightarrow \mathbb{F}_{c}(\Re)$ is called superquadratic $F_{I.V.F}$ on $\mathrm{I}$ if the subsequent inequality

holds $\forall {\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}\in I$, ${{\lambda_{o}}}\in [0, 1]$, and $\mathfrak{f}({\mathfrak{a}_{o}})\succeq{\tilde{0}}$.

Remark 3.1. If the inequality in (3.1) reverses, then $\mathfrak{f}$ is called subquadratic $F_{I.V.F}$ on $\mathrm{I}$.

Remark 3.2. If the inequality in (3.1) turns to equality, then $\mathfrak{f}$ is called affine $F_{I.V.F}$ on $\mathrm{I}$.

Remark 3.3. If $\mathfrak{f}$ is superquadratic $F_{I.V.F}$ on $\mathrm{I}$, then for $\mathrm{p}\geq0$, $\mathrm{p}\, \mathfrak{f}$ is superquadratic $F_{I.V.F}$ on $\mathrm{I}$.

Remark 3.4. If $\mathfrak{f}(\varkappa)$ and $\mathfrak{g}(\varkappa)$ are superquadratic $F_{I.V.F}$ on $\mathrm{I}$, then $max(\mathfrak{f}(\varkappa), \mathfrak{g}(\varkappa))$ is superquadratic $F_{I.V.F}$ on $\mathrm{I}$, $\forall \varkappa \in \mathrm{I}$.

Theorem 3.1. Let $\mathfrak{f}:\mathrm{I}\rightarrow \mathbb{F}_{c}(\Re)$ be a $F_{I.V.F}$ on $\mathrm{I}$ with $\mathfrak{f}(\varkappa)\succeq\tilde{0}$, whose ${{ß}}$-cuts or ${{ß}}$-levels define the family of I.V.Fs, such that $\mathfrak{f}_{{{ß}}}:\mathrm{I}\subset\Re\rightarrow \mathbb{K}^{+}_{c}\subset\mathbb{K}_{c}$, which are provided by

then $\mathfrak{f}$ is superquadratic on $\mathrm{I}$ if and only if the functions $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$ and $\mathfrak{f}^{\ast}(\varkappa, {{ß}})$ both are superquadratic, $\forall\varkappa \in \mathrm{I}$, and ${{ß}}\in [0, 1]$.

Proof. Let $\mathfrak{f}$ is a superquadratic $F_{I.V.F}$ on $\mathrm{I}$, then $\forall {{\lambda_{o}}}\in\; [0, 1]$ and $\varkappa, {\mathrm{y}}\in\mathrm{I}$, and we attain

Therefore, according to (3.2), the left term and right term of (3.3) can be expressed in the following fashion:

and

respectively. So it implies that

and it follows from (3.6) that

and

$\forall {{ß}}\in[0, 1]$.

Inequalities (3.7) and (3.8) obviously illustrate that $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$ and $\mathfrak{f}^{\ast}(\varkappa, {{ß}})$ are superquadratic functions.

Conversely: Assume that $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$ and $\mathfrak{f}^{\ast}(\varkappa, {{ß}})$ are superquadratic functions, therefore, they have to satisfy the inequality given by the Definition 1.1. So, we attain

and

$\forall {{ß}} \in[0, 1]$ and $\varkappa, {\mathrm{y}}\in \mathrm{I}$.

From (3.9) and (3.10), we attain

From (3.2) as well as using the basic fuzzy arithmetical properties, we attain that

thus,

$\forall {{\lambda_{o}}}\in[0, 1]$, and $\varkappa, {\mathrm{y}}\in \mathrm{I}$.

Hence, $\mathfrak{f}$ is superquadratic $F_{I.V.F}$ on $\mathrm{I}$. □

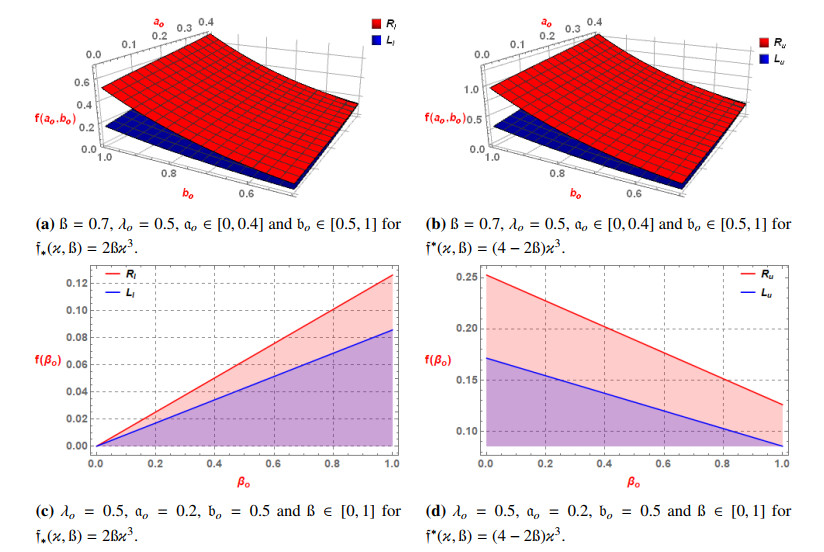
Example 3.1 Consider the $I_{V.F}$, $\mathfrak{f}:[0, 1]\rightarrow \mathbb{F}_{c}(\Re)$, defined as follows:

Then, $\forall {{ß}}\in[0, 1],$ and we have

Since each function in (3.14), which are designated by $\mathfrak{f}_{\ast}(\varkappa, {{ß}}) = 2{{ß}} \varkappa^3$ and $\mathfrak{f}^{\ast}(\varkappa, {{ß}}) = (4-2{{ß}})\varkappa^3$ are superquadratic functions by utilizing Lemma 1.2. From Theorem 3.1, $\mathfrak{f}(\varkappa)$ is then superquadratic $F_{I.V.F}$.

Beside this, the subsequent graphs which are based on the values of $L_{\mathfrak{l}}$, $R_{\mathfrak{l}}$, $L_{\mathrm{u}}$, and $R_{\mathrm{u}}$ also confirm that $\mathfrak{f}(\varkappa)$ is superquadratic $F_{I.V.F}$. As we mentioned earlier, $\mathfrak{f}(\varkappa)$ is superquadratic $F_{I.V.F}$ or $\mathfrak{f}(\varkappa)$ satisfies the condition given by Definition 3.1, from Theorem 3.1, the condition of Definition 3.1 holds if the functions $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$ and $\mathfrak{f}^{\ast}(\varkappa, {{ß}})$ are superquadratic and we know that a function is superquadratic if it satisfies the condition or inequality (3.1) given by Definition 1.1. Therefore, the notations $L_{\mathfrak{l}}$ and $R_{\mathfrak{l}}$ are supposed to be the representations for left and right terms of $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$ via Definition 1.1, respectively. Similarly, $L_{\mathrm{u}}$ and $R_{\mathrm{u}}$ are the representations for left and right terms of $\mathfrak{f}^{\ast}(\varkappa, {{ß}})$ via Definition 1.1, so their values are given as follows:

Figures (1a) and (1c) show that $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$ is superquadratic while the Figures 2 and (1d) show that $\mathfrak{f}^{\ast}(\varkappa, {{ß}})$ is superquadratic. So according to Theorem 3.1, the function $\mathfrak{f}(\varkappa)$ satisfies inequality (3.1) of the Definition 1.1. Hence, $\mathfrak{f}(\varkappa)$ is superquadratic $F_{I.V.F}$.

Similarly consider the following example.

Example 3.2. Consider the $I_{V.F}$, $\mathfrak{f}: [1, 4] \rightarrow \mathbb{F}_{c}(\Re)$, defined as follows:

Then, $\forall {{ß}}\in[0, 1],$ and we have

Since each function in (3.15) is represented by $\mathfrak{f}_{\ast}(\varkappa, {{ß}}) = ({{ß}}+1)e^{2\varkappa}$ and $\mathfrak{f}^{\ast}(\varkappa, {{ß}}) = (4-2{{ß}})e^{2\varkappa}$, to show that $\mathfrak{f}$ is superquadratic $F_{I.V.F}$, it is mandatory that $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$ and $\mathfrak{f}^{\ast}(\varkappa, {{ß}})$ should be superquadratic. So moving in the same fashion as in Example 3.1, we obtain the 2D Graphs (Figure (2c,d)) and 3D Graphs (Figure (2a,b)).

$L_{\mathfrak{l}}$ and $R_{\mathfrak{l}}$ are supposed to be the representations for left and right terms of $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$ via Definition 1.1, respectively. Similarly, $L_{\mathrm{u}}$ and $R_{\mathrm{u}}$ are the representations for left and right terms of $\mathfrak{f}^{\ast}(\varkappa, {{ß}})$ via Definition 1.1, so their values are given as follows:

Hence, $\mathfrak{f}(\varkappa)$ is superquadratic $F_{I.V.F}$.

Remark 3.5. If $\mathfrak{f}^{\ast}(\varkappa, {{ß}}) = \mathfrak{f}_{\ast}(\varkappa, {{ß}})$ with ${{ß}} = 1$, then we attain the classical superquadratic function.

Now we provide the proof of the inequality of Jensen's type for superquadratic $F_{I.V.F}$, which is more refined than the Jensen's inequality for convex $F_{I.V.F}$.

Theorem 3.2. Let $\omega_{i}\in{\mathfrak{R}^+}, {\varkappa_{i}}\in[\mathfrak{a}_{o}, \mathfrak{b}_{o}], i = 1, 2, 3, ..., k, \; k\geq2$, and let $\mathfrak{f}\colon[\mathfrak{a}_{o}, \mathfrak{b}_{o}]\longrightarrow \mathfrak{f}_{c}(\mathfrak{R})$ be a superquadratic $F_{I.V.F}$, whose ${{ß}}$-levels or cuts define the family of I.V.Fs such that, $\mathfrak{f}_{{{ß}}}:[\mathfrak{a}_{o}, \mathfrak{b}_{o}]\rightarrow \mathbb{K}^{+}_{c}\subset\mathbb{K}_{c}$, which are provided by

$\forall \varkappa \in [\mathfrak{a}_{o}, \mathfrak{b}_{o}]$ and ${{ß}} \in [0, 1]$, then

where ${{\mathrm{W}_{\mathrm{k}}}} = \Sigma^{\mathfrak{n}}_{i = 1}\omega_{i}.$

Proof. According to (3.16), the inequality (3.17) can be stated as

Thus, it may be shown that

and

We derive this theorem by employing the mathematical induction principle; therefore, by taking $\mathrm{k} = 2$ in (3.19), we obtain

Similarly, by putting $\mathrm{k} = 2$ in (3.20), we get

According to (3.16), the results (3.21) and (3.22) can be expressed as follows:

It implies that

Thus, the inequality (3.23) reflects the Definition 3.1. Hence, the result (3.17) is true for $\mathrm{k} = 2.$ Next, we assume that (3.17) is valid for $\mathrm{k}-1$; therefore, we have

Let us now demonstrate the validity of (3.17) for $\mathrm{k}$. Thus, we look at the left hand side (L.H.S.) of (3.17), which is alternatively expressed as $\bigg[\mathfrak{f}_{\ast}\bigg(\frac{1}{\mathrm{W}_{\mathrm{k}}}\sum_{{i = 1}}^{{\mathrm{k}}}\omega_{i}\mathfrak{\varkappa}_{i}, {{ß}} \bigg), \mathfrak{f}^{\ast}\bigg(\frac{1}{{\mathrm{W}_{\mathrm{k}}}}\sum_{{i = 1}}^{{\mathrm{k}}}\omega_{i}\mathfrak{\varkappa}_{i}, {{ß}} \bigg)\bigg]$. Here, first we take $\mathfrak{f}_{\ast}\bigg(\frac{1}{{\mathrm{W}_{\mathrm{k}}}}\sum_{{i = 1}}^{{\mathrm{k}}}\omega_{i}\mathfrak{\varkappa}_{i}, {{ß}} \bigg)$ into account, i.e.,

Using (3.24) in (3.25), we get

Similarly, by taking $\mathfrak{f}^{\ast}\bigg(\frac{1}{{\mathrm{W}_{\mathrm{k}}}}\sum_{{i = 1}}^{{\mathrm{k}}}\omega_{i}\mathfrak{\varkappa}_{i}, {{ß}} \bigg)$ into account, we have

Inequalities (3.25) and (3.26) imply that

By Theorem 3.1, the inequality (3.28) is equivalent to the following:

Thus, (3.17) is true for $\mathrm{k}$. Hence, this concludes the proof. □

Remark 3.6. If $\mathfrak{f}_{\ast}(\varkappa, {{ß}}) = \mathfrak{f}^{\ast}(\varkappa, {{ß}})$, with ${{ß}} = 1$, then the result of Theorem 3.2 shrinks to the classical Jensen inequality for the superquadratic function.

If $\omega_{1} = \omega_{2} = ... = \omega_{k} = 1$, then the Theorem 3.2 will reduce to the subsequent result.

Corollary 3.1. Let ${\varkappa_{i}}\in[\mathfrak{a}_{o}, \mathfrak{b}_{o}], \; i = 1, 2, 3, ..., k, \; k\geq2$, and let $\mathfrak{f}\colon[\mathfrak{a}_{o}, \mathfrak{b}_{o}]\longrightarrow \mathfrak{f}_{c}(\mathfrak{R})$ be a superquadratic $F_{I.V.F}$, whose ${{ß}}$-levels or cuts define the family of I.V.Fs such that $\mathfrak{f}_{{{ß}}}:[\mathfrak{a}_{o}, \mathfrak{b}_{o}]\rightarrow \mathbb{K}^{+}_{c}\subset\mathbb{K}_{c}$, which are provided by

$\forall {{ß}} \in [0, 1]$, then

Remark 3.7. In the case of subquadratic $F_{I.V.F}$, we have

Next we propose inequalities of H.H's type for superquadratic $F_{I.V.F}$, which is more sharp than inequalities of H.H's type for convex $F_{I.V.F}$. Additionally, a number of instances are offered to show how the theory developed in this study is applicable.

Theorem 3.3. Let $\mathfrak{f}\colon[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}]\longrightarrow {F_{c}}(\Re)$ be a superquadratic $F_{I.V.F}$, whose ${{ß}}$-levels or cuts define a family of I.V.Fs such that $\mathfrak{f}_{{{ß}}}:[\mathfrak{a}_{o}, \mathfrak{b}_{o}]\rightarrow \mathbb{K}^{+}_{c}\subset\mathbb{K}_{c},$ which are provided by

$\forall \varkappa \in [\mathfrak{a}_{o}, \mathfrak{b}_{o}]$ and ${{ß}} \in [0, 1]$. If $\mathfrak{f}\in {FR}_{([{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}], {{ß}})}$, then

Proof. Let $\mathfrak{f}\colon[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}]\longrightarrow {F_{c}}(\Re)$ be a superquadratic $F_{I.V.F}$, then from Definition 3.1, we have

Inequality (3.35), according to Theorem 3.1, can be written as

It implies that

and

First taking (3.37) into account and setting ${{\lambda_{o}}} = \frac{1}{2}$ in (3.37), we get

Choosing $\mathfrak{\varkappa}_{1} = {\mathfrak{a}_{o}}{{\lambda_{o}}}+(1-{{\lambda_{o}}}){\mathfrak{b}_{o}}$ and $\mathfrak{\varkappa}_{2} = {\mathfrak{b}_{o}}{{\lambda_{o}}}+(1-{{\lambda_{o}}}){\mathfrak{a}_{o}}$, in (3.39), we obtain

Integrating (3.40) w.r.t ${{\lambda_{o}}}$ on [0, 1], we attain

It implies that

Likewise, if we take inequality (3.38) into account, we obtain

According to (3.33), the inequalities (3.41) and (3.42) can be viewed as follows:

It implies that

Next, we prove the other half of the inequality. Since $\mathfrak{f}$ is a superquadratic $F_{I.V.F}$ on $[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}]$, we have from Definition 3.1 that

The inequality (3.44), according to (3.33), can be written as

It implies that

and

Replacing ${\mathfrak{a}_{o}}{{\lambda_{o}}}+(1-{{\lambda_{o}}}){\mathfrak{b}_{o}}$ by ${\mathfrak{b}_{o}}{{\lambda_{o}}}+(1-{{\lambda_{o}}}){\mathfrak{a}_{o}}$ in inequalities (3.45) and (3.46), we obtain the following inequalities:

and

By the addition of inequalities (3.45), and (3.47), we attain

After integrating (3.49) via ${{\lambda_{o}}}$ on [0, 1], and then changing the variables $\mathfrak{\varkappa} = ({\mathfrak{a}_{o}}{{\lambda_{o}}}+(1-{{\lambda_{o}}}){\mathfrak{b}_{o}}), {\mathfrak{b}_{o}}+{\mathfrak{a}_{o}}-\mathfrak{\varkappa} = ({\mathfrak{b}_{o}}{{\lambda_{o}}}+(1-{{\lambda_{o}}}){\mathfrak{a}_{o}}), 1-{{\lambda_{o}}} = \frac{\mathfrak{\varkappa}-{\mathfrak{a}_{o}}}{{\mathfrak{b}_{o}}-{\mathfrak{a}_{o}}}$ and ${{\lambda_{o}}} = \frac{{\mathfrak{b}_{o}}-\mathfrak{\varkappa}}{{\mathfrak{b}_{o}}-{\mathfrak{a}_{o}}}$, we obtain

Similarly, adding (3.46) and (3.48) and continuing in the same manner, we arrive at

According to Theorem 3.1, the inequalities (3.50) and (3.51) can be viewed as follows:

It implies that

The combination of (3.43) and (3.53) yields the desired outcome. This ends the proof. □

Remark 3.8. If $\mathfrak{f}_{\ast}(\varkappa, {{ß}}) = \mathfrak{f}^{\ast}(\varkappa, {{ß}})$, with ${{ß}} = 1$, then the result of Theorem 3.3 shrinks to the classical H.H inequality for the superquadratic function proved by ^[22].

Remark 3.9. For subquadratic $F_{I.V.F}$, we attain the subsequent result

In the subsequent example, we show how Theorem 3.3 holds graphically and numerically.

Example 3.3. Consider the $F_{I.V.F}$ $\mathfrak{f}:[0, 2]\rightarrow \mathbb{F}_{c}(\Re)$, defined by

Then, $\forall {{ß}}\in[0, 1],$ and we have

Since the functions of (3.55), which are represented by $\mathfrak{f}_{\ast}(\varkappa, {{ß}}) = 2{{ß}} \varkappa^3$ and $\mathfrak{f}^{\ast}(\varkappa, {{ß}}) = (4-2{{ß}})\varkappa^3$ and are superquadratic functions by utilizing Lemma 1.2, then $\forall {{ß}}\in[0, 1]$.

Thus, $\mathfrak{f}(\varkappa)$ is superquadratic $F_{I.V.F}$. So in the subsequent we calculate the values for the right, middle and left terms of H.H's type inequality over $[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}] = [0, 2]$ for the functions $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$ and $\mathfrak{f}^{\ast}(\varkappa, {{ß}})$.

Figure 3 provided below assures the authenticity of H.H's inequality for the function $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$.

Similarly, we have

Figure 4 provided below assures the authenticity of H.H's inequality for the function $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$.

Next, we consider the Table 1, which displays the values of right, middle and left terms of H.H's type for both $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$ and $\mathfrak{f}^{\ast}(\varkappa, {{ß}})$. Right, middle, and left terms of H.H's type for $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$ are designated by ${^{R}\mathfrak{f}_{\ast}}(\varkappa, {{ß}})$, ${^{M}\mathfrak{f}_{\ast}}(\varkappa, {{ß}})$, and ${^{L}\mathfrak{f}_{\ast}}(\varkappa, {{ß}})$, respectively, while right, middle, and left terms of H.H's type for $\mathfrak{f}^{\ast}(\varkappa, {{ß}})$ are designated by ${^{R}\mathfrak{f}^{\ast}}(\varkappa, {{ß}})$, ${^{M}\mathfrak{f}^{\ast}}(\varkappa, {{ß}})$, and ${^{L}\mathfrak{f}^{\ast}}(\varkappa, {{ß}})$, respectively.

From the aforementioned figures and table, it is obvious that

Hence, we have

4.   Fuzzy interval fractional H.H type inequalities for fuzzy interval valued superquadratic functions

In this section, the proof of the fractional version of the inequalities of H.H's type for superquadratic $F_{I.V.F}$ via fuzzy interval Riemann-Liouville fractional integral operators along with graphical and numerical illustration is provided.

Theorem 4.1. Let $\mathfrak{f}\colon[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}]\longrightarrow {F_{c}}(\Re)$ be a superquadratic $F_{I.V.F}$ whose ${{ß}}$-levels, or cuts define a family of I.V.Fs such that, $\mathfrak{f}_{{{ß}}}:[\mathfrak{a}_{o}, \mathfrak{b}_{o}]\rightarrow \mathbb{K}^{+}_{c}\subset\mathbb{K}_{c}$, which are provided by

$\forall \varkappa \in [\mathfrak{a}_{o}, \mathfrak{b}_{o}]$, ${{ß}} \in [0, 1]$ and ${{\gamma}_{o}} > 0$. If $\mathfrak{f}\in {(FR)}_{([{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}], {{ß}})}$, then

Proof. Let $\mathfrak{f}\colon[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}]\longrightarrow {F_{c}}(\Re)$ be a superquadratic $F_{I.V.F}$, then from Definition 3.1, we attain

Inequality (4.3), according to Theorem 3.1, can be written as

It implies that

and

First, taking (4.5) into account and setting ${{\lambda_{o}}} = \frac{1}{2}$ in (4.5), we get

Choosing $\mathfrak{\varkappa}_{1} = {\mathfrak{a}_{o}}{{\lambda_{o}}}+(1-{{\lambda_{o}}}){\mathfrak{b}_{o}}$ and $\mathfrak{\varkappa}_{2} = {\mathfrak{b}_{o}}{{\lambda_{o}}}+(1-{{\lambda_{o}}}){\mathfrak{a}_{o}}$ in (4.7), we obtain

Multiplying (4.8) on both sides by ${{\lambda_{o}}}^{{{\gamma}_{o}}-1}$ and then taking integration w.r.t ${{\lambda_{o}}}$ on (0, 1), we attain

Next, setting $\varkappa = {\mathfrak{a}_{o}}{{\lambda_{o}}}+(1-{{\lambda_{o}}}){\mathfrak{b}_{o}}$ and ${\mathrm{y}} = {\mathfrak{b}_{o}}{{\lambda_{o}}}+(1-{{\lambda_{o}}}){\mathfrak{a}_{o}}$ in (4.9), we get

Similarly, by considering inequality (4.6), we get

According to (4.1), the results (4.10) and (4.11) can be viewed as follows:

It implies that

Next, we provide the proof of the other half of the inequality. Since $\mathfrak{f}$ is a superquadratic $F_{I.V.F}$ on $[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}]$, we have from Definition 3.1, $\forall {{\lambda_{o}}}\in[0, 1]$,

The inequality (4.13), according to (4.1), can be written as

It implies that

and

Replacing ${\mathfrak{a}_{o}}{{\lambda_{o}}}+(1-{{\lambda_{o}}}){\mathfrak{b}_{o}}$ by ${\mathfrak{b}_{o}}{{\lambda_{o}}}+(1-{{\lambda_{o}}}){\mathfrak{a}_{o}}$ in inequalities (4.14) and (4.15), we get the following inequalities:

and

Adding the inequalities (4.14) and (4.16), we obtain

Multiplying (4.18) on both sides by ${{\lambda_{o}}}^{{{\gamma}_{o}}-1}$ and then taking integration w.r.t ${{\lambda_{o}}}$ on [0, 1], we get

Setting $\varkappa = {\mathfrak{a}_{o}}{{\lambda_{o}}}+(1-{{\lambda_{o}}}){\mathfrak{b}_{o}}$ and ${\mathrm{y}} = {\mathfrak{b}_{o}}{{\lambda_{o}}}+(1-{{\lambda_{o}}}){\mathfrak{a}_{o}}$ in (4.19), we get

It implies that

Similarly, adding (4.15) and (4.17) and continuing in the same manner, we arrive at

The findings (4.21) and (4.22) can be interpreted as follows in accordance with Theorem 3.1:

It implies

When we combine (4.12) and (4.24), we obtain the desired outcome.

This brings the proof to its end. □

Remark 4.1. If ${{\gamma}_{o}} = 1$, then the result of Theorem 4.1 reduces to the result of Theorem 3.3.

Remark 4.2. If $\mathfrak{f}_{\ast}(\varkappa, {{ß}}) = \mathfrak{f}^{\ast}(\varkappa, {{ß}})$, with ${{ß}} = 1$, then the result of Theorem 4.1 reduces to the fractional H.H inequality for the superquadratic function proved by ^[23].

Remark 4.3. If $\mathfrak{f}_{\ast}(\varkappa, {{ß}}) = \mathfrak{f}^{\ast}(\varkappa, {{ß}})$, with ${{ß}} = 1$ and ${{\gamma}_{o}} = 1$, then the result of Theorem 4.1 shrinks to the traditional H.H inequality for the superquadratic function proved by ^[22].

Remark 4.4. In the case of subquadratic $F_{I.V.F}$, then we attain the following result:

In the subsequent example, we show how Theorem 4.1 holds graphically and numerically.

Example 4.1. Consider the $F_{I.V.F}$ $\mathfrak{f}:[0, 2]\rightarrow \mathbb{F}_{c}(\Re)$, defined as follows:

Then, $\forall {{ß}}\in[0, 1],$ and we have

Since each functions of (4.26), which are represented by $\mathfrak{f}_{\ast}(\varkappa, {{ß}}) = 2{{ß}} \varkappa^3$ and $\mathfrak{f}^{\ast}(\varkappa, {{ß}}) = (4-2{{ß}})\varkappa^3$ and are superquadratic functions, $\forall {{ß}}\in[0, 1]$.

Thus, $\mathfrak{f}(\varkappa)$ is superquadratic $F_{I.V.F}$. So in the subsequent, we calculate the values for the right, middle, and left terms of Theorem 4.1 over $[{\mathfrak{a}_{o}}, {\mathfrak{b}_{o}}] = [0, 2]$ and ${{\gamma}_{o}} = \frac{1}{2}$, for the function $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$,

Figure 5 provided below assures the authenticity of H.H's inequality for the function $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$.

Similarly, for $\mathfrak{f}^{\ast}(\varkappa, {{ß}})$ and ${{\gamma}_{o}} = \frac{1}{2}$, we have

Figure 6 provided below assures the authenticity of H.H's inequality for the function $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$.

Next, we consider the Table 2, which displays the values of right, middle, and left terms of H.H's type for both $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$ and $\mathfrak{f}^{\ast}(\varkappa, {{ß}})$. Right, middle, and left terms of H.H's type for $\mathfrak{f}_{\ast}(\varkappa, {{ß}})$ are designated by ${^{R}\mathfrak{f}_{\ast}}(\varkappa, {{ß}})$, ${^{M}\mathfrak{f}_{\ast}}(\varkappa, {{ß}})$, and ${^{L}\mathfrak{f}_{\ast}}(\varkappa, {{ß}})$, respectively, while right, middle, and left terms of H.H's type for $\mathfrak{f}^{\ast}(\varkappa, {{ß}})$ are designated by ${^{R}\mathfrak{f}^{\ast}}(\varkappa, {{ß}})$, ${^{M}\mathfrak{f}^{\ast}}(\varkappa, {{ß}})$, and ${^{L}\mathfrak{f}^{\ast}}(\varkappa, {{ß}})$, respectively.

From the aforementioned graphs and table, it is obvious that

Hence, we have

5.   Conclusions

We introduced the notion of superquadratic $F_{I.V.Fs}$, significantly advancing the field of fuzzy mathematics. We developed discrete type Jensen and H.H inequalities for superquadratic $F_{I.V.Fs}$ using fuzzy order relations, providing a refined framework beyond traditional convexity-based approaches. The study extended these inequalities to their fractional versions using fuzzy interval Riemann-Liouville fractional integral operators. The robustness and authenticity of our results were confirmed through reduced results, numerical computations, and graphical illustrations. Our work enhances the theoretical foundation of superquadraticity in fuzzy intervals and has practical applications in optimization, decision-making, and control theory. It adds substantial scientific value by expanding the mathematical toolkit for handling fuzzy data. The study primarily focused on a specific class of superquadratic functions and their inequalities. Future research should explore other classes of superquadraticity, as well as interval-valued and $F_{I.V.F}$. We suggest to investigate further inequalities for superquadratic $F_{I.V.Fs}$ such as Jensen-Mercer, midpoint, trapezoidal and Fejér type as well as their fractional perspective via different fractional calculus models, including conformable, Atangana-Baleanu, k-Riemann-Liouville, Caputo-Hybrid and Prabhakar fractional operators suggesting a wide range of practical applications. The concept presented in this study can be considered as a cornerstone in developing the notions such that h-superquadratic $F_{I.V.F}$, m-superquadratic $F_{I.V.F}$, P-superquadratic $F_{I.V.F}$, and (P, m)-superquadratic $F_{I.V.F}$.

Author contributions

Dawood Khan: Conceptualization, Investigation, Writing–original draft & editing; Saad Ihsan Butt: Formal Analysis, Methodology, Supervision; Asfand Fahad: Software, Writing–review; Yuanheng Wang: Supervision, Funding Acquisition; Bandar Bin Mohsin: Formal Analysis, Supervision, Funding Acquisition. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was supported by Researcher Supporting Project number (RSP2024R158), King Saud University, Riyadh, Saudi Arabia. This work was partially supported by the National Natural Science Foundation of China under Grant 12171435, and the Postdoctoral Fellowship at Zhejiang Normal University, China, Grant No. YS304023966.

Conflict of interest

All authors declare no conflicts of interest in this paper.