Explainable artificial intelligence with fusion-based transfer learning on adverse weather conditions detection using complex data for autonomous vehicles

1.   Introduction

Cancer immunotherapy is a promising strategy to treat cancer and consists of activating and harnessing the immune system to fight cancers ^[1,2]. The therapy consists of several different approaches such as immune checkpoint inhibitors, adoptive cell transfer, monoclonal antibodies, cancer vaccines, and oncolytic virus therapy (OVT) ^[1,2]. The OVT is perhaps the next major breakthrough in cancer treatment following the success in immunotherapy using immune checkpoint inhibitors ^[2,3,4]. Oncolytic viruses (OVs) are defined as genetically engineered or naturally occurring viruses that selectively replicate in and kill cancer cells without harming the normal tissues ^[2,3]. The therapy takes advantage of the oncolytic nature of the viruses to replicate inside the infected cells and spread between tumor cells with the goal to eradicate tumor cells ^[2,3,4].

The inhibition of the IFN pathway, the major anti-viral response of the cells, is frequently dysfunctional in cancer cells ^[2,4,5], which causes the OVs to infect the transformed cells much more easily. However, normal cells recognize the invasion of viruses as foreign pathogens and mount strong anti-viral responses through pattern-recognition receptors by the innate immune cells. Detection of viral components by innate immune cells then activates a cascade of intracellular signaling, leading to the secretion of type I IFNs, pro-inflammatory cytokines and chemokines, and increased expression of co-stimulatory molecules ^[2,4,5]. These result in the activation of adaptive immunity that eventually kills viruses.

In recent years, an array of oncolytic viruses have demonstrated anti-tumor efficacy, including adenoviruses, herpes simplex viruses, measles viruses, vesicular stomatitis virus and Newcastle disease virus ^[2,4]. The most successful example of OVT is given by Talimogene Laherparepvec, known as T-Vec. This is a modified herpes simplex virus that has two viral gene deletions and is armed with the human GM-CSF gene. The inserted human GM-CSF gene in the virus results in local GM-CSF production, which enhances the influx and activation of dendritic cells needed to start a systemic antitumor response ^[6]. T-Vec has been shown in a phase II study to increase the number of tumor-specific CD8$^+$ T cells and to reduce the number of regulatory and suppressor T cells ^[2,3,4]. Indeed, oncolysis is a form of immunogenic cell death that results in the release of immune-stimulatory molecules such as cytokines and tumor associated antigens ^[2,7]. This can then stimulate the recruitment of both the innate and adaptive immune cells and in particular the CD8$^+$ T cells that kill tumor cells ^[2,7]. Due to the breakthrough results obtained from T-Vec, a variety of OVs have been tested in clinical trials over the last few years ^[2,3,4]. Despite these intense studies, however, anti-tumor efficacy is still limited and, as a result, new strategies are needed for further improvement of OVT ^[2,8,9].

The immune system interacts intimately with tumors over the entire process of disease development and progression. This complex cross talk between immunity and cancer cells can both inhibit and enhance tumor growth ^[1,7,10]. In order to rapidly proliferate and acquire effector functions, activated CD8$^+$ T cells rely heavily on aerobic glycolysis as a quick source of energy ^[1,7]. Tumor cells also utilize this metabolic pathway for energy and thus compete with CD8$^+$ T cells for glucose. In fact, reprogramming energy metabolism is one of the hallmarks of cancers outlined in Hanhan and Weinberg ^[11]. Cancer cells can reprogram their glucose metabolism and thus their energy production by limiting their energy metabolism largely to glycolysis ^[7,11]. Markedly increased uptake and utilization of glucose have been documented in many human tumor types ^[7,11]. A glucose-poor tumor-microenvironment therefore results in T cell suppression ^[1,7]. There are numerous other ways that cancer cells can evade immune response. In particular, PD-L1 expression by tumor cells is an important mechanism used by tumors. When PD-1 positive T cells come to tumor sites, their PD-1 will be engaged by PD-L1 expressed by cancer cells to suppress immune function and promote T cell apoptosis ^[1,7].

The combinations of stimulation and suppression of growth between cancer and immune cells may act simultaneously ^[1,7]. The majority of mathematical models, however, assume that tumor cells facilitate immune cell growth and proliferation ^[12], which may not be appropriate from the above elaboration. Recently, Garcia et al. ^[13] proposed mathematical models of tumor-immune system interaction to study the effect of immunosuppression by cancer cells. In particular, tumor cells are able to reduce immune cell growth. Their results suggest that one mechanism to generate biologically plausible bistability is consistent with situations in which the cancer's immunosuppressive effects outweigh its immunoproliferative effects ^[13]. Here, bistability is in the sense of dynamical systems, meaning that the model has two stable equilibria.

The goal of this work is to study the effects of oncolytic viral therapy (OVT) when cancer cells are not only able to evade immune cell detection but can also facilitate immune cell death. In any OVTs, the immune cells play a double-edged sword role against tumor cells. They are able to kill cancer cells but can also eliminate viruses as foreign pathogens from the therapy. Additionally, immune cells may be stimulated to proliferate or be impaired to reduce their growth by tumor cells. We will derive a threshold based on the tumor killing rate for which tumors can be eradicated for all sizes if the tumor killing rate by immune cells is above the threshold. This threshold is shown to depend on whether the immune cells are proliferative or immunosuppressive. Numerical bifurcation analysis with respect to various model parameters is performed to explore therapy outcomes. Bistability exists in a large parameter space when the tumor killing rate by immune cells is below the threshold and the immune cells are suppressive. Reducing the virus killing rate by immune cells, however, always increases the effectiveness of the viral therapy.

In the following section, the mathematical model is introduced and the system with no OVT is analyzed. Section 3 studies asymptotic dynamics of the full model, and global sensitivity analysis is performed in Section 4 by applying plausible parameter values obtained from the literature. Numerical bifurcation analysis is provided in Section 5 and the final section ends with a brief summary and conclusions.

2.   Model development and asymptotic dynamics of the system with no OVT

In this section, we first derive the mathematical model. The analysis of the tumor-immune system without OVT is carried out in Section 2.2.

2.1.   Model description

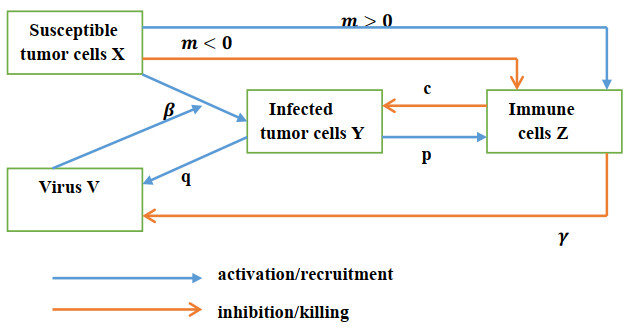
The tumor cells are classified into susceptible $x$ and infected $y$. The compartment of free viral particles is denoted by $v$, and $z$ is the collection of immune cells including both the innate and adaptive immune cells. The susceptible tumor population grows logistically with intrinsic growth rate $r$ and carrying capacity $1/b$ for all tumor cells ^{[14,15,16,17]}. Here, the logistic growth is adopted as several experimental studies have shown evidence of a reduced rate of tumor growth at larger sizes both in vivo and in vitro of various human and mouse solid tumors ^[18,19]. The mass action kinetics has been used by numerous researchers to describe viral infection of susceptible tumor cells. This assumption follows largely from the work of Nowak and May ^[20], which is based on the infectious disease models in reference ^[21] by assuming perfect mixing of populations. However, virus spread is likely to be slower, limited by spatial constraints ^[22]. Since viruses released from one infected cell cannot reach all susceptible tumor cells, the infection rate must be a saturating function of susceptible tumor cells ^[22]. In addition to the Michaelis-Menten form, several authors ^[23,24] use the frequency-dependent transmission $\cfrac{\beta xv}{x+y}$. In this work, the infection process is modeled by a Michaelis-Menten term as in references ^[25,26] with a half saturation constant $g$ and a maximum infection rate $\beta$. How the immune cells detect cancer cells and kill them is a complicated process ^[1]. We assume that the tumor killing by immune cells follows a mass action law ^[13,27] and let $k$ denote the rate for which susceptible tumor cells are killed by immune cells. The corresponding killing rate of infected tumor cells by immune cells is given by $c$. The infected tumor cells have an extra death rate $a$ due to infection ^{[14,15,16,28]}.

Upon lyses, new progeny virions are released from infected tumor cells and the viral burst size per infected tumor cell is denoted by $q$ ^{[14,15,16,28]}. As elaborated in Section 1, immune cells can kill viruses and this killing is modeled by the law of mass action with rate $\gamma$ ^[29]. The natural death rates of viruses and immune cells are constant and are denoted by $\delta$ and $d$, respectively ^[15,16]. As in ^[13,27], it is assumed that there is a constant supply of immune cells at a rate $s$. When OVs infect and destroy cancer cells, specific antigens are released into the tumor micro-environment allowing immune cells to be activated ^[4,5]. We use a Michaelis-Menten mechanism to model this activation from infected tumor cells ^[14,15,30] with $p$ denoting the maximum rate and $h$ the half saturation constant.

There are numerous mechanisms used by tumors to counter effect immune cells ^[1,11]. In particular, tumor cells can actively release soluble molecules to create an environment that is harsh to immune cells ^[1,11]. For example, tumor cells produce VEGF not only to promote blood supply for themselves, but also to suppress the function of antigen-presenting cells ^[1,11]. Cancer cells also release cytokines such as TGF-$\beta$, IL-10, etc., that directly inhibit the activation or function of immune cells ^[1]. They also use PD-L1 to promote T cell death by engaging PD-L1 with PD-1 on activated T cells. Therefore, immune cells can either be stimulated to proliferate or be impaired to reduce their growth by susceptible cancer cells. A combination of stimulation and suppression on growth between cancer and immune cells may act simultaneously and may be modeled by the simple mass action at a rate $m$ as in reference ^[13]. The net growth increases or decreases due to presence of cancer cells can either be positive ($m > 0$), negative ($m < 0$) or null ($m = 0$). Negative $m$ indicating tumor cells exert significant effect on the immune system leading to immunosuppression.

Recall that the compartments of susceptible and infected tumor cells are denoted by $x$ and $y$, respectively. The variable $v$ is the compartment of free viral particles and $z$ is the collection of immune cells. The unit of the cell populations is the number of cells while the unit of viral particles is given by pfu, the plaque-forming unit, and the time unit is a day. Based on the above descriptions, the model takes the following form

All of the parameters $r, \ b, \ \beta, \ k, \ a, \ c, \ q, \ \delta, \ \gamma, s, \ d, \ p, \ h$ are positive except $m$ which can be any real number. The negative $m$ indicating the net effect of tumor on immune cells decreases their growth. Figure 1 presents a schematic diagram of the model (2.1).

Once the model is derived, it can be verified easily that solutions of the model are nonnegative and bounded. We proceed to study dynamics of model (2.1) by first investigating its subsystem.

2.2.   Analysis of the $xz$-subsystem

When $v(0) = 0 = y(0)$ and there is no oncolytic virus treatment, then $v(t) = 0 = y(t)$ for $t > 0$ and system (2.1) is reduced to the following $xz$-subsystem

Model (2.2) has been studied in reference ^[13] by determining the number of positive equilibria and their local stability. In this study, we shall provide global asymptotic dynamics of the model.

We first show that the $xz$-subsystem (2.2) has only equilibrium dynamics by applying the Dulac criterion ^[31] with $B(x, z) = \cfrac{1}{xz}$, $x, z > 0$. To this end, since

system (2.2) has no positive periodic solutions.

Proposition 2.1. System (2.2) has no positive periodic solutions.

We proceed to discuss the existence of positive equilibria. The nontrivial $x$-isocline and the $z$-isocline of (2.2) are given respectively by

where $f$ is strictly decreasing with $f(0) = r/k$ and $f(1/b) = 0$. The shape of the graph of $g$ depends on $m$ with $g(0) = s/d$. If $m > 0$, then $g$ is strictly increasing on $[0, \ d/m)$, $g((d/m)^-) = \infty$ and $g(x) < 0$ on $(d/m, \ \infty)$. It follows that (2.2) has no positive equilibrium if $sk > rd$ and there exists a unique positive equilibrium $(x^+, z^+)$ if $sk < rd$, where $0 < x^+ < \mbox{min}\{1/b, \ d/m\}$ and $s/d < z^+ < r/k$. If $m < 0$, then $g$ is strictly decreasing with $g(\infty) = 0$ and (2.2) has a unique positive equilibrium $(x^-, z^-)$ if $sk < rd$, where $0 < x^- < 1/b$ and $0 < z^- < s/d$. However, if $sk > rd$, there can be either zero, one, or two positive equilibria, which will be discussed below. The case of $m = 0$ is trivial since the graph of $g$ is a horizontal line.

The Jacobian matrix of (2.2) at the equilibrium $(0, s/d)$ has the following form

Therefore, $(0, s/d)$ is asymptotically stable if $sk > rd$ and a saddle point if $sk < rd$. The Jacobian matrix at a positive equilibrium $(x, z)$ is given by

Notice $-d+mx < 0$ by the $z$ equation in (2.2) and the trace, $tr(J(x, z))$, is thus always negative for all $m$. The determinant, $det(J(x, z))$, is positive if $m\geq 0$, and therefore a positive equilibrium is always locally asymptotically stable provided $m\geq 0$. By the Poincar$\acute{\mbox{e}}$-Bendixson Theorem, the dynamics of (2.2) are simple and are summarized in Theorem 2.1(i)(b) without proofs for $m\geq 0$.

Consider the case $m < 0$. We shall derive conditions for which there are two positive equilibria. Observe from (2.3) that any intersection of the isoclines in $\mathbb{R}_+^2$ results in a positive equilibrium. Setting $f(x) = g(x)$ and simplifying, the $x$ component of a positive equilibrium is a positive root of

where $H_1(1/b) = -sk < 0$. The vertex of $H_1$ is at $(\cfrac{bd+m}{2mb}, \Delta_1)$ with

If $sk < rd$, it is clear that (2.2) has a unique positive equilibrium $(x^-, z^-)$ where $x^- < 1/b$ and $z^- = g(x^-) < s/d$. Notice $tr(J(x^-, z^-)) < 0$ and $det(J(x^-, z^-)) = rx^-(-2mb x^-+bd+m) > 0$ since $x^- > \cfrac{bd+m}{2mb}$, which implying $(x^-, z^-)$ is locally stable. Moreover, the equilibrium is globally asymptotically stable in $R_x$ by a similar argument as in Theorem 2.1(i)(b).

Consider the case of $sk > rd$, where the tumor-free equilibrium $(0, s/d)$ is locally asymptotically stable. If $m+bd\geq 0$, it is clear that $H_1(x)$ has no positive roots since $H_1(x) < 0$ for $x\geq 0$ and thus $(0, s/d)$ is globally asymptotically stable by the Poincar$\acute{\mbox{e}}$-Bendixson Theorem. Let $m+bd < 0$. Then (2.2) has no positive equilibrium if $\Delta_1 < 0$ and in this instance $(0, s/d)$ is globally asymptotically stable in $\mathbb{R}_+^2$. If $\Delta_1 > 0$, (2.2) has two positive equilibria $(x_i^-, z_i^-)$, $i = 1, 2$, where $x_1^- < \cfrac{bd+m}{2mb} < x_2^-$ and $z_i^- = \cfrac{r(1-b x_i^-)}{k}$, $i = 1, 2$. From (2.5), we obtain $tr(J(x_i^-, z_i^-)) < 0$ and $det(J(x_i^-, z_i^-)) = rx_i^-(-2mb x_i^-+bd+m)$ for $i = 1, 2$. As a result, $(x_1^-, z_1^-)$ is always a saddle point and $(x_2^-, z_2^-)$ is locally asymptotically stable. Since (2.2) has no positive periodic solutions by Proposition 1, we conclude that the stable manifold of $(x_1^-, z_1^-)$ separates $\mathbb{R}_+^2$ into two positively invariant regions such that $(0, s/d)$ and $(x_2^-, z_2^-)$ are globally asymptotically stable in the corresponding region. When $\Delta_1 = 0$, there is a unique positive equilibrium $(x^-, z^-)$, where $x^- = \cfrac{bd+m}{2mb}$ and $z^- = \cfrac{r(1-b x^-)}{k}$. Therefore, $det(J(x^-, z^-)) = 0$ and $(x^-, z^-)$ is nonhyperbolic. We summarize the discussion as follows by letting

Theorem 2.1. The following statements hold for (2.2).

(i) Let $m\geq 0$.

(a) If $sk > rd$, then $(0, s/d)$ is globally asymptotically stable in $\mathbb{R}_+^2$.

(b) If $sk < rd$, then there is a unique positive equilibrium $(x^+, z^+)$, which is globally asymptotically stable in $R_x$.

(ii) Let $m < 0$.

(a) If $sk < rd$, there is a unique positive equilibrium $(x^-, z^-)$ which is globally asymptotically stable in $R_x$.

(b) If $sk > rd$ and $m+bd\geq 0$, then there is no positive equilibrium and $(0, s/d)$ is globally asymptotically stable in $\mathbb{R}_+^2$.

(c) Let $sk > rd$ and $m+bd < 0$. If $\Delta_1 < 0$, then (2.2) has no positive equilibrium and $(0, s/d)$ is globally asymptotically stable in $\mathbb{R}_+^2$. System (2.2) has a unique positive equilibrium which is nonhyperbolic if $\Delta_1 = 0$.

(d) If $sk > rd$, $m+bd < 0$ and $\Delta_1 > 0$, then (2.2) has two positive equilibria $(x_i^-, z_i^-)$, $i = 1, 2$, $x_1^- < x_2^-$, where $(x_2^-, z_2^-)$ is asymptotically stable and $(x_1^-, z_1^-)$ is a saddle point. The stable manifold of $(x_1^-, z_1^-)$ separates $\mathbb{R}_+^2$ into two positively invariant regions $R_1$ and $R_2$ such that $(0, s/d)$ is globally asymptotically stable in $R_1$ and $(x_2^-, z_2^-)$ is globally asymptotically stable in $R_2$.

When the tumor is not aggressive so that the immune system is not dysfunctional, i.e., $m > 0$, the tumor cells can be eradicated completely if the tumor killing rate is large. If the tumor killing rate is not large, then the tumor cells will be stabilized at a positive level that is smaller than its carrying capacity as illustrated in Theorem 2.1(i).

Notice $\Delta_1 < 0$ is equivalent to $k > \cfrac{r}{s}\Big(d-\cfrac{(bd+m)^2}{4mb}\Big)$. We interpret our results of Theorems 2.1(i) and (ii) in terms of the tumor killing rate $k$. If the suppressive effects of tumor cells on immune cells are not too large so that the tumor can either stimulate the immune activity or its effect on the immune cells is null, $m\geq 0$, then the tumor will be eliminated completely if $k > \cfrac{rd}{s}$, whereas the tumor will be stabilized at a size that is smaller than the carrying capacity if $k < \cfrac{rd}{s}$. See Theorem 2.1(i). In this instance, the final tumor size depends on other parameters. If the suppressive effects of cancer cells exceed the proliferative effort of immune cells, i.e., $m < 0$, then the fate of the tumor also depends on $k$. Specifically, if $k < \cfrac{rd}{s}$, then the tumor will be stabilized at a size depending on other parameters. If $k > \cfrac{rd}{s}$, then several scenarios can occur as illustrated in Theorem 2.1(ii)(b)–(d). In particular, if the suppressive effort of tumor is large but not large enough, $m+bd\geq 0$, the tumor can be eradicated completely for all sizes. If the tumor can exert substantial suppressive effort so that $m+bd < 0$ but the tumor killing rate $k$ is large enough, $k > \cfrac{r}{s}\Big(d-\cfrac{(bd+m)^2}{4mb}\Big)$, the tumor can also be eliminated eventually. However, if the tumor killing rate is not sufficiently large, $\cfrac{rd}{s} < k < \cfrac{r}{s}\Big(d-\cfrac{(bd+m)^2}{4mb}\Big)$, the fate of tumor then depends on its size when first detected as shown in Theorem 2.1(ii)(d). The tumor can be eliminated by the immune cells if its size upon detection is small, whereas the tumor will be stabilized at a positive level if its initial size is large. The stable manifold of the smaller positive equilibrium provides a threshold for tumor elimination and persistence.

Using the parameter values given in Figure 2 of ^[13], where $m = -10^{-6}$, $s = 10$, $d = 2\times 10^{-2}$, $b = 1.02\times 10^{-9}$, and $r = 0.514$, we have $m+bd\approx -10^{-6} < 0$. Consequently, the tumor will eventually stabilize for all sizes if $k < 1.028\times 10^{-3}$ whereas the tumor can be eliminated if $k > 12.5985$. When the tumor killing rate satisfies $1.028\times 10^{-3} < k < 12.5985$, the fate of tumor depends on its size upon detection. The tumor with a small size can be eradicated completely and the tumor will be stabilized if the size is large when detected. We remark that (2.2) has no periodic solutions and therefore the tumor cannot have dormant and relapse phenomena that frequently observed clinically.

3.   Analysis of the full system

In this section, we first derive a sufficient condition for which the OVT fails and study stability of the boundary equilibria. We then separate the discussion into $m\geq 0$ and $m < 0$ for the discussion of asymptotic dynamics.

First, a sufficient condition for which the viral therapy is ineffective is provided. As a consequence, the model (2.1) cannot have any positive equilibrium. Under the oncolytic viral treatment, if the product of infection rate $\beta$ and virus burst size $q$ is small, eventually there will be no virus and infected cancer cells present in the tumor-immune interaction and the therapy fails.

Proposition 3.1. If $\beta q < \delta (bg+1)$, then solutions of (2.1) satisfy $\lim\limits_{t\rightarrow \infty}y(t) = 0 = \lim\limits_{t\rightarrow \infty}v(t)$.

Proof. Since $\limsup\limits_{t\rightarrow \infty}x(t)\leq 1/b$, for any $\epsilon > 0$ there exists $t_0 > 0$ such that $x(t) < 1/b+\epsilon$ for $t\geq t_0$. By the assumption, we can choose $\epsilon > 0$ so that $\beta q < \cfrac{\delta(bg+1+b\epsilon)}{1+b\epsilon}$. Then for $t\geq t_0$, there holds $y^\prime\leq \cfrac{\beta(1/b+\epsilon)v}{g+1/b+\epsilon}-ay$ and $v^\prime\leq qay-\delta v$. Consider the following linear, two-dimensional cooperative system

By the choice of $\epsilon$, solutions of the linear cooperative system satisfy $\lim\limits_{t\rightarrow \infty}x_i(t) = 0$, $i = 1, 2$. Since $0\leq y(t)\leq x_1(t)$ and $0\leq v(t)\leq x_2(t)$ for $t\geq t_0$, the assertion is therefore proven.

The asymptotic autonomous is a method of model reduction. The asymptotic dynamics of the original system can be deduced from its limiting system under some mild conditions, and the original system is said to be asymptotically autonomous to the limiting system ^[32]. In particular, we will use Proposition 3.1 to study the full model (2.1).

System (2.1) always has the tumor-free equilibrium $E_0 = (0, 0, 0, s/d)$ and its stability depends on the following matrix

As a result, $E_0$ is locally asymptotically stable if $sk > rd$ and a saddle point if $sk < rd$. In particular, if the tumor growth rate $r$ is small and the tumor killing rate $k$ by the effector cells is large, then small tumors can be eliminated completely. However, since the basin of attraction of the tumor-free equilibrium is not known, the maximum tumor size that can be eradicated is unknown.

To discuss the existence of a positive equilibrium, we set the right hand side of (2.1) to zero,

From the third equation, we obtain

Substituting the expression into the second equation in (3.1) and dividing the equation by $v > 0$, results in

Substituting these expressions into the first equation of (3.1), we have

Consequently, from the last equation in (3.1), the $z$ component of any interior equilibria is the positive root of

which results in a polynomial of degree 6 in $z$ with a negative leading coefficient and $H(0) = s\Big(h+\cfrac{\beta gr(\beta q-\delta-bg\delta)}{(\beta q-\delta)(rb\delta g+\beta qa-\delta a)}\Big)$. The other components of the equilibria are given by

provided $r(1-bf_1(z))-kz > 0$ and $\beta q a > a\delta+(a\gamma+c\delta)z+c\gamma z^2$. It is not easy to determine the conditions analytically, we will study the existence of positive equilibria numerically.

We next separate the discussion of asymptotic dynamics of (2.1) into the cases of $m\geq 0$ and $m < 0$.

3.1.   The case of $m\geq 0$

When $m\geq 0$, we derive a sufficient condition based on the tumor killing rate for which the tumor can be eradicated eventually for all sizes.

Theorem 3.1. Let $m\geq 0$ and $sk > rd$. Then $E_0 = (0, 0, 0, s/d)$ is globally asymptotically stable in $\mathbb{R}_+^4$.

Proof. As $m\geq 0$, $z^\prime\geq s-dz$ implies $\liminf\limits_{t\rightarrow \infty}z(t)\geq s/d$. Therefore for any $\epsilon > 0$ there exists $t_0 > 0$ such that $z(t) > s/d-\epsilon$ for $t\geq t_0$. We choose $\epsilon > 0$ such that $s/d > r/k+\epsilon$. It follows that

As a result, $\lim\limits_{t\rightarrow \infty}x(t) = 0$, and hence $\lim\limits_{t\rightarrow \infty}y(t) = 0 = \lim\limits_{t\rightarrow \infty}v(t)$ and $\lim\limits_{t\rightarrow \infty}z(t) = s/d$. Therefore, $E_0$ is globally asymptotically stable since it is locally asymptotically stable and globally attracting.

If susceptible tumor cells exerted on the immune cells cannot prevent effector cells from proliferations, i.e., $m > 0$, and if the tumor growth rate $r$ is small or if the tumor killing rate $k$ is large, $k > \cfrac{rd}{s}$, the tumor can be completely eradicated for all sizes. No treatment is needed in this scenario as the immune system is effective and the tumor is not aggressive. A similar interpretation can be made if $m = 0$.

Let $sk < rd$. Then (2.1) has another boundary equilibrium $E_1^+ = (x^+, 0, 0, z^+)$, where $(x^+, z^+)$ is the unique positive equilibrium of (2.2). The Jacobian matrix of (2.1) evaluated at $E_1^+$ has the following form

which is similar to the following triangular block matrix

Let $J_1$ and $J_2$ denote the upper left and lower right $2 \times 2$ submatrices of (3.4), respectively. Notice $-d+m x^+ < 0$ and hence $tr(J_i) < 0$, $i = 1, 2$. Moreover, $J_1$ is the $J(x, {z})$ given in (2.5) and thus $det(J_1) > 0$. Consequently, local stability of $E_1$ depends on $det(J_2)$.

Next, a sufficient condition for which the tumor can be stabilized at the level $x^+$ that is smaller than $1/b$ and $d/m$ is derived. In particular, if either the tumor killing rate $k$ by immune cells is small or the tumor has a large growth rate $r$, then the tumor will be stabilized at a size smaller than the carrying capacity but maybe near to its carrying capacity. Denote

Theorem 3.2. Let $m\geq 0$, $sk < rd$ and $\beta q < \delta(gb+1)$. Then $E_1^+ = (x^+, 0, 0, z^+)$ is globally asymptotically stable in $\Gamma_x$.

Proof. By the assumption, $E_0$ is unstable and $E_1^+$ exists. To show $E_1^+$ is locally asymptotically stable, noticing as $\beta q < \delta(gb+1)$,

i.e., $E_1^+$ is locally asymptotically stable. Since system (2.1) is asymptotically autonomous ^[32] to the $xz$ subsystem (2.2) by Proposition 3.1, $E_1^+$ is therefore globally asymptotically stable in $\Gamma_x$.

If $sk < rd$ and $\beta q > \delta(gb+1)$, then since $H(0) > 0$, $H(z) = 0$ has at least one positive root $z^*$. However, $\beta q < \delta(gb+1)$ is only a sufficient condition for $E_1^+$ to be asymptotically stable. The boundary equilibrium $E_1^+$ may remain stable in the parameter space of $\beta q > \delta(gb+1)$. We now turn to the discussion of the case $m < 0$.

3.2.   The case of $m < 0$

Let $m < 0$. We provide a sufficient condition in terms of the tumor killing rate $k$ for which the tumor can be eradicated for all sizes.

Theorem 3.3. Let $m < 0$ and $k > \cfrac{r(bd-m)}{sb}$. The tumor-free equilibrium $E_0 = (0, 0, 0, s/d)$ is globally asymptotically stable in $\mathbb{R}_+^4$.

Proof. Since $\limsup\limits_{t\rightarrow \infty}x(t)\leq 1/b$, for any given $\epsilon > 0$ we can find $t_0 > 0$ such that $x(t) < 1/b+\epsilon$ for $t\geq t_0$. Using $m < 0$, we have $z^\prime(t)\geq s-dz+mxz\geq s-dz+m(1/b+\epsilon)z$ for $t\geq t_0$. Therefore, $\liminf\limits_{t\rightarrow \infty}z(t)\geq\cfrac{s}{d-m(1/b+\epsilon)}$, and by letting $\epsilon\rightarrow 0^+$, we have

For any $\epsilon > 0$, there exists $t_1 > t_0$ such that $z(t) > \cfrac{sb}{bd-m}-\epsilon$ for $t\geq t_1$. By the given assumption, we can choose $\epsilon > 0$ such that $r-\cfrac{ksb}{bd-m} < -k\epsilon$. It then follows from the first equation of (2.1) that for $t\geq t_1$

As a result, $\lim\limits_{t\rightarrow \infty}x(t) = 0$, $\lim\limits_{t\rightarrow \infty}y(t) = 0 = \lim\limits_{t\rightarrow \infty}v(t)$ and $\lim\limits_{t\rightarrow \infty}z(t) = s/d$. Further, $k > \cfrac{r(bd-m)}{sb} > \cfrac{rd}{s}$ implies that $E_0$ is locally asymptotically stable, and hence $E_0$ is globally asymptotically stable.

We next derive a sufficient condition for which the OVT fails in the sense that both viruses and infected tumor cells will go extinct eventually.

Theorem 3.4. Let $m < 0$. If $\beta q a < (gb+1)(a+\cfrac{csb}{bd-m})(\delta+\cfrac{\gamma sb}{bd-m})$, then solutions of (2.1) satisfy $\lim\limits_{t\rightarrow \infty}y(t) = 0 = \lim\limits_{t\rightarrow \infty}v(t)$.

Proof. Applying a similar analysis as in the proof of Theorem 3.3, (3.6) implies that for any given $\epsilon > 0$ there exists $t_1 > 0$ such that $z(t) > \cfrac{sb}{bd-m}-\epsilon$ and $x(t) < 1/b+\epsilon$ for all $t\geq t_1$. By the given assumption, we can choose $\epsilon > 0$ such that

Therefore, for $t\geq t_1$, there hold $y^\prime\leq \cfrac{\beta(1+b\epsilon)v}{gb+1+b\epsilon}-y\Big(a+c(\cfrac{sb}{bd-m}-\epsilon)\Big)$ and $v^\prime(t)\leq qay-v\Big(\delta+\gamma(\cfrac{sb}{bd-m}-\epsilon)\Big)$. Consider the following linear, cooperative system for $t\geq t_1$

By the choice of $\epsilon$ satisfying (3.7), the equilibrium $(0, 0)$ is globally asymptotically stable for (3.8) and thus solutions of (3.8) satisfying $\lim\limits_{t\rightarrow \infty}x_1(t) = 0 = \lim\limits_{t\rightarrow \infty}x_2(t)$. Since system (3.8) is cooperative with $x_1(t_1) = y(t_1)$ and $x_2(t_1) = v(t_1)$, we have $y(t)\leq x_1(t)$ and $v(t)\leq x_2(t)$ for $t\geq t_1$ and therefore $\lim\limits_{t\rightarrow \infty}y(t) = 0 = \lim\limits_{t\rightarrow \infty}v(t)$.

Clearly, $(gb+1)(a+\cfrac{csb}{bd-m})(\delta+\cfrac{\gamma sb}{bd-m}) > \delta a(gb+1)$. Therefore, with respect to the infection rate $\beta$, the condition derived in Theorem 3.4 provides a larger parameter space than the region given in Proposition 3.1 for which the OVT fails when the immune system is immunosuppressive due to tumor cells.

Suppose now $sk < rd$. Then in addition to the tumor-free equilibrium $E_0$, system (2.1) has another boundary equilibrium $E_1^- = (x^-, 0, 0, z^-)$, where $(x^-, z^-)$ is globally asymptotically stable in $R_x$ for the $xz$ subsystem (2.2) by Theorem 2.1(ii)(a). The following theorem provides a sufficient condition for which $E_1^-$ is globally asymptotically stable.

Theorem 3.5. Let $m < 0$, $sk < rd$ and $\beta q < (gb+1)\Big(1+\cfrac{csb}{a(bd-m)}\Big)\Big(\delta+\cfrac{\gamma sb}{bd-m}\Big)$. Then $E_1^- = (x^-, 0, 0, z^-)$ is globally asymptotically stable in $\Gamma_x$.

Proof. The assumptions indicating $E_0 = (0, 0, 0, s/d)$ is a saddle point and $E_1^- = (x^-, 0, 0, z^-)$ exists, where $(x^-, z^-)$ is globally asymptotically stable in $R_x$ for the $xz$ subsystem (2.2) by Theorem 2.1(ii). Using (3.4) with $E_1^+$ being replaced by $E_1^-$, the stability of $E_1^-$ then depends on the sign of $det(J_2) = (\delta+\gamma z^-)(a+cz^-)-\cfrac{\beta aq x^-}{g+x^-}$. By the proof of Theorem 3.3, it is known that $z^-\geq\cfrac{sb}{db-m}$. As a result,

and $E_1^-$ is locally asymptotically stable. Moreover, the last assumption and Theorem 3.4 imply that the full model (2.1) is asymptotically autonomous to the $xz$ subsystem (2.2). Consequently, $E_1^-$ is globally asymptotically stable in $\Gamma_x$.

Suppose now $sk > rd$. System (2.2) has two positive equilibria $(x_i^-, z_i^-)$, $i = 1, 2$, $x_1^- < x_2^-$, under the conditions given in Theorem 2.1. In particular, $(x_1^-, z_1^-)$ is always a saddle point and $(x_2^-, z_2^-)$ is asymptotically stable. Denote $E_{1i} = (x_i^-, 0, 0, z_i^-)$, $i = 1, 2$, whenever they exist. Then $E_{11}$ is always a saddle point and $E_{12}$ is asymptotically stable if $\beta q < (gb+1)\Big(1+\cfrac{csb}{a(db-m)}\Big)\Big(\delta+\cfrac{\gamma sb}{db-m}\Big)$ by a similar argument as in the proof of Theorem 3.5 with $E_1^-$ being replaced by $E_{12}$. Under this later inequality and applying Theorem 3.4, system (2.1) is asymptotically autonomous to the $xz$-subsystem (2.2). Recall that $\Delta_1 < 0$ is equivalent to $k > \cfrac{r}{s}\Big(d-\cfrac{(bd+m)^2}{4mb}\Big)$ and we have the following asymptotic dynamics.

Theorem 3.6. Let $m < 0$, $\cfrac{rd}{s} < k < \cfrac{r(bd-m)}{sb}$, and $\beta q < (gb+1)\Big(1+\cfrac{csb}{a(bd-m)}\Big)\Big(\delta+\cfrac{\gamma sb}{bd-m}\Big)$. The following statements hold

(a) If $m+bd\geq 0$, then $E_0 = (0, 0, 0, s/d)$ is globally asymptotically stable in $\mathbb{R}_+^4$.

(b) If $m+bd < 0$ and $k > \cfrac{r}{s}\Big(d-\cfrac{(bd+m)^2}{4mb}\Big)$, then $E_0 = (0, 0, 0, s/d)$ is globally asymptotically stable in $\mathbb{R}_+^4$.

(c) If $m+bd < 0$ and $k < \cfrac{r}{s}\Big(d-\cfrac{(bd+m)^2}{4mb}\Big)$, then except on a set of initial conditions of Lebesgue measure zero, solutions of (2.1) converge to either $E_0 = (0, 0, 0, s/d)$ or $E_{12} = (x_2^-, 0, 0, z_2^-)$.

It can be shown directly that $\cfrac{r(bd-m)}{sb} > \cfrac{r}{s}\Big(d-\cfrac{(bd+m)^2}{4mb}\Big)$ when $m+bd < 0$ so that Theorem 3.3 gives a smaller region in $k$ than Theorem 3.6 for which the tumor can be eradicated. However, the condition $bd+m < 0$ is not required in Theorem 3.3.

We now summarize our analytical results of model (2.1). To simplify the notation, we label one of the inequalities in Theorems 3.5 and 3.6 as

and the results of Section 3 are summarized in the following table. Here, GAS means global asymptotic stability and for the last case, denoted by *, solutions converge to either $E_0$ or $E_{12}$ except those on the stable manifold of $E_{11}$. From Table 1, we see that the dynamics of model (2.1) is not clear if the inequality (3.10) is reversed when $m < 0$ or if $\beta q > \delta(gb+1)$ and $sk < rd$ hold when $m\geq 0$.

4.   Sensitivity analysis

Sensitivity analysis is a method for identifying critical inputs of a model. In the mathematical model (2.1), input factors are parameters and initial conditions. In this section, we use sensitivity analysis to identify parameters that contribute the most to output uncertainty. This analysis also helps with selecting parameters for the bifurcation analysis which is to be performed in the next section.

Local sensitivity analysis is used when input factors are known with little uncertainty. Such analysis focuses on the sensitivity in vicinity of nominal values of factors and can be evaluated by the partial derivative of the output with respect to the input factors ^[33]. In contrast, global sensitivity analysis (GSA) is the study of the uncertainty in outputs apportioned to the uncertainty in input factors over their entire ranges of interest ^[34]. A parameter value in a mathematical model often varies over a wide range (e.g., parameter ranges shown in Table 2) and thus GSA is more appropriate than local sensitivity analysis ^[33].

In this paper, Latin hypercube sampling (LHS) and partial rank correlation coefficient (PRCC) ^[33] are used to perform GSA and determine critical parameters. Before GSA is explored, a plausible range of parameter values and their sources are provided in Table 2, where the baseline values given in Table 3 are clearly within the ranges in Table 2. There is a wide range of tumor growth rates in the literature. For example, $r = 0.18$ in reference ^[27], $r = 0.514$ in reference ^[13,35], and $r\in(0.69, 0.97)$ are adopted in reference ^[25]. In the review paper ^[25], tumor growth rates of either $0.23$, $0.43$ or $1.636$ are simulated in the numerical examples to demonstrate model outcomes. Motivated by the work in reference ^[36], the tumor growth rate is estimated using the doubling time of about 48–60 hours of the BxPC-3 cell line ^[37] by assuming an initial exponential growth phase.

GSA is performed based on the parameter ranges in Table 2 except for a selected range $[-1, 1.5\times 10^{-9}]$ for $m$. This is due to the fact that although $m = -10^{-6}$ is given in reference ^[13]HY__HY, Table 1], the authors also use the values of $-10^{3}$ to $-10^{-3}$ for a modified model in Table 2 and so the range of -1 to $1.5\times 10^{-9}$ is adopted for our GSA. Let $p_k$, $k = 1, 2, \cdots, n$, be the parameters included in GSA with parameter ranges $[a_k, b_k]$ shown in Table 2, and let $N = 1000$ be the sample size. Uniform distributions are used for parameters with $b_k/a_k < 1000$, and loguniform distributions are used for parameters with $b_k/a_k\geq1000$. Each random parameter distribution is divided into $N$ equal probability intervals. A probability is randomly selected from each probability interval, and one parameter value is obtained by the inverse of the cumulative distribution function. The list of $N$ samples is then shuffled. Let $p_{ki}$, $1\leq k\leq N$ and $1\leq i\leq n$, be the parameter samples. For each parameter set $(p_{k1}, p_{k2}, \cdots, p_{kn})$, (2.1) is solved over the time interval $[0, t]$ and $x(t)$ is used as the output. Then the function partialcorr in Matlab is applied, and the output of this function gives the partial rank correlation coefficient. Note that the range for $m$ $[-1, 1.5\times 10^{-9}]$ contains both positive and negative values. The sampling process is modified as follows. The interval $[-1, 1.5\times 10^{-9}]$ is divided and modified into two intervals $[-1, -10^{-11}]$ and $[10^{-11}, 1.5\times 10^{-9}]$. Let $p_1 = -1$, $p_2 = -10^{-11}$, $p_3 = 10^{-11}$, $p_4 = 1.5\times 10^{-9}$, $N_1 = N\times (\log(-p_1)-\log(-p_2))/(\log(-p_1)-\log(-p_2)+\log(p_4)-\log(p_3))$, and $N_2 = N\times (\log(p_4)-\log(p_3))/(\log(-p_1)-\log(-p_2)+\log(p_4)-\log(p_3))$. Note that $N_1$ and $N_2$ are rounded and $N_1+N_2 = N$. Loguniform distributions are used for GSA in both intervals $[-1, -10^{-11}]$ and $[10^{-11}, 1.5\times 10^{-9}]$ with sample sizes $N_1$ and $N_2$, respectively.

The global sensitivity analysis is performed with two different endpoints at $t = 2$ and $t = 20$. Research studies have pointed out that most tumor cells entering the circulation were eliminated during the first 24 hours ^[38,39]. Using $t = 2$ for a short time scale allows to identify the parameters that may have a correlation with the formation of a tumor. We use $t = 20$ for a longer time scale to identify the parameters that may have a correlation with tumor growth and the outcome of OVT.

Figure 2 shows the PRCC for each parameter with initial susceptible tumor population at $x(0) = 10^5$ and $x(0) = 10^8$. Note that a tumor of $x(0) = 10^5$ cells has a size about 1 mm in diameter, while a tumor of $x(0) = 10^8$ cells has a size about 1 cm in diameter. The former is undetectable while the latter is detectable. From Figure 2, parameters $m$, $k$, $r$ and $\beta$ have stronger correlations with the final tumor size than the rest of the parameters. For these four parameters, the magnitude of the correlation coefficients is grater than 0.3 in at least two cases (Figure 2). This criterion is used as a threshold for identifying critical parameters in this paper. The time scale does not influence the results of GSA in this simulation.

In all cases, the parameter $m$, which represents the stimulation, recruitment, or impairment of immune cells, has the strongest correlation with the final tumor size. Also, the tumor elimination rate, $k$, by immune cells has a moderate correlation with the final tumor size when the initial tumor size is small ($x(0) = 10^5$). However, it loses its significance when the initial tumor size becomes $x(0) = 10^8$. Our observations agree with research studies ^[38,39,40] indicating that the immune response were able to detect early-stage developing tumors and effectively eliminate them. Adaptive immune system is activated when the innate immune response is insufficient to destroy the pathogens. The immune system is crucial in the surveillance against tumors ^[41].

The growth rate, $r$, has a weak correlation with the final tumor size for a microscopic tumor (Figure 2(a), (b)) but the correlation increases as the tumor size increases (Figure 2(c), (d)). The growth rate $r$ in the plausible parameter range has a moderate positive correlation with the final tumor size when the immune system fails to detect a tumor at an early stage. The viral infection rate $\beta$ and the virus elimination rate $\gamma$ by immune cells have moderate or weak associations with the final tumor size. Immune cells kill not only tumor cells but also viruses ^[29] resulting in positive and negative effects on the outcome of OVT. All other parameters show no correlation with the final tumor size in this numerical experiment.

Because the plausible range for $m$ is uncertain, additional GSA (Figures are not shown here) is performed using different parameter ranges for $m$, $[-10^{-3}, 1.5\times 10^{-9}]$, $[-10^{-6}, 1.5\times 10^{-9}]$ and $[-10^{-3}, 10^{-3}]$, along with the parameter ranges shown in Table 2 for other parameters. This additional GSA shows that the parameters $m$, $k$, $\beta$ are critical parameters in all cases according to the above threshold. The parameters $\gamma$ and $r$ are weakly correlated with the final tumor size in some cases. Again, All other parameters show no correlation with the final tumor size in the additional GSA.

5.   Numerical bifurcation analysis

Bifurcation analysis is the study of changes in asymptotic model behavior under parameter variation and can provide a complete picture of asymptotic dynamics on a parameter domain. Bifurcation analysis usually begins with the identification of equilibria. However, analytical solutions of positive equilibria are infeasible. A numerical method for locating all of the positive equilibria must be constructed for this purpose.

5.1.   Numerical methods for bifurcation analysis

A positive equilibrium satisfies the following equations:

Solving for $v$ in the third equation, we obtain $v = aqy/(\delta+\gamma z)$. Substitute $aqy/(\delta+\gamma z)$ for $v$ in the second equation. The second equation is equivalent to

Equation (5.2) has at most one positive solution for each fixed $x\geq 0$ since the coefficients of $z^2$ and $z$ are both positive. The second equation implies $\beta xv/(g+x) = ay+cyz$. Replacing $\beta xv/(g+x)$ by $ay+cyz$ in the fist equation, we can write $y$ in terms of $x$ and $z$. Let $K_1 = 1/b$ be the carrying capacity of the tumor. Using $n$ equally spaced intervals for $\log(x)$ with $x\in[0.1, K_1]$ gives $x_i$ for $i = 0, 1, 2, \cdots, n$ with $\log(x_i) = -1+i\cdot(\log(K_1)+1)/n$. Then the fourth equation of (5.1) is used as a test equation. Let

For $x_i$, $0\leq i \leq n$, $z_i$ is solved using (5.2) and $y_i$ is solved using the first equation. Then, $F(x_i)$ is calculated. If $F(x_{i-1})$ and $F(x_i)$ have the opposite sign, the Newton method is used to solve (5.1) with the initial guess $(x_i, y_i, z_i)$. It is known that the Newton method converges quadratically provided that (i) $F(x)$ is twice differentiable on an interval containing the root, (ii) the derivative of $F$ does not vanish at the root, and (iii) the initial guess is sufficiently close to the root. Equation (5.3) involving rational expressions and square root functions which are twice differentiable at the interior points of their domains. Thus the Newton method for solving $F(x) = 0$ is expected to converge if $[x_{i-1}, x_i]$ contains a root at which the derivative of $F$ does not vanish and the interval is sufficiently small so that $x_i$ is sufficiently close to the root in $[x_{i-1}, x_i]$. Given a set of parameter values, this numerical method can be used to locate all the positive equilibria of the system (2.1) and the mathematical analysis given in Section 3 can be used to find all the boundary equilibria.

After solving for all the equilibria, an adaptive grid method developed by Wei ^[42,43] is employed for locating bifurcations of equilibrium points. This numerical method does not use continuation technique and is highly parallelable. It can be directly applied to the computation of three-dimensional bifurcation diagrams. For the details of the method, we refer the reader to Section 2.2 in reference ^[42] or Section 3.1 in reference ^[43].

5.2.   Bifurcation analysis of immune response and viral infection rate

In the previous section, GSA shows that the stimulation, recruitment, or impairment of tumor cells $m$, the viral infection rate $\beta$, the killing rates $k$, and the tumor growth rate $r$ are important parameters that influence the model output. Evidence has shown that antiviral immune response may inhibit the effectiveness of OVT ^[2,8,9]. The killing rate $\gamma$ of viruses by immune cells is also included in the bifurcation analysis. Bifurcation analysis using $\beta$, $k$ and $\gamma$ is studied in this subsection, and bifurcation analysis using $m$ and $r$ is to be studied in the next subsection.

Consider the parameter values given in Table 3 and use $\beta$, $k$ and $\gamma$ as bifurcation parameters. Figure 3(a) shows the regions in which the system (2.1) has different asymptotic properties. The stability property of equilibria is summarized in Table 4. Note that $E^-$ represents a tumor with tumor population $x_2^- > (bd+m)/2mb = 4.89\times 10^8$ (Section 2.2). Considering a carrying capacity of $9.8\times 10^8$ in (2.1), $E^-$ is called a large tumor equilibrium in this case. There are six regions in the parameter domain $[0, 1]\times[10^{-6}, 1]\times[0, 2]$. The equilibrium $E_0$ is locally stable in the regions II, IV, and VI, where $k > \cfrac{rd}{s} = 1.384\times 10^{-4}$. This stability condition can be justified by the mathematical analysis given in Section 3. When $k < 1.384\times 10^{-4}$, the positive equilibrium $E_2$ and the boundary equilibrium $E_1^-$ are stable in the regions III and V, respectively.

Bistability exists when the parameter values lie in regions IV and VI. The OVT is successful for the tumor with a restricted initial size. The tumor-free equilibrium $E_0$ becomes the only stable equilibrium when immune response increases and satisfies $k > 0.01703$. The OVT is able to eliminate a large tumor. Note that $k > 0.01703$ is out of the plausible range of $k$ values shown in Table 2, indicating unlikelihood of occurrence. Nevertheless, the above observation also suggests that early treatment and strengthening the immune system are important for successful treatment. The condition $k > 0.01703$ provides a larger parameter space than the region of $k > 0.067982$ derived in Theorem 3.3 given that $m$ is fixed at $-10^{-6}$. From Theorem 3.5, $E_{1}^-$ is globally asymptotically stable when $m < 0$, $k < rd/s$, and $\beta < \Big((gb+1)(a+\cfrac{csb}{bd-m})(\delta+\cfrac{\gamma s b}{bd-m})\Big)/(qa)$. The region satisfying these stability conditions coincides with the region V. Theorem 3.5 accurately predicts the region where $E_{1}^-$ is globally asymptotically stable. Also from Theorem 3.6(c), solutions of (2.1) converges to either $E_0$ or $E_{12}$ when $m < 0$, $rd/s < k < \cfrac{r}{s}\Big(d-\cfrac{(bd+m)^2}{4mb}\Big)$, $bd+m < 0$ and $\beta < \Big((gb+1)(a+\cfrac{csb}{bd-m})(\delta+\cfrac{\gamma s b}{bd-m})\Big)/(qa)$. The region satisfying these stability conditions almost coincides with the region VI. Theorem 3.6(c) gives a sharp approximation for region VI.

To illustrate the bifurcations between these regions, a two-dimensional bifurcation diagram is constructed and shown in Figure 3(b) where $\beta$ is fixed at 0.6 and $k$ and $\gamma$ are used as bifurcation parameters. It consists of two transcritical bifurcation curves, one saddle-node bifurcation curve and one Hopf bifurcation curve. The saddle-node bifurcation curve shown in Figure 3(b) satisfies $k = 0.01703$. Note that Theorem 2.1(ii) (c) and (d) imply that $(x_1^-, y_1^-)$ and $(x_2^-, y_2^-)$ disappear simultaneously when $\Delta_1 = 0$. This condition can be applied to the full system (2.1) and gives $k = 0.01703$ along with all other parameter values kept the same as in Table 3. The line $k = 1.384\times 10^{-4}$ represents transcritical bifurcations, the curve between $\mbox{III}\cup\mbox{IV}$ and $\mbox{V}\cup\mbox{VI}$ also represents transcritical bifurcations, and Hopf bifurcations occur on the curve between $\mbox{I}\cup\mbox{II}$ and $\mbox{III}\cup\mbox{IV}$. Periodic solutions are expected in the regions below the Hopf bifurcation curve.

A one-parameter bifurcation diagram is the plot of a phase variable against a parameter. It depicts the changes in the properties of equilibria at bifurcation points giving biological implication of the bifurcations. Furthermore, it may be used to approximate the boundary of the basins of attraction when bistability occurs ^[44]. Figure 4 shows two one-parameter bifurcation diagrams. One uses $k$ as a bifurcation parameter with $\beta = 0.6$ and $\gamma = 1$ (Figure 4(a)). The other uses $\gamma$ as a bifurcation parameter with $\beta = 0.6$ and $k = 10^{-5}$ (Figure 4(b)). Note that the boundary equilibrium $E_{12}$ is a continuation of $E_1^-$ in Figure 4(a).

A one-parameter bifurcation diagram is the plot of a phase variable against a parameter. It depicts the changes in the properties of equilibria at bifurcation points giving biological implication of the bifurcations. Furthermore, it may be used to approximate the boundary of the basins of attraction when bistability occurs ^[44]. Figure 4 shows two one-parameter bifurcation diagrams. In Figure 4(a), $k$ is used as a bifurcation parameter with $\beta = 0.6$ and $\gamma = 1$ (Figure 4(a)). In Figure 4(b), $\gamma$ is used as a bifurcation parameter with $\beta = 0.6$ and $k = 10^{-5}$. Note that the boundary equilibrium $E_{12}$ is a continuation of $E_1^-$ in Figure 4(a).

In Figure 4(a), the positive equilibrium with a high tumor population level is stable when $k$ is small. Tumors grow large and the OVT fails if the immune response is weak. As the immune response increases, an unstable boundary equilibrium $E_{11}$ bifurcates from $E_0$ at $k = 1.384\times 10^{-4}$ and the tumor-free equilibrium $E_0$ becomes stable causing bistability which exists in the range $[1.384\times 10^{-4}, 0.01703]$. The OVT may succeed or fail depending on the initial condition. It is desired to determine the maximum tumor size that the OVT can treat successfully. Numerical trials (figures not shown here) using parameter values in this range indicate that the tumor burden represented by the unstable boundary equilibrium $E_{11}$ is a good approximation of the maximum tumor burden that the OVT is able to eliminate. For example, $E_{11}$ represents a tumor of about $1.3\times 10^7$ (5 mm in diameter) cells when $k = 10^{-3}$. Direct integration of (2.1) shows that the OVT is able to eliminate a tumor of $1.4\times 10^7$ cells (Figure 5(a)) while a tumor of $1.5\times 10^7$ grows to near its carrying capacity (Figure 5(b)). The other transcritical bifurcation occurs at $3.71\times 10^{-3}$ where $E_2$ and $E_{12}$ coincide, and then $E_2$ disappears while $E_{12}$ gains its stability. A saddle node bifurcation occurs at $k = 0.01703$ where $E_{11}$ and $E_{12}$ coincide and disappear. The tumor–free equilibrium is globally stable when $k > 0.01703$.

In Figure 4(b), the killing rate $\gamma$ of viruses by the immune cells is used as the bifurcation parameter. Note that $k = 10^{-5}$ is at the lower bound of the plausible range for tumor elimination rate by immune cells representing an immune system with weak immune response against tumor. No stable equilibrium or limit cycle exists for $\gamma < 0.11$. Figure 6(a) depicts population dynamics for $\gamma = 0.07$. The OVT may be successful because of low immune response against viruses. However the tumor-free equilibrium $E_0$ is not stable. A tumor cell is added to the solution at $t = 100$ simulating the formation of a new tumor cell at $t = 100$. The tumor grows large leading to tumor relapse. A stable limit cycle with a large amplitude appears when $\gamma = 0.11$, and populations oscillate wildly with time initially. The amplitude of the stable limit cycle decreases quickly as $\gamma$ increases. Figure 6(b) shows an example of population oscillation when $\gamma = 0.2$. The limit cycle shrinks into a positive equilibrium ($E_2$) when $\gamma = 0.25$, where a Hopf bifurcation occurs. As the immune response against viruses continues to increase, the equilibrium population of the tumor increases meaning that the effect of OVT declines. As $\gamma$ increases further, a transcritical bifurcation occurs at $\gamma = 1.137$, where the positive equilibrium $E_2$ coincides with $E_1^-$ resulting in the disappearance of $E_2$ and the change in stability of $E_1^-$. The equilibrium $E_1^-$ is stable when $\gamma > 1.137$. A high virus elimination rate may cause a poor treatment outcome, and the tumor grows to near its carrying capacity. Strong immune response against viruses may hinder the effectiveness of OVT ^[2]. Figure 3(a), (b) show that the immune response against tumor is an important factor that affects the stability of the tumor-free equilibrium. Immune system is critical for controlling tumor progression.

5.3.   Bifurcation analysis of stimulation for immune system and tumor growth rate

In this section we study the changes in asymptotic population dynamics using $m$ and $r$ as bifurcation parameters (see Figure 7 (a)). All other parameter values are fixed as shown in Table 3 except for $k = 10^{-4}$ and $\gamma = 39$.

In Theorems 3.1 and 3.6(a), we have proven that the tumor-free equilibrium $E_0$ is globally asymptotically stable on the region satisfying: (i) $m\geq 0$ and $r < sk/d$ or (ii) $m < 0$, $m > -bd = -2.04\times 10^{-9}$, $r < sk/d = 0.25$ and $\beta q < (gb+1)\Big(1+\cfrac{csb}{a(bd-m)}\Big)\Big(\delta+\cfrac{\gamma sb}{bd-m}\Big)$. The above region covers almost the entire region II in Figure 7 (a). The treatment is successful and the host remains disease free when the tumor growth rate is small and when the tumor does not or slightly impair the immune cells. Although $r < sk/d = 0.25$ lies outside the plausible range of $r$, the region II in Figure 7 (a) can be extended to cover the plausible range of $r$ if the tumor elimination rate $k$ by immune cells has a slight increase, e.g., a 1.4 fold increase. Increases in immune response are important for the success of treatment and preventing tumor recurrence ^[45].

The boundary equilibria $E_{12}$ and $E_1^-$ are stable in regions I and III, respectively. The treatment is not successful if the tumor growth rate is larger than the threshold $r = sk/d = 0.25$. Bistability occurs in region I where the tumor growth rate is smaller than the threshold $r = 0.25$ and the tumor induces larger impairment to immune cells than the threshold represented by the saddle-node bifurcation curve. The treatment may or may not be successful in region I depending on the initial condition. Recall that the condition $\Delta_1 = 0$ can be applied to the identification of the saddle-node bifurcation curve where $E_{11}$ and $E_{12}$ coincide and disappear. The saddle-node bifurcation curve computed by numerical method (Figure 7 (a)) agrees with the conditions $r < sk/d = 0.25$ and $\Delta_1 = 0$ which is equivalent to $k = \cfrac{r}{s}\Big(d-\cfrac{(bd+m)^2}{4mb}\Big)$. Figure 7 (a) also shows that transcritical bifurcations occur in the parameter domain. One-dimensional bifurcation diagrams are then performed to reveal detailed information about these two bifurcations.

Figure 7 (b) shows the bifurcation diagram using $m$ as the bifurcation parameter with $r = 0.2$. The boundary equilibrium $E_{11}$ exists and is unstable when bistability occurs. Recall that the $x$ value of $E_{11}$ is a good approximation of the largest tumor burden that the OVT is able to eliminate. In Figure 7 (b), $m < 0$ indicates that the tumor can impair the immune cells. As the impairment of immune cells become weaker, the OVT is able to eliminate a larger tumor, and the tumor-free equilibrium $E_0$ becomes globally stable when the impairment of immune cells by the tumor cells is smaller than the threshold where the saddle-node bifurcation occurs. Figure 7 (c) shows the bifurcation diagram using $r$ as the bifurcation parameter with $m = -10^{-7}$. The OVT is able to eliminate a small tumor when the tumor growth rate is small. Note that a tumor of population level less than $5\times 10^6$ cells (3.6 mm in diameter) is undetectable. The OVT is ineffective in this case and the tumor grows to near its carrying capacity. Overcoming the impairment of immune cells by the tumor cells is critical to improving the effectiveness of OVT.

6.   Conclusions

The advantage of oncolytic virus therapy (OVT) may come in part from the way the viruses can be engineering manipulated. Viruses can replicate in cancer cells and the viral genome can be modified to alter its virulence and increase anti-tumor activity ^[1,7]. Although a variety of OVs have been tested in clinical trials over the last several years ^[2,3,4], anti-tumor efficacy is still limited and new strategies are needed for further improvement of OVT ^[2,8,9].

In this study, we proposed a mathematical model to investigate the effectiveness of OVT, where the immune cells may be stimulated to proliferate or be suppressed to reduce their growth by cancer cells. The virus was assumed only to infect a certain proportion of the tumor and a saturation term is used to model the infection rate. The model was then studied both analytically and numerically. We derived a threshold of the tumor killing rate above which the tumor can be eradicated for all sizes. The threshold depends on other model parameters and in particular on whether the immune cells are suppressed by tumor cells or not. If tumor's immunosuppressive effects outweigh its immunoproliferative effects, the threshold tumor killing rate is larger. When the tumor killing rate is smaller than the threshold and the immune system is suppressed by tumor cells, several scenarios can occur and bistability exists in a large parameter space. This bistability implies the importance of early treatment and that strengthening the immune system can lead to therapy success.

Global sensitivity analysis was carried out to determine parameters that are important to tumor growth and effectiveness of OVT. Numerical bifurcation analysis was then performed based on the results of GSA. A three-parameter bifurcation diagram with respect to viral infection rate, tumor killing and viral killing rates by immune cells was presented to illustrate existence of bistability in the tumor-virus-immune interaction. The unstable equilibrium $E_{11}$ can be used to approximate the maximum tumor burden that the OVT is able to eliminate when bistability occurs (e.g., Figure 4(a)). Several two-parameter bifurcation diagrams were constructed. Most bifurcation surfaces and curves were in agreement with the mathematical analysis from Sections 2 and 3. The model exhibits a Hopf bifurcation when the tumor and virus killing rates are small. With a weak immune system, the tumor may relapse if any tumor cell is formed after treatment (Figure 6(a)). Bifurcation analysis and GSA have suggested that the immune system is an important factor in the surveillance against cancer as well as cancer recurrence (Figures 2 and 3) Similar results have been reported in clinical studies ^{[38,39,40,41,45]}. Furthermore, Hale et al. ^[45] suggested priming the immune system through vaccination to prevent cancer recurrence. Bifurcation diagrams for the tumor growth rate and stimulation of immune cells were constructed. The tumor can grow to near its carrying capacity if the tumor growth rate is not small even with a stimulated immune system Figure 7(a).

Various techniques have been developed to increase tumor mediated killing and to reduce virus clearance by immune cells ^[2]. Because anti-viral responses may dampen the effect of OVs by clearing virus prematurely, manipulating the anti-viral immune response by blocking antibody responses to the virus is one way to overcome this problem ^[2]. Chemical modification of viral coat proteins is another strategy used to mask the virus and allow it to reach the tumor tissue ^[2,46]. To facilitate tumor mediated killing, in addition to inserting the human GM-CSF gene to viruses, OVs are engineered to encode a transgene for the tumor protein p53 with the goal of generating more potent OVs that function synergistically with host immunity ^[47]. Other strategies have been developed to include interleukins IL-2 and IL-12 in order to potentiate the adaptive immune response ^[2]. Further, chemokines CCL5 and CCL3 have also been used to engineer OVs to either attract T lymphocytes to the tumor site or to recruit neutrophils into the tumor ^[2].

We conclude from this work that when the immune system is suppressed by tumor cells, in addition to virus infection rate and tumor killing rate, the viral clearance rate by immune cells plays an important role in determining outcomes of the OVT. A smaller virus killing rate in general can increase the effectiveness of the therapy. These findings are consistent with the contemporary medical approaches.

Acknowledgments

We thank the five reviewers for many valuable comments and suggestions that improved the manuscript. H. C. Wei was partially supported by the Ministry of Science and Technology (MOST) of Taiwan under the grant MOST 110-2115-M-035-004.

Conflict of interest

The authors declare there is no conflict of interest.