On fast reconstruction of periodic structures with partial scattering data

1.   Introduction

We consider the inverse scattering problem for two-dimensional periodic structures which are assumed to be unboundedly periodic in the horizontal direction and bounded in the vertical direction. These periodic strutures are motivated by one-dimensional photonic crystals ^[1]. The inverse scattering problem of interest aims to reconstruct the shape of these periodic structures from boundary scattering data. This inverse problem is motivated by applications of nondestructive testing for photonic crystals.

During the past two decades, there has been a considerable amount of research on numerical methods for this inverse problem, see ^{[2,3,4,5,6,7,8,9,10,11]}. A significant portion of these studies involves the factorization method ^[12]. This method, which belongs to the class of sampling or qualitative methods, was introduced by D. Colton and A. Kirsch ^[13,14]. The factorization method aims to construct a necessary and sufficient characterization of the unknown scatterer from multi-static scattering data. It is a fast and non-iterative method that does not require advanced a priori information about the unknown scatterers. However, it is not very robust against noise in the data when imaging periodic structures ^[2]. For periodic scattering structures modeled by a smooth periodic function multiplied by a small surface deformation parameter, the near-field imaging method ^[3,15] can provide reconstruction with super resolution.

Inspired by the direct or orthogonality sampling methods ^{[16,17,18,19]}, a sampling method with novel imaging functions has been recently developed in ^[20,21] for imaging periodic structures from scattering data. Similar to the direct sampling method, this new sampling method is fast, stable, and simple to implement, avoiding the need to solve an ill-posed problem. Numerical studies also show that this method is more accurate than the direct sampling method and more stable than the factorization method for imaging periodic structures. This paper extends the results in ^[20]. Specifically, we modify the imaging function developed in ^[20] to use only half the data required by the original imaging function. Additionally, this imaging function is fast, simple to implement, and very robust against noise in the data. We study the modified imaging function for both isotropic and anisotropic cases of periodic scattering media. Numerical examples are presented to demonstrate the performance of the numerical method and to compare it with the direct sampling method and the factorization method.

The paper is organized as follows. The basics of the scattering from periodic media and the inverse problem of interest are described in Section 2. The modified imaging function and its analysis for the isotropic case are discussed in Section 3. Results for the case of anisotropic media are presented in Section 4. Finally, Section 5 is dedicated to a numerical study of the sampling method and its comparison to the factorization method and the orthogonality sampling method.

2.   Problem setup

We consider a two-dimensional medium that is $2\pi$ periodic in the $x_1$-direction and bounded in the $x_2$-direction. While we choose the period to be $2\pi$ for convenience, the medium can have any arbitrary period. For $\alpha \in \mathbb{R}$, a function $f: \mathbb{R}^2 \to \mathbb{C}$ is $\alpha$-quasiperiodic in $x_1$ if

Let $q: \mathbb{R}^2 \to \mathbb{R}$ be a bounded function that represents the material parameter of the medium relative to that of the background. Assume that $q$ is $2\pi$-periodic in $x_1$, $\text{supp}(q)$ is bounded in $x_2$, and $q = 0$ outside of the medium. We consider an $\alpha$-quasiperiodic incident field, $u_{in}$, to illuminate the medium. The medium scatters the incident field and produces a scattered field, $u_{sc}$, which satisfies the Helmholtz equation,

where $u: = u_{sc}+u_{in}$ is the total field, and $k > 0$ is the wave number. It is well known that $u_{sc}$ is also $\alpha$-quasiperiodic in $x_1$. Thus, the problem can be reduced to one period:

Let $D: = \text{supp}(q) \cap \Omega$ and $h > 0$ such that

To ensure that the direct scattering problem is well-posed, we impose the Rayleigh radiation condition for the scattered field as

where

and $u_j^{\pm}$, $j\in \mathbb{Z}$, are called the Rayleigh coefficients of the scattered field. The condition (2.3) means that $u_{sc}$ is an outgoing wave. Note that we exclude the case where $k = \alpha_j$ for some $j$, which is known as Wood's anomaly. See ^[22] for a detailed discussion on well-posedness of the direct problem under some assumption on $q$ and wave number $k$. For the study of the inverse problem of this paper, we will assume that the direct problem (2.1)–(2.3) is well-posed. Let

and the inverse problem of interest can be stated as follows.

Inverse problem: Using multiple incident fields at a fixed wave number $k$ to illuminate an unknown scattering medium, determine the geometry $D$ of the medium from the measurement of the scattered fields on either $\Gamma_{+h}$ or $\Gamma_{-h}$.

To solve this inverse problem, we introduce a new imaging function, which is inspired by that for the case of full measurement on $\Gamma_{+h} \cup \Gamma_{-h}$ in ^[20].

3.   The imaging function and its properties

For $N \in \mathbb{N}$ and $l = 1, 2, \dots, N$, we denote by $u_{in}(x, l)$ the incident fields used to illuminate the unknown medium. The corresponding scattered fields and total fields are denoted by $u_{sc}(x, l)$ and $u(x, l)$, respectively. It is well-known that the scattered fields satisfy the Lippmann-Schwinger integral equation ^[23]:

where $G(x, y)$ is the $\alpha$-quasiperiodic Green's function, which admits the following series representation ^[1]:

Note that $G(\cdot, y)$ also admits a Rayleigh expansion similar to (2.3), and its Rayleigh coefficients $g_j^{\pm}(y)$ are given by

Now, let us discuss the following lemma, which is the motivation behind the definition of the imaging function.

Lemma 1. Let $\Omega_h: = (-\pi, \pi) \times (-h, h)$ and

Then, for $x\in \Gamma_{+h} \cup \Gamma_{-h}$ and $y\in \Omega_h$,

Moreover, for $y, z\in \Omega_h$,

where $\nu(x)$ denotes the normal vector.

Proof. For $x \in \Gamma_{+h}$ and $y \in \Omega_h$, we have $x_2 > y_2$ and

From these two expressions, we can see that the terms for which $\beta_j$ is complex-valued in $G(x, y)$ coincide with their counterparts in $\overline{G(y, x)}$. Thus,

Next, for fixed $z, y\in \Omega_h$,

Note that

and therefore,

Similarly, for $x \in \Gamma_{-h}$ and $y\in \Omega_h$, we have $x_2 < y_2$, and we can show that

Moreover, by the same reasoning, we can also show that

Therefore,

The reason why (3.4) helps us define the imaging function is as follows. Using the Rayleigh expansion of the Green's function, the left-hand side of (3.4) becomes

Then, as done in ^[20], we can show that

So, if we define the imaging function as

we would have

From this equation, we can expect the imaging function to exhibit behaviors similar to the kernel $F(z, y)$. We will discuss this in detail shortly. In the case of data measured on either $\Gamma_{+h}$ or $\Gamma_{-h}$, we will only have either $u^+_j$ or $u^-_j$, respectively. A natural way to modify the imaging function is to omit the term for which data is not available. For example, when data is measured only on $\Gamma_+$, the term $\overline{g_j^-(z)}u_j^-(l)$ will be dropped.

For $z \in \Omega_h$, we define the (general) imaging function $\mathcal{I}(z)$ as

where $p \in \mathbb{N}$ is used to sharpen the resolution of the imaging function, $t \in \{\text{U, L, B}\}$ (abbreviations for Upper, Lower, and Both), and

The choice of $t$ here allows the imaging function to apply to scattering data measured on either one side (Upper or Lower) or both sides (Both) of the periodic structures. The imaging function defined above satisfies the following property.

Theorem 2. For all $z\in \Omega_h$, the imaging function $\mathcal{I}(z)$ satisfies

where

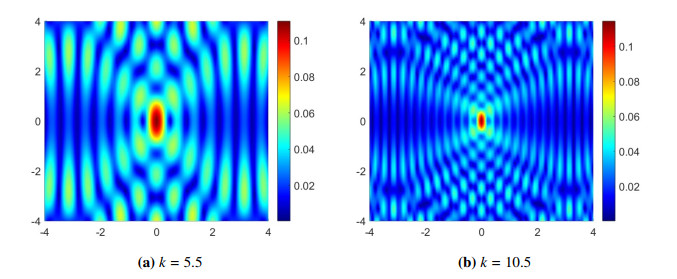
Remark 3. Graphical observations display that the kernel functions (3.8) exhibit a peak when $z \approx y$ and decay rapidly as $z$ and $y$ are apart from each other. Moreover, this peak becomes more distinct with larger values of $k$, as shown in Figure 1.

The behavior of the kernel can be justified in some simple cases. For example, in the context of near-field measurements, where $\Gamma_{\pm h}$ are very close to periodic scatterer $D$, we can reasonably assume that $z_2 \approx y_2$. Furthermore, if we consider $\alpha \approx 0$ in the incident field, the kernel $F_U(z, y)$ simplifies to

When $z_1 = y_1$, the terms $\cos(j(z_1-y_1))$ all reach their maximum value simultaneously. However, for $z_1 \neq y_1$, these terms also have other maxima, but they no longer align at the same point as $j$ varies, since the periods of the cosine functions differ. Therefore, $F_U(z, y)$ will have a larger value when $z \approx y$. As $z$ moves farther from $y$, the cosine terms are more likely to differ in sign at $z$, leading to cancellations in their sum. As a result, $F(z, y)$ becomes significantly smaller. A larger $k$ results in the summation of more maximal values when $z \approx y$ and more cancellations as $z$ and $y$ are apart from each other. Thus, the peak of $F_U(z, y)$ appears more distinct for larger $k$, as illustrated in Figure 1. This justification certainly applies to $F_t(z, y)$ for $t = L$ or $t = B$. Based on the behavior of $F_t(z, y)$, we expect $\mathcal{I}(z)$ to take relatively small values when $z$ is outside $D$ and significantly larger values when $z$ is inside $D$.

It is worth noting that Theorem 2 can be proved using the integral representation (3.4) by following a similar approach as in ^[20]. However, in this paper, we propose an alternative simple proof. This proof does not rely on Green's identities, which allows us to study the imaging function using scattering data measured from only one side of the periodic structure.

Proof. Case $\mathbf{t = U}$. Note that the Rayleigh coefficients of the scattered field satisfy

Substituting the Lippmann-Schwinger equation (3.1) into the integral (3.9) gives

Note that the integrand is bounded and $D$ and $\Gamma_{+h}$ are bounded sets. Therefore, by Fubini's theorem,

Plugging this into the definition of $\mathcal{I}(z)$ gives

By (3.3), for $j$ such that $\beta_j > 0$,

Therefore,

and thus,

Case $\mathbf{t = L}$. By similar reasoning, we can show that

and

and the result then follows.

Case $\mathbf{t = B}$. Adding (3.10) and (3.11) together gives

Therefore,

□

Theorem 2 and Remark 3 partly justify the resolution of the imaging function $\mathcal{I}(z)$. The next theorem shows that $\mathcal{I}(z)$ is stable with respect to noise in the data.

Theorem 4. For $\delta > 0$, let $u_{sc, \delta}(\cdot, l)$ be the noisy scattered fields that satisfy

and let $u_{j, \delta}^\pm(l)$ be the corresponding Rayleigh coefficients. We define $\mathcal{I}_\delta(z)$ as the imaging function as in (3.7) where $u_{j}^\pm(l)$ are replaced by $u_{j, \delta}^\pm(l)$. Then, for all $z \in \Omega$, the following stability property holds:

where $C > 0$ is a constant independent of $z$ and $\delta$.

The proof of this theorem follows a similar approach to that in ^[20] and is therefore omitted here. In summary, we have introduced an imaging function for reconstructing the unknown isotropic scatterer $D$ using scattering data measured either above or below the periodic structures. We also provided partial justification for its resolution and stability. In the next section, we extend the analysis of this imaging function to the case of anisotropic media.

4.   The case of anisotropic media

In the case of scattering from anisotropic media, let $Q: \mathbb{R}^2 \to \mathbb{R}^{2\times 2}$ be the material parameter of the periodic scattering medium. We assume that $Q$ is a matrix-valued bounded function which is $2\pi$-periodic with respect to $x_1$, $Q$ is zero outside of the medium, and $\text{supp}(Q)$ is bounded in $x_2$. We consider the following equation:

where $u_{sc}$ satisfies the radiation condition (2.3). We refer to ^[22] for results on the well-posedness of the direct problem under some assumption on $Q$ and wave number $k$. As in the isotropic case, we assume that the direct problems is well-posed for the study of the inverse problem. Again we denote $D : = \text{supp}(Q) \cap \Omega$ and the inverse problem is to determine $D$ from given data of $u_{sc}$ on $\Gamma_{+h}$ or $\Gamma_{-h}$. From ^[24], we know that the corresponding Lippmann-Schwinger equation is given by

To simplify the presentation, we will analyze the imaging function for the case of measured data on $\Gamma_{+h}$, and the other cases can be derived through a similar process as in the isotropic case. Recall that the imaging function for this case is

for $z \in \Omega_h$. The following theorem is an extension of Theorem 2 to anisotropic media.

Theorem 5. The imaging function satisfies

where

Proof. Plugging (4.1) into (3.9) gives

Swapping the integrals, we obtain,

Since $G(x, y)$ satisfies the radiation condition, so do $\partial_{x_1}G(x, y)$ and $\partial_{x_2}G(x, y)$, and their Rayleigh coefficients are $i\alpha_j g_j^+(y)$ and $i\beta_j g_j^+(y)$, respectively. Thus,

Plugging into (4.2), we obtain

This completes the proof. □

The kernel $\mathbf{F}(z, y)$ has a similar behavior as $F_U(z, y)$ defined in (3.8). This means that, for any vector $v \in \mathbb{R}^2$ and $z, y \in \Omega_h$, $\mathbf{F}(z, y) \cdot v$ has a large value when $z \approx y$ and has a much smaller value when $z$ moves away from $y$. Therefore, we can expect the imaging function to have a large value when the sampling point is inside the medium and a much smaller value when the sampling point moves away from the medium. We will confirm this numerically in the next section.

5.   Numerical study

In this section, we present numerical results on the performance of our imaging function. We only present results for the case of transmission data, in which the incident sources are placed below the scatterer and the receivers are placed above the scatterer. Numerical results for full-aperture data can be found in ^[20]. We also compare our method with the orthogonality sampling method (OSM) and the factorization method (FM). Recall that the imaging function for our method is

and the imaging function of the OSM is given by

For the factorization method, we employ a singular value decomposition and regularize the method by truncating all singular values that are less than $0.1$. The parameters used in the simulation are as follows.

● $h = 1$, $\alpha = 0$.

● Wave number: $k = 10.5$.

● Sampling domain: $(-\pi, \pi)\times (-1, 1)$, partitioned into a grid of $128 \times 64$ sampling points.

● Number of incident sources: $N = 128$, placed on $\Gamma_{-3} = (-\pi, \pi)\times \{-3\}$.

● Number of receivers: $128$, placed on $\Gamma_{+1} = (-\pi, \pi) \times \{1\}$.

● Noise level: $\delta = 20\%$. The noise is added to the scattered fields according the following model:

where $\mathbf{n}: \Gamma_{+h} \to \mathbb{C}$ is the noise function whose values are random numbers such that $\| \mathbf{n} \|_{L^2} = 1$.

● Exponent of the imaging functions: $p = 5$.

We refer to ^[20] for a detailed study of the behavior of the imaging function for different sets of parameters, including different values of $h$, $\alpha$, $k$, and $\delta$, as well as different numbers of incident sources and receivers. The imaging function behaves similarly in the case of limited-aperture data with respect to these parameters.

To generate synthetic data for the inverse problem, we solve the direct problem using a spectral method studied in ^[25]. We compute the scattered fields at the receivers' location, add noise to them, and then compute the corresponding Rayleigh coefficients via (3.9). The incident fields we used are of the form

where $x_l$ is the receivers' location, $l = 1, \dots, N$.

5.1.   Results for isotropic media

First, we show numerical examples of some isotropic media. Recall that in this case, the medium is characterized by the function $q(x)$. In all examples, the function $q(x)$ has the form

We consider four periodic media with four different geometries $D$.

Aligned ellipses (Figure 2). This medium consists of two horizontally aligned ellipses in each period. The radii of each ellipse are $\pi/4$ and $0.4$.

Aligned squares (Figure 3). This medium consists of two horizontally aligned squares in each period. The side of each square is $0.4$.

Aligned crosses (Figure 4). This medium consists of two horizontally aligned crosses in each period. Each cross is made up of one horizontal $0.55 \times 0.18$ rectangle and vertical $0.18 \times 0.45$ rectangle.

Aligned kites (Figure 5). This medium consists of a kite-shaped object in each period.

In all cases, the proposed imaging function outperforms the OSM. The FM simply fails because of a high level of noise and a lack of data. Note again that we aim to solve the inverse problem under a lack of data, which is extremely challenging. Nevertheless, the proposed method is able to provide reasonable results.

5.2.   Results for anisotropic media

In this part, we present results for some anisotropic media. In this case, the medium is characterized by a $2\times 2$ matrix-valued function $Q(x)$. In all examples, $Q(x)$ has the form

where $\text{diag}(0.5, 0.25)$ is a $2\; \times\; 2$ diagonal matrix whose first and second diagonal entries are $0.5$ and $0.25$, respectively. We consider the same geometries as in the isotropic case. Figures 6–9 show the reconstructions of the proposed imaging function versus those of the OSM and FM. The comparison result is similar to the isotropic case, with the proposed method outperforming both the OSM and FM.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research is partially supported by the National Science Foundation Grants DMS-2208293 and DMS-2243854.

Conflict of interest

The authors declare there are no conflicts of interest.