1.
Introduction
Predator-prey interactions have been an interesting and challenging issue that is frequently discussed in marine ecosystems, especially in fish populations. Predator-prey interactions are the most important component of ecology, determining various factors such as community composition, species behavior and dynamics. Mathematical modeling helps to provide insights into the dynamics of the system, which was investigated in the early pioneering work of Lotka[1] and Volterra[2]. In dynamical systems, continuity, equilibrium stability, bifurcation, and control problems are also often studied[3,4,5,6,7]. Traditionally, predators could be distinguished as specialists or generalists based on whether they ate only one or more types of prey. In general, a predator-prey model can be described by the following ordinary differential equation for both specialists and generalist predators[8]:
where P and N denote the prey and predator's population densities at moment t, respectively. F(⋅) and H(⋅) represent the growth of the species in the absence of the other one. G(⋅) is known as the functional response, which characterizes the average individual of prey consumed by a predator; γ represents the conversion rate from prey consumption to predator, υ(⋅) is a monotonically increasing function. For specialist predators, there is H(N)=−d<0; and for generalist predators, it is required that γυ(G(0,N))+H(N)>0. In literature, different type of functional responses were adopted to model different species, which can be prey dependent[9,10] or prey and predator dependent[11,12,13,14,15].
The classical view of population dynamics claims that the higher the population density, the lower the overall growth rate due to the competition for resources. The lower the density, the higher the overall growth rate. However, when the population density is low, Allee[16] introduced the opposite view that the lower the population density, the lower the overall growth rate, that is, the Allee effect. The Allee effect is a common phenomenon in marine populations[17,18,19]. When the population density is low, it may affect population development due to pairing restrictions, dispersal, habitat changes, cooperative foraging, cooperative defense, and predator saturation. Therefore, the study of the Allee effect on ecosystems has attracted the attention of many scholars. In general, the Allee effect can be represented by a multiplier of the form P-L[20,21,22], where L is the threshold for the Allee effect. When L<0, it is a weak Allee effect, and the Allee effect is always positive no matter how much the prey growth rate decreases. When L>0, it is a strong Allee effect. The strong Allee effect indicates that in order for the population to grow, the population size or density must be higher than L; otherwise, the population will die out. Scholars have analyzed the dynamics of the system with the Allee effect of the form P-L, and discussed the existence of the equilibrium of the system and various bifurcation phenomena such as saddle-node bifurcation and B-T bifurcation[23,24,25].
Fish is a kind of important ecological resources. In view of the fish resources development problems, scholars studied population behavior by adding harvest items on the basis of continuous systems. However, fishing activities are not continuous, so continuous dynamic systems cannot accurately describe the actual fishing process. In the process of fish harvesting, the periodic harvesting of fish is a kind of human-controlled behavior that can be described by an impulse differential equation, and it has been found that the impulse differential equation is more accurate in describing and portraying the dynamical behavior of the population[26]. The theory of semi-continuous dynamic systems has been widely used in modeling research on pest management modeling[27,28,29,30,31]. Based on the analysis of the literature, due to the fact that impulsive differential systems (semi-continuous dynamical systems) have the characteristics of both continuous and discrete dynamical systems, there are some studies applying the theory to the development of fish populations in deterministic environments[32,33,34,35,36] and uncertain environment[37,38,39]. In addition, most of the studies considered fish harvesting or fish protection only (unilateral control); in this study, a bilateral state control[40,41,42] is considered, and a predator-prey model for conservation and harvesting of two fish species is developed by constructing a semi-continuous dynamical system. When designing the state feedback control strategy, the number of objective fish was used as the state variable for feedback control. On the one hand, when the number of prey fish is small, the Allee effect will lead to their extinction, which will lead to the lack of enough food for prey fish and destroy the balance of the ecosystem. Therefore, it is necessary to release a certain amount of prey fish when the number of prey fish decreases to a certain threshold. When the number of prey fish is high, it is necessary to catch prey fish from the economic point of view. Since the fishing behavior will also lead to the harvesting of some predator fish, in order to maintain the ecological balance and avoid the extinction of predator fish caused by the fishing behavior, it is necessary to release a certain amount of predator fish larvae at the same time. Based on the above two aspects, we propose a bilateral control strategy to maintain the population size of the two species in a suitable range.
This paper considers a predator-prey model in which the predator is a generalist and the growth of the prey is affected by the Allee effect. The structure is as follows: In Section Ⅱ, we describe the fishery model, non-negativity, persistent survivability and discuss the existence and stability of equilibria of the model. In Section Ⅲ, the bifurcation dynamics of the model are discussed using bifurcation theory. In Section Ⅳ, based on this model, we analyze the model of marine fish harvesting and conservation with bilateral controls. The existence and stability of the order-1 and order-2 periodic solutions of the system are analyzed by using the geometry theory of differential equations. In the fifth section, we performed numerical simulations using MATLAB to verify the correctness of the results.
2.
Mathematical model and basic knowledge
2.1. Fishery model with Allee effect
In this paper, we present a predator-prey model in which predators are generalists, prey growth rates are logical and subject to strong Allee effects, and the functional response is a Holling-Ⅰ type, while the conversion from prey consumption to predator species is saturated,
where p(T), N(T) denote the prey and predator's densities at the moment of T; K denotes the prey's environmental holding capacity; L is the threshold of the prey's Allee effect; r and s represent the intrinsic growth rates of prey and predator, respectively; A is the capture rate of prey by the predator; e is the efficiency with which prey is converted to predator; B is the half-saturation constant; f is the intensity of predator density dependence, and d is the predator mortality rate. Since the predators are generalist, it requires that eA≤Bd, s>d, and all parameters of model (2.1) are positive.
To facilitate the analysis, let x=PK, y=N, t=rKT, α=ArK, β=LK, γ=eAr, δ=BK, s1=srK, d1=drK. Then system (2.1) is simplified to system (2.2):
and from the biological point of consideration, the model (2.2) is limited in the region
On the other hand, as a renewable resource, fish species are closely related to human life. In order to maintain the balance of the ecosystem during the fishing process, we consider a fish stock control strategy with a combination of fishing and investment. First, to avoid the distinction of prey fish caused by the Allee effect, a quantity (η) of juvenile prey fish is released when the prey density declines to the level x=h1. But at a higher level x=h2, a proportion a of prey fish together with a proportion b of predator fish will also be caught for economic purposes, and simultaneously, a quantity τ of juvenile predator fish is released into the system to maintain the level of predator fish. Based on the control measures, the model can be described as follows:
where η, a, b, τ are all positive, and a,b∈(0,1).
2.2. Impulsive semi-continuous system
For a given planar model
Definition 1 (Order-k periodic solution[32,33,36]) The solution ˜z(t)=(˜x(t),˜y(t)) is called periodic if there exists m(⩾1) satisfying ˜zm=˜z0. Furthermore, ˜z is an order-k T-periodic solution with k≜min{j|1≤j≤m,˜zj=˜z0}.
Lemma 1 (Analogue of Poincaré Criterion[32,33,36]). The order-k T-periodic solution z(t)=(ξ(t),η(t))T is orbitally asymptotically stable if |μq|<1, where
with
f+1=f1(ξ(θ+j),η(θ+j)), f+2=f2(ξ(θ+j),η(θ+j)) and f1, f2, ∂I1∂x, ∂I1∂y, ∂I2∂x, ∂I2∂y, ∂ω∂x, ∂ω∂y are calculated at (ξ(θj),η(θj)).
3.
Dynamic properties of Model (2.2)
In this section, the bounded-ness of the solution for Model (2.2) is discussed. Moreover, the existence, type, and local stability of the equilibrium as well as the bifurcation properties are verified.
Define
3.1. Positivity and bounded-ness of the solution
Theorem 1. The solution of Model (2.2) with non-negative initial values will remain non-negative for all time and is bounded on R2+.
Proof. By Eq (2.2), it can be obtained that
for all t≥0, as long as x(0) and y(0) are non-negative, then x(t) and y(t) are also non-negative.
Next, we define a function u(t)=γαx(t)+y(t). Then
which implies that
so long as u0=γαx0+y0 is bounded, u(t) is bounded in Ω. To sum up, any solution of Model (2.2) starting with a non-negative bounded initial condition is non-negative and bounded in Ω. □
3.2. Existence and stability of equilibrium
Obviously, four equilibria always exist
Define
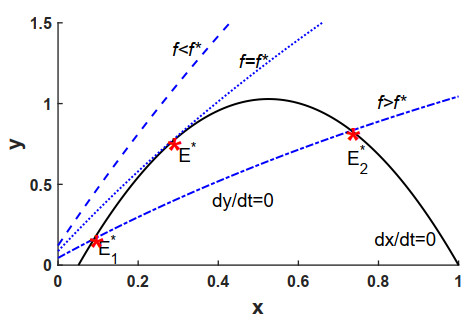
and denote ¯γ1≜d1δ. Due to the assumptions eA≤Bd and s>d, then γ<¯γ1, i.e., y2(x)<s1δ¯γ1−γ. The positional relationship between y1(x) and y2(x) for different cases is shown in Figure 1.
Let y1(x)=y2(x). Then it has
where
Define
Theorem 2. For any of the following cases: C1) α<¯α, δ<¯δ2, γ<¯γ1; C2) α<¯α, ¯δ2<δ<¯δ3, ¯γ2<γ<¯γ1; C3) α>¯α, δ<¯δ2, 0<γ<−¯γ2, if ρ<0 holds, there exists two interior equilibria in Model (2.2); if ρ=0, there exists a unique interior equilibrium in Model (2.2); if ρ>0, there doesn't exists interior equilibrium in Model (2.2).
Proof. Clearly, the existence of an interior equilibrium is equivalent to that of a positive root of Eq (3.3) in the interval (0, 1). Since
and
then for any of the cases C1)–C3), there is a3<0. Moreover, g′(0)<0, g′(xd)=0, g″(xd)>0 and
so that for x∈(0,xd), g′(x)<0, for x∈(xd,0), g′(x)>0. If ρ<0, Eq (3.3) has two distinct positive roots x∗i∈(0,1), i=1,2. Denote y∗i=y1(x∗i), i=1,2. Then two interior equilibria exist in Model (2.2), denoted by E∗1(x∗1,y∗1) and E∗2(x∗2,y∗2). If ρ=0, Eq (3.3) has a unique positive root x∗=xd∈(0,1), then a unique positive equilibrium exists in Model (2.2), denoted by E∗(x∗,y1(x∗); when ρ>0, Eq (3.3) does not have positive root, and thus there does not exist interior equilibrium in Model (2.2). □
3.2.1. Type and stability of equilibrium
For any equilibrium ¯E(¯x,¯y), there is
its characteristic equation is
where
1) Boundary equilibria
At O(0,0), there is
since λ1=−β<0, λ2=s1−d1>0, then O is an unstable higher-order singularity.
At E1(0,1f(s1−d1d1)), there is
since λ1=0, λ2=−αf(s1−d1d1)<0, so that E1 is locally stable.
At E2(β,0), there is
since λ1=β(1−β)>0, λ2=γβ1+δβ+s1−d1>0, then E2 is unstable.
At E3(1,0), there is
since λ1=β−1<0, λ2=γ1+δ+s1−d1>0, then E3 is unstable.
2) Interior equilibrium
At E∗(x∗,y∗), there are g1(x∗,y∗)=0 and g2(x∗,y∗)=0, then
thus,
where x∗y∗∂g1∂y∂g2∂y|x∗,y∗>0, then the sign of DET(J(E∗)) is identical to that of dy1dx|x=x∗−dy2dx|x=x∗. Next, it will discuss the sign of dy1dx|x=x∗−dy2dx|x=x∗ for different cases in Theorem 2.
ⅰ) When ρ<0 holds, two interior equilibria E∗1(x∗1,y∗1) and E∗2(x∗2,y∗2) with 0<x∗1<x∗2<1 exists in Model (2.2), as illustrated in Figure 2(a). It can be easily checked that
Besides, at E∗1, there is dy1dx|x=x∗1>dy2dx|x=x∗1, thus
i.e., E∗1 is unstable. Similarly, at E∗2, there is dy1dx|x=x∗2<dy2dx|x=x∗2, thus
i.e., E∗2 is a locally asymptotically stable node.
ⅱ) When ρ=0 holds, system (2.2) has a unique interior equilibrium E∗(x∗,y∗), as shown in Figure 2(b). Let X=x−x∗,Y=y−y∗, then E∗ is converted to the origin O(0,0), and the model is written as
where,
and P3(X,Y) is a function of (X,Y) with degree of three or higher. The Jacobian matrix at E∗ is
thus
a) If TR(J(E∗))=a11+a22=0, then λ1=λ2=0. Make the transformation
then Model (3.5) is converted into the following standard form:
where
and ˉP3(X,Y) is a function of three or more degrees about (X,Y).
Let τ=ˉa12t. For convenience, t is still used to represent τ, then it has
where
and ˜P3(X,Y) is a function of (X,Y) with three or higher degree. Model (3.6) can be transformed into the following form[43]:
and if ˜B1≠0, then E∗ is a cusp point.
Meanwhile, if ˜B2+2˜A1≠0, E∗ is a cusp of codimension two. If ˜B2+2˜A1=0, E∗ is a cusp with at least codimension three.
b) If TR(J(E∗))=a11+a22≠0, then λ1=0, λ2≠0. Make the transformation
system (3.5) is converted into the following standard form
where
Next, introduce a new variable τ=a′22t (for convenience, is represented by t), then
where, ˆAi=A′ia′22,ˆBi=B′ia′22,i=1,2,3.
If ˆA1≠0 then E∗ is unstable. Meanwhile, E∗ is a saddle node of attraction.
To sum up, the following result hold.
Theorem 3. For Model (2.2), 1) O(0,0) is unstable, E1(0,1f(s1−d1d1)) is locally stable, E2(β,0), E3(1,0) is unstable; 2) For the interior equilibrium, when ρ>0, E∗1(x∗1,y∗1) is a saddle (unstable), and E∗2(x∗2,y∗2) is a stable node; when ρ=0, if TR(J(E∗))=0 and ˜B1≠0, E∗(x∗,y∗) is a cusp of codimension two in case of ˜B2+2˜A1≠0, and a cusp with at least codimension three in case of ˜B2+2˜A1=0; If TR(J(E∗))≠0 and ˆA1≠0, E∗(x∗,y∗) is an attractive saddle node.
4.
Parameter's influence
4.1. Saddle-node bifurcation
Let α=α0 satisfy
Denote
and define
Theorem 4. Let the parameters of Model (2.2) satisfy TR(J(E∗))≠0 and ˆA1≠0. If Φ2≠0, system (2.2) undergoes a saddle node bifurcation near E∗(x∗,y∗) when α=α0.
Proof. At E∗(x∗,y∗), there is
Let V=(V1,V2)T (W=(W1,W2)T) be the eigenvector corresponding to the zero eigenvalue of J(E∗) ((J(E∗))T). Then V=(ω1,−ξ1)T, W=(−ξ2,ξ1)T. Let g=(g1,g2)T. Then
and
Since
and
then according to Sotomayor's theorem[44], Model (2.2) undergoes a saddle-node bifurcation near E∗(x∗,y∗) when α=α0. □
Remark 1. For Model (2.2), it can be concluded that for a lager α, the interior equilibrium does not exist. When α decreases to α=α0, a unique equilibrium exists in the system. As α decreases below α0, the system undergoes a saddle-node bifurcation at the interior equilibrium E∗, giving rise to two interior equilibria E∗1 and E∗2.
4.2. Bogdanov-Takens bifurcation
According to Theorem 3, when ρ=0, TR(J(E∗))=0, ˜B1≠0 and ˜B2+2˜A1≠0, Model (2.2) to undergo a Bogdanov-Takens bifurcation of codimension two near E∗ when (α,β)=(α0,β0). Next, it will show the universal unfolding of the Bodmanov-Takens bifurcation of codimension two under parameter perturbation when α and β are taken as bifurcation parameters.
Define
Let (ϵ1,ϵ2) be a parameter vector in a small neighborhood of (0,0). Then
Theorem 5. Let the parameters of Model (2.2) satisfy ρ=0, TR(J(E∗))=0, ˜B1≠0, ˜B2+2˜A1≠0 and |∂(O1,O2)∂(ϵ1,ϵ2)|≠0. When (α,β) varies in the neighborhood of (α0,β0), Model (2.2) changes in the small neighborhood of E∗(x∗,y∗), and a codimensional 2 Bogdanov-Takens branching occurs.
Proof. Consider the perturbation system
For (α,β)=(α0,β0), there is DET(J(E∗))=0,TR(J(E∗))=0. With the transformation x1=x−x∗, y1=y−y∗, we can obtain
where N3(x1,y1,ϵ1,ϵ2)∈C∞.
Make the following transformation:
then Model (4.1) is converted to
where N′3(x2,y2,ϵ1,ϵ2)∈C∞ with coefficients depending smoothly on ϵ1,ϵ2.
Next, introduce the variable τ, denoted as dt=(1−H6x2)dτ (still denote τ as t), then
Let x3=x2,y3=(1−H6x2)y2, then the above system of equations is transformed into
where ˜N3(x3,y3,ϵ1,ϵ2)∈C∞ with coefficients depending smoothly on ϵ1,ϵ2.
(ⅰ) When J4<0, the following transformations are applied to the variables:
still denote τ as t, there is
where M3(x4,y4,ϵ1,ϵ2)∈C∞ with at least third order.
Let x5=x4−K22, y5=y4, and obtain
where M′3(x5,y5,ϵ1,ϵ2)∈C∞ with at least third order.
If set J5≠0, then L3≠0. Define new variables: x6=−L23x5, y6=L33y5, τ=−tL3, and denote x6 by x, y6 by y, and τ by t, which yields that
where ˜N3(x2,y2,ϵ1,ϵ2)∈C∞ with at least third order, and O1, O2 can be represented by ϵ1 and ϵ2.
(ⅱ) When J4>0, the following transformations are applied
still denote τ by t, it has
where N3(x4,y4,ϵ1,ϵ2)∈C∞ with at least third order, and
Let x5=x4+K′2/2,y5=y4. Then it has
where N′3(x5,y5,ϵ1,ϵ2)∈C∞ with at least third order, and
If set J5≠0, then L′3≠0. Define new variables: x6=L′32x5, y6=L′33y5, τ=t/L′3, and still denote x6 by x, y6 by y, τ by t, which yields that
where O′1=L′1L′34,O′2=L′2L′3, and ϵ1, ϵ2 can be represented by O′1, O′2.
For convenience of discussion, O′1, O′2 is still denoted by O1,O2. When |∂(O1,O2)∂(ϵ1,ϵ2)|≠0, Models (4.2) and (4.3) are the cardinal folds of the Bogdanov-Takens bifurcation[44], when (α,β) varies in the vicinity of (α0,β0), Model (2.2) undergoes a codimension 2 Bogdanov-Takens bifurcation in a small neighborhood of E∗(x∗,y∗). □
5.
Complex dynamics of control-Model (2.3)
It only focuses on the case of ρ<0 in Theorem 3. For Model (2.3), there are
5.1. Order-1 periodic solution
Denote l1=1α(1−x)(x−β) as the prey isocline, l2=(s1−d1)(1+δx)−γxf[d1+(d1δ−γ)x] as the predator's isocline, l3, l4, l5, l6 as the saddle point separatrix of E∗1 in different directions. The intersection point between l1 and N2 is denoted by A3. The intersection point between l4 and N2 is denoted by M. The trajectory from A3 intersects M2 at the point B3. Define ¯τ2≜yM−(1−b)yB3. Denote
Definition 2 (Successor function). For a point S∈N1, if the trajectory from S intersects M1, then denote the intersection point by S−∈M1. Under the impulse effect, the point S− is mapped to S+∈N1. In such a case, we can define fISOR1: N1→R, S→fISOR1(S)≜yS+−yS. If the trajectory from S intersects M2, then denote the intersection point by S−. Under the impulse effect, the point S− is mapped to S+∈N2. If the trajectory from S+ intersects M1, denote the intersection point by S+−∈M1. Under the impulse effect, the point S+− is mapped to S++∈N1. In such cases, we can define fIISOR1: N1→R, S→fIISOR1(S)≜yS++−yS. Similarly, For a point S′∈N2, define fISOR2: N2→R, S′→fISOR2(S′)≜yS′+−yS′.
Theorem 6. For system (2.3) with model parameters satisfying any one of C1)–C3) and ρ>0, if D-1) h1+η<x∗1<(1−a)h2<h2<x∗2, y2(h1)≥y1(h1+η) and τ<¯τ2, an order-1 periodic solution exists in each Ωi, i=1,2; if D-2) h1<(1−a)h2<h1+η<x∗1<h2<x∗2 and y2(h1)≥y1(h1+η), an order-1 periodic solution exists in Ω1; if D-3) h1<x∗1<h1+η<(1−a)h2<h2<x∗2 and τ<¯τ2, an order-1 periodic solution exists in Ω2.
Proof. For case D-1) h1+η<x∗1<(1−a)h2<h2<x∗2 and y2(h1)≥y1(h1+η), denote the intersection point between l2 and N1 by A0. Select a point A1∈N1 above A0; the trajectory from A1 intersects M1 at B1. Under the impulse effect, the point B1 is mapped to A+1∈N1. Since g1(xA1,yA1)<0, g2(xA1,yA1)<0, then we have fISOR1(A1)=yA+1−yA1=yB1−yA1<0. Besides, denote the intersection between l1 and N1 by A2. Since g1(xA2,yA2)=0, g2(xA2,yA2)>0 and g1(xS,yS)<0 for S∈U(A1,ϵ) with xS<h1+η and yS<yA1, then we have fISOR1(A2)=yA+2−yA2=yB2−yA2>0 due to y2(h1)≥y1(h1+η). The continuity of fISOR1 implies that a point S∈¯A1A2 exists so that fISOR1(S)=0, i.e., an order-1 periodic solution exists in Ω1 (Figure 3(a)). Similarly, it can be proved that an order-1 periodic solution exists in Ω1 for case D-2).
Under the impulse effect, B3 is mapped to A3+∈N2, where yA3+=(1−b)yB3+τ. Define ¯τ1≜yA3−(1−b)yB3.
ⅰ) If τ=¯τ1, then fISOR2(A3)=yA3+−yA3=0, i.e., an order-1 periodic solution exists in Ω1 (Figure 3(a)).
ⅱ) If τ<¯τ1, then fISOR2(A3)=yA3+−yA3<0. On the other hand, for A4((1−a)h2,τ), there is fISOR2(A4)=yA4+−yA4>0. The continuity of fISOR2 implies that a point S′∈¯A3A4 exists so that fISOR2(S′)=0, i.e., an order-1 periodic solution exists in Ω2 (Figure 3(b)).
ⅲ) If ¯τ1<τ<¯τ2, then fISOR2(A3)=yA3+−yA3>0. According to the trend of the trajectory and the fact that any two trajectories cannot be intersected, select D∈N2 above and sufficiently close to the A3, then fISOR2(D)=yD+−yD>0. On the other hand, for C=A+3, there is fISOR2(C)=yC+−yC<yA+3−yC=0. The continuity of fISOR2 implies that a point S′∈¯CD exists so that fISOR2(S′)=0, i.e., an order-1 periodic solution exists in Ω2 (Figure 3(c)).
Similarly, system (2.3) has an order-1 periodic solution in Ω2 for case D-3).
To sum up, an order-1 periodic solution exists in Model (2.3) for case D-1). □
Let zi(t)=(ϕi(t),φi(t)) (k−1)Ti≤t≤kTi, k∈N be the order-1 periodic solution in Ωi, i=1,2. For z1(t)=(ϕ1(t),φ1(t)) (k−1)T1≤t≤kT1, denote
For z2(t)=(ϕ2(t),φ2(t)) (k−1)T2≤t≤kT2, denote
Theorem 7. For the model parameters with any one of C1)–C3), ρ>0 and D-1), zi(t)=(ϕi(t),φi(t)) (k−1)Ti≤t≤kTi is orbitally asymptotically stable if μi<1, where
with Λ(t)=exp{∫T20+[ϕ2(t)(β+1−2ϕ2(t))−s1fφ2(t)(1+fφ2(t))2]dt}.
Proof. For system (2.3), there are
and ω1(x,y)=x−h1,I11(x,y)=η,I21(x,y)=0, So it can be concluded that
Denote f1+≜f1(ϕ1(T+1),φ1(T+1)),f2+≜f2(ϕ1(T+1),φ1(T+1)). Then by Lemma 1, there are
and
If μ1<1, the order-1 periodic solution z1(t)=(ϕ1(t),φ1(t)) (k−1)T1≤t≤kT1 is orbitally asymptotically stable.
Similarly, for the order-1 periodic solution z2(t)=(ϕ2(t),φ2(t)) (k−1)T2≤t≤kT2, there is
where Λ(t)≜exp{∫T20+[ϕ2(t)(β+1−2ϕ2(t))−s1fφ2(t)(1+fφ2(t))2]dt}. By Lemma 1, if μ2<1, the order-1 periodic solution z2(t)=(ϕ2(t),φ2(t)) (k−1)T2≤t≤kT2 is orbitally asymptotically stable. The proof is completed. □
5.2. Order-2 periodic solution
Here only the case for h1<(1−a)h2<x∗1<h1+η<h2<x∗2 is considered. Let G1(h1+η,yG1) be the intersection point between l1 and N1, G2(h1,yG2) be the intersection point between l2 and M1. The trajectory that starts with G1 intersects M2 at B1(h2,yB1). Define ¯τ3≜yG1−(1−b)yB1.
Theorem 8. For the model parameters with any one of C1)-C3), ρ>0 and D-4) h1<(1−a)h2<x∗1<h1+η<h2<x∗2, if byG2≤τ≤min{yG2,¯τ3} holds, an order-2 periodic solution exists in system (2.3).
Proof. For G1∈N1, the trajectory starting from G1 intersects with M2 at B1. Then B1 is mapped to B″1∈N2, and next intersects with M1 at ˆB1, and then ˆB1 is mapped to G+1 under impulse effect. Since τ<¯τ3, then yB″1=(1−b)yB1+τ<yG1. Since g1(B″1)<0 and g2(B″1)<0, it has yˆB1<yB″1, then yG+1=yˆB1<yB″1=(1−b)yB1+τ<yG1, i.e., fIISOR1(G1)=yG+1−yG1<0.
On the other hand, since τ≤yG2, then G2∈N1. The trajectory starting from A1∈N1 with yA1=yG2 intersects with M2 at A−1, and then A−1 is mapped to A+1. Then it intersects with M1 at A+−1, and next A+−1 is mapped to A++1. Since yA+1=(1−b)yA−1+τ>(1−b)yG2+τ>yG2, so fIISOR1(A1)=yA++1−yA1=yA+−1−yG2>0.
The continuity of fIISOR1 implies that a point S∈¯A1G1⊂N1 exists so that fIISOR1(S)=0, i.e., an order-2 periodic solution exists (Figure 4(a)).
Similarly, a point S′∈¯A2B2⊂N2 exists so that fIISOR2(S′)=0, i.e., an order-2 periodic solution exists (Figure 4(b)). □
Let z3(t)=(ϕ3(t),φ3(t)) (k−1)(T1+T2)≤t≤k(T1+T2), k∈N be the order-2 periodic solution. Denote
Define
where
Theorem 9. For the model parameters with any one of C1)–C3), ρ>0 and D-4) h1<(1−a)h2<x∗1<h1+η<h2<x∗2, and byG2≤τ≤min{yG2,¯τ3}, if
then z3(t)=(ϕ3(t),φ3(t)) (k−1)(T1+T2)≤t≤k(T1+T2) is orbitally asymptotically stable.
Proof. For convenience, denote the intersection point between z3(t)=(ϕ3(t),φ3(t)) and N1 (M2, N2, M1) by L1(h1+η,δ3) (L2(h2,δ4), L3((1−a)h2,(1−b)δ4+τ), L4(h1,δ3)). Then, according to analogue of Poincaré Criterion, there are
and
Then
If μ<1, then z3(t)=(ϕ3(t),φ3(t)) (k−1)(T1+T2)≤t≤k(T1+T2) is orbitally asymptotically stable. □
6.
Numerical simulations and verification
6.1. Numerical simulations for system (2.2)
For system (2.2) with model parameters α=0.09, β=0.15, γ=0.6, δ=0.9, s1=1.12, d1=1.1, f=0.21, there is ρ<0, then two interior equilibria exist in the system, and the phase diagram is presented in Figure 5(a); For the model parameters α=0.219, β=0.051, γ=0.6, δ=0.9, s1=1.12, d1=1.1, f=0.21, there is ρ=0, then a unique equilibrium exists in system (2.2), which is a sharp point. The phase diagram of the system (2.2) for such a case is presented in Figure 5(b). Moreover, system (2.2) undergoes a Bogdanov-Takens bifurcation of codimension two in a very small neighborhood of the unique interior equilibrium.
While for system (2.2) with model parameters α=0.09, β=0.29, γ=0.6, δ=0.9, s1=1.12, d1=1.1, f=0.21, there is also ρ=0, in such case a unique equilibrium exists in system (2.2), which is a saddle node, and the phase diagram is presented in Figure 5(c). System (2.2) undergoes a saddle-node bifurcation of codimension one in a very small neighborhood of the interior equilibrium.
For system (2.2) with model parameters α=0.09, β=0.35,γ=0.6, δ=0.9, s1=1.12, d1=1.1, f=0.21, there is ρ>0. In such a case, system (2.2) does not have interior equilibrium, and the phase diagram of the system (2.2) is presented in Figure 5(d).
For system (2.2) with parameters β=0.051, γ=0.6, δ=0.9, s1=1.12, d1=1.1, f=0.21, the bifurcation diagrams of the residual dimension 1 for the system (2.2) are shown in Figure 6(a), (b) when α is selected as the bifurcation parameter. The result shows that for larger α, the interior equilibrium does not exist. When α decreases to α=α0, a unique equilibrium exists in the system. As α decreases below α0, the system undergoes a saddle-node bifurcation at the interior equilibrium E∗, giving rise to two interior equilibria E∗1 and E∗2.
6.2. Simulations for system (2.3)
For system (2.3) with model parameters α=0.1, β=0.15, γ=0.6, δ=0.9, s1=1.12, d1=1.1, f=0.21, the control parameters: h1=0.07, η=0.1, h2=0.6, a=0.35, b=0.38, τ=0.51, an order-1 periodic solution can be formed in both Ω1 and Ω2 (Theorem 6), as presented in Figure 7(a); For model parameters α=0.1, β=0.15, γ=0.6, δ=0.9, s1=1.12, d1=1.1, f=0.21 and control parameters h1=0.07, η=0.128, h2=0.44, a=0.7, b=0.08, τ=0.51, an order-1 periodic solution can be formed in Ω1 (Theorem 6), as presented in Figure 7(b); while for control parameters h1=0.14, η=0.16, h2=0.6, a=0.25, b=0.38, τ=0.51, an order-1 periodic solution can be formed (Theorem 6), as presented in Figure 7(c).
For system (2.3) with given model parameters α=0.09, β=0.215, γ=0.6, δ=0.9, s1=1.12, d1=1.1, f=0.21 and control parameters h1=0.07, η=0.1, h2=0.4, a=0.65, b=2, τ=3, an order-2 periodic solution can be formed in system (2.3) (Theorem 3.2), as presented in Figure 8(a); while for the control parameters h1=0.07, η=0.4, h2=0.68, a=0.65, b=0.85, τ=0.5, a different order-2 periodic solution can be formed in system (2.3) (Theorem 8), as presented in Figure 8(b).
7.
Conclusions
Considering that the Allee effect is an important mechanism in ecosystems and a realistic description of the interaction between species, we presented a model of prey-predator system with prey's Allee effect and generalist predator in the context of fish resources (Models (2.1) or (2.2)). We investigated the dynamic properties of Model (2.2) such as the type and stability of the boundary equilibria as well as the existence and stability of the interior equilibrium in detail (Theorems 1–3, Figure 5).
To show the influence of the parameters on the dynamics of Model (2.2), we analyzed the bifurcations in the predation system by selecting the capture rate of prey by predator and Allee threshold as key parameters. We showed that Model (2.2) will undergo a saddle-node bifurcation as changing of the capture rate α (Figure 6), and undergo a Bogdanov-Takens bifurcation of codimension at least 2 and 3 as changing of (α,β).
To achieve sustainable and efficient exploitation of fish stocks, we adopted a bilateral intervention strategy, i.e., to avoid the distinction of prey fish caused by the Allee effect, releasing juvenile prey fish is adopted at a lower-level x=h1; while for economic purposes, capturing both prey and predator fish is adopted at a higher-level x=h2. We obtained the conditions for the existence and stability of the order-1 periodic solution (Theorems 6, 7, Figure 7) and order-2 periodic solution (Theorems 8, 9, Figure 8) of the control system (2.3). The results showed that the extinction can be prevented by control even when the prey density is low, while in the case of the prey density increasing to a certain extent, fishing activities can be taken in a periodic way (periodic solution) to obtain the fish resources. Therefore, as long as the fish stocks are properly managed, the number of fish stocks can be controlled within an appropriate range, and the sustainable development and utilization of biological resources can be realized.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The work was supported by the National Natural Science Foundation of China (No. 11401068).
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.









 DownLoad:
DownLoad:









