Reliable analysis for obtaining exact soliton solutions of (2+1)-dimensional Chaffee-Infante equation

1.   Introduction

We consider the system of Hamilton-Jacobi equations

where $\lambda > 0$ is a given constant, the functions $H_i : \mathbb{R}^n\to \mathbb{R}$ and $B_i : \mathbb{R}^2 \to \mathbb{R}$, with $i = 1, 2$, are given continuous functions, and $\mathbb{T}^n$ denotes the $n$-dimensional flat torus $\mathbb{R}^n/ \mathbb{Z}^n$.

In a recent paper ^[6], the authors have investigated the vanishing discount problem for a nonlinear monotone system of Hamilton-Jacobi equations

and established under some hypotheses on the $G_i \in C(\mathbb{T}^n \times \mathbb{R}^n \times \mathbb{R}^m)$ that, when $u_ \lambda = (u_{ \lambda, 1}, \ldots, u_{ \lambda, m})\in C(\mathbb{T}^n)^m$ denoting the (viscosity) solution of (1.2), the whole family $\{u_ \lambda\}_{ \lambda > 0}$ converges in $C(\mathbb{T}^n)^m$ to some $u_0\in C(\mathbb{T}^n)^m$ as $\lambda\to 0+$. The constant $\lambda > 0$ in the above system is the so-called discount factor.

The hypotheses on the system are the convexity, coercivity, and monotonicity of the $G_i$ as well as the solvability of (1.2), with $\lambda = 0$. Here the convexity of $G_i$ is meant that the functions $\mathbb{R}^n \times \mathbb{R}^m\ni (p, u)\mapsto G_i(x, p, u)$ are convex. We refer to ^[6] for the precise statement of the hypotheses.

Prior to work ^[6], there have been many contributions to the question about the whole family convergence (in other words, the full convergence) under the vanishing discount, which we refer to ^{[1,3,4,6,8,9,10]} and the references therein.

In the case of the scalar equation, B. Ziliotto ^[11] has recently shown an example of the Hamilton-Jacobi equation having non-convex Hamiltonian in the gradient variable for which the full convergence does not hold. In Ziliotto's approach, the first step is to find a system of two algebraic equations

with two unknowns $u, v\in \mathbb{R}$ and with a parameter $\lambda > 0$ as the discount factor, for which the solutions $(u_ \lambda, v_ \lambda)$ stay bounded and fail to fully converge as $\lambda \to 0+$. Here, an "algebraic" equation is meant not to be a functional equation. The second step is to interpolate the two values $u_ \lambda$ and $v_ \lambda$ to get a function of $x\in \mathbb{T}^1$ which satisfies a scalar non-convex Hamilton-Jacobi equation in $\mathbb{T}^1$.

In the first step above, Ziliotto constructs $f, g$ based on a game-theoretical and computational argument, and the formula for $f, g$ is of the minimax type and not quite explicit. In ^[5], the author has reexamined the system given by Ziliotto, with a slight generality, as a counterexample for the full convergence in the vanishing discount.

Our purpose in this paper is to present a system (1.3), with an explicit formula for $f, g$, for which the solution $(u_ \lambda, v_ \lambda)$ does not fully converge to a single point in $\mathbb{R}^2$. A straightforward consequence is that (1.1), with $B_1(u_1, u_2) = f(u_1-u_2)$ and $B_2(u_1, u_2) = g(u_2-u_1)$, has a solution given by

under the assumption that $H_i(x, 0) = 0$ for all $x\in \mathbb{T}^n$, and therefore, gives an example of a discounted system of Hamilton-Jacobi equations, the solution of which fails to satisfy the full convergence as the discount factor goes to zero.

The paper consists of two sections. This introduction is followed by Section 2, the final section, which is divided into three subsections. The main results are stated in the first subsection of Section 2, the functions $f, g$, the key elements of (1.3), are contstructed in the second subsection, and the final subsection provides the proof of the main results.

2.   A system of algebraic equations and the main results

Our main focus is now the system

where $f, g\in C(\mathbb{R}, \mathbb{R})$ are nondecreasing functions, to be constructed, and $\lambda > 0$ is a constant, to be sent to zero. Notice that (2.1) above is referred as (1.3) in the previous section.

We remark that, due to the monotonicity assumption on $f, g$, the mapping $(u, v)\mapsto (f(u-v), g(v-u)), \, \mathbb{R}^2\to \mathbb{R}^2$ is monotone. Recall that, by definition, a mapping $(u, v)\mapsto (B_1(u, v), B_2(u, v)), \, \mathbb{R}^2\to \mathbb{R}^2$ is monotone if, whenever $(u_1, v_1), (u_2, v_2)\in \mathbb{R}^2$ satisfy $u_1-u_2\geq v_1-v_2$ (resp., $v_1-v_2\geq u_1-u_2$), we have $B_1(u_1, v_1)\geq B_1(u_2, v_2)$ (resp., $B_2(u_1, v_1)\geq B_2(u_2, v_2)$).

2.1.   Main results

Our main results are stated as follows.

Theorem 1. There exist two increasing functions $f, g\in C(\mathbb{R}, \mathbb{R})$ having the properties $\textrm{(a)–(c):}$

$\textrm{(a)}$ For any $\lambda > 0$ there exists a unique solution $(u_ \lambda, v_ \lambda)\in \mathbb{R}^2$ to (2.1),

$\textrm{(b)}$ the family of the solutions $(u_ \lambda, v_ \lambda)$ to (2.1), with $\lambda > 0$, is bounded in $\mathbb{R}^2$,

$\textrm{(c)}$ the family $\{(u_ \lambda, v_ \lambda)\}_{ \lambda > 0}$ does not converge as $\lambda\to 0+$.

It should be noted that, as mentioned in the introduction, the above theorem has been somewhat implicitly established by Ziliotto ^[11]. In this note, we are interested in a simple and easy approach to finding functions $f, g$ having the properties (a)–(c) in Theorem 1.

The following is an immediate consequence of the above theorem.

Corollary 2. Let $H_i\in C(\mathbb{R}^n, \mathbb{R})$, $i = 1, 2$, satisfy $H_1(0) = H_2(0) = 0$. Let $f, g\in C(\mathbb{R}, \mathbb{R})$ be the functions given by Theorem 1, and set $B_1(u_1, u_2) = f(u_1-u_2)$ and $B_2(u_1, u_2) = g(u_2-u_1)$ for all $(u_1, u_2)\in \mathbb{R}^2$. For any $\lambda > 0$, let $(u_{ \lambda, 1}, u_{ \lambda, 2})$ be the (viscosity) solution of (1.1). Then, the functions $u_{ \lambda, i}$ are constants, the family of the points $(u_{ \lambda, 1}, u_{ \lambda, 2})$ in $\mathbb{R}^2$ is bounded, and it does not converge as $\lambda\to 0+$.

Notice that the convexity of $H_i$ in the above corollary is irrelevant, and, for example, one may take $H_i(p) = |p|^2$ for $i\in \mathbb{I}$, which are convex functions.

We remark that a claim similar to Corollary 2 is valid when one replaces $H_i(p)$ by degenerate elliptic operators $F_i(x, p, M)$ as far as $F_i(x, 0, 0) = 0$, where $M$ is the variable corresponding to the Hessian matrices of unknown functions. (See ^[2] for an overview on the viscosity solution approach to fully nonlinear degenerate elliptic equations.)

2.2.   The functions $f, g$

If $f, g$ are given and $(u, v)\in \mathbb{R}^2$ is a solution of (2.1), then $w: = u-v$ satisfies

Set

which defines a continuous and nondecreasing function on $\mathbb{R}$.

To build a triple of functions $f, g, h$, we need to find two of them in view of the relation (2.3). We begin by defining function $h$.

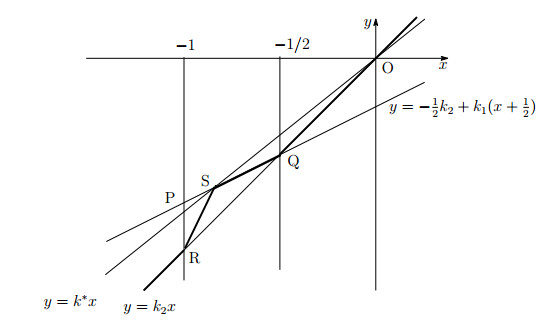
For this, we discuss a simple geometry on $xy$-plane as depicted in Figure 1 below. Fix $0 < k_1 < k_2$. The line $y = -\frac 12k_2 +k_1(x+\frac 12)$ has slope $k_1$ and crosses the lines $x = -1$ and $y = k_2 x$ at $\mathrm{P}: = (-1, -\frac 12(k_1+k_2))$ and $\mathrm{Q}: = (-\frac 12, -\frac 12 k_2)$, respectively, while the line $y = k_2x$ meets the lines $x = -1$ and $x = -\frac 12$ at $\mathrm{R}: = (-1, -k_2)$ and $\mathrm{Q} = (-\frac 12, -\frac 12 k_2)$, respectively.

Choose $k^* > 0$ so that $\frac 12(k_1+k_2) < k^* < k_2$. The line $y = k^*x$ crosses the line $y = -\frac 12k_2 +k_1(x+\frac 12)$ at a point $\mathrm{S}: = (x^*, y^*)$ in the open line segment between the points $\mathrm{P} = (-\frac 12, -\frac 12(k_1+k_2))$ and $\mathrm{Q} = (-\frac 12, -\frac 12 k_2)$. The line connecting $\mathrm{R} = (-1, -k_2)$ and $\mathrm{S} = (x^*, y^*)$ can be represented by $y = -k_2+k^+(x+1)$, with $k^+: = \frac{y^*+k_2}{x^*+1} > k_2$.

We set

It is clear that $\psi\in C(\mathbb{R})$ and increasing on $\mathbb{R}$. The building blocks of the graph $y = \psi(x)$ are three lines whose slopes are $k_1 < k_2 < k^+$. Hence, if $x_1 > x_2$, then $\psi(x_1)-\psi(x_2)\geq k_1(x_1-x_2)$, that is, the function $x\mapsto \psi(x)-k_1 x$ is nondecreasing on $\mathbb{R}$.

Next, we set for $j\in \mathbb{N}$,

It is clear that for all $j\in \mathbb{N}$, $\psi_j\in C(\mathbb{R})$, the function $x\mapsto \psi_j(x)-k_1 x$ is nondecreasing on $\mathbb{R}$, and

We set

It is clear that $\eta\in C(\mathbb{R})$ and $x\mapsto \eta(x)-k_1x$ is nondecreasing on $\mathbb{R}$. Moreover, we see that

and that if $-2^{-j} < x < -2^{-j-1}$ and $j\in \mathbb{N}$,

Note that the point $\mathrm{S} = (x^*, y^*)$ is on the graph $y = \psi(x)$ and, hence, that for any $j\in \mathbb{N}$, the point $(2^{-j}x^*, 2^{-j}y^*)$ is on the graph $y = \eta(x)$. Similarly, since the point $\mathrm{S} = (x^*, y^*)$ is on the graph $y = k^*x$ and for any $j\in \mathbb{N}$, the point $(2^{-j}x^*, 2^{-j}y^*)$ is on the graph $y = k^*x$. Also, for any $j\in \mathbb{N}$, the point $(-2^{-j}, -k_2 2^{-j})$ lies on the graphs $y = \eta(x)$ and $y = k_2 x$.

Fix any $d\geq 1$ and define $h\in C(\mathbb{R})$ by

For the function $h$ defined above, we consider the problem

Lemma 3. For any $\lambda\geq 0$, there exists a unique solution $z_ \lambda\in \mathbb{R}$ of (2.4).

Proof. Fix $\lambda\geq 0$. The function $x\mapsto h(x)+ \lambda x$ is increasing on $\mathbb{R}$ and satisfies

Hence, there is a unique solution of (2.4).

For any $\lambda\geq0$, we denote by $z_ \lambda$ the unique solution of (2.4). Since $h(d) = 0$, it is clear that $z_0 = d$.

For later use, observe that if $\lambda > 0$, $k > 0$, and $(z, w)\in \mathbb{R}^2$ is the point of the intersection of two lines $y = - \lambda x$ and $y = k(x-d)$, then $w = - \lambda z = k(z-d)$ and

Lemma 4. There are sequences $\{\mu_j\}$ and $\{\nu_j\}$ of positive numbers converging to zero such that

Proof. Let $j\in \mathbb{N}$. Since $(-2^{-j}, -k_2 2^{-j})$ is on the intersection of the graphs $y = k_2x$ and $y = \eta(x)$, it follows that $(-2^{-j}+d, -k_2 2^{-j})$ is on the intersection of the graphs $y = k_2(x-d)$ and $y = h(x)$. Set

and note that $\mu_j > 0$ and that

which says that the point $(d-2^{-j}, -k_22^{-j})$ is on the line $y = -\mu_j x$. Combining the above with

shows that $d-2^{-j}$ is the unique solution of (2.4). Also, since $(d-2^{-j}, -\mu_j(d-2^{-j})) = (d-2^{-j}, -k_2 2^{-j})$ is on the line $y = k_2(x-d)$, we find by (2.5) that

Similarly, since $(2^{-j} x^*, 2^{-j}y^*)$ is on the intersection of the graphs $y = k^*x$ and $y = \eta(x)$, we deduce that if we set

then

It is obvious by (2.6) and (2.7) that the sequences $\{\mu_j\}_{j\in \mathbb{N}}$ and $\{\nu_j\}_{j\in \mathbb{N}}$ are decreasing and converge to zero.

We fix $k_0\in(0, k_1)$ and define $f, g\in C(\mathbb{R})$ by $f(x) = k_0(x-d)$ and

It is easily checked that $g(x)-(k_1-k_0)x$ is nondecreasing on $\mathbb{R}$, which implies that $g$ is increasing on $\mathbb{R}$, and that $h(x) = f(x)-g(-x)$ for all $x\in \mathbb{R}$. We note that

2.3.   Proof of the main results

We fix $f, g, h$ as above, and consider the system (2.1).

Lemma 5. Let $\lambda > 0$. There exists a unique solution of (2.1).

The validity of the above lemma is well-known, but for the reader's convenience, we provide a proof of the lemma above.

Proof. By choice of $f, g$, the functions $f, g$ are nondecreasing on $\mathbb{R}$. We show first the comparison claim: if $(u_1, v_1), (u_2, v_2)\in \mathbb{R}^2$ satisfy

then $u_1\leq u_2$ and $v_1\leq v_2$. Indeed, contrary to this, we suppose that $\max\{u_1-u_2, v_1-v_2\} > 0$. For instance, if $\max\{u_1-u_2, v_1-v_2\} = u_1-u_2$, then we have $u_1-v_1\geq u_2-v_2$ and $u_1 > u_2$, and moreover

yielding a contradiction. The other case when $\max\{u_1-u_2, v_1-v_2\} = v_1-v_2$, we find a contradiction, $0 > \lambda v_2+g(v_2-u_2)$, proving the comparison.

From the comparison claim, the uniqueness of the solutions of (2.1) follows readily.

Next, we may choose a constant $C > 0$ so large that $(u_1, v_1) = (-C, -C)$ and $(u_2, v_2) = (C, C)$ satisfy (2.9) and (2.10), respectively. We write $S$ for the set of all $(u_1, u_2)\in \mathbb{R}^2$ such that (2.9) hold. Note that $(-C, -C)\in S$ and that for any $(u, v)\in S$, $u\leq C$ and $v\leq C$. We set

It follows that $-C\leq u^*, v^*\leq C$. We can choose sequences

such that $\{u_n^1\}, \{v_n^2\}$ are nondecreasing,

Observe that for all $n\in \mathbb{N}$, $u_n^2\leq u^*$, $v_n^1\leq v^*$, and

which yields, in the limit as $n\to\infty$,

Similarly, we obtain $0\geq \lambda v^*+g(v^*-u^*)$. Hence, we find that $(u^*, v^*)\in S$.

We claim that $(u^*, v^*)$ is a solution of (2.1). Otherwise, we have

For instance, if the former of the above inequalities holds, we can choose $\varepsilon > 0$, by the continuity of $f$, so that

Since $(u^*, v^*)\in S$, we have

Accordingly, we find that $(u^*+ \varepsilon, v^*)\in S$, which contradicts the definition of $u^*$. Similarly, if $0 > \lambda v^*+g(v^*-u^*)$, then we can choose $\delta > 0$ so that $(u^*, v^*+ \delta)\in S$, which is a contradiction. Thus, we conclude that $(u^*, v^*)$ is a solution of (2.1).

Theorem 6. For any $\lambda > 0$, let $(u_ \lambda, v_ \lambda)$ denote the unique solution of (2.1). Let $\{\mu_j\}, \{\nu_j\}$ be the sequences of positive numbers from Lemma 2.4. Then

In particular,

With our choice of $f, g$, the family of solutions $(u_ \lambda, v_ \lambda)$ of (2.1), with $\lambda > 0$, does not converge as $\lambda\to 0$.

Proof. If we set $z_ \lambda = u_ \lambda-v_ \lambda$, then $z_ \lambda$ satisfies (2.4). By Lemma 4, we find that

Since $u_ \lambda$ satisfies

we find that

which shows that

A parallel computation shows that

Recalling that $0 < k^* < k_2$, we conclude that

We remark that, since

We give the proof of Theorem 1.

Proof of Theorem 1. Assertions (a) and (c) are consequences of Lemma 5 and Theorem 6, respectively.

Recall (2.8). That is, we have $f(d) = h(d) = g(-d) = 0$. Setting $(u_2, v_2) = (d, 0)$, we compute that for any $\lambda > 0$,

By the comparison claim, proved in the proof of Lemma 5, we find that $u_ \lambda \leq d$ and $v_ \lambda\leq 0$ for any $\lambda > 0$. Similarly, setting $(u_1, v_1) = (0, -d)$, we find that for any $\lambda > 0$,

which shows by the comparison claim that $u_ \lambda \geq 0$ and $v_ \lambda\geq -d$ for any $\lambda > 0$. Thus, the sequence $\{(u_ \lambda, v_ \lambda)\}_{ \lambda > 0}$ is bounded in $\mathbb{R}^2$, which proves assertion (b).

Proof of Corollary 2. For any $\lambda > 0$, let $(u_ \lambda, v_ \lambda)\in \mathbb{R}^2$ be the unique solution of (2.1). Since $H_1(0) = H_2(0) = 0$, it is clear that the constant function $(u_{ \lambda, 1}(x), u_{ \lambda, 2}(x)): = (u_ \lambda, v_ \lambda)$ is a classical solution of (1.1). By a classical uniqueness result (see, for instance, [7,Theorem 4.7]), $(u_{ \lambda, 1}, u_{ \lambda, 2})$ is a unique viscosity solution of (1.1). The rest of the claims in Corollary 2 is an immediate consequence of Theorem 1.

Some remarks are in order. (ⅰ) Following ^[11], we may use Theorem 6 as the primary cornerstone for building a scalar Hamilton-Jacobi equation, for which the vanishing discount problem fails to have the full convergence as the discount factor goes to zero.

(ⅱ) In the construction of the functions $f, g\in C(\mathbb{R}, \mathbb{R})$ in Theorem 6, the author has chosen $d$ to satisfy $d\geq 1$, but, in fact, one may choose any $d > 0$. In the proof, the core step is to find the function $h(x) = f(x)-g(-x)$, with the properties: (a) the function $x\mapsto h(x)- \varepsilon x$ is nondecreasing on $\mathbb{R}$ for some $\varepsilon > 0$ and (b) the curve $y = h(x)$, with $x < d$, meets the lines $y = p(x-d)$ and $y = q(x-d)$, respectively, at $P_j$ and $Q_j$ for all $j\in \mathbb{N}$, where $p, q, d$ are positive constants such that $\varepsilon < p < q$, and the sequences $\{P_j\}_{j\in \mathbb{N}}, \, \{Q_j\}_{j\in \mathbb{N}}$ converge to the point $(d, 0)$. Obviously, such a function $h$ is never left-differentiable at $x = d$ nor convex in any neighborhood of $x = d$. Because of this, it seems difficult to select $f, g\in C(\mathbb{R}, \mathbb{R})$ in Theorem 1, both smooth everywhere. In the proof of Theorem 6, we have chosen $\varepsilon = k_0$, $p = k^*$, $q = k_2$, $P_j = (u_{\nu_j}, k^*(u_{\nu_j}-d))$, and $Q_j = (u_{\mu_j}, k_2(u_{\mu_j}-d))$

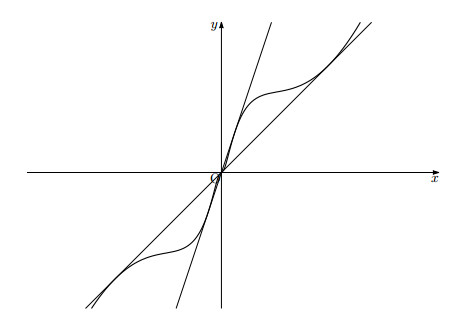
Another possible choice of $h$ among many other ways is the following. Define first $\eta \, :\, \mathbb{R}\to \mathbb{R}$ by $\eta(x) = x(\sin(\log|x|)+2)$ if $x\not = 0$, and $\eta(0) = 0$ (see Figure 2). Fix $d > 0$ and set $h(x) = \eta(x-d)$ for $x\in \mathbb{R}$. we remark that $\eta\in C^\infty(\mathbb{R} \setminus \{0\})$ and $h\in C^\infty(\mathbb{R} \setminus\{d\})$. Note that if $x\not = 0$,

and that if we set $x_j = -\exp(-2\pi j)$ and $\xi_j = -\exp\left(-2\pi j+\frac \pi 2\right)$, $j\in \mathbb{N}$, then

The points $P_j: = (x_j+d, 2x_j)$ are on the intersection of two curves $y = h(x)$ and $y = 2(x-d)$, while the points $Q_j: = (d+\xi_j, 3\xi_j)$ are on the intersection of $y = h(x)$ and $y = 3(x-d)$. Moreover, $\lim P_j = \lim Q_j = (d, 0)$.

Acknowledgments

The author would like to thank the anonymous referees for their careful reading and useful suggestions. He was supported in part by the JSPS Grants KAKENHI No. 16H03948, No. 20K03688, No. 20H01817, and No. 21H00717.

Conflict of interest

The author declares no conflict of interest.