Analyticity and uniqueness of the fractional electromagnetic boundary value problem

1.   Introduction

Understanding the analytic behavior of the electromagnetic field is crucial for addressing various theoretical electromagnetic problems, particularly in resolving uniqueness issues. Previous discussions ^{[1,2,3,4,5,6,7]} have explored electromagnetic (EM) wave propagation using fractional calculus, emphasizing its practical relevance in communication, plasma, fluids, and various media applications ^{[8,9,10,11,12,13,14,15,16]}. Additionally, studies focusing on local fractional calculus and its applications have been investigated ^{[17,18,19,20,21,22]}.

The authors in ^[23,24,25] demonstrated the uniqueness of solutions in time-harmonic electromagnetic boundary-value problems (BVPs) within homogeneous regions with free source, based on the analyticity of the electromagnetic field components in these regions, specifically in the usual integer space. However, the scope of applications for electromagnetic field analyticity has been limited to homogeneous dielectric regions.

Expanding research to encompass dielectric materials with non-constant analytic dielectric characteristics, such as analytically inhomogeneous "lossy" or "lossless" regions within the rest (stable) region, becomes crucial to broaden the uniqueness of time-harmonic EM BVP. Notably, recent works delved into optical soliton solutions and the wave equation, respectively ^[26,27]. Recent literature explores diverse computational methodologies for fractional differential equations across different physical domains. Ali et al. ^[28] likely explored electromagnetic wave behavior in plasma-filled rectangular waveguides using fractional space and the local fractional derivative (LFD) technique, aiming to enhance our understanding of wave propagation in complex plasma environments. Concurrently, the research ^[29,30] delved into multistep schemes for electromagnetic wave models using fractional derivatives, emphasizing numerical approaches. Singh et al. ^[31] analyzed implicit schemes for stochastic fractional diffusion wave models. Together, these works showcase a breadth of numerical methods and applications for understanding physical phenomena governed by fractional differential equations. There are some papers that delve into studying the fractional perspective of infectious diseases ^[32], dynamical analysis in plant infections ^[33], and optimization of fractional-order parameters in disease modeling ^[34]. These studies deepen our understanding of disease dynamics and control strategies.

In this manuscript, the authors venture into a pioneering extension, transcending the conventional realm of integer space to explore the uncharted territory of fractional space within the context of electromagnetic BVPs. Unlike prior references that predominantly navigate the integer domain, this paper introduces an innovative study delving into the distinctive and analytical facets of fractional solutions within a fractional electromagnetic BVP framework. The focal point revolves around delineating the tangential components of the electromagnetic field, specifically characterizing the fractional electromagnetic fields. A fundamental revelation arises from proving the non-vanishing nature of these analytical expressions within designated subregions, underscoring their persistence and continuity throughout space. Notably, this paper elucidates the uniqueness of the solution, ensuring equivalence between, while obviating any existence of singular fields within the same spatial domain. Furthermore, the manuscript rigorously establishes the analyticity of the fractional time-harmonic electromagnetic field within both lossy and lossless dielectric regions, serving as a comprehensive generalization of prior works in the domain of electromagnetic BVPs, specifically referencing seminal works ^{[23,24,25,35,36,37]}. The main purpose of this paper is to generalize the uniqueness and analyticity of the solution from integer space to fractals, as well as to extend the works of ^{[23,24,25,35,36]}. This paper has proved the uniqueness and analyticity of fractional solutions for the fractional electromagnetic boundary value problem, which had not previously been studied. The usual uniqueness in the integer space has been checked as a special case when the fractional parameter $\alpha = 1$. Moreover, the goal of this paper is to move toward such a generalization of the analytic behavior of the electromagnetic field in fractional space.

Novelty and expansion:

1) This work explores fractional space, pioneering the investigation of fractional electromagnetic boundary value problems, departing from traditional integer domain solutions.

2) This methodology delves into analytical facets, characterizing fractional electromagnetic fields and presenting their unique properties and analytical expressions.

3) The non-vanishing nature of analytical expressions within designated subregions establishes persistence and continuity, a fundamental aspect of this methodology.

4) The methodology ensures solution equivalence and eliminates singular fields within the same spatial domain, highlighting its robustness and reliability.

5) This paper comprehensively generalizes prior works in electromagnetic boundary value problems, extending beyond existing literature and referencing seminal works.

6) This paper uniquely contributes by proving the uniqueness and analyticity of fractional solutions for the fractional electromagnetic boundary value problem, a previously unexplored area.

7) This work acts as a bridge towards generalization of the analytic behavior of electromagnetic fields in fractional space, paving the way for future research and understanding in this domain.

8) This paper generalizes the previously published works ^{[23,24,25,35,36]}.

The paper is organized as follows: Section 1 represents an introduction on fractional electromagnetic fields as well as discussing both the uniqueness and analyticity of BVPs; Section 2 focuses on the mathematical formulation of the fractional BVP; Section 3 investigates the proof of the uniqueness of the solution; Section 4 is devoted to the analyticity of the fractional EM BVP; and Section 5 is devoted to the conclusion.

2.   Fractional boundary value problem

2.1.   Mathematical formulation

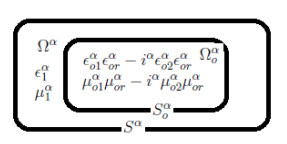
Consider the following fractional boundary value problem with fractional parameter $\alpha$ such that $0 < \alpha\leqslant1$. Assume that $S^\alpha$ is the whole boundary for the homogeneous dielectric region $\Omega^\alpha$, which is specified by the permittivity $\epsilon_1^\alpha$ and the permeability $\mu_1^\alpha$. Furthermore, suppose $S_o^\alpha$ is the boundary for $\Omega_o^\alpha$, which is characterized by complex permittivity $\epsilon_{o1}^\alpha\epsilon_{or}^\alpha-i^\alpha \epsilon_{o2}^\alpha\epsilon_{or}^\alpha$ and complex permeability $\mu_{o1}^\alpha\mu_{or}^\alpha-i^\alpha \mu_{o2}^\alpha\mu_{or}^\alpha$. The typical regions are indicated in Figure 1. Between the regions $\Omega^\alpha-\Omega_o^\alpha$, the dielectric is assumed to be lossless, i.e., the conductivity $\sigma < \omega\epsilon$, $\epsilon = \epsilon_o\epsilon_r$, $\mu = \mu_o\mu_r$, where $\epsilon_o$ and $\epsilon_r$ is permittivity in the free space and the dielectric, respectively. The tangential electromagnetic fields over $S^\alpha$ are denoted by $E^\alpha (r^\alpha)$ and $H^\alpha(r^\alpha)$, which follow the time-harmonic with factor $e^{i^\alpha\omega^\alpha t^\alpha}$, where $i^\alpha$ is complex indeterminate and $\omega^\alpha$ is the fixed angular frequency.

In the fractional form, we can define the following electromagnetic quantities as:

The classical constitutive relations are obtained when $\alpha = 1$ as

Also, we can define the fractional vector operators as:

where $\Gamma(1+\alpha)$ is the Gamma function. By using Caputo derivatives, we have

where ${^c_o} D^\alpha_{x\ell}$ is a fractional Caputo derivative which is defined by

where $n-1 < \alpha < n.$

2.2.   Fractional Maxwell's equations

The fractional Maxwell's equations are given by:

where the magnetic permeability $\mu'$ is

and the permittiviy $\epsilon'$ is

In the lossless dielectric region $\Omega^\alpha_o$, $\mu^\alpha_{o1}\mu^\alpha_{or}$, $\mu^\alpha_{o2} \mu^\alpha_{or}$, $\epsilon^\alpha_{o1}\epsilon^\alpha_{or}$, and $\epsilon^\alpha_{o2} \epsilon^\alpha_{or}$ are the real and imaginary parts of fractional permeability and permittivity, respectively. $n^\alpha$ is the unit vector to $S^\alpha$.

The solution of the boundary problem that described by Eqs (2.6)–(2.8) is unique if and only if

3.   Proof of the solution's uniqueness

We will employ the method of proof by contradiction in this case. Let us assume that the fractional Maxwell Eqs (2.6) and (2.7) do not yield unique solutions, implying the existence of multiple solutions for the electric field as $E^\alpha$ and $E^{\alpha}$, as well as multiple solutions for the magnetic field as $H^\alpha$ and $H^{\alpha}$ across potential internal interfaces. The continuity of the tangential magnetic components $H^\alpha$ and $H^{*\alpha}$ can be described using Gauss's theorem over the entire domain $\Omega^\alpha$. Furthermore,

where $J_M^{1-\alpha}$ is an integrated vector field expressed the fractional flux.

By applying the fractional vector identities, we get

and by using the Maxwell equations, we obtain

since $n^\alpha\wedge H^\alpha = 0$, over $S^\alpha$, and also $n^\alpha\wedge H^{*\alpha} = 0$, over $S^\alpha$. Then, these conditions are satisfied over $\Omega^\alpha$ as a part of $S^\alpha$. This leads to the left hand side (L.H.S.) of Eq (3.3) vanishing, i.e.,

and consequently

where the permittivity $\epsilon'$ takes the form of Eq (2.10) as

by dividing on $\Gamma(1+\alpha)$. Then, the Eq (3.4) can be written as:

By equating both the real and imaginary parts with zero, we get

where $i^{2^\alpha}$ is a real number and $\omega^\alpha$ is a fixed angular frequency. This leads to

because of $d^\alpha v$ is an arbitrary volume, this leads to $d^\alpha v \neq0$ in $\Omega^\alpha_o$. Therefore,

$\Longrightarrow$

But, from the Maxwell equations,

Equations (3.12) and (3.13) are satisfied in $\Omega^\alpha$ under the conditions

Therefore, the solutions of Eq (3.9) are

So, by combining these solutions in the same subregion, we have

Equation (3.14) is satisfied in $\Omega^\alpha_o$. Hence,

where $\omega^\alpha \epsilon^\alpha_{or}\epsilon^\alpha_{o2}$ is strictly positive.

In the region $\Omega^\alpha$-$\Omega^\alpha_o$, the dielectric is linear and homogeneous. Within $S^\alpha_o$, we obtained

So, the solutions $H^{\alpha} \neq 0$ and $H^{*\alpha} \neq 0$ are satisfied also in region $\Omega^\alpha-\Omega^\alpha_o$. Finally, we get

and then we deduce that

By the same method, the divergence theorem to the whole domain $\Omega^\alpha$ can be applied on the tangential components of $E^\alpha$, $E^{*\alpha}$ within $S^\alpha$; $\Rightarrow$

Special case

To test the validity of the results, when we put $\alpha = 1$, we get in $\Omega$

Equation (3.22) is in good agreement with previously published results in ^[23,24,25].

4.   Analyticity of fractional EM BVP

The fractional electromagnetic field within a homogeneous lossless dielectric region was analyzed using the analyticity method. We will now demonstrate the analytic behavior in the presence of a source for the electromagnetic field, considering the conduction current

Both the electric field $E^\alpha$ and the magnetic field $H^\alpha$ are analytic in a medium if they are defined and analytic in some arbitrary volume $\Omega^\alpha\subset R^3$. This means that the electromagnetic field can be developed in multiple power series in a neighborhood of each point in the region ^[36]. Let $E^\alpha$ and $H^\alpha$ be continuously differentiable vector fields in $\Omega^\alpha$, i.e., $E^\alpha$ and $H^\alpha$ $\in$ $[C^2(\Omega^\alpha)]^3$.

Maxwell equations can be rewritten to include the current source as

By taking the curl for Eq (4.2), while employing both Eq (4.1) and the vector identity

we obtain

By taking the divergence for Eq (4.1) and using the concept of the vanishing of Div (Curl), we get

This leads to

and, by substituting Eq (4.5) into Eq (4.3), we get

The characteristic determinant classifies this linear partial differential equations system Eq (4.6) by considering a diagonal matrix $\Bbbk_{3\times3}$ whose diagonal values $m_{\imath\jmath}$, $m_{\imath\jmath}$ are expressed as the sum of the coefficients $b_{mn}$ of the second-order partial derivative $\frac{\partial^{2\alpha} H^\alpha_\ell}{\partial x_m \partial x_n}$ multiplied by real polynomials of second-order $\lambda_m \lambda_n$; $m, n = 1, 2, 3$. System (4.6) can be characterized by ^[37]

i.e.,

or

with characteristic determinant

From Eq (4.9), system (4.6) is considered as elliptic ^[37], and therefore system (4.6) can characterized by analytic coefficients in $\Omega^\alpha$, and this means that both $E^\alpha$ and $H^\alpha$ are analytic in $\Omega^\alpha$.

Examples on uniqueness/analyticity of electromagnetic fields

(1) Illustrating the uniqueness and analyticity of fractional electromagnetic waves, the phenomenon of energy distribution within enclosures featuring irregular boundaries is prevalent across various electromagnetic domains. When the wavelength of an injected wave is considerably smaller than the size of the structure, even minute alterations in geometry or wave frequency significantly impact the scattering characteristics of the enclosure. Under such circumstances, statistical models become essential. One of these models, the random coupling model, has undergone exploration via experiments and theoretical studies.

Earlier investigations involved injecting waves into high Q cavities in an almost omnidirectional manner. However, when employing a directed beam approach and considering relatively low Q cavities, the assumption based on the random plane wave hypothesis, fundamental to the random coupling model formulation, becomes invalid. Observations indicate that injecting such directed beams results in substantial deviations in wave statistics for individual realizations of enclosure geometry. Nevertheless, despite these variations, the electromagnetic fields themselves remain consistent.

(2) Reference ^[15] serves as an exemplar showcasing the constancy and analytic nature of electromagnetic fields in fractional space. Within this framework, electromagnetic fields maintain consistency along the waveguide, ensuring that solutions remain unique at any distance throughout the propagation process within the waveguide.

5.   Conclusions

In conclusion, this paper generalizes previously published works ^[23,24,25] as well as ^[35,36]. This paper marks a pioneering step in the study of electromagnetic BVPs by extending the analysis from the conventional integer space to the unexplored realm of fractional space. The exploration of fractional electromagnetic fields has revealed distinct analytical facets, emphasizing their non-vanishing nature within designated subregions and their persistent continuity across space. The methodology not only establishes equivalence between solutions, but also eliminates the existence of singular fields within the same spatial domain, ensuring robustness and reliability.

Moreover, this work stands as a comprehensive generalization and extension of prior research, advancing the understanding of electromagnetic BVPs by proving the uniqueness and analyticity of fractional solutions, a dimension previously unexplored. The confirmed uniqueness in the integer space acts as a validation, showcasing the broader applicability of the methodology. Ultimately, this paper not only contributes to the immediate field of study, but also serves as a catalyst for future research, laying the groundwork for a more comprehensive understanding of electromagnetic fields in fractional space. The findings presented herein open avenues for further exploration and development, propelling the study of electromagnetic phenomena into new and promising directions.

Both the uniqueness and analyticity of the time harmonic fractional electromagnetic fields are proven. The fractional electromagnetic fields components $E^{\alpha}$, $E^{*\alpha}$, $H^{\alpha}$, and $H^{*\alpha}$ do not vanish and, furthermore, $E^{\alpha} = E^{*\alpha}$ and $H^{\alpha} = H^{*\alpha}$. This proves that the solution of fractional electromagnetism is unique in the fractional space. The good agreement of these results matches published results in ^[23,24,25]. The proof and comparison of uniqueness solutions and analyticity for the fractional electromagnetic boundary value problem have been conducted, extending the analysis to a special case in integer space. The analyticity method was employed in both lossy and lossless media, encompassing homogeneous and inhomogeneous dielectrics.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors extend their appreciation to Taif University, Saudi Arabia, for supporting and funding this work through project number (TU-DSPP-2024-xx).

Conflict of interest

The authors declare that there are no conflicts of interest to this work.