A fractional dual-phase-lag thermoelastic model for a solid half-space with changing thermophysical properties involving two-temperature and non-singular kernels

Nomenclature

1.   Introduction

Studying heat transfer through conduction, taking into account the variation of thermophysical properties such as specific heat capacity and thermal conductivity with temperature, poses major challenges in both experimental studies and mathematical modeling ^[1]. The concept of variable material properties pertains to the phenomenon wherein a material's mechanical and physical characteristics can alter or fluctuate under diverse conditions, including temperature, pressure, stress, or strain. The comprehension of how material characteristics undergo alterations in different conditions is crucial within the fields of engineering, physics, and materials science. This understanding has great significance as it has the potential to exert a substantial influence on the behavior and effectiveness of structures and materials ^[2]. The constancy of thermal conductivity is an important characteristic attributed to materials, acknowledged by numerous researchers. Nevertheless, numerous theoretical and practical investigations have demonstrated that thermal conductivity is not an unchanged property, but exhibits a strong temperature dependence ^[3]. Temperature variations can modify the mechanical characteristics of materials, including their strength, stiffness, and ductility. Certain materials may exhibit a reduction in strength and stiffness when subjected to higher temperatures, rendering them more susceptible to deformation or failure. On the other hand, some materials may have enhanced mechanical characteristics when exposed to higher temperatures. As temperature rises, metals have the potential to undergo expansion, decreased hardness, and alterations in their thermal conductivity and electrical resistance. Comprehending these fluctuations is crucial for developing systems functioning in diverse thermal conditions ^[4]. For the majority of materials, thermal conductivity frequently rises with temperature. However, some materials could behave oddly. For instance, phonon-phonon scattering may cause a material to lose thermal conductivity at extremely high temperatures. ^[5,6]. In various applications, varying thermal conductivity can be both a disadvantage and a benefit. Engineers and scientists must consider these variances when constructing systems that require heat transmission, such as electrical devices, thermal insulation, or materials used in harsh environments. For such systems to operate at their peak efficiency, it is essential to comprehend how and why thermal conductivity changes ^[7,8]. Many researchers have solved various problems of thermal conduction and diffusion to study the effect of the dependence of physical properties on temperature and the extent of its effect on the behavior of materials. A more detailed discussion of this topic is available in the literature ^{[9,10,11,12,13]}.

The prevailing assumption in traditional thermoelasticity is that thermal waves propagate at infinite speeds and that heat transfer occurs instantaneously. As a result, theories of extensional thermoelasticity were considered in order to address this expectation. These theories with hyperbolic equation systems confirmed that heat waves have a limited speed in accordance with physical phenomena ^[14]. The study of thermal shock in materials, the modeling and simulation of biological tissues, and the study of heat propagation in semiconductors are just a few examples of the many applications of thermoelasticity theory.

Hyperbolic heat transfer models are used in extensional thermoelasticity instead of the hyperbolic heat transfer equation used in conventional thermoelasticity. Thermal delays are a common element in the development of these models, and they determine how long it takes a temperature change to propagate through the material ^[15]. A single relaxation time was postulated in the general theory of thermoelasticity by Lord and Shulman ^[16]. Green and Lindsay ^[17] proposed a hyperbolic model of thermoelasticity that is an alternative to the classical system and includes two distinct relaxation periods. In this context, using a two-phase delay strategy for both the heat flow vector and the temperature gradient, Tzou ^[18,19] presented a thermoelastic model. Roy Choudhuri ^[20] also relied on the DPL model to determine the three-phase lag equation for thermal conductivity (TPL). The TPL model is developed instead of the traditional Fourier law of heat transfer by considering the delay phase component of heat flow, temperature gradient, and thermal displacement. Also, Green and Naghdi ^[21,22,23] have put forward three models, designated as types I, II, and III. Type I theories, when linearized, are equivalent to the classical heat equation derived from Fourier's law. On the other hand, linearized types of type II and type III theories allow for the transmission of thermal waves at a limited velocity. Both Type-II and Type-III theories of thermoelasticity employ the potential to determine the entropy flow vector. Type-II models do not involve energy dissipation, whereas Type-III models incorporate energy dissipation. The potential also determines the strains. When Fourier transmission is the primary factor, the temperature equation simplifies to the classical Fourier law of heat transfer. Conversely, when the influence of conductivity is insignificant, the equation exhibits undamped thermal wave solutions that do not include energy loss. Recently, higher-order time derivative terms have been introduced into modified forms of heat transfer by Abouelregal et al. ^{[24,25,26,27,28]}.

Gurtin and Williams ^[29,30] propose that it is not reasonable to assume that the second law of thermodynamics for continuous bodies is solely dependent on a single temperature. Instead, they contend that it makes more sense to take into account a second law in which one temperature controls the entropy contribution from heat transfer while another temperature controls the contribution from heat supply. The authors Chen and Gurtin ^[31], as well as Chen et al. ^[32,33], have developed a theory of heat conduction in deformable structures that relies on two separate temperatures: the conductive temperature $\phi$, and the thermodynamic temperature $\theta$. In instances where time does not play a role, the disparities between these two temperatures are directly related to the amount of heat provided. If no heat is supplied, the two temperatures will be the same ^[33]. In the case of issues that change over time, and especially in difficulties involving the movement of waves, the two temperatures are often different, regardless of whether there is a source of heat. Within the framework of the two-temperature thermoelasticity model (2TT), Quintanilla ^[34] discussed the existence of a solution, structural stability, and spatial behavior of the model. The material coefficient $\beta \ge 0$, also known as the temperature discrepancy ^[35], is what sets two-temperature thermoelasticity (2TT) apart from the traditional theory of thermoelasticity (CTE). More precisely, when $\beta$ is equal to zero, the value of $\phi$ is equal to $\theta$. As a result, the field equations of the 2TT may be simplified to match those of the CTE thermoelasticity model.

Classical derivatives, normally specified for integer orders, can be extended to accommodate non-integer orders, thanks to the concept of fractional derivatives. The concept of derivatives makes it possible to calculate the rate of change of a function at a given point or interval, including non-integer orders. Fractional calculus places heavy emphasis on the concept of fractional derivatives. When integral operators are used, fractional derivatives are often established ^[36,37]. The two definitions of fractional derivatives offered by Riemann-Liouville and Caputo, according to the majority of experts, are the most widely used. Choosing a definition depends on the nature of the issue at hand. Many fields, including physics, engineering, the field of economics, biological sciences, and control theory, have found uses for fractional derivatives. Anomalous diffusion, viscoelasticity, and fractional Brownian motion are only a few examples of the types of phenomena that these mathematical frameworks are used to depict and investigate ^[38,39].

It is possible to see fractional derivatives with non-singular kernels as an extension of traditional derivatives. Classical calculus uses derivatives, usually represented as integer-order derivatives, to describe the rate of change of a function at a given point in space. The use of non-singular (or non-local) kernels is a key component of the definition of fractional derivatives, which broadens the concept of differentiation to encompass orders that are not integers. Hydrodynamics, viscoelasticity, physics, biology, and mechanical engineering are just a few of the fields that need accurate simulations of real-world events. To meet this need, researchers have realized how important it is to find new fractional derivatives that use distinct, unique, or non-singular kernels ^[40]. It is fairly uncommon for non-singular kernels to use transcendental functions like the gamma, exponential, or Mittag-Leffler functions. The goal in choosing these kernels is to ensure that the fractional derivatives display clearly defined mathematical traits that are also of practical value in a wide range of contexts.

Existing definitions of fractional derivatives, such as Liouville-Caputo and Riemann-Liouville fractional derivatives, have difficulty with a single kernel, which Caputo and Fabrizio ^[41] suggest a solution for. An exponential function was used to calculate the answer. Still, there were difficulties with this operator, one of which was its non-locality. It is also important to remember that the integral corresponding to the fractional order derivative is not a fractional integral. Atangana and Baleanu ^[42] effectively overcame these difficulties. Derivatives of the Liouville-Caputo and Riemann-Liouville varieties of the fractional kind were introduced. To define these derivatives, the extended Mittag-Leffler function is used. In ^[43], a complete formulation was provided that includes all known fractional derivative operators with non-singular kernels. Several models ^{[44,45,46,47,48,49]} have been updated to incorporate the clarified definitions.

Fractional thermoelasticity is an advancing field that integrates the ideas of fractional calculus and thermoelasticity to elucidate the intricate response of materials to heat and mechanical pressures. As the main objective of this study, we provide a novel thermoelasticity system with two temperatures. This model was derived in the context of a new study of two-phase heat conduction with fractional orders and fractional operators. For the purpose of comparison, the use of fractional derivative operators with traditional singular and non-singular kernels was taken into account. This approach facilitates the acquisition of knowledge regarding heat transfer and the intricate interplay between thermal and mechanical properties in materials with complex microstructures. The new framework of fractional thermoelasticity can be used to study how heat moves through nanostructures like nanowires and nanotubes. It can help us learn more about how the thermal properties of these materials change with size. Additional research is required to thoroughly investigate the capabilities of this novel framework for analyzing thermoelastic materials.

The current study is structured into the following sections: The first section provides an introduction to the topic of the paper and states the research objectives and questions. It also includes a brief review of relevant literature and previous work on the research topic. The second section presents a theoretical framework and fractional mathematical model of two-temperature thermoelasticity used in the study, including assumptions, hypotheses, and limitations. The proposed model is applied to study the thermodynamic behavior of a one-dimensional elastic material subjected to thermal laser pulses and decreasing external force in fourth section. The basic equations were solved using the Laplace transform methodology in the fifth and sixth sections. The numerical results, which were shown in figures and tables, were examined and discussed in the seventh section. The most significant findings and deductions drawn from the article were included in the last section.

2.   Derivation of the two-temperature thermoelastic model

The concept of Fourier's law is of great significance in the field of heat transfer, as it serves as a fundamental principle for understanding the methods by which heat is transferred in both solid and liquid media. This law explains the relationship between heat flow $\boldsymbol{\mathcal{H}}$, which quantifies the amount of heat transferred per unit area, and thermal gradient $\nabla \theta$, which indicates the spatial variation in temperature within a substance. The theoretical formula of Fourier's law can be expressed as:

The second law of thermodynamics introduces entropy, which is a measure of the disorder or unpredictable nature of a system. According to the law, the total entropy $\eta$ of a closed system cannot decrease over time; in fact, it tends to rise as it grows. Because it places restrictions on the maximum efficiency of heat engines and other devices that involve the transformation of energy from one form to another, this principle has significant repercussions for the design of thermal systems. The following equations may be derived using the increase in entropy $\eta$ represented by ^[19,20]

The energy equation may be derived by utilizing Eqs (2) and (3) in the following manner:

The following changes were suggested by Quintanilla ^[21] to the conventional form of Fourier's law (1):

Chen and Gurtin ^[30] and Chen et al. ^[31,32] have created a theoretical framework for analyzing heat transmission in flexible structures. This theory relies on considering two distinct temperatures: the conductive temperature, denoted as $\phi$, and the thermodynamic temperature, represented by $\theta$. The mathematical expression representing the correlation between the two temperatures, $\theta$ and $\phi$, may be expressed as ^[30,31,32]:

where $\beta$ represent the distinguished factor between the two temperatures.

Tzou ^[6] proposed the use of two-phase-lag models (DPL) for both the heat flow vector and the temperature gradient. Quintanilla ^[34] has examined the presence, structural integrity, and spatial dynamics of the solution in 2TT. Moreover, the uniqueness and reciprocity theorems for the 2TT have been successfully demonstrated by Lesan ^[50]. The DPL law is modified by taking into account two distinct phase delays, one for the heat flow vector (${\tau }_{q}$), and the other for the conductive temperature gradient (${\tau }_{\phi }$) as follows ^[51]:

The Taylor series expansion of Eq (7) is employed to approximate the modified heat transfer rule at a specific position $\boldsymbol{r}$ and time $t$, using just the first-order variables in ${\tau }_{q}$ and ${\tau }_{\phi }$ ^[51]:

The fractional heat equation is a theoretical framework used to describe heat transfer. The concept of fractional heat equations is introduced to describe the heat transfer phenomenon in accordance with experimental results. Such models demonstrate how the temperature history of the surrounding area as well as the current temperature gradient affect the rate of heat transfer from one point to another. The formula that is commonly used to represent the Caputo time fractional derivative of a function $𝒻\left(t\right)$ concerning time $t$ of order $\alpha$ ($0 < \alpha < 1$) is as follows ^[36,39]:

A new definition of the fractional derivative of fractional order was proposed by Caputo and Fabrizio ^[41] in 2015. This concept is a departure from the traditional definition of the Caputo fractional derivative. The formula that follows corresponds to the definition that Caputo and Fabrizio would want to have implemented ^[41]:

Choosing the kernel function that is utilized in the definition is the primary distinction that can be made between the Caputo-Fabrizio fractional derivative and the typical Caputo fractional derivative. The kernel function is characterized as an exponential function in the Caputo-Fabrizio formulation, but in the Caputo definition, the kernel function is characterized as a power-law function. The Caputo-Fabrizio fractional derivative possesses several appealing qualities. These characteristics include its straightforwardness, its ability to handle initial and boundary conditions simply, and its simplicity. Viscoelastic materials, electrical circuits, and heat conduction are only a few of the physical systems that have benefited from their application.

The physical interpretation and application of the Caputo-Fabrizio fractional derivative in modeling real-world events have been the subject of several studies that have prompted individuals to raise issues regarding these aspects. The fact that the Caputo-Fabrizio fractional derivative is more akin to a filter than a genuine fractional derivative is one of the critiques that might be leveled against it. Because it does not have a lot of memory, the exponential kernel function used to make the Caputo-Fabrizio fractional derivative does not show the long-range interactions and memory effects that are usually part of fractional derivatives.

The Atangana-Baleanu fractional time derivative ^[42] is a recently introduced concept of the fractional derivative, which was suggested in 2016. It is determined utilizing the following formula:

The function ${\mathrm{E}}_{\alpha }\left(z\right)$ denotes a Mittage-Laffer function, which may be expressed as

The Fourier law (8) can be transformed into a more accurate fractional-order expression by replacing the time derivative with a non-integer order derivative, as follows:

By performing the divergence operation on each side of Eq (13), the following equation can be obtained

The fractional heat transfer equation for two temperatures and two-phase delays can be obtained by merging Eq (14) with Eq (4) as follows:

Moreover, the stress-strain-temperature relationships, which describe the material characteristics, as well as the correlation between strain and displacement for thermoelastic isotropic materials at a consistent ambient temperature ${T}_{0}$, may be expressed as follows:

3.   Special cases

In the absence of the discrepancy factor and fractional derivatives ($\beta = 0, \; \alpha = 1$), it is possible to develop three prior models of thermal elasticity with one temperature. The models under consideration encompass the conventional thermoelasticity (CTE) model with ${{\tau }_{q} = \tau }_{\phi } = 0$, the Lord and Shulman (LS) model with a solitary delay coefficient (${\tau }_{\phi } = 0$), and the two-phase delay model (DPL). Moreover, when the discrepancy factor ($\beta$) disappears ($\beta = 0$) and fractional differential derivatives ($0 < \alpha < 1$) are taken into account, it is possible to develop two independent fractional models of thermoelasticity at a certain temperature. These fractional thermal models are denoted by the symbols FLS and FDPL. Finally, the inclusion of the theory of thermoelasticity with two temperatures at $\beta > 0$ and the use of fractional operators when ($0 < \alpha < 1$), leads to the extraction of two other models in the field of fractional thermoelasticity, referred to as 2TFLS and 2TFDPL.

4.   Problem formulation

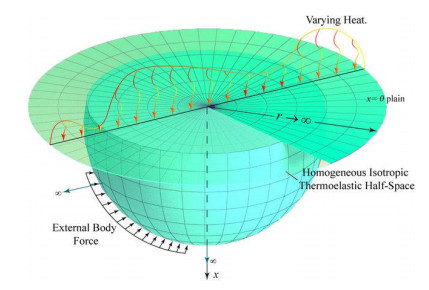
The accuracy of the proposed model is evaluated by examining its application in the context of a thermoelastic issue. This investigation aims to investigate the thermoelastic behavior of a half-space with an infinite area ($x\ge 0$). The x-axis is oriented inward into the medium and is perpendicular to the surface $x = 0$, as seen in Figure 1. The medium being studied is initially in a state of rest, devoid of any pressure or strain, and is characterized by an initial temperature denoted as ${T}_{0}$. A laser pulse characterized by a consistent intensity is directed towards the medium, with its entry point specified by the surface at $x = 0$. This work conceptualizes a one-dimensional problem as a dynamic problem occurring within a half-space. Therefore, all regions under examination are contingent solely upon time and space variables, denoted as $x$ and $t$.

The displacement elements can be mathematically described as follows:

Also, the expression for the only non-zero strain is provided by

External forces acting on objects are important in many physical phenomena and are often crucial in the design and analysis of engineering systems. By understanding the behaviors and interactions of external forces acting on a continuous body, engineers and scientists can devise superior and more productive solutions to a variety of engineering problems. In the current work, it was taken into account that the external body force components take the form

in which the decay rate is determined by the parameter $𝒷 > 0$. In the case of a problem with just one dimension, the fundamental Eqs (6), (15), (16), and (18) may be represented as

where $k = \frac{K}{\rho {C}_{s}}$ denotes the thermal diffusivity (constant).

The differences in the properties and behavior of materials that are impacted by changes in temperature are referred to as temperature-dependent characteristics at this point. Depending on the particular material and the kind of application, these qualities can be classified into a variety of distinct kinds, such as mechanical, thermal, electrical, and others. Changes in the elastic modulus, yield strength, and other mechanical properties are examples of temperature-dependent mechanical characteristics. These changes have an impact on the deformation and failure nature of materials when they are subjected to stress. Some polymers, for instance, may become more malleable and flow when subjected to high temperatures, but the stiffness and strength of a great number of metals and alloys reduce as the temperature rises. Changes in thermal conductivity, specific heat, and other thermal properties are examples of thermal temperature-dependent features. These changes have an impact on the capacity of materials to move heat and store energy.

In this analysis, thermal conductivity and specific heat capacity will be expressed as linear functions of thermodynamic temperature ^[5,6]

The symbols ${K}_{0}$ and ${C}_{s0}$ represent the thermal conductivity and specific heat of the material at the reference temperature ${T}_{0}$. On the other hand, the parameter ${K}_{1}$ is a minor, non-positive factor that explains the effect of temperature changes on thermal conductivity and specific heat. By substituting Eq (22) into Eq (26), we can get

In Eq (27), the term $\beta {K}_{1}\frac{{\partial }^{2}\phi }{\partial {x}^{2}}$ can be ignored due to its small value, leading to

The previous equation means that the physical properties ($K$ and ${C}_{s}$) depend linearly on the conduction temperature. The following Kirchhoff transformation can be taken into account

By repeating the differentiation twice for the variable $x$ in Eq (29), the following expression can be derived:

By differentiating Eq (29) with respect to time, we get:

By time differentiation of Eq (29) and then multiplying by $K\left(\phi \right)$, we acquire

The term $\beta K\left(\phi \right)\frac{{\partial }^{3}\phi }{\partial t\partial {x}^{2}}$ can be ignored due to its very small value and due to linearity. Using Eq (31), we reach

When Eqs (30) and (33) are combined, the nonlinear fractional heat transfer Eq (25) turns into a linear equation and takes the following form:

Also, the following mapping will be used:

Also, in order to achieve linearity, Eqs (22) and (24) can be approximated with the following formulas:

Dimensionless formulas play a crucial role in physical and mathematical modeling, facilitating simplification and enabling meaningful comparisons across different systems or contexts. The following non-dimensional variables can be taken into account to facilitate the system of governing equations:

where ${c}_{0}^{2} = \frac{\lambda +2\mu }{\rho }$ and $\chi = \frac{\rho {C}_{s}}{K}$.

As a result, Eqs (34)–(37) can be expressed in dimensionless forms using Eq (26) and deleting the primes to become

where $\varepsilon = \frac{{\gamma }^{2}{T}_{0}}{{\rho }^{2}{{c}_{0}^{2}C}_{s}}$.

The initial and regularity conditions can be taken into account as follows:

This study is based on the assumption that the surface $x = 0$ remains constrained. This implies that the material at this surface experiences either no displacement or deformation or that it remains constant. As a result, we have

Pulses from non-Gaussian thermal lasers can cause temperature differences and changes in the material that can happen in a variety of ways and at different times. This can lead to a wide range of mechanical and thermal reactions. Different thermal laser sources and processing circumstances allow for a broad variety of pulse forms and durations in on-Gaussian lasers. It will be assumed that the surface $x = 0$ experiences a pulsating heat flux $\mathcal{H}\left(x, t\right)$ in the form of non-Gaussian laser pulses as follows ^[52]:

where $j$ is the amplitude of the heat flow or laser fluence, $R$ is the reflection coefficient, $\delta$ is the penetration depth, and ${t}_{p}$ is the pulse duration. Due to the nature of the thermal boundary condition, the modified Fourier law (13) involving heat flux will be taken into account:

Using Eqs (30) and (45), condition (46) can be reformulated as follows:

where ${\alpha }_{0} = \frac{\delta {t}_{p}{K}_{0}}{j\left(1-R\right)}\sqrt{\frac{\pi }{4ln\left(2\right)}}$.

5.   The methodology used to solve the problem

The Laplace transform is a valuable mathematical technique used in analyzing and solving differential equations across many scientific and engineering fields, especially for linear systems that exhibit time-dependent behavior. This approach allows complex systems to be solved by transforming them from the space-time domain to the space domain. The Laplace transform of the function $ℊ\left(x, t\right)$, denoted by $\overline{ℊ}\left(x, s\right)$, can be defined as follows:

By applying Laplace transformations, Eqs (39)–(42) can be rewritten to become:

where

Equations (51) and (52) may be reformulated as

where

By removing the variable $\overline{e}$ from Eqs (54) and (55), we can obtain the following differential equation:

where

The solution to Eq (57) can be expressed, satisfying the regularity condition, as follows:

where ${\mathcal{M}}_{3} = {\alpha }_{4}/\left({𝒷}^{4}-ℓ{𝒷}^{2}+𝓂\right)$ and ${\mathcal{M}}_{1}$ and ${\mathcal{M}}_{2}$ are the integration constants.

Moreover, the parameters ${𝒽}_{1}$ and ${𝒽}_{1}$ satisfy the solutions of the equation

By inserting (59) into Eq (55), we can obtain a solution for $\overline{e}$ as follows:

Also, when substituting Eq (61) into relationship (20), we can obtain the expression formula for the displacement $\overline{𝓊}$ in the transformed field as follows:

The conductive temperature $\overline{\phi }$ can be determined in the Laplace transform field by solving Eq (29) and using the solution of the function $\overline{{\Psi }}$ to obtain

Moreover, by substituting Eq (63) into Eq (22), we can conclude:

Finally, by substituting Eqs (55) and (64) into Eq (50), we can derive

Using the Laplace transform, the boundary conditions (44) and (47) can be rewritten in the following forms:

where

In Eq (68), $\mathrm{E}\mathrm{r}\mathrm{f}\mathrm{c}\left(\mathrm{z}\right)$ denotes the complementary error function.

By substituting the expressions $\overline{{\Psi }}$ and $\overline{𝓊}$ given in Eqs (59) and (62) into boundary conditions (66) and (67), the integration coefficients ${\mathcal{M}}_{1}$ and ${\mathcal{M}}_{2}$ can be determined.

6.   Numerical techniques for Laplace transform inversions

After obtaining the analytical formulas for the physical fields, the inverse Laplace transform (LT) is then applied to obtain the functions in the time domain. Instead of employing direct methods, approximate numerical methods are frequently utilized since it is difficult to acquire inverse solutions to Laplace transforms using direct methods. On the other hand, approximate numerical approaches can produce reliable estimations of the inverse LT without the requirement of inverting the variables directly. These approaches may be implemented using a wide variety of software tools and packages, and they can be based on a variety of numerical techniques, which include numerical integration, interpolation, or rational function approximation. The particular situation at hand, in addition to the amount of accuracy and efficiency that is sought, should be taken into consideration while selecting the specific numerical approach to use. For particular kinds of functions or applications, certain approaches could be more appropriate than others, while others might be more effective or accurate for a variety of parameter ranges.

The Fourier series approach is one of the many methods that may be utilized to quantify the inverse Laplace transform. Through the utilization of the Fourier series, this is a technique that may be utilized to approximate the inverse LT. To implement this approach, first, the function in question is approximated as a sum of sinusoidal functions, and then the inverse LT of each sinusoidal function is computed by making use of the features of the LT. Additional information about this technique can be found in the study presented by Honig and Hirdes in ^[53].

7.   Numerical results

To assess the credibility of the suggested fractional thermal model, which incorporates phase delay and two temperatures, we can examine a numerical illustration involving an elastic substance like copper. This section will analyze the behaviors of non-dimensional field variables, such as displacement variation, temperature rise, and stress distributions. The study will focus on how these variables change with different contrast coefficients and fractional operators. The analysis will be presented using various graphical and tabular forms. Numerical data on the physical characteristics of materials like copper were utilized for the purpose of comparison and computation. The numerical computations included the following physical characteristics of copper ^[54]:

Numerical values of the fields were calculated using programming tools such as Mathematica. Presenting the data obtained in tabular form facilitates the use of these results by other researchers, as it enables them to easily conduct comparative studies and verify the results. For the computations, three separate scenarios might be utilized, as outlined below.

7.1.   The effect of the temperature discrepancy

In this section of the discussion, the effect of the temperature discrepancy coefficient ($\beta$) on the thermophysical variables under study will be studied. Under conditions where time does not play a role, the disparities between the conductive temperature $\phi$ and the thermodynamic temperature $\theta$ are directly related to the amount of heat being provided. When there is no heat source present, the two temperatures are equal. For issues that vary with time, especially those related to wave propagation, the two temperatures are often distinct, regardless of the existence of a heat source.

The application of the fractional two-phase heat transfer model (FDPL), which incorporates the Atangana-Baleanu fractional derivative operator, will be considered. It is worth noting here that if the discrepancy factor $\beta$ is set to zero, the results are consistent with the one-temperature fractional DPL (1TFDPL) model. When the value of the parameter $\beta$ is greater than zero, we will have a two-temperature fractional DPL (2TFDPL) model. Figures 2–5 display the thermodynamic and conductive temperature variations ($\theta$ and $\phi$), displacement ($𝓊$), and normal stress ($\sigma$) over different distances ($x$). Moreover, for computational analysis, the values of other constants were considered as follows:${\tau }_{\phi } = 0.02$, ${\tau }_{q} = 0.05$, ${t}_{0} = 0.1$, $\alpha = 0.85$, and ${K}_{1} = -0.04$.

By examining the curves of the figures, the limited transfer of wave speed can be deduced, which confirms the principle of the proposed model. The results show the prominent effect of the discrepancy factor $\beta$ on the field differences. It is also clear from the graphs presented that the different models show large differences in values near the surface boundary, and the observed differences diminish steadily as the distance from the boundary increases. This observed phenomenon can be attributed to the effect of laser thermal flux pulses that were applied to the outer boundaries of the surface. Figures 2 and 3 show that the two temperature distributions take maximum values at the surface $x = 0$ due to the presence of convection, and then gradually decrease after that until they disappear within the medium.

Figure 2 shows the decreasing path of the conductive heat field $\phi$ with increasing depth within the semi-medium. The figure also shows that the magnitude of the function $\phi$ in the case of the 1TFDPL model scenario (at $\beta = 0$) is larger than that of the 2TFDPL model with two temperatures. Moreover, it has been observed that the parameter "$\beta$", which refers to the two-temperature coefficient, significantly affects the conductive heat distribution $\phi$. Therefore, in light of the results, it is necessary to differentiate between thermodynamic and conductive temperatures. Figure 3 depicts the effect of the two temperature distinction coefficients on the behavior of the thermodynamic temperature $\theta$. Figure 3 depicts the relationship between $\theta$ and the distance coordinate $x$ in the case of both the 1FDPL and 2FDPL models, taking into account distinct values of the discrepancy parameter $\beta$. Specifically, $\beta = 0$ refers to the one-temperature thermal model, while $\beta > 0$ refers to the two-temperature thermal model. As a result of the presence of heat flux from laser pulses affecting the surface, the temperature $\theta$ is initially higher and then gradually decreases as one goes deeper into the material. The results obtained are consistent with consistent physical features of thermoelasticity and provide experimental support for the accuracy and applicability of generalized models, as described in ^[55]. In light of the results of the proposed thermoelastic framework, it is necessary to build a new system for classifying and evaluating the thermal conductivity of materials based on the coefficient of contrast between the two temperatures ^[56].

Figure 4 illustrates the relationship between the displacement $𝓊$ and the change in distance $x$ for both the 1TFDPL and 2TFDPL systems. The diagram illustrates the alteration in the displacement field $𝓊$ within the elastic body, resulting in deformations and variations in thermal stress. This phenomenon occurs due to exposure to a time-dependent, fluctuating thermal field, which allows the molecules in the half-space next to the boundary surface to expand freely in a certain direction. Figure 4 demonstrates that the displacement field $𝓊$ satisfies the mechanical requirement set for the issue. Due to the assumption of surface restriction, the displacement $𝓊$ first becomes zero and subsequently grows until it reaches peak points before gradually diminishing inside the medium. The impact of altering the thermal contrast coefficient values on the displacement distribution $𝓊$ is also seen. Regarding the 2TFDPL model, the curves exhibit a lower position in comparison to the outcomes of the 1TFDPL model, which aligns with the findings mentioned in article ^[57].

Figure 5 illustrates the relationship between thermal stress $\sigma$ and depth $x$. The graphs demonstrate the significant impact of thermal stress $\sigma$ on the variation of the contrast coefficient $\beta$ over time. The stress differences exhibit similar characteristics in both fractional thermal models, with the differences becoming more noticeable toward the surface of the elastic medium. It is important to mention that the thermal stress $\sigma$ increases as the parameter $\beta$ increases, independent of the value of $x$. The shown curves indicate that the pressure exhibits negative values for the 1TFDPL model, but it exhibits positive values for the 2TFDPL model. From the previous results, it is clear that the generalized two-temperature fractional thermoelasticity model gives results about the importance of knowing the difference between the conductive temperature wave and the thermodynamic temperature wave. This differentiation is crucial to prevent the formation of discontinuous patches or sudden peaks in stresses and deformations within elastic media.

7.2.   Comparison of fractional differentiation operators

The use of fractional calculus has been prevalent in mathematical modeling and the examination of many physical phenomena. This is because it has the ability to depict complex and non-local behavior that conventional integer-order models are unable to adequately represent. Fractional calculus has several advantages compared to conventional integer-order models. These include the capacity to depict long-range interactions, non-local memory effects, and intricate dynamical behavior. Additionally, fractional calculus exhibits flexibility and adaptation across various systems and sizes. In recent years, many academics have studied the challenges related to heat transfer in various mechanical and thermal conditions using fractional Caputo derivatives (C) and Riemann-Liouville fractional derivatives (RL). The Atangana-Baleanu (AB) time-fractional derivative has been suggested as a more modern and modified alternative to the Caputo-Fabrizio (CF) approach. The AB time-fractional derivative is a mathematical operator that is both non-singular and non-local. It is known for its ability to capture memory effects and transmission phenomena. This operator has found applications in modeling many physical phenomena, including viscoelasticity, anomalous diffusion, and electrical circuits.

The current study presented a fractional heat conduction model that includes the fractional differential operators $\left({D}_{t}^{\left(\alpha \right)}\right)$ and two distinct temperatures. In this subsection of the discussion, a comparative analysis of the fractional derivatives AB, CF, and C will be presented with an emphasis on the differences in the associated results between them. Due to the convergence of the numerical values, the effect of the difference of the fractional differentiation operators and the fractional parameter $\alpha$ has been presented tabularly. These effects on areas of the system, such as temperature, displacement, and thermal stress, were studied and then analyzed geometrically and physically. The study also included a comparison between the results of thermoelastic models that include fractional derivatives and those that include integer derivatives ($\alpha = 1$). Furthermore, for the purposes of computational analysis, the values of ${\tau }_{\phi }$, ${\tau }_{q}$, ${t}_{0}$, and $\beta$ were assumed to be 0.02, 0.05, 0.1, and 0.001, respectively.

The most significant inferences that can be drawn from the numerical findings are summarized in the following points:

● The new FDPL thermoelastic model appears to reduce the temperature field diffusion compared to the traditional model with integer operators, as can be seen from the results of Table 1. This reduction can be attributed to the incorporation of fractional operators with fractional derivatives, which effectively reduces the thermal diffusion within the medium. This observation is consistent with both experimental results and proven physical facts.

● Compared to the Caputo-Fabrizio fractional thermoelastic model (2TFDPL-CF) and the Atangana-Baleanu thermoelastic fractional model (2TFDPL-AB), the thermodynamic and conductive temperatures ($\theta$ and $\phi$) in the case of the two-temperature thermoelastic Caputo fractional thermoelastic model with phase delays (2TFDPL-C) are shown to be significantly greater as the value of the fractional parameter is increased.

● It is imperative to acknowledge that the transmission of thermal and mechanical waves within an elastic media is contingent upon the specific fractional order derivative operator utilized. Hence, it can be inferred that the fractional arrangement considers the variability of the elastic medium, as each operator and fractional order signifies a distinct characteristic of elasticity.

● The theoretical results obtained can provide potential benefit in addressing some practical issues involving fractional models. Based on theoretical results and experimental evidence, it is possible to choose a fractional mathematical model that shows the correspondence between experimental results and theoretical results.

● Tables 1 to 4 showcase the empirical results, which suggest that the power-law kernel exhibits a resilient memory effect in long-term historical data. On the other hand, non-singular kernels may be more suitable for describing relaxation or diffusion processes characterized by exceptionally strong memory.

● The decay rate of the Caputo-Fabrizio type derivative relaxation model with a stretched exponential kernel is shown to be significantly faster than the decay rate of the model with a power-law kernel. This suggests that utilizing a Caputo-Fabrizio-type derivative model with a stretched exponential kernel allows for describing a broader spectrum of relaxation phenomena, in contrast to employing a power-law kernel.

● It is important to acknowledge that a mathematical model employing the Atangana-Baleanu type derivative, with a stretched Mittag–Leffler function kernel, exhibits a slower diffusive motion compared to a model utilizing an exponential kernel.

● Furthermore, it is highly anticipated that the novel fractional derivatives of Atangana-Baleanu (AB) and Caputo-Fabrizio (CF) would significantly contribute to the investigation of the macroscopic characteristics of particular materials associated with nonlocal exchanges. These exchanges predominantly govern the properties of these materials.

7.3.   Effect of changing properties depending on temperature

The variation in thermal conductivity can present challenges and advantages in many applications. Engineers and scientists must consider these variances when constructing systems that include heat transmissions, such as electrical devices, thermal insulation, or materials utilized in harsh environments. Gaining a comprehensive understanding of the factors influencing the variability of thermal conductivity is of utmost importance to effectively enhance these systems' operational efficiency. The motivation behind this study is to provide a novel model that accurately represents the behavior of thermoplastic materials whose thermal characteristics vary with temperature.

This study examines the relationship between temperature and physical quantities, namely thermal conductivity and specific heat, inside a two-temperature extended fractional thermoelasticity model. It aims to determine how these values vary with temperature and if they exhibit linear changes. Figures 6–9 illustrate the comparisons between the distribution patterns of the analyzed fields and the change in dimensionless distance, $x$. In order to elucidate the distinction between a scenario where the characteristics are constant and a scenario where they are mutable, we have considered the following values of the parameter that governs this dependency: The values of ${K}_{1}$ are 0, -0.02, -0.04, and -0.06. The current discussion and presentation of numerical calculations uses the fractional thermoelasticity model (2TFDPL-AB) with the Atangana-Baleanu fractional derivative operator, which takes into account the effects of the two-temperature parameter ($\beta$). Moreover, to perform the numerical analysis, the following values were assigned: ${\tau }_{\phi } = 0.02$, ${\tau }_{q} = 0.05$, ${t}_{0} = 0.1$, $\alpha = 0.85$, and $\beta = 0.04$.

Unsurprisingly, it is evident that the alteration of the thermal conductivity significantly impacts the characteristics and dynamics of the analyzed physical parameters. Although the observed events in the researched fields exhibit comparable behavior, there is a variation in the amplitude of each. Upon analyzing Figures 6 and 7, it is evident that the thermodynamic and conductive temperatures ($\theta$ and $\phi$) exhibit a positive correlation with the coefficient of variation of thermal conductivity, ${K}_{1}$. Examining Figures 6 and 7 reveals that, when the coefficient of variation of thermal conductivity ${K}_{1}$ grows, both the displacement and thermal stress ($𝓊$ and $\sigma$) decrease significantly.

The results show that it is important to use fractional generalized thermoelasticity models with changing specific heat and thermal conductivity when studying isotropic elastic materials. By incorporating variable thermal conductivity and specific heat into the theoretical model of the system, the resulting model can provide a more accurate depiction of the system's behavior and can include the complex interactions between its many components. Through the comparison of findings and curves derived from various models and assumptions, one may evaluate the reliability and precision of the models and determine the most favorable methodologies and techniques for modeling and evaluating system behavior ^[58,59,60].

In contemporary engineering, structural components frequently experience temperature fluctuations of significant size, leading to a situation where the material characteristics of these parts may no longer be considered as having constant values, even in an approximate manner. The thermal and mechanical characteristics of materials exhibit temperature-dependent behavior, necessitating the inclusion of temperature dependency in the thermal stress measurement in these components.

8.   Conclusions

The objective of this research is to introduce a novel framework for two-degree and two-phase generalized thermoelasticity, specifically in relation to the fractional heat conduction equation. The analysis focuses on fractional-order differential operators that are both single and non-singular. The conventional power-law kernel is substituted with a Mittag-Leffler function and a non-singular exponential kernel.

The suggested model examines the effects of elastic thermal stress, strain, displacement, conductive temperature, and thermodynamic temperature in an infinite, isotropic, and homogeneous elastic half-space that is exposed to heat flow in the form of laser pulses. In addition, it has been considered that thermal characteristics change linearly with temperature variation. The equations controlling the two-temperature fractional generalized thermoelasticity theory were solved using the Laplace transform method. Numerical inversion of the altered solutions was carried out utilizing a Fourier series expansion methodology. Ultimately, a quantitative assessment of the different thermophysical properties of copper materials was achieved. An exhaustive study of the data was provided, encompassing the examination of the operators, the fractional order parameter, the discrepancy coefficient, and the variable thermal conductivity and their respective consequences.

The findings suggest that field variables, such as temperature, displacement, and thermal stress, are influenced by both spatial position ($x$) and instantaneous time ($t$), as well as the two temperature factors ($\beta$) and fractional order differential operators. The results also indicate that the influence of fractional differential operators on the analyzed system variables is particularly significant in the theoretical investigation of heat conduction issues. The fractional coefficient plays a crucial role in minimizing the thermal diffusion of a thermoplastic material. Therefore, it is essential to consider this component while investigating and creating new types of elastic materials, particularly those with high viscosity. Furthermore, it is highly anticipated that the distinct fractional derivatives introduced by Atangana-Baleanu (AB) and Caputo-Fabrizio (CF) will have a substantial impact on the investigation of the macroscopic characteristics of certain materials that include nonlocal interactions. These interactions mostly govern the characteristics of these materials.

The phenomenon of finite speeds of propagation is evident in all the illustrated figures and tables. This outcome is anticipated as the thermal wave propagates at a limited velocity. Noticeable disparities in the physical magnitudes are seen between the one-temperature theory and the two-temperature theory. In the context of generalized fractional thermoelasticity, the two-temperature theory is considered to be more realistic compared to the one-temperature theory.

In general, the fractal thermoelasticity model is a promising and active area of research and development. It has the potential to offer new insights and answers to complicated issues occurring in the field of thermoelasticity, as well as in other areas of study. Despite this, the model has several restrictions and difficulties, and it is necessary to do further study and validation to advance the current level of knowledge and comprehension of the subject matter.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors express their gratitude to the Deanship of Scientific Research at Jouf University for providing financial support for this study through research grant No. (DSR-2021-03-03193).

Conflicts of interest

The authors assert that there are no conflicts of interest.