Condition numbers of the generalized ridge regression and its statistical estimation

1.   Introduction

Ridge regression ^[1] is a classical and powerful statistical method to inhibit the multicollinearity among covariates in the following linear regression model:

where $y\in\mathbb{R}^{n}$ is the observations of response, $X\in \mathbb{R}^{n\times p}$ is the design matrix of covariates, $\beta \in \mathbb{R}^{p}$ is the unknown parameter vector, and $\epsilon\sim \mathcal{N}(0, \sigma^2 I_n)$ with $I_n$ being the identity matrix of order $n$. The ridge estimator of model (1.1) is given by

where $\lambda > 0$ is the ridge parameter. Finding the ridge estimator (1.2) is also equivalent to solving the following optimization problem:

where $\|\cdot\|_2$ is the Euclidian vector norm. Equation (1.3) is also known as the famous Tikhonov regularization technique dealing with discrete ill-posed problems ^[2]. Incorporating weights to the observations and generalizing the ridge penalty leads to the following generalized ridge regression (GRR) model:

where $\Sigma\in \mathbb{R}^{n\times n}$ is a diagonal matrix with nonnegative elements on its diagonal, $\Theta\in\mathbb{R}^{p\times p}$ is a symmetric positive definite matrix and determines the speed and direction of shrinkage, and $\beta_0$ is a user-specified, non-random target vector ^[3]. By the Karush-Kuhn-Tucker (KKT) optimality condition, taking the derivative of the objective function in (1.4) with respect to $\beta$ shows that the generalized ridge estimator (GRE) denoted by ${\hat{\beta}_{gr}}$ satisfies the following normal equation:

and ${\hat{\beta}_{gr}}$ is given by

Though the diagonal matrix $\Sigma$ can give different weights to the observations, the correlation structure between observations cannot be captured. For this reason, we relax the assumption and allow $\Sigma$ to be a symmetric positive definite matrix, which makes (1.4) the exact combination of weighted least squares loss and the generalized ridge penalty. By varying the weighting matrices $\Sigma$ and $\Theta$, the generalized Tikhonov regularization ^[2] can also be derived from (1.4).

The multicollinearity in covariates often leads to a large condition number of $X^TX$, which plays a central role in the sensitivity analysis of the least squares estimate of model (1.1) [4,Ch. 5]. Condition number is a powerful tool in measuring the sensitivity of a problem and gives the maximum amplification of the resulting change in solution, with respect to a small perturbation in the input data, and has been studied for too many numerical linear algebra problems to list here. {The development of the definition of condition number and their comparison should be referred to ^[5,6,7,8,9]. In this paper, we employ the following very general definition of condition number given by ^[6], which covers most of the popular condition numbers in the current literature as its special cases.

Definition 1. (projected condition number) ^[6] Let ${\mathcal{F}}: \mathbb{R}^{p}\rightarrow \mathbb{R}^{q}$ be a continuous map defined on an open set $Dom({\mathcal{F}})$, the domain of definition of ${\mathcal{F}}$, and $L\in \mathbb{R}^{q\times k}$, then the projected condition number of ${\mathcal{F}}$ at $x\in Dom({\mathcal{F}})$ with respect to $L\in \mathbb{R}^{q\times k}$ is defined by

where $\cdot/\cdot$ is the componentwise division satisfying that a nonzero numerator divided by a zero denominator remains unchanged, $\xi_L\in \mathbb{R}^{k}$ and $\alpha\in\mathbb{R}^{p}$ are parameters with a requirement that if some element of $\alpha$ is zero, then the corresponding element of $\Delta x$ must also be zero, and $\|\cdot\|_\mu$ and $\|\cdot\|_\nu$ are two vector norms defined on $\mathbb{R}^{p}$ and $\mathbb{R}^{k}$, respectively.

In Definition 1, the matrix $L$ can be treated as an operator to transform the image vector of ${\mathcal{F}}$, for example, when we set $L = e_i$, the $i$-th element of the canonical base of $\mathbb{R}^q$, Definition 1 gives the condition number of the $i$-th element of the image vector. The two vector norms $\|\cdot\|_\mu$ and $\|\cdot\|_\nu$ also enable us to give different measures of the perturbations in the input and output spaces, respectively. When the map ${\mathcal{F}}$ is Fréchet differentiable, we can get the following Theorem 1.1, which largely reduces the difficulty of finding the supremum of (1.7) to establishing the Fréchet derivative of ${\mathcal{F}}$. The rationality of Definition 1 and its relationship with other popular condition numbers has been extensively discussed, and the interested readers are referred to ^[6,7,8] and the references therein.

Theorem 1. ^[6] When the map ${\mathcal{F}}$ in Definition 1 is Fréchet differentiable at $x$, the explicit expression of the projected condition number $\kappa_{L{\mathcal{F}}}(x)$ is given by

where $D{\mathcal{F}}(x)$ is the Fréchet derivative of ${\mathcal{F}}$ at $x$, $\xi_L^{\ddagger}$ is a vector with $\xi_{Li}^{\ddagger} = \left\{ \begin{array}{ll} 1/\xi_{Li}, & \hbox{ $\xi_{Li}\neq 0$, } \\ 1, & \hbox{ $\xi_{Li} = 0, $ } \end{array} \right.$ ${\mathrm{Diag}}(\xi_L^{\ddagger})$ and ${\mathrm{Diag}}(\alpha)$ are diagonal matrices with the elements of the vector on the diagonal, and $\|\cdot\|_{\mu\nu}$ is the matrix norm induced by the vector norms $\|\cdot\|_\mu$ and $\|\cdot\|_\nu$.

The condition number theory of some special cases of model (1.4) have been well studied in the literature, like (weighted) linear least squares problem ^[6,7,10,11] and (generalized) Tikhonov regularization ^[12,13,14]. In this paper, we will extend the current results and consider the condition number theory of the GRR model (1.4). To compute the exact value of the condition number is usually expensive, we also propose some efficient statistical condition estimation methods to reduce the computation burden but still give reasonable estimates. The rest of the paper is organized as follows. In Section 2, we present the explicit expressions of condition numbers for the GRR model (1.4). Section 3 contains the statistical condition estimation method for estimating the condition numbers of the GRR model (1.4). Numerical experiments and a conclusion of the whole paper are given as Sections 4 and 5, respectively.

2.   The condition number of the GRR problem

In order to present the condition number of the GRR model (1.4), we first explicitly define the map ${\mathcal{F}}$ in (1.7) as follows:

Let $\tilde{y} = y +\Delta y$, $\tilde{X} = X +\Delta X$, $\tilde{\Sigma} = \Sigma +\Delta \Sigma$, $\tilde{\Theta} = \Theta +\Delta \Theta$ and $\tilde{\beta}_0 = \beta_0 +\Delta \beta_0$, then the perturbed GRR model is given by

where $\hat{\beta}_{\tilde{gr}}$ is the GRE of the perturbed GRR model (2.2) and satisfies the following normal equation:

For simplicity of presentation and with a little abuse of notation, we set

then the projected condition number of the GRR model (1.4) can be defined as follows.

Definition 2. Considering the perturbed GRR model (2.2), the projected condition number of the GRR model (1.4), with respect to $L\in \mathbb{R}^{q\times k}$, is defined by

where $\xi_L\in \mathbb{R}^{k}$, $\gamma\in \mathbb{R}^{n}$, $\Psi\in\mathbb{R}^{n\times p}$, $\Phi\in\mathbb{R}^{n\times n}$, $\Upsilon\in\mathbb{R}^{p\times p}$, $\varpi\in\mathbb{R}^{p}$ are parameters with a requirement that if some element is zero, then the corresponding element in the numerator must also be zero, and $\|\cdot\|_\mu$ and $\|\cdot\|_\nu$ are two vector norms defined on $\mathbb{R}^{n+np+n^2+p^2+p}$ and $\mathbb{R}^{k}$, respectively.

If we set $\hat{\beta}_{\tilde{gr}} = \hat{\beta}_{gr} + \Delta\beta$ and further assume that

with $\|\cdot\|$ denoting appropriate norm and $\epsilon$ being a sufficiently small positive real number, then with some algebra and omitting the higher order terms, we can get the following equality by subtracting (1.5) from (2.3)

where $\mathcal{W} = X^T\Sigma X + \Theta$ and $r = y - X{\hat{\beta}_{gr}}$. Backing to Definition 2, we have

and

With (2.5), the first order expansion of $\Delta \beta$, we can establish the explicit expression of the projected condition number for the GRR model (1.4).

Theorem 2. For the GRR model (1.4), when $\Sigma$ and $\Theta$ are symmetric positive definite matrices, the explicit expression of its projected condition number can be established and given as

where $\mathcal{W} = X^T\Sigma X + \Theta$, $r = y - X{\hat{\beta}_{gr}}$, ${\mathcal{M}} = {\mathcal{W}}^{-1}\otimes(\Sigma r)^T - \hat{\beta}_{gr}\otimes ({\mathcal{W}}^{-1}X^T\Sigma)$ and ${\mathcal{N}} = (\beta_{0} - \hat{\beta}_{gr})^T\otimes {\mathcal{W}}^{-1}$.

Proof. Since ${\mathrm{vec}}(ABC) = \left(C^T\otimes A\right) {\mathrm{vec}}(B)$, we apply ${\mathrm{vec}}(\cdot)$ operator to $\Delta\beta$ and get

Let ${\mathcal{M}} = {\mathcal{W}}^{-1}\otimes(\Sigma r)^T - \hat{\beta}_{gr}^T\otimes ({\mathcal{W}}^{-1}X^T\Sigma)$ and ${\mathcal{N}} = (\beta_{0} - \hat{\beta}_{gr})^T\otimes {\mathcal{W}}^{-1}$. We can rewrite (2.6) as

With (2.7), we can get the following Fréchet derivative of ${\mathcal{F}}$

and complete the proof by Theorem 1. □

Theorem 2 presents the generic form of the condition number for the GRR problem (1.4). For practical applications, we need to specify the norms and the parameters with respect to concrete backgrounds. We also note that the explicit expression of the condition number contains specific structures due to the Kronecker product, which enlarges the size of the matrix and increases its computational burden. In the following, we will discuss some specific forms of the condition number and its computational issues.

2.1.   The normwise condition number

When $\mu = \nu = 2$, the parameter vectors and matrices $\gamma$, $\Psi$, $\Phi$, $\Upsilon$, and $\varpi$ reduce to real numbers and equal to $\left\|{\mathrm{vec}}([y, X, \Sigma, \Theta, \beta_0])\right\|_2$ and $\xi_L = \|L^T\hat{\beta}_{gr}\|_2\neq 0$, $\kappa_{L{\mathcal{F}}}$ gives an overall treatment of the perturbations, then we can obtain the projected relative normwise condition number of the GRR model (1.4) from Theorem 2, which is given as follows.

Theorem 3. When $\mu = \nu = 2$, $\gamma = \Psi = \Phi = \Upsilon = \varpi = \left\|{\mathrm{vec}}(y, X, \Sigma, \Theta, \beta_0)\right\|_2$, and $\xi_L = \|L^T\hat{\beta}_{gr}\|_2\neq 0$, the projected relative normwise condition number of the GRR model (1.4) is given by

where $\|\cdot\|_2$ denotes the spectral norm of a matrix or the Euclidian norm of a vector, $\mathcal{W} = X^T\Sigma X + \Theta$, $r = y - X{\hat{\beta}_{gr}}$, ${\mathcal{M}} = {\mathcal{W}}^{-1}\otimes(\Sigma r)^T - \hat{\beta}_{gr}^T\otimes ({\mathcal{W}}^{-1}X^T\Sigma)$ and ${\mathcal{N}} = (\beta_{0} - \hat{\beta}_{gr})^T\otimes {\mathcal{W}}^{-1}$.

Note that the main difficulty for explicitly computing the value of $\kappa_{L{\mathcal{F}}}^2$ lies in the following term

which contains the Kronecker product and is also called the projected absolute normwise condition number. To remove the Kronecker product in $\kappa_{L{\mathcal{F}}}^{2a}$, the matrix cross-product and Cholesky factorization techniques may be used to establish the compact but equivalent forms of the normwise condition number ^[6,7]. However for large problems, there is no need to form the condition number explicitly and a suitable estimate will be enough [15,Ch. 15]. Here, we present a compact form of $\kappa_{L{\mathcal{F}}}^{2a}$ that not only removes the Kronecker product, but also provides important support for its estimation procedure described in Section 3.

Theorem 4. When $\mu = \nu = 2$, $\gamma = \Psi = \Phi = \Upsilon = \varpi = \left\|{\mathrm{vec}}(y, X, \Sigma, \Theta, \beta_0)\right\|_2$, and $\xi_L = \|L^T\hat{\beta}_{gr}\|_2\neq 0$, the projected absolute normwise condition number $\kappa_{L{\mathcal{F}}}^{2a}$ of the GRR model (1.4) can also be written as

In particular, when $L = e_i$, we can get the projected absolute normwise condition number of the $i$-th element in the solution

where $\mathcal{W} = X^T\Sigma X + \Theta$, $r = y - X{\hat{\beta}_{gr}}$ and $\mathcal{K} = \left(1+\|\hat{\beta}_{gr}\|^2_2\right)X^T\Sigma^2X + \|r\|_2^2X^TX + \left(\|\beta_0 - \hat{\beta}_{gr}\|_2^2 + r^T\Sigma^2 r\right)I_p + \Theta^2$.

Proof. For the spectral norm, we have $\|A\|_2 = \|AA^T\|_2^{\frac{1}{2}}$ with $A\in\mathbb{R}^{m\times n}$. We apply this equality to $\kappa_{L{\mathcal{F}}}^{2a}$ and get its equivalent form

Since

and

we can easily get

with $\mathcal{K} = \left(1+\|\hat{\beta}_{gr}\|^2_2\right)X^T\Sigma^2X + \|r\|_2^2X^TX + \left(\|\beta_0 - \hat{\beta}_{gr}\|_2^2 + r^T\Sigma^2 r\right)I_p + \Theta^2$. □

Remark 1. Theorem 4 presents a compact but equivalent form $\kappa_{L{\mathcal{F}} 1}^{2a}$ of the absolute condition number $\kappa_{L{\mathcal{F}}}^{2a}$ that does not contain the Kronecker product. Comparing the size of the matrix, we can find that $\kappa_{L{\mathcal{F}} 1}^{2a}$ requires much less storage memory compared with $\kappa_{L{\mathcal{F}}}^{2a}$. When the exact value of the normwise condition number is computed, $\kappa_{L{\mathcal{F}} 1}^{2a}$ also needs much less Central Processing Unit (CPU) time on a computer, and this will be illustrated through numerical experiment in Section 4. Here, we also need to point out that the Cholesky factorization technique was not employed to derive the compact form of $\kappa_{L{\mathcal{F}}}^{2a}$. The main reason is that the Cholesky factorization based compact form only gives a moderate size of matrix, which is still larger than $\kappa_{L{\mathcal{F}} 1}^{2a}$, though much smaller than $\kappa_{L{\mathcal{F}}}^{2a}$. Thus, considering the economics of storage space, we only derived $\kappa_{L{\mathcal{F}} 1}^{2a}$.

2.2.   The mixed and componentwise condition numbers

Since the normwise condition number gives an overall treatment of all the parameters and ignores the data structure and scaling of the input data, the mixed and componentwise condition numbers are proposed ^[8,9]. By varying the norms and parameters in Theorem 2, we can also obtain the mixed and componentwise condition numbers of the GRR model (1.4).

Theorem 5. When $\mu = \nu = \infty$, $\gamma = y$, $\Psi = X$, $\Phi = \Sigma$, $\Upsilon = \Theta$, $\varpi = \beta_0$, $\xi_L = \|L^T\hat{\beta}_{gr}\|_{\infty}$, and $L^T\hat{\beta}_{gr}$ in sequel, the projected mixed and componentwise condition numbers of the GRR model (1.4) are given by

and

respectively, where $\|\cdot\|_{\infty}$ is the infinite norm giving the largest magnitude among each element of a vector.

Proof. The proof is quite easy due to the following fact that for matrix $A$ and vector $d$, the following equalities hold

Applying the above equalities to Theorem 2 gives the desired results. □

For the mixed and componentwise condition numbers, the aforementioned matrix-cross product techniques cannot be used to remove its Kronecker product. Here, we present some upper bounds that require little storage space and can be efficiently computed.

Theorem 6. The mixed and componentwise condition numbers of the GRR model (1.4) can be correspondingly bounded as follows:

where

Proof. The explicit expression of $\mathcal{G}^{ubd}$ is derived with the Lemma 5 in ^[10], which is straightforward and omitted here. □

The condition number not only gives a measure of the sensitivity of the problem, but also can be used to give the first order estimate of the forward error. Thus, in many practical applications, the exact value of the condition number is usually not needed and within a 10 factor estimate will be enough. Many techniques have been proposed to estimate the normwise, mixed, and componentwise condition numbers, like the power method ^[15], probabilistic, and statistical based methods ^[16]. Considering the computational efficiency and its powerful adaptability, we would like to employ the statistical condition estimation method to estimate the condition numbers of the GRR model.

3.   The small-sample statistical condition estimation

The small-sample statistical condition estimation (SSCE) theory has been widely applied to estimate the normwise, mixed, and componentwise condition numbers of many numerical linear algebra problems, and examples include the linear system ^[17], least squares problem ^[18,19], matrix factorization ^[20,21], eigenvalue problem ^[22], matrix function ^[16], Sylvester equation ^[23], and so on.

To introduce the framework of SSCE, we consider the following differentiable function $f: \mathbb{R}^{p}\rightarrow \mathbb{R}$, and its Taylor expansion is given by

where $\delta$ is a small positive real number, $\nabla f(x)$ is the gradient vector of $f$ at $x$, and $z$ is a unit 2-norm vector. It is well known that $\|\nabla f(x)\|_2$ is the absolute condition number and gives an appropriate measure of the local sensitivity of $f$ at $x$. According to ^[16], if we choose $z$ uniformly and randomly from a unit sphere $\mathcal{S}_{p-1}$, then the expected value of $|\nabla f(x)^Tz|$ is

where $E_1 = 1$, $E_2 = \frac{\pi}{2}$, and for $p > 2$,

$E_p$ is the Wallis factor and can be approximated by $E_p \approx \sqrt{\frac{2}{\pi(p-\frac{1}{2})}}$ with high accuracy ^[18], then we can define

as the condition estimator, which can give a very reliable estimate of $\|\nabla f(x)\|_2$; specifically, the following probability inequality holds

The accuracy of condition estimator can be further improved by adding $k$ samples

where $[z_1, z_2, \cdots, z_k]$ is the orthonormalization of $z_1, z_2, \cdots, z_k$ being selected uniformly and randomly from $\mathcal{S}_{p-1}$. The $k$-sample condition estimator $\eta(k)$ can achieve a very high accuracy with a small size of samples, for example, when $k = 3$ and $\tau = 10$, we have

which means the reliability of a condition estimate within a factor 10 can be improved from 0.936338 ($k = 1$) to 0.9988389 by just adding 2 extra samples.

3.1.   Normwise condition estimation

Note that the SSCE method is very suitable for estimating the condition number of certain elements in the solution. However, for the normwise condition number derived in Section 2.1, what we need to estimate is the spectral norm of a large matrix. This means we need to make some modification on the SSCE method to estimate the normwise condition number of the GRR model (1.4). Here, we employ the strategy proposed by ^[19] for estimating the normwise condition number of the linear least squares problem.

According to ^[19], to estimate the normwise condition number of the GRR model (1.4), we first need to estimate the condition number of $z^T_ix$ with

and then the normwise condition number can be estimated by

where $[z_1, \cdots, z_k]$ can be obtained via QR factorization [4,Ch. 5] of a random matrix $Z\in\mathbb{R}^{p\times k}$. Note that when ${\mathcal{W}}$ and $\mathcal{K}$ are available, the main computational cost for computing $\kappa_i$ is $\mathcal{O}(\frac{1}{3}p^3)$ when Cholesky factorization is used to compute ${\mathcal{W}}^{-1}z_{i}$. If we further take the QR factorization into account, then we can find that the total computational cost for estimating the normwise condition number is $\mathcal{O}(\frac{k}{3}p^3+pk^2)$. We summarize the above procedure as the following Algorithm 1.

3.2.   Mixed and componentwise condition estimation

From Theorem 5, we note that computing the mixed and componentwise condition numbers is equivalent to finding the largest elements in a vector. The SSCE method can be easily applied to estimate the mixed and componentwise condition numbers by extending the aforementioned SSCE procedure from scalar valued function to vector valued function. We present it in the following Algorithm 2. Note that when the orthonormal vectors are obtained, the computational complexity of SSCE for mixed and componentwise condition numbers also lies in solving the positive definite linear system, which makes it similar to that of Algorithm 1.

4.   Numerical experiment

To illustrate our theoretical results, we will use a randomly generated GRR model with a known solution. The desired GRR model is constructed as follows. The coefficient matrices are given by

where $U_i$ and $V_i$ ($i = 1, 2$) are random orthogonal matrices and $\Lambda_i$ $(i = 1, 2, 3)$ are diagonal matrices with $\lambda_{ij}$ arranged in a descending order on its diagonal. Actually, (4.1) exactly gives the eigenvalue decomposition of $\Sigma$ and $\Theta$ and the singular value decomposition of $X$ ^[4]. $\Lambda_1$ and $\Lambda_2$ contain the eigenvalues of $\Sigma$ and $\Theta$, and $\Lambda_3$ the singular values of $X$. $\beta$ is a random vector generated from the standard normal distribution. $r$ is a random vector with specified magnitude, that is, $\|r\|_2$ is given. Then, based on the normal Eq (1.5), we set

and get the random GRR model with specified solution. To compute $\hat{\beta}_{gr}$, the preconditioned conjugate gradients (PCG) method will be employed to solve the normal Eq (1.5). With the above setting, we can control the condition number of the coefficient matrices and easily get

All the experiments are performed in Matlab R2018a on a PC with Intel i7-10700 CPU @ 2.90 GHz and 16.00 GB random access memory.

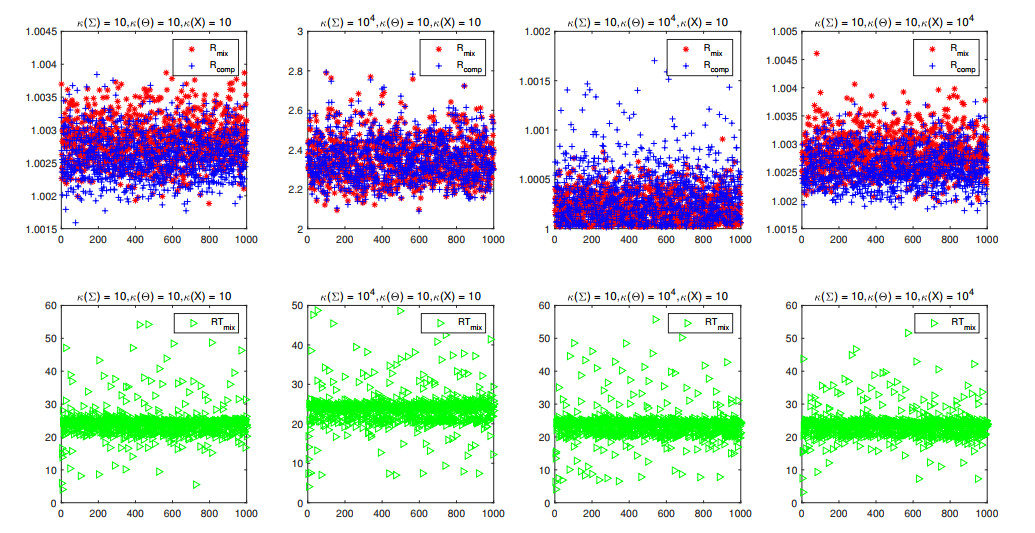
Example 1. In this example, we will test the tightness and computational efficiency of the upper bounds of the mixed and componentwise condition numbers derived in Theorem 6. For this, we define the following ratios:

$\mathrm{R}_{\mathrm{mix}}$ and $\mathrm{R}_{\mathrm{comp}}$ demonstrate that the closer of the ratios are to 1, the tighter the upper bounds are. $\mathrm{RT}_{\mathrm{mix}}$ and $\mathrm{RT}_{\mathrm{comp}}$ measure the computational efficiency of the upper bounds with respect to CPU time and the larger value shows better computational efficiency. For a clear presentation, we present the numerical results in Figure 1, using a red asterisk and blue plus sign to denote $\mathrm{R}_{\mathrm{mix}}$ and $\mathrm{R}_{\mathrm{comp}}$, correspondingly. Note that there is very little difference in computational complexity between mixed and componentwise condition numbers and its upper bounds. We only present the results of CPU time comparison of the mixed condition number and its upper bound denoted by a green square.

In our computation, we set $L = I_n$, $n = 100$, $p = 60$, $\|r\|_2 = 10^{-2}$, $\lambda_{ij}$s in the denominator of (4.2) are equal to 1, $\lambda_{i1}$ in the numerator are set to accommodate the given condition number, and the rest $\lambda_{ij}$s are equally spaced. The normal Eq (1.5) is solved with the Matlab command $\texttt{pcg}$ with relative residual smaller than $10^{-10}$ and maximum iterations smaller than 100. By varying the condition numbers of coefficient matrices (4.2), we repeat 1000 times for each setting and present the numerical results in Figure 1. From the first row of Figure 1, we observe that the majority of the ratios are close to 1. This indicates that the derived upper bounds for the mixed and componentwise condition numbers of the GRR model (1.4) are quite tight. On the other hand, from the second row of Figure 1, we notice that most of the ratios exceed 20. This implies that these upper bounds can be computed efficiently, resulting in a significant improvement in CPU time by a factor of 20. Thus, in practical applications, we can use the upper bounds to measure the illness of the GRR model rather than the exact mixed and componentwise condition numbers.

Example 2. In this example, we will check the efficiency of the SSCE of condition numbers of the GRR model (1.4) with respect to accuracy and CPU time. Similar to the former example, we also define some ratios

The first row of the above ratios measures the accuracy of the SSCE method and the second row measures the efficiency. Specifically, although $\kappa_{L{\mathcal{F}}}^{2a}$ in (2.9) and $\kappa_{L{\mathcal{F}}1}^{2a}$ in (2.10) give the same values, they have very different storage requirement and computational efficiency. Thus, we only give $\mathrm{R_{\mathbf{N1}}}$ to measure the accuracy of the normwise SSCE condition estimator, whereas $\mathrm{RT_{\mathbf{N1}}}$ and $\mathrm{RT_{\mathbf{N2}}}$ are employed to compare the computational efficiency. Moreover, note that the computational complexities of computing or estimating the mixed and componentwise condition numbers have very little difference, so we only present the CPU time comparison via $\mathrm{RT}_{\mathbf{C}}$. For a clarity, we also use figures to present our results.

In our experiment, we set $L = I_n$, $n = 200$, $p = 100$, $\|r\|_2 = 10^{-1}$, $\kappa(\Sigma) = 10$, $\kappa(\Theta) = 10$, $\kappa(X) = 10$, and the other settings are the same as that in Example 1. The numerical results are reported in Figure 2. From the first row in Figure 2, we can find that the SSCE method can give reliable estimates of the mixed and componentwise condition numbers for its ratios within a factor of 10. For the normwise condition number, the SSCE method may give slight overestimates, which coincides with the phenomenon in ^[19]. From the second row in Figure 2, we note that the ratios are much smaller than 1, which means, in general, the SSCE condition number estimates require much less CPU time compared with the explicit computation of the condition numbers. Comparing the first and second panels in the second row, we can also find that the compact form of the normwise condition number gives much gain of computational efficiency compared with its original form.

5.   Conclusions

In this paper, we extended the GRR model given in ^[3] by allowing the serial dependence of the observations and investigated the condition number theory of the new model. We first established the generic expression of the condition number of the GRR model (1.4). By varying the norms and parameters in the generic expression, the popular normwise, mixed, and componentwise condition numbers can be obtained as its special cases. Considering the computational difficulty in calculating the exact value of the condition number, we provided the compact form of the normwise condition number and the upper bounds of the mixed and componentwise condition numbers. We also proposed the SSCE condition number estimators for the normwise, mixed, and componentwise condition numbers. Numerical experiments were given to show the tightness and efficiency of the upper bounds and the proposed condition estimators.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The work was supported by Shandong Provincial Natural Science Foundation (Grant No. ZR2020QA034). WSX was also supported by Shandong Province Higher Education Youth Innovation and Technology Support Program (Grant No. 2023KJ199).

The authors would like to give their sincere thanks to the anonymous five reviewers for their detailed and helpful comments, which led to a much better presentation of their work.

Conflict of interest

The authors affirm that they have no conflicts of interest to disclose.