Microscopic mechanism of subgrade vibration compaction based on discrete element method

1.   Introduction

Fractional calculus (FC) is an appropriate tool to describe the physical properties of materials. Currently mathematical theories and realistic applications of FC are recognized. Thus fractional-order differential equations (FDEs) have been established for modeling of real phenomena in various fields such as physics, engineering, mechanics, control theory, economics, medical science, finance and etc. There are a lot of studies which deal with the numerical methods for FDEs. Modeling of spring pendulum in fractional sense and its numerical solution ^[1], numerical solution of fractional reaction-diffusion problem ^[2], study of the motion equation of a capacitor microphone in fractional calculus ^[3], fractional modeling and numerical solution of two coupled pendulums^[4], fractional telegraph equation with different types of solution such as fractional homotopy analysis transform method ^[5] and homotopy perturbation transform method ^[6] can be found in literatures.

Time fractional telegraph equation with Riesz space fractional derivative is a typical fractional diffusion- wave equation which is applied in signal analysis and the modeling of the reaction diffusion and the random walk of suspension flows and so on. Lately numerical methods such as finite element approximation ^[7], L1/L2 – approximation method, the standard/shifted Grunwald method and the matrix transform method ^[8], Chebyshev Tau approximation ^[9], radial basis function approximation ^[10], Low-rank solvers ^[11], and some other useful methods are used to find the approximate solutions of fractional diffusion equation with Riesz space fractional derivative. Differential transform method (DTM) is a reliable and effective method which was constructed by Zhoue ^[12] for solving linear and nonlinear differential equations arising in electrical circuit problems. This method constructs an analytical solution in the form of a polynomial based on Taylor expansion, which is different from traditional high order Taylor series method. DTM makes an iterative procedure to obtain Taylor series expansion, which needs less computational time compared to the Taylor series method. DTM was extended by Chen and Ho ^[13] into two dimensional functions for solving partial differential equations. One and two dimensional differential transform methods were generalized for ordinary and partial differential equations of fractional order (GDTM) by Odibat and Momani ^[14,15]. DTM and GDTM were applied by many authors to find approximate solution for different kind of equations. S. Ray ^[16] used the modification of GDTM to find numerical solution for KdV type equation ^[17]. More over, Soltanalizadeh, Sirvastava and Garg ^[18,19,20] applied GDTM and DTM to find exact and numerical solutions for telegraph equations in the cases of one-space dimensional, two and three dimensional and space –time fractional derivatives. Furthermore GDTM were applied to find numerical approximations of time fractional diffusion equation and differential-difference equations ^[21,22], as well as DTM was used to obtain approximate solution of telegraph equation ^[23].

In previous studies all types of partial differential equations such as telegraph equation, which were solved by DTM and GDTM were not involved Riesz space fractional derivative operator. This work investigates an improved scheme for fractional partial differential equations with Riesz space fractional derivative to obtain semi analytical solution for these types of equations. For the simplicity we consider a kind of telegraph equation with Riesz operator on a finite one dimensional domain in the form:

subject to the initial conditions

and boundary conditions

where $k > v \ge 0$ and $\eta > 0$ are constants.

Generally the Riesz space-fractional operator $\dfrac{\partial^\gamma}{\partial |x|^\gamma}$ over $[a, b]$ is defined by:

We suppose that $1 < \gamma < 2$, and $u(x, t), f(x, t), \phi(x)$ and $\psi(x)$ are real-valued and sufficiently well-behaved functions.

The main goal of this paper is providing an improved scheme based on GDTM to obtain numerical solution for Eq (1.1). To implement this technique we separate the main equation into sub equations by means of new theorems and definitions. This separation enable to derive a system of fractional differential equations. Then we apply improved GDTM for system of fractional differential equations to obtain system of recurrence relations. The solution will be attained with inverse transformation to the last system.

The rest of this study is organized as follows. Section 2 discusses preliminary definitions of fractional calculus. In section 3 we give some knowledge of two dimensional generalized differential transform method and two dimensional differential. transform method, afterward in section 4 the implementation of the method accompanied by new definitions and theorems are described while the equation contains Riesz space fractional derivative. Section 5 provides an error bound for two-dimensional GDTM. In section 6 some numerical examples are presented to demonstrate the efficiency and convenience of the theoretical results. The concluding remarks are given in section 7.

2.   Some definitions of fractional calculus

In this section some necessary definitions of fractional calculus are introduced. Since the Riemann-Liouville and the Caputo derivatives are often used, as well as the Riesz fractional derivative is defined based on left and right Riemann-Liouville derivatives, we focus on these definitions of fractional calculus. Furthermore in the modeling of most physical problems, the initial conditions are given in integer order derivatives and the integer order derivatives are coincided with Caputo initial conditions definition; therefore the Caputo derivative is used in numerical algorithm.

Definition 2.1. The left and right Riemann-Liouville integrals of order $\alpha > 0$ for a function $f(x)$ on interval $(a, b)$ are defined as follows,

where $\Gamma(z) = \int_0^{\infty}e^{-t}t^{z-1}dt, z \in C$ is the Gamma function.

Definition 2.2. The left and right Riemann-Liouville derivatives of order $\alpha > 0$ for a function $f(x)$ defined on interval $(a, b)$ are given as follows,

where $m-1 < \alpha \le m.$

Remark 2.3. From the Riemann-Liouville derivatives definition and the definition of the Riesz space fractional derivative one can conclude for $0 \le x \le L$

$\dfrac{\partial ^\gamma}{\partial |x|^\gamma}u(x, t) = - \xi_\gamma(_0^{R}D_x^\gamma+ _x^{R}D_L^\gamma)u(x, t)$ while $\xi_\gamma = \dfrac{1}{2 \cos \dfrac{ \gamma \pi}{2}}, \, \, \gamma \ne 1$, and $_0^{R}D_x^\gamma$ and $_x^{R}D_L^\gamma$ are left and right Riemann-Liouville derivatives.

Definition 2.4. The left and right Caputo derivatives of order $\alpha$ for a function $f(x)$ are defined as

There are relations between Riemann-Liouville and Caputo derivatives as follows:

It is clear that if $f^{(k)}(a) = 0, \, \, k = 0, 1, ..., m-1$ then the Riemann-Liouville and Caputo derivatives are equal. For comprehensive properties of fractional derivatives and integrals one can refer to the literatures ^[24,25].

3.   Generalized two dimensional differential transform and differential transform methods

Generalization of differential transform method for partial differential equation of fractional order was proposed by Odibat et al. ^[15]. This method was based on two-dimensional differential transform method, generalized Taylor's formula and Caputo fractional derivatives.

Consider a function of two variables $u(x, t)$ and suppose that it can be represented as a product of two single-variable functions, i.e $u(x, t) = f(x)g(t).$ If $u(x, t)$ is analytic and can be differentiated continuously with respect to x and t in the domain of interest, then the function $u(x, t)$ is represented as

where $0 < \alpha, \beta \le 1, \, U_{\alpha, \beta}(k, h) = F_{\alpha}(k)G_{\beta}(h)$ is called the spectrum of $u(x, t)$. The generalized two-dimensional differential transform of the function $u(x, t)$ is as follows

where $(D_{x_0}^{\alpha})^k = D_{x_0}^{\alpha} \cdot D_{x_0}^{\alpha} \cdots D_{x_0}^{\alpha}, \, \, k-$times, and $D_{x_0}^{\alpha}$ represents the derivative operator of Caputo definition.

On the base of notations (3.1) and (3.2), we have the following results.

Theorem 3.1. Suppose that $U_{\alpha, \beta}(k, h), V_{\alpha, \beta}(k, h)$ and $W_{\alpha, \beta}(k, h)$ are differential transformations of the functions $u(x, t), v(x, t) and \, \, w(x, t)$, respectively; then

(a) If $u(x, t) = v(x, t)\pm w(x, t)$ then $U_{\alpha, \beta} (k, h) = V_{\alpha, \beta} (k, h) \pm W_{\alpha, \beta} (k, h),$

(b) If $u(x, t) = cv(x, t), c \in R$ then $U_{\alpha, \beta} (k, h) = cV_{\alpha, \beta} (k, h),$

(c) If $u(x, t) = v(x, t)w(x, t)$ then $U_{\alpha, \beta}(k, h) = \sum_{r = 0}^{k} \sum_{s = 0}^{h} V_{\alpha, \beta}(r, h-s)W_{\alpha, \beta}(k-r, s),$

(d) If $u(x, t) = (x-x_0)^{n \alpha}(t-t_0)^{m \beta}$ then $U_{\alpha, \beta}(k, h) = \delta(k-n) \delta(h-m),$

(e) If $u(x, t) = D_{x_0}^{\alpha} v(x, t), \, \, 0 < \alpha \le 1$ then $U_{\alpha, \beta}(k, h) = \dfrac{\Gamma(\alpha(k+1)+1)}{\Gamma(\alpha k+1)}V_{\alpha, \beta}(k+1, h)$

Theorem 3.2. Suppose that $u(x, t) = f(x)g(t)$ and the function $f(x) = x^{\lambda}h(x),$ where $\lambda > -1$ and $h(x)$ has the generalized Taylor series expansion i.e. $h(x) = \sum_{n = 0}^{\infty}a_n(x-x_0)^{\alpha k},$ and

(a) $\beta < \lambda+1$ and $\alpha$ is arbitrary or

(b) $\beta\ge \lambda+1, \alpha$ is arbitrary, and $a_k = 0$ for $k = 0, 1, .., m-1,$ where $m-1 \le \beta \le m.$

Then the generalized differential transform (3.2) becomes

Theorem 3.3. Suppose that $u(x, t) = f(x)g(t)$ and the function $f(x)$ satisfies the condition given in theorem 3.2 and $u(x, t) = D_{x_0}^\gamma v(x, t)$ then

where $\alpha$ is selected such that $\gamma/ \alpha \in Z^+$.

The method and proofs of the theorems 3.1, 3.2 and 3.3 are well addressed in literature ^[14].

In case $\alpha = \beta = 1$, GDTM reduces to DTM which is briefly introduced as follows.

Definition 3.4. Suppose that $u(x, t)$ is analytic and continuously differentiable with respect to space $x$ and time t in the domain of interest, then

where the spectrum function $U(k, h)$ is the transformed function, which also is called T-function and $u(x, t)$ is the original function. The inverse differential transform of $U(k, h)$ is defined as

From these equations we have

Definition 3.4 eventuates the following relations

(a) If $u(x, t) = v(x, t)\pm w(x, t)$ then $U (k, h) = V (k, h) \pm W(k, h),$

(b) If $u(x, t) = cv(x, t)$ then $U(k, h) = cV (k, h),$

(c) If $u(x, t) = \dfrac{\partial}{\partial x}v(x, t)$ then $U(k, h) = (k+1)V(k+1, h),$

(d) If $u(x, t) = \dfrac{\partial^{r+s}}{\partial x^r \partial t^s}v(x, t)$ then $U(k, h) = \dfrac{(k+r)! (h+s)!}{k!h!}V(k+r, h+s),$

(e) If $u(x, t) = v(x, t)w(x, t)$ then $U(k, h) = \sum_{r = 0}^k \sum_{s = 0}^h V(r, h-s)W(k-r, s).$

The basic definitions and fundamental operations of two-dimensional differential transform can be found in literature ^[13].

4.   Description of the method

To gain an algorithm for applying GDTM to Eq (1.1) we need some new theorems and definitions which are presented as follows.

Theorem 4.1. Suppose $u(x, t) = \sum\nolimits_{k = 0}^{\infty} \sum_{h = 0}^{\infty} U(k, h)x^kt^h$ and $v(x, t) = _0^{R}D_x^\gamma u(x, t)$, $1 < \gamma < 2$, is the left Riemann-Liouville derivative then

Proof. By replacing $u(x, t) = \sum\nolimits_{k = 0}^{\infty} \sum_{h = 0}^{\infty} U(k, h)x^kt^h$ in the left Riemann-Liouville derivative definition it is easy to achieve

Theorem 4.2. Suppose $u(x, t) = \sum\nolimits_{k = 0}^{\infty} \sum_{h = 0}^{\infty}U(k, h)x^kt^h$ and $v(x, t) = _x^{R}D_l^{\gamma}u(x, t)$, $1 < \gamma < 2$, is the right Riemann-Liouville derivative, then

Proof. By replacing $u(x, k) = \sum\nolimits_{k = 0}^{\infty} \sum_{h = 0}^{\infty} U(k, h)x^kt^h$ in the right Riemann-Liouville derivative definition it is easy to obtain

With replacing $\xi-x = t$ and then $l-x = y$ we have

In both theorems 4.1 and 4.2 $L$ is Laplace transform operator which is defined as $L(f) = \int_0^{\infty}f(t)e^{-st}dt$ and $(f*g)$ represents the convolution of $f$ and $g$ which is defined as $(f*g) = \int_0^t f(t- \tau)g(\tau) d \tau.$

As it is observed in calculation of left and right Riemann-Liouville derivatives for function $u(x, t)$, coefficients of variables $x^{k-\gamma} t^h$ and $(l-x)^{k-\gamma}t^h$ are appeared, respectively. Therefore we expect to see functions of $x^{k-\gamma} t^h$ and $(l-x)^{k-\gamma}t^h$ in equations which involves Riesz space fractional derivatives. In DTM, it is traditional to expand the function $u(x, t)$ with respect to integer order of $x$ and $t$, i.e.

which means that $u(x, t)$ has Taylor series expansion. However $x^{k-\gamma}$ and $(l-x)^{k- \gamma}$ are not smooth enough on $[0, l]$, in this case we define different notation for differential transformation.

Definition 4.3. we use $\overline{U}_{\gamma, 0}(k, h)$ as a notation for differential transform of function $u(x, t)$ where $u(x, t)$ has the series representation in the form of $u(x, t) = \sum\nolimits_{k = 0}^{\infty}\sum\nolimits_{h = 0}^{\infty} \overline{U}_{\gamma, 0}(k, h)(x-x_0)^{k-\gamma}(t-t_0)^h$.

Definition 4.4. we use $\overline{\overline{U}}_{\gamma, 0}(k, h)$ as a notation for differential transform of function $u(x, t)$ where $u(x, t)$ has the series representation in the form of $u(x, t) = \sum\nolimits_{k = 0}^{\infty}\sum\nolimits_{h = 0}^{\infty} \overline{\overline{U}}_{\gamma, 0}(k, h)(l-(x-x_0))^{k-\gamma}(t-t_0)^h$.

Theorem 4.5. If $v(x, t) = _0^{R}D_x^\gamma u(x, t)\, \, \, 1 < \gamma < 2$, then $\overline{V}_{\gamma, 0}(k, h) = \dfrac{\Gamma(k+1)}{\Gamma(k+1-\gamma)}U(k, h)$ The proof follows directly from theorem 4.1 and definition 4.3 at $(x_0, t_0) = (0, 0)$.

Theorem 4.6. If $v(x, t) = _x^RD_l^\gamma u(x, t), \; 1 < \gamma < 2$, then

The proof follows directly from theorem 4.2 and definition 4.4 at $(x_0, t_0) = (0, 0)$.

These definitions and theorems assist to describe the implementation of the method. For this aim recall Eq (1.1), since $u(x, t)$ is supposed to be smooth enough, we primarily focus on special separation of $f(x, t)$ in Eq (1.1) into three functions $f_1, f_2, f_3$ as follows

where $f_1$ is a function which contains integer order of $x$ and fractional order of $t$ with the series representation as $f_1(x, t) = \sum\nolimits_{k = 0}^{\infty} \sum_{h = 0}^{\infty} F_1(k, h)(x-x_0)^k(t-t_0)^{\beta h}$ and $f_2$ is a function which contains $x^{k-\gamma}$ and t which has the series representation as $f_2 (x, t) = \sum\nolimits_{k = 0}^{\infty} \sum_{h = 0}^{\infty} \bar{F}_2(k, h)(x-x_0)^{k-\gamma}(t-t_0)^h$ and $f_3$ is a function involves $(l-x)^{k-\gamma}$ and t with the series representation as $f_3 (x, t) = \sum\nolimits_{k = 0}^{\infty} \sum_{h = 0}^{\infty} \bar{\bar{F}}_3(k, h)(l-(x-x_0))^{k-\gamma}(t-t_0)^h$, then we take the following three steps

Step1. The left parts of Eq (1.1) which do not have Riesz space derivatives are equivalent with the inhomogeneous part, which have integer order of $x$ and fractional order of t. i.e:

Now we apply GDTM as follows

where $F_1 (k, h)$ is the differential transform of $f_1 (x, t).$

Step2. As mentioned in remark 2.3 Riesz space derivative contains left and right Riemann-Liouville derivatives, i.e. $\dfrac{\partial^{\gamma}}{\partial |x|^{\gamma}}u(x, t) = -\xi_{\gamma}(_0^{R}D_x^{\gamma}+_x^{R}D_L^{\gamma})u(x, t)$, for the next step we set

then with using differential transform method according to theorem 4.5 we get

Step3. For the last step we set

Then with applying differential transform by means of new notation according to the theorem 4.6 we obtain,

The differential transform of initial and boundary conditions are

where $\Phi(k)$ and $\Psi(k)$ are differential transforms of $\phi(k)$ and $\psi(k)$, respectively. The recurrence relations (4.2), (4.4), and (4.6) are compatible and we calculate $U(k, h), \; \; k, h = 0, 1, 2, ...$, with using of each one and (4.7). Then with the inverse transformation we find the approximate solution of $u(x, t)$ as follows

5.   Error estimation

In this section we find an error bound for two dimensional GDTM. As we know DTM is obtained from GDTM when the fractional powers reduce to integer order, therefore one can find an error bound for two dimensional DTM at the same manner.

As mentioned before we assume that $u(x, t)$ is analytic and separable function which has the series representation in the form of $u(x, t) = \sum\nolimits_{k = 0}^{\infty} \sum_{h = 0}^{\infty} U(k, h)(x-x_0)^{\alpha k}(t-t_0)^{\beta h}$, then we have the following theorems.

Theorem 5.1. Suppose $v(x) = \sum\nolimits_{k = 0}^{\infty}a_k(x-x_0)^{\alpha k}$ and let $\phi_k(x) = a_k(x-x_0)^{\alpha k},$ then the series solution $\sum\nolimits_{k = 0}^{\infty} \phi_k(x)$ converges if $\exists \, 0 < \gamma_1 < 1$ Such that $\| \phi_{k+1}(x) \| \le \gamma_1 \| \phi_k(x) \|, \, \, \forall k \ge k_0 \, for \, some\, k_0 \in N$, where $\| \phi_{k}(x)\| = \max_{x \in I} | \phi_k(x) |$ and $I = (x_0, x_0+r)$, $r > 0$.

Remark 5.2. The series solution $v(x) = \sum\nolimits_{k = 0}^{\infty}a_k(x-x_0)^{\alpha k}$ converges if $\lim_{k \to \infty} \left| \dfrac{a_{k+1}}{a_k} \right| < 1/ \max_{x \in I}(x-x_0)^ \alpha, I = (x_0, x_0+r), \, \, r > 0$, in this case the function $v(x)$ is called $\alpha$-analytic function at $x_0$.

Remark 5.3. Suppose $S_n = \phi_0(x)+\phi_1(x)+ \cdots + \phi_n(x)$, where $\phi_k(x) = a_k(x-x_0)^{\alpha k}$ then for every $n, m \in N, \, \, n \ge m > k_0$ we have $\| S_n-S_m\| \le \dfrac{1-\gamma_1^{n-m}}{1-\gamma_1}\gamma_1^{m-k_0+1} \max_{x \in I}| \phi_{k_0}(x)|.$ Notice that when $n \to \infty$ then

The proof of theorem 5.1 and remarks 5.2 and 5.3 are given in literature ^[26]. Now suppose that $v(x)$ and $w(t)$ are $\alpha$-analytic and $\beta$-analytic functions respectively such that $v(x) = \sum\nolimits_{k = 0}^{\infty} a_k(x-x_0)^{\alpha k}$ and $w(t) = \sum_{h = 0}^{\infty} b_k(t-t_0)^{\beta h}$, then the truncated error of $u(x, t) = v(x)w(t)$ is found according to the next theorem.

Theorem 5.4. Assume that the series solution $v(x) = \sum_{k = 0}^\infty \phi_k(x)$ with $\phi_k(x) = a_k(x-x_0)^{\alpha k}$ and $w(x) = \sum_{h = 0}^\infty \psi_h(x)$ where $\psi_h(x) = a_h(t-t_0)^{\beta h}$ converges, then the maximum absolute truncated error of function $u(x, t) = v(x)w(t)$ is estimated by

where $M = \max_{x \in I}|v(x)|, \, N = \max_{t \in J}|w(t)|$, $I = (x_0, x_0+r)$, $J = (t_0, t_0+l)$, $\gamma_1$ and $\gamma_2$ are determined by theorem 5.1.

Proof. from remark 5.3 for $n \ge m \ge m_0$ for any $m_0 \ge 0$ $\|S_n-S_m\| \le \dfrac{1-\gamma_1^{n-m}}{1-\gamma_1}\gamma_1^{m-m_0+1} \max_{x \in I}| a_{m_0}(x-x_0)^{\alpha m_0}|$ where $S_n = \phi_0(x)+\phi_1(x)+ \cdots + \phi_n(x)$, and $a_{m_0} \ne 0$,

as well we conclude that if $T_p = \psi_0(t)+\psi_1(t)+ \cdots + \psi_p(t)$, for $p \ge q \ge q_0$ for any $q_0 \ge 0$ then

It is clear that, when $n \to \infty$ then $S_n \to v(x)$, and when $p \to \infty$ then $T_p \to w(t)$, now

Since $0 < \gamma_1, \gamma_2 < 1$, we have $(1-\gamma_1^{n-m}) < 1$ and $(1-\gamma_2^{p-q}) < 1$, and the last inequality reduces to

It is clear that when $m \rightarrow \infty$ and $q \rightarrow \infty$ the right hand side of last inequality tends to zero, therefore $\sum_{k = 0}^m \sum_{h = 0}^q \phi_k(x) \psi_h(t) \rightarrow u(x, t)$.

We refer the readers to Anastassiou et al. ^[29] to see the monotone convergence of extended iterative methods.

6.   Numerical results

In this section, some examples are illustrated to verify the applicability and convenience of the mentioned scheme. It is notable that if the partial derivative in equation is integer order, DTM is used and in the case that the equation has fractional order derivatives then GDTM is used. The examples are presented in both cases.

Example 6.1. Consider the following Riesz -space fractional telegraph equation with constant coefficients ^[27]

where the initial and boundary conditions are

and the inhomogeneous term is

Under these assumptions, the exact solution of Eq (6.1) is $u(x, t) = x^2(1-x)^2 \sin t$.

For using mentioned algorithm, first we separate $f(x, y)$ in the form of

where $f(x, t) = f_1 (x, t)+f_2 (x, t)+f_3 (x, t)$, with this separation we set

With applying differential transform method and using theorems (4.5) and (4.6) to system (6.3) we get

Where $S(h)$ and $C(h)$ indicate differential transforms of sint and cost, respectively which are obtained as

The differential transform of initial and boundary conditions are

From (6.6) it is easy to get $U(0, 1) = U(1, 1) = 0$ and $U(2, 1) = 1, \; \; U(3, 1) = -2, \; \; U(4, 1) = 1$ and $U(k, 1) = 0$ for$k\ge 5$.

From (6.4) with simple calculation we obtain

$U(k, 2) = 0$ for$k = 0, 1, 2, ...$

With using inverse differential transform method we have

Which is the exact solution.

Chen et al. ^[27] proposed a class of unconditionally stable difference scheme (FD) based on the Pade approximation to solve the problem (6.1) at $t = 2.0$ with several choices for $h$ and $\tau$, where $h$ and $\tau$ are the space and time step sizes, respectively. In Table 1, we compare $\| u-u_{N} \|_2$ at $t = 2.0$ with different choice for $N$. The results show that our method is more accurate than the three schemes which were proposed on their work. The main advantage of this method is lower computational work than Chen et al. ^[27], where with $\tau = 10^{-4}$ as a time step length they need to evaluate 2000 iterations to reach $t = 2$.

Example 6.2. Consider the following partial differential equation with Riesz space fractional derivative ^[28]

with initial condition

and boundary conditions

where the forced term is

The exact solution of Eq (6.7) is $u(x, t) = x^2(1-x)^2(t+1)^4.$

For using the method, we separate the force term as

Now we set

With using differential transform method for system (6.9) and applying theorems 4.5 and 4.6 we get

Differential transform of initial and boundary conditions are

From (6.11) we have

From (6.10) we obtain

and $U(k, h) = 0$ for $h\ge 5$, and $k = 0, 1, 2, ...$.

Therefore with using inverse differential transform we have

Zhang et al. ^[28] achieved numerical results based on difference scheme for Eq (6.7) with different values for $\gamma$. However with our proposed improved GDTM, an analytical solution for Eq (6.7) is found.

Example 6.3. Consider the following fractional telegraph equation with Riesz space fractional derivative ^[7]

with initial condition

and boundary conditions

where the inhomogeneous term is

The exact solution of Eq (6.12) is $u(x, t) = (4t^2-4t+1)x^2(1-x)^2.$

For using mentioned algorithm, we set

Suppose $2\beta = 1.6$, we choose $\alpha = 0.2$ and using GDTM and theorems 4.5 and 4.6 for fractional partial differential equation we get

Generalized differential transform for initial and boundary conditions are

Form (6.15) we obtain $U(2, 0) = 1, \; U(3, 0) = -2, \; U(4, 0) = 1$ and $U(k, 0) = 0$ for$k = 0, 1, 5, 6, ...,$

$U(2, 5) = -4, \; U(3, 5) = 8, \; U(4, 5) = -4$ and $U(k, 5) = 0$ for $k = 0, 1, 5, 6, ...$

From (6.14) it is easy to find

$U(2, 10) = -4, \; U(3, 10) = 8, \; U(4, 10) = -4$ and $\; U(k, 10) = 0$ for $k = 0, 1, 5, 6, ...$

Otherwise $U(k, h) = 0.$

With using inverse generalized differential transform we obtain

Zhao et al. ^[7] used fractional difference and finite element methods in spatial direction to obtain numerical solution for Eq (6.12).Contrary, with our method the exact solution is achieved for this equation which demonstrate that this method is effective and reliable for fractional telegraph equation with Riesz space-fractional derivative.

Example 6.4. For the last example consider the following Riesz space fractional telegraph equation

where the initial and boundary conditions are

and the inhomogeneous term is

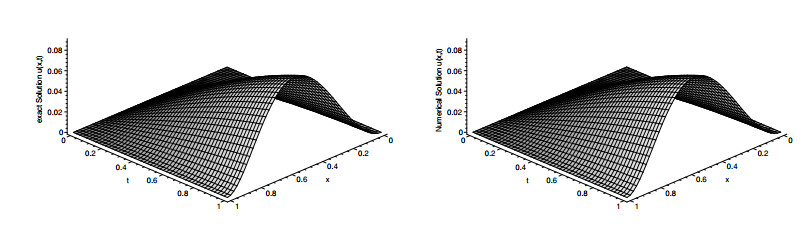
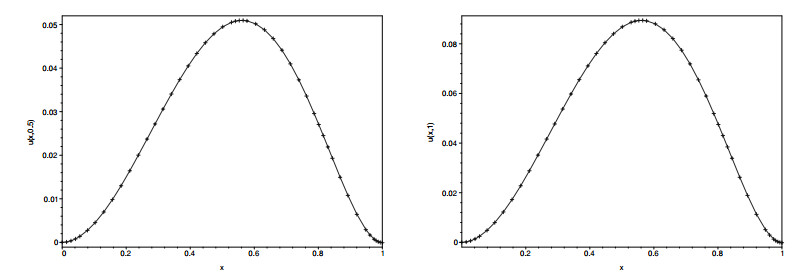
Under these assumptions, the exact solution of Eq (6.16) is $u(x, t) = x^2(1-x)^2e^x \sin t.$ The approximate solution (with $m = q = 10$) and exact solution of example 6.4 are illustrated in Figure 1. Also the exact solution and approximate solution in cases $t = 0.5$ and $t = 1$ are demonstrated in Figure 2, which shows the accuracy of the method.

7.   Conclusion

Riesz derivative operator appears in some partial differential equations such as telegraph equation, wave equation, diffusion equation, advection-dispersion equation and some other partial differential equations. These types of equations previously were solved by GDTM without considering Riesz derivative operator. In this paper an improved scheme based on GDTM was developed for solution of fractional partial differential equations with Riesz space fractional derivative. For this purpose the main equation was separated into sub-equations, in a manner which GDTM can be applied. With this trend the main equation reduces to system of algebraic recurrence relations which can be solved easily. The acquired results demonstrated that this method required less amount of computational work compared to the other numerical methods; moreover it was efficient and convenient technique. Providing convergent series solution with fast convergence rate was the advantage of the proposed method, which the numerical examples revealed these facts.

Acknowledgments

The authors would like to express his gratitude to the anonymous referees for their helpful comments and suggestions, which have greatly improved the paper.

Conflict of interest

The authors declare no conflict of interests in this paper.