Unbalanced signed graphs with eigenvalue properties

1.   Introduction

For a simple connected graph $H = (V(H), E(H))$ on $n$ vertices, a signed graph (S.G) $\hat{H} = (H, \Psi)$ is a graph obtained by assigning weights ${\pm1}$ to the edges of $H$ by a signature function $\Psi:$E(H)$\longrightarrow \{1, -1\}$. The matrix $A(\hat{H}) = [a_{rs}]$ is referred as the adjacency matrix of $\hat{H}$ with order $n \times n$, where

The collection $\sigma(A(\hat{H}))$ of all eigenvalues of $A(\hat{H})$ is referred as spectrum of $\hat{H}$, that is:

where $m_{i}$ are multiplicities of $\hat{h} _{i}(\hat{H})$, for $i = 1, 2, \cdots n$.

A non singular S.G is a graph with a non singular adjacency matrix. An S.G with a cycle as an underlying graph is referred to as a signed cycle. If the number of edges with weight -1 in a cycle is even (odd), then the cycle is referred to as a balanced (unbalanced) signed cycle. The S.Gs can be categorized into two families (balanced and unbalanced). If all the cycles in an S.G are balanced, then that S.G is referred to as a balanced S.G, otherwise, it is referred to as an unbalanced S.G.

If two S.Gs have identical spectra, then they are referred to as co-spectral S.Gs.

Theorem 1.1. ^[11] An S.G is balanced $\Longleftrightarrow$ it has the same the spectrum as that of its underlying unsigned graph.

Definition 1.1. If for every $(\hat{h_{i}}(\hat{H}), m_{i})\in\sigma (A(\hat{H}))$, its additive inverse $(\hat{-h_{i}}(\hat{H}), m_{j})$ is also in $\sigma (A(\hat{H}))$ then $\hat{H}$ is said to fulfill the symmetric eigenvalue property. Furthermore, if $m_{i} = m_{j}$, then the symmetric eigenvalue property becomes strong symmetric eigenvalue property.

Definition 1.2. If each $(\hat{h_{i}}(\hat{H}), m_{i})\in\sigma (A(\hat{H}))$ implies $1/(\hat{h_{i}}(\hat{H}), m_{\acute{j}})\in\sigma (A(\hat{H}))$, then, $\hat{H}$ is said to fulfill reciprocal eigenvalue property, that is, the property $(\mathcal{R})$. Furthermore, if $m_{i} = m_{j}$, then, $\hat{H}$ is said to fulfill strong reciprocal eigenvalue property, the property $(\mathcal{SR})$.

Definition 1.3. If each $(\hat{h_{i}}(\hat{H}), m_{i})\in\sigma (A(\hat{H}))$ implies $-1/(\hat{h_{i}}(\hat{H}), m_{\acute{j}})\in\sigma (A(\hat{H}))$, then, $\hat{H}$ is said to fulfill anti-reciprocal eigenvalue property, that is, the property $(\mathcal{-R})$. Furthermore, if $m_{i} = m_{j}$, then, $\hat{H}$ is said to fulfill strong reciprocal eigenvalue property, the property $(\mathcal{-SR})$.

If $\hat{H}$ fulfills both the properties $(\mathcal{SR})$ and $(-\mathcal{SR})$, then $\hat{H}$ also fulfills the symmetric eigenvalue property. A graph is bipartite if it contains only even cycles, otherwise, it is non bipartite. Degree one vertex is known as a pendent vertex.

Theorem 1.2. A balanced S.G $\hat{H} = (H, \Psi)$ is bipartite $\Longleftrightarrow$ it fulfills the symmetric eigenvalue property.

Proof. Using Theorem 1.1, $\hat{H}$ and $H$ are co-spectral and by ^[3], $H$ is bipartite $\Longleftrightarrow$ it fulfills the symmetric eigenvalue property.

A polynomial $P(s)$ is said to fulfill the property ($\mathcal{-SR}$), whenever for each root $\hat{h}$, $-1/\hat{h}$ is root of $P(s)$ with the same multiplicity.

The following Propositions 1.1 and 1.2 give necessary and sufficient conditions for a polynomial to fulfill the property ($\mathcal{-SR}$), the property ($\mathcal{SR}$) and the symmetric eigenvalue property.

Proposition 1.1. ^[1] A polynomial $P(s) = a_{0}+ a_{1}s+... +a_{2k}s^{2k}$ fulfills property ($\mathcal{-SR}$) $\Longleftrightarrow$

Proposition 1.2. ^[14] A polynomial $P(s) = \sum_{i = 0}^{2k} a_{i}s^{i}$ fulfills property ($\mathcal{SR}$) if and only if $a_{2k-i} = a_i$ or $a_{2k-i} = -a_i$ for $i = 0, 1, 2 \cdots, 2k$, that is palindromic or anti-palindromic, respectively.

S.Gs are applicable in various fields of mathematics. In 1953, Harary ^[12] presented the notion of S.Gs. In ^[5], construction of pair of equienergetic S.Gs was given. In ^[7], authors characterized simple connected S.Gs with at most degree $4$ and with exact two distinct adjacency eigenvalues and constructed four different regular S.Gs with two distinct eigenvalues. In ^[9], Ghorbani et al. in 2020 answered the problem proposed by Belardo et al. (2018) by constructing symmetric spectra of S.Gs, which are not sign-symmetric. So far, a lot of research has been done on spectra of S.Gs but very little effort has been made on eigenvalue properties (symmetric, $(\mathcal{R})$, $(-\mathcal{R})$, $(\mathcal{SR})$ and $(-\mathcal{SR})$). However, for unsigned graphs, extensive research work can be found for these properties. In ^[3], it was proved that for a graph $H$, $H$ is bipartite $\Longleftrightarrow$ for every $\hat{h} _{i}(H)\in\sigma (A(H))$, its additive inverse is also in $\sigma (A(H))$. In ^[4], it was proved that if a unicyclic graph $H$ fulfills the property $(\mathcal{SR}),$ then it is bipartite and is simple corona graph for $g\neq4$, where $g$ is the girth of $H$. Also, some non-corona graphs with girth 4, fulfilling the property $(\mathcal{SR}),$ were constructed. In ^[6], it was proved that if a connected unicyclic bipartite graph having unique perfect matching fulfills the property $(\mathcal{SR})$, then the graph is invertible and its inverse is also a unicyclic graph. In ^[1], it was proved that a weighted graph $H_{w}$ (with unique perfect matching), in which non-matching edges are given positive weights, where as matching edges are given weight 1 fulfills the property $(-\mathcal{SR})$ if and only if $H_{w}$ is simple corona. In ^[8], a family of weighted graphs (with unique perfect matching) was presented in which diagonal entries are zero in the inverse of its adjacency matrix. Furthermore, it was shown that, in this family, non-corona graphs with the property $(-\mathcal{SR})$ cannot be obtained even for a sole weight function. In ^[10], Ahmad et al. constructed seven different non-corona classes using corona triangles, corona squares and corona pentagons, which fulfill the property $(-\mathcal{SR})$. Moreover, they concluded that the property $(-\mathcal{SR})$ can be proved for classes formed by corona cycles of finite length in the similar way. In ^[2], more general families of non-corona graphs fulfilling the property $(-\mathcal{SR})$ were constructed.

Theorem 1.3. ^[13] If an S.G $\hat{H}$ is bipartite, then for each $\hat{h} _{i}(\hat{H})\in\sigma (A(\hat{H}))$, its additive inverse is also in $\sigma (A(\hat{H}))$.

Now the questions arise "Does the symmetric eigenvalue property hold for non bipartite S.Gs?" and "Are there any classes of non bipartite S.Gs with the symmetric eigenvalue property or any of the reciprocal eigenvalue properties?". Our aim is to investigate the symmetric and reciprocal eigenvalue properties in non bipartite S.Gs.

Notations: Throughout this paper, $\underline{{\bf{1}}}$ represents a column vector with all entries 1, $\underline{{\bf{0}}}$ represents column vector having all entries 0. $O$ denotes a matrix with all entries 0. $P_{2}^{+}$ represents a signed path on 2 vertices with edge assigned $+$ sign whereas $P_{2}^{-}$ represents a signed path on 2 vertices with edge assigned $-$ sign. $P(G; s)$ denotes the characteristic polynomial for the adjacency matrix in the variable $s$.

2.   The symmetric and reciprocal eigenvalue properties in non bipartite S.Gs

In this section, we will construct unbalanced S.Gs $\hat{\mathfrak{C}}^{(m, 1)}_{3}$ and $\hat{\mathfrak{C}}^{(m, 2)}_{5}$, for each even positive integer $m$, which are non bipartite and prove that for all even positive integers $m$, $\hat{\mathfrak{C}}^{(m, 1)}_{3}$ fulfills the symmetric eigenvalue property as well as properties $(-\mathcal{SR})$ and $(\mathcal{SR})$, where as the graphs $\hat{\mathfrak{C}}^{(m, 2)}_{5}$, for all even positive integers $m$ fulfills the symmetric eigenvalue property and is close to fulfill the property $(-\mathcal{SR})$ and $(\mathcal{SR})$.

The following lemma will be used in the proofs of Theorems 2.3 and 2.4.

Lemma 2.1 gives determinant of a block matrix and will be used in the proofs of our theorems to evaluate the determinant of a block matrix.

Lemma 2.1. ^[2] Let $\dot{R} = \left[\begin{array}{cc} K & L \\ M & N \\ \end{array} \right]$ be a block matrix such that $K$ and $N$ are square matrices, then,

Let ${G}_1$ and ${G}_2$ be two connected graphs of order $n$ and $m$, respectively. The corona product ${G}_1\circ {G}_2$ is a graph formed by one copy of graph ${G}_1$ and $n$-copies of ${G}_2$ and by connecting each vertex of $jth$ copy of ${G}_2$ with the $jth$ vertex of ${G}_1$, for $1\leq j\leq n$. If ${G}_2\cong {K}_1$ then ${G}_1\circ {K}_1$ is a corona graph. We will use Lemma 2.2 in the proofs of Theorems 2.3 and 2.4.

Lemma 2.2. ^[2] Consider a $k$ regular graph $H$ on $n$ vertices and $H_1 = H\circ K_{1}$, then,

Hence, we can obtain the following lemma because $P_2$ is the corona graph obtained form corona product of $K_1$ with $K_1$.

Lemma 2.3. Consider a signed path graph $P_{2}^{+}$ in which the edge is given sign +1, then,

Lemma 2.4. Consider a signed path graph $P_{2}^{-}$ in which the edge is given sign -1, then,

Proof. As

Let

and

Now,

□

Now, we construct a family of S.Gs, which fulfills eigenvalue properties such as (the property $(-\mathcal{SR})$, the property $(\mathcal{SR})$ and the strong symmetric eigenvalue property).

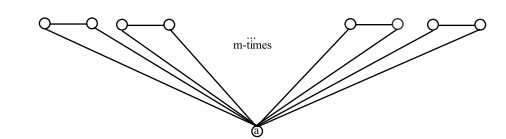
Definition 2.1. Consider $m$ duplicates $\mathfrak{C}_{3}^{1}, \mathfrak{C}_{3}^{2}, ..., \mathfrak{C}_{3}^{m}$ of cycle graph $\mathfrak{C}_{3}$ on 3 vertices, where $m \in E^{+}$ (even positive integers). Now, identify a vertex of each duplicate $\mathfrak{C}_{3}^{2}, ..., \mathfrak{C}_{3}^{m}$ to the vertex $a$ of $\mathfrak{C}_{3}^{1}$. Name this graph $\mathfrak{C}_{3}^{m}$ as shown in Figure 1.

Now, join the vertex $a$ of $\mathfrak{C}_{3}^{m}$ to an isolated vertex, by an edge and the resulting graph named $\mathfrak{C}_{3}^{(m, 1)}$ is given in Figure 2.

Now, with $\mathfrak{C}^{(m, 1)}_{3}$ we construct an unbalanced S.G $\hat{\mathfrak{C}}^{(m, 1)}_{3}$ by giving -1 sign to the edge joining vertices of degree two, in $m$/2 duplicates of $\mathfrak{C}_{3}$ and give +1 sign to all the other remaining edges. Name this graph $\hat{\mathfrak{C}}^{(m, 1)}_{3}$ as given in Figure 3.

Each $\hat{\mathfrak{C}}^{(m, 1)}_{3}$, where $m$ is an even positive integer is a non bipartite unbalanced S.G. In Theorem 2.3, it is shown that the $\hat{\mathfrak{C}}^{(m, 1)}_{3}$, where $m$ is an even positive integer fulfills the property ($\mathcal{-SR}$).

Theorem 2.3. For each even positive integer $m$, $\hat{\mathfrak{C}}^{(m, 1)}_{3}$ fulfills the strong symmetric eigenvalue property and the properties ($\mathcal{SR}$) and ($\mathcal{-SR}$).

Proof. Consider $\hat{\mathfrak{C}}^{(m, 1)}_{3}$, where $m$ is an even positive integer, then the adjacency matrix $A(\hat{\mathfrak{C}}^{(m, 1)}_{3})$ of $\hat{\mathfrak{C}}^{(m, 1)}_{3}$ can be written as

$P(\hat{\mathfrak{C}}^{(m, 1)}_{3};s)$ of $\hat{\mathfrak{C}}^{(m, 1)}_{3}$ can be written as

Let

Using Lemma 2.1 we have

From Lemmas 2.3 and 2.4, we have

Therefore,

Each factor in $P(\hat{\mathfrak{C}}^{(m, 1)}_{3};s)$ fulfills the property ($\mathcal{-SR}$) by Definition 1.2. Therefore, $P(\hat{\mathfrak{C}}^{(m, 1)}_{3};s)$ fulfills the property ($\mathcal{-SR})$.

Remark 2.1. Table 1 shows the roots of all the factors of $P(\hat{\mathfrak{C}}^{(m, 1)}_{3};s)$.

Table 1 shows that every factor of $P(\hat{\mathfrak{C}}^{(m, 1)}_{3};s)$ fulfills the symmetric eigenvalue property. Therefore, $P(\hat{\mathfrak{C}}^{(m, 1)}_{3};s)$ fulfills the property ($\mathcal{SR})$.

Example 2.1 exhibits that the graph $\hat{\mathfrak{C}}^{(6, 1)}_{3}$ fulfills the symmetric eigenvalue property, the property ($\mathcal{SR}$) and the property ($\mathcal{-SR}$).

Example 2.1. A non bipartite unbalanced S.G $\hat{\mathfrak{C}}^{(6, 1)}_{3}$ is shown in Figure 4.

The spectrum of $\hat{\mathfrak{C}}^{(6, 1)}_{3}$ is shown in Table 2.

Table 2 represents that $\hat{\mathfrak{C}}^{(6, 1)}_{3}$ fulfills the symmetric eigenvalue property, the property ($\mathcal{SR}$) and the property ($\mathcal{-SR}$).

Now we construct a family of S.Gs which fulfills the eigenvalue properties (the property $(-\mathcal{SR})$, the property $(\mathcal{SR})$ and the symmetric eigenvalue property).

Definition 2.2. Consider $m$ duplicates $\mathfrak{C}_{5}^{1}, \mathfrak{C}_{5}^{2}, ..., \mathfrak{C}_{5}^{m}$ of cycle graph $\mathfrak{C}_{5}$ on 5 vertices, where $m \in E^{+}$. Now identify a vertex of each duplicate $\mathfrak{C}_{5}^{2}, ..., \mathfrak{C}_{5}^{m}$ to the vertex $a$ of $\mathfrak{C}_{5}^{1}$. Name this graph $\mathfrak{C}_{5}^{m}$ as shown in Figure 5.

Now, join the vertex $a$ of $\mathfrak{C}_{5}^{m}$ to 2 isolated vertices, by an edge and the resulting graph named $\mathfrak{C}_{5}^{(m, 2)}$ is given in Figure 6.

Now, with $\mathfrak{C}^{(m, 2)}_{5}$ we construct an unbalanced S.G $\hat{\mathfrak{C}}^{(m, 2)}_{5}$ by giving -1 sign to the edge joining vertices of degree 2 which are non adjacent to $a$, in $m$/2 duplicates of $\mathfrak{C}_{5}$ and give sign +1 otherwise. Name this graph as $\hat{\mathfrak{C}}^{(m, 2)}_{5}$ given in Figure 7.

Each $\hat{\mathfrak{C}}^{(m, 2)}_{5}$, where $m$ is an even positive integer is a non bipartite unbalanced S.G. The following result gives that the $\hat{\mathfrak{C}}^{(m, 2)}_{5}$, for each even positive integer $m$ is close to fulfill the property $(\mathcal{-SR})$.

Theorem 2.4. For each even positive integer $m$, $\hat{\mathfrak{C}}^{(m, 2)}_{5}$ fulfills the strong symmetric eigenvalue property. Furthermore, all eigenvalues of $\hat{\mathfrak{C}}^{(m, 2)}_{5}$ except $(\pm\sqrt{2}, 1)$ and (0, 1) fulfill the properties $(\mathcal{SR})$ and $(\mathcal{-SR})$.

Proof. Consider $\hat{\mathfrak{C}}^{(m, 2)}_{5}$, where $m$ is an even positive integer, then the adjacency matrix $A(\hat{\mathfrak{C}}^{(m, 2)}_{5})$ of $\hat{\mathfrak{C}}^{(m, 2)}_{5}$ can be written as

$P(\hat{\mathfrak{C}}^{(m, 2)}_{5};s)$ of $\hat{\mathfrak{C}}^{(m, 2)}_{5}$ can be written as

Let

Using Lemma 2.1, we have

where

${P(\hat{\mathfrak{C}}^{(m, 2)}_{5};s)} = s^{2m+2} det(P-\frac{1}{s}S),$ where

Now here let

Again from Lemma 2.1 we have

From Lemmas 2.3 and 2.4, we have

Therefore,

Therefore, we have

Table 3 shows that the $\pm\sqrt{2}$ and 0 are eigenvalues of $\hat{\mathfrak{C}}^{(m, 2)}_{5}$, each with multiplicity 1, and the other $4m$ eigenvalues of $\hat{\mathfrak{C}}^{(m, 2)}_{5}$ fulfill the property $(\mathcal{-SR})$.

Table 3 illustrates that $\hat{\mathfrak{C}}^{(m, 2)}_{5}$ also fulfills the symmetric eigenvalue property, and hence therefore close to fulfill the property $(\mathcal{SR})$.

The following example gives a non bipartite unbalanced S.G $\hat{\mathfrak{C}}^{(4, 2)}_{5}$ and we can see from Table 4 that $\pm\sqrt{2}$ and 0 are eigenvalues of $\hat{\mathfrak{C}}^{(4, 2)}_{5}$, each with multiplicity 1, and the other $16$ eigenvalues of $\hat{\mathfrak{C}}^{(4, 2)}_{5}$ fulfill properties $(\mathcal{-SR})$ and $(\mathcal{SR})$.

Example 2.2. The S.G $\hat{\mathfrak{C}}^{(4, 2)}_{5}$ is given in Figure 8 and $\sigma(A(\hat{\mathfrak{C}}^{(4, 2)}_{5}))$ is shown in Table 4.

3.   Conclusions

For each even positive integer $m$, non bipartite unbalanced S.Gs $\hat{\mathfrak{C}}^{(m, 1)}_{3}$ and $\hat{\mathfrak{C}}^{(m, 2)}_{5}$ are constructed. The S.Gs $\hat{\mathfrak{C}}^{(m, 1)}_{3}(m \in E^{+})$ are shown in Figure 3, each $\hat{\mathfrak{C}}^{(m, 1)}_{3}$ is an unbalanced S.G, which is constructed with the help of $m$/2 unbalanced and $m$/2 balanced signed triangles by identifying a vertex of each of $m-1$ triangles to one vertex of the remaining one triangle and then joining 1 isolated vertex to the identified vertex, by an edge. Similarly, S.Gs $\hat{C}^{(m, 2)}_{5} (m \in E^{+}$) are shown in Figure 7, each $\hat{\mathfrak{C}}^{(m, 2)}_{5}$ is an unbalanced S.G, which can be constructed with the help of $m$ signed pentagons. It is proven that $\hat{\mathfrak{C}}^{(m, 1)}_{3}(m \in E^{+})$ fulfills the property $(-\mathcal{SR})$, the property $(\mathcal{SR})$ and the symmetric eigenvalue property, whereas $\hat{C}^{(m, 2)}_{5}(m \in E^{+}$) fulfills the symmetric eigenvalue property and is close to fulfill the property $(-\mathcal{SR})$ and the property $(\mathcal{SR})$.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgement

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through Large Group Research Project under grant number R.G.P.2/163/44.

Conflict of interest

The authors declare that they have no conflicts of interest.