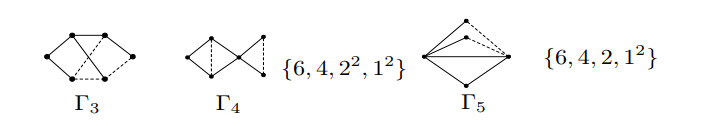Laplacian integral signed graphs with few cycles

1.   Introduction

All graphs considered here are simple and undirected. The vertex set and edge set of a graph $G$ will be denoted by $V (G)$ and $E(G)$, respectively. A signed graph $\Gamma = (G, \sigma)$ consists of an unsigned graph $G = (V, E)$ and a sign function $\sigma: E(G)\rightarrow \{+1, -1\}.$ The $G$ is its underlying graph, while $\sigma$ its sign function (or signature). An edge $v_iv_j$ is positive (negative) if $\sigma(v_iv_j) = +1$ (resp. $\sigma(v_iv_j) = -1$). If a signed graph has the all-positive (resp. all-negative) signature, then it is denoted by $(G, +)$ (resp. $(G, -)$).

The adjacency matrix of a signed graph $\Gamma$ is defined by $A_\sigma = A(\Gamma) = (\sigma_{ij}),$ where $\sigma_{ij} = \sigma(v_iv_j)$ if $v_i \sim v_j,$ and $\sigma_{ij} = 0$ otherwise. The Laplacian matrix of a signed graph $\Gamma$ is defined by $L_\sigma = L(\Gamma) = L(G, \sigma) = D(G)-A(\Gamma),$ where $D(G)$ is the diagonal matrix of vertex degrees. The Laplacian eigenvalues $\mu_1\geq \mu_2\geq \dots \geq \mu_n$ of a signed graph $\Gamma$ are identified to be the eigenvalues of $L(\Gamma)$. Recently, the spectra of the signed graphs have attracted many studies, see ^{[1,2,3,7,18,19]}.

A graph is called integral (resp. Laplacian integral, signless Laplacian integral) if all eigenvalues of its adjacency matrix (resp. Laplacian matrix, signless Laplacian matrix) are integers. This notion was first introduced by Harary and Schwenk in ^[8], who proposed the problem of classifying all integral graphs. The study of this problem has fascinated many mathematicians. In ^[4] and ^[16], Cvetković and Schwenk classified the connected integral graphs of maximum degree at most 3. In ^[14], Kirkland proved that there are 21 connected Laplacian integral graphs of maximum degree 3 on at least 6 vertices. For more results about (Laplacian) integral graphs see ^[5,6,9]. Integral and Laplacian integral signed graphs are defined in the same way. Very recently, there have some interests in characterizing the (Laplacian) integral signed graphs. In ^[18] and ^[19], the authors characterized all connected integral subcubic signed graphs and all connected Laplacian integral subcubic signed graphs, respectively. In ^[17], Stani$\acute{c}$ determined all integral 4-regular net-balanced signed graphs and the integral 4-regular net-balanced signed graphs whose net-balance is a simple eigenvalue.

A connected graph with $n$ vertices and $m$ edges is called a $k$-cyclic graph if $k = m-n+1.$ A $k$-cyclic graph ($k\ge 1$) is said to be a $k$-cyclic base graph if contains no pendent vertices. In particular, the tree and unicyclic, bicyclic and tricyclic graph are respectively defined as the $k$-cyclic graph with $k = 0, 1, 2$ and 3. In ^[15], Liu and Liu determined all Laplacian integral unicyclic and bicyclic graphs. In ^[12], Huang et al. determined all Laplacian integral tricyclic graphs. In ^[13], Zhang et al. determined all signless Laplacian integral unicyclic, bicyclic and tricyclic graphs. Note that $L(G, +) = L(G)$ and $L(G, -) = Q(G) = D(G)+A(G),$ where $L(G)$ and $Q(G)$ are the Laplacian matrix and the signless Laplacian matrix of $G,$ respectively. Thus $L(G, \sigma)$ can be viewed as a common generalization of the $L(G)$ and $Q(G)$ of the underlying graph $G$. So there arises a natural problem: which unicyclic, bicyclic and tricyclic signed graphs are Laplacian integral? In this paper, we will generalize the results of ^[12,13,15] and characterize all connected Laplacian integral signed trees, unicyclic, bicyclic and tricyclic signed graphs.

Most of the concepts defined for graphs can be directly extended to signed graphs. For example, the degree of a vertex $v$ in $G$ (denoted by $d_v$) is also its degree in $\Gamma,$ $\Delta(\Gamma)$ and $\delta(\Gamma)$ denote the maximum degree and minimum degree of vertex, respectively. If $d_v = 1,$ then we call $v$ a pendent vertex of $\Gamma.$ Let $K_{n, m}$ denote the complete bipartite graph. In all figures of signed graphs in this paper, positive edges are depicted as thin lines, while negative edges are depicted as dashed lines. For other undefined notationss and terminology from the theory of signed graphs, we refer to Zaslavsky ^[20].

2.   Preliminaries

First we will present some basic results about signed graphs. Let $\Gamma = (G, \sigma)$ be a signed graph and $C$ a cycle of $\Gamma$. The sign of $C$ is denoted by $\sigma(C) = \prod_{e\in C}\sigma (e)$. A cycle whose sign is $+1$ (resp. $-1$) is called positive (resp. negative). A signed graph is called balanced if all its cycles are positive, otherwise it is called unbalanced. Throughout this paper, we denote a positive and a negative cycle of length $n$ by $C_n^+$ and $C_n^-,$ respectively.

For $\Gamma = (G, \sigma)$ and $U\subset V (G),$ let $\Gamma^U$ be the signed graph obtained from $\Gamma$ by reversing the signatures of the edges in the cut $[U, V (G) \setminus U],$ namely $\sigma_{\Gamma^U}(e) = -\sigma_{\Gamma}(e)$ for any edge $e$ between $U$ and $V(G) \setminus U,$ and $\sigma_{\Gamma^U}(e) = \sigma_{\Gamma}(e)$ otherwise. The signed graph $\Gamma^U$ is said to be switching equivalent to $\Gamma,$ and we write $\Gamma \sim \Gamma^U$. Switching equivalence leaves the many signed graphic invariants, such as adjacency spectrum and Laplacian spectrum.

The following lemma is used to prove two signed graphs are switching equivalent.

Lemma 2.1. [20, Lemma 3.1] Let G be a connected graph and T a spanning tree of G. Then each switching equivalent class of signed graphs on the graph G has a unique representative which is +1 on T. Indeed, given any prescribed sign function $\sigma_T : T \longrightarrow \{+1, -1\}$, each switching class has a single representative which agrees with $\sigma_T$ on T.

Hou et al. ^[11] provided a basic result about the $\mu_n(\Gamma)$ of a signed graph $\Gamma$.

Lemma 2.2. [11, Theorem 2.5] Let $\Gamma = (G, \sigma)$ be a connected signed graph with $n$ vertices. Then $\mu_n(\Gamma) = 0$ if and only if $\Gamma$ is balanced.

From Lemma 2.2, we have the following observations.

Proposition 2.3. Let $\Gamma = (G, \sigma)$ be a connected unbalanced Laplacian integral signed graph. Then

$(i)$ $\mu_n(\Gamma)\ge 1.$

$(ii)$ $L_\sigma -I$ is positive semi-definite $($if $\mu_n(\Gamma) = 1)$ or positive definite $($if $\mu_n(\Gamma) > 1).$

By Proposition 2.3, we can obtain that if $\Gamma = (G, \sigma)$ is a connected unbalanced Laplacian integral signed graph, then $\delta(\Gamma)\ge 2$ and hence $\Gamma$ has no pendent vertex.

Lemma 2.4. Let $\Gamma = (G, \sigma)$ be a connected unbalanced Laplacian integral signed graph. Then $\delta(\Gamma)\ge 2$.

Proof. Suppose $u$ is a pendent vertex and $v$ is the neighbor of $u,$ then $2\times2$ principal submatrix of $L_\sigma -I$ corresponding to $u$ and $v$ equals

We have $\det S = -1,$ which contradicts to Proposition 2.3 ($ii$). Hence $\delta(\Gamma)\ge 2$.

Corollary 2.5. Let $\Gamma = (G, \sigma)$ be a connected unbalanced Laplacian integral $k$-cyclic signed graph. Then the underlying graph $G$ is a $k$-cyclic base graph.

Proof. By Lemma 2.4, we know that $\Gamma$ has no pendent vertex. Hence the underlying graph $G$ is a $k$-cyclic base graph.

By Proposition 2.3 $(ii)$, we can also give a considerable reduction on the possible induced subgraphs.

Lemma 2.6. Let $\Gamma = (G, \sigma)$ be a connected unbalanced Laplacian integral signed graph. If there are two vertices of degree 2 such that they are adjacent, then there must exist one negative 3-cycle that contains vertices $u$ and $v$.

Proof. Suppose that $w$ is the another neighbor of $u,$ by Lemma 2.1, we can assume that $\sigma(vu) = \sigma(uw) = +1.$ Then the $3\times3$ principal submatrix of $L_\sigma -I$ corresponding to $v, u, w$ equals

By direct calculations, we have $\det S = -1$ if $\sigma(vw) = 0$ and $\det S = -4$ if $\sigma(vw) = +1,$ which contradicts to Proposition 2.3 $(ii)$. Thus $\sigma(vw) = -1$ and $\{v, u, w\}$ is a negative 3-cycle. This completes the proof.

It is straightforward to see that if $\Gamma = (G, \sigma)$ is a connected signed graph with maximam degree at most $2,$ then the necessarily the underlying graph $G$ is a path or cycle.

Lemma 2.7. ^[1,19] Let $\Gamma = (G, \sigma)$ be a connected signed graph with maximam degree at most $2,$ then $\Gamma$ is Laplacian integral if and only if it is switching equivalent to one of the $K_1,$ $(P_2, \sigma),$ $(P_3, \sigma),$ $C_3^+,$ $C_3^-,$ $C_4^+$ or $C_6^+.$

The connected Laplacian integral signed graphs $\Gamma = (G, \sigma)$ of maximum degree 3 have been determined by Schwenk^[16], Kirkland^[14], Wang and Hou ^[19]. The following result showes all connected unbalanced Laplacian integral signed graphs of maximum degree 3.

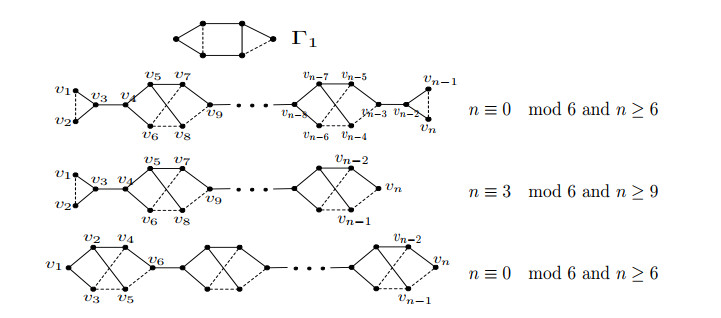
Lemma 2.8. ^[19] Let $\Gamma = (G, \sigma)$ be a connected unbalanced Laplacian integral signed graph of maximum degree 3. Then $\Gamma$ is switching equivalent to one of the signed graphs of Figure 1.

The following three lemmas characterize the connected Laplacian integral unicyclic, bicyclic and tricyclic unsigned graphs. Let $S_1(n)$ $(n \ge 4)$ denote the (unique) unicyclic graph obtained from $K_{1, n-1}$ by adding one edge between pendent vertices of $K_{1, n-1}.$

Lemma 2.9. [15, Theorem 3.2] If $G$ is a connected unicyclic graph of order $n$ $(n \ge 3),$ then $G$ is Laplacian integral if and only if $G\cong S_1(n),$ $G\cong C_3,$ $G\cong C_4,$ $G\cong C_6.$

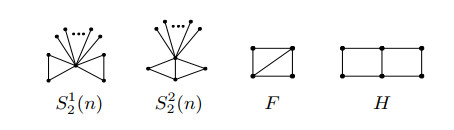
Let $S^1_2(n)$ and $S^2_2(n)$ $(n \ge 5)$ denote the two bicyclic graphs obtained from $K_{1, n-1}$ by adding two edge to the pendent vertices of $K_{1, n-1}$. See Figure 2.

Lemma 2.10. [15, Theorem 3.3] If $G$ is a connected bicyclic graph of order $n$ $(n\ge 4),$ then $G$ is Laplacian integral if and only if $G\cong S^1_2(n), S^2_2(n), K_{2, 3},$ $F,$ $H$ in Figure 2.

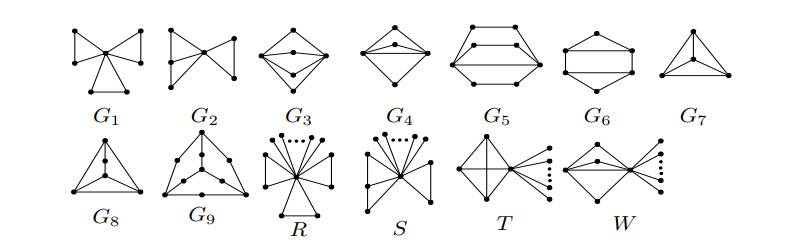
Lemma 2.11. [12, Theorems 4.1 and 5.1] If $G$ is a connected tricyclic graph of order $n$ $(n\ge 4),$ then $G$ is Laplacian integral if and only if $G\cong G_i,$ $i = 1, 2, \dots, 9,$ $R,$ $S,$ $T,$ $W$ in Figure 3.

3.   Laplacian integral signed graphs with few cycles

In this section, we will characterize the connected Laplacian integral $k$-cyclic signed graphs with $k = 0, 1, 2$ and $3.$ If $k = 0$, it is known that the underlying graph $G$ is a tree. Then

Theorem 3.1. If $\Gamma = (T, \sigma)$ is a signed tree of order $n$ $(n\ge 2)$, then $\Gamma$ is Laplacian integral if and only if $\Gamma$ is switching equivalent to $(K_{1, {n-1}}, +).$

Proof. Note that any signed tree shares the same $L$-spectrum with its underlying graph. Hence by Corollary 3.1 of ^[15], $\Gamma$ is Laplacian integral if and only if $\Gamma\sim (K_{1, {n-1}}, +)$.

Now we will determine all connected Laplacian integral unicyclic signed graphs.

Theorem 3.2. If $\Gamma = (G, \sigma)$ is a connected unicyclic signed graph of order $n$ $(n\ge 3),$ then $\Gamma$ is Laplacian integral if and only if $\Gamma$ is switching equivalent to $C_3^+,$ $C_3^-,$ $C_4^+,$ $C_6^+$ or $(S_1(n), +)$.

Proof. If $\Gamma$ is balanced, then $\Gamma$ is Laplacian integral if and only if it is switching equivalent to $C_3^+,$ $C_4^+,$ $C_6^+$ or $(S_1(n), +)$ (by Lemma 2.9). Then we consider the unbalanced case. By Corollary 2.5, we know that the the underlying graph $G$ must be a cycle. So $\Gamma$ is an unbalanced signed cycle $C_n^-$. Hence by Lemma 2.7, we can obtain that $\Gamma$ is switching equivalent to $C_3^-.$ This completes the proof.

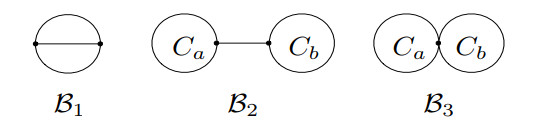
Next we consider the connected Laplacian integral bicyclic signed graphs. It is well-known that there are three types of bicyclic graphs in term of their base graph as described next (see Figure 4).

The type $\mathcal{B}_1$ is the union of three internally disjoint paths $P_{p+2},$ $P_{q+2}$, and $P_{r+2}$ which have the same two distinct end vertices, where $p\geq 0,$ $q \geq0$ and $r\geq 0.$

The type $\mathcal{B}_2$ consists of two vertex disjoint cycles $C_a$ and $C_b$ joined by a path $P_r$ having only its end vertices in common with the cycles, where $a\geq 3,$ $b \geq3$ and $r\geq 2.$

The type $\mathcal{B}_3$ is the union of two cycles $C_a$ and $C_b$ with precisely one vertex in common, where $a\geq 3$ and $b \geq 3.$

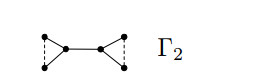
Theorem 3.3. If $\Gamma = (G, \sigma)$ is a connected bicyclic signed graph of order $n$ $(n\ge 4),$ then $\Gamma$ is Laplacian integral if and only if it is switching equivalent to $(S^1_2(n), +),$ $(S^2_2(n), +)$ $(K_{2, 3}, +),$ $(F, +),$ $(H, +)$ or $\Gamma_2$, where $\Gamma_2$ is shown in Figure 5.

Proof. If $\Gamma$ is balanced, then $\Gamma$ is Laplacian integral if and only if it is switching equivalent to $(S^1_2(n), +),$ $(S^2_2(n), +)$ $(K_{2, 3}, +),$ $(F, +)$ or $(H, +)$ (by Lemma 2.10). Then we consider the unbalanced case. By Corollary 2.5, then the underlying graph $G$ is a bicyclic base graph. Further, note that all bicyclic signed graphs of types $\mathcal{B}_1$ and $\mathcal{B}_2$ have maximum degree 3. Thus, by Lemma 2.8, we can get that $\Gamma = (G, \sigma)$ (where $G\in \mathcal{B}_1$ or $\mathcal{B}_2$) is Laplacian integral if and only if $\Gamma\sim \Gamma_2.$ Hence it suffices to consider that the underlying graph $G\in \mathcal{B}_3.$ By Lemma 2.6, we can obtain that $a = b = 3$, because otherwise there have at least one pair of adjacent vertices of degree 2 and no triangle contains these two vertices. Thus the underlying graph $G$ is graph that two triangles meet at one vertex.

It is easy to check that there is no Laplacian integral signed graph on $G$. So we complete the proof.

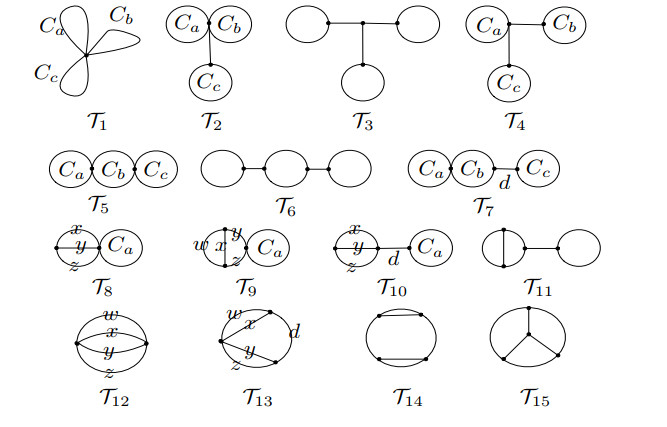
By Corollary 2.5, to determine the Laplacian integral tricyclic signed graph, it suffices to consider that the underlying graph is the tricyclic base graph. It is well-known that there are exactly 15 types of tricyclic base graphs ^[10] (see Figure 6), which are denoted by $\mathcal{T}_i$, for $i = 1, 2, \dots, 15.$ Let $\mathcal{T}_i^\sigma$ $(i = 1, 2, \dots, 15)$ be the set of tricyclic signed graphs whose underlying graph belongs to $\mathcal{T}_i.$

Because of Lemma 2.11, we will focus on the connected unbalanced Laplacian integral tricyclic signed graphs.

Lemma 3.4. Let $\Gamma = (G, \sigma)\in \cup_{i\in X}\mathcal{T}_i^\sigma$ with $X = \{3, 6, 11, 14, 15\}$ and unbalanced. Then $\Gamma$ is Laplacian integral if and only if it is switching equivalent to $\Gamma_1$ or $\Gamma_3$, which is depicted in Figures 1 and 7.

Proof. It is clear that for any signed graph $\Gamma = (G, \sigma)\in \cup_{i\in X}\mathcal{T}_i^\sigma$ with $X = \{3, 6, 10, 11,$ $14, 15\},$ it has the maximum degree of 3. Hence $\Gamma\sim \Gamma_1$ or $\Gamma_3$ by Lemma 2.8.

Lemma 3.5. Let $\Gamma = (G, \sigma)\in \cup_{i\in X}\mathcal{T}_i^\sigma$ with $X = \{1, 2, 4, 5, 7\}.$ Then $\Gamma$ is not Laplacian integral.

Proof. First let $\Gamma = (G, \sigma)\in \mathcal{T}_i^\sigma$ for $i = 1, 2, 4,$ we have $a = b = c = 3$ and $\sigma(C_a) = \sigma(C_b) = \sigma(C_c) = -1$ (by Lemma 2.6). Clearly, we can get that such signed graph is switching equivalent to the all-negative signature, it suffices to find out all graphs $G\in \mathcal{T}_i$ ($i = 1, 2, 4$) that is signless Laplacian integral. By [13, Theorem 3.12], Zhang et al. proved that there is no graph $G\in \mathcal{T}_i$ ($i = 1, 2, 4$) that is signless Laplacian integral. So there is no Laplacian integral signed graph $\Gamma\in \mathcal{T}_i^\sigma$ ($i = 1, 2, 4$).

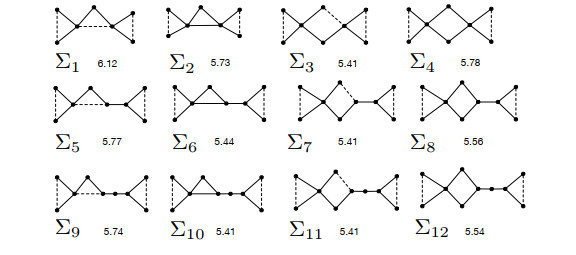
Next let $\Gamma\in \mathcal{T}_i^\sigma$ for $i = 5, 7,$ by Lemma 2.6, we have $a = c = 3,$ $3\le b \le 4$ and $\sigma(C_a) = \sigma(C_c) = -1.$ Thus,

if $\Gamma\in \mathcal{T}_5^\sigma$, then $\Gamma\sim \Sigma_1, \Sigma_{2}, \Sigma_{3}$ or $\Sigma_{4}$ (see Figure 8);

if $\Gamma\in \mathcal{T}_7^\sigma$, by Lemma 2.6, we have $1\le d \le 2.$ Then $\Gamma\sim \Sigma_5, \Sigma_{6}, \Sigma_{7}$ or $\Sigma_{8}$ (if $d = 1$) or $\Gamma\sim \Sigma_9, \Sigma_{10}, \Sigma_{11}$ or $\Sigma_{12}$ (if $d = 2$). See Figure 8.

From Figure 8, we can see that each $\Sigma_i$ ($i = 1, 2, \dots, 12$) has a non-integral Laplacian eigenvalue. Hence $\Gamma$ is not Laplacian integral.

Lemma 3.6. Let $\Gamma = (G, \sigma)\in \cup_{i\in X}\mathcal{T}_i^\sigma$ with $X = \{8, 9, 10, 12, 13\}.$ Then $\Gamma$ is unbalanced and Laplacian integral if and only if it is switching equivalent to $\Gamma_4$ or $\Gamma_5$.

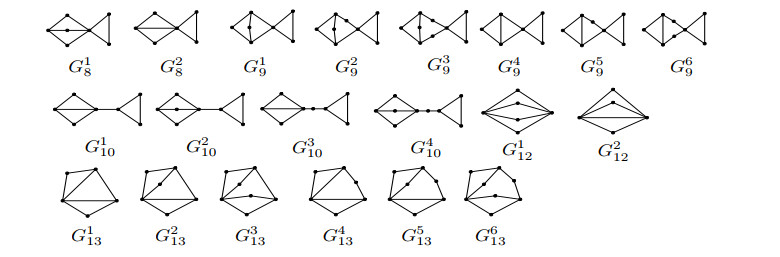
Proof. If $\Gamma\in \mathcal{T}_8^\sigma$, by Lemma 2.6, we have $a = 3$, $1\le x\le 2,$ $1\le y\le 2,$ $1\le z\le 2$ and at most one of $x, y, z$ equals to 1, as we only consider simple. Then the underlying graph $G$ is isomorphism to $G^1_8$ or $G_8^2$ (see Figure 9). By Lemma 2.1, for each graph $G^1_8,$ $G_8^2,$ there are at most $2^3$ nonequivalent signatures. So by direct calculations, it is not too difficult to get that there is no Laplacian integral signed graph $\Gamma$ on $G^1_8$ or $G_8^2.$

If $\Gamma\in \mathcal{T}_9^\sigma$, by Lemma 2.6, we have $a = 3$, $1\le w\le 2,$ $1\le x\le 2,$ $1\le y\le 2,$ $1\le z\le 2$ and at most one of $w, x$ equals to 1. Then the underlying graph $G$ is isomorphism to $G^1_9,$ $G_9^2,$ $G_9^3$ ($w = x = 2$) or $G^4_9,$ $G_9^5,$ $G_9^6$ (otherwise). See Figure 9. By similar calculations, we can check that there is no Laplacian integral signed graph on $G^i_{9}$ ($i = 1, 2, 3, 5, 6$) and $\Gamma = (G_{9}^4, \sigma)$ is Laplacian integral if and only if $\Gamma\sim \Gamma_4$ (see Figure 9).

If $\Gamma\in \mathcal{T}_{10}^\sigma$, by Lemma 2.6, we have $a = 3$, $1\le x\le 2,$ $1\le y\le 2,$ $1\le z\le 2$ and at most one of $x, y, z$ equals to 1. Then the underlying graph $G$ is isomorphism to $G^1_{10},$ $G_{10}^2,$ $G_{10}^3$ or $G^4_{10}$. See Fig. 9. By similar calculations, we can check that there is no Laplacian integral signed graph on $G^i_{10}$ ($i = 1, 2, 3, 4$).

If $\Gamma\in \mathcal{T}_{12}^\sigma$, by Lemma 2.6, we have $1\le w\le 2,$ $1\le x\le 2,$ $1\le y\le 2,$ $1\le z\le 2$ and at most one of $w, x, y, z$ equals to 1. Then the underlying graph $G$ is isomorphism to $G^1_{12}$ or $G_{12}^2$. See Figure 9. By similar calculations, we can check that there is no Laplacian integral signed graph on $G^1_{12}$ and $\Gamma = (G_{12}^2, \sigma)$ is Laplacian integral if and only if $\Gamma\sim \Gamma_5$ (see Figure 7).

If $\Gamma\in \mathcal{T}_{13}^\sigma$, by Lemma 2.6, we have $1\le d\le 2,$ $1\le w\le 1,$ $1\le x\le 2,$ $1\le y\le 2,$ $1\le z\le 2$ and at most one of $w, x$ equals to 1, at most one of $y, z$ equals to 1. Then the underlying graph $G$ is isomorphism to $G^1_{13}$, $G_{13}^2$ or $G_{13}^3$ (if $d = 1$) or $G^4_{13}$, $G_{13}^5$ or $G_{13}^6$ (if $d = 2$). See Fig. 9. By similar calculations, we can check that there is no Laplacian integral signed graph on $G^i_{13}$ ($i = 1, 2, 3, 4, 5, 6$).

This completes the proof.

Combining with Lemmas 2.11, 3.4, 3.5 and 3.6, we have

Theorem 3.7. If $\Gamma = (G, \sigma)$ is a connected tricyclic signed graph of order $n$ $(n\ge 4),$ then $\Gamma$ is Laplacian integral if and only if it is switching equivalent to $(G_i, +)$ for $i = 1, 2, \dots, 9,$ $(R, +)$, $(S, +),$ $(T, +),$ $(W, +)$, $\Gamma_1$, $\Gamma_3, \Gamma_4$ or $\Gamma_5$.

4.   Conclusions

In this research work, we analyzed some properties of the connected unbalanced Laplacian integral $k$-cyclic signed graphs and investigated all connected Laplacian integral $k$-cyclic signed graphs with $k = 0, 1, 2,$ $3$. In future work, we will study the integral $k$-cyclic signed graphs for more general sets of matrices than Laplacian matrix.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (No.11971164, 12101557, 12271484), the Zhejiang Provincial Natural Science Foundation of China (LQ21A010004), the Talent Foundation of Tongling University(2021tlxyrc24) and the Key Projects of Science Research in University of Anhui Province(KJ2021A1049, 2022AH040248).

Conflict of interest

The authors declare that they have no conflict of interest.