Topological indices of linear crossed phenylenes with respect to their Laplacian and normalized Laplacian spectrum

Zhi-Yu Shi; Jia-Bao Liu; Zhi-Yu Shi; Jia-Bao Liu

doi:10.3934/math.2024262

AIMS Mathematics

2024, Volume 9, Issue 3: 5431-5450. doi: 10.3934/math.2024262

Previous Article Next Article

Research article

Topological indices of linear crossed phenylenes with respect to their Laplacian and normalized Laplacian spectrum

Zhi-Yu Shi ^{1
,
,},
Jia-Bao Liu ²

1.
Engineering Department, Anhui Sanlian University, Hefei 230601, China
2.
School of Mathematics and Physics, Anhui Jianzhu University, Hefei 230601, China

Received: 23 November 2023 Revised: 31 December 2023 Accepted: 10 January 2024 Published: 29 January 2024
MSC : 05C50, 05C90

As a powerful tool for describing and studying the properties of networks, the graph spectrum analyses and calculations have attracted substantial attention from the scientific community. Let $C_{n}$ represent linear crossed phenylenes. Based on the Laplacian (normalized Laplacian, resp.) polynomial of $C_{n}$ , we first investigated the Laplacian (normalized Laplacian, resp) spectrum of $C_{n}$ in this paper. Furthermore, the Kirchhoff index, multiplicative degree-Kirchhoff, index and complexity of $C_{n}$ were obtained through the relationship between the roots and the coefficients of the characteristic polynomials. Finally, it was found that the Kirchhoff index and multiplicative degree-Kirchhoff index of $C_{n}$ were approximately one quarter of their Wiener index and Gutman index, respectively.

Keywords:

Citation: Zhi-Yu Shi, Jia-Bao Liu. Topological indices of linear crossed phenylenes with respect to their Laplacian and normalized Laplacian spectrum[J]. AIMS Mathematics, 2024, 9(3): 5431-5450. doi: 10.3934/math.2024262

Related Papers:

[1]	Ze-Miao Dai, Jia-Bao Liu, Kang Wang . Analyzing the normalized Laplacian spectrum and spanning tree of the cross of the derivative of linear networks. AIMS Mathematics, 2024, 9(6): 14594-14617. doi: 10.3934/math.2024710
[2]	Jahfar T K, Chithra A V . Central vertex join and central edge join of two graphs. AIMS Mathematics, 2020, 5(6): 7214-7233. doi: 10.3934/math.2020461
[3]	Jia-Bao Liu, Kang Wang . The multiplicative degree-Kirchhoff index and complexity of a class of linear networks. AIMS Mathematics, 2024, 9(3): 7111-7130. doi: 10.3934/math.2024347
[4]	Muhammad Ajmal, Xiwang Cao, Muhammad Salman, Jia-Bao Liu, Masood Ur Rehman . A special class of triple starlike trees characterized by Laplacian spectrum. AIMS Mathematics, 2021, 6(5): 4394-4403. doi: 10.3934/math.2021260
[5]	Wafaa Fakieh, Amal Alsaluli, Hanaa Alashwali . Laplacian spectrum of the unit graph associated to the ring of integers modulo $pq$ . AIMS Mathematics, 2024, 9(2): 4098-4108. doi: 10.3934/math.2024200
[6]	Zhen Lin . The biharmonic index of connected graphs. AIMS Mathematics, 2022, 7(4): 6050-6065. doi: 10.3934/math.2022337
[7]	Meiling Hu, Shuli Li . Cospectral graphs for the normalized Laplacian. AIMS Mathematics, 2022, 7(3): 4061-4067. doi: 10.3934/math.2022224
[8]	In Hyoun Kim, Yun-Ho Kim . Existence, uniqueness, and localization of positive solutions to nonlocal problems of the Kirchhoff type via the global minimum principle of Ricceri. AIMS Mathematics, 2025, 10(3): 4540-4557. doi: 10.3934/math.2025210
[9]	Milica Anđelić, Saleem Khan, S. Pirzada . On graphs with a few distinct reciprocal distance Laplacian eigenvalues. AIMS Mathematics, 2023, 8(12): 29008-29016. doi: 10.3934/math.20231485
[10]	Yinzhen Mei, Chengxiao Guo . The minimal degree Kirchhoff index of bicyclic graphs. AIMS Mathematics, 2024, 9(7): 19822-19842. doi: 10.3934/math.2024968

Abstract

1. Introduction

In recent years, researchers have been interested in the study of complex networks ^[1,2,3,4]. Three common characteristics of complex networks are: small-world, scale-free, and fractal. Yang and Huang et al. ^[5,6] have determined the Kirchhoff index and multiplicative degree-Kirchhoff index of hexagonal chains, and they obtained that the Kirchhoff index and multiplicative degree-Kirchhoff index of hexagonal chains are approximately half of their Wiener index and Gutman index, respectively. In particular, Peng et al. ^[7] studied the Kirchhoff index and complexity for linear phenylenes, and determined that the Kirchhoff index of linear phenylenes is approximately half of its Wiener index. In addition, Z. Zhu and J.-B. Liu ^[8] obtained the multiplicative degree-Kirchhoff index and complexity of generalized phenylenes. In 2018, Pan and Li ^[9] determined the Kirchhoff index, multiplicative degree-Kirchhoff index, and complexity of linear crossed hexagonal networks, and obtained that the Kirchhoff index and multiplicative degree-Kirchhoff index of linear crossed hexagonal chains are approximately one quarter of their Wiener index and Gutman index, respectively. For other networks, see ^{[10,11,12,13,14]}.

Motivated by these, we investigate the Laplacian and normalized Laplacian spectra of linear crossed phenylenes. We also obtain that the Kirchhoff index and multiplicative degree-Kirchhoff index of linear crossed phenylenes are approximately one quarter of their Wiener index and Gutman index, respectively.

In this paper, we suppose $G = (E_{G}, V_{G})$ is a graph with edge set $E_{G} = \{e_1, e_2, \cdots, e_m\}$ and vertex set $V_{G} = \{v_1, v_2, \cdots, v_n\}$ . For more notations, one can be referred to ^[15].

Let $D(G) = diag\{d_{1}, d_{2}, \cdots, d_{n}\}$ represent a degree matrix, and $A(G)$ be the adjacency matrix, where $d_{i}$ is the degree of $v_{i}$ . Therefore, we can calculate the Laplacian matrix and normalized Laplacian matrix, which are defined as $L(G) = D(G)-A(G)$ and $\mathcal{L}(G) = D(G)^{-\frac{1}{2}}LD(G)^{-\frac{1}{2}}$ , respectively. The Laplacian matrix is

$\begin{eqnarray} (L(G))_{ij} = \begin{cases} d_{i}, & i = j;\\ -1, & i\neq{j}, \; v_{i} \; and \; v_{j} \; are \; adjacent;\\ 0, & otherwise. \end{cases} \end{eqnarray}$

(1.1)

The normalized Laplacian matrix is

$\begin{eqnarray} (\mathcal{L}(G))_{ij} = \begin{cases} 1, & i = j, \; d_{i}\neq 0;\\ -\frac{1}{\sqrt{d_{i}d_{j}}}, & i\neq{j}, \; v_{i} \; and \; v_{j} \; are \; adjacent; \\ 0, & otherwise. \end{cases} \end{eqnarray}$

(1.2)

The distance between vertices $v_i$ and $v_j$ , denoted by $d_{ij}$ , is defined as the length of the shortest path between vertices $v_i$ and $v_j$ . The Wiener index ^[16,17] is defined as

$\begin{eqnarray} W(G) = \sum\limits_{i < j}d_{ij}. \end{eqnarray}$

(1.3)

In 1994, the Gutman index ^[18] is defined as

$\begin{eqnarray} Gut(G) = \sum\limits_{i < j}d_{i}d_{j}d_{ij}. \end{eqnarray}$

(1.4)

Klein and Randić ^[19] were the first to put forward the concept of resistance distance, and the resistance distance between vertices $v_i$ and $v_j$ is denoted by $r_{ij}$ . Klein et al. ^[20,21] introduced the Kirchhoff index as $Kf(G) = \sum_{i < j}r_{ij}$ . In 2007, Chen et al. ^[22] proposed the multiplicative degree-Kirchhoff index as $Kf^{*}(G) = \sum_{i < j}d_{i}d_{j}r_{ij}$ . Gutman and Mohar ^[23] introduced the Kirchhoff index as

$\begin{eqnarray} Kf(G) = n\sum\limits_{k = 2}^{n}\frac{1}{\mu_{k}}, \end{eqnarray}$

(1.5)

where $0 = \mu_{1} < \mu_{2}\leq\cdots\leq\mu_{n}(n\geq2)$ are the eigenvalues of $L(G)$ .

According to the normalized Laplacian, Chen et al. ^[22] proposed the multiplicative degree-Kirchhoff index as

$\begin{eqnarray} Kf^{*}(G) = 2m\sum\limits_{k = 2}^{n}\frac{1}{\lambda_{k}}, \end{eqnarray}$

(1.6)

where $\lambda_{1}\leq\lambda_{2}\leq\cdots\leq\lambda{n}$ are the normalized Laplacian eigenvalues of $\mathcal{L}(G)$ .

The number of spanning trees of $G$ can also be called the complexity of $G$ ^[15], denoted by $\tau(G)$ .

In Section 2, we mainly introduce some notations and theorems. Next, applying the relationship between the roots and coefficients of $C_n$ , the Laplacian spectrum of $C_{n}$ is determined in Section 3. In Section 4, we obtain the normalized Laplacian spectrum of $C_{n}$ in the same way as in Section 3. The conclusion is summarized in Section 5.

2. Preliminary

First, we state some notations and theorems, which will be used later.

Given an $n\times n$ matrix $M$ , the submatrix of $M$ is represented by $M[i_{1}, \cdots, i_{k}]$ , where $M[i_{1}, \cdots, i_{k}]$ is formed by removing the $i_{1}$ -th, $\cdots$ , $i_{k}$ -th rows and columns of $M$ . Let $P_{M}(x) = det(xI-M)$ represent the characteristic polynomial of $M$ .

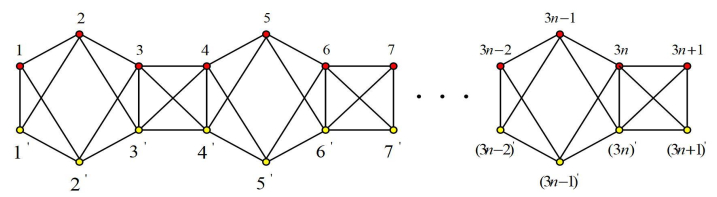
Label linear crossed phenylenes as shown in . Evidently, $|V(C_{n})| = 6n+2, |E(C_{n})| = 14n+1$ and $\pi = (1, 1')(2, 2')\cdots\big(3n+1, (3n+1)'\big)$ is an automorphism of $C_{n}$ . Set $V_{1} = \{1, 2, \cdots, 3n+1\}, V_{2} = \{1', 2', \cdots, (3n+1)'\}$ .

Figure 1. Linear crossed phenylenes

$C_n$ .

DownLoad: Full-Size Img PowerPoint

Thus, $L(C_n)$ and $\mathcal{L}(C_n)$ can be expressed by

$\begin{equation*} L(C_{n}) = \left( \begin{array}{cc} L_{V_{1}V_{1}}& L_{V_{1}V_{2}}\\ L_{V_{2}V_{1}}& L_{V_{2}V_{2}}\\ \end{array} \right),\; \mathcal{L}(C_{n}) = \left( \begin{array}{cc} \mathcal{L}_{V_{1}V_{1}}& \mathcal{L}_{V_{1}V_{2}}\\ \mathcal{L}_{V_{2}V_{1}}& \mathcal{L}_{V_{2}V_{2}}\\ \end{array} \right), \end{equation*}$

where

$\begin{equation*} L_{V_{1}V_{1}} = L_{V_{2}V_{2}},\; L_{V_{1}V_{2}} = L_{V_{2}V_{1}},\; \mathcal{L}_{V_{1}V_{1}} = \mathcal{L}_{V_{2}V_{2}},\; \mathcal{L}_{V_{1}V_{2}} = \mathcal{L}_{V_{2}V_{1}}. \end{equation*}$

Let

$\begin{equation*} T = \left( \begin{array}{cc} \frac{1}{\sqrt{2}}I_{3n+1}& \frac{1}{\sqrt{2}}I_{3n+1}\\ \frac{1}{\sqrt{2}}I_{3n+1}& -\frac{1}{\sqrt{2}}I_{3n+1} \end{array} \right), \end{equation*}$

then

$\begin{equation*} TL(C_{n})T' = \left( \begin{array}{cc} L_{A}& 0\\ 0& L_{S} \end{array} \right),\; T\mathcal{L}(C_{n})T' = \left( \begin{array}{cc} \mathcal{L}_{A}& 0\\ 0& \mathcal{L}_{S} \end{array} \right), \end{equation*}$

where $T'$ is the transpose of the matrix $T$ and

$\begin{eqnarray*} L_{A} = L_{V_{1}V_{1}}+L_{V_{1}V_{2}}, L_{S} = L_{V_{1}V_{1}}-L_{V_{1}V_{2}}, \mathcal{L}_{A} = \mathcal{L}_{V_{1}V_{1}}+\mathcal{L}_{V_{1}V_{2}}, \mathcal{L}_{S} = \mathcal{L}_{V_{1}V_{1}}-\mathcal{L}_{V_{1}V_{2}}. \end{eqnarray*}$

Theorem 2.1. ^[24] If $L_{A}, L_{S}, \mathcal{L}_{A}, \mathcal{L}_{S}$ are defined as above, the following formula can be obtained:

$\begin{eqnarray*} P_{L(C_{n})}(x) = P_{L_{A}}(x)P_{L_{S}}(x), P_{\mathcal{L}(C_{n})}(x) = P_{\mathcal{L}_{A}}(x)P_{\mathcal{L}_{S}}(x). \end{eqnarray*}$

Theorem 2.2. ^[15] If $G$ is a graph with $|V_G| = n$ and $|E_G| = m$ , then

$\begin{eqnarray*} 2m\tau(G) = \prod\limits_{i = 1}^{n}d_i\cdot\prod\limits_{i = 2}^{n}\lambda_i, \end{eqnarray*}$

where $\tau(G)$ is the complexity of $G$ , and $\lambda_{i}$ is the normalized Laplacian eigenvalue of $\mathcal{L}(G)$ .

3. The Kirchhoff index and Wiener index of $C_{n}$ in terms of the Laplacian spectrum

In this section, we mainly calculate the Kirchhoff index and Wiener index of $C_{n}$ .

According to (1.1), we can get $L_{V_1 V_1}$ and $L_{V_1 V_2}$ :

$\begin{eqnarray*} L_{V_1 V_1}& = & \left( \begin{array}{ccccccccccc} 3 & -1 & & & & & & & & &\\ -1 & 4 & -1 & & & & & & & &\\ & -1 & 5 & -1 & & & & & & &\\ & & -1 & 5 & -1 & & & & & &\\ & & & -1 & 4 & -1 & & & & &\\ & & & & -1 & 5 & -1 & & & &\\ & & & & & & \ddots & & & &\\ & & & & & & -1 & 5 & -1 & &\\ & & & & & & & -1 & 4 & -1 &\\ & & & & & & & & -1 & 5 & -1\\ & & & & & & & & & -1 & 3\\ \end{array} \right)_{(3n+1)\times(3n+1)}, \end{eqnarray*}$

$\begin{eqnarray*} L_{V_1 V_2}& = & \left( \begin{array}{ccccccccccc} -1 & -1 & & & & & & & & &\\ -1 & 0 & -1 & & & & & & & &\\ & -1 & -1 & -1 & & & & & & &\\ & & -1 & -1 & -1 & & & & & &\\ & & & -1 & 0 & -1 & & & & &\\ & & & & -1 & -1 & -1 & & & &\\ & & & & & & \ddots & & & &\\ & & & & & & -1 & -1 & -1 & &\\ & & & & & & & -1 & 0 & -1 &\\ & & & & & & & & -1 & -1 & -1\\ & & & & & & & & & -1 & -1\\ \end{array} \right)_{(3n+1)\times(3n+1)}. \end{eqnarray*}$

Based on Theorem 2.1, the Laplacian spectrum consists of the eigenvalues of $L_{A}$ , and $L_{S}$ of $C_{n}$ can be obtained.

$\begin{eqnarray*} L_A& = & \left( \begin{array}{ccccccccccc} 2 & -2 & & & & & & & & &\\ -2 & 4 & -2 & & & & & & & &\\ & -2 & 4 & -2 & & & & & & &\\ & & -2 & 4 & -2 & & & & & &\\ & & & -2 & 4 & -2 & & & & &\\ & & & & -2 & 4 & -2 & & & &\\ & & & & & & \ddots & & & &\\ & & & & & & -2 & 4 & -2 & &\\ & & & & & & & -2 & 4 & -2 &\\ & & & & & & & & -2 & 4 & -2\\ & & & & & & & & & -2 & 2\\ \end{array} \right)_{(3n+1)\times(3n+1)}, \end{eqnarray*}$

$\begin{eqnarray*} L_S = diag(4,4,6,6,4,6,\cdots,6,4,6,4)_{(3n+1)}. \end{eqnarray*}$

Assume that $0 = \alpha_{1} < \alpha_{2}\leq\alpha_{3}\leq\cdots\leq\alpha_{3n+1}$ are the roots of $P_{L_{A}}(x)$ , and $0 < \beta_{1}\leq\beta_{2}\leq\beta_{3}\leq\cdots\leq\beta_{3n+1}$ are the roots of $P_{L_{S}}(x)$ . By (1.5), we have

$\begin{eqnarray} Kf(C_{n}) = (6n+2)\Big(\sum\limits_{i = 2}^{3n+1}\frac{1}{\alpha_{i}}+\sum\limits_{i = 1}^{3n+1}\frac{1}{\beta_{i}}\Big). \end{eqnarray}$

(3.1)

It is obvious from the matrix $L_S$ that the following expression can be obtained:

$\begin{eqnarray} \sum\limits_{i = 1}^{3n+1}\frac{1}{\beta_{i}} = \frac{1}{4}\times(n+2)+\frac{1}{6}\times(2n-1) = \frac{7n+4}{12}. \end{eqnarray}$

(3.2)

Thus, we need to calculate the first sum in (3.1).

Let

$\begin{eqnarray*} P_{L_{A}}(x) = det(xI-L_{A}) = x^{3n+1}+a_{1}x^{3n}+\cdots+a_{3n}x. \end{eqnarray*}$

Based on the Vieta $^{'}$ s Theorem of $P_{L_{A}}(x)$ , we can get

$\begin{eqnarray} \sum\limits_{i = 2}^{3n+1}\frac{1}{\alpha_{i}} = \frac{(-1)^{3n-1}a_{3n-1}}{(-1)^{3n}a_{3n}}. \end{eqnarray}$

(3.3)

Obviously, we obtain that $(-1)^{3n}a_{3n}$ is the sum of all the principal minors of order 3n of $L_{A}$ and $(-1)^{3n-1}a_{3n-1}$ is the sum of all the principal minors of order $3n-1$ of $L_{A}$ . So, let $F_{k}$ be the $k$ -th order principal submatrix, which consists of the first $k$ columns and $k$ rows of $L_{A}$ , and $f_{k} = det(F_{k})$ , $k = 1, 2, \cdots, 3n$ . Thus, we can get $f_{1} = 2, f_{2} = 4$ , and for $1\leq{i}\leq3n$ ,

$\begin{eqnarray*} f_{i} = 4f_{i-1}-4f_{i-2}. \end{eqnarray*}$

The solution of the previous recurrence relation is

$\begin{eqnarray*} f_{i} = 2^{i}. \end{eqnarray*}$

Now, let $H_{k}$ be the $k$ -th order principal submatrix, which consists of the last $k$ columns and $k$ rows of $L_{A}$ , and $h_{k} = det(H_{k})$ , $k = 1, 2, \cdots, 3n$ . Based on the symmetry matrix $L_A$ , one gets $h_k = f_k$ , and let $f_0 = 1$ .

Fact 1. $(-1)^{3n}a_{3n} = (3n+1)2^{3n}.$

Proof. Since $(-1)^{3n}a_{3n}$ is the sum of all the principal minors of order 3n of $L_{A}$ , we have

$\begin{eqnarray*} (-1)^{3n}a_{3n}& = &2f_{3n}+\sum\limits_{i = 2}^{3n}f_{i-1}f_{3n+1-i}\\ & = &\sum\limits_{i = 1}^{3n+1}f_{i-1}f_{3n+1-i}\\ & = &(3n+1)2^{3n}. \end{eqnarray*}$

This completes the proof. ■

Fact 2. $(-1)^{3n-1}a_{3n-1} = n(3n+1)(3n+2)2^{3n-2}$

Proof. Since $(-1)^{3n-1}a_{3n-1}$ is the sum of all the principal minors of order $3n-1$ of $L_{A}$ , we obtain

$\begin{eqnarray*} (-1)^{3n-1}a_{3n-1} = \sum\limits_{1\leq{i} < j\leq3n+1}N_{ij}f_{i-1}f_{3n+1-j}, \end{eqnarray*}$

where

$\begin{eqnarray*} N_{ij}& = & \left| \begin{array}{ccccccc} 4 & -2 & & & & &\\ -2 & 4 & -2 & & & &\\ & -2 & 4 & -2 & & &\\ & & & \ddots & & &\\ & & & -2 & 4 & -2 &\\ & & & & -2 & 4 & -2\\ & & & & & -2 & 4 \\ \end{array} \right|_{(j-i-1)\times(j-i-1)}\\ & = &(j-i)2^{j-i-1}. \end{eqnarray*}$

Therefore, we can have

$\begin{eqnarray*} (-1)^{3n-1}a_{3n-1}& = &\sum\limits_{1\leq{i} < j\leq3n+1}(j-i)2^{j-i-1}f_{i-1}f_{3n+1-j}\\ & = &\sum\limits_{1\leq{i} < j\leq3n+1}(j-i)2^{3n-1}\\ & = &n(3n+1)(3n+2)2^{3n-2}. \end{eqnarray*}$

The result is as desired. ■

Together with (3.3) and Facts 1 - 2, we obtain the following lemma.

Lemma 3.1. If $0 = \alpha_{1} < \alpha_{2}\leq\alpha_{3}\leq\cdots\leq\alpha_{3n+1}$ are the eigenvalues of $L_A$ , one gets

$\begin{eqnarray*} \sum\limits_{i = 2}^{3n+1}\frac{1}{\alpha_{i}} = \frac{n(3n+2)}{4}. \end{eqnarray*}$

Applying (3.1) - (3.2) and Lemma 3.1, we obtain the following theorem.

Theorem 3.2. For linear crossed phenylenes $C_n$ , we have

$\begin{eqnarray*} Kf(C_{n}) = \frac{27n^{3}+48n^{2}+25n+4}{6}. \end{eqnarray*}$

The Kirchhoff indices of $C_{n}$ are shown in , where $1\leq{n}\leq15$ .

Table 1. Kirchhoff indices from

$C_{1}$ to

$C_{15}$ .

$G$	$Kf(G)$	$G$	$Kf(G)$	$G$	$Kf(G)$	$G$	$Kf(G)$	$G$	$Kf(G)$
$C_{1}$	$17.33$	$C_{4}$	$433.33$	$C_{7}$	$1965.33$	$C_{10}$	$5342.33$	$C_{13}$	$11293.33$
$C_{2}$	$77.00$	$C_{5}$	$784.00$	$C_{8}$	$2850.00$	$C_{11}$	$7004.00$	$C_{14}$	$13975.00$
$C_{3}$	$206.67$	$C_{6}$	$1285.67$	$C_{9}$	$3966.67$	$C_{12}$	$8978.67$	$C_{15}$	$17050.67$

| Show Table

DownLoad: CSV

Theorem 3.3. Assume that $C_n$ are the linear crossed phenylenes, then

$\begin{eqnarray*} \lim\limits_{n\rightarrow \infty}\frac{Kf(C_{n})}{W(C_{n})} = \frac{1}{4}. \end{eqnarray*}$

Proof. By first classifying and discussing the following cases of vertices, the Wiener index of $C_n$ is obtained.

● Vertex $3j-1(j = 1, 2, \cdots, n)$ of $C_n$ :

$\begin{eqnarray*} w_{1}(i) = 2+2\Big(\sum\limits_{k = 1}^{i-1}k+\sum\limits_{k = 1}^{3n+1-i}k\Big),i = 3j-1. \end{eqnarray*}$

● Vertex $3j(j = 1, 2, \cdots, n)$ of $C_n$ :

$\begin{eqnarray*} w_{2}(i) = 1+2\Big(\sum\limits_{k = 1}^{i-1}k+\sum\limits_{k = 1}^{3n+1-i}k\Big),i = 3j. \end{eqnarray*}$

● Vertex $3j+1(j = 1, 2, \cdots, n-1)$ of $C_n$ :

$\begin{eqnarray*} w_{3}(i) = 1+2\Big(\sum\limits_{k = 1}^{i-1}k+\sum\limits_{k = 1}^{3n+1-i}k\Big),i = 3j+1. \end{eqnarray*}$

● Vertex $1$ of $C_n$ :

$\begin{eqnarray*} w_{4}(i) = 1+2\Big(\sum\limits_{k = 1}^{3n}k\Big). \end{eqnarray*}$

In view of (1.3), we have

$\begin{eqnarray*} W(C_{n})& = &\frac{2\sum\nolimits_{i = 3j-1}w_{1}(i)+2\sum\nolimits_{i = 3j}w_{2}(i)+2\sum\nolimits_{i = 3j+1}w_{3}(i)+4w_{4}(i)}{2}\\ & = &\frac{2\sum\nolimits_{j = 1}^{n}[2+2(\sum\nolimits_{k = 1}^{3j-2}k+\sum\nolimits_{k = 1}^{3n-3j+2}k)]+2\sum\nolimits_{j = 1}^{n}[1+2(\sum\nolimits_{k = 1}^{3j-1}k+\sum\nolimits_{k = 1}^{3n-3j+1}k)]}{2}\\ &&+\frac{2\sum\nolimits_{j = 1}^{n-1}[1+2(\sum\nolimits_{k = 1}^{3j}k+\sum\nolimits_{k = 1}^{3n-3j}k)]+4(1+2\sum\nolimits_{k = 1}^{3n}k)}{2}\\ & = &18n^{3}+18n^{2}+8n+1. \end{eqnarray*}$

Combining with $Kf(C_n)$ and $W(C_n)$ , we have

$\begin{eqnarray*} \lim\limits_{n\rightarrow \infty}\frac{Kf(C_{n})}{W(C_{n})} = \frac{1}{4}, \end{eqnarray*}$

as desired. ■

4. The multiplicative degree-Kirchhoff index, Gutman index, and complexity of $C_{n}$ in terms of the normalized Laplacian spectrum

In this section, we mainly calculate the multiplicative degree-Kirchhoff index, Gutman index, and complexity of $C_{n}$ .

According to (1.2), we can get $\mathcal{L}_{V_1 V_1}$ and $\mathcal{L}_{V_1 V_2}$ :

$\begin{eqnarray*} \mathcal{L}_{V_1 V_1}& = & \left( \begin{array}{cccccccccc} 1 & \frac{-1}{\sqrt{12}} & & & & & & & &\\ \frac{-1}{\sqrt{12}} & 1 & \frac{-1}{\sqrt{20}} & & & & & & &\\ & \frac{-1}{\sqrt{20}} & 1 & \frac{-1}{\sqrt{25}} & & & & & &\\ & & \frac{-1}{\sqrt{25}} & 1 & \frac{-1}{\sqrt{20}} & & & & &\\ & & & \frac{-1}{\sqrt{20}} & 1 & \frac{-1}{\sqrt{20}} & & & &\\ & & & & & \ddots & & & &\\ & & & & & \frac{-1}{\sqrt{25}} & 1 & \frac{-1}{\sqrt{20}} & &\\ & & & & & & \frac{-1}{\sqrt{20}} & 1 & \frac{-1}{\sqrt{20}} &\\ & & & & & & & \frac{-1}{\sqrt{20}} & 1 & \frac{-1}{\sqrt{15}}\\ & & & & & & & & \frac{-1}{\sqrt{15}} & 1\\ \end{array} \right)_{(3n+1)\times(3n+1)}, \end{eqnarray*}$

$\begin{eqnarray*} \mathcal{L}_{V_1 V_2}& = & \left( \begin{array}{cccccccccc} \frac{-1}{3} & \frac{-1}{\sqrt{12}} & & & & & & & &\\ \frac{-1}{\sqrt{12}} & 0 & \frac{-1}{\sqrt{20}} & & & & & & &\\ & \frac{-1}{\sqrt{20}} & \frac{-1}{5} & \frac{-1}{\sqrt{25}} & & & & & &\\ & & \frac{-1}{\sqrt{25}} & \frac{-1}{5} & \frac{-1}{\sqrt{20}} & & & & &\\ & & & \frac{-1}{\sqrt{20}} & 0 & \frac{-1}{\sqrt{20}} & & & &\\ & & & & & \ddots & & & &\\ & & & & & \frac{-1}{\sqrt{25}} & \frac{-1}{5} & \frac{-1}{\sqrt{20}} & &\\ & & & & & & \frac{-1}{\sqrt{20}} & 0 & \frac{-1}{\sqrt{20}} &\\ & & & & & & & \frac{-1}{\sqrt{20}} & \frac{-1}{5} & \frac{-1}{\sqrt{15}}\\ & & & & & & & & \frac{-1}{\sqrt{15}} & \frac{-1}{3}\\ \end{array} \right)_{(3n+1)\times(3n+1)}. \end{eqnarray*}$

Based on Theorem 2.1, the normalized Laplacian spectrum consists of the eigenvalues of $\mathcal{L}_{A}$ , and $\mathcal{L}_{S}$ of $C_{n}$ can be obtained.

$\begin{eqnarray*} \mathcal{L}_A& = & \left( \begin{array}{ccccccccccc} \frac{2}{3} & \frac{-1}{\sqrt{3}} & & & & & & & & &\\ \frac{-1}{\sqrt{3}} & 1 & \frac{-1}{\sqrt{5}} & & & & & & & &\\ & \frac{-1}{\sqrt{5}} & \frac{4}{5} & \frac{-2}{\sqrt{25}} & & & & & & &\\ & & \frac{-2}{\sqrt{25}} & \frac{4}{5} & \frac{-1}{\sqrt{5}} & & & & & &\\ & & & \frac{-1}{\sqrt{5}} & 1 & \frac{-1}{\sqrt{5}} & & & & &\\ & & & & \frac{-1}{\sqrt{5}} & \frac{4}{5} & \frac{-2}{\sqrt{25}} & & & &\\ & & & & & & \ddots & & & &\\ & & & & & & \frac{-2}{\sqrt{25}} & \frac{4}{5} & \frac{-1}{\sqrt{5}} & &\\ & & & & & & & \frac{-1}{\sqrt{5}} & 1 & \frac{-1}{\sqrt{5}} &\\ & & & & & & & & \frac{-1}{\sqrt{5}} & \frac{4}{5} & \frac{-2}{\sqrt{15}}\\ & & & & & & & & & \frac{-2}{\sqrt{15}} & \frac{2}{3}\\ \end{array} \right)_{(3n+1)\times(3n+1)}, \end{eqnarray*}$

$\begin{eqnarray*} \mathcal{L}_S = diag\Big(\frac{4}{3},1,\frac{6}{5},\frac{6}{5},1,\frac{6}{5},\cdots,\frac{6}{5},1,\frac{6}{5},\frac{4}{3}\Big)_{(3n+1)}. \end{eqnarray*}$

Assume that $0 = \gamma_{1} < \gamma_{2}\leq\gamma_{3}\leq\cdots\leq\gamma_{3n+1}$ are the roots of $P_{\mathcal{L}_{A}}(x)$ , and $0 < \delta_{1}\leq\delta_{2}\leq\delta_{3}\leq\cdots\leq\delta_{3n+1}$ are the roots of $P_{\mathcal{L}_{S}}(x)$ . By (1.6), we have

$\begin{eqnarray} Kf^{*}(C_{n}) = (28n+2)\Big(\sum\limits_{i = 2}^{3n+1}\frac{1}{\gamma_{i}}+\sum\limits_{i = 1}^{3n+1}\frac{1}{\delta_{i}}\Big). \end{eqnarray}$

(4.1)

It is obvious from the matrix $\mathcal{L}_S$ that the following expression can be obtained:

$\begin{eqnarray} \sum\limits_{i = 1}^{3n+1}\frac{1}{\delta_{i}} = 1\times{n}+\frac{5}{6}\times(2n-1)+\frac{3}{4}\times2 = \frac{8n+2}{3}. \end{eqnarray}$

(4.2)

Therefore, we need to calculate the first sum in (4.1).

Let

$\begin{eqnarray*} P_{\mathcal{L}_{A}}(x) = det(xI-\mathcal{L}_{A}) = x^{3n+1}+b_{1}x^{3n}+\cdots+b_{3n}x. \end{eqnarray*}$

Based on the Vieta $^{'}$ s Theorem of $P_{\mathcal{L}_{A}}(x)$ , we can get

$\begin{eqnarray} \sum\limits_{i = 2}^{3n+1}\frac{1}{\gamma_{i}} = \frac{(-1)^{3n-1}b_{3n-1}}{(-1)^{3n}b_{3n}}. \end{eqnarray}$

(4.3)

Obviously, we obtain that $(-1)^{3n}b_{3n}$ is the sum of all the principal minors of order $3n$ of $\mathcal{L}_{A}$ and $(-1)^{3n-1}b_{3n-1}$ is the sum of the principal minors of order $3n-1$ of $\mathcal{L}_{A}$ . So, let $T_{k}$ be the $k$ -th order principal submatrix, which consists of the first $k$ columns and $k$ rows of $\mathcal{L}_{A}$ , and $t_{k} = det(T_{k})$ , $k = 1, 2, \cdots, 3n$ . Thus, we can get $t_{1} = \frac{2}{3}, t_{2} = \frac{1}{3}, t_{3} = \frac{2}{15}$ , and for $1\leq{i}\leq{n-1}$ ,

$\begin{eqnarray*} \begin{cases} t_{3i+1} = \frac{4}{5}t_{3i}-\frac{4}{25}t_{3i-1};\\ t_{3i+2} = t_{3i+1}-\frac{1}{5}t_{3i};\\ t_{3i+3} = \frac{4}{5}t_{3i+2}-\frac{1}{5}t_{3i+1}. \end{cases} \end{eqnarray*}$

The solution of the previous recurrence relation is

$\begin{eqnarray*} \begin{cases} t_{3i-2} = \frac{25}{3}\cdot(\frac{2}{25})^{i};\\ t_{3i-1} = \frac{25}{6}\cdot(\frac{2}{25})^{i};\\ t_{3i} = \frac{5}{3}\cdot(\frac{2}{25})^{i}; \end{cases} \end{eqnarray*}$

where $1\leq{i}\leq{n}$ .

Now, let $S_{k}$ be the $k$ -th order principal submatrix, which consists of the last $k$ columns and $k$ rows of $\mathcal{L}_{A}$ , and $s_{k} = det(S_{k})$ , $k = 1, 2, \cdots, 3n$ . Thus, we can get $s_{1} = \frac{2}{3}, s_{2} = \frac{4}{15}, s_{3} = \frac{2}{15}$ , and for $1\leq{i}\leq{n-1}$ ,

$\begin{eqnarray*} \begin{cases} s_{3i+1} = \frac{4}{5}s_{3i}-\frac{1}{5}s_{3i-1};\\ s_{3i+2} = \frac{4}{5}s_{3i+1}-\frac{4}{25}s_{3i};\\ s_{3i+3} = s_{3i+2}-\frac{1}{5}s_{3i+1}. \end{cases} \end{eqnarray*}$

The solution of the previous recurrence relation is

$\begin{eqnarray*} \begin{cases} s_{3i-2} = \frac{25}{3}\cdot(\frac{2}{25})^{i};\\ s_{3i-1} = \frac{10}{3}\cdot(\frac{2}{25})^{i};\\ s_{3i} = \frac{5}{3}\cdot(\frac{2}{25})^{i}; \end{cases} \end{eqnarray*}$

where $1\leq{i}\leq{n}$ .

Without loss of generality, let $t_0 = 1$ and $s_0 = 1$ .

Fact 1. $(-1)^{3n}b_{3n} = \frac{5}{9}(14n+1)(\frac{2}{25})^{n}.$

Proof. By a similar discussion as in Section 3, we obtain that $(-1)^{3n}b_{3n}$ is the sum of all the principal minors of order $3n$ of $\mathcal{L}_{A}$ ,

$\begin{eqnarray*} (-1)^{3n}b_{3n}& = &\sum\limits_{j = 1}^{3n+1}t_{j-1}s_{3n+1-j}\\ & = &t_{3n}+s_{3n}+\sum\limits_{j = 2}^{3n}t_{j-1}s_{3n+1-j}\\ & = &2\cdot\frac{5}{3}\cdot\Big(\frac{2}{25}\Big)^{n}+\sum\limits_{i = 1}^{n}\frac{25}{3}\cdot\Big(\frac{2}{25}\Big)^{i}\cdot\frac{10}{3}\cdot\Big(\frac{2}{25}\Big)^{n-i+1} +\sum\limits_{i = 1}^{n}\frac{25}{6}\cdot\Big(\frac{2}{25}\Big)^{i}\cdot\frac{25}{3}\cdot\Big(\frac{2}{25}\Big)^{n-i+1}\\ &&+\sum\limits_{i = 1}^{n-1}\frac{5}{3}\cdot\Big(\frac{2}{25}\Big)^{i}\cdot\frac{5}{3}\cdot\Big(\frac{2}{25}\Big)^{n-i}\\ & = &\frac{5}{9}(14n+1)\Big(\frac{2}{25}\Big)^{n}. \end{eqnarray*}$

The result is as desired. ■

Fact 2. $(-1)^{3n-1}b_{3n-1} = \frac{98n^{3}+21n^{2}+9n}{45}(\frac{2}{25})^{n-1}.$

Proof. Since $(-1)^{3n-1}b_{3n-1}$ is the sum of all the principal minors of order $3n-1$ of $\mathcal{L}_{A}$ , one has

$\begin{eqnarray} (-1)^{3n-1}b_{3n-1} = \sum\limits_{1\leq{i} < j\leq3n+1}det\mathcal{L}_{A}[i,j]t_{i-1}s_{3n+1-j}. \end{eqnarray}$

(4.4)

In view of (4.4), all possible cases are listed.

Case 1. $i = 3p, j = 3q, 1\leq{p} < q\leq{n},$

$\begin{eqnarray*} det\mathcal{L}_{A}[3p,3q]& = & \left| \begin{array}{cccccccc} \frac{4}{5} & \frac{-1}{\sqrt{5}} & & & & & &\\ \frac{-1}{\sqrt{5}} & 1 & \frac{-1}{\sqrt{5}} & & & & &\\ & \frac{-1}{\sqrt{5}} & \frac{4}{5} & \frac{-2}{\sqrt{25}} & & & &\\ & & & \ddots & & & &\\ & & & \frac{-1}{\sqrt{5}} & 1 & \frac{-1}{\sqrt{5}} & &\\ & & & & \frac{-1}{\sqrt{5}} & \frac{4}{5} & \frac{-2}{\sqrt{25}} &\\ & & & & & \frac{-2}{\sqrt{25}} & \frac{4}{5} & \frac{-1}{\sqrt{5}}\\ & & & & & & \frac{-1}{\sqrt{5}} & 1\\ \end{array} \right|_{(3q-3p-1)\times (3q-3p-1)}\\ & = &\frac{3}{5}(q-p)\Big(\frac{2}{25}\Big)^{q-p-1}. \end{eqnarray*}$

Case 2. $i = 3p, j = 3q+1, 1\leq{p}\leq{q}\leq{n},$

$\begin{eqnarray*} det\mathcal{L}_{A}[3p,3q+1]& = & \left| \begin{array}{cccccccc} \frac{4}{5} & \frac{-1}{\sqrt{5}} & & & & & &\\ \frac{-1}{\sqrt{5}} & 1 & \frac{-1}{\sqrt{5}} & & & & &\\ & \frac{-1}{\sqrt{5}} & \frac{4}{5} & \frac{-2}{\sqrt{25}} & & & &\\ & & & \ddots & & & &\\ & & & \frac{-1}{\sqrt{5}} & \frac{4}{5} & \frac{-2}{\sqrt{25}} & &\\ & & & & \frac{-2}{\sqrt{25}} & \frac{4}{5} & \frac{-1}{\sqrt{5}} &\\ & & & & & \frac{-1}{\sqrt{5}} & 1 & \frac{-1}{\sqrt{5}}\\ & & & & & & \frac{-1}{\sqrt{5}} & \frac{4}{5}\\ \end{array} \right|_{(3q-3p)\times (3q-3p)}\\ & = &\frac{2}{25}[3(q-p)+1]\Big(\frac{2}{25}\Big)^{q-p-1}. \end{eqnarray*}$

Case 3. $i = 3p, j = 3q+2, 1\leq{p}\leq{q}\leq{n-1},$

$\begin{eqnarray*} det\mathcal{L}_{A}[3p,3q+2]& = & \left| \begin{array}{cccccccc} \frac{4}{5} & \frac{-1}{\sqrt{5}} & & & & & &\\ \frac{-1}{\sqrt{5}} & 1 & \frac{-1}{\sqrt{5}} & & & & &\\ & \frac{-1}{\sqrt{5}} & \frac{4}{5} & \frac{-2}{\sqrt{25}} & & & &\\ & & & \ddots & & & &\\ & & & \frac{-2}{\sqrt{25}} & \frac{4}{5} & \frac{-1}{\sqrt{5}} & &\\ & & & & \frac{-1}{\sqrt{5}} & 1 & \frac{-1}{\sqrt{5}} &\\ & & & & & \frac{-1}{\sqrt{5}} & \frac{4}{5} & \frac{-2}{\sqrt{25}}\\ & & & & & & \frac{-2}{\sqrt{25}} & \frac{4}{5}\\ \end{array} \right|_{(3q-3p+1)\times (3q-3p+1)}\\ & = &\frac{2}{5}[3(q-p)+2]\Big(\frac{2}{25}\Big)^{q-p}. \end{eqnarray*}$

Case 4. $i = 3p+1, j = 3q, 0\leq{p} < q\leq{n},$

$\begin{eqnarray*} det\mathcal{L}_{A}[3p+1,3q]& = & \left| \begin{array}{cccccccc} 1 & \frac{-1}{\sqrt{5}} & & & & & &\\ \frac{-1}{\sqrt{5}} & \frac{4}{5} & \frac{-2}{\sqrt{25}} & & & & &\\ & \frac{-2}{\sqrt{25}} & \frac{4}{5} & \frac{-1}{\sqrt{5}} & & & &\\ & & & \ddots & & & &\\ & & & \frac{-1}{\sqrt{5}} & 1 & \frac{-1}{\sqrt{5}} & &\\ & & & & \frac{-1}{\sqrt{5}} & \frac{4}{5} & \frac{-2}{\sqrt{25}} &\\ & & & & & \frac{-2}{\sqrt{25}} & \frac{4}{5} & \frac{-1}{\sqrt{5}}\\ & & & & & & \frac{-1}{\sqrt{5}} & 1\\ \end{array} \right|_{(3q-3p-2)\times (3q-3p-2)}\\ & = &\frac{1}{2}[3(q-p)-1]\Big(\frac{2}{25}\Big)^{q-p-1}. \end{eqnarray*}$

Case 5. $i = 3p+1, j = 3q+1, 0\leq{p} < q\leq{n},$

$\begin{eqnarray*} det\mathcal{L}_{A}[3p+1,3q+1]& = & \left| \begin{array}{cccccccc} 1 & \frac{-1}{\sqrt{5}} & & & & & &\\ \frac{-1}{\sqrt{5}} & \frac{4}{5} & \frac{-2}{\sqrt{25}} & & & & &\\ & \frac{-2}{\sqrt{25}} & \frac{4}{5} & \frac{-1}{\sqrt{5}} & & & &\\ & & & \ddots & & & &\\ & & & \frac{-1}{\sqrt{5}} & \frac{4}{5} & \frac{-2}{\sqrt{25}} & &\\ & & & & \frac{-2}{\sqrt{25}} & \frac{4}{5} & \frac{-1}{\sqrt{5}} &\\ & & & & & \frac{-1}{\sqrt{5}} & 1 & \frac{-1}{\sqrt{5}}\\ & & & & & & \frac{-1}{\sqrt{5}} & \frac{4}{5}\\ \end{array} \right|_{(3q-3p-1)\times (3q-3p-1)}\\ & = &\frac{3}{5}(q-p)\Big(\frac{2}{25}\Big)^{q-p-1}. \end{eqnarray*}$

Case 6. $i = 3p+1, j = 3q+2, 0\leq{p}\leq{q}\leq{n-1},$

$\begin{eqnarray*} det\mathcal{L}_{A}[3p+1,3q+2]& = & \left| \begin{array}{cccccccc} 1 & \frac{-1}{\sqrt{5}} & & & & & &\\ \frac{-1}{\sqrt{5}} & \frac{4}{5} & \frac{-2}{\sqrt{25}} & & & & &\\ & \frac{-2}{\sqrt{25}} & \frac{4}{5} & \frac{-1}{\sqrt{5}} & & & &\\ & & & \ddots & & & &\\ & & & \frac{-2}{\sqrt{25}} & \frac{4}{5} & \frac{-1}{\sqrt{5}} & &\\ & & & & \frac{-1}{\sqrt{5}} & 1 & \frac{-1}{\sqrt{5}} &\\ & & & & & \frac{-1}{\sqrt{5}} & \frac{4}{5} & \frac{-2}{\sqrt{25}}\\ & & & & & & \frac{-2}{\sqrt{25}} & \frac{4}{5}\\ \end{array} \right|_{(3q-3p)\times (3q-3p)}\\ & = &[3(q-p)+1]\Big(\frac{2}{25}\Big)^{q-p}. \end{eqnarray*}$

Case 7. $i = 3p+2, j = 3q, 0\leq{p} < q\leq{n},$

$\begin{eqnarray*} det\mathcal{L}_{A}[3p+2,3q]& = & \left| \begin{array}{cccccccc} \frac{4}{5} & \frac{-2}{\sqrt{25}} & & & & & &\\ \frac{-2}{\sqrt{25}} & \frac{4}{5} & \frac{-1}{\sqrt{5}} & & & & &\\ & \frac{-1}{\sqrt{5}} & 1 & \frac{-1}{\sqrt{5}} & & & &\\ & & & \ddots & & & &\\ & & & \frac{-1}{\sqrt{5}} & 1 & \frac{-1}{\sqrt{5}} & &\\ & & & & \frac{-1}{\sqrt{5}} & \frac{4}{5} & \frac{-2}{\sqrt{25}} &\\ & & & & & \frac{-2}{\sqrt{25}} & \frac{4}{5} & \frac{-1}{\sqrt{5}}\\ & & & & & & \frac{-1}{\sqrt{5}} & 1\\ \end{array} \right|_{(3q-3p-3)\times (3q-3p-3)}\\ & = &[3(q-p)-2]\Big(\frac{2}{25}\Big)^{q-p-1}. \end{eqnarray*}$

Case 8. $i = 3p+2, j = 3q+1, 0\leq{p} < q\leq{n},$

$\begin{eqnarray*} det\mathcal{L}_{A}[3p+2,3q+1]& = & \left| \begin{array}{cccccccc} \frac{4}{5} & \frac{-2}{\sqrt{25}} & & & & & &\\ \frac{-2}{\sqrt{25}} & \frac{4}{5} & \frac{-1}{\sqrt{5}} & & & & &\\ & \frac{-1}{\sqrt{5}} & 1 & \frac{-1}{\sqrt{5}} & & & &\\ & & & \ddots & & & &\\ & & & \frac{-1}{\sqrt{5}} & \frac{4}{5} & \frac{-2}{\sqrt{25}} & &\\ & & & & \frac{-2}{\sqrt{25}} & \frac{4}{5} & \frac{-1}{\sqrt{5}} &\\ & & & & & \frac{-1}{\sqrt{5}} & 1 & \frac{-1}{\sqrt{5}}\\ & & & & & & \frac{-1}{\sqrt{5}} & \frac{4}{5}\\ \end{array} \right|_{(3q-3p-2)\times (3q-3p-2)}\\ & = &\frac{2}{5}[3(q-p)-1]\Big(\frac{2}{25}\Big)^{q-p-1}. \end{eqnarray*}$

Case 9. $i = 3p+2, j = 3q+2, 0\leq{p} < q\leq{n-1},$

$\begin{eqnarray*} det\mathcal{L}_{A}[3p+2,3q+2]& = & \left| \begin{array}{cccccccc} \frac{4}{5} & \frac{-2}{\sqrt{25}} & & & & & &\\ \frac{-2}{\sqrt{25}} & \frac{4}{5} & \frac{-1}{\sqrt{5}} & & & & &\\ & \frac{-1}{\sqrt{5}} & 1 & \frac{-1}{\sqrt{5}} & & & &\\ & & & \ddots & & & &\\ & & & \frac{-2}{\sqrt{25}} & \frac{4}{5} & \frac{-1}{\sqrt{5}} & &\\ & & & & \frac{-1}{\sqrt{5}} & 1 & \frac{-1}{\sqrt{5}} &\\ & & & & & \frac{-1}{\sqrt{5}} & \frac{4}{5} & \frac{-2}{\sqrt{25}}\\ & & & & & & \frac{-2}{\sqrt{25}} & \frac{4}{5}\\ \end{array} \right|_{(3q-3p-1)\times (3q-3p-1)}\\ & = &\frac{12}{25}(q-p)\Big(\frac{2}{25}\Big)^{q-p-1}. \end{eqnarray*}$

Therefore, we can get

$\begin{eqnarray*} (-1)^{3n-1}b_{3n-1}& = &\sum\limits_{1\leq{i} < j\leq3n+1}det\mathcal{L}_{A}[i,j]t_{i-1}s_{3n+1-j}\\ & = &X_{1}+X_{2}+X_{3}, \end{eqnarray*}$

where

$\begin{eqnarray*} X_{1}& = &\sum\limits_{1\leq{p} < q\leq{n}}det\mathcal{L}_{A}[3p,3q]t_{3p-1}s_{3n-3q+1}+\sum\limits_{1\leq{p}\leq{q}\leq{n}}det\mathcal{L}_{A}[3p,3q+1]t_{3p-1}s_{3n-3q}\\ &&+\sum\limits_{1\leq{p}\leq{q}\leq{n-1}}det\mathcal{L}_{A}[3p,3q+2]t_{3p-1}s_{3n-3q-1}\\ & = &\frac{14n^{3}-5n^{2}-3n}{18}\Big(\frac{2}{25}\Big)^{n-1}, \end{eqnarray*}$

$\begin{eqnarray*} X_{2}& = &\sum\limits_{0\leq{p} < q\leq{n}}det\mathcal{L}_{A}[3p+1,3q]t_{3p}s_{3n-3q+1}+\sum\limits_{0\leq{p} < q\leq{n}}det\mathcal{L}_{A}[3p+1,3q+1]t_{3p}s_{3n-3q}\\ &&+\sum\limits_{0\leq{p}\leq{q}\leq{n-1}}det\mathcal{L}_{A}[3p+1,3q+2]t_{3p}s_{3n-3q-1}\\ & = &\frac{70n^{3}+31n^{2}+37n}{90}\Big(\frac{2}{25}\Big)^{n-1}, \end{eqnarray*}$

$\begin{eqnarray*} X_{3}& = &\sum\limits_{0\leq{p} < q\leq{n}}det\mathcal{L}_{A}[3p+2,3q]t_{3p+1}s_{3n-3q+1}+\sum\limits_{0\leq{p} < q\leq{n}}det\mathcal{L}_{A}[3p+2,3q+1]t_{3p+1}s_{3n-3q}\\ &&+\sum\limits_{0\leq{p} < q\leq{n-1}}det\mathcal{L}_{A}[3p+2,3q+2]t_{3p+1}s_{3n-3q-1}\\ & = &\frac{2}{45}(14n^{3}+9n^{2}-n)\Big(\frac{2}{25}\Big)^{n-1}. \end{eqnarray*}$

Thus, we can obtain

$\begin{eqnarray*} (-1)^{3n-1}b_{3n-1} = X_{1}+X_{2}+X_{3} = \frac{98n^{3}+21n^{2}+9n}{45}\Big(\frac{2}{25}\Big)^{n-1}, \end{eqnarray*}$

which is the desired result. ■

Together with (4.3) and Facts 1 - 2, one can get the following lemma.

Lemma 4.1. Assume that $0 = \gamma_{1} < \gamma_{2}\leq\gamma_{3}\leq\cdots\leq\gamma_{3n+1}$ are the eigenvalues of $\mathcal{L}_A$ , then one gets

$\begin{eqnarray*} \sum\limits_{i = 2}^{3n+1}\frac{1}{\gamma_{i}} = \frac{98n^{3}+21n^{2}+9n}{28n+2}. \end{eqnarray*}$

According to (4.1) - (4.2) and Lemma 4.1, we obtain the following theorem.

Theorem 4.2. For linear crossed phenylenes $C_n$ , we have

$\begin{eqnarray*} Kf^{*}(C_{n}) = \frac{294n^{3}+287n^{2}+99n+4}{3}. \end{eqnarray*}$

The multiplicative degree-Kirchhoff indices of $C_{n}$ are shown in , where $1\leq{n}\leq15$ .

Theorem 4.3. Assume that $C_n$ are the linear crossed phenylenes, then

$\begin{eqnarray*} \lim\limits_{n\rightarrow \infty}\frac{Kf^{*}(C_{n})}{Gut(C_{n})} = \frac{1}{4}. \end{eqnarray*}$

Proof. By first classifying and discussing the following cases of vertices, the Gutman index of $C_n$ is obtained.

Table 2. Multiplicative degree-Kirchhoff indices from

$C_{1}$ to

$C_{15}$ .

$G$	$Kf^{*}(G)$	$G$	$Kf^{*}(G)$	$G$	$Kf^{*}(G)$	$G$	$Kf^{*}(G)$	$G$	$Kf^{*}(G)$
$C_{1}$	$208.00$	$C_{4}$	$7688.00$	$C_{7}$	$37806.00$	$C_{10}$	$106438.00$	$C_{13}$	$229460.00$
$C_{2}$	$1166.00$	$C_{5}$	$14428.00$	$C_{8}$	$55620.00$	$C_{11}$	$140618.00$	$C_{14}$	$285298.00$
$C_{3}$	$3463.33$	$C_{6}$	$24271.33$	$C_{9}$	$78301.33$	$C_{12}$	$181429.33$	$C_{15}$	$349531.33$

| Show Table

DownLoad: CSV

● Vertex $3i-1(i = 1, 2, \cdots, n)$ of $C_n$ :

$\begin{eqnarray*} g_{3i-1}& = &2\sum\limits_{i = 1}^{n}\big[4\times4\times2+2\times3\times4\times(3i-2)+2\times3\times4\times(3n-3i+2)\\ &&+2\sum\limits_{k = 1}^{i-1}4\times4\times3\times(i-k)+2\sum\limits_{k = i+1}^{n}4\times4\times3\times(k-i)\\ &&+2\sum\limits_{k = 2}^{i}4\times5\times(3i-3k+1)+2\sum\limits_{k = i+1}^{n}4\times5\times(3k-3i-1)\\ &&+2\sum\limits_{k = 1}^{i-1}4\times5\times(3i-k-1)+2\sum\limits_{k = i}^{n}4\times5\times(3k-3i+1)\big]\\ & = &8(28n^{3}+3n^{2}+5n). \end{eqnarray*}$

● Vertex $3i(i = 1, 2, \cdots, n)$ of $C_n$ :

$\begin{eqnarray*} g_{3i}& = &2\sum\limits_{i = 1}^{n}\big[5\times5\times1+2\times3\times5\times(3i-1)+2\times3\times5\times(3n-3i+1)\\ &&+2\sum\limits_{k = 1}^{i}4\times5\times(3i-3k+1)+2\sum\limits_{k = i+1}^{n}4\times5\times(3k-3i-1)\\ &&+2\sum\limits_{k = 2}^{i}5\times5\times(3i-3k+2)+2\sum\limits_{k = i+1}^{n}5\times5\times(3k-3i-2)\\ &&+2\sum\limits_{k = 1}^{i-1}5\times5\times3\times(i-k)+2\sum\limits_{k = i+1}^{n}5\times5\times3\times(k-i)\big]\\ & = &10(28n^{3}+3n^{2}). \end{eqnarray*}$

● Vertex $3i-2(i = 2, 3, \cdots, n)$ of $C_n$ :

$\begin{eqnarray*} g_{3i-2}& = &2\sum\limits_{i = 2}^{n}\big[5\times5\times1+2\times3\times5\times(3i-3)+2\times3\times5\times(3n-3i+3)\\ &&+2\sum\limits_{k = 1}^{i-1}4\times5\times(3i-3k-1)+2\sum\limits_{k = i}^{n}4\times5\times(3k-3i+1)\\ &&+2\sum\limits_{k = 2}^{i-1}5\times5\times3\times(i-k)+2\sum\limits_{k = i+1}^{n}5\times5\times3\times(k-i)\\ &&+2\sum\limits_{k = 1}^{i-1}5\times5\times(3i-3k-2)+2\sum\limits_{k = i}^{n}5\times5\times(3k-3i+2)\big]\\ & = &10(28n^{3}-39n^{2}+16n-5). \end{eqnarray*}$

● Corner vertex of $C_n$ :

$\begin{eqnarray*} g_o& = &2\big[3\times3\times1+2\times3\times3\times3n+2(\sum\limits_{i = 1}^{n}3\times4(3i-2)\\ &&+\sum\limits_{i = 1}^{n}3\times5\times(3i-1)+\sum\limits_{i = 2}^{n}3\times5\times(3i-3))\big]\\ &&+2\big[3\times3\times1+2\times3\times3\times3n+2(\sum\limits_{i = 1}^{n}3\times4\times(3n-3i+2)\\ &&+\sum\limits_{i = 1}^{n}3\times5\times(3n-3i+1)+\sum\limits_{i = 2}^{n}3\times5\times(3n-3i+3))\big]\\ & = &504n^{2}+36n+36. \end{eqnarray*}$

Applying (1.4), we obtain

$\begin{eqnarray*} Gut(C_{n}) = \frac{g_{o}+g_{3i-1}+g_{3i-2}+g_{3i}}{2} = 392n^{3}+84n^{2}+118n-7. \end{eqnarray*}$

Combining with $Kf^{*}(C_n)$ and $Gut(C_n)$ , one has

$\begin{eqnarray*} \lim\limits_{n\rightarrow \infty}\frac{Kf^{*}(C_{n})}{Gut(C_{n})} = \frac{1}{4}. \end{eqnarray*}$

This completes the proof. ■

In the following, we can calculate the complexity of $C_{n}$ .

Theorem 4.4. For linear crossed phenylenes $C_{n}$ , we have

$\begin{eqnarray*} \tau(C_{n}) = 2^{7n+2}\cdot3^{2n-1}. \end{eqnarray*}$

Proof. Based on Theorem 2.2, we can get $\prod_{i = 1}^{6n+2}d_{i}\prod_{i = 2}^{3n+1}\gamma_{i}\prod_{i = 1}^{3n+1}\delta_{i} = 2(14n+1)\tau(C_{n}),$

where

$\begin{eqnarray*} \prod\limits_{i = 1}^{6n+2}d_{i} = 3^{4}\cdot4^{2n}\cdot5^{4n-2}, \end{eqnarray*}$

$\begin{eqnarray*} \prod\limits_{i = 2}^{3n+1}\gamma_{i} = (-1)^{3n}b_{3n} = \frac{5}{9}\cdot(14n+1)\cdot\Big(\frac{2}{25}\Big)^{n}, \end{eqnarray*}$

$\begin{eqnarray*} \prod\limits_{i = 1}^{3n+1}\delta_{i} = \Big(\frac{4}{3}\Big)^{2}\cdot\Big(\frac{6}{5}\Big)^{2n-1}. \end{eqnarray*}$

Hence,

$\begin{eqnarray*} \tau(C_{n}) = 2^{7n+2}\cdot3^{2n-1}. \end{eqnarray*}$

The result is as desired. ■

The complexity of $C_{n}$ is shown in , where $1\leq{n}\leq12$ .

Table 3. The complexity from

$C_{1}$ to

$C_{12}$ .

$G$	$\tau(G)$	$G$	$\tau(G)$
$C_{1}$	$1536$	$C_{7}$	$3590096234354105647104$
$C_{2}$	$1769472$	$C_{8}$	$4135790861975929705463808$
$C_{3}$	$2038431744$	$C_{9}$	$4764431072996271020694306816$
$C_{4}$	$2348273369088$	$C_{10}$	$5488624596091704215839841452032$
$C_{5}$	$2705210921189376$	$C_{11}$	$6322895534697643256647497352740864$
$C_{6}$	$3116402981210161152$	$C_{12}$	$7283975655971685031657916950357475328$

| Show Table

DownLoad: CSV

5. Conclusions

Based on the Laplacian (normalized Laplacian, resp) polynomial of $C_{n}$ , we determined the Kirchhoff index, multiplicative degree-Kirchhoff index, and complexity of linear crossed phenylenes through the decomposition theorem and Vieta $^{'}$ s Theorem. In addition, we found that the Kirchhoff index and multiplicative degree-Kirchhoff index of linear crossed phenylenes were approximately one quarter of their Wiener index and Gutman index, respectively, which further enriched the results of the Kirchhoff index, multiplicative degree-Kirchhoff index, and complexity for the linear crossed chains.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported in part by Anhui Provincial Natural Science Foundation Project under Grant KJ2021A1175, Funding project for cultivating top-notch talents in universities under Grant gxgnfx2022096, Anhui Provincial Education Reform Research Project under Grant 2022jyxm481, Anhui Provincial Natural Science Foundation Project under Grant 2023AH051697.

Conflict of interest

All authors declare no conflicts of interest in this paper.

References

[1]	J. Chen, A. B. Le, Q. Wang, L. Xi, A small-world and scale-free network generated by Sierpinski Pentagon, Physica A, 449 (2016), 126–135. https://doi.org/10.1016/j.physa.2015.12.089 doi: 10.1016/j.physa.2015.12.089
[2]	W. Sun, M. Sun, J. Guan, Q. Jia, Robustness of coherence in noisy scale-free networks and applications to identification of influential spreaders, IEEE T. Circuits-Ⅱ, 67 (2019), 1274–1278. https://doi.org/10.1109/TCSII.2019.2929139 doi: 10.1109/TCSII.2019.2929139
[3]	W. Sun, Q. Ding, J. Zhang, F. Chen, Coherence in a family of tree networks with an application of Laplacian spectrum, Chaos, 24 (2014), 043112. https://doi.org/10.1063/1.4897568 doi: 10.1063/1.4897568
[4]	X. Qi, E. Fuller, R. Luo, G. Guo, C. Zhang, Laplacian energy of digraphs and a minimum Laplacian energy algorithm, Int. J. Found. Comput. Sci., 26 (2015), 367–380. https://doi.org/10.1142/S0129054115500203 doi: 10.1142/S0129054115500203
[5]	Y. J. Yang, H. P. Zhang, Kirchhoff index of linear hexagonal chains, Int. J. Quantum Chem., 108 (2008), 503–512. https://doi.org/10.1002/qua.21537 doi: 10.1002/qua.21537
[6]	J. Huang, S. C. Li, L. Sun, The normalized Laplacians degree-Kirchhoff index and the spanning trees of linear hexagonal chains, Discrete Appl. Math., 207 (2016), 67–79. https://doi.org/10.1016/j.dam.2016.02.019 doi: 10.1016/j.dam.2016.02.019
[7]	Y. J. Peng, S. C. Li, On the kirchhoff index and the number of spanning trees of linear phenylenes, Match Communications in Mathematical and in Computer Chemistry, 77 (2017), 765–780.
[8]	Z. X. Zhu, J. B. Liu, The normalized Laplacian, degree-Kirchhoff index and the spanning tree numbers of generalized phenylenes, Discrete Appl. Math., 254 (2019), 256–267. https://doi.org/10.1016/j.dam.2018.06.026 doi: 10.1016/j.dam.2018.06.026
[9]	Y. Pan, J. Li, Kirchhoff index, multiplicative degree-Kirchhoff index and spanning trees of the linear crossed hexagonal chains, Int. J. Quantum Chem., 118 (2018), e25787. https://doi.org/10.1002/qua.25787 doi: 10.1002/qua.25787
[10]	D. Zhao, Y. Zhao, Z. Wang, X. Li, K. Zhou, Kirchhoff index and degree Kirchhoff index of Tetrahedrane-derived compounds, Symmetry, 15 (2023), 1122. https://doi.org/10.3390/sym15051122 doi: 10.3390/sym15051122
[11]	J. Wang, L. Liu, H. Zhang, On the Laplacian spectra and the Kirchhoff indices of two types of networks, Optimization, (2023). https://doi.org/10.1080/02331934.2023.2268631
[12]	X. Geng, P. Wang, L. Lei, S. Wang, On the Kirchhoff indices and the number of spanning trees of M $\ddot{o}$ bius phenylenes chain and Cylinder phenylenes chain, Polycycl. Aromat. Comp., 41 (2021), 1681–1693. https://doi.org/10.1080/10406638.2019.1693405 doi: 10.1080/10406638.2019.1693405
[13]	X. Ma, H. Bian, The normalized Laplacians, degree-Kirchhoff index and the spanning trees of hexagonal M $\ddot{o}$ bius graphs, Appl. Math. Comput., 355 (2019), 33–46. https://doi.org/10.1016/j.amc.2019.02.052 doi: 10.1016/j.amc.2019.02.052
[14]	J. Huang, S. C. Li, X. Li, The normalized Laplacian, degree-Kirchhoff index and spanning trees of the linear polyomino chains, Appl. Math. Comput., 289 (2016), 324–334. https://doi.org/10.1016/j.amc.2016.05.024 doi: 10.1016/j.amc.2016.05.024
[15]	F. R. K. Chung, Spectral Graph Theory, American Mathematical Society Providence, RI, 1997.
[16]	H. Wiener, Structural determination of paraffin boiling points, J. Am. Chem. Soc., 69 (1947), 17–20. https://doi.org/10.1021/ja01193a005 doi: 10.1021/ja01193a005
[17]	A. Dobrynin, Branchings in trees and the calculation of the Wiener index of a tree, Match Communications in Mathematical and in Computer Chemistry, 41 (2000), 119–134.
[18]	I. Gutman, Selected properties of the Schultz molecular topological index, Journal of Chemical Information and Computer Sciences, 34 (1994), 1087–1089. https://doi.org/10.1021/ci00021a009 doi: 10.1021/ci00021a009
[19]	D. J. Klein, M. Randić, Resistance distances, J. Math. Chem., 12 (1993), 81–95. https://doi.org/10.1007/BF01164627 doi: 10.1007/BF01164627
[20]	D. J. Klein, Resistance-distance sum rules, Croat. Chem. Acta, 75 (2002), 633–649. https://hrcak.srce.hr/127542
[21]	D. J. Klein, O. Ivanciuc, Graph cyclicity, excess conductance, and resistance deficit, J. Math. Chem., 30 (2001), 271–287. https://doi.org/10.1023/A:1015119609980 doi: 10.1023/A:1015119609980
[22]	H. Y. Chen, F. J. Zhang, Resistance distance and the normalized Laplacian spectrum, Discrete Appl. Math., 155 (2007), 654–661. https://doi.org/10.1016/j.dam.2006.09.008 doi: 10.1016/j.dam.2006.09.008
[23]	I. Gutman, B. Mohar, The quasi-Wiener and the Kirchhoff indices coincide, J. Chem. Inf. Model., 36 (1996), 982–985. https://doi.org/10.1021/ci960007t doi: 10.1021/ci960007t
[24]	Y. L. Yang, T. Y. Yu, Graph theory of viscoelasticities for polymers with starshaped, multiple-ring and cyclic multiple-ring molecules, Macromol. Chem. Phys., 186 (1985), 609–631. https://doi.org/10.1002/macp.1985.021860315 doi: 10.1002/macp.1985.021860315

This article has been cited by:

1.	Wensheng Sun, Muhammad Shoaib Sardar, Yujun Yang, Shou-Jun Xu, On the Resistance Distance and Kirchhoff Index of $K_n$ -chain(Ring) Network, 2024, 43, 0278-081X, 4728, 10.1007/s00034-024-02709-y
2.	Muhammad Shoaib Sardar, Shou-Jun Xu, Resistance Distance and Kirchhoff Index in Windmill Graphs, 2025, 22, 15701794, 159, 10.2174/0115701794299562240606054510

Reader Comments

Your name:*

Email:*
© 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(1058) PDF downloads(72) Cited by(2)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(1) / Tables(3)

AIMS Mathematics

Topological indices of linear crossed phenylenes with respect to their Laplacian and normalized Laplacian spectrum

Related Papers:

Abstract

1. Introduction

2. Preliminary

3. The Kirchhoff index and Wiener index of $C_{n}$ in terms of the Laplacian spectrum

4. The multiplicative degree-Kirchhoff index, Gutman index, and complexity of $C_{n}$ in terms of the normalized Laplacian spectrum

5. Conclusions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Mathematics

Topological indices of linear crossed phenylenes with respect to their Laplacian and normalized Laplacian spectrum

Related Papers:

Abstract

1. Introduction

2. Preliminary

3. The Kirchhoff index and Wiener index of Cn C_{n} in terms of the Laplacian spectrum

4. The multiplicative degree-Kirchhoff index, Gutman index, and complexity of Cn C_{n} in terms of the normalized Laplacian spectrum

5. Conclusions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

3. The Kirchhoff index and Wiener index of $C_{n}$ in terms of the Laplacian spectrum

4. The multiplicative degree-Kirchhoff index, Gutman index, and complexity of $C_{n}$ in terms of the normalized Laplacian spectrum