1.
Introduction
The quantification of uncertainty in probability distributions is fundamental to information theory. Among its most important measures, Shannon's entropy [1] stands out. Entropy for a continuous random variable X, characterized by a probability density function (PDF) h(x), is calculated as E[−logh(X)], assuming that the expectation is well-defined. Entropy measures the deviation from a uniform distribution. Since the uniform distribution represents the least concentrated distribution, entropy quantifies the concentration of f and thus the unpredictability of the system in terms of X. Zellner [2], an advocate for information-theoretic approaches, made significant contributions to integrating information and Bayesian methods, inspiring many to explore these techniques. For instance, Ebrahimi et al. [3] examined the relationship between reliability and econometrics by introducing an information relationship between a system and its components by using Shannon entropy. This approach is particularly useful for ranking the importance of components on the basis of their information's dependence on the operational status or lifespan of the system. Asadi et al. [4] introduced the Jensen-Shannon information criteria for comparing systems on the basis of the complexity of the system. This scalar function of the signature ranks systems based on their design. It quantifies the remaining uncertainty about the system's lifetime, the dependency between lifetime and component failures, and applies Bayesian decision theory. These results prompted us to explore uncertainty measures as valuable tools in reliability and engineering systems. Extropy, the mirror image of entropy, was recently introduced by Lad et al. [5] as a complementary measure of uncertainty. Extropy, denoted as J(X), for a non-negative random variable X with a PDF h(x) and a cumulative distribution function (CDF) H(x), is expressed as follows:
where U is a uniform random variable on the interval [0,1], H−1(u)=inf{x:H(x)≥u}, u∈[0,1], signifies the quantile function of H, and E(⋅) means the expectation. Similar to entropy, extropy measures the deviation from a uniform distribution and quantifies the concentration of f, thereby gauging the unpredictability of the system in terms of X. While entropy and extropy quantify the uncertainty, the lack of a simple relationship between orderings of a distribution by the two measures arises from some substantial and subtle differences. For example, the differential entropy takes values in [−∞,∞] while extropy takes values in [−∞,0); for more details, see Toomaj et al. [6]. A significant statistical use of extropy lies in assessing predictive distributions through the total logarithmic scoring rule. Readers seeking a deeper understanding will find comprehensive insights in the work of Agro et al. [7], Capotorti et al. [8], and Gneiting and Raftery [9]. An alternative and valuable representation for the extropy by using (1) can be written as
where λ(x)=h(x)/S(x) represents the hazard rate function, S(x)=P(X>x) is the reliability function of X, and X12 follows a PDF given by Toomaj et al. [6]:
The aim of this paper was to investigate the properties of extropy in a linear consecutive r-out-of-n:G system and apply them to testing for exponentiality. A linear consecutive r-out-of-n:G system is a system that comprises n independent and identically distributed (iid) components arranged in a linear configuration, where the system operates successfully if and only if at least r consecutive components remain functional. These systems are used in communication systems, road parking plans, and oil pipeline networks. Consecutive n-out-of-n:G systems represent series systems, while consecutive 1-out-of-n:G systems correspond to parallel systems, both of which are crucial for reliability modeling. Fundamental works in this field include Gera [10], Chang et al. [11], Boland and Samaniego [12] and Eryılmaz [13,14]. In addition, studies such as [15,16,17] investigated different configurations of consecutive r-out-of-n systems and emphasized their relevance in real-world scenarios. Research on the information properties of ordered data has been extensively explored, as evidenced by the work in [18,19,20]. Recently, extropy has gained prominence as a key metric for measuring uncertainty. Fundamental contributions in this field include the work of Qiu [21] and Qiu and Jia [22,23]. Subsequent studies by Kayid and Alshehri [24] investigated the extropy of past lifetimes in coherent systems, including cases where all components remain inactive within a given timeframe. Shrahili and Kayid [25] studied the residul extropy of order statistics, while Shrahili et al. [26] made further progress in this area. Building on these fundamental studies, the present work aimed to deepen the understanding of extropy by investigating its properties and behavior specifically in the context of consecutive r-out-of-n:G systems.
While previous research has examined the extropy of order statistics and record values, its properties in consecutive systems remain largely unexplored. This study addresses this gap by investigating the extropy of such systems. Specifically, we leverage extropy's computational advantages over other information measures, such as Shannon entropy, to facilitate more tractable computations for consecutive systems, even with complex distribution functions. This enhancement makes our approach both practical and widely applicable. Furthermore, while prior studies, such as Navarro et al. [27,28], have explored the preservation of dispersive order and reliability properties in coherent systems, our work extends these findings by introducing extropy as a complementary measure for assessing uncertainty in consecutive r-out-of-n:G systems. In particular, we establish new results on the preservation of aging properties and stochastic orders in the context of extropy, providing insights beyond classical entropy-based approaches. These contributions bridge the gap between stochastic order theory and information measures, offering a novel perspective on systems' reliability. The applicability of our results is demonstrated through an image processing example, where the proposed extropy-based estimator is used to assess uncertainty in grayscale image distributions.
The structure of this paper is organized as follows: in Section 2, we introduce a formulation for the extropy of Tr∣n:G, the lifetime of the consecutive system, assuming a general continuous distribution function H. This representation is expressed as the extropy of such systems when the underlying distribution is uniform, establishing a link between the extropy measures in different distribution constellations. Deriving explicit formulas for the extropy of order statistics is often challenging across various statistical frameworks. To solve this problem, some bounds are derived in Section 3. Section 4 focuses on the characterization of the extropy for consecutive systems, where the main results are presented. In particular, the exponential distribution is characterized in this context. To substantiate the theoretical developments, the computational results are presented in Section 5. In this section, a nonparametric estimator for the extropy of consecutive systems is introduced, and its application in image processing is presented as an example of its practical implementation. Furthermore, a novel test statistic for exponentiality is proposed, and its critical values are determined numerically. The validity of this test is evaluated against a number of alternative distributions. Finally, Section 6 summarizes the main results and contributions, and highlights their importance in both theoretical and applied contexts.
2.
Extropy of consecutive r-out-of-n:G systems
Hereafter, we focus on deriving an expression for the extropy associated with consecutive r-out-of-n:G systems. Assume that X1,X2,⋯,Xn represent the iid component lifetimes within the systems, where each follows the same h(x), H(x), and reliability function S(x). The lifetime of the overall system is represented by Tr∣n:G. Eryilmaz [29] showed that the system's reliability function can be formulated as follows when 2r≥n:
It follows that
where h1:j(t) is the PDF of the series system with a lifetime X1:j=min(X1,⋯,Xj). In the subsequent paragraphs, we derive a formulae for extropy Tr|n:G by utilizing the probability integral transformation Ur|n:G=H(Tr|n:G). It is established that the transformed components of the system, defined as Ui=H(Xi) for i=1,…,n, are iid random variables with a uniform distribution. For 2r≥n and 0<u<1, the probability density function of Ur|n:G is given by
On the basis of the previously introduced transformations, we now present the following theorem.
Theorem 2.1. For 2r≥n, the extropy of Tr|n:G can be expressed as follows:
where gr|n:G(u) is given by (6).
To illustrate (7), we provide the following example.
Example 2.1. Consider
where Xj:m=min(Xj,…,Xm) for 1≤j<m≤n, as the lifetime of a linear consecutive r-out-of-n:G system. Assume that the component lifetimes are iid with a common CDF defined as
It should be noted that Eq (8) represents the cumulative distribution function of a Weibull random variable, with a shape parameter α > 0 and a unit scale parameter. It can be observed that h(H−1(u))=α(1−u)(−log(1−u))α−1α,0<u<1. From Eq (7),
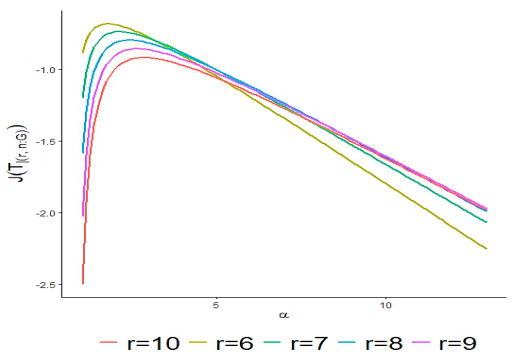
Numerical methods are used to study the relationship between the entropy of J(Tr|n:G) and the shape parameter α, since it is inherently difficult to obtain an explicit expression. The analysis focuses on consecutive r-out-of-10:G systems, where r is between 6 and 10. As shown in Figure 1, the extropy of the system initially increases with α and reaches a peak value before decreasing for α>1. The results for 0<α<1 are not shown due to the divergence of the integral. The findings emphasize the notable impact of the shape parameter on the system's extropy. Furthermore, no correlation is observed between the monotonicity of the extropy and the number of functioning components.
Let us consider X and Y with the PDFs hX(x) and hY(x), and the reliability functions SX(x) and SY(x), respectively. Recall that X is considered to be smaller than Y in the dispersive order, expressed as X≤dispY, if
holds for all 0<v<1. In addition, X is said to have the decreasing failure rate (DFR) property if the ratio hX(x)/SX(x) decreases with x>0. For further details, we direct the reader to the comprehensive work of Bagai and Kochar [30]. Based on the expression in Eq (7), the following theorem is derived. Hereafter, we use CX to denote the class of all consecutive r-out-of-n:G systems with a lifetime TXr|n:G consisting of n iid components with the CDF HX and the PDF hX.
Theorem 2.2. Assume that TXr|n:G∈CX and TXr|n:G∈CY. If X≤dispY, then J(TXr|n:G)≤J(TYr|n:G) for 2r≥n.
It is worth noting that the above results can be derived by applying Part (i) of Theorem 2.9 from Navarro et al. [31], along with the observation that the disperive order implies the extropy order in the sense that TXr|n:G≤dispTYr|n:G yields J(TXr|n:G)≤J(TYr|n:G). For further details on the results related to stochastic orders and the preservation properties of coherent and mixed systems, we refer the readers to Navarro et al. [32]. Before introducing the next corollary, we first present the following lemma from Bagai and Kochar [30].
Lemma 2.1. For the random variables X and Y, if X≤hrY and either X or Y has a DFR, then X≤dispY.
The following corollary can be derived from the lemma above and Theorem 2.2.
Corollary 2.1. Under the assumptions of Theorem 2.2, if X≤hrY and either X or Y has a DFR, then J(TXr|n:G)≤J(TYr|n:G).
The following example illustrates Corollary 2.1.
Example 2.2. Define TXr|n:G=max(min(X1,X2), min(X2,X3)) as the lifetime of a consecutive 2-out-of-3:G system, where the iid components' lifetimes {X1,X2,X3} follow a Makeham distribution with the reliability function SX(x)=e−x−a(x+e−x−1) for x>0 and a>0. Moreover, let TYr|n:G=max(min(Y1,Y2),min(Y2,Y3)) be the lifetime of a consecutive 2-out-of-3:G system having iid component lifetimes {Y1,Y2,Y3} following an exponential distribution with the reliability function SY(x)=e−x, where x>0. It is not hard to see that the hazard rate function of X is λX(x)=1+a(1−e−x), while the hazard rate function of Y is λY(x)=1. It can be shown that X≤hrY for a>0, and Y has a DFR. As a consequence, Corollary 2.1 becomes applicable, implying that J(TXr|n:G)≤J(TYr|n:G).
The next theorem demonstrates that for consecutive r-out-of-n:G systems where the components' lifetime has a DFR, the series system achieves the lowest extropy.
Theorem 2.3. Assume that Tr|n:G∈CX such that X has a DFR. Under the condition 2r≥n, the following statements then hold:
(i)J(X1:n)≤J(Tr|n:G).
(ii)J(X1:r)≤J(Tr|n:G).
Proof. (i) It is evident that the function
is increasing in t for all 1≤r≤n, indicating that X1:n≤hrTr|n:G. Furthermore, if X exhibits the DFR property, then it follows that X1:n also possesses the DFR property. By applying Lemma 2.1, we conclude that X1:n≤dispTr|n:G. This relationship implies that J(X1:n)≤J(Tr|n:G), since X≤dispY entails J(X)≤J(Y).
(ii) According to the findings presented in Proposition 3.2 of Navarro and Eryilmaz [33], it can be inferred that X1:r≤hrTr|n:G. Consequently, employing analogous reasoning to that employed in Part (i) leads to the acquisition of similar results. □
We proceed to extend Theorem 2.3, addressing cases where the number of systems and their respective component lifetimes are not necessarily identical.
Theorem 2.4. Assume that X1:n1∈CX and TYr|n2:G∈CY for all 2r≥n2, and n1≠n2. If X has a DFR and X≤dispY, then J(X1:n1)≤J(TYr|n2:G) for all 2r≥n2 such that 1≤r≤min(n1,n2).
Proof. Assume that TXr|n2:G∈CX for 2r≥n2. It is clear that the function
is increasing in t for all 1≤r≤min(n1,n2) with n1≠n2. This indicates that X1:n1≤hrTXr|n2:G. Following the approach in the proof of Theorem 2.3, we can conclude that X1:n1≤dispTXr|n2:G, since X has a DFR, which implies that J(X1:n1)≤J(TXr|n2:G) for 2r≥n2. Furthermore, the assumption X≤dispY leads to J(TXr|n2:G)≤J(TYr|n2:G) according to Theorem 2.2. By combining these results, we complete the proof. □
3.
Bounds on the extropy of consecutive systems
Obtaining explicit expressions for the extropy of consecutive systems poses significant computational challenges, particularly for systems with many components or intricate lifetime distributions. In such cases, bounding techniques provide a practical and efficient alternative for characterizing the extropy of these systems. This section examines the use of bounding techniques to analyze the extropy of these systems. A theorem is presented that establishes explicit bounds on the extropy, supported by a concise and rigorous proof. These findings provide valuable insights into the behavior of the extropy and enable its application in scenarios where analytical solutions are impractical.
Theorem 3.1. Let TXr|n:G∈CX.
(i) If M=h(m)<∞, where m=sup{x:h(x)≤M} designates the mode of the PDF h, for 2r≥n, we have J(Tr|n:G)≥MJ(Ur|n:G).
(ii) For 2r≥n, we have
where B=infv∈(0,1)gr|n:G(v) and D=supv∈(0,1)gr|n:G(v).
Theorem 3.1(i) provides a lower bound for the extropy of Tr∣n:G by utilizing J(Ur|n:G) and the mode of the original distribution.
Part (ii) of Theorem 3.1 provides bounds on Tr∣n:G with respect to the extropy of each component under certain conditions. These bounds are further illustrated by analyzing consecutive r-out-of-n:G systems with Weibull-distributed components.
Example 3.1. Consider a linear consecutive 6-out-of-10:G system with the lifetime T6|10:G=max(X1:6,X2:7,…,X5:10), where Xj:m=min(Xj,…,Xm) for 1≤j<m≤10. For this analysis, it is assumed that X W(α,1), as defined in (8). We can easily verify that B=infu∈(0,1)g6|10:G(u)=0 and D=supu∈(0,1)g6|10:G(u)=2.837134. Furthermore, it is apparent that J(U6|10:G)=−1.062937. Notably, the mode of X is given by m=(α−1α)1α. Consequently, we can establish lower bounds for J(T6|10:G) based on Theorem 3.1. Specifically, the lower bounds are given for X and m, respectively, by
and
where J(X)=−α21αΓ(2−1α)8 for α>12 and h(m)=α(α−1α)α−1αe−α−1α for α>0. One can see that Part (i) of Theorem 3.1 does not exist when 0<α≤12. As illustrated in Figure 2, the lower bound from Part (i) of Theorem 3.1 is higher than that of Part (ii). Additionally, the figure indicates a decreasing trend for both lower bounds as α increases.
Unlike Theorem 3.1, this section introduces further bounds on the extropy of consecutive r-out-of-n:G systems' lifetimes, derived using the extropy and imprecision associated with a series of system lifetimes. First, let us recall the concept of the inaccuracy measure based on extropy as follows (see Hashempour and Mohammadi [34]).
where hX and hY denote the PDFs of X and Y, respectively.
Theorem 3.2. Let TXr|n:G∈CX. Then the following inequality holds:
which is valid for 2r≥n.
Proof. Another useful representation based on the relations in (5) is as follows:
where
represents the inaccuracy measure of h1:r(x) relative to h1:r+1(x) or vice versa. Since J(X1:rX1:r+1)≤0, one can see that −(n−r+1)(n−r)J(X1:rX1:r+1)≥0, and hence the lower bound is easily obtained. This completes the proof. □
In the next theorem, we establish bounds for consecutive r-out-of-n:G systems that relate to the hazard rate function of the components' lifetimes.
Theorem 3.3. Let Tr|n:G represent the lifetime of a consecutive r-out-of-n:G system, where the components' lifetimes X1,X2,⋯,Xn follow a common failure rate function λ(x). For all 2r≥n, we have
where T12r|n:G has the PDF h12r|n:G(x)=2hr|n:G(x)Sr|n:G(x) for all x>0.
Proof. Note that
where
Given that ψr,n'(z)<0 for 2r≥n and 0<z<1, it follows that ψr,n(z) is identified as a monotonically decreasing function of z. Given that ψr,n(0)=r and ψr,n(1)=2r−n, we have 2r−n≤ψr,n(S(x))≤r for 0<H(x)<1, which implies that 2r−nλ(x)≤λr|n:G(S(x))≤rλ(x), for x>0. Combining this result with the relationship between extropy and the hazard rate (as defined in Eq (2)) completes the proof. □
Let us consider an illustrative example for the preceding theorem.
Example 3.2. We now analyze a linear consecutive 2-out-of-3:G system characterized by its lifetime
where Xi is iid, following an exponential distribution with the CDF H(x)=1−e−λx for x>0. The exponential distribution exhibits a constant hazard rate, λ(x)=λ, which implies that E(λ(T122|3:G))=λ. Applying Theorem 3.3 yields the following bounds on the extropy of the system −0.5λ≤J(T2|3:G)≤−0.25λ. We note that the exact value is J(T2|3:G)=−0.35λ.
The next theorem holds, provided that the expected value of the squared hazard rate function for X is finite.
Theorem 3.4. Given the conditions in Theorem 3.3, where E(λ2(X))<∞, for 2r≥n, it holds that
where Ωr,n=∫10(1−v)2g4r|n:G(v)dv.
Proof. The PDF of Tr|n:G can be rewritten as hr|n:G(x)=h(x)gr|n:G(H(x)), while its failure rate function is given by
for x>0. Consequently, by (2) and using the Cauchy–Schwarz inequality, we obtain
This equality arises from the variable substitution v=H(x), completing the proof. □
4.
Results of characterization
This section focuses on the characterization of extropy in consecutive r-out-of-n:G systems, starting with a lemma based on the Muntz-Szász Theorem, as referenced in Kamps [35].
Lemma 4.1. If ψ(x) is an integrable function on the finite interval (a,b) and ∫baxnjψ(x)dx=0forj≥1, it follows that ψ(x)=0 almost everywhere in (a,b), where {nj,j≥1} represents a strictly increasing sequence of positive integers with ∑∞j=11nj=∞.
It is important to note that Lemma 4.1 is a well-established result in functional analysis, asserting that the set {xn1,xn2,…;1≤n1<n2<⋯} constitutes a complete sequence. Notably, Hwang and Lin [36] extended the scope of the Müntz-Szász Theorem to the functions {ϕnj(x),nj≥1}, where ϕ(x) is both absolutely continuous and monotonic over the interval (a,b).
Theorem 4.1. Let TXr|n:G and TYr|n:G be the lifetimes of two consecutive r-out-of-n:G systems consisting of n iid component lifetimes with the common PDFs hX(x) and hY(x) and the CDFs HX(x) and HY(x), respectively. Here, HX and HY have the same family of distributions, but for a change in location, if and only if
Proof. For the necessity part, since HX and HY belong to the same family of distributions, but for a change in location, HY(y)=HX(y−a) for all a∈R. Thus, it is clear that
To prove the sufficiency part, it is clear that for odd values of n, r ranges from [n/2]+1 to n, so r∈{[n/2]+1,…,n−1,n}. For even values of n, r ranges from [n/2] to n, resulting in r∈{[n/2],…,n−1,n}, where [x] represents the integer part of x. Therefore, we can express r as r=n−[i2] for i=1,2,…,n. Thus, we have
Using this relation, Eq (7) can be reformulated as
for i=1,2,…,n. The same argument also holds for Y. Given the assumption that J(TXr|n:G)=J(TYr|n:G), using relation (10), we can write
Thus, it holds that
Where, for 0<u<1,
By taking z=1−u, Eq (11) can be rewritten as follows:
By applying Lemma 4.1 with the function
and considering the complete sequence {z2n,n≥1}, one can conclude that
or, equivalently, hX(H−1X(x))=hY(H−1Y(x) for all x∈(0,1). It follows that H−1X(x)=H−1Y(x)+d for a constant d. This indicates that X and Y share identical distribution functions except for a shift in location, thereby concluding the proof. □
As a consecutive n-out-of-n:G system represents a specific case of a series system, the subsequent corollary characterizes its extropy.
Corollary 4.1. Let TXn|n:G and TYn|n:G represent two series systems with the shared PDFs hX(x) and hY(x), and the CDFs HX(x) and HY(x), respectively. In this case, HX and HY belong to the same distribution family, differing only by a location shift, if and only if
An additional useful characterization is presented in the following theorem.
Theorem 4.2. According to the conditions of Theorem 4.1, HX and HY are part of the same family of distributions, differing only in location and scale, if and only if
Proof. The necessity is evident; therefore, we now focus on establishing sufficiency. Using Eqs (9) and (10), we can deduce the following:
An analogous argument can be made for J(TYr|n:G)/J(Y). If Eq (12) applies to two cumulative distribution functions HX and HY, it follows from Eq (13) that
Let us set
Following an approach similar to the proof of Theorem 4.1, we can express
The proof concludes by employing arguments analogous to those in Theorem 4.1. □
Applying Theorem 4.2, we obtain the following corollary.
Corollary 4.2. Assuming the conditions in Corollary 4.1, HX and HY are part of the same distribution family, differing only in location and scale, if and only if
The following theorem uses the extropy of consecutive r-out-of-n:G systems to characterize the exponential distribution.
Theorem 4.3. Let TXr|n:G∈CX. In this case, the random variable X has an exponential distribution with the parameter λ if and only if
Proof. Given an exponentially distributed random variable X, its extropy, directly calculated using (1), is J(X)=−λ4. Furthermore, since h(H−1(u))=λ(1−u), application of Eq (7) yields
where the third equality is obtained by noting that
To prove sufficiency, we assume that Eq (14) holds for a fixed value of r. By following the proof of Theorem 4.1 and applying the result from Eq (15), we obtain the following relation:
which is equivalent to
where
Thus, it holds that
where, for 0<u<1,
As in the proof of Theorem 4.1, this implies that
Applying Lemma 4.1 to the function
and utilizing the complete sequence {z2n,n≥1}, we can deduce that
which is equivalent to
by taking w=1−z. This implies that
Integrating the equation from 0 to x gives H−1(x)=log(1−x)4J(X)+d, where d represents an arbitrary constant. If we apply the boundary condition limx→0H−1(x)=0, it follows that d=0. Consequently, this leads to H−1(x)=log(1−x)4J(X) for x>0. This implies the CDF H(x)=1−e4J(Y)x,x>0, confirming that X E(−4J(X)), establishing the theorem. □
5.
Nonparametric inference
Here, we present a nonparametric methodology for the estimation of the extropy of a consecutive r-out-of-n:G system using a series of absolutely continuous, non-negative iid random variables X1,X2,…,XN. Let X1:N≤X2:N≤⋯≤XN:N symbolize the order statistics of this random sample. As shown before, for 2r≥n, the extropy of Tr|n:G from (7) can be written as
For estimating J(Tr|n:G), we use an estimator for dH−1(u)/du as proposed by Vasicek [36]. This method replaces the differential operator with a difference. The estimator for J(Tr|n:G) is derived and can be represented as follows:
where any m that is lower than N/2, known as the window size, is a positive integer, and in scenarios where i−m≤1,Xi−m:N=X1:N and i+m≥N,Xi+m:N=XN:N. For ease of computation, the value of m is determined using the heuristic formula proposed in [37]
Now, we assess the performance of ˆJ(Tr|n:G) using simulated standard exponential data by examining its average bias and mean squared error (MSE). These metrics were computed for various sample sizes (N = 20, 30, 40, 50,100) and parameter values of r and n. The estimates were based on 5000 replicates. The results are shown in Table 1. The table reveals that the MSE of the extropy estimator decreases as the sample size grows. Conversely, the bias demonstrates the opposite trend, increasing with larger sample sizes. This finding suggests that while the estimator's precision and reliability improve with larger sample sizes, the slight increase in bias should be accounted for in practical applications.
5.1. An application to image processing
Information-theoretic measures have gained significant popularity in defining optimized cost functions for image alignment. Rao et al. [37] proposed cross-cumulative residual entropy as a measure to tackle both unimodal and multimodal alignment challenges. In a related field, Tahmasebi et al. [38] proposed a weighted extended cumulative entropy estimator that is used to evaluate image quality without the need to know the true reference or original versions of the images. In addition, Toomaj and Atabay [39] and Toomaj [40] investigated the application of cumulative residual Tsallis entropy and generalized cumulative residual Tsallis entropy in image quality assessments and demonstrated the potential of these entropy measures for image quality and fidelity assessments.
In this study, we illustrate an application of nonparametric estimation of the extropy of a consecutive system in the field of image processing. The dataset comprises a grayscale reference image labeled z, representing boats, and five modified versions of the reference image labeled z1,z2,…,z5. Figure 3 shows images from the dataset, each measuring 768 pixels in width and 512 pixels in height. The pixel values, which represent the intensity of the grayscale, were originally between 0 and 255. For the analysis and calculations, these values were normalized to a standardized range of 0 to 1, where 0 represents black and 1 represents white. This normalization ensures consistency and uniformity in image processing and enables accurate and comparable results for different analysis methods.
The means and standard deviations of the gray levels of these modified images are presented in Table 2.
To evaluate and compare the degree of uncertainty in extropy between the original image and its customized versions, we applied the method described in Eq (16) to estimate the extropy for all six images. The extropy was calculated for various values of r and n, with calculations performed individually for each image. Figure 4 presents the grayscale histograms of the images.
A comparison of Figures 3 and 4 reveals that the adjusted image z1 is the most similar to the original image z, followed by z2. In contrast, z3, z4, and z5 exhibit the largest deviations from the original image z. Figure 4 presents the histograms of the grayscale levels for each image. Table 3 provides the estimated extropy values for various combinations of r and n across all six images. The estimated extropy values for the adjusted images z1 and z2 closely align with the extropy value of the original image, as shown in Table 3.
Conversely, the extropy values for images z3, z4, and z5 significantly deviate from the extropy value of the original image as the parameters r and n increase. Moreover, the results indicate that the estimated extropy is influenced by the skewness of the data, with a pronounced sensitivity toward left skewness. This observation underscores the utility of extropy as a metric for quantifying uncertainty in image processing tasks. It enables meaningful comparisons between images and facilitates the measurement of discrepancies within a single image, thereby providing valuable insights into uncertainty assessments.
5.2. Test of exponentiality
The widespread applicability of the exponential distribution has led researchers to develop a variety of test statistics for evaluating exponentiality. These statistics are based on various fundamental concepts from the field of statistics. The main objective is to verify whether the random variable X follows an exponential distribution. Let X1,X2,…,XN denote a random sample of size N drawn from the CDF H. Let X1:N≤X2:N≤⋯≤XN:N represent the corresponding order statistics. Assuming that H0 signifies the CDF of the exponential distribution, defined as H0(x)=1−e−λx, for x>0, the primary hypothesis under consideration is
Extropy has recently garnered considerable attention within the research community as a valuable metric for goodness-of-fit testing. Qin and Jia [22] introduced two consistent extropy estimators based on the concept of distances and developed a goodness-of-fit test for the uniform distribution using the more effective estimator. In a related study, Xiong et al. [41] utilized the unique properties of classical datasets to derive a characterization result for the exponential distribution, leading to the development of a novel exponentiality test. Their research detailed the formulation of the test statistic and emphasized the significant advantage of the proposed method, showcasing its strong performance with small sample sizes.
Building on these developments, Jose and Sathar [42] introduced a new exponentiality test derived from a characterization result based on the extropy of lower k-record values. In this section, we extend these advancements by examining the extropy of consecutive systems. Theorem 4.3 demonstrates that the exponential distribution can be uniquely characterized by the extropy of consecutive systems. On the basis of this result, we propose a new test statistic for uniformity, denoted TEXr,n and defined as follows:
with 2r≥n. Directly for 2r≥n, Theorem 4.3 implies that TEXr,n=0 if and only if X is exponentially distributed. This fundamental property establishes TEXr,n as a viable measure of exponentiality and a suitable candidate for a test statistic. For a given random sample X1,X2,…,XN, the estimator ^TEXr,n of TEXr,n serves as a viable test statistic. Substantial deviations of ^TEXr,n from its expected value under the null hypothesis (assuming an exponential distribution) suggest nonexponentiality, leading to rejection of the null hypothesis.
To illustrate, we focus on the specific case where n=3 and r=2, utilizing ^TEX2,3 as the test statistic. To derive an expression for ^TEX2,3, we recall that Qiu and Jia's [22] estimator for J(X), denoted JQ2mn and defined by
for all i=m+1,m+2,...,N−m, where m is a positive integer smaller than n2, which is known as the window size. Here, ci depends on the window size m and the sample size N, and is defined as
Therefore, a reasonable estimator for ^TEX2,3 can be derived using Eq (16) and the JQ2mn estimator as follows:
Ensuring the consistency of an estimator is essential, especially when evaluating estimators for parametric functions. The following theorem justifies the result presented in Eq (13). The proof follows a similar approach as Theorem 1 in the work of Vasicek [36]. It is noteworthy that Park [43] and Xiong et al. [41] have also used the consistency proof method of Vasicek [36] to demonstrate the consistency of their respective proposed test statistics.
Theorem 5.1. Suppose X1,X2,…,XN represents a random sample of size N taken from a population with the PDF h and the CDF H and assume that the random variable has finite variance. Then ^TEX2,3p→TEX2,3 as N→+∞,m→+∞, and mN→0, where p→ stands for the convergence in probability.
Proof. From Part (2) of Theorem 2.1 in Qiu and Jia [22], we establish the consistency of their estimator, demonstrating that JQ2mnp→J(X) as N→+∞,m→+∞, and mN→0. Furthermore, by applying the methodology employed in Theorem 1 of Vasicek [36], it can be shown that ˆJ(TX2|3:G)p→J(TX2|3:G) under the same asymptotic conditions. Leveraging the well-known properties of convergence in probability, these individual convergences collectively imply that ^TEX2,3p→TEX2,3 as N→+∞,m→+∞, and mN→0, thus completing the theorem. □
In the next result, we show that the root mean square error (RMSE) of ^TEX2,3 remains invariant under shifts in the random variable X. However, this invariance property does not extend to scale transformations. The proof of these assertions can be readily derived by adapting the arguments presented by Ebrahimi et al. [44].
Theorem 5.2. Assume that X1,X2,…,XN is a random sample of size N taken from a population with the PDF h and the CDF H and Yi=aXi+b,a>0,b∈R. We denote the estimators for TEX2,3 on the basis of Xi and Yi as ^TEXX2,3 and ^TEXY2,3, respectively. Then the following properties apply:
(i).E(^TEXY2,3)=E(^TEXX2,3)/a,
(ii).Var(^TEXY2,3)=Var(^TEXX2,3)/a2,
(iii).RMSE(^TEXY2,3)=RMSE(^TEXX2,3)/a.
Under the null hypothesis, H0, the value of ^TEX2,3 asymptotically converges to zero as the sample size N approaches infinity. Conversely, under an alternative distribution with an absolute CDF H, the value of ^TEX2,3 converges to a positive value as N→+∞. On the basis of these asymptotic properties, we reject the null hypothesis at a given significance level α for a finite sample size N if the observed value of the test statistic ^TEX2,3 exceeds the critical value ^TEX2,3(1−α). The asymptotic distribution of ^TEX2,3 is intricate and analytically intractable due to its dependence on both the sample size N and the window parameter m. To address this challenge, we employed a Monte Carlo simulation approach. Specifically, we generated 10,000 samples of sizes N=5,10,20,30,40,50,100 from the standard exponential distribution under the null hypothesis. For each sample size, we determined the (1−α)-th quantile of the simulated ^TEX2,3 values to establish the critical value for significance levels of α=0.05,0.01, while varying the window size m from 2 to 30. Tables 4 and 5 present the resulting critical values for the sample sizes and significance levels.
5.3. Power comparisons
A Monte Carlo simulation study involving nine alternative probability distributions was performed to evaluate the significance of the ^TEX2,3 test. For every sample size N, a total of 10,000 samples of size N were drawn from each of the alternative distributions.
The ^TEX2,3 statistic was computed for each generated sample. The significance of the ^TEX2,3 test at a given significance level α was determined by calculating the proportion of the 10,000 samples whose test values surpassed the critical value.
The performance and efficiency of the ^TEX2,3-based test was assessed by comparing its performance with various established tests for exponentiality reported in the literature.
Table 6 provides the PDFs of the alternative distributions considered. The distributions and their parameters used in the simulations align with those utilized by Jose and Sathar [42].
The selected distributions represent a diverse range of reliability behaviors commonly encountered in applied settings. The Weibull and Gamma distributions were chosen, as they are widely used in modeling lifetimes, with the Weibull distribution capturing both increasing and decreasing failure rates through its shape parameter, and the Gamma distribution serving as a flexible alternative for modeling skewed lifetime data. The uniform distribution is included as a contrasting case where all failure times are equally probable, providing a baseline for comparison. The half-normal distribution, often used in reliability analyses and statistical modeling, represents cases where the failure times are positively skewed. By considering these distributions, we ensured a comprehensive evaluation of extropy's performance in different stochastic scenarios.
Now, we compare the efficiency of the new proposed test based on the ^TEX2,3 statistic against established tests for exponentiality available in the literature, as detailed in Table 7.
The efficacy of the ^TEX2,3 statistic is influenced by the chosen window size, m. Selecting an appropriate m value is crucial for achieving adequate adjusted statistical power. On the basis of simulations across different sample sizes, a heuristic formula was derived, namely m=[0.4N], where [x] represents the largest integer less than or equal to x. This formula provides a practical guideline for selecting m, aiming to ensure robust and generally effective power performance across diverse distributions.
To evaluate the performance of ^TEX2,3, we selected 10 competing tests for exponentiality and assessed their power against various alternative distributions.
Notably, Xiong et al. [41] proposed a test statistic based on the extropy of classical records, while Jose and Sathar [42] characterized the exponential distribution using extropy derived from lower k-records and subsequently constructed a test statistic. These tests, denoted T9 and T10 in Table 7, are included in our comparative analysis. The authors of these tests provided valuable insights regarding their applicability and suitability for testing exponentiality.
The power analysis involved simulating 10,000 samples with sizes N=10,20, and 50 from each alternative distribution listed in Table 6. The power values of ^TEX2,3 were computed at the 5% significance level. Subsequently, the power values for ^TEX2,3 and 11 competing tests were evaluated for the same sample sizes and distributions. The results are summarized in Table 8.
5.3.1. Analysis of the results
For N=10, the ^TEX2,3 test shows the expected low power against the exponential distribution (Table 8). However, it excels in distinguishing Gamma distributions from exponential distributions, achieving high power as the Gamma shape parameter decreases. Against Weibull distributions, ^TEX2,3's power is competitive, ranking among the top 4 of the 11 tests. While it is not the best performer against the half-normal and log-normal distributions, ^TEX2,3 demonstrates exceptional power against the uniform distribution, outperforming all its competitors.
For N=20, ^TEX2,3 demonstrates the highest power across all tests for the Gamma and uniform distributions. Although its performance against the Weibull, half-normal, and log-normal distributions is competitive, it stands out in identifying deviations from the exponential distribution.
Finally, for N=50, a larger sample size, ^TEX2,3 demonstrates the highest power (shared with some competitors) against the Gamma, half-normal, and uniform distributions. Although its performance against the Weibull and log-normal distributions is not the best, these results affirm ^TEX2,3's competitive performance across larger sample sizes.
5.3.2. A real data example
To demonstrate the practical application of our proposed test, we present an analysis of a real-world dataset. Specifically, we examine data on the time, in hours of operation, between successive failures of air-conditioning equipment in 13 aircraft to study their aging properties, as reported by Proschan [54]. The data are as follows: 90, 10, 60,186, 61, 49, 14, 24, 56, 20, 79, 84, 44, 59, 29,118, 25,156,310, 76, 26, 44, 23, 62,130,208, 70,101, and 208.
The proposed test statistic ^TEX2,3 was used to assess exponentiality. Table 9 presents the calculated test statistic values and corresponding p-values for each dataset.
The window size, m, was determined using the formula m=[0.4N]. For comparison, Table 9 also includes p-values obtained from the Kolmogorov–Smirnov (KS), Anderson-Darling (AD), and Cramer-von Mises (CVM) tests for exponentiality. Consequently, the test fails to reject the null hypothesis, indicating that the failure times are consistent with an exponential distribution at a significance level of α = 0.05. Lawless [55] confirmed this conclusion by applying three additional test statistics to the same failure dataset, yielding identical results.
6.
Conclusions
This study explores the extropy of consecutive r-out-of-n:G systems, providing a comprehensive framework for both theoretical analysis and practical applications. Exact expressions for systems' lifetime extropy were derived and evaluated across various lifetime distributions. The theoretical contributions include new bounds, characterization results, and insights into the variability of extropy, enhancing its applicability in reliability analyses. To address the computational challenges associated with extropy in systems with large component sizes or complex distributions, practical bounds were introduced to facilitate estimation. These bounds were validated through numerical examples, demonstrating their effectiveness. Additionally, a nonparametric extropy estimator was developed and applied to image processing, highlighting its practical significance.
A key contribution of this study is the development of a novel test statistic for exponentiality, with numerically computed critical values and an extensive performance assessment against alternative distributions. The results indicate that the test is particularly effective in distinguishing the exponential from the Gamma and uniform distributions, though its sensitivity varies in the cases of Weibull and half-normal distribution. The test's power was benchmarked against 11 competing goodness-of-fit tests, demonstrating strong and consistent performance across different sample sizes. A heuristic formula was also introduced to optimize the selection of window size, ensuring robust test implementation.
In summary, this research bridges the gap between theoretical stochastic order analysis and real-world statistical inference. It provides valuable tools for reliability modeling, particularly in consecutive system analysis, goodness-of-fit testing, and nonparametric estimation. The findings emphasize the utility of extropy as a computationally efficient and informative measure in both reliability engineering and broader statistical applications.
Author contributions
F. Alrewely: Writing-review and editing, writing-original draft, visualization, validation, resources, investigation, conceptualization; M. Kayid: writing-review and editing, writing-original draft, visualization, validation, software, resources, funding acquisition, data curation, conceptualization.
Use of Generative AI tools declaration
The authors declare they have not used artificial intelligence (AI) tools in the creation of this article.
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work is supported by Researchers Supporting Project number (RSP2025R392), King Saud University, Riyadh, Saudi Arabia.









 DownLoad:
DownLoad: