Zeroing neural networks for computing quaternion linear matrix equation with application to color restoration of images

1.   Introduction

Quaternions, introduced by Hamilton in 1843 ^[1,2], are important in many fields including but not limited to computer graphics ^[3,4,5,6], modeling human motions ^[7], kinematic modeling of manipulators ^[8,9], robotic controllers ^[10,11], spacecraft maneuvering ^[12,13,14] and physics and mathematics, namely quantum fields ^[15,16], quantum mechanics ^[17,18,19], electromagnetism ^[20,21], mathematical physics ^[22,23] and linear algebra ^[24,25]. Quaternions consist of a skew-field or a division algebra over the field of real numbers^[26]. As such, the set of quaternions $\mathbb{H}$ is not commutative under the operation of multiplication and thus, in practical applications, complexity quickly becomes an issue ^[27]. On the other hand, a scalar quaternion may be readily represented by either a complex $2\times 2$ or a real $4\times 4$ matrix ^[26,28,29]. This property also extends to matrices of quaternions, with the dimensions of the representation matrices scaling appropriately. Therefore, in solving problems involving quaternions, it has become common practice to solve an equivalent problem in the real or complex domain and then convert the solution back to quaternion form. This technique, arguably powerful, even in a static environment, proves especially useful in problems of time-varying nature.

Time-varying (TV) problems involving quaternions and matrices of quaternions have recently started to attract research attention. Inversion of TV matrices of quaternions has been studied in ^[27], whereas the dynamic Sylvester quaternion matrix equation has been solved in ^[30] and the TV inequality-constrained quaternion matrix least-squares problem has been dealt with in ^[31]. Furthermore, a practical application involving a problem in robotics has been studied in ^[32]. Last but not least, the TV quaternion valued linear matrix equation (TV-QLME) for square matrices has been solved in ^[33] through transformation of the quaternion valued equation to an equivalent real representation. All these articles share a common theme, in that an online solution is derived through use of zeroing neural networks (ZNNs).

ZNNs, originated by Zhang et al. in a series of papers, comprise a class of recurrent neural networks, with strong parallel processing properties, that is dedicated to solving TV problems. Originally, ZNNs were designed to deal with the problem of matrix inversion ^[34]. Nowadays, their application has extended to solving problems of matrix and/or tensor inversion ^[35], as well as generalized inversion ^[36], solving systems of linear equations and systems of matrix equations ^[37,38,39], solving linear and quadratic optimization problems ^[40,41,42] and approximating miscellaneous matrix functions. Robot control ^[43,44], financial portfolio optimization ^[45,46] and text classification ^[47] are other common ZNNs practical applications.

In this paper, drawing motivation from ^[33], we shall also study the TV-QLME in view of generalizing its solution to rectangular matrices and, more importantly, examining whether direct solution of the problem in the quaternion domain or indirect solution through representation in the complex domain is more effective than the already proposed solution in the real domain. To this end, we shall develop three ZNNs in total, one for each domain, which we shall thoroughly test on four simulation examples. Their effectiveness shall be further examined by application in two tasks of color restoration of contaminated images. This piece of research further contributes to the literature by conducting theoretical analysis as well as analyzing the computational complexity of all discussed models.

The rest of the paper is organized as follows. Preliminaries, notation and the TV-QLME problem are presented in Section 2. The three ZNN models are developed in Section 3. Section 4 includes theoretical analysis whereas computational complexity is discussed in Section 5. Simulation examples and applications to color restoration of images are then presented in Section 6. Finally, concluding comments and remarks are given in Section 7.

2.   Preliminaries and problem formulation

This section lays out certain preliminaries regarding matrices of quaternions, the TV-QLME problem, ZNNs and finally, the notation to be used throughout the rest of the paper as well as the main results to be discussed.

Let $\mathbb{H}: = \{q = q_1 + q_2i + q_3j + q_4k:q_1, q_2, q_3, q_4\in\mathbb{R}\}$ denote the set of quaternions and let $\mathbb{H}^{m\times n}: = \{Q = Q_1 + Q_2i + Q_3j + Q_4k:Q_1, Q_2, Q_3, Q_4\in\mathbb{R}^{m\times n}\}$ denote the set of all $m\times n$ quaternion matrices with entries from $\mathbb{R}$. Note that $Q_1, Q_2, Q_3, Q_4$, also called the coefficient matrices of the quaternion matrix $Q$, are real matrices of the same dimension as $Q$. All things considered, let us now turn our attention to the following general form of a TV-QLME:

where $\tilde{A}(t)\in\mathbb{H}^{m\times n}, \tilde{X}(t)\in\mathbb{H}^{n\times r}$ and $\tilde{B}(t)\in\mathbb{H}^{m\times r}$ with $m\geq n\geq r$. The matrix $\tilde{X}(t)$ is unknown whereas $\tilde{A}(t) = A_1(t)+A_2(t)\imath+A_3(t)\jmath+A_4(t)k$ and $\tilde{B}(t) = B_1(t)+B_2(t)\imath+B_3(t)\jmath+B_4(t)k$ are smoothly TV matrices whose coefficient matrices $A_i(t)\in\mathbb{R}^{m\times n}$ and $B_i(t)\in\mathbb{R}^{m\times r}$, $i = 1, 2, 3, 4$, along with the coefficient matrices of their derivatives, are either given or can be accurately estimated.

The product of the two TV quaternion matrices $\tilde{A}(t)$ and $\tilde{X}(t)$ is the following:

where

with $C_i(t)\in\mathbb{R}^{m\times r}$ for $i = 1, \cdots, 4$.

One complex representation of the TV quaternion matrix $\tilde{A}(t)\in\mathbb{H}^{m\times n}$ is the following:

With the process of multiplying two quaternion matrices and subsequently computing the complex representation of the result being equal to the process of multiplying the respective complex representations of the matrices in the first place [30,Theorem 1], solving (2.1) is equivalent to solving the complex matrix equation:

where $\hat{X}(t)\in\mathbb{C}^{2n\times 2r}$ and $\hat{B}(t)\in\mathbb{C}^{2m\times 2r}$. Note that the construction of $\hat{X}(t)$ and $\hat{B}(t)$ follows the same pattern as that of $\hat{A}(t)$ in (2.4).

One real representation of the TV quaternion matrix $\tilde{A}(t)\in\mathbb{H}^{m\times n}$ is the following:

With the process of multiplying two quaternion matrices and subsequently computing the real representation of the result being equal to the process of multiplying the respective real representations of the matrices in the first place, [33,Corollary 1], solving (2.1) is equivalent to solving the real matrix equation:

where $X(t)\in\mathbb{R}^{4n\times 4r}$ and $B(t)\in\mathbb{R}^{4m\times 4r}$. Note that the construction of $X(t)$ and $B(t)$ follows the same pattern as that of $A(t)$ in (2.6).

For the rest of this paper, $I_r$ will refer to the identity $r\times r$ matrix whereas ${\bf{0}}_{r}$ and ${\bf{0}}_{m\times n}$ will refer to the zero $r\times r$ and $m\times n$ matrices, respectively. Furthermore, ${\mathrm{vec}}(\cdot)$ will denote the vectorization process and $\otimes$ will denote the Kronecker product. Last but not least, $()^ {\mathrm T}$ will refer to the transpose operator, $(\dot{})$ will be used to denote the time derivative of an expression and $\left\lVert{\cdot}\right\rVert_F$ will denote the matrix Frobenius norm. Lastly, Table 1 includes a list of all the abbreviations used in this paper along with their full names.

The development of a ZNN consists of two universal steps. First, one defines an error function $E(t)$, also called a Zhang function or error matrix equation (EME). Note that the expression for $E(t)$ has to involve the unknown TV matrix $X(t)$. It is also worth mentioning that each unique Zhang function defines a class of ZNNs. With $E(t)$ determined, a ZNN must satisfy

with $\dot{E}(t)$ referring to the time derivative of $E(t)$, $\lambda > 0$ being a positive real number through one may adjust the convergence rate of the model and ${\cal F}$ denoting an increasing, odd activation function that acts element-wise on $E(t)$. Substituting in (2.8) the expressions for $E(t)$ and $\dot{E}(t)$, one is then to derive the Zhang dynamics model; an explicit or implicit expression for $\dot{X}(t)$, the time derivative of the unknown TV matrix $X(t)$. The Zhang function $E(t)$, coupled with the choice of activation function ${\cal F}$ and the Zhang dynamics model, are the three defining components of a ZNN.

Learning continuously from non-stationary data, coupled with concurrent transfer and preservation of previous knowledge, is known as continual learning. It is a fact that the ZNN design revolves around forcing every entry of the error function $E(t)$ to 0, as time evolves. This is achieved through the continuous-time learning rule, which results from the definition of the error function (2.8). As a result, the error function may be perceived as a means of monitoring the ZNN models learning. In this paper we shall discuss the linear ZNN dynamical system:

Note that a higher value for the gain parameter $\lambda$ will result in the model converging even faster.

The following are the key results of the paper.

(1) Three new ZNN models for solving TV-QLME problems are presented.

(2) The proposed models are applicable to matrices of arbitrary dimension.

(3) Supportive theoretical analysis is conducted.

(4) Simulation experiments with illustrations as well as applications to color restoration of images are performed to support the theoretical research.

3.   ZNN models in solving the TV-QLME

In this section we shall develop three ZNN models, each one operating on a different domain. We assume that $\tilde{A}(t)\in\mathbb{H}^{m\times n}$ and $\tilde{B}(t)\in\mathbb{H}^{m\times r}$ are differentiable TV quaternion matrices, and $\tilde{X}(t)\in\mathbb{H}^{n\times r}$ is the unknown quaternion matrix to be found.

3.1.   The ZNNQ model

According to (2.2), the following equation is satisfied in the case of the TV-QLME:

Further, according to (2.3) and (3.1), the following are satisfied in the case of the TV-QLME:

Then, setting

we have the following EME:

where its first derivative is:

When $E(t)$ and $\dot{E}(t)$ from (2.9) are replaced with $E_Q(t)$ defined in (3.4) and $\dot{E}_Q(t)$ defined in (3.5), respectively, solving the equation in terms of $\dot{Y}(t)$ yields the following result:

Then, with the aid of the Kronecker product and the vectorization process, the dynamic model of (3.6) may be simplified:

Furthermore, after setting:

we derive the following ZNN model:

where $D_1^ {\mathrm T}(t)D_1(t)\in\mathbb R^{4nr\times 4nr}$ is a, nonsingular, mass matrix and $D_1^ {\mathrm T}(t)D_2(t)\in\mathbb R^{4nr}$. The dynamic model of (3.9), termed ZNNQ, is the proposed ZNN model to be used in solving the TV-QLME of (2.1).

3.2.   The ZNNQC model

According to (2.7), the following equation is satisfied in the case of the TV-QLME through complex representation of the quaternion matrix:

where $\hat{A}(t)\in\mathbb C^{2m\times 2n}$, $\hat{X}(t)\in\mathbb C^{2n\times 2r}$ and $\hat{B}(t)\in\mathbb C^{2m\times 2r}$. As a result, we can set the following EME:

where its first derivative is:

When $E(t)$ and $\dot{E}(t)$ from (2.9) are replaced with $E_C(t)$ defined in (3.11) and $\dot{E}_C(t)$ defined in (3.12), respectively, solving the equation in terms of $\dot{\hat{X}}(t)$ yields the following result:

Then, with the aid of the Kronecker product and the vectorization process, the dynamic model of (3.13) may be simplified:

Furthermore, after setting:

we derive the following ZNN model:

where $G_1^ {\mathrm T}(t)G_2(t)\in\mathbb C^{4nr}$ and $G_1^ {\mathrm T}(t)G_1(t)\in\mathbb C^{4nr\times 4nr}$ is a, nonsingular, mass matrix. The dynamic model of (3.16), termed ZNNQC, is the proposed ZNN model to be used in solving the TV-QLME of (2.1) through complex representation of the quaternion matrix.

3.3.   The ZNNQR model

According to (2.7), the following equation is satisfied in the case of the TV-QLME through real representation of the quaternion matrix:

where $A(t)\in\mathbb R^{4m\times 4n}$, $X(t)\in\mathbb R^{4n\times 4r}$ and $B(t)\in\mathbb R^{4m\times 4r}$. As a result, we can set the following EME:

where its first derivative is:

When $E(t)$ and $\dot{E}(t)$ from (2.9) are replaced with $E_R(t)$ defined in (3.18) and $\dot{E}_R(t)$ defined in (3.19), respectively, solving the equation in terms of $\dot{X}(t)$ yields the following result:

Then, with the aid of the Kronecker product and the vectorization process, the dynamic model of (3.20) may be simplified:

Furthermore, after setting:

we derive the following ZNN model:

where $R_1^ {\mathrm T}(t)R_2(t)\in\mathbb R^{16nr}$ and $R_1^ {\mathrm T}(t)R_1(t)\in\mathbb R^{16nr\times 16nr}$ is a, nonsingular, mass matrix. The dynamic model of (3.23), termed ZNNQR, is the proposed ZNN model to be used in solving the TV-QLME of (2.1) through real representation of the quaternion matrix.

4.   Theoretical analysis

The convergence and the stability analysis of the ZNNQ (3.9), ZNNQC (3.16) and ZNNQR (3.6) models are presented in this section.

Theorem 4.1. Assuming that $Z(t) \in \mathbb R^{4m\times 4n}$ and $W(t) \in \mathbb R^{4m\times r}$ are differentiable, the dynamical system (3.6) converges to the theoretical solution (TSOL) $Y^*(t)$ of the TV-QLME (2.1). The solution is then stable, based on Lyapunov.

Proof. The substitution $\tilde{Y}(t): = Y^*(t)-Y(t)$ implies $Y(t) = Y^*(t)-\tilde{Y}(t)$, where $Y^*(t)$ is a TSOL. The time derivative of $Y(t)$ is $\dot{Y}(t) = \dot{Y}^*(t)-\dot{\tilde{Y}}(t)$. Notice that

and its first derivative

As a result, following the substitution of $Y(t) = Y^*(t)-\tilde{Y}(t)$ into (3.4), one can verify

Further, the implicit dynamics (2.9) imply

We then determine the candidate Lyapunov function so as to confirm convergence:

Then, the next identities can be verified:

Consequently, it hold that

With $\tilde{Y}(t)$ being the equilibrium point of the system (4.4) and $E_Q(0) = 0$, we have that:

By the Lyapunov stability theory, we infer that the equilibrium state $\tilde{Y}(t) = Y^*(t)-Y(t) = 0$ is stable. Thus, $Y(t)\rightarrow Y^*(t)$ as $t\rightarrow \infty$. □

Theorem 4.2. Let $Z(t) \in \mathbb R^{4m\times 4n}$ and $W(t) \in \mathbb R^{4m\times r}$ be differentiable. For any initial value ${\bf{y}}$ (0) that one may consider, the ZNNQ model (3.9) converges exponentially to the TSOL ${\bf{y}}^*(t)$ at each time $t\in[0, t_f)\subseteq[0, +\infty)$.

Proof. The EME of (3.4) is declared so as to determine the TSOL of the TV-QLME. The model (3.6) is developed utilizing the linear ZNN design (2.9) for zeroing (3.4). When $t\rightarrow \infty$, $Y(t)\rightarrow Y^*(t)$ for any choice of initial value, according to Theorem 4.1. As a result, the ZNNQ model (3.9) also converges to the TSOL ${\bf{y}}^*(t)$ for any choice of initial value ${\bf{y}}(0)$ when $t\rightarrow \infty$, as it is simply an alternative version of (3.6). Therefore, the proof is finished. □

Theorem 4.3. Assuming that $\hat{A}(t) \in \mathbb R^{2m\times 2n}$ and $\hat{B}(t) \in \mathbb R^{2m\times 2r}$ are differentiable, the dynamical system (3.13) converges to the TSOL $\hat{X}^*(t)$ of the TV-QLME (2.1). The solution is then stable, based on Lyapunov.

Proof. The proof is omitted, being that it resembles the proof of Theorem 4.1. □

Theorem 4.4. Let $\hat{A}(t) \in \mathbb R^{2m\times 2n}$ and $\hat{B}(t) \in \mathbb R^{2m\times 2r}$ be differentiable. For any initial value ${\bf{h}}(0)$ that one may consider, the ZNNQ model (3.16) converges exponentially to the TSOL ${\bf{h}}^*(t)$ at each time $t\in[0, t_f)\subseteq[0, +\infty)$.

Proof. The proof is omitted, being that it is identical to the proof of Theorem 4.2 once we replace Theorem 4.1 with Theorem 4.3. □

Theorem 4.5. Assuming that $A(t) \in \mathbb R^{4m\times 4n}$ and $B(t) \in \mathbb R^{4m\times 4r}$ are differentiable, the dynamical system (3.20) converges to the TSOL $X^*(t)$ of the TV-QLME (2.1). The solution is then stable, based on Lyapunov.

Proof. The proof is omitted, being that it resembles the proof of Theorem 4.1. □

Theorem 4.6. Let $A(t) \in \mathbb R^{4m\times 4n}$ and $B(t) \in \mathbb R^{4m\times 4r}$ be differentiable. For any initial value ${\bf{x}}(0)$ that one may consider, the ZNNQ model (3.23) converges exponentially to the TSOL ${\bf{x}}^*(t)$ at each time $t\in[0, t_f)\subseteq[0, +\infty)$.

Proof. The proof is omitted, being that it is identical to the proof of Theorem 4.2 once we replace Theorem 4.1 with Theorem 4.3. □

5.   Computational complexity of the ZNN models

The complexity of producing and solving (3.9), (3.16) and (3.23) contributes to the overall computational complexity of the ZNNQ, ZNNQC and ZNNQR models, respectively. In particular, the computational complexity of producing (3.9) is $\mathcal{O}((4nr)^2)$ operations as in each iteration of the equation we perform $(4nr)^2$ multiplications and $4nr$ additions/subtractions. For the same reasons, the computational complexity of computing (3.23) is $\mathcal{O}((16nr)^2)$ operations. However, the ZNNQC model deals with complex numbers. It is worth pointing out that if we multiply two complex numbers, the calculation works out to $(a+b\imath)(c+d\imath) = ac-bd+ad\imath+bc\imath$, which requires a total of four multiplications and two addition/subtraction operations. As a result, the computational complexity of computing (3.16) is $\mathcal{O}((8nr)^2)$ as each iteration of the equation has $4(4nr)^2$ multiplication and $2(4nr)$ addition/subtraction operations.

Additionally, the linear system of equations is, at each step, solved through use of the implicit MATLAB solver ${\tt ode15s}$. The complexity of solving (3.9) is $\mathcal{O}((4nr)^3$ as it involves a $(4nr)\times (4nr)$ matrix. In the same manner, the complexity of solving (3.16) is $\mathcal{O}((8nr)^3$ and the complexity of solving (3.23) is $\mathcal{O}((16nr)^3$. Therefore, the overall computational complexity of the ZNNQ model is $\mathcal{O}((4nr)^3)$, while that of the ZNNQC model is $\mathcal{O}((8nr)^3)$ and that of the ZNNQR model is $\mathcal{O}((16nr)^3)$. The overall computational complexity of the ZNN models is also presented in Table 2.

6.   Simulation experiments

In this section we shall present four simulation examples (SE) and two applications to color restoration of images. Following are a few important clarifications. The ZNN design parameter $\lambda$ is used with value $10$, while the initial values of the ZNNQ, ZNNQC and ZNNQR models have been set to ${\bf{y}}(0) = {\bf{0}}_{4nr}$, ${\bf{h}}(0) = {\bf{0}}_{4nr}$ and ${\bf{x}}(0) = {\bf{0}}_{16nr}$, respectively. For convenience purposes, applying to all SEs, we have set $\alpha(t) = \sin(t)$ and $\beta(t) = \cos(t)$. Last but not least, a MATLAB ode solver, namely ${\tt ode15s}$, is used in the computations throughout all SEs and applications, with the time interval being set to $[0, 10]$.

6.1.   Simulation examples

Example 6.1. The coefficients of the input matrix $\tilde{A}(t)$ have been set to

and the coefficients of the input matrix $\tilde{B}(t)$ have been set to

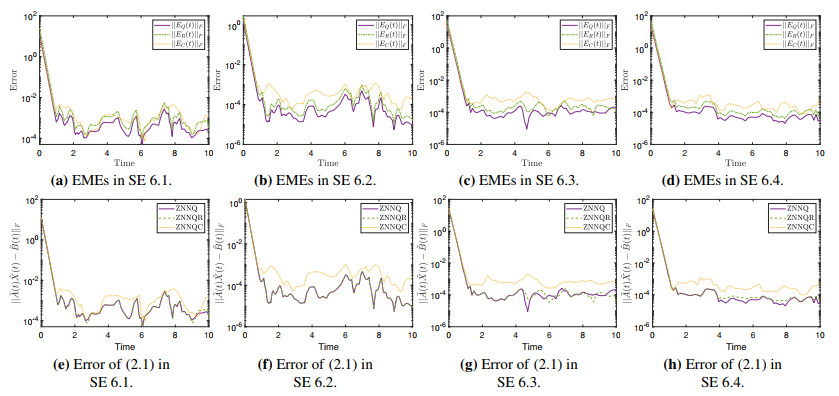
Figures 1 and 2 depict certain aspects of the simulation experiments on the TV-QLME defined by these matrices.

Example 6.2. This example considers the matrices $A_1(t), A_2(t), A_3(t)$ and $A_4(t)$ of NE 1. In view of inverting $A(t)$, the coefficients of $B(t)$ have been set to $B_i(t) = {\bf{0}}_2, i = 1, \dots, 4$. The generated results are presented in Figures 1b, 1f.

Example 6.3. The coefficients of the input matrix $\tilde{A}(t)$ have been set to

and the coefficients of the input matrix $\tilde{B}(t)$ have been set to

Generated results are presented in Figure 1c, 1g.

Example 6.4. The coefficients of the input matrix $\tilde{A}(t)$ have been set to

and the coefficients of the input matrix $\tilde{B}(t)$ have been set to

The results are presented in Figures 1d, 1h.

6.2.   Simulation examples discussion

The performance of the ZNNQ (3.9), ZNNQC (3.16) and ZNNQR (3.6) models for solving the TV-QLME (2.1) is investigated throughout the SEs in Sections 1–4. To each section corresponds a different TV-QLME problem, defined by an appropriate pair of matrices $\tilde{A}(t), \tilde{B}(t)$.

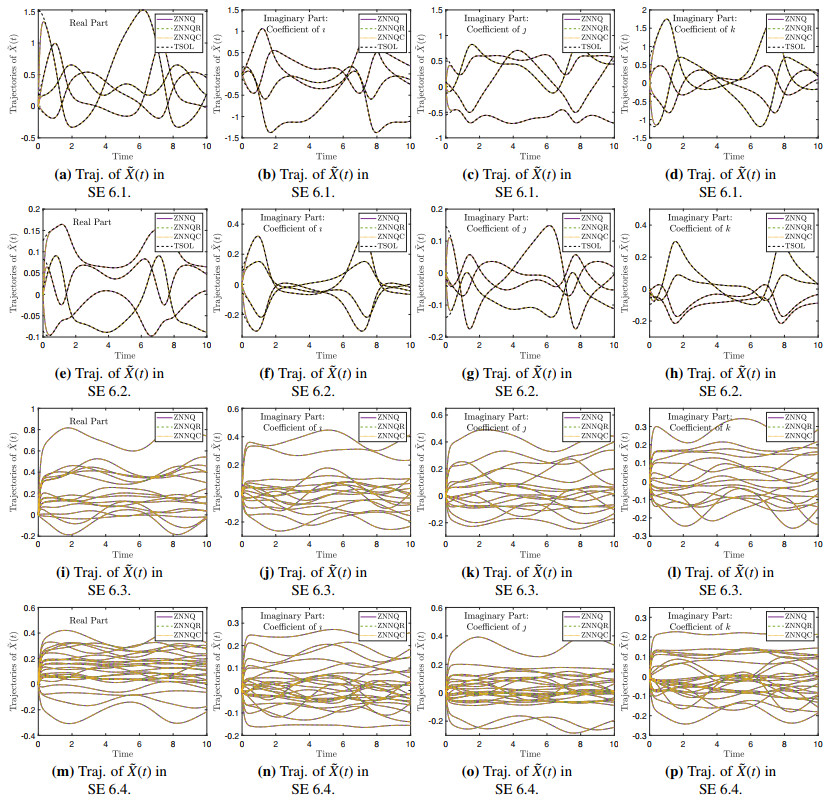
For each such problem, Figure 1a–1d depict the corresponding error paths of the models; that is, the value of the Frobenius norm of their EMEs in the time interval between $t = 0$ and $t = 10$. These curves convey information about the convergence of each model. Notice that, with the value of the parameter $\lambda$ being set to 10, the error values in all SEs experience a steep decline which, by the time-mark of $t\approx 1.5$, brings them to the range $[10^{-5}, 10^{-3}]$. Generally, a larger value for $\lambda$ will force the ZNN models to converge even faster. It bears mentioning that, throughout all SEs, the corresponding error curves of the ZNNQ model are positioned lower than those of the other two models. That is, the ZNNQ model displays better convergence. The successful convergence of all models is further stressed in Figure 2, where the theoretical trajectories of the real as well as the three imaginary parts of the quaternion TV matrix $\tilde{X}(t)$ are compared with the trajectories obtained by the three models. Namely, Figure 2a–2d corresponds to the SE of section 6.1, Figure 2e–2h corresponds to the SE of section 6.2, Figure 2i–2l corresponds to the SE of section 6.3 and, last but not least, Figure 2m–2p corresponds to the SE of section 6.4. For all SEs, the generated trajectories of the three models match the theoretical trajectories.

At this point, ZNNQ, ZNNQC and ZNNQR have generated, for each SE, the previously unknown TV matrices $\tilde{X}(t), \hat{X}(t)$ and $X(t)$, respectively, for $t\in[0, 10]$. In order to validate the models, we shall evaluate $||\tilde{A}(t)\tilde{X}(t)-\tilde{B}(t)||_F$; that is, the error on the given TV-QLME, for each model and SE. In order for this to be accomplished, $\hat{X}(t)$ and $X(t)$, the complex and real representations of the TV solution matrix, respectively, are converted back to quaternion form. Figure 1e–1h demonstrates the respective paths for the SEs of sections 6.1–6.4, respectively. It is interesting to note that, as far as Figure 1e and 1f are concerned, the corresponding curves of the ZNNQ and ZNNQR model are almost identical. Overall, the ZNNQ seems to have a slight competitive edge as its respective $||\tilde{A}(t)\tilde{X}(t)-\tilde{B}(t)||_F$ curves are positioned, for the most part, lower than those of the other two models, for the remaining two SEs.

Last but not least, the results above can be put into better perspective once we take the complexity of each model into account. Namely, in line with the analysis of Section 5, the ZNNQR has by far the highest complexity as the dimensions of the corresponding real valued matrices $A(t), X(t)$ and $B(t)$ are two times bigger than those of the complex valued matrices $\hat{A}(t), \hat{X}(t)$ and $\hat{B}(t)$ and four times bigger than those of the quaternion valued matrices $\tilde{A}(t), \tilde{X}(t)$ and $\tilde{B}(t)$. On that account, as the dimensions of the matrices $\tilde{A}(t)$ and $\tilde{B}(t)$ grow, opting to solve the TV-QLME problem in the real domain comes with a serious cost of memory, with RAM quickly becoming a limiting factor. Furthermore, the choice of programming language (and in some cases, linear algebra libraries) also starts to become important. All things considered, the ZNNQ seems to be the model with the highest potential.

6.3.   Applications to color restoration of images

This section presents applications to color restoration of images. Using the the ZNNQ, ZNNQC and ZNNQR models to restore the color of two contaminated images, their applicability can be further stressed. The first image, shown in Figure 3a, is a thumbnail of Mona Lisa at $256\times 256$ pixels, and the second image, shown in Figure 3d, is a thumbnail of Lena Soderberg at $256\times 256$ pixels.

Following is a description of the task of image restoration. Suppose that a pure quaternion matrix $\tilde{S} = R_e\imath +G_r\jmath +B_lk$ is used to represent a colored image. Then the three imaginary parts of the quaternion $\tilde{S}\in\mathbb Q^{256\times 256}$ are pixel matrices of $R_e$ (red), $G_r$ (green), and $B_l$ (blue) channels of the color image. Given the quaternion matrix $\tilde{A} = 1.2I_{256}\imath +0.8I_{256}\jmath +0.2I_{256}k$, the quaternion matrix $\tilde{B}$ representing the contaminated image is produced by $\tilde{B} = \tilde{A}\tilde{S}$. To restore the image back to its original state, we should solve (2.1) to get $\tilde{X} = \tilde{S}$. One should keep in mind that the coefficient matrices of $\tilde{S}, \tilde{A}$ and $\tilde{B}$ are sparse matrices.

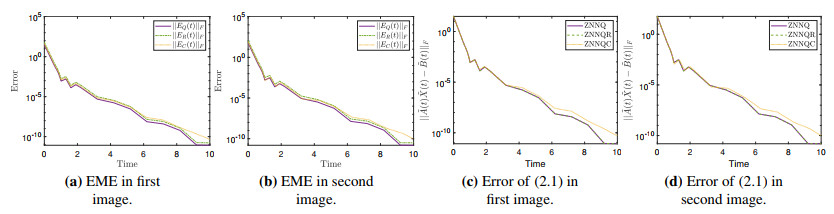
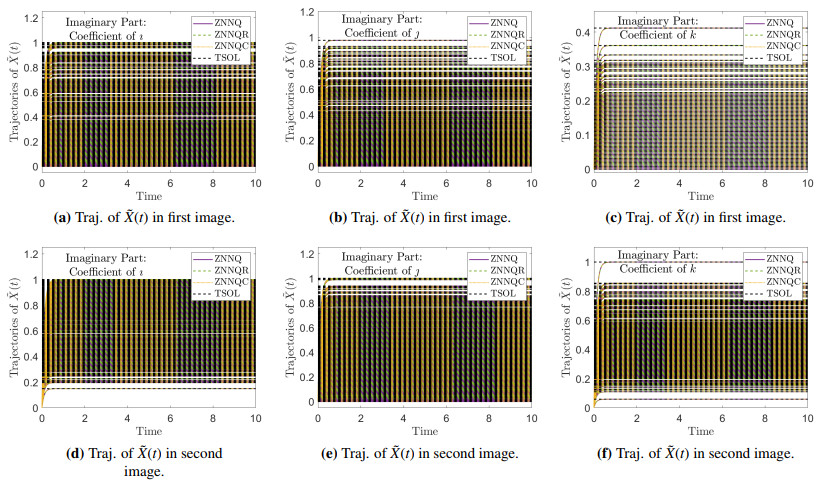
On a similar note to the analysis in Section 6.2, Figure 4a and 4b depict the paths of the EMEs of each model, from which we can draw conclusions regarding the convergence of the models. With the parameter $\lambda$ being set to 10, the values of the EMEs of all three ZNNs steadily decrease as $t$ increases from $0$ to $10$. For both images, the ending values of the EMEs of the models are in the neighborhood of $10^{-10}$. Thus, all three ZNNs have converged. This is further stressed by Figure 5, where the theoretical trajectories of the imaginary parts of $\tilde{X}(t)$ are compared to the trajectories obtained by the three models. Namely, Figure 5a–5c corresponds to the imaginary parts of $\tilde{X}(t)$, relative to the first image, whereas Figure 5d–5f corresponds to the imaginary parts of $\tilde{X}(t)$, relative to the second image. In both cases, the generated trajectories match the theoretical trajectories.

On the other hand, the performance of each model on the task of color restoration of images can be better evaluated by examining Figure 4c and 4d. Once again, we have transformed all involved matrices back to quaternion form and have plotted, for each model and image, the corresponding $||\tilde{A}(t)\tilde{X}(t)-\tilde{B}(t)||_F$ curves of the models. For both images, the respective curves of the ZNNQ and ZNNQR models follow identical paths and are positioned lower than those of the ZNNQC.

Observing the original images (Figure 3a and 3d), the contaminated images (Figure 3b and 3e) and lastly the restored images (Figure 3c and 3f), it is evident that the color restoration process has been successful. Thus, the developed models may be effectively used to restore contaminated images to their original colors. In line with the analysis in Section 6.2, opting to work with the ZNNQ seems to be a more efficient choice.

7.   Conclusions

In view of handling the TV-QLME problem for matrices of arbitrary dimension, three models; namely, ZNNQ, ZNNQC and ZNNQR, have been proposed. Along with simulation examples and practical applications to color restoration of images, the development of those models has been supported by theoretical analysis and analysis of their computational complexity. With the TV-QLME problem having been effectively solved both directly in the quaternion domain as well as indirectly, by representation in the complex and real domains and subsequent conversion of the solutions back to the quaternion domain, the direct method, implemented by the ZNNQ model, has been proposed as the most efficient and effective of the three. All things considered, the established results open the way for more interesting research endeavors. A few considerations are the following:

● One may investigate application of nonlinear ZNNs to quaternion valued TV problems.

● One could also consider the task of pseudo-inversion of quaternion valued TV matrices.

● Using the predefined-time ZNN architecture to quaternion valued TV problems is something that can be looked into.

● Utilizing carefully chosen design parameters specified in fuzzy environments to speed up the convergence of ZNN models is another area of investigation.

Acknowledgments

This work was supported by a Mega Grant from the Government of the Russian Federation within the framework of federal project No. 075-15-2021-584.

Conflict of interest

The authors declare no conflict of interest.