Adaptive estimation for spatially varying coefficient models

1.   Introduction

In spatial data analysis, a common problem is determining the nature of the relationship between variables. In many cases, a simple global model often fails to explain the relationships between certain sets of variables, as the relationships between them may change with the change of position, which is known as spatial heterogeneity. In order to deal with this heterogeneity, the model needs to reflect the structure of spatial variation in the data. Suppose that the spatial data of $n$ positions are randomly selected in the spatial region $D \subseteq R^2$, let ${\mathit{\boldsymbol{u}}}_i = (u_{i1}, u_{i2})^\top \in D$ is the position of the point $i, i = 1, \cdots, n$, $y_i$ is the response variable, ${\bf{x}}_i = (x_{i1}, x_{i2}, \cdots, x_{ip})^\top$ is the explanatory variable and $x_{i1}\equiv 1$, allowing a varying intercept in the model. $\{y_i, {\bf{x}}_i, u_i\}$ satisfy the following spatially varying coefficient models (SVCM) ^[1,2,3]:

where ${\mathit{\boldsymbol{\beta}}}({\mathit{\boldsymbol{u}}}_i) = (\beta_1({\mathit{\boldsymbol{u}}}_i), \beta_2({\mathit{\boldsymbol{u}}}_i), \cdots, \beta_{p}({\mathit{\boldsymbol{u}}}_i))^\top$ is a vector of $p$-dimensional unknown space-varying functional coefficients defined on $D$, $\varepsilon_i$ is an independent and and identically distributed random noise, with $E(\varepsilon_{i}) = 0, var(\varepsilon_{i}) = \sigma^2$, and are independent of ${\bf{x}}_i$. Over the past few decades, SVCM has been widely used in geography ^[4], econometrics ^[5], meteorology ^[6], and environmental science ^[7]. When $\beta_k(\cdot)$ is a univariate function, the model (1.1) is a varying coefficient model and has been extensively studied ^[8,9]. In this study, $\beta_k(\cdot)$ is a bivariate function of the location-specific, and our main goal is to estimate ${\mathit{\boldsymbol{\beta}}} = (\beta_1, \beta_2, \cdots, \beta_p)$ and explore the spatial heterogeneity of regression relations based on the given observations $\{(y_i, {\bf{x}}_i, {\mathit{\boldsymbol{u}}}_i)\}_{i = 1}^{n}$.

In the rich literature on how to estimate the regression coefficients of SVCM, the Bayesian approach and the smoothing approach are two competing methods. Firstly, the Bayesian approach is an important spatial modeling method that assumes that the regression coefficients obey a certain prior distribution and calculates their posterior distribution for estimation and inference. For example, Gelfand et al. ^[10] developed a Bayesian hierarchical framework of spatial point reference data by formulating a Gaussian process for spatially varying coefficients, and Assuncao ^[11] introduced the Bayesian space-varying coefficient model (BVCM) for areal data. Recently, Kim and Lee ^[12] extended BVCM to handle mixed data with point reference data and areal data. Luo et al. ^[13] built the Bayesian spatially clustered coefficient (BSCC) model from the spanning trees of a graph. However, Bayesian methods require careful selection of prior distributions and face the high computational cost issue. Secondly, the smoothing method is a traditional framework for regression, divided into kernel smoothing and smoothing splines. For example, Fotheringham et al. ^[1] adopted a locally weighted least squares method of constructing weights by spatial kernel functions, namely geographically weighted regression (GWR), which is essentially a local constant kernel smoother. Mu et al. ^[14] used binary splines over triangulation to estimate regression coefficients, which solves the problem of inappropriate smoothness of complex regional boundary features and processes large data sets quickly and effectively enough. Yet, the kernel-based method needs to solve an optimization problem at each sample position which is computationally intensive, and smoothing splines method inference for spatially varying coefficients relies on a bootstrap method.

Currently, there are also numerous studies on variable selection in SVCM. Shin et al. ^[15] proposed penalized quasi-likelihood methods with spatial dependence. Wang and Sun ^[16] represented the space-varying coefficients as a combination of local polynomials at anchor points and applying the least squares with an additive form of lasso and fused-lasso penalties. Li and Sang ^[17] proposed a spanning tree graph fused lasso-based spatially clustered coefficient regression (SCC) model with the assumption of spatial clusters, and the regularization term of the SCC model is generalized by a chain graph guided fusion penalty plus a group lasso penalty ^[18]. However, each of these methods estimated space-varying coefficients by the least squares criterion, corresponding to the likelihood function when the error term is normally distributed. In practice, the error density was unknown, so it is not appropriate to use the least squares method, which will lose some efficiency, but the adaptive estimation method provides an alternative way.

The adaptive estimation method was first studied to consider the problem of estimating and inferring an infinite dimensional parameter ^[19]. This method replaces the Gaussian density function with a nonparametric estimate of the score function of the log-likelihood estimation and proves that efficiency gain can be achieved in both varying coefficient models ^[20] and varying coefficient models with non-stationary covariates ^[21]. In this study, we propose an adaptive estimation method to estimate spatially varying coefficients, different from the least squares criterion, the logarithmic function of the new adaptive estimation method is similar to the likelihood structure of the mixed density function, without an explicit solution, and we use the generalized Modal EM (GMEM) algorithm to achieve parameter estimation ^[22]. Simulation results show that when the error distribution deviates from the normal distribution, the new estimation is more effective than the existing GWR estimation based on least squares. In addition, the new method is also comparable with existing GWR methods when the error is completely normal. Finally, we illustrate the effectiveness of the proposed adaptive estimation method through two real data examples.

The rest of this study is organized below. In Section 2, the adaptive estimation of spatial varying coefficient models and the generalized Modal EM algorithm are introduced. In Section 3, through simulation research, the proposed method is compared with the GWR method under five different error densities. In Section 4, the new method is applied to two real-world data examples. This article is briefly discussed in Section 5. All technical conditions and certifications are given in Section Appendix A.

2.   Adaptive kernel estimation method

For any given ${\mathit{\boldsymbol{u}}}_0$, approximating the spatially varying coefficients by Taylor's expansion as

where ${\mathit{\boldsymbol{u}}}_i$ is in a neighborhood of ${\mathit{\boldsymbol{u}}}_0$, $\dot{ {\mathit{\boldsymbol{\beta}}}}_k({\mathit{\boldsymbol{u}}}_0) = \{\partial(\beta_k({\mathit{\boldsymbol{u}}})/\partial{u_1}, \partial(\beta_k({\mathit{\boldsymbol{u}}})/\partial{u_2}\}_{ {\mathit{\boldsymbol{u}}} = {\mathit{\boldsymbol{u}}}_0}$. Using the above approximation, we have the following objective function for estimating $(b_1, \cdots, b_p)$ and $({\mathit{\boldsymbol{c}}}_1, \cdots, {\mathit{\boldsymbol{c}}}_p)$

where $K_h(\cdot) = K(\cdot/h)/h^2$, $K(\cdot)$ is a kernel function, $h$ is a bandwidth, and $\vert|{\mathit{\boldsymbol{s}}}\vert| = ({\mathit{\boldsymbol{s}}}^\top {\mathit{\boldsymbol{s}}})^{\frac{1}{2}}$ for a vector ${\mathit{\boldsymbol{s}}}$. Throughout this study, a Gaussian kernel will be used for $K(\cdot)$. Due to the least squares in (2.2), the resulting estimate may lose some efficiency when the error distribution is not normal. Therefore, we develop an adaptive estimation procedure that can adapt to different error distributions.

Let $f(\varepsilon)$ be the density function of $\varepsilon$. If $f(\varepsilon)$ were known, it would be natural to estimate the parameters in (2.1) by maximizing the following log-likelihood function

However, in practice, $f(\varepsilon)$ is generally unknown but can be replaced by a leave-one-out kernel density estimator

where $\tilde{\varepsilon}_j = y_j-\sum_{k = 0}^p x_{jk}\tilde{\beta}_k({\mathit{\boldsymbol{u}}}_j)$ is a preliminary estimation of $\varepsilon_j$ based on initial estimator $\tilde{\beta}_k$, +and $\tilde{\beta}_k = \tilde{b}_k$, which can be estimated by local linear regression estimator (2.2). Let $\mathit{\boldsymbol{\theta}} = (b_1, \cdots, b_p, \mathit{\boldsymbol{c}}_1, \cdots, \mathit{\boldsymbol{c}}_p)^\top$. Then our proposed adaptive estimate for the parameter $\mathit{\boldsymbol{\theta}}$ is

where

Since the logarithmic function of (2.6) has an internal sum, which is similar to the objective function from a random sample of mixed density, so there is no explicit solution. In the following, we use the generalized Modal EM algorithm proposed in Yao ^[22] to calculate the parameters.

Generalized Modal EM algorithm (GMEM): GMEM algorithm is the generalization of Modal EM (MEM) algorithm ^[23] that finds the mode of the mixture density and does nonparametric clustering. The MEM algorithm comprises two steps similar to the expectation and the maximization steps in EM algorithm, which aims at maximizing the likelihood function for finite mixture models when the model contains unobserved latent variables. Especially, suppose an m-component finite mixture density be

where $\pi_j$ is the mixing proportions of mixture component $j$, and $f_j(x)$ is the density of component $j$. Given any initial value $x^{(0)}$, in the $(l+1)th$ step of the MEM algorithm solves a local maximum of the mixture by the following two steps:

1) let

2) update

The first step is the "Expectation" step where the probability of each mixture component $j, 1 \leq j \leq m$, at the current point $x^{(r)}$ is computed. The second step is the "Maximization" step, similar to EM algorithm, which is usually much easier than the original objective function. Detailed properties of MEM algorithms refer to Li et al. ^[23]. Yao ^[22] proves that the MEM algorithm can be applied to maximize a general mixture-type objective function

where $w_k$ and $a_{kl}$ are known positive constants, $f_{jk}(x)$ is positive known function, when $j = 1$, the objective function (2.7) is simplified to

Therefore, the MEM algorithm in Eq (2.7) is a special case of the generalized Modal EM algorithm (GMEM) if $\sum_{k = 1}^Ka_{1k} = 1$ and $f_{1k}(x)$ are density functions. Specifically, given the initial value $x^{(0)}$, in the $(l+1)th$ step of the GMEM algorithm are following:

E-step: let

M-step: update

In this study, we note that the objective function $Q({\mathit{\boldsymbol{\theta}}})$ of (2.6) has the mixture form of (2.7). Specially, $K_h({\mathit{\boldsymbol{u}}}_i- {\mathit{\boldsymbol{u}}}_0), \frac{1}{n}, K_{h_0} [y_i-\sum_ {k = 1}^p \{b_k+\mathit{\boldsymbol{c}}_k ({\mathit{\boldsymbol{u}}}_i- {\mathit{\boldsymbol{u}}}_0)\}x_{ik}-\tilde{\varepsilon}_j]$ in (2.6) corresponds to $w_j, a_{jk}, f_{jk}(x)$ in (2.7), respectively. Therefore, GMEM could be directly applied to estimate the parameters of $b_k$, $\mathit{\boldsymbol{c}}_k$ in (2.6). Let ${\mathit{\boldsymbol{\theta}}}^{(0)}$ be the initial estimator obtained by minimizing (2.2), $\mathit{\boldsymbol{\theta}}^{(l)} = (b_1^{(l)}, \cdots, b_p^{(l)}, \mathit{\boldsymbol{c}}_1^{(l)}, \cdots, \mathit{\boldsymbol{c}}_p^{(l)})^\top$ is the estimator of (l)th iteration, $\tilde{\varepsilon}_j$ is a preliminary estimation of $\varepsilon_j$ and no need to update, ${\mathit{\boldsymbol{z}}}_{i} = \{ {\bf{x}}_{i}^\top, ({\bf{x}}_{i}\otimes({\mathit{\boldsymbol{u}}}_{i}- {\mathit{\boldsymbol{u}}}_{0}))^\top\}^\top$. At the $(l+1)$th iteration, steps E and M are as follows:

E-step: calculate the classification probabilities $p_{ij}^{(k+1)}$,

M-step: update ${\mathit{\boldsymbol{\theta}}}^{(l+1)}$

where ${\mathit{\boldsymbol{Z}}} = ({\mathit{\boldsymbol{Z}}}_{1, n-1}, \cdots, {\mathit{\boldsymbol{Z}}}_{n, n-1})^\top$,

${\mathit{\boldsymbol{W}}} = diag(p_{12}^{(l+1)}K_h(\vert| {\mathit{\boldsymbol{u}}}_1- {\mathit{\boldsymbol{u}}}_0\vert|), \cdots, p_{1n}^{(l+1)}K_h(\vert| {\mathit{\boldsymbol{u}}}_1- {\mathit{\boldsymbol{u}}}_0\vert|), \cdots, p_{n, n-1}^{(l+1)}K_h(\vert| {\mathit{\boldsymbol{u}}}_n- {\mathit{\boldsymbol{u}}}_0\vert|))$, ${\mathit{\boldsymbol{Y}}} = (y_1-\tilde{\varepsilon}_2, \cdots, y_1-\tilde{\varepsilon}_n, \cdots, y_n-\tilde{\varepsilon}_{n-1})^\top$, and the second equation follows the use of Gaussian kernel. If $\vert| {\mathit{\boldsymbol{\theta}}}^{(l+1)}- {\mathit{\boldsymbol{\theta}}}^{(l)}\vert| \leq 10^{-5}$, the algorithm ends. Otherwise, the E and M steps of the algorithm continue to iterate.

Proposition 2.1. Each iteration of the above E and M steps will monotonically increase $Q(\mathit{\boldsymbol{ \theta}})$ in the Eq (2.6), i.e., for any $l$,

The consistency and asymptotic of ${\mathit{\boldsymbol{\theta}}}$ are established. Let ${\mathit{\boldsymbol{H}}} = diag(1, h, h) \otimes {\mathit{\boldsymbol{I}}}_p$, where $\otimes$ is the Kronecker product and $I_p$ is the unit matrix of $p\times p$. For $i, j = 0, 1, 2$, $k = 1, 2$, denote $\gamma_{ij} = \int{u_{k}^{i}K^{j}(\|{\mathit{\boldsymbol{u}}}\|) d{\mathit{\boldsymbol{u}}}}$ with ${\mathit{\boldsymbol{u}}} = (u_1, u_2)$, and $q(\cdot)$ is the marginal density function of ${\mathit{\boldsymbol{u}}}$.

Theorem 2.1. Under the regularity conditions in the A, there exists a consistent maximizer $\hat{\mathit{\boldsymbol{\theta}}} = (\hat b_1, \cdots, \hat b_p, \hat{\mathit{\boldsymbol{c}}}_1, \cdots, \hat{\mathit{\boldsymbol{c}}}_p)^\top$ of (2.6) with probability approaching 1 such that

Based on Theorem 2.1, we can know that the proposed adaptive estimator of ${\mathit{\boldsymbol{\theta}}}$ is consistent and its proof is provided in the Appendix. Next, we provide the asymptotic distribution of the proposed estimator.

Theorem 2.2. Suppose that the regularity conditions in the A hold. Then $\hat{ {\mathit{\boldsymbol{\theta}}}}$, given in Theorem 2.1, has the following asymptotic distribution

where $\rho(\cdot) = \log f(\cdot)$, ${\mathit{\boldsymbol{S}}} = diag(\gamma_{01}, \gamma_{21}, \gamma_{21})\otimes {\bf{\Gamma}}(\mathit{\boldsymbol{u}}_0)$, ${\bf{\Gamma}}(\mathit{\boldsymbol{u}}_0) = \{\Gamma_{kj}({\mathit{\boldsymbol{u}}}_0)\}_{1\leq k, j \leq p}$, $\Gamma_{kj}({\mathit{\boldsymbol{u}}}_0) = E(x_{ik}x_{ij}\vert {\mathit{\boldsymbol{u}}}_0)$, ${\bf{\Lambda}} = diag(\gamma_{02}, \gamma_{22}, \gamma_{22})\otimes {\bf{\Gamma}}({\mathit{\boldsymbol{u}}}_0)$, and $\mathit{\boldsymbol{\psi}}_k = \binom{\gamma_{21}}{{{\bf{0}}}_{2 \times 1}}\otimes (\Gamma_{kj}({\mathit{\boldsymbol{u}}}_0))_{1\leq j \leq p}^\top$.

3.   Simulation study

This section simulates the proposed adaptive estimation method and compares it with that of the local linear geographically weighted regression (LL) ^[24] and the Geographically Weighted Regression Model (GWR). In numerical experiments, the following four designs of error structure are considered:

$1)$ $\varepsilon \sim N(0, 1)$;

$2)$ $\varepsilon \sim t_3$;

$3)$ $\varepsilon \sim 0.5N(-1, 0.5^2)+0.5N(1, 0.5^2)$;

$4)$ $\varepsilon \sim e^T-E(e^T)$, where $T \sim N(0, 1)$.

The first is the standard normal distribution as a benchmark for comparison, and the second is the $t$ distribution with 3 degrees of freedom. The distributions of the third are doublet and left-biased, and the last one has a long right tail. For the above error distribution, the population positions are located at the $N = 25 \times 25$ regular grid in the square region of $D = [0, 1]^2$, and the distance between any two adjacent points in the horizontal and vertical directions is equal. At each location, the response variable $y_1, \cdots, y_n$ is generated by $y_i = \beta_1({\mathit{\boldsymbol{u}}}_i)x_{i1}+\beta_2({\mathit{\boldsymbol{u}}}_i)x_{i2}+\varepsilon_i$, where $x_1$ and $x_2$ follow $N(0, 1)$ with correlation coefficient $\rho = 1/\sqrt{2}$, and the regression coefficient function is as follows:

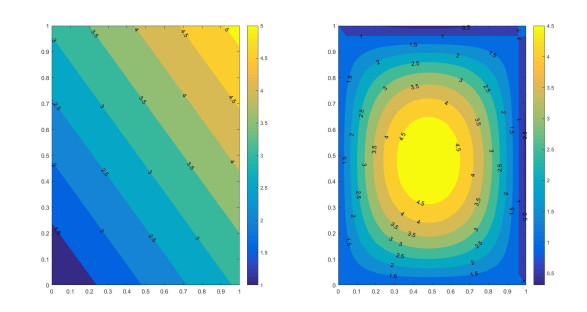
the true coefficient functions contour plots of $\beta_1({\mathit{\boldsymbol{u}}})$ and $\beta_2({\mathit{\boldsymbol{u}}})$ are shown in Figure 1. We randomly sample $n = 200$ and 400 points from the $25\times 25$ points in each of the 100 Monte Carlo experiments.

There are two bandwidths $h$ and $h_0$ in the estimate, we use the leave-one-out cross-validation method to select $h$, and the choice of $h_0 = h/\log(n)$ follows Linton and Xiao ^[25]. The performance of the estimator $\hat{\beta}(\cdot)$ is evaluated by the square root of the average squared errors (RASE), which calculated as follows:

The simulation results are summarized in Table 1. It can be clearly seen that when the error is non-normal, the proposed adaptive estimation is better than LL and GWR, and the improvement of estimation efficiency may also be considerable. When the error is fully normally distributed, our method is still comparable to the LL and GWR method.

Figure 2 visualizes the estimated surfaces of $\beta_1(\cdot)$ and $\beta_2(\cdot)$ using adaptive estimation method, LL and GWR based on sample size $n = 400$ when the error distribution of $\varepsilon$ is the case 3, These results highlight that the adaptive estimation method can capture more accurate spatial pattern than the LL and GWR method.

4.   Real data analysis

Example 1. (Dublin Voter Turnout Data) This section applies the proposed methodology to Dublin Voter data. This dataset includes the proportion of the voting population in 322 areas, as well as several variables that may explain the change in the proportion of the voting population. Specifically, we will explore how the unemployment rate (Unempl), the proportion of ages 25 to 44 (Age 25_44) and no formal education (LowEduc) affect the proportion of the voting population in each region (GenEl2004). Figure 3 shows the spatial distribution of the dependent variable and the three independent variables.

The dependent variable $GenEl2004$ and the independent variable $Unempl$, $Age 25\_44$, $LowEduc$ are $y, x_2, x_3, x_4$, respectively, $x_1 = 1$ as intercept terms. We use the spatially varying coefficient models to fit the data as follows:

Figure 4 summarizes estimated coefficient functions using the adaptive method, LL, and GWR respectively, which are considerably in space. Figure 7(a) shows a residual QQ-plot of the Dublin voter turnout via the adaptive method. From the plot, we can see that the distribution of the residual is very close to normal.

To evaluate the prediction accuracy of the adaptive method, we set aside 50 observations for comparing the mean squared prediction error (MSPE) of the adaptive method, LL, and GWR. The MSPE is computed as follows:

where $m = 50$ and $\hat{y}_j = \hat{\beta}_1({\mathit{\boldsymbol{u}}}_j)+\sum_{k = 2}^{4}\hat{\beta}_p({\mathit{\boldsymbol{u}}}_j)x_{jk}$. The MSPE values by three methods are comparable, which are 0.018, 0.015 and 0.017, respectively. The QQ-plot of residuals from the Fingure 7(a) are close to the normal distribution, which explains why the MSPE of the adaptive method is very close to the MSPE of the GWR and the LL.

Example 2. (England and Wales House Price Data) England and Wales house price data is publicly available in the R package GWmodel. The dataset includes 10 variables, namely: house sale price $(PurPrice)$, $BldIntWr$, $BldPostW$, $bld 60$, $bld 70$, $bld 80$, $TypDetch$, $TypSemiD$, $TypFlat$ and floor area $(FlrArea)$. With the exception of the floor area $(FlrArea)$, all independent variables are indicative variables (1 or 0). Figure 5 is shown Spatial distribution of $PurPrice$ and $FlrArea$.

We take the house sale price ($y$) as the dependent variable, FlrArea($x_2$) as the independent variable, $x_1 = 1$ as the intercept term, and the spatially varying coefficient models of the fitted data is:

The estimated coefficient function is shown in Figure 6, and Figure 7(b) shows a residual QQ plot via adaptive method for England and Wales house price data. Similar to the analysis in example 1, we set aside 50 observations as the test set. The MSPE of the adaptive approach, LL and GWR are 0.302, 0.339 and 0.548, respectively. The QQ-plot of residuals from the above fit showed a clear deviation from normality, which explains why the MSPE from the adaptive approach is smaller than LL and GWR.

5.   Concluding remarks

In this article, we proposed an adaptive estimation for spatially varying coefficient models. The new estimation procedure can adapt to different errors and improve estimation efficiency than the LL and the GWR method. Simulation studies and two real data applications confirmed our theoretical findings.

The proposed method in this article can be easily extended to semiparametric varying-coefficient partially linear models, where some coefficients in the model are assumed to be constant and the remaining coefficients are allowed to spatially vary across the studied region. Another interesting future work is the spatiotemporal extension to analyze data collected across time and space.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant No. 11871173), the National Statistical Science Research Project (Grant No. 2020LZ09).

Conflict of interest

The authors declare that there is no conflict of interest.

A.   Appendix

This section will give proofs of propositions 2.1, theorem 2.1 and theorem 2.2, with the required regular conditions as follows:

$1)$ $K(\cdot)$ is bounded, symmetric, and has bounded support and bounded derivatives;

$2)$ $\{ {\bf{x}}_i\}_{i = 1}^{n}$, $\{ {\mathit{\boldsymbol{u}}}_i\}_{i = 1}^{n}$, $\{\varepsilon_i\}_{i = 1}^{n}$ are independent and identically distributed and $\{\varepsilon_i\}_{i = 1}^{n}$ is independent of $\{ {\bf{x}}_i\}_{i = 1}^{n}$ and $\{ {\mathit{\boldsymbol{u}}}_i\}_{i = 1}^{n}$. In addition, the independent variable ${\bf{x}}$ has bounded support;

$3)$ The probability density function $f(\varepsilon)$ of $\varepsilon$ has fourth-order bounded continuous derivative. Assume $E[\rho'(\varepsilon)] = 0$, $E[\rho''(\varepsilon)] < \infty$, $E[\rho'(\varepsilon)^2] < \infty$ and $\rho'''(\cdot)$ is bounded;

$4)$ The marginal density $q({\mathit{\boldsymbol{u}}})$ of ${\mathit{\boldsymbol{u}}}$ has a continuous second derivative in some neighborhood of ${\mathit{\boldsymbol{u}}}_0$ and $q({\mathit{\boldsymbol{u}}}_0)\neq0$;

$5)$ $h\rightarrow0$, when $n\rightarrow \infty$, $nh\rightarrow \infty$, $h_0 = h/\log(n)$;

$6)$ $\beta_k(\cdot), k = 1, \cdots, p$ has bounded and continuous third derivative.

Proof of propositions 2.1: Note that

where

From Jensen's inequality,

Based on the properties of step M of formula (2.9), it is proved that $Q ({\mathit{\boldsymbol{\theta}}} ^ {(k+1)}) - Q ({\mathit{\boldsymbol{\theta}}} ^ {(k)}) \geq 0$.

Proof of theorem 2.1: According to the the result of Linton and Xiao ^[25], the asymptotic behaviour of $\hat{ {\mathit{\boldsymbol{\theta}}}}$ in (7) is the same as that obtained from (4). Therefore, we prove the asymptotic properties of $\hat{ {\mathit{\boldsymbol{\theta}}}}$ based on (2.3).

Denote ${\mathit{\boldsymbol{\theta}}}^* = {\mathit{\boldsymbol{H}}} {\mathit{\boldsymbol{\theta}}}$, ${\mathit{\boldsymbol{x}}}_i^* = \left(x_{i1}, \cdots, x_{ip}, (\frac{ {\mathit{\boldsymbol{u}}}_i- {\mathit{\boldsymbol{u}}}_0}{h})^\top x_{i1}, \cdots, (\frac{ {\mathit{\boldsymbol{u}}}_i- {\mathit{\boldsymbol{u}}}_0}{h})^\top x_{ip}\right)^\top$, $K_i = K_h(\vert| {\mathit{\boldsymbol{u}}}_i- {\mathit{\boldsymbol{u}}}_0\vert|)$, $R({\mathit{\boldsymbol{u}}}_i, {\mathit{\boldsymbol{x}}}_i) = \sum_{k = 1}^p\beta_k({\mathit{\boldsymbol{u}}}_i)x_{ik}-\sum_{k = 1}^p \{b_k+\mathit{\boldsymbol{c}}_k ({\mathit{\boldsymbol{u}}}_i- {\mathit{\boldsymbol{u}}}_0)\}x_{ik}$, and $a_n = (nh^2)^{-1/2}+h^2$. Let $\rho(\cdot) = \log f(\cdot)$, objective function (2.3) is written as

Based on the definition of ${\mathit{\boldsymbol{\theta}}}^*$, it is sufficient to show that for any given $\eta > 0$, there exists a large constant $c$ such that

where $\mu$ has the same dimension as ${\mathit{\boldsymbol{\theta}}}$, $a_n$ is the convergence rate. By using Taylor expansion, it follows that

where $z_i$ is a value between $\varepsilon_i+R({\mathit{\boldsymbol{u}}}_i, {\mathit{\boldsymbol{x}}}_i)-a_n\mu^\top {\mathit{\boldsymbol{x}}}_i^*$ and $\varepsilon_i+R({\mathit{\boldsymbol{u}}}_i, {\mathit{\boldsymbol{x}}}_i)$.

For $I_1 = -\frac{1}{n}\sum_{i = 1}^n K_i\rho'(\varepsilon_i+R({\mathit{\boldsymbol{u}}}_i, {\mathit{\boldsymbol{x}}}_i))a_n\mu^\top {\mathit{\boldsymbol{x}}}_i^*$, Let $\delta_1 = E[\rho''(\varepsilon_i)]$. Since $R({\mathit{\boldsymbol{u}}}_i, {\mathit{\boldsymbol{x}}}_i) = \sum_{k = 0}^p\beta_k({\mathit{\boldsymbol{u}}}_i)x_{ik}-\sum_{k = 0}^p \{b_k+\mathit{\boldsymbol{c}}_k ({\mathit{\boldsymbol{u}}}_i- {\mathit{\boldsymbol{u}}}_0)\}x_{ik} = O_p(h^2) = o_p(1)$ and $E[\rho'(\varepsilon)] = 0$, so

By using $\mu^\top {\mathit{\boldsymbol{x}}}_i^* \leq \|\mu\| \cdot \|{\mathit{\boldsymbol{x}}}_i^*\|$, we have $E(I_1) = O(a_nh^2)$.

where $A = K_i\rho'(\varepsilon_i+R({\mathit{\boldsymbol{u}}}_i, {\mathit{\boldsymbol{x}}}_i))a_n\mu^\top {\mathit{\boldsymbol{x}}}_i^*$. Let $\delta_2 = E[\rho'(\varepsilon_i)^2]$, then

Note that ${\mathit{\boldsymbol{x}}}_i^* {\mathit{\boldsymbol{x}}}_i^{*\top} = \left(x_{ij}x_{ik}(\frac{ {\mathit{\boldsymbol{u}}}_i- {\mathit{\boldsymbol{u}}}_0}{h})^l((\frac{ {\mathit{\boldsymbol{u}}}_i- {\mathit{\boldsymbol{u}}}_0}{h})^{l'})^\top\right)_{1 \leq j, k\leq p; l, l' = 0, 1}$, $\Gamma_{jk}({\mathit{\boldsymbol{u}}}_i) = E(x_{ij}x_{ik}\vert {\mathit{\boldsymbol{u}}}_i)$, $\int_{R^2} {\mathit{\boldsymbol{u}}} K(\| {\mathit{\boldsymbol{u}}}\|)d {\mathit{\boldsymbol{u}}} = {\bf{0}}_{2\times1}$, $\int_{R^2} {\mathit{\boldsymbol{u}}} {\mathit{\boldsymbol{u}}}' {\mathit{\boldsymbol{u}}} K(\| {\mathit{\boldsymbol{u}}}\|)d {\mathit{\boldsymbol{u}}} = {\bf{0}}_{2\times1}$, $\int_{R^2}u_1u_2K(\| {\mathit{\boldsymbol{u}}}\|)d {\mathit{\boldsymbol{u}}} = {\bf{0}}_{2\times1}$, for $1 \leq j, k\leq p$, then

The second equation follows the Taylor expansion, and the assumption $\varepsilon$ is independent of ${\mathit{\boldsymbol{u}}}$ and ${\mathit{\boldsymbol{x}}}$. Then, $E\{E[{\mathit{\boldsymbol{x}}}_i^* {\mathit{\boldsymbol{x}}}_i^{*\top} \vert {\mathit{\boldsymbol{u}}}_i]K_i^2\} = \frac{1}{h^2}q({\mathit{\boldsymbol{u}}}_0){\bf{\Lambda}}$, where ${\bf{\Lambda}} = diag(1, \nu_2, \nu_2)\otimes {\bf{\Gamma}}({\mathit{\boldsymbol{u}}}_0)$ is a $3p \times 3p$ matrix. Thus,

Note that $[E(A)]^2 = [E(I_1)]^2 = [O(a_nh^2]^2 \ll E(A^2)$, then $var(I_1)\approx\frac{1}{n}[E(A)]^2 = O(a_n^2\frac{1}{nh^2})$. Hence,

Similarly,

and

Assume $\delta_1 > 0$, we can choose $c$ large enough such that $I_1+I_2+I_3 < 0$ with probability at least $1-\eta$. Thus $P\left\{\mathop{\sup}\limits_{\|\mu\| = c}L({\mathit{\boldsymbol{\theta}}}^*+a_n\mu) < L({\mathit{\boldsymbol{\theta}}}^*)\right\} \geq 1-\eta$.

Proof of theorem 2.2: Since $\hat {\mathit{\boldsymbol{\theta}}}^*$ maximizes $L({\mathit{\boldsymbol{\theta}}}^*)$, then $L'(\hat {\mathit{\boldsymbol{\theta}}}^*) = 0$. By Taylor expansion,

thus

For $L''({\mathit{\boldsymbol{\theta}}}^*)$, since $L({\mathit{\boldsymbol{\theta}}}^*) = \frac{1}{n}\sum_{i = 1}^n K_i\rho(y_i- {\mathit{\boldsymbol{\theta}}}^{*\top}{\mathit{\boldsymbol{x}}}_i^*)$, and $y_i- {\mathit{\boldsymbol{\theta}}}^{*\top}{\mathit{\boldsymbol{x}}}_i^* = \varepsilon_i+R({\mathit{\boldsymbol{u}}}_i, {\mathit{\boldsymbol{x}}}_i$), then $L''({\mathit{\boldsymbol{\theta}}}^*) = \frac{1}{n}\sum_{i = 1}^n K_i\rho''(\varepsilon_i+R({\mathit{\boldsymbol{u}}}_i, {\mathit{\boldsymbol{x}}}_i)){\mathit{\boldsymbol{x}}}_i^* {\mathit{\boldsymbol{x}}}_i^{*\top}$, and the expectation is

where ${\mathit{\boldsymbol{S}}} = diag(\gamma_{01}, \gamma_{21}, \gamma_{21})\otimes {\bf{\Gamma}}({\mathit{\boldsymbol{u}}}_0)$, the last equation follow (A.1). In this study, we consider the element-wise variance of a matrix, then

Based on the result $L''({\mathit{\boldsymbol{\theta}}}^*) = E[L''({\mathit{\boldsymbol{\theta}}}^*)] + O_p{\sqrt{var[L''({\mathit{\boldsymbol{\theta}}}^*)]}}$ and the assumption $nh \rightarrow \infty$, it follows that $L''({\mathit{\boldsymbol{\theta}}}^*) = \delta_1 q({\mathit{\boldsymbol{u}}}_0){\mathit{\boldsymbol{S}}} (1+o_p(1))$.

For $L'({\mathit{\boldsymbol{\theta}}}^*)$,

The asymptotic result is determined by ${\mathit{\boldsymbol{w}}}_m$. Next, calculating the order of $\mathit{\boldsymbol{\nu}}_n$.

For $R({\mathit{\boldsymbol{u}}}_i, {\mathit{\boldsymbol{x}}}_i) x_i^*$, since $\beta'''_j(\cdot)$ is bounded, then we have

where $\mathcal{H}_{\beta_k}$ is Hessian matrix. By ${\mathit{\boldsymbol{x}}}_i^* = (x_{i1}, \cdots, x_{ip}, (\frac{ {\mathit{\boldsymbol{u}}}_i- {\mathit{\boldsymbol{u}}}_0}{h})^\top x_{i1}, \cdots, (\frac{ {\mathit{\boldsymbol{u}}}_i- {\mathit{\boldsymbol{u}}}_0}{h})^\top x_{ip})^\top$,

The expectation about the first item is

and the expectation on second item is

then

where $\mathit{\boldsymbol{\psi}}_k = \binom{\gamma_{21}}{{{\bf{0}}}_{2 \times 1}}\otimes (\Gamma_{kj}({\mathit{\boldsymbol{u}}}_0))_{1\leq j \leq p}^\top$ is a $3p \times 1$ vector for $j = 1, \cdots, p$. Since $var(\mathit{\boldsymbol{\nu}}_n) = \frac{1}{n} var\{K_i\rho''(\varepsilon_i)R({\mathit{\boldsymbol{u}}}_i, {\mathit{\boldsymbol{x}}}_i)){\mathit{\boldsymbol{x}}}_i^*\} = O(h^2/n)$, then based on the result $\mathit{\boldsymbol{\nu}}_n = E(\mathit{\boldsymbol{\nu}}_n) + var(\sqrt{\mathit{\boldsymbol{\nu}}_n})$ and the assumption $nh \rightarrow \infty$, it follows that

Then

For ${\mathit{\boldsymbol{w}}}_n$, based on the assumption $E[\rho'(\varepsilon_i)] = 0$, we can easily get $E({\mathit{\boldsymbol{w}}}_n)$ = 0, and

Based on Lyapunov Central Limit Theorem, we have the following result

By $\delta_ 1^{-1} = \delta_ 2$, the theorem is proved.