Under nonlinear prey-harvesting, effect of strong Allee effect on the dynamics of a modified Leslie-Gower predator-prey model

1.   Introduction

The future of human civilization depends on sustainable natural resources such as forestry, wildlife, marine life, and many more, as they not only provide food, energy, medicines, and other necessities for the human population but also help to regulate the Earth's biodiversity. The increasing food demand has led to an increase in the exploitation of these resources, which is exerting a negative impact on the environment. As a result, it is critical to devise harvesting tactics that maximize economic rewards while simultaneously considering the ecological-health of the related ecological-system. Predator-prey interactions, which are ubiquitous in nature, have a wide-ranging impact on our biological-system. Lotka ^[1] and Volterra ^[2] devised separately the first mathematical model to examine predator-prey interactions, and later it was referred to as the Lotka-Volterra predator-prey model. In the conceptualization of this model, all the components, like growth rate, predator's mortality rate and altering the rate of prey biomass into predator reproduction, are assumed to be linear functions ^[3], but predator-prey interactions depend on nonlinear components in nature. As a consequence, the model fails to account for specific real-world scenarios, so a number of improvements have been suggested by researchers. Leslie and Gower devised the Leslie-Gower predator-prey (LGPP) model ^[4], where the growth function of predator species is distinct from the predation function of predator species. In ^[5], the authors have investigated this model and found that for all ecologically acceptable parameters, there exists a unique, globally asymptotically stable, co-existing equilibrium point. Aziz-Alaoui and Okiye ^[6] enhanced the realism of this model, and later it was termed the modified Leslie-Gower prey-predator (MLGPP) model.

Multiple biological resources are being overused because of the increasing demand for food and other supplies. However, protecting the environment as a whole is a topic of concern on a worldwide scale. In light of these two opposing realities, it is necessary for the commercial use of renewable biological resources, such as fisheries and forestry, to be managed scientifically and to search for a sustainable development strategy. In 1976, Clark ^[7] made the first attempt to develop a mathematical model to examine the challenges and strategies of harvesting renewable natural resources. In mathematical ecology, harvesting is classified into three forms: constant harvesting, linear harvesting and nonlinear harvesting; see ^[8,9]. The nonlinear harvesting is one of the most feasible options ^[9,10]. Hu and Cao ^[11] examined a predator-prey system in which non-linear harvesting regulates the proliferation of predator species. They obtained certain parametric conditions for the existence of several bifurcations: namely, Hopf bifurcation, transcritical bifurcation, saddle-node bifurcation and Bogdanov-Takens bifurcation. The qualitative behavior of a ratio-dependent Holling-Tanner predator-prey system with prey harvesting of nonlinear type was examined by Singh and Bhadauria ^[12], where the system's behavior in the neighborhood of its origin was studied and found to be non-hyperbolic. Abid et al. ^[13] examined the dynamics of a harvested MLGPP model. Al-Momen and Naji ^[14] investigated the impact of the fear effect on the dynamics of a harvested MLGPP model.

W. C. Allee ^[15] suggested an inspiring biological phenomenon termed the Allee effect (mechanism that results in a positive association between an aspect of the individual's fitness and the density/quantity of conspecifics) or negative competition effect ^[16]. It is a widespread phenomenon in many animals that can be caused by a variety of reasons ^[17]. One of the key reasons is that it is difficult to find partners within the same species in the case of low population density. The Allee effect enhances the likelihood of local/global extinction of a predator-prey system ^[18]. In recent decades, many mathematicians/ecologists have employed the Allee effect to improve the realism of mathematical models. AlSharawi et al. ^[19] provided experimental evidence of the Allee effect in a range of natural species. Based on how much the per capita growth rate is slowed down for the low population densities, the Allee effect is classified in two classes: strong Allee effect (in case the per capita growth rate is negative at the limit of low density) and weak Allee effect (in case the per capita growth rate is positive at zero density) ^[20,21]. In the literature, a lot of research demonstrated that the Allee effect makes a predator-prey system more dynamic and fascinating, providing new insights into the connections between the two species ^[22,23]. When the proliferation of prey species is subjected to the double Allee effect, Singh et al. ^[24] examined how this affects the stability and bifurcations of the MLGPP model. Feng and Kang ^[25] reported a comprehensive qualitative study of the MLGPP model that assumes the Allee effect influences the proliferation of both species. In ^[26], a comprehensive study of a modified Volterra predator-prey model in which the prey population is growing under the influence of the double Allee effect has been provided. One of the most interesting results they found was that the Allee effect can change the number of limit cycles. A Holling-Tanner predator-prey system was investigated by Arancibia-Ibarra et al. ^[27], where prey species experience a strong Allee effect. Recently, Zhu et al. ^[28] improved the MLGPP model by incorporating the Allee effect and analyzed its qualitative behaviors.

In the present study, the MLGPP model is made more realistic by incorporating nonlinear prey harvesting and a strong Allee-effect within the prey species. The remaining part of the paper is laid out as shown below. The described model is developed in Section 2. Additionally, the solutions to the model are analyzed for their positivity as well as their boundedness. Section 3 deals with the emergence of system equilibrium points and their local stability. In Section 4, two local bifurcations (saddle node and Hopf bifurcations), the nature of Hopf-bifurcating periodic solutions and a global bifurcations (Bogdanov-Takens bifurcation) are examined. The analytical findings are verified numerically in Section 5. In Section 6, the combined impact of nonlinear harvesting and the Allee effect on the dynamics of the MLGPP system is reported. Finally, the results obtained with biological conclusions are discussed in Section 7.

2.   Model formulation and basic properties

2.1.   Model formulation

Gupta and Chandra ^[8] proposed the following continuous-time two species MLGPP model, where prey growth is governed by nonlinear harvesting:

where, at time $t$, $u = u(t)$ and $v = v(t)$ denote the densities of prey and predator, respectively. All parameter values ($r, s, a_1, sa_2, n, K, E$ and $q$) are positive and have the following ecological meanings: $r$ and $s$ are the maximum specific growth rates of prey and predator, $a_1$ is the encounter rate of predators, $n$ is the degree to which the ecosystem protects prey and predator, $K$ is the carrying capacity for the prey species, $sa_2$ is the maximum value of the per capita decreasing rate of the predator, $E$ represents harvesting effort, and $q$ represents the catchability coefficient. Further, $m_1$ and $m_2$ are suitable constants. Here, the authors assumed that the degree of the environment's protection is equal for both species. Consider that the growth of the first species of system (2.1) is subjected to a strong Allee effect. This consideration leads to the following form:

where $(u-M)$ stands for Allee effect, and $-K \leq M < K$ is its threshold value. This variable determines how much the Allee effect affects the system. Since the strong Allee effect is of interest in this study, so we have $0 < M\leq K$. Consider the following transformations to make the analysis easier.

The system (2.2) transforms into the following non-dimensionalized system:

where $a = \frac{n}{K}, \; m = \frac{M}{K}, \; \beta = \frac{a_1}{a_2r K }, \; h = \frac{qE}{r m_2K^2}, \; \gamma = \frac{s}{r}, \; c = \frac{m_1E}{m_2 K}$.

Consider $dt = Kd\tau$ and $\gamma = K \rho$ to eliminate the parameter $K$ from the system (2.3), and we get

2.2.   Positivity/Boundedness

Some results are provided to confirm that the proposed system is well posed.

Lemma 2.1. (a) Let $\left(x(t), \; y(t)\right)$ be a solution behavior of model (2.4) with initial conditions (I-Cs) $x(0) > 0, \; y(0) > 0$. Then, $x(t) > 0, \; y(t) > 0, \; \; \forall t \geq 0$.

(b) Each solution of the model Eq (2.4) with the I-Cs starting in the positive quadrant is bounded for every $t \geq 0.$

Proof. ${\rm{(a)}}$ The prey and predator behavior for the model Eq (2.4) can be evaluated as follows:

and

From (2.5) one can see that for all $t \geq 0$ the solution $x(t)$ will be non-negative whenever I-C $x(0)$ is non-negative. The similar finding for predator species, $y(t)$, holds true from (2.6), so the set $R^2_+$ = $\{(x, y) : x, y \geq 0\}$ is an invariant set.

(b) Suppose $\left(x(t), \; y(t)\right)$ is a non-negative solution behavior of the model Eq (2.4), among them the behavior of prey species is as follows:

For the sake of convenience, take $F\Big(x(z), y(z)\Big) = \left((1-x(z))(x(z)-m)-\frac{\beta y(z)}{a+x(z)}-\frac{h}{c+x(z)}\right)$.

Now, we have the two cases that are explained below:

Case ($i$) When $x(0) \leq 1$. Our goal is to show $x(t) \leq 1, \; \; \forall\; \; t \geq 1$.

Suppose that our claim is not correct. In this case, two positive reals, say, $t_1$ and $t_2$, exist ($t_2 > t_1$) with the property that $x(t_1) = 1$, $x(t) > 1, \; \forall t \in (t_1, t_2).$ This yields

Equation (2.8) leads to

As $F\Big(x(t), y(t) \Big) < 0, \; \forall t \in (t_1, t_2)$, we have a contradiction, and our claim is accepted.

Case ($ii$) When $x(0) > 1.$ Clearly, $F\Big(x(t), y(t) \Big) < 0$ whenever $\; x(t)\geq 1,$ so, as long as $x(t) \geq 1$,

From cases (ⅰ) and (ⅱ), we get

Inequality (2.9) with the predator equation in (2.4) leads to

The inequality (2.10) implies

Hence the result.

3.   Equilibria and the conditions for their stability

3.1.   Equilibria and their existence

This portion deals with the number of feasible equilibria admitted by model (2.4). The nullclines of model (2.4) are given by

Thus, the model (2.4) always admits the trivial equilibrium point $E_0 = (0, 0)$ and the prey free equilibrium point $E_5 = (0, a)$. In addition to the above, two types of equilibrium points are evaluated as follows:

$(i)$ Predator Free Equilibrium Points: $E_i = (x_i, 0)$, where $x_i$ can be evaluated by the cubic equation

where $T(c, m) = 1-c+m$, and $L(c, m) = c(1+m)-m.$ Descartes' sign rule assures that Eq (3.2) always has a negative root if any of the conditions $i) \; T > 0, L \geq 0, \; \; ii)\; T > 0, L \leq 0$ and $iii)\; T \leq 0, L > 0$ holds true.

Let us assume this negative root to be $x_1 = -\alpha, \; \alpha > 0$. To obtain the other two roots of the Eq (3.2), we divide it by $(x+\alpha)$, and consequently, the following quadratic equation is obtained.

$(ii)$ Interior Equilibrium Points: $E^*_i = (x_i^*, \; a+x_i^*)$, where $x_i^*$ is the root of the cubic equation

where $T(c, m) = 1- c + m$, and $R(c, m, \beta) = (1+m)c - m -\beta.$ Descartes' sign rule assures that Eq (3.4) always admits a negative root if any of the conditions $i)$ $T > 0, R \geq 0, \; \; ii)$ $T > 0, R \leq 0$ and $iii)$ $T \leq 0, R > 0$ holds true. Let us assume the negative root to be $x^*_1 = -\xi, \; \xi > 0$, and the remaining two roots are obtained by finding the roots of the following quadratic equation, obtained by dividing Eq (3.4) by $x^*+\xi$:

Take $\Delta_1 = \Big(\alpha+T(c, m)\Big)^2-4\Big(\alpha\Big(\alpha+T(c, m)\Big)-L(c, m)\Big),$ $\Delta_2 = \Big(\xi+T(c, m)\Big)^2-4\Big(\xi\Big(\xi+T(c, m)\Big)-R(c, m, \beta)\Big)$, $\alpha^* = \frac{-T(c, m)+2\sqrt{T^2(c, m)+3L(c, m)}}{3},$ and $\xi^* = \frac{-T(c, m)+2\sqrt{T^2(c, m)+3R(c, m, \beta)}}{3},$ provided $L(c, m) \geq 0$ and $R(c, m, \beta) \geq 0$.

As a summary of the preceding discussion, we get the following.

Lemma 3.1. If any of the conditions i) $T > 0, L \geq 0,$ ii) $T > 0, L \leq 0$ and $iii)$ $\; T \leq 0, L > 0$ holds true, then the model Eq (2.4) has

$(a)$ no predator-free point of equilibrium whenever $\alpha > \alpha^*,$

$(b)$ a unique predator-free point equilibrium $E_2(x_2, 0)$ whenever $\alpha = \alpha^*,$ where $x_2 = \frac{1-c+m+\alpha}{2},$ and

$(c)$ two distinct predator-free point equilibrium points $E_3(x_3, 0)$ and $E_4(x_4, 0)$ whenever $0 < \alpha < \alpha^*,$ where $x_3 = \frac{\alpha + T(c, m)+\sqrt{\Delta_1}}{2},$ and $x_4 = \frac{\alpha+T(c, m)-\sqrt{\Delta_1}}{2}.$

Lemma 3.2. If any of the conditions i) $T > 0, R \geq 0,$ ii) $T > 0, R \leq 0$ and $iii)$ $\; T \leq 0, R > 0$ holds true, then the model (2.4) has

$(a)$ no interior point of equilibrium whenever $\xi > \xi^*,$

$(b)$ a unique interior equilibrium point $E^*_2(x^*_2, a+x^*_2)$ if $\xi = \xi^*,$ where $x^*_2 = \frac{1-c+m+\alpha^*}{2},$

$(c)$ two distinct interior equilibrium points $E^*_3(x^*_3, a+x^*_3)$ and $E^*_4(x^*_4, a+x^*_4)$ if $0 < \xi < \xi^*,$ where $x^*_3 = \frac{\alpha^*+T(c, m)+\sqrt{\Delta_2}}{2}$ and $x^*_4 = \frac{\alpha^*+T(c, m)-\sqrt{\Delta_2}}{2}.$

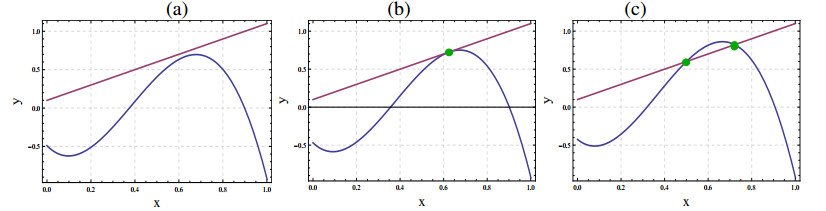
Using the conditions of Lemma 3.2, Figure 1 depicts the numbers of interior equilibrium points.

3.2.   Local stability analysis

This portion deals with the linearization approach to examine local stability of equilibria for model (2.4).

Theorem 3.1. Always, the trivial point $E_0$ is a saddle.

Proof. The Jacobian matrix of model (2.4) at $E_0(0, 0)$ is

whose eigenvalues are $\lambda_1 = -\frac{1}{c} (mc+h) < 0$ and $\lambda_2 = \rho > 0$. We get the result from the fact that these eigenvalues are of opposite signs.

Theorem 3.2. Always, the point $E_3$ is a saddle, whereas $E_4$ is unstable.

Proof. The Jacobian matrix for model (2.4) at an axial feasible point $E(x, 0)$ of equilibrium is given by

whose eigenvalues are $\lambda_1 = x\Big(1-2x+m+\frac{h}{(c+x)^2}\Big)$ and $\lambda_2 = \rho.$

Interpreting $x\Big(1-2x+m+\frac{h}{(c+x)^2}\Big)$ at $x_3 = \frac{1-c+m+\alpha+\sqrt{\Delta_1}}{2}$, the eigenvalue $\lambda_1 = -\frac{x_3\sqrt{\Delta_1}}{(c+x_3)}\Big(\alpha + x_3\Big) < 0$. Since the eigenvalues of the matrix $J_{E(x_3, 0)}$ are of opposite signs, the point $E_3$ is always a saddle point.

Interpreting $x\Big(1-2x+m+\frac{h}{(c+x)^2}\Big)$ at $x_4 = \frac{1-c+m+\alpha-\sqrt{\Delta_1}}{2}$, the eigenvalue $\lambda_1 = \frac{x_4\sqrt{\Delta_1}}{(c+x_4)}\Big(\alpha +x_4\Big) > 0$. Since the eigenvalues of the matrix $J_{E(x_3, 0)}$ are of positive signs, the point $E_4$ is always an unstable point.

Theorem 3.3. The equilibrium point $E_5 = (0, \; a)$ is always asymptotically stable.

Proof. The Jacobian matrix for model (2.4) at $E_5 = (0, a)$ is given by

and eigenvalues of this are $\lambda_1 = -(m+\beta+\frac{h}{c}) < 0$ and $\lambda_2 = - \rho < 0$. Since both eigenvalues are of negative sign, the point $E_5$ is always stable.

Theorem 3.4. The point $E^*_4$ is a saddle point always, while point $E^*_3$ is

(i) unstable if $x^*_3\Big(1-2x^*_3+m+\frac{\beta}{a+x^*_3}+\frac{h}{(c+x^*_3)^2}\Big) > \rho,$

(ii) stable if $x^*_3\Big(1-2x^*_3+m+\frac{\beta}{a+x^*_3}+\frac{h}{(c+x^*_3)^2}\Big) < \rho.$

Proof. The Jacobian matrix for model (2.4) at $E = (x, y)$ is

The determinant and trace of the above matrix are evaluated as

$detJ_E = \rho x\Big(2x-(1+m+\frac{h}{(c+x)^2})\Big),$ and $trJ_E = x(1-2x+m+\frac{\beta}{(a+x)}+\frac{h}{(c+x)^2}) - \rho.$

Computing $x\Big (2x-(1+m+\frac{h}{(c+x)^2})\Big)$ at $x^*_4 = \frac{1-c+m+\alpha^*-\sqrt{\Delta_2}}{2}$ yields

$x^*_4\Big(2x^*_4-(1 +m+\frac{h}{(c+x^*_4)^2})\Big) = \frac{x^*_4\sqrt{\Delta_2}}{2(c+x^*_4)}\Big(-1-m+c-3\alpha^*+\sqrt{\Delta_2}\Big)$ $= -\frac{x^*_4\sqrt{\Delta_2}}{(c+x^*_4)}\Big(\alpha^*+x^*_4\Big),$

which indicates that the determinant $\det J_{E^*_4}$ is negative, so the point $E^*_4$ is always a saddle point.

Now, interpreting $x\Big(2x-(1+m+\frac{h}{(c+x)^2})\Big)$ at $x^*_3 = \frac{1-c+m+\alpha^*+\sqrt{\Delta_2}}{2}$ yields

$x^*_3\Big(2x^*_3-(1+m+\frac{h}{(c+x^*_3)^2})\Big) = \frac{x^*_3\sqrt{\Delta_2}}{2(c+x^*_3)}\Big(1+m-c+3\alpha^*+\sqrt{\Delta_2}\Big)$ $= \frac{x^*_3\sqrt{\Delta_2}}{(c+x^*_3)}\Big(\alpha^*+x^*_3\Big),$

which shows that the determinant $detJ_{E^*_3}$ is positive, and the Routh-Hurwitz criterion confirms the conclusion.

Theorem 3.5. The equilibrium point $E_2^*$ of the model Eq (2.4) is

(i) a stable saddle node whenever $\frac{\beta x^*_2}{a+x^*_2} < \rho$ and an unstable saddle node whenever $\frac{\beta x^*_2}{a+x^*_2} > \rho,$

(ii) a cusp of codimension $2$ whenever $\frac{\beta x^*_2}{a+x^*_2} = \rho$ and $\frac{a \beta }{(a+x^*_2)^2}-\frac{2{x^*_2}^2}{(c+x^*_2)}\neq 0$.

Proof. $(i)$ Use the transformation $\check{x} = x-x^*_2, \check{y} = y-y^*_2$ in the model (2.4) to shift the equilibrium point $E_2^*$ to the origin $(0, 0)$, and the Taylor series expansion at $(0, 0)$ reduces the corresponding model equation to

where $a_{20} = \frac{a \beta }{(a+x^*_2)^2}-\frac{{x^*_2}^2 }{c+x^*_2}, \; a_{11} = -\frac{a \beta }{(a+x^*_2)^2}.$

Evidently, if $\frac{\beta x^*_2}{a+x^*_2}\neq \rho$, then the trace $\mbox{tr}J_{E^*_2} \neq 0$, but the determinant $\mbox{det}J_{E^*_2} = 0$, which confirms that the equilibrium point $E^*_2$ is a saddle node. Additionally, $\mbox{tr}J_{E^*_2} < 0$ whenever $\frac{\beta x^*_2}{a+x^*_2} < \rho$, so $E_2^*$ is a stable saddle node. $\mbox{tr}J_{E^*_2} > 0$ whenever $\frac{\beta x^*_2}{a+x^*_2} > \rho$, so the point $E_2^*$ is an unstable saddle node.

$(ii)$ Let us consider $\frac{\beta x^*_2}{a+x^*_2} = \rho$, (3.6) can be expressed as

Let us consider $\tau = \rho t$, the system (3.7) becomes

where $b_{20} = \frac{a_{20}}{\rho}, \; b_{11} = \frac{a_{11}}{\rho}.$

The system (3.8) under the transformation $\tilde{x} = \check{x}, \; \tilde{y} = \check{x}-\check{y}$ reduces to

where $\overline{b_{20}} = b_{20}+b_{11}.$ Further, under the transformation $x_1 = \tilde{x}, \; x_2 = \tilde{y}-\frac{1}{a+x^*_2}\tilde{x}\tilde{y}$, the system (3.9) reduces to

where $\overline{b_{11}} = (\frac{1}{a+x^*_2}-b_{11}).$ Finally, with the transformation $y_1 = x_1-\frac{1}{2}\overline{b_{11}}x^2_1, \; y_2 = x_2+\overline{b_{20}}x^2_1+o|(x_1, x_2)^3|$, (3.10) reduces to

As $2\overline{b_{20}} -b_{11} = \frac{1}{\rho}\Big(\frac{a\beta }{(a+x^*_2)^2}-\frac{2{x^*_2}^2}{(c+x^*_2)}\Big)\neq 0$, and $\overline{b_{20}} = -\frac{{x^*_2}^2}{\rho(c+x^*_2)}\neq 0$, $E^*_2$ is a cusp of codimension $2$ in the $xy$ plane.

4.   Bifurcation analysis

This section deals with the existence of various types of bifurcations for the model (2.4): saddle node bifurcation, Hopf bifurcations, Bogdanov-Takens bifurcation and homoclinic bifurcation.

4.1.   Saddle-node bifurcation

It is proven in Lemma 3.2 that there is a unique degenerate positive equilibrium $E^*_2 = (x^*_2, y^*_2)$ that develops as a result of the annihilation of the two internal equilibrium points $E^*_3 = (x^*_3, y^*_3)$ and $E^*_4 = (x^*_4, y^*_4)$. Thus, there is a chance of occurrence of a saddle-node bifurcation at $E^*_2 = (x^*_2, y^*_2)$. Satomayor's criterion, which is described in the following theorem, is utilized to ensure the occurrence of saddle-node bifurcation.

Theorem 4.1. The model (2.4) exhibits a saddle-node bifurcation in the vicinity of the point $E^*_2(x^*_2, y^*_2)$ w.r.t. the parameter $m$ whenever $\frac{\beta (1- c+ m+\alpha^*)}{(2a+1-c+m+\alpha^*)} \neq \rho.$

Proof. The Jacobian matrix of the model (2.4) at $E_2^*,$ is

The determinant det$J_{E_2^*} = 0$, and trace tr$J_{E_2^*} = \frac{\beta (1- c+ m+\alpha^*)}{(2a+1-c+m+\alpha^*)} - \rho$. So, we can conclude that whenever $\frac{\beta (1- c+ m+\alpha^*)}{(2a+1-c+m+\alpha^*)} \neq \rho$, one eigenvalue of $J_{E^*_{2}}$ is zero, and the other is non-zero. Let $V$ and $U$ represent eigenvectors of matrices $J_{E^*_{2}}$ and $J^{T}_{E^*_{2}},$ respectively, associated with zero-eigenvalue of the matrices. A simple computation implies

Consider,

Now,

Thus,

and

The two preceding transversality conditions for saddle-node bifurcation indicate the occurrence of saddle-node bifurcation for the model (2.4) at $E_2^*$.

Theorem 4.2. The model (2.4) exhibits a saddle-node bifurcation in the vicinity of the point $E_2(x_2, 0)$ w.r.t. the parameter $m$.

4.2.   Hopf bifurcation

It is proven in Theorem 3.4 that the point $E^*_3$ is unstable whenever $x^*_3\Big(1-2x^*_3+m+\frac{\beta}{a+x^*_3}+\frac{h}{(c+x^*_3)^2}\Big) > \rho$, and it is stable whenever $x^*_3\Big(1-2x^*_3+m+\frac{\beta}{a+x^*_3}+\frac{h}{(c+x^*_3)^2}\Big) < \rho$. It is now fascinating to look into the property of the point when $x_3^*\Big(1-2x_3^*+m+\frac{\beta}{(a+x_3^*)}+\frac{h}{(c+x_3^*)^2}\Big)-\rho = 0$. For this parametric condition, tr$(J_{E_3^*}) = 0$, whereas det$(J_{E_3^*}) > 0$, which leads to the appearance of the Hopf bifurcation at $E^*_3$.

Theorem 4.3. The model (2.4) experiences a Hopf bifurcation around the point $E_3^*$ w.r.t. the parameter $\rho$ in the presence of the parametric condition $x_3^*\Big(1-2x_3^*+m+\frac{\beta}{(a+x_3^*)}+\frac{h}{(c+x_3^*)^2}\Big)-\rho = 0$.

Proof. For $\rho = x_3^*\Big(1-2x_3^*+m+\frac{\beta}{(a+x_3^*)}+\frac{h}{(c+x_3^*)^2}\Big),$ we get det$J_{E_3^*} > 0,$ tr$J_{ E_3^*} = x_3^* \Big(1-2x_3^*+m+\frac{\beta}{(a+x_3^*)}+\frac{h}{(c+x_3^*)^2}\Big)-\rho$, and $\frac{d}{d \rho}\Big(trJ_{E_3^*}\Big)\Big|_{\rho = \rho^{[hf]}} = -1$.

This confirms that the transversality conditions of Hopf bifurcation hold true, and the model (2.4) undergoes a Hopf bifurcation around $E_3^*$ w.r.t. the parameter $\rho$.

The above theorem ensures the existence of a limit cycle. Next, the first Lyapunov coefficient is computed for model (2.4) at $E_3^*$ to examine the stability of the limit cycle.

Take $x = \bar{x}-x_3^*$, $y = \bar{y}-y_3^*$ to shift the equilibrium $E_3^*$ to the origin $(0, 0)$, and the model (2.4) reduces to

where, $a_{10} = x_3^*-2 {x_{3}^{*}}^{2}+m x_3^*+\frac{\beta x_3^*y_3^*}{(a+x_3^*)^2}+\frac{ h x_3^*}{(c+x_3^*)^2},$ $a_{01} = \frac{- \beta x_3^*}{(a+x_3^*)},$ $a_{20} = (1-x_3^*)+\frac{\beta y_3^*}{(a+x_3^*)^2}+\frac{h }{(c+x_3^*)^2}-(x_3^*-m)-x_3^*-\frac{\beta x_3^*y_3^*}{(a+x_3^*)^3}-\frac{ h x_3^*}{(c+x_3^*)^3},$ $a_{11} = \frac{- \beta a}{(a+x_3^*)^2},$ $a_{02} = 0,$ $a_{30} = \frac{\beta x_3^*y_3^*}{(a+x_3^*)^4}+\frac{ h x_3^*}{(c+x_3^*)^4}-\frac{h }{(c+x_3^*)^3}-\frac{\beta y_3^*}{(a+x_3^*)^3} - 1,$ $a_{21} = \frac{\beta a}{(a+x_3^*)^3},$ $a_{12} = 0,$ $a_{03} = 0,$ $b_{10} = \frac{\rho {y_3^*}^2}{(a+x_3^*)^2},$ $b_{01} = \frac{-\rho y_3^*}{(a+x_3^*)},$ $b_{20} = \frac{-\rho {y_3^*}^2}{(a+x_3^*)^3},$ $b_{11} = \frac{2\rho y_3^*}{(a+x_3^*)^2},$ $b_{02} = \frac{-\rho }{(a+x_3^*)},$ $b_{30} = \frac{\rho {y_3^*}^2}{(a+x_3^*)^4},$ $b_{21} = \frac{-2\rho y_3^*}{(a+x_3^*)^3},$ $b_{12} = \frac{\rho }{(a+x_3^*)^2},$ $b_{03} = 0$, $f_1(\bar{x}, \bar{y}) = \sum_{i+j = 4}^\infty a_{ij}\bar{x}\bar{y},$ $f_2(\bar{x}, \bar{y}) = \sum_{i+j = 4}^\infty b_{ij}\bar{x}\bar{y}.$

As a result, the first Lyapunov number $\sigma$ at the origin is evaluated as in Perko ^[29], as follows:

$\sigma = \frac{-3\pi}{2 a_{01}\Delta^{3/2}}[a_{10}b_{10}({a_{11}}^2+$$a_{11}b_{02}+a_{02}b_{11})+a_{10}a_{01}({b_{11}}^2+a_{20}b_{11}+$$a_{11}b_{02}) +{b_{10}}^2(a_{11}a_{02}+$$2a_{02}b_{02})-2a_{10}b_{10}({b_{02}}^2-a_{20}a_{02})-$$2a_{10}a_{01}({a_{20}}^2-b_{20}b_{02})-{a_{01}}^2(2a_{20}b_{20}+b_{11}b_{20})+$$(a_{01}b_{10}-2{a_{10}}^2)(b_{11}b_{02}-a_{11}a_{20})]-$$({a_{10}}^2+a_{01}b_{10})[3(b_{10}b_{03}-$$a_{01}a_{30})+2a_{10}(a_{21}+b_{12})+(b_{10}a_{12}-a_{01}b_{21})],$ where $\Delta = \rho x_3^*\Big(2x_3^*-(1+m+\frac{h}{(c+x_3^*)^2})\Big).$

An unstable limit cycle appears around $E^*_3$ whenever $\sigma > 0$; otherwise, a stable limit cycle appears around $E^*_3$.

4.3.   Bogdanov-Taken bifurcation

The Jacobian matrix of model (2.4) at $E_2^* = (x_2^*, y_2^*)$ is

det$(J_{E_2^*}) = 0$, whereas the trace tr$(J_{E_2^*}) = 0$, under the parametric condition $\frac{\beta x_2^*}{(a+x_2^*)} = \rho$. As a result of this, the non-zero Jacobian matrix $J_{E_2^*}$ has a zero-eigenvalue of multiplicity two, which means that the Bogdanov - Takens (BT) bifurcation may occur in the model (2.4). As the parameters $m, \; \rho$ play vital roles in the dynamics of the model equation, it is worthwhile to regard them as bifurcation parameters. The BT point in the parameter space is associated with the point at which the saddle-node bifurcation curve and Hopf-bifurcation curve cross. To ensure the appearance of the BT bifurcation, the non-degeneracy criteria are shown by using the technique introduced in ^[30].

Theorem 4.4. Bogdanov-Takens bifurcation occurs in the model Eq (2.4) w.r.t. bifurcation parameters $m, \; \rho$ around the instantaneous point $E_2^*$ whenever $\rho = \frac{\beta x_2^*}{(a+x_2^*)}$ and $\dfrac{a \rho }{x^*_2(a+x^*_2)}-\frac{2x^*_2(\alpha^*+x_2^*)}{(c+x^*_2)} \neq 0$.

Proof. Suppose $m, \rho$ vary in a small neighborhood of BT point $(m^{*}, \rho^{*})$ and let $(m, \rho) = (m^{*}+\lambda_1, \rho^{*}+\lambda_2)$ be a neighboring point of the BT point, where $\lambda_1, \; \lambda_2$ are very small, and the model (2.4) reduces to

Under $u_1 = x-x_2^*, u_2 = y-y_2^*$ the BT point is shifted to $(0, 0)$. As a result, the system (4.3) reduces to

where $p, q, r$ and $s$ are the Jacobian coefficients calculated at the equilibrium point $E_2^*$, and the coefficients $a_{ij}$ and $b_{ij}$ are determined by

$a_{11} = \Big[\frac{\partial^2g_1}{\partial x^2}\Big]_{(x^*_2, \; y^*_2, \; m^{*}, \; \rho^{*})} = 2\Big(\frac{a \beta}{(a+x_2^*)^2}-x^*_2-\frac{hx^*_2}{(c+x^*_2)^3}\Big)+2 \lambda_1,$

$a_{12} = \Big[\frac{\partial^2g_1}{\partial x \partial y}\Big]_{(x^*_2, \; y^*_2, \; m^{*}, \; \rho^{*})} = -\frac{a \beta }{(a+x^*_2)^2},$

$a_{22} = \Big[\frac{\partial^2g_1}{\partial y^2}\Big]_{(x^*_2, \; y^*_2, \; m^{*}, \; \rho^{*})} = 0,$

$b_{11} = \Big[\frac{\partial^2g_2}{\partial x^2}\Big]_{(x^*_2, \; y^*_2, \; m^{*}, \; \rho^{*})} = \frac{-2\rho}{(a+x^*_2)} - \frac{2\lambda_2}{(a+x^*_2)},$

$b_{12} = \Big[\frac{\partial^2g_2}{\partial x \partial y}\Big]_{(x^*_2, \; y^*_2, \; m^{*}, \; \rho^{*})} = \frac{2\rho}{(a+x^*_2)} + \frac{2\lambda_2}{(a+x^*_2)},$

$b_{22} = \Big[\frac{\partial^2g_2}{\partial y^2}\Big]_{(x^*_2, \; y^*_2, \; m^{*}, \; \rho^{*})} = \frac{-2\rho}{(a+x^*_2)} - \frac{2\lambda_2}{(a+x^*_2)}.$

Making the affine transformations $v_1 = u_1$ and $v_2 = pu_1+qu_2$, the system (4.4) reduces to

where,

$\xi_{00}(\lambda) = g_{1}(x^*_2, y^*_2, \lambda_1),$ $\xi_{10}(\lambda) = \lambda_1(2x^*_2-1), \; \; \; \xi_{01}(\lambda) = 1, \; \; \; \xi_{20}(\lambda) = a_{11}-\frac{2p}{q} a_{12}+\frac{p^2}{q^2}a_{22},$

$\xi_{11}(\lambda) = \frac{a_{12}}{q}-\frac{p}{q^2}a_{22}, \; \; \; \xi_{02}(\lambda) = \frac{a_{22}}{q^2}, \; \; \; \eta_{00}(\lambda) = p g_{1}(x^*_2, y^*_2, \lambda_1)+qg_{2}(x_2^*, y^*_2, \lambda_2),$

$\eta_{10}(\lambda) = p\lambda_1(2x^*_2-1), \; \; \; \eta_{01}(\lambda) = -\lambda_2,$

$\eta_{20}(\lambda) = \Big(pa_{11}+qb_{11}-\frac{2p}{q}(pa_{12}+qb_{12})+\frac{p^2}{q^2}(pa_{22}+qb_{22})\Big),$

$\eta_{11}(\lambda) = \Big(\frac{pa_{12}+qb_{12}}{q}-\frac{p}{q^2}(pa_{22}+qb_{22})\Big), \; \; \; \eta_{02}(\lambda) = \frac{(pa_{22}+qb_{22})}{q^2}.$

In order to ensure the existence of Bogodanov-Takens bifurcation, we examine the following non-degeneracy conditions ^[30]:

$i)$ $\left[\begin{array}{cc} p & \qquad q\\ r & \qquad s \end{array} \right] = \theta_{2\times 2},$

$ii)$ $\xi_{20}(0)+\eta_{11}(0)\neq 0,$

$iii)$ $\eta_{20}(0)\neq 0.$

The first restriction is obvious. Using the values of $a_{ij}, \; b_{ij}, \; p$ and $q$, we get

$\xi_{20}(0)+\eta_{11}(0) = \dfrac{a \rho }{x^*_2(a+x^*_2)}-\frac{2x^*_2(\alpha^*+x_2^*)}{(c+x^*_2)}.$

$\eta_{20} = -\frac{2\rho x^*_2(\alpha^*+x^*_2)}{a+x^*_2} \neq 0.$

Hence, the proof is complete.

5.   Numerical simulations

This section deals with the numerical simulations to validate the presented analytical findings. For computations and plotting phase portrait diagrams, we utilized the MATHEMATICA 10.0 software.

$1)$

From an ecological point of view, $\rho < 1$. The model (5.1) exhibits six feasible equilibrium points: $E_0 = (0, 0),$ $E_3 = (0.902701, 0) \; E_4 = (0.351066, 0),$ $E_5 = (0, 0.1), \; E^*_3 = (0.665439, 0.765439)$ and $E^*_4 = (0.583736, 0.683736)$. The natures of the equilibrium points are shown in Table 1.

$2)$

There are four axial equilibrium points, $E_0 = (0, \; 0), \; E_3 = (0.901899, \; 0), \; E_4 = (0.356186, \; 0)$ and $E_5(0, 0.1)$ in the model (5.2), along with a unique interior point $E^*_2(0.626768, 0.726768)$. Quantitatively, the points of axial equilibria are identical with the axial equilibria of the model (5.1). Unique interior equilibrium point $E^*_2$ occurs due to collision of the interior points $E^*_3$ and $E^*_4$ of model (5.1). The nature of $E^*_2$ is reported in Table 2.

$3)$

The model Eq (5.3) consists of only axial equilibrium points, and their number depends upon the parameter $m$. Table 3 records the numbers of axial equilibrium points and their natures.

$4)$

The saddle-node bifurcation curve for the model (5.4) is $m = 0.193603.$ The hopf-bifurcation curve for the model Eq (5.4) is $\rho = x_3^*(1-2x_3^*+m+\frac{0.0799}{0.08+x_3^*}+\frac{0.08}{(0.35+x_3^*)^2}).$ The intersection point of these two curves (BT point) is $(m^*, \rho^*) = (0.193603, 0.070995)$. These two curves divide the feasible region into three distinct regions: Region Ⅰ, Region Ⅱ and Region Ⅲ. The behaviors of these regions are reported in Table 4 and depicted in Figure 5.

6.   Combined influence of non-linear harvesting and Allee effect

This work deals with a MLGPP model with two important phenomena, the Allee effect and nonlinear harvesting. These two phenomena have strong impacts on the dynamics of a predator-prey system. Also, the phenomenon of the Allee effect is natural as it occurs frequently in species. It has been found that at low population density, it may enhance the risk of extinction ^[21]. On the other hand, the harvesting provides a scientific study of the exploitation of renewable resources. Thus, a predator-prey model that includes the Allee effect and non-linear harvesting in prey species is more realistic. To the best of the authors' knowledge, this is the first effort to study any predator-prey model experiencing both the Allee effect and non-linear prey harvesting.

The model (2.4) with no Allee effect undergoes a number of bifurcations, known as saddle-node bifurcation, Hopf bifurcation, transcritical bifurcation and Bogdanov-Takens bifurcation ^[8]. Meanwhile, the considered model equation with Allee effect experiences all aforesaid bifurcations except the transcritical one, but this model provides more general parametric conditions for appearance of these bifurcations. The dynamics of the populations of the model (2.4) in the $hm-$ plane have been plotted in Figure 6, which provides the maximum harvesting rate for a threshold value of Allee effect.

7.   Conclusions

In the present work, the dynamics of a harvested MLGPP model have been studied in the case of a strong Allee effect. It has been assumed that the growth of the prey species is subjected to non-linear harvesting. The analysis was simplified by the study of the equivalent system (2.4). It has been found that the model (2.4) has at most six equilibrium points, in which the trivial equilibrium point and a predator-free equilibrium are always saddle points, whereas another predator-free equilibrium point is unstable. The prey-free equilibrium point is always asymptotically stable. Ecologically speaking, predator species are always active in the ecosystem. If two interior points of equilibrium exist, then one of them is always a saddle, whereas the other's behavior depends on parametric conditions. It has been proven that this point is enclosed by unstable limit cycles in the presence of certain parametric conditions. Thus, the system exhibits bistability and oscillatory coexistence for both the populations for a given parametric domain. The first Lyapunov number has been calculated for studying the stability of limit cycles.

The equivalent model (2.4) can have 0 to 2 interior equilibrium points as the bifurcation parameter $m$ crosses a certain threshold value. The appearance of saddle-node bifurcation has been demonstrated via Sotomayor's theorem. Ecologically speaking, if $m$ is less than the maximum of the threshold value of $m$, then both species will coexist; and above that, extinction is faced by the prey species. Moreover, the model (2.4) undergoes Bogdanov-Taken bifurcation near the degenerate equilibrium point. The parameters $m$ and $\rho$ are used as bifurcation parameters, and the system is reduced to standard form. In terms of ecology, a small disturbance in the bifurcation parameters can lead to coexistence, oscillation, or even extinction. Finally, we have discussed the combined influence of the non-linear harvesting and the Allee effect, which may be useful to protect the system at low population density of prey species.

Acknowledgments

The second author is thankful to Banasthali Vidyapith for giving an opportunity and motivation to write this research paper.

Conflict of interest

The authors declare there is no conflict of interest.