Bayesian inference in epidemics: linear noise analysis

1.   Introduction

Computational models in epidemics are commonly relied upon to estimate the disease spread at fairly large spatial- and temporal scales, often referred to as scenario generation. With the increasing volumes and improved resolution of data from, e.g., mobile apps and disease testing time series from hospitals and nursing homes, predictive data-driven models formed from first principles are within reach. The accuracy of such models is ultimately limited by the specifics of the available disease surveillance data. In this paper we attempt to gain a qualitative understanding of how Bayesian inference of epidemiological parameters may be expected to perform and what the limiting factors are.

Epidemiological models are typically formed by postulating laws for the flow of individuals between different compartments in a large population and have been studied in this form for a long time. When connected with data in the form of observations, the associated inference problem is also a fairly mature field, see, e.g., ^[1,2,3]. With the increasing qualities and quantities of data, the various incarnations of data-driven modeling allow for substantially higher modeling resolution compared to traditional macroscopic approaches ^[4,5,6,7,8]. For example, individual-level contact tracing has been used to study disease spread models at various population sizes ^{[9,10,11,12,13]}. Data-driven models have allowed epidemic and endemic conditions to be investigated at a level of detail not previously possible ^[14,15,16].

The identification of the epidemiological parameters from data falls under the scope of problems formally studied in System Identification ^[17]. However, a 'system' viewpoint of epidemiological modeling is not yet standard, and identification of parameters is rather more often approached through calibration of residuals ^[5,16,18], sometimes also blending in aspects of Bayesian arguments. Fully Bayesian approaches are rarer, albeit with some exceptions ^[8,19], typically due to the technical difficulties with formulating suitable (pseudo-)likelihoods and the slow convergence associated with the conditioning of the problem. Although Bayesian inference is notably well-posed thanks to its use of prior distributions, the posterior distribution itself is often a computationally ill-conditioned object whenever strong parameter correlations are present, e.g., resulting from nearly singular maps from parameters to observables. These conditions, together with the societal importance of this modeling domain, make it relevant to reason around the limits of fully Bayesian techniques.

Fundamental questions concerning Bayesian convergence in general settings, including infinite-dimensional ones, have been treated ^[20,21], and have also been revisited with specific tools and applications in mind, e.g., Gaussian processes and other machine learning algorithms ^[22,23]. "Brittleness" ^[24,25], or high sensitivity to small perturbations have been proposed to be a problematic phenomenon under certain conditions. For applications, this points to the importance of striking a balance between the granularity of the model and the information content and level of detail of the available data.

With the specific aim of reaching qualitative conclusions for Bayesian modeling in epidemiology, we will connect some usual modeling approaches in infectious disease spread with a basic linear stochastic differential equation. We analyze the pre-asymptotic Bayesian posterior in the high-quality data regime as well as the estimate's convergence under weakly informative disease measurements. This is motivated by current trends in disease spread monitoring through for example sewage water analysis and symptoms data collection using smartphones ^[26,27].

The rest of the paper is organized as follows. In §2 we suggest the Ornstein-Uhlenbeck process as a meta-model of epidemiological models, covering various Susceptible-Infected-Recovered (SIR)-type models locally in time, during endemic as well as under epidemic conditions. In §3 we briefly analyze the posterior convergence when accurate full state measurements are available. The main results are found in §4 where we more fully develop an analysis for the case of poorly informative data. We offer some examples of relevance in §5 and a summarizing discussion is found in §6.

2.   The Ornstein-Uhlenbeck process

We connect in this section the Ornstein-Uhlenbeck process with some basic epidemiological models via linearization and quasi steady-state arguments. We also briefly discuss, by means of a backward analysis, how continuous and discrete time in this setting can be connected in probability law under a certain parameter map.

2.1.   Disease spread modeling

Epidemiological modeling typically involves ordinary differential equations (ODEs), e.g., the SIR-model which is often used to model the annual flu ^[1,28],

in terms of Susceptible, Infected, and Recovered individuals, respectively, and for a total population size $\Sigma \equiv S+I+R$. The model parameters $\beta$ and $\gamma$ define the transmission and recovery rates, and the basic reproduction number is then given by $R_0 = \beta/\gamma$, that is, the expected number of new infections resulting from a single index case ^[1].

Simplifying the SIR-model by removing the $R$-compartment one obtains the SIS-model, where the recovered state has been removed and hence effectively identified with the susceptible state,

and with the same $R_0$ as the SIR-model. It is sometimes useful to add an environmental compartment expressing the infectious pressure $\varphi$, i.e., the amount of infectious substance per unit of space. This defines the SIS$_{\text{E}}$-model ^[29], where the $E$ stands for the Environmental compartment,

where the indicated governing equation for $\varphi$ is just a basic example. The SIS$_{\text{E}}$-model is convenient to adapt to spread over a network and to detection situations involving sampling the environment ^[19]. Due to the indirect transmission the basic reproduction number now scales as a square root, with $R_0 = \sqrt{\beta/(\gamma\rho)}$.

The use of ODEs can be justified for epidemiological models in sufficiently large populations. In smaller populations, e.g., networks of small communities, stochastic variants are necessary to properly capture the underlying dynamics of the spread ^[3,30]. For example, a stochastic differential equation (SDE)-version of (2.2) was analyzed in ^[31] which essentially replaces $\beta \, dt$ by a Brownian diffused version $\beta \, dt+\eta \, dB(t)$. This has the effect of lowering the basic reproduction number to $R_0 = (\beta-\eta^2/2)/\gamma$. A first-principle stochastic approach is to rather express the dynamics as a continuous-time discrete state Markov chain (CTMC). The SIS-model above is then defined via discrete transitions with exponentially distributed waiting times,

meaning, e.g., that one infectious individual may infect one susceptible individual, and such that $\beta$ and $\gamma$ are now understood as rate parameters in the driving Poissonian processes. One can show that now $R_0 = (1-\Sigma^{-1}/2) \times \beta/\gamma$ such that consistency with the previous SDE formulation would require that $\eta^2 = \Sigma^{-1} \beta$ and hence follows from the typical Poissonian population-dependent noise scaling $\eta \propto \Sigma^{-1/2}$.

Let $P(t)$ be some given measure of the intensity of the disease, such as the absolute or relative disease prevalences, $I(t)$ or $\Sigma^{-1}I(t)$, respectively. Another alternative could be the infectious pressure $\varphi(t)$, which also informs on the current disease intensity. Gathering data from the disease spread means collecting information about $P(t)$, typically in the form of a time-series, $(F(P(t_i))_i$, say, for some measurement operator $F$. Consider endemic conditions first, that is, $P$ is considered stationary. As an ansatz, suppose

for some epidemiological potential $E$. Under endemic conditions we can expect this to be a single well potential, say,

or at least can locally be approximated by this form. This is consistent with the Ornstein-Uhlenbeck ($\mathcal{OU}$-) process ^[32],

where $X(t) \in {\bf R}$ and where the parameters of the model are $\theta = [k, \mu, \sigma] \in {\bf R}_+^3$ and in (2.6), $\alpha = k/\mu$.

As a concrete example, we may approximate the continuous-time Markov chain (2.4) by linearizing the rates around the non-trivial stationary state $I_\infty = \Sigma (1-\gamma/\beta)$ of (2.2). Similarly, the noise term $\sigma$ can be determined by inspecting the total variance of the Poissonian rates in (2.4) around this equilibrium. This yields a linear noise $\mathcal{OU}$-approximation to the state variable $I$ of the SIS-model (2.4) with parameters

where we use the approximation $R_0 = (1-\Sigma^{-1}/2) \times \beta/\gamma \approx \beta/\gamma$. Hence, with this specific interpretation of the $\mathcal{OU}$-process,

The quality of this approximation is exemplified in Figure 1; the effect of linearizing around the stationary state can be seen as a slightly too fast transient compared to the Markov chain.

During epidemic conditions we are rather sampling a transient of the process and, moreover, there are also typically many kinds of feedback involved, e.g., from minor adjustments of individual level behavior, to major societal changes and governmental intervention strategies. Although this means that there is now a greater challenge in formulating a data-centric meta-model of the situation we may still consider a window of time for which the disease spread parameters are approximately constant and such that (2.7)–(2.8) remain a relevant model of the situation. A difference is then that data is gathered out of equilibrium (hence away from $\alpha$) and presumably also under more noisy conditions with larger values of $\sigma$. More general epidemiological potentials could be considered through the SDE in gradient formulation,

for which the stationary measure is still given by (2.5). For general SDE models, a change of variables allows us to locally consider an SDE with constant noise ^[33] and, in turn, any time-homogeneous SDE with constant noise,

is of course readily linearized into an $\mathcal{OU}$-process.

2.2.   Exact sampling

The $\mathcal{OU}$-process (2.7)–(2.8) is a Gaussian continuous process with mean and covariance given by

such that the stationary distribution is $X_\infty \sim \mathcal{N}(k/\mu, \sigma^2/(2\mu))$.

Numerical simulation procedures are typically based on Euler-type discretization methods. Assume for convenience a fixed numerical time step $\Delta t$ and compute

with $\Delta W_n$ being i.i.d. normally distributed numbers of zero mean and variance $\Delta t$. The numerical trajectory $(X_n)$ is then an approximation to the $\mathcal{OU}$-process $(X(t_n))$ at discrete times $t_n = n\Delta t$ for $n = 0, 1, \ldots$ and is also a Gaussian vector with mean and covariance

Actually, (2.15) forms an $AR(1)$-sequence ^[34]. Comparing (2.13)–(2.14) with (2.16)–(2.17) we readily find the following useful result.

Proposition 2.1. (Exact $\mathcal{OU}$-samples and backward analysis). The discrete process $(X_n)$ given by the explicit Euler method (2.15) follows the law of the discrete samples of an exact $\mathcal{OU}$-process with perturbed parameters $(k_{\Delta t}, \mu_{\Delta t}, \sigma_{\Delta t})$, where

This system of equations can be solved explicitly provided $\Delta t < \mu^{-1}$,

These perturbed parameters are all first order perturbations in $\Delta t$ of the exact parameters.

The inverse of (2.19) is that

It follows that, for given parameters $[k_{\Delta t}, \mu_{\Delta t}, \sigma_{\Delta t}]$, a forward Euler simulation using the new set of parameters $[k, \mu, \sigma]$ defined by (2.20) will produce a sample trajectory obeying the law of the $\mathcal{OU}$-process with the given parameters exactly.

3.   Bayesian filtering with full information

We first briefly consider in this section the behavior of the Bayesian posterior as a function of the prior and of data in the sense of full state measurements. Hence we suppose that sampled process data $D_ N = (d_i)_{i = 0}^{ N}$ is available at some fixed time step $h$, that is, $d_i = X(t_i)$ with $t_i = ih$ and $X(\cdot)$ an $\mathcal{OU}$-process with $X_0$ for simplicity considered a known sure number.

It will be convenient to consider the following reparametrization of the $\mathcal{OU}$-process

and we put $u \equiv [\alpha, \beta, \gamma]$ for brevity, also defining $u_0 \equiv [\alpha_0, \beta_0, \gamma_0]$, i.e., the true parameters generating the data.

Under this reparametrization we readily find from Proposition 2.1 that the exact discrete process can be written in the $AR(1)$-sequence form

where the $\xi_i \sim \mathcal{N}(0, 1)$ are independent. Writing $\delta : = \alpha(1-\beta)$, explicit least squares estimators for the parameters can be found by solving

where the brackets over the data form column vectors. The residual of this solution implies the corresponding estimator for $\gamma$,

By the Gaussian character of the $\mathcal{OU}$-process these estimators coincide with the maximum likelihood estimators.

The Bayesian convergence to the true parameters as $N \to \infty$ can be characterized by either the Bernstein von Mises theorem (BvM), for $h$ fixed, or by contrast functions convergence for a fixed time window $t \in [0, T]$. BvM states that the Bayesian posterior converges to a normal distribution centered at the maximum likelihood estimate with the inverse Fisher information matrix (FIM) as covariance ^[35,36,37]. Similarly, the contrast functions approach considers the convergence of the approximation of discretized observations, approaching the same normal distribution for $N$ large enough ^[38,39,40]. In the present case the FIM can be determined explicitly using the log-likelihood $\log\mathcal{L}(X_{i+1} | X_i; \; u)$ induced by (3.2) and the definition

The result is that

Proposition 3.1. (BvM Theorem for (3.2)). Provided that the prior has a continuous and positive density in an open neighborhood of $(\alpha, \beta, \gamma)$, as $N \to \infty$ we have that the ML-estimators (3.3)–(3.4) converge to the true values as

(convergence in the sense of distribution) with $\Sigma$ defined by (3.6). Alternatively, (3.7) dictates the asymptotic convergence of the mean of the Bayesian posterior.

To summarize, the asymptotic variances of all parameters are independent of $\alpha_0$. The noise term $\gamma_0$ mainly affects the convergence of $\alpha_0$ (and $\gamma_0$ in an absolute sense). Finally, an increase of $\beta_0$ implies a faster convergence towards $\beta_0$ at the cost of a slower convergence towards $\alpha_0$. Under the interpretation of an SIS-model (2.9)–(2.10), the parameter $\alpha_0$ is in one-to-one correspondence with the basic reproduction number $R_0$, hence its central interest here.

The asymptotic nature of both the BvM Theorem and the contrast function convergence is a poor match in epidemiological situations where data is often scarce and poorly informative at the time scale over which the parameters can be considered static. This motivates our interest in also the pre-asymptotic regime of the Bayesian posterior. We therefore consider prior densities of the specific form

where, for integrability, $P$ is to be a polynomial of degree $2$ in $\alpha$ and nonnegative for $\beta\in(0, 1)$. This choice has the convenient property that the posterior measure after $N$ observations is

where

and where $d_i = X(t_i)$ is the observation at time $t_i$.

Remark. To include also the case of flat priors, while avoiding technicalities for nonintegrable densities, we note that, since the value of a constant prior has no influence on the posterior, we can still determine a posterior after a single initial observation, and then use this posterior as a prior for the rest of the observations.

The following result examines the convergence of the Bayesian posterior.

Theorem 3.2. (Convergence of log-likelihood). Consider the polynomial $q_ N$:

Then as $N \to \infty$ we have the almost everywhere uniform convergence on every compact of $q_ N$ towards the function $f$,

Proof. For a general point $(\alpha, \beta)$, we rely on the ergodic theory of Markov chains [41,p. 472] to get that $N^{-1}\sum g(d_i, d_{i+1})$ converges almost surely towards $\mathbb{E}[g(d_i, d_{i+1})]$ for $g$ integrable against the stationary measure. Using (2.13)–(2.14) this implies the limits:

Combined, we obtain the claimed limit in a pointwise sense. As each $(q_N)$ is a polynomial in $(\alpha, \beta)$ of bounded degree, pointwise convergence is equivalent to convergence of the coefficients, and hence implies the convergence on all compact sets.

An obvious extension is to consider measurements polluted by noise, say, $d_i = X_i+\eta_i$, for i.i.d. $\eta_i \sim \mathcal{N}(0, \eta)$ and some variance $\eta$. The posterior so obtained is readily computed via a recursive Kalman filter but does not have a simple analytic form. To first order in $\eta$, however, (3.8)–(3.9) still holds provided $\gamma$ is replaced with $[1/\gamma+\eta(1+\beta^2)]^{-1}$ and $Q_N$ in (3.10) is replaced with

where the right $\eta\beta\gamma$-term is skipped when $i = 0$. Intuitively, the first order effect of noise in data is to broaden the posterior with the variance of this noise. We next proceed to investigate more severe truncations of the measurements from the epidemiological process.

4.   Bayesian filtering of surveillance data

In the previous section we considered full process data to be available without any extrinsic noise. This models the best possible Bayesian setup but is also clearly unrealistic in epidemics. As a model of a more challenging situation we consider in this section the recorded data to be some (possibly stochastic) function of the $\mathcal{OU}$-process $X(\cdot)$, which itself is considered a latent variable. We are initially concerned with binary data of the form $D_ N = (d_i)_{i = 0}^ N$ where $d_i = Y_i = {\bf 1}_{X(t_i) \ge c}$, again over a uniform grid in time $t_i = ih$, and for a known filter cut-off value $c$ (see also the related setup in ^[42]). That is, the epidemiological interpretation is that the data is considered to be time-discrete information about whether or not the prevalence $X(\cdot)$ of the population is above or below a certain known threshold $c$. With the prevalence process hidden one is forced to estimate it simultaneously with any parameter estimates. Using the $AR(1)$-form (3.2) we have that the stationary measure for the $(p+1)$ steps $(X_i, \ldots, X_{i+p})$ is Gaussian $\mathcal{N}(\alpha, \Sigma)$ with $\Sigma$ given by (for $p \ge 0$)

In order to be able to conduct an analysis where information is obtained only from the observable $Y(\cdot)$, we take (4.1) as a motivation for the following:

Assumption 4.1 ($p$-step Markovian stationary assumption). We say that we work under the stationary assumption whenever we assume that the law of the latent variable $Y(\cdot)$ can be directly inferred from the stationary $p$-step law (4.1).

We stress that it is known that this type of clipped Gaussian processes are not $p$-step Markov for any $p$ ^[43]. Assumption 4.1 rather serve as an approximation where we approximately model $Y(\cdot)$ as if it was $p$-step Markov with law deduced from (4.1). The pseudo-likelihood for the filtered variable $Y$ then becomes

where $\varphi_u(e)$ denotes the probability for a Gaussian stationary filtered process with parameters $u$ to be $e\in\{0, 1\}^{p+1}$. We also define the pseudo-potential

We show below in §4.1 that the stationary assumption allows for converging posterior estimates for the parameter $\beta$, but leaves any prior density unchanged over a certain curve in $(\alpha, \gamma)$. In §4.2 we briefly consider the filter cutoff value $c$ (the sensitivity) to be uncertain and straightforwardly show that any prior density on $c$ is unaffected by data. We next replace the sharp deterministic filter by a stochastic filter implementing a sigmoidal response function and sharpen our results in this more general setting in §4.3. Finally, in §4.4 we consider slightly more informative measurements consisting of a finite discrete response and we show that this resolves the singularity issues associated with purely binary measurements.

4.1.   Binary measurements

We first show that under the $p$-fold stationary assumption one can estimate the correlation term $\beta$ rather well, but increasing the gap between the filter threshold $c$ and the mean $\alpha$ has an effect on the likelihood which is indistinguishable in law from increasing the noise $\gamma$.

We start with a technical lemma.

Lemma 4.1 (Equality in law). For $u$ in any admissible set of parameters, let $p_u$ be the law of $(Y_0, \ldots, Y_p)$ under Assumption 4.1 corresponding to $\mathcal{N}(\alpha_u, \Sigma_u)$. Then $p_u = p_{w}$ if and only if $\beta_u = \beta_{w}$ and $\sqrt{\gamma_u}(c-\alpha_u) = \sqrt{\gamma_{w}}(c-\alpha_{w})$.

Proof. $(\Longrightarrow)$ Suppose $p_u = p_{w}$. Consider $(X_0^u, \ldots, X_p^u)$ a Gaussian vector with law $\mathcal{N}(\alpha_u, \Sigma_u)$. As ${\bf P}(X_0^u\leq c) = \sum_{e \in \{0, 1\}^{p}}\varphi(0, e)$, we deduce that ${\bf P}(X_0^u\leq c) = {\bf P}(X_0^{w}\leq c)$. This can be written as an equality between standard cumulative distribution functions of Gaussians, since $\sqrt{\gamma_u(1-\beta_u^2)}(X_0^u-\alpha_u)$ and $\sqrt{\gamma_w(1-\beta_w^2)}(X_0^w-\alpha_w)$ are standard Gaussians. This translates into:

We also have ${\bf P}(X_0^u, X_1^u\leq c) = {\bf P}(X_0^{w}, X_1^{w}\leq c)$, and this implies, with $A = \sqrt{\gamma_u(1-\beta_u^2)}(c-\alpha_u)$,

This last expression shows that the map $\beta_u\mapsto {\bf P}(X_0^u, X_1^u\leq c)$ is locally analytic. As a corollary of Slepian's lemma ^[44], this map is also increasing and hence strictly increasing. It follows that the last equality implies $\beta_u = \beta_w$.

$(\Longleftarrow)$ The law $p_u$ is uniquely determined by its $2^{p+1}$ values. All these values are of the type

where $Q(A)$ is a product of $p+1$ intervals, each being either $(-\infty, A]$ or $[A, +\infty)$. And so, if $\beta_u = \beta_w$ and $\sqrt{\gamma_u}(c-\alpha_u) = \sqrt{\gamma_{w}}(c-\alpha_{w})$, the laws $p_u$ and $p_{w}$ are indeed equal.

Theorem 4.2 (Non-identifiability). Assume $p\geq 1$. For any integrable prior $\pi$, non-zero on $\mathcal{E}$, and for $f$ bounded, as $N \to \infty$,

where $\mathcal{E} \equiv \{u; \; \sqrt\gamma(c-\alpha) = \sqrt\gamma_0(c-\alpha_0), \, \beta = \beta_0\}$ and $\tilde{\pi}$ is the prior restricted to the set $\mathcal{E}$.

Proof. At first, thanks to Lemma 4.1, the law $\varphi(Y_i\ldots, Y_{i+p})$ is not characterized by $u_0 = [\alpha_0, \beta_0, \gamma_0]$, but rather by $[\sqrt{\gamma_0}(c-\alpha_0), \beta_0]$. As the $Y_i$'s are binary, the quantity $\varphi(Y_i, \ldots, Y_{i+p})$ can only take $2^{p+1}$ values, which we denote by $\varphi_e$ for $e\in\{0, 1\}^{p+1}$. This means that the log-likelihood under Assumption 4.1 can be written as a finite sum:

where

Now, as the discrete $\mathcal{OU}$-process is an $AR(1)$-sequence ^[34], we may infer the convergence of $N(e)/ N$ towards a stationary value:

where $\varphi_e^u$ denotes the law of a stationary filtered process with parameter $u$. We note that

Up to a constant this limit is the negative of the Kullback-Leibler divergence between the laws $\varphi^u$ and $\varphi^{u_0}$, which vanishes if and only if the two distributions are equal. We already know that the laws of $\varphi^u$ and $\varphi^{u_0}$ are equal if and only if $\beta = \beta_0$ and $\sqrt{\gamma}(c-\alpha) = \sqrt{\gamma_0}(c-\alpha_0)$, i.e., if $u \in \mathcal E$. Consider the associated relation:

It is straightforward to show that this relation is reflexive, symmetric, and transitive, thus forming an equivalence relation. Thanks to Lemma 4.1, we know that the map $u\mapsto\mathcal{L}_ N(u)$ factorizes through the equivalence relation to a map $w\mapsto\tilde{\mathcal{L}}_ N(w)$ where $w$ ranges over the different equivalence classes of $u$.

Lemma 4.1 also allows us to state that the map $\tilde{\mathcal{L}_ N}$ is injective. Consider $w_0$ in the equivalence class of $u_0$. Then for any neighborhood $W$ of $w_0$, there is a $\delta > 0$ such that for $N$ large enough, $w \not \in W$ implies

which means that the posterior measure of $W$ converges towards 1. Since the factorized map $\tilde{\mathcal{L}}_ N \rightarrow \delta_{w_0}$, the theorem follows.

The same argument implies that, if we consider the case $p = 0$, the posterior will be even more degenerate. For $p = 0$ one gets the convergence

where now $\tilde\pi$ is the prior restricted to $\mathcal{E}'$:

This case is relevant whenever we consider large gaps of time in between the measurements such that they can be considered practically independent.

At this point, let us remind that the quantities $\mathcal{L}_ N(u)$ and $\Phi_ N^p(u)$ are defined in Eqs (4.2) and (4.3).

Theorem 4.3 (Rate of convergence of pseudo-potential). Under the $p$-Markovian stationary Assumption 4.1 there exists a mapping $f_p$ and a constant $\sigma_p > 0$ such that, as $N \to \infty$, we have the convergence in law:

Proof. This is a direct consequence of the Central Limit Theorem, with $f_p(u)$ being the mean value of $\Phi_N^p(u)$ and $\sigma_p$ a nonnegative constant.

4.2.   Propagation of filter uncertainty

A relevant variation of the theme is to consider the parameter $c$ (the "test sensitivity") an uncertain parameter. Mathematically, this means considering the likelihood $\mathcal L_N$ a function of $(\alpha, \beta, \gamma, c)$, and priors and posteriors depending also on $c$. However, the following result shows that this setup will not produce any more information about the parameters.

Theorem 4.4 (Translation of filter uncertainty). Consider a prior of the form $\mu(\alpha)\pi(c-\alpha, \beta, \gamma)$ and the pseudo-likelihood in §4.1. Then the resulting posterior measure will be of the form $\mu(\alpha)\Pi(c-\alpha, \beta, \gamma)$, where, for fixed $c$, $\Pi(c-\cdot, \cdot, \cdot)$ is the pseudo-posterior from the prior $\pi(c-\cdot, \cdot, \cdot)$.

Proof. This result is immediate once one realizes that the pseudo-likelihood has the property that, for any $t\in {\bf R}$,

In other words, the only information we can infer on the parameters $(c, \alpha)$ is the gap $c-\alpha$. Any uncertainty of $c$ can be understood as an uncertainty on $\alpha$, and vice-versa.

4.3.   Non-perfect binary measurements

Rather than a sharp cut-off value $c$, most environmental sampling methods obey some kind of sensitivity response, e.g., of sigmoid character, with a quick rise in the detection probability as one progresses through some threshold region. Examples here could include sampling and subsequent analysis of sewage water or animal droppings, but this would also be a relevant model in the case of statistical regression estimates using data obtained via self-reporting smartphones applications.

A general ansatz to capturing this situation is to consider

where $s$ is a map from ${\bf R}$ to $[0, 1]$ and $\mathcal B$ denotes the Bernoulli law. Typically, the map $s$ is sigmoidal with a gradient around the threshold $c$ which depends on the sensitivity and specificity of the test. We naturally ask that the efficiency of the filter does not depend on its previous use, i.e., that $(Y_i|X_i)_i$ is an independent family. To construct such an object, one may consider an i.i.d. family of uniformly distributed variables $(\xi_i)$ on $(0, 1)$, independent from $(X_i)$, and set

This object clearly fulfills all properties mentioned and is general enough to capture also quite specific situations.

We will now establish our result in this more general setting. Consider a bounded and continuous map $f: {\bf R}^{p+1}\rightarrow {\bf R}$. We observe the $\mathcal{OU}$-process $X(t)$ through the map $f$, so the observations are $Y_i = f(X_i, \ldots, X_{i+p})$ where as before $X_i = X(t_i)$. To define a pseudo-likelihood, we reason as if the observed data can be regarded as stationary. We thus denote by $f_u$ the law of a stationary $\mathcal{OU}$-process with parameters $u$ filtered via the measurement map $f$ and we remind ourselves that the latent process $X(t)$ is not necessarily stationary.

We consider a likelihood of the kind

normalized to mass one, and we denote the potential by

This setup simply corresponds to observing the data portion $(X_i, \ldots, X_{i+p})$ via the filter $f$ and, assuming stationarity, building a pseudo-likelihood. Unfortunately this does not directly include the intended case of a sigmoid filter, as this would rather involve measurements $h(\xi_i, X_i, \ldots, \xi_{i+p}, X_{i+p})$ with $(\xi_i)$ an i.i.d. sequence independent from $(X_i)$ and uniform on $(0, 1)$. However, once the proposed case is examined, one can get to the latter case by exchanging the order of integration using the Fubini property, i.e., studying the behavior of $h(t_0, X_i, \ldots, t_p, X_{i+p})$ and then integrate over $(t_0, \ldots, t_p)$. For example, consider the case $p = 1$. Then the intended map $h$ would be

For a fixed $u$, $f_u$ can take at most $4$ values, e.g.,

where $(Z_0, Z_1)$ is a stationary $\mathcal{OU}$-process of parameter $u$, and similarly for $f_u(0, 1)$, $f_u(1, 0)$, and $f_u(0, 0)$. As this technique would render the proof lengthy, we decided to put it aside.

In order to state our result, we need to specify some minimal set of regularity conditions. Convergence of the potential is required as well as definiteness in the Kullback-Leibler divergence (${\rm{D}}_{\rm{KL}}$). Additionally, we shall also require a separation condition in the large data limit.

Assumption 4.2 (Regularity). We assume the following specifics:

$1)$ The potential $g_N$ converges uniformly on the compacts of $u$.

$2)$ ${\rm{D}}_{\rm{KL}}(f_{u_0}, f_u) = 0 \Longrightarrow u = u_0$.

$3)$ There is a $\delta > 0$ and a compact neighborhood $K$ of $u_0$ such that, for $N$ large enough and for $u \in K^\complement$, $g_N(u_0) > g_N(u)+\delta$.

Theorem 4.5 (Weak convergence). Under Assumption 4.2, we have the weak convergence

This theorem can be adapted to cover other situations:

● If ${\rm{D}}_{\rm{KL}}(f_{u_0}, f_u) = 0$ does not imply $u = u_0$, one can try to factorize the map through an equivalence relation (as in the proof of Theorem 4.2) to get the convergence towards the indicative function of the set $\{u; \; {\rm{D}}_{\rm{KL}}(f_{u_0}, f_u) = 0\}$.

● If we only want to consider parameters within a subset $U$ of the set of parameters, one can always consider the assumptions restricted to the set $U$, and then one would have the convergence only for priors with support in $U$.

Proof. We divide the proof in two steps as follows.

Step 1 Let us call $g$ the limit of $(g_N)$, which by assumption is not random. The same argument as in the proof of Theorem 3.2, the ergodicity of the process $(X_t)$, allows us to state that the limit function must be $\mathbb{E}[\log f_u]$ (up to a constant, the limit is actually $-{\rm{D}}_{\rm{KL}}(f_{u_0}, f_u)$). As adding a constant is equivalent to multiplying all posteriors by a nonnegative constant, we may assume the limit function to be equal to $u \mapsto -{\rm{D}}_{\rm{KL}}(f_{u_0}, f_u)$.

Step 2 As $\mathcal{L}_N$ is proportional to $\exp(g_N)$, the assumptions allow us to deduce that the mass of any neighborhood of $u_0$ converges towards $1$. This implies the weak convergence of the posteriors towards the Dirac $\delta_{u_0}$.

4.4.   Non-binary measurements

As a final variation on the theme we now show how Theorem 4.5 can be applied in such a way as to overcome the issues with the non-identifiability of Theorem 4.2. The idea is that the test with one filter $c$ evidently at best gives us a curve containing the parameter $u_0$, namely the one satisfying $\beta = \beta_0$, and $\sqrt{\gamma}(c-\alpha) = \sqrt{\gamma_0}(c-\alpha_0)$. Suppose instead that we have two kinds of tests, one with cut-off $c_1$ and one with cut-off $c_2$. Since the intersection of the two curves implied by the respective filters $c_1$ and $c_2$ is exactly the point $u_0$, it is natural to assume that two filters are enough to get the convergence of the posterior towards $\delta_{u_0}$. We show that this is indeed the case.

Theorem 4.6 (Trinary filter). Let $c_1 < c_2$ and consider the filtered values $Y_i$ to be

and the associated pseudo-likelihood

where $\varphi$ is the multivariate cumulative distribution function of a Gaussian $\mathcal{N}(\alpha, \Sigma)$ (4.1). Then the sequence of pseudo-likelihoods converges weakly:

Proof. It is sufficient to check that the sequence $(Y_i)$ verifies Assumption 4.2. Considering $g_ N : = N^{-1} \log{\mathcal{L}_ N}$, one has

where $N_e$ is the number of times $(Y_i, \ldots, Y_{i+p})$ matches $e$, and $p_u$ is the cumulative distribution function of the underlying Gaussian process $\mathcal{N}(\alpha, \Sigma)$. From this we get directly conditions (4.2) and (4.2) of Assumption 4.2. For condition (4.2), if the Kullback-Leibler divergence is zero, then we must have $p_u(e) = p_{u_0}(e)$ for all $e$. This implies the equalities

As $c_1\neq c_2$ we have $u = u_0$, and so the assumptions are fulfilled.

5.   Illustrations

We devote this section to some illustrations of selected results from §§3 and 4. We shall do this in the intended epidemiological setting and thus no longer assume the $\mathcal{OU}$-process, but rather the SIS- and SIS$_{\text{E}}$-models from §2 in the form of continuous-time Markov chains over a discrete state-space. In §5.1 we investigate the precision of the predicted posterior uncertainty under full state measurements, while in §5.2 we offer a demonstration of the singular behavior under filtered measurements. Finally, in §5.3 we highlight the use of synthetic data when approaching more realistic problems defined over a network.

The software for the numerical experiments is available for download via the corresponding author's web-page^*.

^*Refer to the BISDE-code at https://user.it.uu.se/~stefane/freeware.html

5.1.   Asymptotic uncertainty

We first consider the Bayesian uncertainty under accurate measurements and take the continuous-time Markov chain version of the SIS-model (2.4) as an example. Using the $\text{SIS} \leftrightarrow$ $\mathcal{OU}$ approximate interpretation (2.9) we have from (3.1) the relations

where $\{R_0, \Sigma, \gamma\}$ are the SIS-model parameters.

We generate synthetic data from the Markov chain as illustrated in Figure 1 for $\Sigma = 1000$ and with ranges of values $\gamma \in [0.1, 1]$ and $R_0 \in (1, 3.5]$. We let $I(0) = 0.01\times\Sigma$ and sample exact values of $I(t_i)$ for $t_i = ih$, $i = 1, \ldots, N$, and $h \equiv 1$. This corresponds to 100 perfect samples in a closed population at a rate equivalent to between one to one tenth the disease period unit ($= 1/\gamma$).

We evaluate the posterior over a grid of values in the $(R_0, \gamma)$-plane by simply normalizing the likelihood for the Markov chain given the synthetic data discussed previously. The likelihood of the Markov chain is formally obtained by solving the associated master equation which, however, is inconvenient to do except for small populations $\Sigma$. A more general approach is via a local linear Gaussian approximation and a Kalman filter. Put $I_0 = I(0)$ and define

that is, this is the forward Euler discretization of the Langevin equations approximating the Markov chain. The Kalman filter associated with (5.2) computes a likelihood for each data point, albeit for a perturbed model. The relative error in the Langevin approximation generally scales with the inverse of the population size $\Sigma$, and can be expected to be rather small in the present context (see [45,Ch. 11.3]). Further, Proposition 2.1 suggests analyzing the Euler discretization via backward analysis as a parameter perturbation, but unfortunately this is not generalizable to non-additive noise ^[46]. For a resolved discretization, however, $\gamma \Delta t \ll 1$, weak first order convergence can be expected under broad conditions. We use the constant Kalman resolution $\Delta t = h/4$ and next focus on the estimation error.

We have already evaluated the asymptotic covariance matrix under accurate data in (3.7). Using the linear uncertainty transformation $Q' \approx JQJ^T$, where $J$ is the Jacobian of the parameter map (5.1), and where $Q$ is the (diagonal) covariance matrix in (3.7), we can estimate the posterior variance

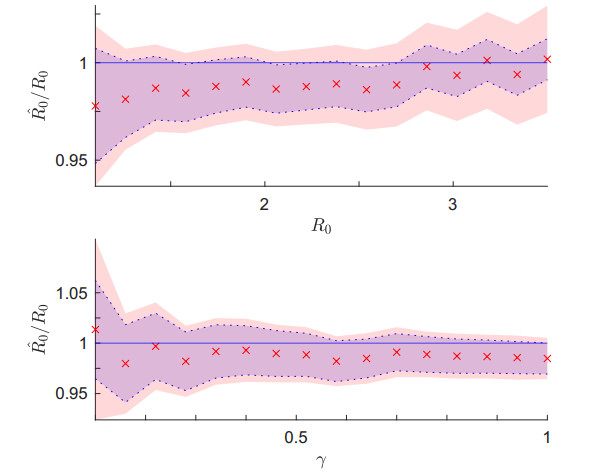
A similar formula can be worked out for the variance of $\gamma$ as well, although a bit more involved. For small enough $h$, the denominator $1-\beta_{{ \mathcal{OU} }} \sim \gamma h (R_0-1)$ in (5.3), and so the relative uncertainty in any consistent estimator of $R_0$ can be expected to depend weakly on $R_0$ itself. This effect is seen for $R_0 > 1$ in Figure 2 (top), where it can also be seen that the approximation (5.3) derived from the $\mathcal{OU}$-approximation is somewhat optimistic. Similarly, we find that the relative uncertainty of $R_0$ goes down with increasing values of $\gamma$, or, which by (5.1) is the same thing, with decreasing correlation $\beta_{{ \mathcal{OU} }}$ (cf. Figure 2, bottom).

5.2.   Limits of convergence

The SIS-model investigated previously was dependent on two parameters only and hence the singularity detected in §4 is not likely to be limiting any convergence. While various model modifications naturally lead to additional independent parameters, e.g., an extra transition $S \to I$ modeling external infectious events, the most immediate modification is to simply consider the population size $\Sigma$ uncertain. For instance, this is a possible setup for inference relying on sewage water analysis, where the data is binary according to whether the infectious substance is above or below some known threshold value $c$, but the sewage uptake area is populated with an unknown number of individuals.

We remark that this is a considerably challenging task, and although we are able to demonstrate the sharpness of our negative results from §4 in this setting, the fact that this problem can at all be approached is quite remarkable.

As ground truth we use the same parameters as in the previous section, but with $\gamma = 1/10$ (time$^{-1}$) and $R_0 = 1.5$ fixed, and we need to sample more, $N = 1000$ points equispaced with $h = 1$. The data is then taken to be the filtered sequence $Y_i = {\bf 1}_{X_i \ge c}$ with $c = 0.9 \times I_\infty = 0.9 \times \Sigma(1-R_0^{-1})$.

The measurement map is strongly nonlinear and so the Kalman filter needs to be extended in some way. We took an immediate approach by simply discretizing the state variable $I$ into $M = 100$ Gaussian particles, distributed according to the percentiles of the stationary measure for a given proposed set of parameters. Each particle is evolved in time $[0, h]$ using steps of size $\Delta t$ according to the Kalman filter (5.2), after which the prior distribution is formed by aggregating the probability mass in the vicinity of each particle. This yields the likelihood for a single data point after which the posterior distribution for the state is obtained by setting selected particles' mass to zero (according to the data point) and rescaling appropriately.

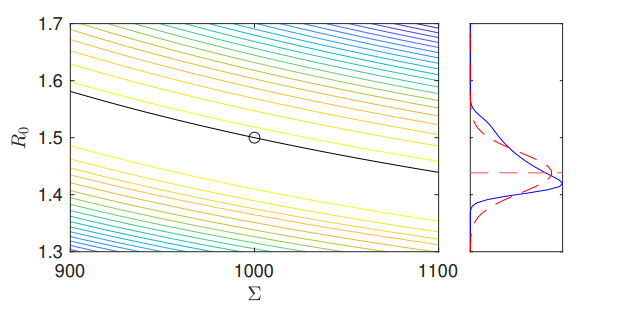
From Theorem 4.2 we have the singular curve $\sqrt{\gamma_{{ \mathcal{OU} }}}(c-\alpha_{{ \mathcal{OU} }}) = \mbox{constant}$, which gets transferred via the map (5.1) into a surface in $(R_0, \Sigma, \gamma)$-space. After arbitrarily fixing $\gamma$ we thus obtain a curve in the $(R_0, \Sigma)$-plane. Since the SIS-to- $\mathcal{OU}$ map (2.9) is an approximation and, moreover, the likelihood is approximated via a Kalman filter, this analytical curve can be expected to be a perturbation of the observed numerical posterior level curves. As shown in Figure 3 the match is quite remarkable.

5.3.   Network epidemics

Epidemic models on networks can give rise to phenomena not observed in single-node systems, e.g., the rescue effect ^[1], where the infection is "rescued" from extinction through the network structure. Here we consider both the SIS- and the SIS$_{\text{E}}$-model, respectively, cf. (2.2)–(2.3). We assume these models at each node in a network implicitly defined by pre-recorded movements of individuals between the nodes. As a concrete example this would be an appropriate model for estimating disease parameters in a monitoring program for bovine animals using cheap, but low-informative, tests collected on a weekly basis for a subsample of sentinel nodes.

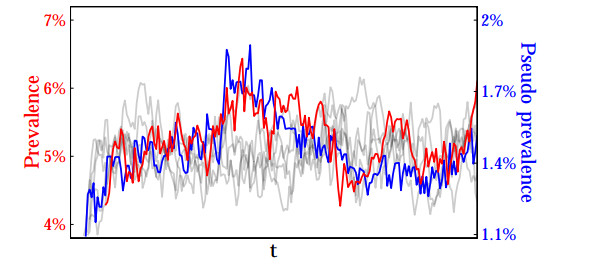
The nodal model is replicated across 1600 nodes, populated with 196,168 individuals, and the nodes are connected using 466,692 prescribed movements of individuals over four years, see Figure 4. The system is not well stirred on the aggregate level, but events occur frequently; the average # of events per sample node and day $= 0.20\, [0.19, 0.21]$ with 50% credible interval (CrI). This particular network was constructed by anonymizing a set of recorded cattle movements and can be accessed through the publicly available R-package SimInf ^[19,47]. We extract model measurements from the same 100 randomly pre-selected sentinel nodes every 7th day for a total of 4 years. Each measurement is the outcome of a binary test: if the prevalence ($P = \Sigma^{-1} I$) in the node is above a threshold value ($c =$ 30% or 4% for the SIS- or the SIS$_{\text{E}}$-model, respectively), where all nodes are seeded at 10% or 2% initially. In Figure 5, we illustrate the sampling output in time for the SIS$_{\text{E}}$-model.

A challenging aspect of many data-driven inference problems, e.g., including network, dynamics is that the likelihood function is intractable and must be estimated through repeated simulations. Bayesian inference in this setting is termed Likelihood-free inference (LFI), or Approximate Bayesian Computations (ABC); see ^[48,49] for reviews. In this example, we consider the Sequential Monte Carlo (SMC) adaptation of ABC (SMC-ABC) implemented in SimInf and described in ^[50].

Our SMC-ABC implementation determines proposal rejections per generation $n$ using the normalized Euclidean kernel $K_\varepsilon(x, y) = \sqrt{\sum_i ((x_i-y_i)/x_i)^2} < \varepsilon_n$ for statistics of the simulation proposal $y$ and observation $x$ and with a series of decreasing tolerances $\varepsilon_n$. The statistics are computed as follows. Each simulation generates a time series of pseudo prevalences, i.e., a population-weighted sum of positive samples. We interpret the time series as an $\mathcal{OU}$-process and select the least square estimates (3.3)–(3.4) as indirect summary statistics ^[51]. A word in favor of this particular choice of statistics for other ABC implementations, e.g., synthetic likelihoods ^[52], is that least square estimates are asymptotically normally distributed under broad assumptions ^[53]. Notably, we get away with using statistics with one more or equal dimension as the parameter set, suggesting that this characterization is indeed very fitting.

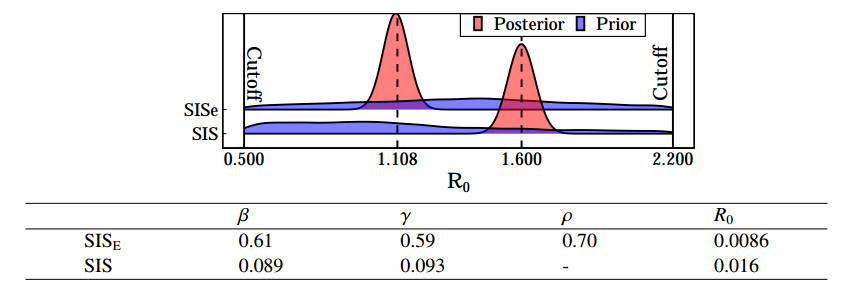
For the inference we use a single initial simulation with the true parameters $(\beta, \gamma, R_0)_{\text{SIS}} = (0.16, 0.1, = 1.6)$ and $(\beta, \gamma, \rho, R_0)_{\text{SIS}_{\text{E}}} = (0.054, 0.1, 0.44, = 1.108)$, respectively, and we infer all parameters simultaneously. For priors, since we have no likelihood and thus cannot easily produce a strictly non-informative prior, we take uniform distributions over quite large intervals in parameter space: $\beta$ and $\gamma \sim \mathcal{U}(0, 1)$ in both cases and $\rho \sim \mathcal{U}(0.4, 0.5)$. We use the decreasing ABC tolerances $\varepsilon_n = 100 \exp(-0.25 (n-1))$, for $n = 1\ldots 15$ and 1000 SMC particles.

We found that $\rho$ requires a tighter prior than the others for the computations to complete in a reasonable time: the SIS$_{\text{E}}$-model is considerably more challenging but is also more realistic, particularly so in our setting on a network where rather large prevalences are required for the SIS-model to not simply die out.

The results for the $R_0$-marginals are displayed in Figure 6, where we also investigate the concentration effect of data through the relative change in quartile coefficient of dispersion (QCD); a small concentration factor indicates an accurately identifiable parameter. Although the SIS$_{\text{E}}$-model is clearly more challenging, $R_0$ is still well reconstructed for both models.

Binary data implies identifiability when given multiple observations at the same time, e.g., over a small collection of nodes in a network rather than on a single node, as indicated in a qualitative sense by Theorem 4.6. Additionally, $R_0$ is identifiable with quite high accuracy even when the dependent parameters covaries. The example is prototypical of using synthetic data to evaluate the feasibility of an intended setup. Since the posteriors are robust with respect to capturing the synthetic truth, we have good reasons to also have some faith in the design when approaching real data.

6.   Conclusions

Throughout this work we have employed the Ornstein-Uhlenbeck process as a meta-model of more involved epidemiological models. We indicated in §3 a convergence analysis of the Bayesian posterior under direct process observations. Since this is an unrealistic setup in most epidemiological applications, one can think of these results as best possible.

We next took the opposite standpoint and considered data to be severely filtered such that, literally, each data point contributed only a single bit of information. For instance, this could be a model of pooled data obtained through environmental sampling and subsequent analysis. To obtain a closed framework we added a fairly general stationary $p$-step Markov assumption and worked out conditions on the data to obtain a non-singular inverse problem.

With increasing compute power and improving possibilities for gathering data, fully Bayesian first-principle epidemiological models can be realized. As a minimum standard, we propose, such methods should be preceded by a proof of self-consistency: data generated from the model itself and chosen "nearby" the actual data should allow for accurate parameter identifiability. Under this basic standard, Bayesian epidemiological modeling with both short-term prediction and generation of forecasting scenarios can be included as an integrated part of the public health's methodological arsenal.

Acknowledgment

This work was financially supported by the ENS Paris (S. Bronstein) and in part by the Swedish Research Council Formas (S. Engblom) and the Swedish Innovation Agency Vinnova (S. Engblom, R. Marin). Several helpful comments and kind suggestions on earlier versions of the manuscript were offered by friends and colleagues. These helped to improve the presentation considerably.

Conflict of interest

The authors declare there is no conflict of interest.