A study on the factors influencing the transfer of COVID-19 severe illness patients out of the ICU based on generalized linear mixed effect model

1.   Introduction

Fractional partial differential equations (FPDEs) are the generalizations of classical partial differential equations with integer orders, which are used to describe several phenomena in many fields of sciences, such as mechanics, signal processing, plasma physics, systems identification, electricity, chemistry, biology, control theory and other areas.

The exact solutions of FPDEs play a crucial role in the study of nonlinear sciences. It is used to describe observed various qualitative and quantitative features of nonlinear phenomenons in many fields of mathematical physics, it can let our better understand some complex physics phenomena. Therefore, it is an important task to seek more exact solutions of different forms for the FPDEs.

In recent decades, with the development of science and technology, especially symbolic computation package such as Maple and Mathematica, many researchers have presented many direct and powerful approaches to establish exact solutions of fractional partial differential equations. For example, the fractional sub-equation method ^[1,2], the first integral method ^[3], the extended fractional Riccati expansion method ^[4], the fractional complex transform ^[5], the Jacobi elliptic equation method ^[6], the fractional mapping method ^[7], the $(G'/G)$-expansion method ^[8], the improved fractional $(D^\alpha G/G)$ method ^[9], the extended fractional $(D_\xi^\alpha G/G)$-expansion method ^[10], the separation variables approach ^[11], the modified extended tanh method ^[12], the $\rm{exp}(-\Phi(\xi))$ method ^[13,14], the invariant subspace method ^[15], and other methods ^{[16,17,18,19]}. Due to these methods, various exact solutions or numerical solutions of FPDEs have been established successfully.

The two variable $(\phi'/\phi, 1/\phi)$-expansion method is the generalization of $(G'/G)$-expansion method, the main idea of this method is that the solutions to FPDEs are represented as a polynomial in two variables $(\phi'/\phi)$ and $(1/\phi)$, wherein $\phi = \phi(\xi)$ satisfies the second order ODE $\phi''+\delta \phi = \mu,$ where $\delta$ and $\mu$ are constants. The objective of this article is to establish further general and some fresh close form solitary wave solution to the time-fractional Kuramoto-Sivashinsky (K-S) equation, (3+1)-dimensional time-fractional KdV-Zakharov-Kuznetsov (KdV-ZK) equation and time-fractional Sharma-Tasso-Olver (FSTO) equation by means of the two variable $(\phi'/\phi, 1/\phi)$-expansion method, the results suggest that the method is significative and further general.

The organization of the paper is as follows. In Section 2, the description of conformable fractional derivative and its properties are given. In Section 3, we describe the algorithm for solving time-fractional partial differential equations by using the two variable $(\phi'/\phi, 1/\phi)$-expansion method with the help of fractional complex transform. In Section 4, we apply the two variable $(\phi'/\phi, 1/\phi)$-expansion to the time-fractional K-S equation, (3+1)-dimensional KdV-ZK equation and FSTO equation. In Section 5, some typical wave figures of the exact solutions are given. Results and discussion part are added in Section 6. The conclusion part is in Section 7.

2.   Conformable fractional derivative and its properties

In fractional calculus, the most famous fractional derivatives are the Riemann-Liouville and the Caputo fractional derivatives, the Riemann-Liouville fractional derivative is defined as follows ^[20]:

If $n$ is $a$ positive integer and $\alpha \epsilon[n-1, n]$, the $\alpha$ derivative of a function $f$ is given by

Also, the Caputo fractional derivative is defined as follows ^[20]

Some flaws arise in these definitions of these fractional derivatives, for example, all these derivatives do not satisfy: the known formula of the derivative of the product of two functions, the known formula of the derivative of the quotient of two functions and the chain rule of two functions.

In 2014, Khalil et al. ^[21] introduced a novel definition of fractional derivative named the conformable fractional derivative to overcome the flaws found in Riemann-Liouville and the Caupto fractional derivatives.

Definition 1. Suppose $f$: $[0, \infty) \rightarrow R$ is a function. Then, the conformable fractional derivative of $f$ of order $\alpha$ is defined as

for all $t > 0$ and $\alpha\in(0, 1]$. If $f$ is $\alpha$-differentiable in some $(0, a)$, $a > 0$, and $lim_{t\rightarrow 0^+}f^{(\alpha)}(t)$ exists, then $f^{(\alpha)}(0) = lim_{t\rightarrow 0^+}f^{(\alpha)}(t)$.

Some properties of the conformable fractional derivative are given below as in ^[21]

Thereom 1. Suppose $\alpha\in(0, 1]$, and $f = f(t)$ and $g = g(t)$ are $\alpha-$differentiable at $t > 0$. Then

If, in addition to $f$ differentiable, then

Thereom 2. Suppose functions $f, g$: $[0, \infty) \rightarrow R$ be $\alpha-$differentiable, where $(0 < \alpha \leq1)$. Then the following rule is obtained

The above equations play an important role in fractional calculus in the following sections.

3.   The two variable $(\phi'/\phi, 1/\phi)$-expansion method

In this section we give the description of the two variable $(\phi'/\phi, 1/\phi)$-expansion method to find exact traveling wave solutions of time-fractional partial differential equation.

Suppose that a time-fractional partial differential equation in the variables $x, y, z, t$ is given by

where $D_{t}^{\alpha}u, D_{tt}^{2\alpha}u$ are fraction-order derivatives of $u$ with respect to $t$, $P$ is a polynomial of $u = u(x, y, z, t)$ and its various partial conformable derivatives including the highest order derivatives and nonlinear terms.

We use the conformable wave transformation:

where $c$ and $\upsilon$ are constant to be determine later, the FPDE (3.1) is reduced to the following nonlinear ordinary differential equation (ODE) for $u(x, y, z, t) = u(\xi)$:

where $u' = u_\xi, u'' = u_{\xi\xi}, \cdots.$

We suppose the solution $u$ of (3.3) can be expressed in the following form:

where $a_i, b_j(i = 0, 1, 2, \ldots, n; j = 0, 1, 2, \ldots, n-1)$ are constants and $a_nb_{n-1}\neq 0$. The positive number $n$ can be determined by considering the homogeneous balance between the highest order derivatives and nonlinear terms appearing in (3.3). The function $\phi = \phi(\xi)$ satisfies the second order linear ODE in the form

where $\delta$ and $\mu$ are constants. Equation (3.5) has three types of general solution with double arbitrary parameters as follows ^[22]:

and

where $A_1, A_2$ are arbitrary constants.

By substituting (3.4) into (3.3) and using the second order linear ODE (3.5) and (3.7), collecting all terms with the same order of $\frac{1}{\phi^i}$ and $\frac{1}{\phi^i}\frac{\phi'}{\phi}$ together, the left-hand side of (3.3) is converted into another polynomial in $\frac{1}{\phi^i}$ and $\frac{1}{\phi^i}\frac{\phi'}{\phi}$. Equating each coefficient of this different power terms to zero yields a set of algebraic equations for $a_i, b_j(i = 0, 1, 2, \ldots, n; j = 0, 1, 2, \ldots, n-1), \delta, \mu, c$ and $\upsilon$.

Assuming constants $a_i, b_j(i = 0, 1, 2, \ldots, n; j = 0, 1, 2, \ldots, n-1), \delta, \mu, c$ and $\upsilon$ can be determined by solving the nonlinear algebraic equations. Then substituting these terms and the general solutions (3.6) of (3.5) into (3.4), we can obtain more exact traveling wave solutions of (3.1).

4.   Applications of the two variable $(\phi'/\phi, 1/\phi)$-expansion method

In this subsection, we investigate more general and new exact traveling wave solutions of time-fractional differential equations by means of the two variable $(\phi'/\phi, 1/\phi)$-expansion method.

4.1.   Time-fractional Kuramoto-Sivashinsky (K-S) equation

we consider the time-fractional Kuramoto-Sivashinsky (K-S) equation ^[23]:

where $0 < \alpha\leq 1$ and $a, b, k$ are arbitrary constants.

The K-S equation (4.1) was examined as a prototypical example of spatiotemporal chaos in one space dimension. This equation represents the motion of a fluid going down a vertical wall, the variations of the position of a flame front, or a spatially uniform oscillating chemical reaction in a homogeneous medium.

To solve (4.1), we use the wave transformations:

then (4.1) is reduced into a nonlinear ODE in the form

By reducing (4.3), we get

By balancing the highest order derivative term $u^{(4)}$ and nonlinear term $uu'$ in (4.4), the value of $n$ can be determined, which is $n = 3$ in this problem. Therefore, by (3.4), we have the following ansatz:

where $a_0, a_1, a_2, a_3, b_0, b_1$ and $b_2$ are constants to be determined later, and function $\phi(\xi)$ satisfies (3.5).

By substituting (4.5) into (4.4) and using the second order linear ODE (3.5) and (3.7), collecting all terms with the same order of $\frac{1}{\phi^i}$ and $\frac{1}{\phi^i}\frac{\phi'}{\phi}$ together, the left-hand side of (4.4) is converted into another polynomial in $\frac{1}{\phi^i}$ and $\frac{1}{\phi^i}\frac{\phi'}{\phi}$. Equating each coefficient of this different power terms to zero yields a set of algebraic equations for $a_0, a_1, a_2, a_3, b_0, b_1, b_2, \delta, \mu, k, a, b, c$ and $\upsilon$. Solving this system of algebraic equations, with the aid of Maple, we obtain

where $\Xi_i(i = 1, 2, 3)$ are given later.

Substituting (4.6) and (4.7) and the general solutions (3.6) of Eq. (3.5) into (4.5), we obtain more exact traveling wave solutions of (4.1):

where $\xi = c(x-\frac{(b_2\delta\mu+2a_0\Xi_i)a}{2\Xi_i\alpha}t^\alpha), \ \ b = \pm\frac{19b_2a\delta}{60c\sqrt{\Xi_i}}, \ \ k = \pm\frac{ab_2}{60c^3\sqrt{\Xi_i}}.$

where $\xi = c(x-\frac{(b_2\delta\mu+2a_0\Xi_i)a}{2\Xi_i\alpha}t^\alpha), \ \ b = \mp\frac{19b_2a\delta}{660c\sqrt{\Xi_i}}, \ \ k = \pm\frac{ab_2}{60c^3\sqrt{\Xi_i}}$.

When $i = 1$ for $\delta < 0$, $i = 2$ for $\delta > 0$, $i = 3$ for $\delta = 0$. And

Since $A_1$ and $A_2$ are arbitrary constants, one may choose arbitrarily their values. For example, if we choose $A_1 = 0$, $A_2\neq 0$ and $\mu = 0$ in (4.8), we obtain some traveling wave solutions.

Case 1.1 when $\delta < 0$, we have

where $\xi = c(x-\frac{a_0a}{\alpha}t^\alpha), b = \frac{19b_2a\delta}{60A_2c\sqrt{-\delta}}, \ \ k = \frac{ab_2}{60c^3A_2\sqrt{-\delta}}.$

where $\xi = c(x-\frac{a_0a}{\alpha}t^\alpha), b = -\frac{19b_2a\delta}{60A_2c\sqrt{-\delta}}, \ \ k = -\frac{ab_2}{60c^3A_2\sqrt{-\delta}}.$

Case 1.2 when $\delta > 0$, we have

where $\xi = c(x-\frac{a_0a}{\alpha}t^\alpha), b = \frac{19b_2a\delta}{60A_2c\sqrt{\delta}}, \ \ k = \frac{ab_2}{60c^3A_2\sqrt{\delta}}.$

where $\xi = c(x-\frac{a_0a}{\alpha}t^\alpha), b = -\frac{19b_2a\delta}{60A_2c\sqrt{\delta}}, \ \ k = -\frac{ab_2}{60c^3A_2\sqrt{\delta}}.$

Again if $A_2 = 0$, $A_1\neq 0$ and $\mu = 0$ in (4.8), we obtain some traveling wave solutions.

Case 2.1 when $\delta < 0$, we have

where $\xi = c(x-\frac{a_0a}{\alpha}t^\alpha), b = \frac{19b_2a\delta}{60c\sqrt{A_1^2\delta}}, \ \ k = \frac{ab_2}{60c^3\sqrt{A_1^2\delta}}.$

Case 2.2 when $\delta > 0$, we have

where $\xi = c(x-\frac{a_0a}{\alpha}t^\alpha), b = \frac{19b_2a\delta}{60c A_1\sqrt{\delta}}, \ \ k = \frac{ab_2}{60c^3 A_1\sqrt{\delta}}.$

where $\xi = c(x-\frac{a_0a}{\alpha}t^\alpha), b = -\frac{19b_2a\delta}{60c A_1\sqrt{\delta}}, \ \ k = -\frac{ab_2}{60c^3 A_1\sqrt{\delta}}.$

If we choose $A_1 = 0$, $A_2\neq 0$ and $\mu = 0$ in (4.9), we obtain some traveling wave solutions, for example

Case 3.1 when $\delta < 0$, we have

where $\xi = c(x-\frac{a_0a}{\alpha}t^\alpha), b = -\frac{19b_2a\delta}{660A_2c\sqrt{-\delta}}, \ \ k = \frac{ab_2}{60c^3A_2\sqrt{-\delta}}.$

where $\xi = c(x-\frac{a_0a}{\alpha}t^\alpha), b = \frac{19b_2a\delta}{660A_2c\sqrt{-\delta}}, \ \ k = -\frac{ab_2}{60c^3A_2\sqrt{-\delta}}.$

Case 3.2 when $\delta > 0$, we have

where $\xi = c(x-\frac{a_0a}{\alpha}t^\alpha), b = -\frac{19b_2a\delta}{660A_2c\sqrt{\delta}}, \ \ k = \frac{ab_2}{60c^3A_2\sqrt{\delta}}.$

where $\xi = c(x-\frac{a_0a}{\alpha}t^\alpha), b = \frac{19b_2a\delta}{660A_2c\sqrt{\delta}}, \ \ k = -\frac{ab_2}{60c^3A_2\sqrt{\delta}}.$

Again if $A_2 = 0$, $A_1\neq 0$ and $\mu = 0$ in (4.9), we obtain some traveling wave solutions.

Case 4.1 when $\delta < 0$, we have

where $\xi = c(x-\frac{a_0a}{\alpha}t^\alpha), b = -\frac{19b_2a\delta}{660c\sqrt{A_1^2\delta}}, \ \ k = \frac{ab_2}{60c^3\sqrt{A_1^2\delta}}.$

Case 4.2 when $\delta > 0$, we have

where $\xi = c(x-\frac{a_0a}{\alpha}t^\alpha), b = -\frac{19b_2a\delta}{660A_1c\sqrt{\delta}}, \ \ k = \frac{ab_2}{60c^3A_1\sqrt{\delta}}.$

where $\xi = c(x-\frac{a_0a}{\alpha}t^\alpha), b = \frac{19b_2a\delta}{660A_1c\sqrt{\delta}}, \ \ k = -\frac{ab_2}{60c^3A_1\sqrt{\delta}}.$

4.2.   (3+1)-dimensional time-fractional KdV-Zakharov-Kuznetsov (KdV-ZK) equation

Consider the (3+1)-dimensional time-fractional KdV-Zakharov-Kuznetsov (KdV-ZK) equation ^[24,25]:

where $0 < \alpha\leq 1$ and $a, b$ are arbitrary constants.

It is well known that the Korteweg-de Vries (KdV) equation arises as an model for one-dimensional long wavelength surface waves propagating in weakly nonlinear dispersive media, as well as the evolution of weakly nonlinear ion acoustic waves in plasmas. The ZK equation is one of two well-studied canonical two-dimensional extensions of the Korteweg-de Vries equation. In recent, S. Shoo et al. ^[25] found some new exact traveling wave solutions of Eq. (4.29) by the simplest equation method.

To solve (4.29), we use the wave transformations:

then (4.29) is reduced into a nonlinear ODE in the form

By reducing (4.31), we get

Further by integrating (4.32) with respect to $\xi$, we get

By balancing the highest order derivative term $u''$ and nonlinear term $u^2$ in (4.33), the value of $n$ can be determined, which is $n = 2$ in this problem. Therefore, by equation (3.4), we have the following ansatz:

where $a_0, a_1, a_2, b_0$ and $b_1$ are constants to be determined later, and function $\phi(\xi)$ satisfies (3.5).

By substituting (4.34) into (4.33) and using the second order linear ODE (3.5) and (3.7), collecting all terms with the same order of $\frac{1}{\phi^i}$ and $\frac{1}{\phi^i}\frac{\phi'}{\phi}$ together, the left-hand side of (4.33) is converted into another polynomial in $\frac{1}{\phi^i}$ and $\frac{1}{\phi^i}\frac{\phi'}{\phi}$. Equating each coefficient of this different power terms to zero yields a set of algebraic equations for $a_0, a_1, a_2, b_0, b_1, \delta, \mu, a, b, c$ and $\upsilon$. Solving this system of algebraic equations, with the aid of Maple, we obtain

Substituting (4.35) and (4.36) and the general solutions (3.6) of Eq. (3.5) into (4.34), we obtain more exact solutions of (4.29):

where $\xi = c(x+y+z\mp\frac{\delta ab_1}{6\sqrt{\Xi_i}\alpha}t^\alpha), \ \ b = -\frac{6c^2\sqrt{\Xi_i}\pm ab_1}{12c^2\sqrt{\Xi_i}}$.

where $\xi = c(x+y+z\pm\frac{\delta ab_1}{6\sqrt{\Xi_i}\alpha}t^\alpha), \ \ b = -\frac{6c^2\sqrt{\Xi_i}\pm ab_1}{12c^2\sqrt{\Xi_i}}$, in which $i = 1$ for $\delta < 0$, $i = 2$ for $\delta > 0$, $i = 3$ for $\delta = 0$, and $\Phi_i, \Psi_i, \Xi_i, \ (i = 1, 2, 3)$ see (4.10)-(4.14).

Here $A_1$ and $A_2$ are arbitrary constants. Therefore, one can freely select their values. If we choose $A_1 = 0$, $A_2\neq 0$, $\mu = 0$ and $\delta > 0$ in (4.37), we obtain some traveling wave solutions.

where $\xi = c(x+y+z-\frac{\delta ab_1}{6A_2\alpha\sqrt{\delta}}t^\alpha), b = -\frac{6c^2A_2\sqrt{\delta}+ ab_1}{12c^2A_2\sqrt{\delta}}.$

where $\xi = c(x+y+z+\frac{\delta ab_1}{6A_2\alpha\sqrt{\delta}}t^\alpha), b = \frac{-6c^2A_2\sqrt{\delta}+ ab_1}{12c^2A_2\sqrt{\delta}}.$

If we choose $A_1 = 0$, $A_2\neq 0$, $\mu = 0$ and $\delta < 0$ in (4.38), we obtain some other traveling wave solutions.

where $\xi = c(x+y+z+\frac{\delta ab_1}{6A_2\alpha\sqrt{-\delta}}t^\alpha), b = -\frac{6c^2A_2\sqrt{-\delta}+ ab_1}{12c^2A_2\sqrt{-\delta}}.$

where $\xi = c(x+y+z-\frac{\delta ab_1}{6A_2\alpha\sqrt{-\delta}}t^\alpha), b = \frac{-6c^2A_2\sqrt{-\delta}+ ab_1}{12c^2A_2\sqrt{-\delta}}.$

If we choose $A_1 = 0$, $A_2\neq 0$, $\mu = 0$ and $\delta > 0$ in (4.38), we obtain some traveling wave solutions.

where $\xi = c(x+y+z+\frac{\delta ab_1}{6A_2\alpha\sqrt{\delta}}t^\alpha), b = -\frac{6c^2A_2\sqrt{\delta}+ ab_1}{12c^2A_2\sqrt{\delta}}.$

where $\xi = c(x+y+z-\frac{\delta ab_1}{6A_2\alpha\sqrt{\delta}}t^\alpha), b = \frac{-6c^2A_2\sqrt{\delta}+ ab_1}{12c^2A_2\sqrt{\delta}}.$

Similarly, we can write down the other families of exact solutions of Eq. (4.29) which are omitted for convenience.

4.3.   Time-fractional Sharma-Tasso-Olver (FSTO) equation

Consider the time-fractional Sharma-Tasso-Olver (FSTO) equation ^[26,27]:

where $a$ is an arbitrary constant and $0 < \alpha\leq 1$. The function $u(x, t)$ is assumed to be a causal function of time. i.e. vanishing for $t < 0$. The general response expression contains a parameter describing the order of the fractional derivative that can be varied to obtain various responses. In the case of $\alpha = 1$, Eq. (4.45) reduces to the classical nonlinear STO equation. L. Song ^[26] found a rational approximation solution of Eq. (4.45) by the variational iteration method, the Adomian decomposition method and the homotopy perturbation method.

To solve (4.45), we use the wave transformations:

then (4.45) is reduced into a nonlinear ODE in the form

By reducing (4.47), we get

Further by integrating (4.48) with respect to $\xi$, we get

By balancing the highest order derivative term $u''$ and nonlinear term $u^3$ in (4.49), the value of $n$ can be determined, which is $n = 1$ in this problem. Therefore, by Eq. (3.4), we have the following ansatz:

where $a_0, a_1$ and $b_0$ are constants to be determined later, and function $\phi(\xi)$ satisfies (3.5).

By substituting (4.50) into (4.49) and using the second order linear ODE (3.5) and (3.7), collecting all terms with the same order of $\frac{1}{\phi^i}$ and $\frac{1}{\phi^i}\frac{\phi'}{\phi}$ together, the left-hand side of (4.49) is converted into another polynomial in $\frac{1}{\phi^i}$ and $\frac{1}{\phi^i}\frac{\phi'}{\phi}$. Equating each coefficient of this different power terms to zero yields a set of algebraic equations for $a_0, a_1, b_0, \delta, \mu, a, c$ and $\upsilon$. Solving this system of algebraic equations, with the aid of Maple, we obtain

Substituting (4.51)-(4.54) and the general solutions (3.6) of Eq. (3.5) into (4.50), we obtain more exact solutions of (4.45):

where $\xi = c(x+\frac{ac^2\delta t^\alpha}{\alpha}).$

where $\xi = \pm\frac{2b_0}{\sqrt{\Xi_i}}(x+\frac{b_0^2a\delta t^\alpha}{\Xi_i\alpha}).$

where $\xi = \frac{2b_0}{\sqrt{\Xi_i}}(x+\frac{4b_0^2a\delta t^\alpha}{\Xi_i\alpha}).$

where $\xi = -\frac{2b_0}{\sqrt{\Xi_i}}(x+\frac{4b_0^2a\delta t^\alpha}{\Xi_i\alpha}),$ in which $i = 1$ for $\delta < 0$, $i = 2$ for $\delta > 0$, $i = 3$ for $\delta = 0$, and $\Phi_i, \Psi_i, \Xi_i, \ (i = 1, 2, 3)$ see (4.10)-(4.14).

Here $A_1$ and $A_2$ are arbitrary constants. Therefore, one can freely select their values. If we choose $A_1 = 0$, $A_2\neq 0$, $\mu = 0$ and $\delta < 0$ in (4.55), we the traveling wave solution:

If we choose $A_1 = 0$, $A_2\neq 0$, $\mu = 0$ and $\delta > 0$ in (4.55), we obtain the traveling wave solution:

If we choose $A_2 = 0$, $A_1\neq 0$, $\mu = 0$ and $\delta > 0$ in (4.55), we obtain the traveling wave solution:

where $\xi = c(x+\frac{ac^2\delta}{\alpha}t^\alpha).$

Similarly, we can write down the other families of exact solutions of Eq. (4.45) which are omitted for convenience.

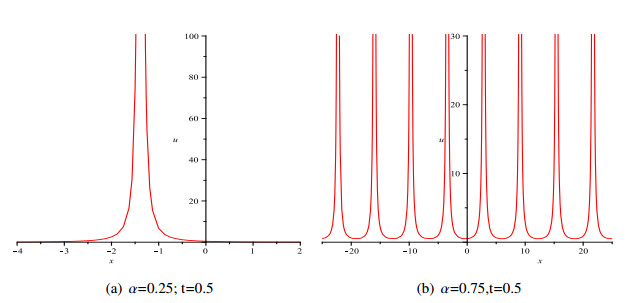
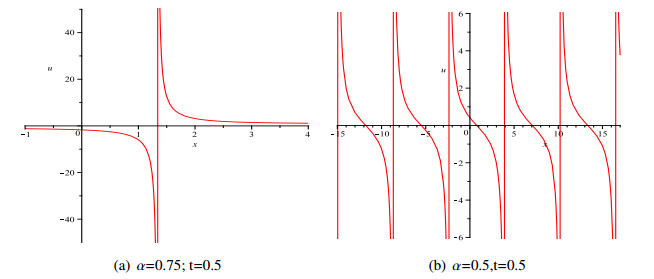
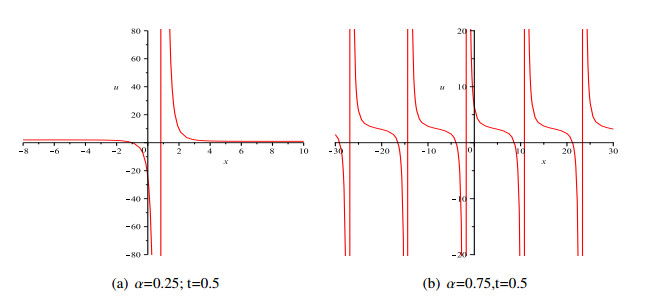
5.   Figures of some exact solutions

In this section, some typical wave figures are given as follows (Figure 1-3):

6.   Results and discussion

The basic idea of the two variable $(\phi'/\phi, 1/\phi)$-expansion method is to research the new exact traveling wave solutions of the mentioned Eqs. (4.1), (4.29) and Eq. (4.45). The Eqs. (4.1), (4.29) and (4.29) have been studied using various techniques, among them, Authors obtained some new solutions, but the researches considered the Jumaries modified Riemann-Liouville derivative sense for their solution techniques. Nonetheless, the existing analytical solutions reported in ^[23,24,27] are not correct because the utilized definitions of fractional derivative have some shortcomings that could not be overlooked ^[21]. Chen et al. ^[25] found some new solutions of Eq. (4.29) expressed by tanh, coth, tan and cot form. In our case, first time we considered the conformable fractional derivative sense and two variable $(\phi'/\phi, 1/\phi)$-expansion method for the Eqs. (4.1), (4.29) and (4.45), we found some new solutions expressed by tanh, coth, sech, csch, tan, cot, sec and csc form. To our knowledge, the solutions obtained have not been reported in former literature. So, all the solutions are new in this article.

7.   Conclusion

In this study, the two variable $(\phi'/\phi, 1/\phi)$-expansion method with the help of conformable wave transformation has been applied to find out exact traveling wave solutions of time-fractional differential equations. We have obtained some new and further general solitary wave solutions to three nonlinear time fractional differential equation, namely, time-fractional K-S equation, (3+1)-dimensional KdV-ZK equation and FSTO equation in terms of hyperbolic, trigonometric and rational function solution involving parameters. These solutions have important physical implications, for example, these solutions forces are convenient to characterize the hydromagnetic waves in cold plasma, acoustic waves in inharmonic crystals and acoustic-gravity waves incompressible fluids. The obtained results show that the two variable $(\phi'/\phi, 1/\phi)$-expansion method is direct, consistent, reliable, very much attractive and an effective powerful mathematical tool for obtaining the exact solutions of other time fractional differential equations, and it can be generalized to nonlinear space-time fractional differential equations and space fractional differential equations. Finally, our results in this article have been checked using the Maple by putting them back into the original equation.

Acknowledgments

The authors would like to express their deepest appreciation to the reviewers for their valuable suggestions and comments to improve the article.

This work was supported by the Middle-Aged Academic Backbone of Honghe University (No. 2014GG0105; No.2015GG0207), Scientific Research Foundation of Yunnan Education Department (No. 2018JS479) Yunnan Applied Basic Research Project(No.2018FH001013; 2018FH001014) and the Natural Science Foundation of Education Committee of Yunnan Province (No. 2019J0558).

Conflict of interest

The authors declare no conflict of interest.