An epidemic-economic model for COVID-19

Jie Bai; Xiunan Wang; Jin Wang; Jie Bai; Xiunan Wang; Jin Wang

doi:10.3934/mbe.2022449

Mathematical Biosciences and Engineering

2022, Volume 19, Issue 9: 9658-9696. doi: 10.3934/mbe.2022449

Previous Article Next Article

Research article Special Issues

An epidemic-economic model for COVID-19

1.
School of Mathematics and Statistics, Liaoning University, Shenyang 110036, China
2.
Department of Mathematics, University of Tennessee at Chattanooga, Chattanooga, TN 37403, USA

Received: 10 April 2022 Revised: 04 June 2022 Accepted: 16 June 2022 Published: 04 July 2022

In this paper, we propose a new mathematical model to study the epidemic and economic consequences of COVID-19, with a focus on the interaction between the disease transmission, the pandemic management, and the economic growth. We consider both the symptomatic and asymptomatic infections and incorporate the effectiveness of disease control into the respective transmission rates. Meanwhile, the progression of the pandemic and the evolution of the susceptible, infectious and recovered population groups directly impact the mitigation and economic development levels. We fit this model to the reported COVID-19 cases and unemployment rates in the US state of Tennessee, as a demonstration of a real-world application of the modeling framework.

Keywords:

Citation: Jie Bai, Xiunan Wang, Jin Wang. An epidemic-economic model for COVID-19[J]. Mathematical Biosciences and Engineering, 2022, 19(9): 9658-9696. doi: 10.3934/mbe.2022449

Related Papers:

[1]	M. Mohseni Takallo, Rajab Ali Borzooei, Seok-Zun Song, Young Bae Jun . Implicative ideals of BCK-algebras based on MBJ-neutrosophic sets. AIMS Mathematics, 2021, 6(10): 11029-11045. doi: 10.3934/math.2021640
[2]	Abdelaziz Alsubie, Anas Al-Masarwah . MBJ-neutrosophic hyper $BCK$ -ideals in hyper $BCK$ -algebras. AIMS Mathematics, 2021, 6(6): 6107-6121. doi: 10.3934/math.2021358
[3]	Amr Elrawy, Mohamed Abdalla . Results on a neutrosophic sub-rings. AIMS Mathematics, 2023, 8(9): 21393-21405. doi: 10.3934/math.20231090
[4]	D. Jeni Seles Martina, G. Deepa . Some algebraic properties on rough neutrosophic matrix and its application to multi-criteria decision-making. AIMS Mathematics, 2023, 8(10): 24132-24152. doi: 10.3934/math.20231230
[5]	Ali Yahya Hummdi, Amr Elrawy, Ayat A. Temraz . Neutrosophic modules over modules. AIMS Mathematics, 2024, 9(12): 35964-35977. doi: 10.3934/math.20241705
[6]	Dongsheng Xu, Huaxiang Xian, Xiewen Lu . Interval neutrosophic covering rough sets based on neighborhoods. AIMS Mathematics, 2021, 6(4): 3772-3787. doi: 10.3934/math.2021224
[7]	Sumyyah Al-Hijjawi, Abd Ghafur Ahmad, Shawkat Alkhazaleh . A generalized effective neurosophic soft set and its applications. AIMS Mathematics, 2023, 18(12): 29628-29666. doi: 10.3934/math.20231517
[8]	D. Ajay, P. Chellamani, G. Rajchakit, N. Boonsatit, P. Hammachukiattikul . Regularity of Pythagorean neutrosophic graphs with an illustration in MCDM. AIMS Mathematics, 2022, 7(5): 9424-9442. doi: 10.3934/math.2022523
[9]	Ning Liu, Zengtai Gong . Derivatives and indefinite integrals of single valued neutrosophic functions. AIMS Mathematics, 2024, 9(1): 391-411. doi: 10.3934/math.2024022
[10]	Mohammad Hamidi, Florentin Smarandache . Valued-inverse Dombi neutrosophic graph and application. AIMS Mathematics, 2023, 8(11): 26614-26631. doi: 10.3934/math.20231361

Abstract

1. Introduction

The development of highway pavement as the basis for maintaining the national economy has led to a large investment in highway infrastructure construction in the early stages of construction worldwide, thus causing a lack of corresponding funds for maintenance and rehabilitation of highways ^[1,2]. Meanwhile, with the continuous development and expansion of China highway network, the durability of various highways in use is facing serious challenges. Pavement maintenance aims to prolong the service life of roads and ensure safe and comfortable driving of vehicles, which has been paid more and more attention by pavement maintenance engineers ^[3].

With the continuous development of pavement maintenance technology, based on which the concept of pavement management system has been proposed, pavement management has also made significant achievements in optimal decision making ^[4,5,6,7,8]. The main purpose of a pavement management system (PMS) is to identify pavement maintenance needs, generate appropriate pavement maintenance schedules, and maintain the pavement in good serviceable condition with limited funds, maximizing the ability to assist highway engineers and pavement managers in making cost-effective and effective pavement rehabilitation decisions ^[9,10]. The PMS includes environmental elements such as weather, traffic levels, axle weights, and detailed information such as pavement structure. It is important to incorporate factors such as pavement-related data into pavement maintenance decisions ^[11,12,13].

Determining the weight of each item factor is the main issue in road maintenance decision making. On the other hand, the hierarchical analysis method (AHP) is a typical systems engineering method that transforms qualitative analysis into quantitative analysis, which not only effectively determines the weight of each factor but also considers both quantitative and qualitative factors ^{[14,15,16,17]}. Applying the AHP method to the road maintenance decision system can solve a decision problem with many decision criteria that are difficult to quantify. At the same time, it is important for determining weights and expressing alternatives based on multiple criteria ^[11]. Network-level pavement maintenance decision-making as a multi-factor, multi-criteria problem determines the maintenance priority of the corresponding section of the road network by considering the performance and other characteristics of all sections ^[18]. The main factors that are usually considered for network-level maintenance decisions are pavement age, performance, load, and structure ^[19]. For network-level pavement maintenance decisions, on the one hand, various maintenance treatments are needed to maintain a high level of pavement performance so as to meet the requirements of road users; on the other hand, pavement maintenance costs need to be minimized ^[20,21]. The network-level pavement maintenance decision requires a reasonable ranking of all maintenance sections based on specific indicators such as performance, traffic volume, and relative importance of the sections to meet the maintenance requirements of individual sections ^[22]. The evolution of intelligent road systems has introduced innovative techniques for road ailment detection and real-time road weight measurements. This includes leveraging technologies such as sensitive surface layers and cement-based sensors, enabling the comprehensive collection and analysis of diverse traffic data within intricate and real-world driving scenarios. In addition, this innovative distress monitoring method will contribute to the intelligent maintenance of highways ^[23,24].

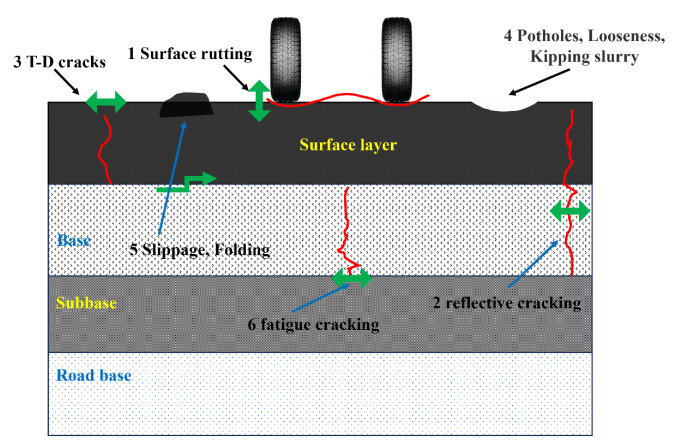
Furthermore, addressing the prevailing damage pattern observed in the semi-rigid base asphalt pavement of Chinese highways, as depicted in Figure 1, entails addressing several key aspects. These primarily encompass: 1) bottom-up fatigue cracks originating from the fatigue-induced fracturing of semi-rigid base layers. 2) Bottom-up reflection cracks stemming from the dry or temperature-induced contraction of semi-rigid base layers. 3) Surface rutting, a consequence of vehicular loading. 4) Top-down T-D cracks are attributed to material aging under conditions of low temperature, load stress, and more. 5) Slippage and folding resulting from inadequate interlayer adhesion. 6) Potholes, loosening, and kipping slurry due to insufficient water stability within the asphalt mixture ^[25,26]. These modes of pavement damage exert a notable impact not only on the comfort and safety of highway travel but also on the overall service quality of highways. These effects are not conducive to the sustained progress of highway construction in the long run.

Figure 1. Damage pattern of asphalt pavement.

DownLoad: Full-Size Img PowerPoint

Given this understanding, a compelling initiative has been undertaken to secure the enduring stability of highway pavement structures. This endeavor is grounded in the pursuit of bolstering the immediate gains stemming from prevailing pavement maintenance decisions. Acknowledging the limitations of solitary maintenance approaches, a strategic and scientifically informed decision-making system for safeguarding pavement structures has been meticulously formulated. This system not only addresses these shortcomings but also elevates the efficacy of short-term maintenance strategies, thereby fostering a comprehensive and forward-looking approach to highway pavement preservation. Simultaneously, this article introduces a novel concept—the notion of long-term preservation for asphalt pavement structures. Employing the analytic hierarchy process and network-level pavement maintenance decision-making, the existing highway maintenance decision tree model is systematically optimized in alignment with this new paradigm. This approach takes into account the prevailing circumstances and maintenance requirements of the pavement. The overarching objective is to circumvent the necessity for major repairs and extensive reconstruction of asphalt pavement structures on highways. By maintaining the long-term stability of pavement structural performance, this approach aims to significantly prolong the service life of the pavement, thereby contributing to the sustainable growth of highway infrastructure.

2. Methodology

2.1. Decision-making methods

When it comes to making maintenance decisions at the project level, decision trees serve a dual purpose. They not only effectively rank the significance of various indicators but also hold the advantage of being straightforward and easily comprehensible to decision-makers ^[27]. Consequently, the decision tree approach is employed as the foundation for conducting the pavement maintenance decision-making study. The key process unfolds as follows: initiating with the selection of the primary decision indicator to establish the primary indicator's branching threshold, progressing to the secondary bifurcation node for the choice of the secondary decision indicator and its corresponding branching threshold, and finally culminating in the tertiary bifurcation node where the conservation program decision is made, illustrated in Figure 2.

Figure 2. Decision tree diagram.

DownLoad: Full-Size Img PowerPoint

2.2. Selection of decision indicators

The maintenance decision is predominantly categorized into three modules: preventive maintenance, structural preservation, and structural overhaul. These categories are determined based on the existing conditions and maintenance requirements of highway pavements ^[28]. In the process of identifying appropriate indicators for preventive maintenance decisions, the central objective revolves around fulfilling the demands of preventive maintenance. Specifically, functional indicators are employed as decision metrics, encompassing aspects like damage condition, levelness, and skid resistance ^[29]. Conversely, when discerning indicators for structural overhaul decisions, the primary focus shifts to ensuring the pavement's structural integrity. In this context, decision indicators encompass both structural criteria, such as the overall structural strength of the pavement (D0) and the structural strength of the subgrade (D20–D60), as well as material-related measures like the bottom tensile stress ratio of the inorganic bond stabilization layer. For the determination of indicators related to structural preservation decisions, the key considerations revolve around characteristic ailments such as rut depth and transverse cracks. Here, the chosen decision indicators span across structural elements, including transverse crack spacing and rut depth/rut annual increment, alongside material factors such as Hamburg rut depth and the composite average strain rate ^[30]. In this study, the evaluation of high-temperature stability was focused on the medium surface layer material for the surface layer. Furthermore, to streamline the maintenance decision-making process and enhance its practicality for maintenance management, design, and implementation, it is advisable to concentrate solely on macroscopic indicators when evaluating pavement crack conditions. Specifically, utilizing the transverse crack spacing indicator for decision-making purposes is recommended. Moreover, it is important to acknowledge that the magnitude of traffic axle load exerts a discernible impact on the optimal selection of maintenance strategies. Consequently, when deliberating over maintenance decisions pertaining to structural preservation and structural overhaul, it is essential to incorporate the traffic class as a significant decision indicator.

2.3. Prioritization of decision indicators

The process of determining the priority of decision indicators requires systematic arrangement and adherence to a hierarchical order of strength and relevance based on specific maintenance requirements. Given the inherent significance of each indicator and the actual maintenance imperatives, this prioritization is essential. Considering that the pavement's structural strength index serves as a fundamental cornerstone for pavement structural design, and given that pavements experiencing greater bending and sinking also exhibit accelerated performance degradation, the initial focal point of pavement maintenance decisions should be the evaluation of structural stability. This pivotal assessment serves as the foremost step, setting the foundation for subsequent considerations. In contrast, the evaluation of functionality, encapsulating indicators such as damage condition and skid resistance, should be the concluding aspect of the decision-making process, as articulated in Figure 3 for reference ^[31]. Firstly, through the assessment of overall pavement condition, it is judged whether to carry out subgrade stability assessment or directly into surface stability assessment. Second, through the assessment of subgrade stability, it is judged whether to carry out structural overhaul or directly enter surface stability assessment. Then, through the assessment of surface stability, it is judged whether to carry out structural preservation or directly engage in functional assessment of the road surface. Finally, through the assessment of road surface functionality, it is judged whether to carry out preventive or routine maintenance.

Figure 3. Classification chart of pavement decision indicators.

DownLoad: Full-Size Img PowerPoint

1) In gauging the comprehensive pavement condition, the foremost criterion employed for evaluation is the overall structural strength, denoted as D0. If the evaluation against this indicator aligns with the stipulated criteria, then an assessment of surface layer stability can be pursued. Conversely, when the criteria are not met, a subsequent examination of subgrade stability becomes necessary. Consequently, the overall structural strength index, D0, serves as the primary, foundational decision indicator for the initial assessment of subgrade stability.

2) In the context of subgrade stability assessment, a twofold approach is adopted. Initial evaluation entails an analysis of macroscopic performance, followed by a more comprehensive exploration of material characteristics. Within this framework, the structural strength of the subgrade (specifically, D20–D60) serves as the second-tier decision index, addressing macroscopic performance. Subsequently, the tensile stress ratio at the base of the inorganic bonded stabilization layer was included as a tertiary decision indicator with focus on material-related properties. To account for the influence of traffic axle load, a fourth-tier decision index is incorporated, reflecting the traffic level. This multifaceted consideration ensures a comprehensive evaluation of subgrade stability, encapsulating both structural and material aspects as well as the impact of varying traffic conditions.

3) When appraising surface layer stability, the emphasis centers on scrutinizing high-temperature stability and resistance against cracking. This evaluation revolves around distinct parameters. At the primary level, the transverse crack spacing stands as the key decision index, reflecting macroscopic performance. Subsequently, rutting depth and its annual increment serve as the second-tier decision index, addressing macro-level characteristics. Furthermore, material performance is taken into account, represented by the third-level decision index—namely, the Hamburg rutting depth of the medium surface layer in tandem with the composite average strain rate. To accommodate the influence of varying traffic axle loads, a fourth-tier decision index is incorporated, encompassing the traffic class as an additional determinant. This comprehensive approach ensures an encompassing assessment of surface layer stability, factoring in macro and material elements as well as the impact of traffic dynamics.

4) For the assessment of road surface functionality, the primary decision indicator is pavement deterioration, the secondary decision indicator is smoothness, and the tertiary decision indicator is skid resistance.

2.4. Decision conditions

Decision conditions play a pivotal role in the construction of decision trees. These conditions serve as the basis for making judgments that dictate the course of the decision tree's branches, subsequently guiding the progression towards the subsequent levels of decision-making. Based on the outcomes derived from the assessment of pavement performance, as depicted in Table 1, the decision conditions associated with each evaluation index have been consolidated. By combining the decision conditions with the decision indicator selection scheme, the decision tree model for highway asphalt pavement maintenance is formulated. This model is visually represented in Figure 4.

Table 1. Decision indicators and conditions for pavement performance.

Decision priority		Level 1	Level 2	Level 3	Level 4
Structural overhaul	Decision indicator	Overall structural strength of the road surface D₀	Structural strength of the subgrade D₂₀-D₆₀	Tensile stress ratio at the base of the inorganic bond stabilized layer	Traffic class
Structural overhaul	Decision conditions	● Level 1 ● Level 2	● Level 1 ● Level 2 ● Level 3		● Light, medium, heavy ● extra heavy, very heavy
Structural preservation	Decision indicator	Transverse crack spacing	Rutting depth/annual increment of rutting	Medium surface layer Hamburg rutting depth/composite mean strain rate	Traffic class
Structural preservation	Decision conditions	● Level 1, 2 ● Level 3	● Level 1 ● Level 2 ● Level 3		● Light, medium, heavy ● extra heavy, very heavy
Preventive maintenance	Decision indicator	Breakage	Flatness	Slip resistance
Preventive maintenance	Decision conditions	● Excellent ● Medium ● Sub-poor	● Excellent ● Medium ● Sub-poor	● Excellent ● Medium、Sub-poor

| Show Table

DownLoad: CSV

Figure 4. Decision tree model for highway asphalt pavement maintenance.

DownLoad: Full-Size Img PowerPoint

3. Optimization of decision methods

3.1. Structure preservation decision optimization

The intelligent execution of structural preservation decisions employs decision trees for decision-making at the project level. This approach involves establishing the maintenance priority for each road section through the selected decision indicators using a ranking methodology. This process identifies the road segments that require immediate maintenance attention. Subsequently, mathematical optimization techniques are employed to strategize and resolve the choice of maintenance measures for the remaining sections. This comprehensive approach culminates in the development of a structured preservation plan, effectively ensuring the longevity and integrity of the infrastructure.

The hierarchical analysis method can better determine the weights of each sub-indicator ^[32], thus providing a basis for the development of comprehensive indicators. Therefore, the degree of urgency in this study can be determined by the target layer (A). The determination of the degree of urgency should take into account the traffic volume, subgrade condition, high temperature, and cracking performance of the pavement. Thus, these four aspects can be determined as the guideline layer (C). The classification of decision indicators D20–D60, traffic volume, rutting depth, and cross-joint spacing can then be used as the bottom layer P.

Expert survey data were meticulously gathered, with 30 sets of survey data chosen as representative samples. The process involved determining the single-layer weight coefficients, which are depicted in Table 2, and subsequently arriving at the ultimate synthetic weights, as illustrated in Table 3.

Table 2. Single-layer weighting factors.

Layer	Indicator	Weighting factor
Guideline layer	Base layer performance	0.37
	High temperature deformation of the pavement	0.29
	Pavement cracking performance	0.23
	Traffic volume	0.11
Indicator layer - high temperature performance	Macroscopic indicator	1
Indicator layer - cracking performance	Macroscopic indicator	1

| Show Table

DownLoad: CSV

Table 3. Synthetic weights.

Indicator	Weighting
Base layer	0.37
High temperature macro-indicator (rutting depth / annual increment of rutting)	0.29
Cracking resistance macro-indicator (cross-seam spacing)	0.23
Traffic volume	0.11

| Show Table

DownLoad: CSV

The sense of urgency directly corresponds to the imperative of promptly initiating the structural preservation initiative. Moreover, when faced with budget constraints, prioritizing the structural preservation of road sections becomes paramount. Utilizing the performance formula outlined earlier, a quantitative analysis is conducted, leveraging the urgency factor. This analysis yields a ranking from highest to lowest urgency values, thus enabling the identification of road sections with pronounced urgency, which are subsequently accorded precedence for structural preservation efforts.

3.2. Network-level intelligent decision optimization

Network-level optimal decision-making typically involves examining a specific-sized road network. The objective is to achieve the optimal synergy between maintenance strategies and fund allocation while considering financial limitations and other resource constraints. This pursuit aims to maximize defined benefits, such as pavement performance. Alternatively, this approach can also involve determining the most suitable maintenance strategies within the confines of prescribed pavement performance thresholds and resource limitations. In this scenario, the primary goal is to minimize various cost-related objectives, including maintenance expenses and user costs ^[33,34].

The optimization of the entire life cycle at the network level builds upon the optimized outcomes of individual section decisions. Each single road section's optimized plan is treated as the foundational unit. The scheme table for each road section is converted into a scheme matrix, while the cost data is transformed into a cost matrix. Similarly, the difference in the Pavement Quality Index (PQI) before and after maintenance for each section is tabulated into a performance matrix. This comprehensive framework enables a holistic approach to optimizing network-wide decisions while preserving the integrity of individual section-level plans.

Assuming section i has p n-year options, then the p-dimensional vector Xi will be the solution of the optimal maintenance solution chosen for section i.

${X}_{i} = \left(\begin{array}{ccc}\begin{array}{cc}{x}_{1}& {x}_{2}\end{array}& \begin{array}{cc}\dots & {x}_{i}\end{array}& \begin{array}{cc}\dots & {x}_{p}\end{array}\end{array}\right)$

(1)

The value of xi in the vector is only 0 or 1, which is a 0–1 planning problem in integer programming. When Xi is 1, it means that the i option is chosen as the maintenance option for the road section, in which the constraint is:

${\sum }_{i = 1}^{p}{x}_{i} = 1$

(2)

Indicating that among the p options for road section i, there is one and only one option that is the eligible n-year optimal maintenance option for that road section.

Denote the maintenance company's budget for year n as an n-dimensional vector $\overrightarrow{F}$ , and f_i denotes the maintenance budget for year i.

$\overrightarrow{F} = \left(\begin{array}{ccc}\begin{array}{cc}{f}_{1}& {f}_{2}\end{array}& \begin{array}{cc}\dots & {f}_{i}\end{array}& \begin{array}{cc}\dots & {f}_{n}\end{array}\end{array}\right)$

(3)

Based on the maintenance budget of the conservation company, the total cost of the selected options for each of the S sections each year cannot exceed the cost budget of the conservation company for that year, whereby the cost constraint equation established is:

${\sum }_{i = 1}^{s}{X}_{i}*{B}_{i}\le F$

(4)

${X}_{i}*{B}_{i} = \left[\begin{array}{ccc}\begin{array}{cc}{x}_{1}& {x}_{2}\end{array}& \begin{array}{cc}\dots & {x}_{i}\end{array}& \begin{array}{cc}\dots & {x}_{p}\end{array}\end{array}\right]*\left[\begin{array}{ccc}\begin{array}{cc}{\mathrm{b}}_{11}& {\mathrm{b}}_{12}\\ {\mathrm{b}}_{21}& {\mathrm{b}}_{22}\end{array}& \begin{array}{cc}{\mathrm{b}}_{13}& {\mathrm{b}}_{14}\\ {\mathrm{b}}_{23}& {\mathrm{b}}_{24}\end{array}& \begin{array}{cc}{\mathrm{b}}_{15}& \dots \\ {\mathrm{b}}_{25}& \dots \end{array}\\ \begin{array}{cc}{\mathrm{b}}_{31}& {\mathrm{b}}_{32}\\ {\mathrm{b}}_{41}& {\mathrm{b}}_{42}\end{array}& \begin{array}{cc}{\mathrm{b}}_{33}& {\mathrm{b}}_{34}\\ {\mathrm{b}}_{43}& {\mathrm{b}}_{44}\end{array}& \begin{array}{cc}{\mathrm{b}}_{35}& \dots \\ {\mathrm{b}}_{45}& \dots \end{array}\\ \begin{array}{cc}{\mathrm{b}}_{51}& {\mathrm{b}}_{52}\\ \dots & \dots \end{array}& \begin{array}{cc}{\mathrm{b}}_{53}& {\mathrm{b}}_{54}\\ \dots & \dots \end{array}& \begin{array}{cc}{\mathrm{b}}_{55}& \dots \\ \dots & \dots \end{array}\end{array}\right]$

(5)

Based on the analysis of the life cycle maintenance objectives, it is clear that the optimal solution to be sought in this paper is to minimize the total cost of the maintenance program during the life cycle and maximize the sum of the PQI differences before and after the implementation of the program to obtain the best performance benefits. The two objective functions are:

$\mathit{min}{\sum }_{i = 1}^{s}{X}_{i}*{B}_{i}^{\text{'}}$

(6)

$\mathit{max}{\sum }_{i = 1}^{s}{X}_{i}*{C}_{i}^{\text{'}}$

(7)

The integrated cost constraint function solved X_i, which is the i section of the road to meet the conditions of the solution, where the solution of X_i for 1 indicates that the section of the alternative program of the i program is the optimal solution to meet the full section of life cycle planning. A complete highway will generally be divided into at least dozens or even hundreds of sections based on the analysis of the actual condition of the highway, solving for:

${X}_{i} = \left(\begin{array}{ccc}\begin{array}{cc}{x}_{1}& {x}_{2}\end{array}& \begin{array}{cc}\dots & {x}_{i}\end{array}& \begin{array}{cc}\dots & {x}_{p}\end{array}\end{array}\right)$

(8)

The solution corresponding to X_i = 1, which is the optimal solution in the section that meets the objective condition constraint, is solved by the multi-section association.

3.3. Decision-making module design

3.3.1. Visualization comprehensive data platform module

This module provides a browsing of the technical condition of the highway pavement of the road network in a province, mainly including the GIS map of the road network, the introduction of management agencies, the traffic axle load situation, weather conditions, the current status of the road network, and statistical analysis. Through this function, the overall situation of the road network can be understood, and it is easy for the management to grasp the road network information on a macro level. Leveraging the GIS platform, the visualization management of highway road maintenance is actualized through the seamless integration of diverse data types. This integration encompasses spatial data, attribute data, road condition data, maintenance records, and visual content such as images and videos. This comprehensive approach enables a dynamic and comprehensive depiction of highway road maintenance activities. This encompasses an electronic map browsing feature and an attribute data query function that collectively enable a comprehensive window display. Additionally, it encompasses the viewing of pavement damage images and road condition videos, facilitating easy understanding of on-site road conditions while significantly streamlining field investigation efforts. The platform also facilitates map-based presentations of traffic volume, road conditions, maintenance history, and other pertinent information. These visualizations provide an intuitive representation of the technical state of the road network. A detailed listing of its functions is visually depicted in Figure 5.

Figure 5. Visualization of the integrated data platform framework.

DownLoad: Full-Size Img PowerPoint

3.3.2. Data quality control module

Pavement technical condition data forms the cornerstone for pavement performance assessment, maintenance determinations, and performance projections. However, because of potential inaccuracies stemming from instrument measurement deviations and human operational missteps, the initial pavement technical condition data may exhibit poor quality and formatting differences. This disparity can hinder an accurate representation of the actual pavement state, thereby compromising the scientific rigor and efficacy of maintenance decisions. To address these challenges, this module undertakes rigorous quality control measures based on the available pavement condition data. It meticulously evaluates the data's accuracy, timeliness, consistency, and comprehensiveness, subsequently refining its quality. This meticulous process safeguards the rationality and precision of the research findings and conclusions.

The data quality inspection process encompasses several stages: data format validation, identification of missing data points, assessment of value range adherence, verification of degradation patterns, and cross-indicator consistency checks. Following the completion of this inspection phase, any anomalous values are treated as missing data, and suitable interpolation techniques are employed to fill in these gaps, thereby achieving data rectification. Initially, the error rate for each dataset is calculated, considering aspects like missing entries. If the error rate, encompassing the missing values, exceeds 50% in the preceding data inspections for a particular dataset, it signifies an inadequate availability of valid information within that dataset for modeling and predicting other data. Consequently, the entirety of the data associated with that dataset is omitted and is substituted by the data from the nearest dataset. This meticulous procedure guarantees the robustness and accuracy of the ensuing analyses and predictive models.

When a substantial portion of the preceding inspection data for the same pile number is deemed accurate—meaning the error rate remains below 50%—only the erroneous segment undergoes processing while the accurate data is preserved. In cases where missing values emerge, several interpolation methods can be employed, including mean interpolation, nearest neighbor interpolation, linear interpolation, and regression interpolation. This approach optimizes the correction process by focusing on rectifying inaccuracies and enhancing the reliability of the data set while ensuring that the majority of trustworthy information is retained.

3.3.3. Pavement performance evaluation and prediction module

Within this module, a comprehensive analysis and assessment of the technical state of all road sections within the network are conducted. This assessment draws upon the analytical outcomes derived from historical pavement technical condition data, enabling the prediction of pavement performance trends. These predictions furnish a foundational basis for evaluating network-wide maintenance decisions, thereby offering a robust framework to guide informed decision-making at a holistic level. The module provides a variety of data query and analysis methods to meet the needs of different users. Through this function, users can grasp the pavement performance status and development trend within the road network in a comprehensive and timely manner. Its functional framework is shown in Figure 6. Expanding upon conventional pavement performance evaluation metrics, additional indices are incorporated, encompassing both functional and structural facets. These encompass pavement driving quality assessment metrics, pavement safety performance indices, and evaluations of pavement rutting conditions. Furthermore, structural considerations are addressed through the inclusion of parameters such as bending and subsidence basin characteristics (D20–D60). To enhance the evaluative scope, material-related indices are introduced, spanning assessments of the stability of semi-rigid base materials, the high-temperature stability of asphalt surface materials, and the performance evaluation of crack resistance. This comprehensive approach ensures a well-rounded evaluation that spans diverse dimensions of pavement performance and integrity ^[35,36,37].

Figure 6. Functional framework for pavement performance evaluation and prediction.

DownLoad: Full-Size Img PowerPoint

Building upon the foundation of performance evaluation, the Garcia model is harnessed for performance prediction. This model comprises three regression coefficients that can be aligned with distinct performance impact indicators. By establishing a multi-factor differentiated performance degradation model, the accuracy of predictions is notably enhanced. It is important to acknowledge that the precision of the regression outcomes hinges on the accuracy of the original data. Inadequate data accuracy not only compromises the reliability of regression results but also casts doubt on the rationality of decision outcomes and the dependability of life cycle optimization findings ^[38].

The comprehensive amalgamation and streamlined analysis of all maintenance, performance, and traffic axle load data are facilitated through diverse methodologies. Simultaneously, cutting-edge data processing and optimization techniques are employed to guarantee users seamless and rapid access to the essential information stored within the extensive pavement database. This approach ensures that users can effortlessly and promptly retrieve the requisite data they need.

3.3.4. Maintenance decision module

The structural maintenance decision module and the network-level maintenance decision module in this study will further optimize the funding allocation scheme to rationally allocate and use the limited funding resources to maximize the system requirements. Four sub-functions are set in the "Maintenance Decision" module: intelligent decision-making, expert decision-making, decision-making scheme, implementation scheme comparison, and maintenance decision report. The functional framework is shown in Figure 7.

Figure 7. Functional framework of the maintenance decision module.

DownLoad: Full-Size Img PowerPoint

The intelligent decision is based on the intelligent maintenance decision optimization method, providing intelligent maintenance decisions and displays under the conditions of financial constraints, pavement performance constraints, and custom constraints. The expert decision can refer to the expert decision result based on the intelligent decision scheme. The query function of the final maintenance decision scheme is displayed in the form of graphs and tables, which can be downloaded and edited at the same time.

4. Project research cases

The Jin-Hang Expressway, Lian-Su Expressway, and Su-Tai Expressway are selected respectively as the relieving sections to carry out the application of pavement structure preservation countermeasures. Based on the survey results, combined with the pavement maintenance decision tree model and pavement structure preservation countermeasures, a maintenance plan that meets the requirements is selected for physical engineering application, and the pavement quality after implementation is tested.

4.1. Investigation of original road condition

1) Traffic load condition

For the purpose of traffic volume analysis, specific road sections were chosen: Sections XY-A and XY-B of the Jin-Hang Expressway; Sections HN-A and HN-B of the Lian-Su Expressway; and Sections GJXC-A and GJXC-B of the Su-Tai Expressway. These selections were subjected to comprehensive traffic volume surveys, and the resultant findings are presented in Table 4.

Table 4. Traffic volume survey results.

Road Section	XY-A	XY-B	HN-A	HN-B	GJXC-A	GJXC-B
Directional coefficient	0.50	0.50	0.52	0.52	0.50	0.50
Lane factor	0.60	0.60	0.42	0.40	0.50	0.55
AADTT (Vehicles/day)	3966	3863	48501	23593	14383	12791
Annual growth rate of traffic volume(%)	8		2		8

| Show Table

DownLoad: CSV

Drawing from historical traffic data and in alignment with the Highway Asphalt Pavement Design Specification (JTG D60-2017), design parameters were meticulously chosen at level three. Conforming to the same specification, the Lian-Su Expressway was classified as TTC2 type, while the Jin-Hang and Su-Tai Expressways were designated as TTC3 type. Vehicle type distribution coefficients were established in accordance with the stipulated specification, as detailed in Table 5. Based on an analysis of the road network surrounding the vehicle's full load scenario and utilizing historical survey data, the complete range of non-full load and full load ratios for various models was derived. Refer to Table 6 for a comprehensive presentation of these findings. Table 7 presents the conversion factors correlating to the equivalent design axle loads for both unladen and laden vehicles across each model.

Table 5. Vehicle type distribution coefficient.

Vehicle type	2	3	4	5	6	7	8	9	10	11
TTC2	22.0	23.3	2.7	0.0	8.3	7.5	17.1	8.5	10.6	0.0
TTC3	17.8	33.1	3.4	0	12.5	4.4	9.1	10.6	8.5	0.7

| Show Table

DownLoad: CSV

Table 6. Percentage of non-full and full vehicles (%).

Vehicle type	2	3	4	5	6	7	8	9	10	11
Proportion of vehicles not fully loaded	85.0	90.0	65.0	75.0	55.0	70.0	45.0	60.0	55.0	65.0
Proportion of fully loaded vehicles	15.0	10.0	35.0	25.0	45.0	30.0	55.0	40.0	45.0	35.0

| Show Table

DownLoad: CSV

Table 7. Conversion factors of equivalent design axle load for non-full load vehicles and full load vehicles.

Design indicator	Permanent deformation of the asphalt mix layer		Fatigue cracking of the inorganic bond layer
Vehicle type	Non-full load vehicle	Full load vehicle	Non-full load vehicle	Full load vehicle
2	0.8	2.8	0.5	35.5
3	0.4	4.1	1.3	314.2
4	0.7	4.2	0.3	137.6
5	0.6	6.3	0.6	72.9
6	1.3	7.9	10.2	1505.7
7	1.4	6.0	7.8	553.0
8	1.4	6.7	16.4	713.5
9	1.5	5.1	0.7	204.3
10	2.4	7.0	37.8	426.8
11	1.5	12.1	2.5	985.4

| Show Table

DownLoad: CSV

Traffic data can be computed by considering the cumulative count of axle load actions across each road section. Additionally, the cumulative count of equivalent design axle load actions that correspond to permanent deformation of the asphalt mixture layer, along with those corresponding to fatigue cracking of the inorganic bond layer over the next eight years, is detailed in Table 8.

Table 8. Calculation results of the cumulative number of equivalent design actions.

Road section	Corresponding to the asphalt mixture layer permanent deformation times	Corresponding to the inorganic bonding material layer fatigue cracking (times)
XY-A	1.44 × 10⁷	8.46 × 10⁹
XY-B	1.41 × 10⁷	8.24 × 10⁹
HN-A	10.57 × 10⁷	2.79 × 10¹⁰
HN-B	4.9 × 10⁷	1.29 × 10¹⁰
GJXC-A	4.36 × 10⁷	2.56 × 10¹⁰
GJXC-B	4.26 × 10⁷	2.27 × 10¹⁰

| Show Table

DownLoad: CSV

2) Pavement technical condition

The technical condition of the original pavement of each road section was tested separately, and the results are shown in Table 9.

Table 9. Results of testing of the technical condition of the original pavement.

Indicators	XY-A	XY-B	HN-A	HN-B	GJXC-A	GJXC-B
D₀ (0.01mm)	6.3	16.1	16.7	6.4	9.6	8.5
D₂₀-D₆₀ (μm)	12.4	24.3	24.5	9.3	20.7	16.9
Rutting depth (mm)	13.5	10.4	10.2	11.3	11.0	13.2
Spacing of transverse cracks (m)	78	93	112	48	108	126

| Show Table

DownLoad: CSV

3) Pavement material performance

The original pavement structure and material parameter information for each road section are shown in Table 10.

Table 10. Material parameters of the original pavement structure.

Road name	Layer	Hanburger rut depth (mm)		Compressive strength (MPa)		Flexural tensile strength (MPa)
Road name	Layer	A	B	A	B	A	B
Jin-Hang	Upper layer	1.2	0.8	/	/	/	/
	Middle layer	2.5	1.5	/	/	/	/
	Lower layer	2.6	2.3	/	/	/	/
	Base layer	/	/	19.0	17.67	3.99	3.71
	Sub-base	/	/	6.95	5.24	1.46	1.1
Lian-Su	Upper layer	0.8	0.7	/	/	/	/
	Middle layer	1.5	1.4	/	/	/	/
	Lower layer	1.9	2.8	/	/	/	/
	Base layer	/	/	20.43	16.9	4.29	3.55
	Sub-base	/	/	9.86	9.14	2.07	1.92
Su-Tai	Upper layer	1.23	1.53	/	/	/	/
	Middle layer	3.69	3.76	/	/	/	/
	Lower layer	2.05	1.73	/	/	/	/
	Base layer	/	/	10.89	14.86	2.29	3.12
	Sub-base	/	/	6.98	6.98	1.47	1.47

| Show Table

DownLoad: CSV

4.2. Structural preservation countermeasures

Drawing upon the preceding road condition inspection outcomes and material test findings, the structural preservation countermeasure decision process for each road section is illustrated in Figure 8. This process adheres to the highway asphalt pavement preservation decision tree while concurrently selecting an appropriate preservation intensity level.

Figure 8. Decision-making process for preservation countermeasures for each section of pavement structure.

DownLoad: Full-Size Img PowerPoint

In accordance with the decision-making procedure, the preliminary pavement preservation alternatives for each segment are outlined in Table 11. Subsequently, the anticipated pavement performance was projected for each section upon implementation of the preliminary structural preservation plan, with the outcomes elaborated in Table 12. The findings reveal that, following an upper layer milling and resurfacing combined with overlay treatment, the projected pavement rutting depth for section XY-A over the upcoming 10 years is anticipated to be 7.37 mm—well within the stipulated 10 mm threshold. In parallel, section XY-B is projected to attain a pavement fatigue life of 8.75 × 10⁹ times over the next 30 years, aligning with axle load criteria. Moreover, the pavement rutting depth of section XY-B is forecast to reach 6.05 mm over the next decade, satisfying the requirement of less than 10 mm. For section HN-A and section HN-B, milling and resurfacing accompanied by a 4 cm overlay and top layer respectively are envisaged. This intervention anticipates pavement rutting depths of 9.98 and 7.64 mm, respectively, over the subsequent 10 years—both well within the 10 mm limit. Following P3 strength maintenance, the projected pavement rutting depths for section HN-A and section HN-B stand at 9.91 and 9.98 mm, respectively, over the upcoming 10 years, both comfortably meeting the less-than-10 mm requirement. These assessments underscore the accomplishment of structural preservation goals.

Table 11. Preliminary proposed surface structure preservation options.

Road section	Maintenance intensity	Maintenance countermeasures
XY-A	P3	Milling 4 cm top layer, back laying 4 cm SMA-13, adding 4 cm SMA-13 overlay
XY-B	P4	Milling 10 cm middle and upper layers, pave back 6 cm SUP-20 + 4 cm SMA-13, add 4 cm SMA-13 overlay
HN-A	P3	Add 4 cm modified asphalt SMA-13 overlay
HN-B	P2	Milling 4 cm top layer, pave back 4 cm modified asphalt SMA-13
GJXC-A	P3	Milling 2.5 cm cover layer, pave back 4 cm modified asphalt SMA-13, add 4 cm modified asphalt SMA-13 cover layer
GJXC-B	P3	Milling 2.5 cm cover layer, back to pave 4 cm modified asphalt SMA-13, plus 4 cm modified asphalt SMA-13 cover

| Show Table

DownLoad: CSV

Table 12. Calculation results of different structural preservation schemes.

Road section	Checking content	Maintenance strength	Calculated value	Contrast value	Meet?
XY-A	Rutting of asphalt layers (mm)	Not maintained	20.96	10.0	No
XY-A	Rutting of asphalt layers (mm)	P3	7.37	10.0	Yes
XY-B	Rutting of asphalt layers (mm)	Not maintained	17.58	10.0	No
	Rutting of asphalt layers (mm)	P4	6.05	10.0	Yes
	Cumulative equivalent axes corresponding to fatigue cracking of semi-rigid layers (times)	Not maintained	17.58 × 10⁹	8.24 × 10⁹	No
		P4	8.75 × 10⁹	8.24 × 10⁹	Yes
HN-A	Rutting of asphalt layers (mm)	Not maintained	20.24	10.0	No
HN-A	Rutting of asphalt layers (mm)	P3	9.99	10.0	Yes
HN-B	Rutting of asphalt layers (mm)	Not maintained	22.0	10.0	No
HN-B	Rutting of asphalt layers (mm)	P2	9.98	10.0	Yes
GJXC-A	Rutting of asphalt layers (mm)	Not maintained	22.33	10.0	No
GJXC-A	Rutting of asphalt layers (mm)	P3	9.91	10.0	Yes
GJXC-B	Rutting of asphalt layers (mm)	Not maintained	24.33	10.0	No
GJXC-B	Rutting of asphalt layers (mm)	P3	9.98	10.0	Yes

| Show Table

DownLoad: CSV

5. Conclusions

This research endeavor has yielded significant outcomes. It encompassed the formulation of comprehensive long-term preservation goals and definitions for pavement structures. A robust decision system was meticulously constructed to facilitate pavement structure preservation. Various structural preservation countermeasures, tailored to distinct maintenance requirements, were systematically identified and consolidated. Additionally, novel methodologies were established for both maintenance design and decision optimization. The principal findings can be summarized as follows.

1) The definition of long-term preservation of asphalt pavement structure and technical measures are proposed, and the objective of long-term preservation of pavement structure is clarified to slow down the deterioration of pavement interior and subgrade through periodic surface maintenance, overlays, and structural reinforcement.

2) A decision tree model for asphalt pavement maintenance was established by combining the needs of pavement preventive maintenance and long-term structural preservation, and countermeasures for long-term preservation of pavement structures were established based on engineering experience and the applicability, service life, and maintenance benefits of various types of maintenance measures.

3) A project-level and network-level structural preservation decision optimization method based on urgency and a life cycle algorithm was established, and the results were intelligently applied.

4) Drawing from the outcomes of road condition assessments and material performance evaluations, the road maintenance decision-making system presented in this study has undergone rigorous validation. This has culminated in the successful implementation of a network-level structural preservation optimization decision-making system and has substantiated the accuracy of asphalt pavement maintenance decision-making. However, it is noteworthy that practical validation of the maintenance plan outlined in this article necessitates further assessment through more maintenance projects, thus advancing the trajectory of sustainable development within highway engineering.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by National Key Research and Development Program of China (No. 2020YFA0714302), Science and Technology Innovation Support Program of Jiangsu Province of China (No. BZ2022019); Nanjing Science and Technology Program Fund (No. 2021-12004).

Conflict of interest

The authors declare there is no conflict of interest.

References

[1]	World Health Organization: Coronavirus Disease (COVID-19) Pandemic, Available from: https://www.who.int/emergencies/diseases/novel-coronavirus-2019.
[2]	N. Chow, K. Fleming-Dutra, R. Gierke, A. Hall, M. Hughes, T. Pilishvili, et al., Preliminary estimates of the prevalence of selected underlying health conditions among patients with coronavirus disease 2019-United States, February 12 – March 28, 2020, Morb. Mortal. Wkly. Rep., 69 (2020), 382–386. https://doi.org/10.15585/mmwr.mm6913e2 doi: 10.15585/mmwr.mm6913e2
[3]	Q. Li, X. Guan, P. Wu, X. Wang, L. Zhou, Y. Tong, et al., Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia, N. Engl. J. Med., 382 (2020), 1199–1207. https://doi.org/10.1056/nejmoa2001316 doi: 10.1056/nejmoa2001316
[4]	S. Garg, L. Kim, M. Whitaker, A. O'Halloran, C. Cummings, R. Holstein, et al., Hospitalization rates and characteristics of patients hospitalized with laboratory-confirmed coronavirus disease 2019-COVID-NET, 14 States, March 1 – 30, 2020, Morb. Mortal. Wkly. Rep., 69 (2020), 458–464. https://doi.org/10.15585/mmwr.mm6915e3 doi: 10.15585/mmwr.mm6915e3
[5]	A. Pan, L. Liu, C. Wang, H. Guo, X. Hao, Q. Wang, et al., Association of public health interventions with the epidemiology of the COVID-19 outbreak in Wuhan, China, J. Am. Med. Assoc., 323 (2020), 1915–1923. https://doi.org/10.1001/jama.2020.6130 doi: 10.1001/jama.2020.6130
[6]	CDC, Coronavirus Disease 2019 (COVID-19): People Who Need to Take Extra Precautions, Acess date: Mar. 25, 2022, Available from: https://www.cdc.gov/coronavirus/2019-ncov/need-extra-precautions/index.html.
[7]	A. Lasry, D. Kidder, M. Hast, J. Poovey, G. Sunshine, K. Winglee, et al., Timing of community mitigation and changes in reported COVID-19 and community mobility-four U.S. metropolitan areas, February 26 – April 1, 2020, Morb. Mortal. Wkly. Rep., 69 (2020), 451–457. https://doi.org/10.15585/mmwr.mm6915e2 doi: 10.15585/mmwr.mm6915e2
[8]	CDC, Implementation of Mitigation Strategies for Communities with Local COVID-19 Transmission, Available from: https://www.cdc.gov/coronavirus/2019-ncov/community/community-mitigation.html.
[9]	M. S. Eichenbaum, S. Rebelo, M. Trabandt, The macroeconomics of epidemics, NBER Working Paper No. 26882, National Bureau of Economic Research, March 2020, Revised April 2021. https://doi.org/10.3386/w26882
[10]	S. R. Baker, R. A. Farrokhnia, S. Meyer, M. Pagel, C. Yannelis, How does household spending respond to an epidemic? Consumption during the 2020 COVID-19 pandemic, NBER Working Paper No. 26949, National Bureau of Economic Research, April 2020. https://doi.org/10.3386/w26949
[11]	J. Bartash, U.S. Leading Economic Indicators Sink Record 6.7% in March as Coronavirus Spreads, MarketWatch, Acess Date: April 17, 2020, Available from: https://www.marketwatch.com/story/us-leading-economic-indicators-post-record-67-plunge-in-march-as-covid-19-pandemic-broke-out-2020-04-17.
[12]	The Becker Friedman Institute for Economics: Key Economic Facts about COVID-19, Available from: https://bfi.uchicago.edu/insight/blog/key-economic-facts-about-covid-19/.
[13]	The Federal Reserve Bank of St. Louis: Tracking the U.S. Economy and Financial Markets During the COVID-19 Outbreak, Available from: https://fredblog.stlouisfed.org/2020/03/tracking-the-u-s-economy-and-financial-markets-during-the-covid-19-outbreak/.
[14]	The U.S. Bureau of Labor Statistics (BLS), Available from: https://data.bls.gov/timeseries/LNS14000000.
[15]	The U.S. Department of Commerce: Advance Monthly Sales for Retail and Food Services March 2020, Release Number: CB20-56, April 15, 2020. Available from: https://www.census.gov/retail/marts/www/marts_current.pdf.
[16]	The International Monetary Fund: World Economic Outlook, April 2020, Available from: https://www.imf.org/en/Publications/WEO/Issues/2020/04/14/weo-april-2020.
[17]	Z. J. Cheng, J. Shan, 2019 Novel coronavirus: where we are and what we know, Infection, 48 (2020), 155–163. https://doi.org/10.1007/s15010-020-01401-y doi: 10.1007/s15010-020-01401-y
[18]	A. Sahin, A. Erdogan, P. M. Agaoglu, Y. Dineri, A. Cakirci, M. Senel, R. Okyay, A. Tasdogan, 2019 Novel coronavirus (COVID-19) outbreak: A review of the current literature, Eurasian J. Med. Oncol., 4 (2020), 1–7. https://doi.org/10.14744/ejmo.2020.12220 doi: 10.14744/ejmo.2020.12220
[19]	A. Vespignani, H. Tian, C. Dye, J. O. Lloyd-Smith, R. M. Eggo, M. Shrestha, et al., Modelling COVID-19, Nat. Rev. Phys., 2 (2020), 279-281. https://doi.org/10.1038/s42254-020-0178-4 doi: 10.1038/s42254-020-0178-4
[20]	A. Afzal, C. A. Saleel, S. Bhattacharyya, N. Satish, O. D. Samuel, I. A. Badruddin, Merits and limitations of mathematical modeling and computational simulations in mitigation of COVID-19 pandemic: A comprehensive review, Arch. Comput. Methods Eng., 29 (2022), 1311–1337. https://doi.org/10.1007/s11831-021-09634-2 doi: 10.1007/s11831-021-09634-2
[21]	C. Anastassopoulou, L. Russo, A. Tsakris, C. Siettos, Data-based analysis, modelling and forecasting of the COVID-19 outbreak, PLOS ONE, 15 (2020), e0230405. https://doi.org/10.1371/journal.pone.0230405 doi: 10.1371/journal.pone.0230405
[22]	J. Bai, J. Wang, A two-patch model for the COVID-19 transmission dynamics in China, J. Appl. Anal. Comput., 11 (2021), 1982–2016. https://doi.org/10.11948/20200302 doi: 10.11948/20200302
[23]	N. Imai, A. Cori, I. Dorigatti, M. Baguelin, C. A. Donnelly, S. Riley, et al., Report 3: Transmissibility of 2019-nCoV, Acess date: January 25, 2020, Available from: https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/news–wuhan-coronavirus/.
[24]	R. Li, S. Pei, B. Chen, Y. Song, T. Zhang, W. Yang, et al., Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV2), Science, 368 (2020), 489–493. https://doi.org/10.1126/science.abb3221 doi: 10.1126/science.abb3221
[25]	K. Liang, Mathematical model of infection kinetics and its analysis for COVID-19, SARS and MERS, Infect. Genet. Evol., 82 (2020), 104306. https://doi.org/10.1016/j.meegid.2020.104306 doi: 10.1016/j.meegid.2020.104306
[26]	J. M. Read, J. R. E. Bridgen, D. A. T. Cummings, A. Ho, C. P. Jewell, Novel coronavirus 2019-nCoV (COVID-19): early estimation of epidemiological parameters and epidemic size estimates, Philos. Trans. R. Soc. B, 376 (2021), 20200265. https://doi.org/10.1098/rstb.2020.0265 doi: 10.1098/rstb.2020.0265
[27]	B. Tang, X. Wang, Q. Li, N. L. Bragazzi, S. Tang, Y. Xiao, et al., Estimation of the transmission risk of 2019-nCoV and its implication for public health interventions, J. Clin. Med., 9 (2020), 462. https://doi.org/10.3390/jcm9020462 doi: 10.3390/jcm9020462
[28]	A. R. Tuite, D. N. Fisman, Reporting, epidemic growth, and reproduction numbers for the 2019 novel coronavirus (2019-nCoV) epidemic, Ann. Intern. Med., 172 (2020), 567–568. https://doi.org/10.7326/m20-0358 doi: 10.7326/m20-0358
[29]	J. Wang, Mathematical models for COVID-19: applications, limitations, and potentials, J. Public Health Emergency, 4 (2020), 9. https://doi.org/10.21037/jphe-2020-05 doi: 10.21037/jphe-2020-05
[30]	J. T. Wu, K. Leung, G. M. Leung, Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study, Lancet, 395 (2020), 689–697. https://doi.org/10.1016/s0140-6736(20)30260-9 doi: 10.1016/s0140-6736(20)30260-9
[31]	C. Yang, J. Wang, A mathematical model for the novel coronavirus epidemic in Wuhan, China, Math. Biosci. Eng., 17 (2020), 2708–2724. https://doi.org/10.3934/mbe.2020148 doi: 10.3934/mbe.2020148
[32]	C. Yang, J. Wang, Modeling the transmission of COVID-19 in the US–-A case study, Infect. Dis. Model., 6 (2021), 195–211. https://doi.org/10.1016/j.idm.2020.12.006 doi: 10.1016/j.idm.2020.12.006
[33]	C. Yang, J. Wang, COVID-19 and underlying health conditions: A modeling investigation, Math. Biosci. Eng., 18 (2021), 3790–3812. https://doi.org/10.3934/mbe.2021191 doi: 10.3934/mbe.2021191
[34]	K. M. Bubar, K. Reinholt, S. M. Kissler, M. Lipsitch, S. Cobey, Y. H. Grad, et al., Model-informed COVID-19 vaccine prioritization strategies by age and serostatus, Science, 371 (2021), 916–921. https://doi.org/10.1126/science.abe6959 doi: 10.1126/science.abe6959
[35]	N. E. Dean, A. Pastore Y Piontti, Z. J. Madewell, D. A.T. Cummings, M. D. T. Hitchings, K. Joshi, et al., Ensemble forecast modeling for the design of COVID-19 vaccine efficacy trials, Vaccine, 38 (2020), 7213–7216. https://doi.org/10.1016/j.vaccine.2020.09.031 doi: 10.1016/j.vaccine.2020.09.031
[36]	B. H. Foy, B. Wahl, K. Mehta, A. Shet, G. I. Menon, C. Britto, Comparing COVID-19 vaccine allocation strategies in India: A mathematical modelling study, Int. J. Infect. Dis., 103 (2021), 431–438. https://doi.org/10.1016/j.ijid.2020.12.075 doi: 10.1016/j.ijid.2020.12.075
[37]	C. M. Saad-Roy, C. E. Wagner, R. E. Baker, S. E. Morris, J. Farrar, A. L. Graham, et al., Immune life history, vaccination, and the dynamics of SARS-CoV-2 over the next 5 years, Science, 370 (2020), 811–818. https://doi.org/10.1126/science.abd7343 doi: 10.1126/science.abd7343
[38]	E. Shim, Optimal allocation of the limited COVID-19 vaccine supply in South Korea, J. Clin. Med., 10 (2021), 591. https://doi.org/10.3390/jcm10040591 doi: 10.3390/jcm10040591
[39]	H. de la Fuente-Mella, R. Rubilar, K. Chahuan-Jimenez, V. Leiva, Modeling COVID-19 cases statistically and evaluating their effect on the economy of countries, Mathematics, 9 (2021), 1558. https://doi.org/10.3390/math9131558 doi: 10.3390/math9131558
[40]	J. Chen, A. Vullikanti, J. Santos, S. Venkatramanan, S. Hoops, H. Mortveit, et al., Epidemiological and economic impact of COVID-19 in the US, Sci. Rep., 11 (2021), 20451. https://doi.org/10.1038/s41598-021-99712-z doi: 10.1038/s41598-021-99712-z
[41]	D. Altig, S. Baker, J. M. Barrero, N. Bloom, P. Bunn, S. Chen, et al., Economic uncertainty before and during the COVID-19 pandemic, J. Public Econ., 191 (2020), 104274. https://doi.org/10.1016/j.jpubeco.2020.104274 doi: 10.1016/j.jpubeco.2020.104274
[42]	P. R. Jena, R. Majhi, R. Kalli, S. Managi, B. Majhi, Impact of COVID-19 on GDP of major economies: Application of the artificial neural network forecaster, Econ. Anal. Policy, 69 (2021), 324–339. https://doi.org/10.1016/j.eap.2020.12.013 doi: 10.1016/j.eap.2020.12.013
[43]	L. Xiang, M. Tang, Z. Yin, M. Zheng, S. Lu, The COVID-19 pandemic and economic growth: theory and simulation, Front. Public Health, 9 (2021), 741525. https://doi.org/10.3389/fpubh.2021.741525 doi: 10.3389/fpubh.2021.741525
[44]	G. Dimarco, L. Pareschi, G. Toscani, M. Zanella, Wealth distribution under the spread of infectious diseases, Phys. Rev. E, 102 (2020), 022303. https://doi.org/10.1103/PhysRevE.102.022303 doi: 10.1103/PhysRevE.102.022303
[45]	M. C. Auld, F. Toxvaerd, The Great COVID-19 Vaccine Rollout: Behavioral and Policy Responses, Centre for Economic Policy Research Discussion Paper, 18271–1619079393, 2021.
[46]	The Tennessee Department of Health, Available from: https://www.tn.gov/health.html.
[47]	The Tennessee Department of Labor and Workforce Development, Available from: https://www.tn.gov/workforce.html.
[48]	C. Rothe, M. Schunk, P. Sothmann, G. Bretzel, G. Froeschl, C. Wallrauch, et al., Transmission of 2019-nCoV infection from an asymptomatic contact in Germany, N. Engl. J. Med., 382 (2020), 970–971. https://doi.org/10.1056/NEJMc2001468 doi: 10.1056/NEJMc2001468
[49]	The U.S. Bureau of Economic Analysis, Available from: https://www.bea.gov/.
[50]	Our World in Data: Policy Responses to the Coronavirus Pandemic, Available from: https://ourworldindata.org/policy-responses-covid.
[51]	J. A. Spencer, D. P. Shutt, S. K. Moser, H. Clegg, H. J. Wearing, H. Mukundan, C. A. Manore, Epidemiological parameter review and comparative dynamics of influenza, respiratory syncytial virus, rhinovirus, human coronavirus, and adenovirus, Available from: https://doi.org/10.1101/2020.02.04.20020404.
[52]	G. Albi, L. Pareschi, M. Zanella, Control with uncertain data of socially structured compartmental epidemic models, J. Math. Biol., 82 (2021), 63. https://doi.org/10.1007/s00285-021-01617-y doi: 10.1007/s00285-021-01617-y
[53]	N. Chitnis, J. M. Hyman, J. M. Cushing, Determining important parameters in the spread of Malaria through the sensitivity analysis of a mathematical model, Bull. Math. Biol., 70 (2008), 1272–1296. https://doi.org/10.1007/s11538-008-9299-0 doi: 10.1007/s11538-008-9299-0
[54]	W. H. Fleming, R. W. Rishel, Deterministic and Stochastic Optimal Control, Springer, New York, 1975.
[55]	S. Lenhart, J. Workman, Optimal Control Applied to Biological Models, Chapman Hall/CRC, 2007.
[56]	L. S. Pontryagin, V. G. Boltyanski, R. V. Gamkrelize, E. F. Mishchenko, The Mathematical Theory of Optimal Processes, Wiley, New York, 1967.
[57]	T. Kruse, P. Strack, Optimal Control of An epidemic through Social Distancing, Cowles Foundation Discussion Papers, 214, (2020), Available from: https://elischolar.library.yale.edu/cowles-discussion-paper-series/214.
[58]	L. Miclo, D. Spiro, J. Weibull, Optimal epidemic suppression under an ICU constraint: An analytical solution, J. Math. Econ., (2022), 102669. https://doi.org/10.1016/j.jmateco.2022.102669 doi: 10.1016/j.jmateco.2022.102669
[59]	R. Rowthorn, F. Toxvaerd, The Optimal Control of Infectious Diseases via Prevention and Treatment, Cambridge-INET Working Paper WP2013, 2020. https://doi.org/10.17863/CAM.52481
[60]	T. Andersson, A. Erlanson, D. Spiro, R. Ostling, Optimal trade-off between economic activity and health during an epidemic, Working Papers, Lund University, Department of Economics, 2020.
[61]	P. van den Driessche, J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Math. Biosci., 180 (2002), 29–48. https://doi.org/10.1016/s0025-5564(02)00108-6 doi: 10.1016/s0025-5564(02)00108-6
[62]	C. Castillo-Chavez, B. Song, Dynamical models of tuberculosis and their applications, Math. Biosci. Eng., 1 (2004), 361–404. https://doi.org/10.3934/mbe.2004.1.361 doi: 10.3934/mbe.2004.1.361

This article has been cited by:

1.	Xin He, Xin Zhao, Tao Feng, Zhipeng Qiu, Dynamical behaviors of a prey-predator model with foraging arena scheme in polluted environments, 2021, 71, 1337-2211, 235, 10.1515/ms-2017-0463
2.	R. Rajaji, M. Pitchaimani, Analysis of stochastic viral infection model with lytic and nonlytic immune responses, 2020, 38, 0736-2994, 490, 10.1080/07362994.2019.1702559
3.	Fathalla A. Rihan, Hebatallah J. Alsakaji, Persistence and extinction for stochastic delay differential model of prey predator system with hunting cooperation in predators, 2020, 2020, 1687-1847, 10.1186/s13662-020-02579-z
4.	Yongzhong Lan, Jianping Shi, Hui Fang, Hopf Bifurcation and Control of a Fractional-Order Delay Stage Structure Prey-Predator Model with Two Fear Effects and Prey Refuge, 2022, 14, 2073-8994, 1408, 10.3390/sym14071408
5.	Feng Rao, Yun Kang, Dynamics of a stochastic prey–predator system with prey refuge, predation fear and its carry-over effects, 2023, 175, 09600779, 113935, 10.1016/j.chaos.2023.113935
6.	Subarna Roy, Subhas Khajanchi, Pankaj Kumar Tiwari, Fear and its carry-over effects in a generalist predator–prey system featuring cooperative hunting, 2025, 1598-5865, 10.1007/s12190-024-02346-3

Reader Comments

Your name:*

Email:*
© 2022 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)