A complex network model for a society with socioeconomic classes

1.   Introduction

A social class can be simplistically defined as a group of individuals with similar socioeconomic status ^[1,2,3,4]. People's social class affects their habits, opportunities, relationships, traditions, values. In addition, the features of the socioeconomic stratification of a society is relevant for governments implementing policies related to education, labor market, public health, public safety ^[1,2,3,4]. These features also influence, for instance, the propagation of a contagious disease like COVID-19 ^[5,6,7,8]. Usually, from an economic perspective, societies are stratified into lower class, middle class, and upper class ^[1,2,3,4]. In this manuscript, these three classes are taken into consideration in a model of scale-free network proposed for representing daily personal contacts.

People primarily interact with family, friends, and neighbors, which usually belong to the same social class; however, face-to-face encounters among individuals belonging to different classes do occur, for instance, in the workplace, in a subway, in a shopping mall, in a park. Interactions among distinct social classes can also occur in virtual environments ^[9].

Social contacts have been theoretically modeled by complex networks ^{[10,11,12,13,14,15]}. Two classic examples are the scale-free graphs representing exchanged e-mails ^[16] and human sexual contacts ^[17]. Recent applications deal with scheduling problem ^[18] and rumor propagation ^[19]. Usually, theoretical studies on social connectivity are based on the three main models of complex networks found in the literature. These well-known models were conceived by Erdös and Rényi, Watts and Strogatz, Barabási and Albert ^{[10,11,12,13,14,15]}. Unfortunately, these models are not suitable for representing social interactions: the Erdös-Rényi network leads to Poissonian degree distribution and low average clustering coefficient; the Watts-Strogatz network leads to Poissonian degree distribution; the Barabási-Albert network leads to low average clustering coefficient ^[11,12,15]. An appropriate network model should present scale-free degree distribution and high average clustering coefficient ^[11,12,15]. The model proposed here presents these features. Notice that a suitable model of social connectivity could be employed in studies on homophily. This sociological concept states that similarities among people facilitate the formation of social bonds ^[20]. Homophily has been investigated by analyzing, for instance, data from mobile phones in Singapore ^[21], the ethnoracial residential segregation in Detroit ^[22], friendship patterns in American high schools ^[23,24], the sociocultural dimension in Dutch urban areas ^[25]. In these analyzes, however, basic statistical measures commonly used to identify the network structure were not computed. For the model proposed here, these measures are computed for three countries and compared. There are also studies on homophily that incorporate game theory ^[26] and degree heterogeneity ^[27]; however, their theoretical predictions were not tested in real-world scenarios.

The aim of this work is to introduce a complex network model to represent the social connectivity of a community with socioeconomic classes. This model is inspired by the coupling pattern originally developed for studying the neurophysiological phenomenon called spreading depression ^[28] and also used in investigations on the spread of contagious diseases in a host population ^[29,30,31].

This manuscript is organized as follows. In Section 2, a new model of complex network is proposed. In Section 3, the topological structures of the networks built with sociodemographic data from France, Peru, and Zimbabwe are characterized by computing average values of node degree, shortest-path length, clustering coefficient, closeness centrality, betweenness centrality, and eigenvector centrality. In Section 4, the numerical results obtained in these computer simulations are discussed from a public health perspective, by taking into account the COVID-19 pandemic.

2.   The model of complex network

Let a square lattice be composed of $\eta \times \eta$ cells, in which each cell corresponds to an individual. Thus, there are $N = \eta^2$ individuals in this society. In order to avoid edge effects, the top and bottom edges are connected and the left and right edges are also connected. Therefore, all individuals living in this lattice are equivalent from a geographical standpoint; that is, their spatial coordinates can be neglected. Consider that the index $\alpha = 1, 2, ..., N$ labels an individual belonging to the social class $x \in \{l, m, u\}$, in which $l$ denotes lower class, $m$ middle class, and $u$ upper class. Undirected connections between individuals are created by a random process, in which the $\alpha$-th individual is connected to $k_\alpha$ others placed within the square matrix of size $2r + 1$ centered in such an individual (self-connections and multiple connections are not allowed). Here, for the $\alpha$-th individual, a number $\sigma_\alpha$ is randomly picked from the standard uniform distribution. Then, the value of $k_\alpha$ is obtained from $\rho(k_\alpha) = \sigma_\alpha$, in which $\rho(\theta)$ is a power law given by $\rho(\theta) \propto \theta^{-\delta}$ with $\delta = 2.5$ (because the degree distribution for most social networks has $2 \leq \delta \leq 3$ ^[11,12,15]). The value of $\delta$ remains fixed and it is equal for the three countries. Also, the minimum and maximum degrees of the degree distribution must be conveniently chosen in order to adjust the average degree of the model to the average degree found in the real-world populations.

In the proposed model, the probability of linking two individuals depends on the distance between them and on their social classes as follows. The distance between the individuals is taken into account in the term $q^i_{\alpha}$, which is the probability of creating a connection between the $\alpha$-th individual and any individual at the $i$-th layer of the square matrix of size $2r + 1$ centered in this $\alpha$-th individual. Here, $q^i_{\alpha}$ is obtained from:

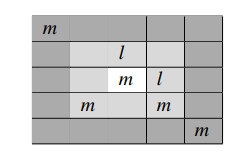
with $i = 1, 2, ..., r$ and $\sum_{i = 1}^r q^i_{\alpha} = 1$. The $i$-th layer is formed by individuals with Moore radius equal to $i$ ^[32]. For instance, for $r = 2$, the square matrix centered in the $\alpha$-th individual is $5 \times 5$. Therefore, there are 8 individuals in the layer $i = 1$ and 16 individuals in the layer $i = 2$ ($8+16$ plus the central $\alpha$-th individual is equal to $5 \times 5 = 25$ individuals). For $r = 2$, Eq. (2.1) gives $q^1_{\alpha} = 2/3$ and $q^2_{\alpha} = 1/3$; thus, the chance of connecting the $\alpha$-th individual to any of the 8 individuals forming the layer $i = 1$ is $2/3$ and to any of the 16 individuals forming the layer $i = 2$ is $1/3$. Table 1 illustrates an individual with six neighbors in a lattice with $r = 2$.

Let $n^y_\alpha$ be the number of neighbors of the $\alpha$-th individual belonging to the social class $y \in \{l, m, u\}$; thus, $n^l_\alpha$ is the number of lower-class neighbors, $n^{m}_\alpha$ the number of middle-class neighbors, and $n^u_\alpha$ the number of upper-class neighbors. Evidently, $n^l_\alpha+n^m_\alpha+n^u_\alpha = k_\alpha$. In the creation of the complex network, the social classes of the individuals are taken into account in the term $s^{xy}_{\alpha}$ defined as:

in which $w_{xy}$ is a weighting factor which depends on the country where these people live. The higher the value of $w_{xy}$, the higher the probability of two individuals of the classes $x$ and $y$ being socially connected. Recall that the $\alpha$-th individual belongs to the social class $x$. Obviously, $\sum_{y = \{l, m, u\}}s^{xy}_{\alpha} = 1$. For instance, assume that the $\alpha$-th individual belongs to the middle class (that is, $x = m$) and $n^l_\alpha = 2$, $n^m_\alpha = 4$, and $n^u_\alpha = 0$ (that is, this individual has two lower-class neighbors and four middle-class neighbors), as in the example shown in Table 1. Also, assume that in the region where they live, $w_{ml} = 4$, $w_{mm} = 8$, and $w_{mu} = 1$. For this $\alpha$-th individual, then $s^{ml}_\alpha = 1/5$, $s^{mm}_\alpha = 4/5$, and $s^{mu}_\alpha = 0$.

In the proposed model, the probability $Q^j_{\alpha}$ of the $\alpha$-th individual of the class $x$ being connected to an individual of the class $y$ in the layer $i$ is given by:

with $\sum_{i = 1}^r \sum_{y = \{l, m, u\}} Q^j_\alpha = 1$. Notice that the number of social classes considered in the model can be easily changed. This network model with $s^{xy}_{\alpha} = 1$ (that is, a single social class) and by taking $k_\alpha$ as a constant (instead of taking $k_{\alpha}$ from a power law $\rho(\theta)$ as done here) was already employed in other works ^{[28,29,30,31]}.

In short, the model parameters are: $\eta$ (the lattice size), $\rho(\theta)$ (the power law used to determine the degree $k_\alpha$ of the $\alpha$-th individual), $r$ (the Moore radius of the area where the connections can be made), $\bf{W}$ (the matrix $3 \times 3$ formed by the weights $w_{xy}$, with $\{x, y\} \in \{l, m, u\}$), and the percentage of individuals in each social class.

3.   Numerical results

Here, the topological structure of each graph is characterized by computing $P(k)$, $\langle k \rangle$, $\langle k_l \rangle$, $\langle k_m \rangle$, $\langle k_u \rangle$, $\langle \ell \rangle$, $\langle c \rangle$, $\langle C_c \rangle$, $\langle C_b \rangle$, and $\langle C_e \rangle$. These symbols and the corresponding measures are defined below.

The degree distribution $P(k)$ expresses how the fraction of individuals with degree $k$ varies with $k$. The average degree of the whole population $\langle k \rangle$ is given by ^{[10,11,12,15]}:

in which $k_{min}$ and $k_{max}$ are the minimum and maximum degrees found in the network, respectively.

Here, the average degree of the lower-class individuals $\langle k_l \rangle$ is also calculated by considering only the links in which at least one endpoint is a lower-class individual. Likewise, the average degrees of middle-class individuals $\langle k_m \rangle$ and of upper-class individuals $\langle k_u \rangle$ are computed.

The average shortest-path length $\langle \ell \rangle$ is obtained from ^{[10,11,12,15]}:

in which $\ell_{\alpha \beta}$ is shortest distance between the individuals $\alpha$ and $\beta$.

For the $\alpha$-th individual, the clustering coefficient $c_\alpha$ is defined as ^{[10,11,12,15]}:

in which $e_\alpha$ is the number of connections among its $k_\alpha$ neighbors.

Centrality measures are usually employed to quantify the relevance of the nodes composing the network. The closeness centrality $C_c(\alpha)$ of the individual $\alpha$ is defined as ^[15,33]:

The betweenness centrality $C_b(\alpha)$ of the individual $\alpha$ is defined as ^[15,33]:

in which $g_{\beta \gamma}$ is the number of shortest paths between the individuals $\beta$ and $\gamma$ and $g_{\beta \gamma}(\alpha)$ is the number of shortest paths between the individuals $\beta$ and $\gamma$ passing through the individual $\alpha$. The eigenvector centrality of the individual $\alpha$ is determined from ^[12,33]:

in which $\lambda$ is the greatest eigenvalue of adjacency matrix $\bf{A}$ formed by the elements $a_{\alpha \beta}$, so that $a_{\alpha \beta} = 1$ if the individuals $\alpha$ and $\beta$ are connected, and $a_{\alpha \beta} = 0$ otherwise.

For the whole network, average values of the measures defined by Eqs. (3.3)-(3.6) are obtained from $\langle c \rangle = \sum_{\alpha = 1}^N c_\alpha/N$, $\langle C_c \rangle = \sum_{\alpha = 1}^N C_c(\alpha)/N$, $\langle C_b \rangle = \sum_{\alpha = 1}^N C_b(\alpha)/N$, and $\langle C_e \rangle = \sum_{\alpha = 1}^N C_e(\alpha)/N$.

Undirected graphs were built by using Eq. (2.3) and sociodemographic data from France, Peru, and Zimbabwe. Table 2 shows the actual percentages of individuals in each social class in these three countries ^[34,35,36]. These percentages determine the numbers of individuals of each class in the graph.

In the simulations, $\eta = 100$ (thus, $N = 10000$), $r = 10$, and the matrix $\bf{W}$ is written in terms of a single parameter $\omega$ as:

Thus, $w_{ll} = w_{mm} = w_{uu} = \omega$, $w_{lm} = w_{ml} = w_{mu} = w_{um} = \omega/2$, and $w_{lu} = w_{ul} = 1$. Assume that the value of $\omega$ decreases with the Human Development Index (HDI) and increases with the Gini coefficient. Since HDI$_{France} >$ HDI$_{Peru} >$ HDI$_{Zimbabwe}$ ^[37] and Gini$_{France} <$ Gini$_{Peru} <$ Gini$_{Zimbabwe}$ ^[37], then $\omega_{France} < \omega_{Peru} < \omega_{Zimbabwe}$. The values chosen for the constant $\omega$ are $\omega = 4$ for France, $\omega = 10$ for Peru, and $\omega = 40$ for Zimbabwe. Thus, the weights $w_{xy}$ are assumed to be more uniform for France and more heterogeneous for Zimbabwe, which is consistent with the HDI and the Gini coefficient for these countries. Notice that the weights for connections between individuals of the same class are privileged, in agreement with results found in studies on homophily ^{[20,21,22,23,24,25]}. Alternatively, the matrix $\bf{W}$ could be written in terms of two or more parameters, in order to represent different connectivity patterns.

For the $\alpha$-th individual (for $\alpha = 1, 2, ..., N$), $k_\alpha$ is obtained from $\rho(\theta) = A \theta^{-2.5}$ for $k_{min} \leq \theta \leq k_{max}$, in which $A = 1/(\sum_{\theta = k_{min}}^{k_{max}} \theta^{-2.5})$ is a normalization constant. Suppose that $k_{min} = 11$ and $k_{max} = 39$ for France; $k_{min} = 11$ and $k_{max} = 36$ for Peru; and $k_{min} = 7$ and $k_{max} = 31$ for Zimbabwe. Let $\bar{k}$ be the average number of daily contacts per individual typical of each country found in the literature. For France, $\bar{k} = 17$ ^[38]; for Peru, $\bar{k} = 16$ ^[39]; and for Zimbabwe, $\bar{k} = 11$ ^[40]. It is assumed that the complex network created according to Eq. (2.3) is suitable to represent the social contacts in each country if $\langle k \rangle \simeq \bar{k}$; that is, if the average degree of the computer-generated network is close to the average degree found in the real world.

Table 3 presents the values of $\langle k \rangle$, $\langle k_l \rangle$, $\langle k_m \rangle$, $\langle k_u \rangle$, $\langle \ell \rangle$, $\langle c \rangle$, $\langle C_c \rangle$, $\langle C_b \rangle$, and $\langle C_e \rangle$. Table 4 exhibits the classes of the 100 individuals with the highest values of $\langle k \rangle$, $\langle c \rangle$, $\langle C_c \rangle$, $\langle C_b \rangle$, and $\langle C_e \rangle$ for the three countries.

Table 3 shows that $\langle k \rangle_{France} \simeq \langle k \rangle_{Peru} > \langle k \rangle_{Zimbabwe}$. Observe that these numbers are close to the values of $\bar{k}$ found in the literature ^[38,39,40] and mentioned above. By considering the average degrees of the social classes given by $\langle k_l \rangle$, $\langle k_m \rangle$, and $\langle k_u \rangle$, the middle class is more connected than the other two classes in France, and the lower class is more connected than the other two classes in Peru and Zimbabwe.

Table 3 also shows that $\langle \ell \rangle_{France} \simeq \langle \ell \rangle_{Peru} < \langle \ell \rangle_{Zimbabwe}$. Since $\langle C_c \rangle$ increases by decreasing $\langle \ell \rangle$, this table consistently shows that $\langle C_c \rangle_{France} \simeq \langle C_c \rangle_{Peru} > \langle C_c \rangle_{Zimbabwe}$. These relations suggest that information travels faster in France and Peru than in Zimbabwe.

Also, $\langle c \rangle_{France} > \langle c \rangle_{Peru} \simeq \langle c \rangle_{Zimbabwe}$ and $\langle C_b \rangle_{France} \simeq \langle C_b \rangle_{Peru} < \langle C_b \rangle_{Zimbabwe}$. Hence, the value of $\langle c \rangle$ does not distinguish Peru from Zimbabwe and the value of $\langle C_b \rangle$ does not distinguish France from Peru. These inequalities suggest that the neighbors of an individual are more connected in France and there are more individuals controlling the flow of information in Zimbabwe. Surprisingly, the values of $\langle C_e \rangle$ were found to be identical for the three countries.

The values of $\langle k_l \rangle$, $\langle k_m \rangle$, and $\langle k_u \rangle$ shown in Table 3 and the results presented in Table 4 reveal that the flow of information is mainly controlled by the middle class in France and by the lower class in Peru and Zimbabwe; however, middle class has a greater influence in Peru than in Zimbabwe. Despite the predominance of the middle class in France and of the lower class in Peru and Zimbabwe, the proportions shown in Table 4 for each topological measure are different from the sociodemographic data shown in Table 2.

This computer experiment was repeated three times for each country. The standard deviations associated with the values shown in Table 3 were about 1%-3% and about $0\%-10\%$ in Table 4. For better readability of the results, the deviations were omitted in these tables.

Figure 1 shows the double-logarithmic plot (log base 10) of the degree distribution $P(k)$ (black dots) and the fitted function $P_0(k) = B_0 k^{-\delta_0}$ (red line) for the three countries for $k_{min} \leq k \leq 2\bar{k}$. Table 5 presents the values of $B_0$, $\delta_0$, and the mean square error determined from the least square fitting method ^[41]. Notice that, for the three countries, the degree distributions follow a power law with $\delta_0 \approx 2.5$, as expected. By considering the whole range of $k$, a better fitting is obtained with the function $P_1(k) = B_1 k^{-\delta_1} 10^{{\delta_2} k^{10}}$ (blue line), as shown in Table 6 and Figure 1. Observe that $\delta_1 \approx 2.5$ for the three countries. The exponential tails exhibited in Figure 1 were already found in other real-world networks ^[16,42]. They appear when the highest connected nodes have degrees lower than those predicted by a pure power law. In our model, this exponential cutoff is affected by $\eta$ and $r$.

4.   Discussion and conclusion

In this work, scale-free graphs were numerically generated and analyzed. These graphs represent the daily personal contacts occurring in a society with three social classes. Socioeconomic data from France, Peru, and Zimbabwe related to the social stratification and the income distribution in these countries were taken into account. For each country, the power-law exponent of the degree distribution and the average degree present realistic values. Here, it is assumed that more contacts mean more information being changed. This assumption concerns the volume of the disseminated information and not its quality. By taking into account this supposition, the results shown in Tables 3 and 4 can help to understand, for instance, the propagation of information on COVID-19 in the considered countries.

Information affects the perception of reality and the decision-making process. In fact, information can become a matter of life and death. Hence, in every country, authorities have been fighting fake news and misinformation on COVID-19. For instance, in France, a website was launched to provide reliable information about the use of drugs during the COVID-19 outbreak ^[43]. In Peru, creating and spreading fake news about COVID-19 could be punished with a prison sentence ^[44]. In Zimbabwe, a social networking service was used to disseminate trustworthy COVID-19 information ^[45]. The results obtained here via computer simulations can help these three countries to realize how the interpersonal communication is influenced by the social stratification.

The COVID-19 pandemic highlighted economic inequality, since individuals belonging to the lower class had higher risk of loosing their jobs and their lives ^[5,6,7,8]. Unfortunately, their fear of unemployment hampered the adherence to movement restriction measures; their low income made it difficult to improve personal hygiene habits.

During the pandemic, there was an overload of technical information, which might sound seemingly contradictory sometimes. Hence, the scientific findings on COVID-19 should have been summarized and rephrased to facilitate its understanding. In addition, public health interventions (such as implementing preventive protocols and conducting vaccination campaigns) should have been planned by taking into account the topological characteristics of the underlying structure of the social contacts. Personal experiences, unverified information, true news, and fake news related to COVID-19 are spread through the same network. This work suggests that middle class in France and lower class in Peru and Zimbabwe primarily affect the volume of information changed in these countries.

In brief, the model of complex network proposed here can stress the influence of each social class in the propagation of information in every country, which can guide the development of strategies for disseminating scientifically accurate information.

Data availability

The data used to support the findings of this study are available from the first author upon request.

Conflicts of interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Acknowledgments

LHAM is partially supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) under the grant #304081/2018-3. This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) - finance code 001.