Spatial segregation limit of traveling wave solutions for a fully nonlinear strongly coupled competitive system

1.   Introduction

We investigate the reaction–diffusion system

where $t$ is a real time variable, $x$ is a one-dimensional real space variable, $u(t, x)$ and $v(t, x)$ are two population densities, $\mathbf{D} = (d_{i, j})_{1\leq i, j\leq 2}$ is a matrix of self- and cross-diffusion rates^*, $\mathbf{H} = (h_{i, j})_{1\leq i, j\leq 2}$ is a matrix of self- and cross-advection rates, $\mathbf{g} = (g_i)_{1\leq i\leq 2}$ is a vector of growth rates per capita accounting for a saturation effect, $\omega$ is an interpopulation competition operator and $k > 0$ and $\alpha k > 0$ are constant interpopulation competition rates exerted respectively by $v$ on $u$ and by $u$ on $v$.

^* Although the word "rate" might be misleading, in the whole paper, rates are not necessarily constant and are in general functions of $(u, v)$.

The three main examples of such systems that we have in mind are the classical Lotka–Volterra competition–diffusion system,

the Potts–Petrovskii competition–diffusion–cross-taxis system ^[1],

and the Shigesada–Kawasaki–Teramoto competition–cross-diffusion system ^[2],

In the above systems, the various parameters are all positive constants, except $\gamma_1$ and $\gamma_2$ that might be of any sign.

Our abstract framework is justified by the fact that we want to deal with all these systems simultaneously. We also want to encompass generalizations of (1.4) of the form

with arbitrary positive exponents $\left(\beta_{i, j} \right)_{1\leq i, j\leq 2}$, that have been considered in the literature ^[3]. Moreover, we want to be able to replace the logistic growth terms $u(1-u)$ and $rv(1-v)$ above by more general monostable reaction terms, for instance with a weak Allee effect (e.g., $u(u+\theta)(1-u)$ with $\theta\in[0, 1)$).

More precisely, we are interested in the singular limit $k\to+\infty$ of the associated traveling wave system satisfied by entire solutions of the form $(u, v):(t, x)\mapsto\left(\phi, \psi \right)(x-ct)$, where $(\phi, \psi)$ is the wave profile and $c$ is the wave speed. From now on, we denote $\xi = x-ct$ the wave variable and $\boldsymbol{\Phi} = (\phi, \psi)$ the wave profile vector. The traveling wave system reads, in vector form,

The notation $\circ$ above stands for the component-by-component product of two vectors, namely the so-called Hadamard product.

The singular limit $k\to+\infty$ of the traveling wave system for (1.2) was studied by the first author and G. Nadin in ^[4]. There, it was proved that the singular limit of the solution $(\phi_k, \psi_k, c_k)$ of

is

where $z^+ = \max(z, 0)$ and $z^- = \max(-z, 0)$ are respectively the positive and negative part of the function $z$ and where $(z, c)$ is the unique (up to shifts of $z$) solution of

The integral equality is the equation $-((\mathbf{1}_{z > 0}+d\mathbf{1}_{z < 0})z')'-cz' = z^+(1-\frac{z}{\alpha})-rz^-(1+z)$ tested against test functions in $L^1(\mathbb{R})$ and where the divergence-form second order term, the first order term and the zeroth order term are all in $L^\infty(\mathbb{R})$. Consequently, $z$ is smooth and a classical solution away from the point $z^{-1}(0)$ and Lipschitz-continuous at $z^{-1}(0)$.

Roughly speaking, the preceding result follows from the combination of $\phi_k\psi_k\to0$ (spatial segregation) and an equation that does not depend explicitly on $k$:

In the present work, we will show that the singular limit $k\to+\infty$ of (1.5) is similarly given, under reasonable assumptions, by the unique (up to shifts) solution of

where

1.1.   Minimal speeds of the underlying monostable problems

In order to state more precisely the assumptions and the results, we need to introduce $c_\star^+\in\mathbb{R}$ the minimal speed of classical traveling wave solutions of

and $c_\star^-\in\mathbb{R}$ the minimal speed of classical traveling wave solutions of

Both are well-defined provided $d$, $h$ and $g$ are continuous away from $0$ and $d$ is positive away from $0$ ^[5].

1.2.   Standing assumptions

The standing assumptions follow.

$({\mathsf{A}}_{1})$ $\mathbf{D}\in \mathscr{C}^1([0, 1]^2)$, $\mathbf{H}\in \mathscr{C}([0, 1]^2)$, $\mathbf{g}\in \mathscr{C}([0, 1]^2)$, $\omega\in\mathscr{C}([0, 1]^2)$.

$({\mathsf{A}}_{2})$ $d_{1, 1}$ and $d_{2, 2}$ are positive in $[0, 1]^2$.

$({\mathsf{A}}_{3})$ $d_{1, 2}(0, \bullet)$, $d_{2, 1}(\bullet, 0)$, $h_{1, 2}(0, \bullet)$ and $h_{2, 1}(\bullet, 0)$ are identically zero in $[0, 1]$.

$({\mathsf{A}}_{4})$ $g_1(\bullet, 0)$ and $g_2(0, \bullet)$ are positive in $(0, 1)$ and $g_1(1, 0) = g_2(0, 1) = 0$.

$({\mathsf{A}}_{5})$ $\omega$ is positive in $(0, 1]^2$ and identically zero on $\{0\}\times[0, 1]\cup[0, 1]\times\{0\}$.

$({\mathsf{A}}_{6})$ $c_\star^+ > -c_\star^-$.

$({\mathsf{A}}_{7})$ There exists $k^\star > 0$ such that, for all $k > k^\star$, the system (1.5) admits a classical solution $(\boldsymbol{\Phi}_k, c_k)$ with nonincreasing $\phi_k$, nondecreasing $\psi_k$, $\lim_{-\infty}\boldsymbol{\Phi}_k = (1, 0)$, $\lim_{+\infty}\boldsymbol{\Phi}_k = (0, 1)$.

$({\mathsf{A}}_{8})$ Any family of wave speeds $(c_k)_{k > k^\star}$ is bounded in $\mathbb{R}$.

$({\mathsf{A}}_{9})$ Any family of wave profiles $(\boldsymbol{\Phi}_k)_{k > k^\star}$ is locally relatively compact in a Hölder space.

Note that the systems (1.2), (1.3), (1.4) all satisfy directly the assumptions $({\mathsf{A}}_{1})$–$({\mathsf{A}}_{5})$. As will be explained in the discussion (cf. Section 3.2.6), they also satisfy $({\mathsf{A}}_{6})$. It will be explained in the discussion (cf. Section 3.2.9) that $({\mathsf{A}}_{9})$ is satisfied for (1.2), (1.4) and (1.3) if $\min\left(\gamma_1, \gamma_2 \right)\geq 0$ (attractive–attractive case). Finally, $({\mathsf{A}}_{7})$ and $({\mathsf{A}}_{8})$ are satisfied for (1.2) ^[6,7] but are, to the best of our knowledge, important open problems for the strongly coupled systems (1.3) and (1.4) that have been solved only in special perturbative cases (cf. Sections 3.2.7 and 3.2.8). Solving these problems away from any such perturbative regime is way outside the scope of this paper.

1.3.   Statement of the main result

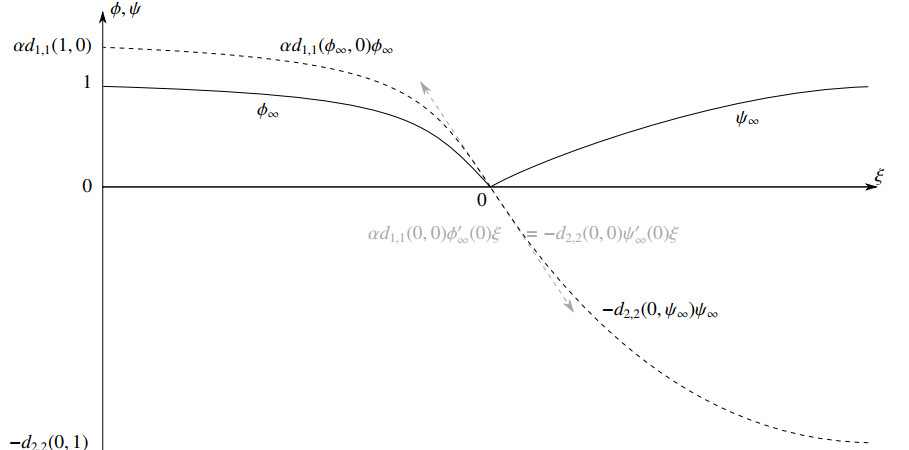
The main result follows. The limiting profiles and their basic properties – spatial segregation and free boundary relation – are illustrated on Figure 1.

Theorem 1.1. Assume $({\mathsf{A}}_{1})$–$({\mathsf{A}}_{9})$.

Then there exists $c_\infty\in\mathbb{R}$ and $\boldsymbol{\Phi}_\infty\in \mathscr{C}^2(\mathbb{R}\backslash\left\{ 0 \right\})\cap W^{1, \infty}(\mathbb{R})$ such that, up to shifting $(\boldsymbol{\Phi}_k)_{k > k^\star}$,

The limit satisfies $\phi_\infty \psi_\infty = 0$ and the pair $(\alpha\phi_\infty-\psi_\infty, c_\infty)$ is the unique solution $(z, c)$ of $(1.7)$ satisfying $z(0) = 0$.

Consequently,

1. the profiles $\phi_\infty$ and $\psi_\infty$ are respectively decreasing in $(-\infty, 0)$ with limit $1$ at $-\infty$ and increasing in $(0, +\infty)$ with limit $1$ at $+\infty$;

2. the free boundary relation reads

3. the speed $c_\infty$ satisfies $-c_\star^- < c_\infty < c_\star^+$;

4. if $h_{1, 1} = h_{2, 2} = h_0\in\mathbb{R}$, then

Below, we specify the theorem for the three main examples. It turns out that (1.2) and (1.3) have the same singular limit whereas (1.4) has a different limit.

Corollary 1.2 ("Disunity is strength" ^[4]). Assume $(1.1)$ has the form $(1.2)$.

Then there exists $c_\infty\in\mathbb{R}$ and $\boldsymbol{\Phi}_\infty\in \mathscr{C}^2(\mathbb{R}\backslash\left\{ 0 \right\})\cap W^{1, \infty}(\mathbb{R})$ such that, up to shifting $(\boldsymbol{\Phi}_k)_{k > k^\star}$,

The limit satisfies $\phi_\infty \psi_\infty = 0$ and the pair $(\alpha\phi_\infty-\psi_\infty, c_\infty)$ is the unique solution $(z, c)$ of

Consequently,

1. the profiles $\phi_\infty$ and $\psi_\infty$ are respectively decreasing in $(-\infty, 0)$ with limit $1$ at $-\infty$ and increasing in $(0, +\infty)$ with limit $1$ at $+\infty$;

2. the free boundary relation reads

3. the speed $c_\infty$ satisfies $-2\sqrt{rd} < c_\infty < 2$;

4. $\operatorname{sign}\left(c_\infty \right) = \operatorname{sign}\left(\alpha^2-rd \right)$.

Corollary 1.3. Assume $(1.1)$ has the form $(1.3)$ and assume furthermore $({\mathsf{A}}_{7})$–$({\mathsf{A}}_{8})$ and, if $\min\left(\gamma_1, \gamma_2 \right) < 0$, assume $({\mathsf{A}}_{9})$.

Then all the conclusions of Corollary 1.2 remain true.

Remark 1.1. The above statement is consistent with the fact that $({\mathsf{A}}_{9})$ is automatic in the attractive–attractive case ($\min \gamma_i \geq 0$), as explained in Section 3.2.9.

Corollary 1.4. Assume $(1.1)$ has the form $(1.4)$ and assume furthermore $({\mathsf{A}}_{7})$–$({\mathsf{A}}_{8})$.

Then there exists $c_\infty\in\mathbb{R}$ and $\boldsymbol{\Phi}_\infty\in \mathscr{C}^2(\mathbb{R}\backslash\left\{ 0 \right\})\cap W^{1, \infty}(\mathbb{R})$ such that, up to shifting $(\boldsymbol{\Phi}_k)_{k > k^\star}$,

The limit satisfies $\phi_\infty \psi_\infty = 0$ and the pair $(\alpha\phi_\infty-\psi_\infty, c_\infty)$ is the unique solution $(z, c)$ of

Consequently,

1. the profiles $\phi_\infty$ and $\psi_\infty$ are respectively decreasing in $(-\infty, 0)$ with limit $1$ at $-\infty$ and increasing in $(0, +\infty)$ with limit $1$ at $+\infty$;

2. the free boundary relation reads

3. the speed $c_\infty$ satisfies $-c_\star^- < c_\infty < c_\star^+$, where $c_\star^+$ is the minimal speed of monotonic traveling wave solutions of

and $c_\star^-$ is the minimal speed of monotonic traveling wave solutions of

4. $\operatorname{sign}\left(c_\infty \right) = \operatorname{sign}\left(\alpha^2(d_1+a_{1, 1})-r(d_2+a_{2, 2}) \right)$.

Remark 1.2. In the preceding corollary, if $d_1\geq a_{1, 1}$, then $z\mapsto(d_1+a_{1, 1}z)z(1-z)$ is concave and therefore the speed $c_\star^+$ is linearly determined ^[5]: $c_\star^+ = 2\sqrt{d_1}$. Similarly, if $d_2\geq a_{2, 2}$, then $c_\star^- = 2\sqrt{rd_2}$.

1.4.   Organization of the paper

In Section 2 we prove the main result. In Section 3 we discuss at length the literature, the assumptions and the results.

2.   Proof of Theorem 1.1

For clarity, we divide the proof in several parts.

2.1.   Existence of limit points

Proof. Up to extraction, the bounded family $(c_k)_{k > k^\star}$ converges to some limit $c_\infty$ (whose uniqueness is unclear at this point).

Now, we fix a family of shifts for the profiles:

1. if $c_\infty\leq \frac12(c_\star^+-c_\star^-)$, the family $(\boldsymbol{\Phi})_{k > k^\star}$ is shifted so that $\phi_k(0) = \frac12$;

2. if $c_\infty > \frac12(c_\star^+-c_\star^-)$, the family $(\boldsymbol{\Phi})_{k > k^\star}$ is shifted so that $\psi_k(0) = \frac12$.

Next, since the family of profiles is locally relatively compact in some Hölder space, up to another (diagonal) extraction, $(\boldsymbol{\Phi}_k)_{k > k^\star}$ converges locally uniformly to some limit $\boldsymbol{\Phi}_\infty$ (whose uniqueness is also unclear at this point).

Since the families of profile derivatives are uniformly bounded in $L^1(\mathbb{R})$, by the Banach–Alaoglu theorem, up to another extraction, the families $(\phi_k' \text{d}\xi)_{k > k^\star}$ and $(\psi_k' \text{d}\xi)_{k > k^\star}$ converge in the weak-$\star$ topology of the set of bounded Radon measures to some limits, $\text{d}\phi_\infty$ and $\text{d}\psi_\infty$ respectively, which are supported in the support of $\phi_\infty$ and $\psi_\infty$ respectively.

We deduce from such a convergence that $\phi_\infty$ and $\psi_\infty$ are continuous, valued in $[0, 1]$, nonincreasing and nondecreasing respectively and with (distributional) derivatives that are bounded Radon measures of total mass smaller than or equal to $1$. Subsequently, $\phi_\infty$ and $\psi_\infty$ have limits at $\pm\infty$.

2.2.   Segregation of the limiting supports

Proof. Testing for all $k > k^\star$ one of the two equations of (1.5), say the first one, against any smooth and compactly supported test function $\chi\in\mathscr{D}(\mathbb{R})$ and using the dominated convergence theorem as well as estimates of the form

where $K\subset\mathbb{R}$ is the support of $\chi$, we find that $\omega(\boldsymbol{\Phi}_k)$ converges to $0$ in the space of distributions. By continuity of $\omega$, $\omega(\boldsymbol{\Phi}_\infty) = 0$, whence at any $\xi\in\mathbb{R}$, $\phi_\infty(\xi) = 0$ or $\psi_\infty(\xi) = 0$. Consequently, the following equalities are true pointwise in $\mathbb{R}$:

1. $\alpha\phi_\infty = \left(\alpha\phi_\infty-\psi_\infty \right)^+$;

2. $\psi_\infty = \left(\alpha\phi_\infty-\psi_\infty \right)^-$.

Recall that $\text{d}\psi_\infty$ is supported in the support of $\psi_\infty$, namely the closure of $\psi_\infty^{-1}\left((0, 1] \right)$. Note that $\psi_\infty^{-1}\left((0, 1] \right)\subset\phi_\infty^{-1}(\left\{ 0 \right\})$. Since $\boldsymbol{\Phi}_\infty$ and $d_{1, 2}$ are continuous with $d_{1, 2}(0, \bullet) = 0$,

Note that this calculation does not require the absolute continuity of $\text{d}\phi_\infty$ with respect to the Lebesgue measure, which is unclear a priori. Repeating this argument, we discover that the equalities

are all true.

2.3.   The limiting equation

Proof. For all $k > k^\star$, the scalar equation

is equivalent to

The equation (2.2) does not depend explicitly on $k$. Our aim is to pass to the limit in this equation. Therefore we test this equation against a smooth and compactly supported test function $\chi\in\mathscr{D}(\mathbb{R})$ and we subtract from the result the equation (1.7) tested against the same $\chi$. Working in the space of distributions, we can write $\phi_\infty'$ and $\psi_\infty'$ without abuse of notation.

The zeroth-order terms converge to $0$ by the dominated convergence convergence.

The first-order terms converge to $0$ by estimates of the form

(where the compact set $K\subset\mathbb{R}$ is the support of $\chi$). The first term on the right-hand side converges to $0$ by $\int_K \left|\psi_k'\right|\leq 1$ and locally uniform convergence of the profiles whereas the second term converges to $0$ by weak-$\star$ convergence of the derivatives (the test function $\left|h_{1, 2}(\boldsymbol{\Phi}_\infty)\chi\right|$ is indeed continuous and zero at infinity).

The second-order terms converge to $0$ by similar estimates with $\chi$ replaced by $\chi'$.

Eliminating all the terms that are actually zero (2.1), we find that $(z, c) = (\alpha\phi_\infty-\psi_\infty, c_\infty)$ is a solution of

where the functions $d$, $h$ and $g$ are defined above in (1.8), (1.9), (1.10).

Note that, when identifying the terms, it can be useful to cut all integrals into three parts: the integral over the set $z^{-1}\left(\left(0, \alpha \right] \right)$, the one over $z^{-1}\left(\left\{ 0 \right\} \right)$ and the one over $z^{-1}\left(\left[-1, 0 \right) \right)$. By monotonicity of $z$, these three sets are intervals, ordered from left to right. Also, some of these sets might be empty (at this point). It turns out that all integrals over the closed interval $z^{-1}\left(\left\{ 0 \right\} \right)$ are zero. Indeed,

1. if this interval is empty or a singleton, then the set is negligible;

2. if this interval is neither empty nor a singleton, then $z = z' = 0$ there.

Remark 2.1. In ^[4], the limiting equation (of the form $-(\alpha\phi_\infty-d\psi_\infty)"-c(\alpha\phi_\infty-\psi_\infty)' = g(\alpha\phi_\infty-\psi_\infty)$ in $\mathscr{D}'(\mathbb{R})$, with a constant diffusion rate $d > 0$) was used to deduce directly the continuity of $(\alpha\phi_\infty-d\psi_\infty)'$, just by taking the antiderivative of the equation. Let us emphasize that here the situation is not so easy: indeed, at this point of the proof, we do not know that the distributional derivative $z'$ is sufficiently regular to write the chain rule $h(z)z' = (H(z))'$ (where $H$ is a Lipschitz-continuous antiderivative of $h$). Therefore more care is needed to obtain the regularity at the free boundary and subsequently the free boundary relation. In order to complete the proof, we will use ideas from ^[8], where the free boundary problem was also more delicate, due to the spatial periodicity of the setting there.

2.4.   Non-triviality, piecewise-smoothness and limits at infinity of the limit points

Proof. By pointwise convergence,

1. if $c_\infty\leq \frac12(c_\star^+-c_\star^-)$, $\phi_\infty(0) = \frac12$;

2. if $c_\infty > \frac12(c_\star^+-c_\star^-)$, $\psi_\infty(0) = \frac12$.

Note that, by $({\mathsf{A}}_{6})$,

We define $\xi^+ = \sup \phi_\infty^{-1}((0, 1])$ and $\xi^- = \inf \psi_\infty^{-1}((0, 1])$. These two quantities, a priori defined in $\overline{\mathbb{R}}$, satisfy $\xi^+\leq\xi^-$ by virtue of $\phi_\infty \psi_\infty = 0$. Moreover, $\xi^+\geq 0$ if $c_\infty\leq \frac12(c_\star^+-c_\star^-)$ and $\xi^-\leq 0$ if $c_\infty > \frac12(c_\star^+-c_\star^-)$.

We are going to prove now the following claim:

Assume for instance $c_\infty\leq \frac12(c_\star^+-c_\star^-)$, so that $\xi^+\geq 0$.

From the equation (2.3) tested against test functions supported in $(-\infty, \xi^+)$, where $\psi_\infty$ is identically zero, we find that $\phi_\infty$ is a weak solution of

By standard elliptic regularity ^[9], $\phi_\infty$ is then $\mathscr{C}^2$ in $(-\infty, \xi^+)$.

Since $(-\infty, \xi^+)$ is not empty and $\phi_\infty$ is non-increasing and larger than or equal to $1/2$ in $(-\infty, 0)$, its limit $C$ at $-\infty$ is well-defined and larger than or equal to $1/2$. Let $(\xi_n)_{n\in\mathbb{N}}$ be a sequence such that $\xi_n\to-\infty$ as $n\to+\infty$ and define, for all $n\in\mathbb{N}$, $\phi^n_\infty:\xi\mapsto\phi_\infty(\xi+\xi_n)$. By standard elliptic estimates, up to extraction of a subsequence, the sequence $(\phi_\infty^n)_{n\in\mathbb{N}}$ converges in $\mathscr{C}^2_{ \text{loc}}$. By uniqueness of the limit, the limit in $\mathscr{C}^2_{ \text{loc}}$ is also the constant $C\geq 1/2$. By (2.6), invariance by translation and convergence in $\mathscr{C}^2_{ \text{loc}}$, we directly deduce that $C\geq 1/2$ satisfies $Cg_1(C, 0) = 0$, whence $C = 1$ by $({\mathsf{A}}_{4})$.

In order to prove the finiteness of $\xi^+$, assume by contradiction $\xi^+ = +\infty$. Then $\psi_\infty = 0$ identically and $\phi_\infty(\xi) > 0$ at any $\xi\in\mathbb{R}$. Hence $\phi_\infty$ is a positive weak solution, and then a positive classical solution by elliptic regularity, of

Repeating the argument, the limit of $\phi_\infty$ at $+\infty$ is then $0$. Hence $(t, x)\mapsto \phi_\infty(x-c_\infty t)$ is a traveling wave solution with speed $c_\infty$, and by (2.4), $c_\infty < c_\star^+$, which contradicts the analysis of monostable equations by Malaguti and Marcelli ^[5]. Therefore $\xi^+ < +\infty$, or in other words $\xi^+\in\mathbb{R}$.

Next, integrating the equation satisfied by $\phi_\infty$ in $(\xi^+-1, \xi^+)$, we infer that the left-sided limit of $\phi_\infty'$ at $\xi^+$ is finite and, by the Hopf lemma, negative. Since $\xi^-\in\left[\xi^+, +\infty \right]$, we infer similarly that one, and only one, of the following two claims is true:

1. $\xi^- = +\infty$,

2. $\psi_\infty$ is $\mathscr{C}^2$ in $(\xi^-, +\infty)$ with $1$ as limit at $+\infty$ and a finite and positive right-sided limit of $\psi_\infty'$ at $\xi^-$.

Integrating the equation (2.3) over $\mathbb{R}$ with an arbitrary test function $\chi\in\mathscr{D}(\mathbb{R})$ and using the fact that $z = 0$ in $(\xi^+, \xi^-)$, we obtain:

Integrating by parts the terms $\int_{-\infty}^{\xi^+}-d(z)z'\chi'$ and $\int_{\xi^-}^{+\infty}-d(z)z'\chi'$, we deduce:

By positivity of the left-hand side, necessarily $\xi^- < +\infty$, or in other words $\xi^-\in\mathbb{R}$. We have thus proved the claim (2.5) in the case $c_\infty\leq \frac12(c_\star^+-c_\star^-)$.

Repeating the argument with the roles of $\phi_\infty$ and $\psi_\infty$ reversed, we find that the claim (2.5) remains true even if $c_\infty < \frac12(c_\star^+-c_\star^-)$, that is for any possible value of $c_\infty$.

2.5.   Triviality of the free boundary, the free boundary relation and regularity of the first derivatives

Proof. It follows from (2.7) that

with $\lim_{\xi-\xi^+\to0^-}\phi_\infty'(\xi) < 0 < \lim_{\xi-\xi^-\to0^+}\psi_\infty'(\xi)$.

We first check that $\xi^+ = \xi^-$. Indeed, if $\xi^+ < \xi^-$, we can choose the test function $\chi$ so that its support contains $\xi^+$ but not $\xi^-$, and then the above equality becomes an equality between a positive term and a zero term, which is contradictory. Therefore $\xi^+ = \xi^-$.

Next, choosing $\chi$ so that its support contains $\xi^+ = \xi^-$ and dividing by $\chi(\xi^+)\neq 0$, we find

In other words, $d(z)z'$ is a well-defined continuous function in $\mathbb{R}$.

In order to simplify the notations, we work from now on with the shifted profiles so that $\xi^+ = \xi^- = 0$. With this convention, the free boundary relation reads

Since the limits of $d(z)z'$ at $\pm\infty$ are zero, we also obtain $d(z)z'\in L^\infty(\mathbb{R})$. We deduce the piecewise-continuity and global boundedness of $z'$. Hence the distribution $z$ is a well-defined function in $W^{1, \infty}(\mathbb{R})$, or in other words a well-defined Lipschitz-continuous, piecewise-$\mathscr{C}^1$, function in $\mathbb{R}$.

Since $z$ has no jump discontinuity at $0$, a standard result of distribution theory yields the identification $z' \text{d}\xi = \alpha \text{d}\phi_\infty- \text{d}\psi_\infty$. This proves that the measures $\text{d}\phi_\infty$ and $\text{d}\psi_\infty$ are absolutely continuous with respect to the Lebesgue measure, or in other words that the derivatives $\phi_\infty'$ and $\psi_\infty'$ are well-defined functions in $L^1(\mathbb{R})$.

2.6.   Regularity of the second derivatives

Proof. From the equality

and the fact that the right-hand side is a well-defined function in $L^\infty(\mathbb{R})$, we infer that $(d(z)z')'\in L^\infty(\mathbb{R})$ (in other words, $d(z)z'$ is Lipschitz-continuous).

We are now in a position to rewrite (2.3) with less regular test functions: by density,

2.7.   Uniqueness of the limit point

Proof. The uniqueness (up to shifts) of the limit point is a direct consequence of the uniqueness (up to shifts) of the bistable traveling wave (Theorem A.1).

By a classical compactness argument, the uniqueness of the limit point implies the convergence of the full initial family $(\boldsymbol{\Phi}_k, c_k)_{k > k^\star}$ (as defined before any extraction of subsequence).

2.8.   Estimates on $c_\infty$

Proof. Similarly, the estimates $-c_\star^- < c_\infty < c_\star^+$ follow directly from Theorem A.1.

The sign of the effective wave speed if $h_{1, 1} = h_{2, 2} = h_0\in\mathbb{R}$ (which implies $h = h_0$) is obtained by testing (1.7) against $d(z)z'$. After an integration by parts and a change of variable, we find

so that the effective wave speed $c_\infty+h_0$ has indeed the sign of the right-hand side. Note that since $z'\in L^1(\mathbb{R})\cap L^\infty(\mathbb{R})$, clearly $z'\in L^2(\mathbb{R})$.

2.9.   Improvement of the convergence

Proof. In view of the limits at $\pm\infty$ of $\phi_\infty$ and $\psi_\infty$, the equalities $\int \phi_k' = -1$ and $\int \psi_k' = 1$ are true for all $k\in(k^\star, +\infty]$. From this remark, it follows that:

1. by a result sometimes known as the second Dini theorem^†, the convergence of the families of monotonic functions $(\phi_k)_{k > k^\star}$ and $(\psi_k)_{k > k^\star}$ is actually uniform in $\mathbb{R}$;

^† The second Dini theorem states that a sequence of nondecreasing functions that converges pointwise in a closed interval of $\overline{\mathbb{R}}$ to a continuous function converges uniformly in this interval; when $\pm\infty$ belong to the interval, the assumption is naturally understood as the convergence of the limits at $\pm\infty$ to the limits at $\pm\infty$ of the continuous limit.

2. by the Prokhorov theorem, the convergence of the tight families of probability measures $(-\phi_k' \text{d}\xi)_{k > k^\star}$ and $(\psi_k' \text{d}\xi)_{k > k^\star}$ actually occurs in the weak-$\star$ topology of the set of probability measures in $\mathbb{R}$ (i.e., the measures converge when tested against any fixed continuous bounded function from $\mathbb{R}$ to $\mathbb{R}$). Since the limits $-\phi_\infty' \text{d}\xi$ and $\psi_\infty' \text{d}\xi$ are absolutely continuous with respect to the Lebesgue measure, this implies the strong convergence of $(\boldsymbol{\Phi}_k')_{k > k^\star}$ in $L^1(\mathbb{R})$ (testing as usual the weak-$\star$ convergence against the test function $\mathbf{1}_{\mathbb{R}}$).

3.   Discussion

Our focus is on the effect of $\mathbf{D}$ and $\mathbf{H}$. For $\mathbf{g}$ and $\omega$, we mostly have in mind the special Lotka–Volterra case:

3.1.   On the literature

To the best of our knowledge, this paper is the very first to consider the spatial segregation limit of traveling waves for general fully nonlinear competitive systems and to show the connection with general fully nonlinear scalar equations.

3.1.1.   Fully nonlinear strongly coupled competitive systems

The semilinear competition–diffusion system (1.6) was studied by the first author and G. Nadin in ^[4] (refer also to ^[8] for an extension to space-periodic media). The spatial segregation limit was used to characterize the sign of the wave speed: $c_\infty$ has in such a case the sign of $\alpha^2-rd$. This was interpreted as a "Unity is not strength"-type result (and, actually, as a "Disunity is strength"-type result): if $\alpha = r = 1$, so that the two species only differ in diffusion rate, then the invader is the fast diffuser (that is, with pure Brownian motion, the winning strategy is to disperse rapidly instead of remaining concentrated). The problem of the sign of the wave speed for finite values of $k$ is the object of a recent survey paper by the first author ^[10].

The paper ^[4] used extensively the ideas of the wide literature on the spatial segregation limit of parabolic or elliptic competition–diffusion systems in bounded domains (e.g., ^{[11,12,13,14,15,16,17]} and references therein).

These ideas were also used in a collection of works by Liu and various collaborators ^[18,19,20] studying the spatial segregation limit of the strongly coupled elliptic system (1.4) with self- and cross-diffusion of Shigesada–Kawasaki–Teramoto type ^[2], where (3.1), $\mathbf{H} = \mathbf{0}$,

all parameters above being constant and positive. The main idea there was to change variables in order to recover an elliptic system with linear diffusion. We point out that although our system can be seen as an elliptic one, the unboundedness of the domain and the generality of the functions $\mathbf{D}$ and $\mathbf{H}$ make the problem quite different. Although the Cauchy problem for the cross- and self-diffusion system in an unbounded domain has been studied more than ten years ago by Dreher ^[21], we believe that the traveling wave problem is still largely open (e.g., ^[22]).

Bistable traveling waves for the competition–diffusion–cross-taxis system (1.3), where

and with finite, but large, values of $k$ were numerically investigated by Potts and Petrovskii in ^[1]. The cross-taxis is attractive if $\gamma_i > 0$ and repulsive if $\gamma_i < 0$. The point there was to show that appropriate choices of $\gamma_i$ can change the sign of the wave speed, or equivalently the invader: roughly speaking, aggressivity can compensate unity. The authors called this conclusion a "Fortune favors the bold"-type result. The well-posedness of this system with $\gamma_1 = \gamma_1(u, v)$ and $\gamma_2 = 0$ was studied independently in a collection of works by Wang and various collaborators ^{[23,24,25,26]} (refer also to ^[27] for a case where $v$ does not diffuse at all).

We also point out a recent analytical and numerical study by Krause and Van Gorder ^[28] of traveling wave solutions to a closely related non-local system with advection toward resource gradients and where each resource density solves an elliptic PDE involving the two population densities (modeling the consumption of resources). Since the resource density converges to a linear combination of both population densities in the vanishing viscosity limit, our model (1.1) can be understood as a singular limit of that model (see [28,Section 2.1]).

3.1.2.   Fully nonlinear scalar equations

Equations of the form

are the object of a specific wide literature (e.g., ^{[5,29,30,31,32,33,34,35,36,37]} and references therein). Generically, the important features of the semilinear equations (existence and uniqueness of waves, estimates for the minimal wave speed, etc.) are recovered but in a loose sense.

We point out that in this literature, it is typically assumed that $d$, $g$ and $h$ are at least continuous. This is true in our case when considering the underlying monostable fronts (i.e., connecting $0$ and $\alpha$ or $0$ and $-1$) but, when considering the bistable fronts (connecting $\alpha$ and $-1$), our functions $d$ and $h$ have a jump discontinuity at $z = 0$. It turns out this obstacle can be easily overcome and we will show in Appendix A how the previously known results can be extended to such cases. Our method of proof uses extensively the results of Malaguti and her collaborators ^[5,33] to characterize the singular limit.

3.2.   On the standing assumptions

3.2.1.   $({\mathsf{A}}_{1})$

This is a very standard regularity assumption. Although it seems to us that the results might remain true with less regularity, our aim here is not to focus on regularity issues and we prefer to assume that everything is "smooth enough". Besides, our proof really needs the continuity of $\mathbf{D}$, $\mathbf{H}$, $\mathbf{g}$ and $\omega$. The continuous differentiability of $\mathbf{D}$ is not explicitly used in our proof but is required for the continuity result of ^[34] (which is used in the proof of Theorem A.1).

3.2.2.   $({\mathsf{A}}_{2})$

This is a very standard ellipticity assumption. Although the main part of our proof does not rely upon the sign of $d_{1, 1}$ and $d_{2, 2}$, we need a strong characterization of the limit points (uniqueness in particular) that is available indeed in the elliptic framework but might be unavailable in a degenerate elliptic or aggregative framework. Furthermore, the compactness assumption $({\mathsf{A}}_{9})$ is natural in the elliptic framework but might be contradictory in an aggregative framework.

We believe that our results, and especially the formula (1.11), remain true in a weakly degenerate setting. On the very special case where $d_{1, 1}(\bullet, 0)$ vanishes at $0$ and at $0$ only, we refer for instance to ^[35,36,37], and references therein. We point out that our results would extend indeed to such a degenerate diffusivity provided a result analogous to Theorem A.1 can be established.

Finally, we point out that there are no sign conditions on the cross-diffusion rates $d_{1, 2}$ and $d_{2, 1}$.

3.2.3.   $({\mathsf{A}}_{3})$

This assumption ensures that the system (1.1) is well-posed in the following sense: if $u = 0$ initially, it should not spontaneously appear, so that

Taking for instance $V(x) = v-x^2$, for some $v\in[0, 1]$, and evaluating at the maximum $x = 0$, we get $d_{1, 2}(0, v) = 0$. Subsequently, we deduce $h_{1, 2}(0, v) = 0$. Similarly, $d_{2, 1}(u, 0) = h_{2, 1}(u, 0) = 0$ for any $u$.

Naturally, all applications we have in mind satisfy this assumption.

Note that with such an assumption, $\mathbf{D}$ and $\mathbf{H}$ are constant if and only if they are constant and diagonal.

3.2.4.   $({\mathsf{A}}_{4})$

This is a loose monostability assumption, ensuring that if $v = 0$ then $u$ follows a monostable equation, and vice versa. The instability of $0$ and the stability of $1$ are not understood here in the linear sense (hyperbolicity of the equilibrium), but truly in the nonlinear sense (say, $\alpha$-limit set and $\omega$-limit set of the associated ODE $u' = ug_1(u, 0)$). It is also in that sense that the function $g$ is of bistable type.

The fact that both carrying capacities are unitary is assumed without loss of generality, up to a nondimensionalization of both densities.

Recall that monostable reaction terms can be either of Fisher–KPP type ($g$ is maximal at $0$, e.g., $g(z) = 1-z$) or have a weak Allee effect ($\max_{[0, 1]} g > g(0)$, e.g., $g(z) = z(1-z)$).

3.2.5.   $({\mathsf{A}}_{5})$

This assumption generalizes the interpopulation competition of Lotka–Volterra type, where $\omega(u, v) = uv$. In view of the proof, it might in fact be weakened in several ways. However, we do not know any reasonable model that satisfies only such a weakened assumption. Since $\omega$ does not play an important role in the paper and since we mostly have in mind $\omega(u, v) = u^p v^q$ with $p, q\geq 1$, we choose to keep the more explicit stronger assumption.

3.2.6.   $({\mathsf{A}}_{6})$

The assumption $-c_\star^- < c_\star^+$ is very natural and we actually expect it to be necessary, in the sense that if it is not satisfied, the existence of bistable waves $({\mathsf{A}}_{7})$ should fail, as will be discussed below in Section 3.2.8.

This assumption basically means that, in a situation where the species $u$ comes from $x\simeq -\infty$ and the species $v$ comes from $x\simeq +\infty$, with negligible strong couplings due to the distance between the two species, their invasion fronts move one toward the other and will eventually meet and form a bistable traveling wave.

Marcelli and Papalini ^[35] recently showed that the minimal wave speeds $c_\star^+$ and $c_\star^-$ satisfy the following upper estimates:

Therefore $({\mathsf{A}}_{6})$ fails if, for instance, $h_{2, 2}$ is a large negative constant whereas $h_{1, 1}$ is a large positive constant. Having in mind the preceding heuristics, this is natural: such an advection term $h$ slows down the invasion of both $u$ and $v$ so strongly that the two fronts never meet, with a buffer zone that is linearly increasing in time. Instead of a traveling wave, this describes the formation of what is nowadays called a propagating terrace ^[38]. Such a phenomenon is standard in bistable dynamics and was first reported by Fife and McLeod ^[39].

On the contrary, various simple conditions can ensure $-c_\star^- < c_\star^+$. Indeed, Malaguti and Marcelli ^[5] established the following lower estimates:

For instance, $-c_\star^- < c_\star^+$ as soon as $h_{1, 1} = h_{2, 2} = 0$ (no self-advection), $g_1(0, 0) > 0$ and $g_2(0, 0) > 0$. In particular, the systems (1.2), (1.3), (1.4) all satisfy $({\mathsf{A}}_{6})$.

3.2.7.   $({\mathsf{A}}_{7})$

This is the first truly restrictive assumption. Indeed, for a system as general as (1.1), the existence of bistable traveling waves connecting $(1, 0)$ and $(0, 1)$ is a completely open and difficult problem and it might very well be false in full generality.

More precisely, although the existence of traveling waves $(u, v)(t, x) = (\phi, \psi)(x-ct)$ connecting $(1, 0)$ and $(0, 1)$ is to be expected under fairly reasonable assumptions, we expect that in some cases their profiles $\phi$ and $\psi$ will not be monotonic. In general, non-monotonic traveling waves connecting $(1, 0)$ and $(0, 1)$ do not satisfy any uniform $L^\infty$ bounds or $L^1$ bounds for the profile derivatives. Clearly, from our proof, we need such bounds. We also used several times the fact that the profile derivatives do not change sign. In particular, the monotonicity of the profiles implies (almost directly) that the free boundary is a point or an interval. With non-monotonic profiles, the free boundary problem will be in general much more difficult. Even though we believe our approach can be successful when studying some specific non-monotonic traveling waves, for which convenient bounds can be a priori established, the setting in the present paper is already quite abstract and we deliberately choose to exclude non-monotonic traveling waves.

It seems to us that there are mainly three ways to solve, at least partially, this problem of existence of monotonic traveling waves.

1. Direct construction: this is what was done in the scalar case by Malaguti, Marcelli and Matucci ^[33]. However the proof there relies upon phase-plane arguments and therefore does not extend easily to systems.

2. Perturbative arguments starting from the semilinear case with (3.1): using a standard implicit function theorem approach for bistable waves in monotone systems (presented in detail in, for instance, ^[40,41]), this approach would give the existence of a neighborhood of any constant pair $(\mathbf{D}, \mathbf{H})$ in which traveling waves exist (see also ^[22] for another type of perturbative result). However the diameter of this neighborhood will depend on $k$ and it is quite difficult to bound it from below. Therefore such an approach is hardly suitable if our ultimate goal is to pass to the limit $k\to+\infty$.

3. Homotopy arguments starting from the limit $k = +\infty$: such an approach has been used repeatedly in the literature on strongly competitive systems (e.g., ^[14,42]). It requires first a good knowledge of the limit. The present paper can therefore be understood as a first step toward existence results proved with this approach.

Consequently, the proof of existence is left as a difficult but interesting open problem and, in this paper, we simply assume a priori the existence.

3.2.8.   $({\mathsf{A}}_{8})$

This is a technical assumption that should always be satisfied as soon as traveling waves exist $({\mathsf{A}}_{7})$. Indeed, it is a quite general feature of bistable waves that their speed is stuck between the minimal wave speeds of the two underlying monostable problems (e.g., ^[6,7,33,43]). Here, these two bounds are precisely $c_\star^+$ and $-c_\star^-$. In other words, we actually expect that $-c_\star^- < c_k < c_\star^+$ is true for all $k > k^\star$.

Nevertheless, since the existence of waves is unclear and since the system does not satisfy the comparison principle (which is the main tool used to prove the above inequalities in the semilinear competition–diffusion case (1.2)), we have no choice but to add this likely superfluous assumption.

3.2.9.   $({\mathsf{A}}_{9})$

This is the second truly restrictive assumption. It is for instance satisfied if an $L^2_{ \text{loc}}$ estimate on $\boldsymbol{\Phi}_k'$ can be proved, but it seems that in general such an estimate is false. Below we give important examples where such an estimate can be proved indeed.

1. If both $d_{1, 2}$ and $d_{2, 1}$ are nonpositive (this applies in particular to the system (1.3) with $\min(\gamma_1, \gamma_2)\geq 0$), then we can multiply the first, respectively second, equation of the system (1.5) by $\phi_k\chi_R$, respectively $\psi_k\chi_R$, where $\chi_R$ is a cut-off function equal to $1$ in $[-R, R]$, smooth and valued in $(0, 1)$ in $[-R-1, -R]\cup[R, R+1]$, and equal to $0$ in $\mathbb{R}\backslash(-R-1, R+1)$. Just as in ^[4], a few integrations by parts lead to an $L^2([-R, R])$ estimate on $\phi_k'$, respectively $\psi_k'$. For completeness, the detailed calculation for the first equation – where subscripts $R$ and $k$ are dropped for ease of reading – follows. Together, the inequality $\int d_{1, 2}(\boldsymbol{\Phi})\psi'\phi'\chi\geq 0$ (where $d_{1, 2}\leq 0$ and $\psi'\phi'\leq 0$ are used) and the equality

imply

It just remains to verify that each term on the right-hand side is bounded uniformly with respect to $k$. The last term is bounded as follows:

All the other terms are handled similarly, using the facts that $(c_k)_{k > k^\star}$ is bounded $({\mathsf{A}}_{8})$ and that $\phi'$ and $\psi'$ both have a unitary $L^1(\mathbb{R})$-norm. For instance,

In the end, using the boundedness from below of $d_{1, 1}$, there exists a constant $C > 0$ that does not depend on $k$ or $R$ such that

Remark that necessarily $\|\chi\|_{W^{1, \infty}}+\|\chi\|_{L^1}$ depends on $R$. We also point out that further integration by parts are possible but do not improve the estimate.

2. If (3.1) and $\mathbf{D}$ is the Jacobian matrix of a $\mathscr{C}^2$-diffeomorphism

then we can multiply the first, respectively second, equation by $d_1(\boldsymbol{\Phi}_k)\chi_R$, respectively $d_2(\boldsymbol{\Phi}_k)\chi_R$, and discover similarly an $L^2([-R, R])$ estimate on $(\mathbf{d}(\boldsymbol{\Phi}_k))'$, that is on $\boldsymbol{\Phi}_k'$ by invertibility of $\mathbf{d}$. This idea is borrowed from ^[18,19,20]. As such, this applies to the system (1.4).

A very important remark is required here: similar estimates cannot be obtained for the general evolution parabolic problem or for the general diffusion–advection elliptic problem, as here we heavily use the monotonicity and the $L^\infty$-boundedness of the profiles for the calculations. More details on the difficult estimates for the evolution problem can be found for instance in ^[3,21] and references therein.

Actually, the monotonicity of the profiles and the uniform $L^\infty$ bounds induced by the traveling wave form, that are heavily used in the above calculations, directly yield some regularity, compactness and convergence properties. Unfortunately, these are not sufficient to derive the limiting problem and $({\mathsf{A}}_{9})$ seems to be truly required. Still, for possible future reference, we list some of these properties below.

1. Since the wave profiles are all of bounded variation and uniformly bounded, we can directly apply Helly's selection theorem: up to extraction, $(\boldsymbol{\Phi}_k)_{k > k^\star}$ converges pointwise and locally in $L^1$ to some limit $\boldsymbol{\Phi}_\infty$. This does not depend on the equations.

2. The families $(-\phi_k' \text{d}\xi)_{k > k^\star}$ and $(\psi_k' \text{d}\xi)_{k > k^\star}$ are families of probability measures in $\mathbb{R}$. By the Banach–Alaoglu theorem, a bounded family of Radon measures in $\mathbb{R}$ is relatively compact in the weak-$\star$ topology of the set of bounded Radon measures, namely the topology of pointwise convergence on the space of continuous functions in $\mathbb{R}$ that converge to $0$ at $\pm\infty$. Again, this does not depend on the equations.

3. A monotone function is differentiable almost everywhere, with a number of discontinuities at most countable, and each discontinuity is a jump discontinuity.

3.3.   On the results

3.3.1.   The limiting equation

The limiting equation in (1.7) does not have classical solutions (namely, solutions of class $\mathscr{C}^2$) in general. In fact, the unique weak solution $z$ is of class $\mathscr{C}^1$ if and only if the left-sided and right-sided limits of $d$ at $0$ coincide (that is $d_{1, 1}(0, 0) = d_{2, 2}(0, 0)$) and of class $\mathscr{C}^2$ if and only if it is of class $\mathscr{C}^1$ and the left-sided and right-sided limits of $h$ at $0$ coincide (that is $h_{1, 1}(0, 0) = h_{2, 2}(0, 0)$). Nevertheless, since the equation implies that $d(z)z'\in W^{1, \infty}(\mathbb{R})$, $d(z)z'$ is at least Lipschitz-continuous. This is where the free boundary relation comes from.

As they are defined in (1.8) and (1.9), the functions $d$ and $h$ both have a zero at $z = 0$. However, Theorem 1.1 does not depend on how the piecewise-continuous functions $d$ and $h$ are defined at $z = 0$. This is classical in such problems (e.g., ^[4,13,15]).

Note that the positivity of the left-sided and right-sided limits of $d$ at $0$, that is the positivity of the essential infimum of $d$, still matters.

3.3.2.   The convergence

The space where the convergence of the profiles occurs might be improved by bootstrap in special cases, using more deeply the structure of the equations. We point out that, in view of the regularity of the limit, the best that can be proved is a uniform Lipschitz bound (implying convergence in all Hölder spaces $\mathscr{C}^{0, \gamma}$) for $(\boldsymbol{\Phi}_k)_k$ and $(\mathbf{D}(\boldsymbol{\Phi}_k)\boldsymbol{\Phi}_k')_k$. This is consistent with the literature on the semilinear problem (refer to Soave–Zilio ^[17] for a detailed review).

3.3.3.   The sign of the effective wave speed when the self-advection is constant

The formula (1.11) is the extension of the "Disunity is strength"-type result for the semilinear competition–diffusion system (1.2) established in ^[4].

It shows for instance that, if $h_0 = 0$, $g_1(\bullet, 0) = g_2(0, \bullet)$, $\alpha = 1$ and $d_{1, 1}(\bullet, 0) < d_{2, 2}(0, \bullet)$, so that the two populations differ only in diffusivity and the diffusivities obtained in absence of the other are strictly ordered, then $c_\infty < 0$: again, a strong diffusivity is a competitive advantage.

Quite interestingly, the formula (1.11) does not depend on the cross-diffusion rates $d_{1, 2}$ and $d_{2, 1}$, on the cross-advection rates $h_{1, 2}$ and $h_{2, 1}$ and on the competition rate $\omega$. In fact, it only depends on the parameter $\alpha$ and on the dynamics of each population in absence of the other: although the system is arbitrarily strongly coupled, its spatial segregation limit is mostly decoupled (more precisely, it is coupled only at the free boundary).

In order to illustrate more directly our result, below, we apply the formula (1.11) to the specific cases studied in the aforementioned earlier literature [1,3,etc.]. This mostly amounts to comparing dispersal strategies, but clearly we can also use the formula (1.11) to compare growth strategies and determine, for instance, the effect of a weak Allee effect.

First, we consider self- and cross-diffusion systems with logistic growth, namely systems generalizing (1.4), where (3.1) holds, $\mathbf{H} = \mathbf{0}$ and $\mathbf{D}(u, v)$ is the following Jacobian matrix:

In such a case, the formula (1.11) reads

In the special case $\beta_{1, 1} = \beta_{2, 2} = 1$, this reads

Hence the sign of the wave speed is determined by the self-diffusivities in absence of the other and at carrying capacity. This illustrates quite interestingly the fact that the coupling at the free boundary is not just local but takes also into account what happens far away from the free boundary. The above formula also shows that there are cases where a population wins despite a smaller linear diffusivity (say, for instance, $\alpha = r = 1$, $d_1+a_{1, 1} > d_2+a_{2, 2}$ and $d_1 < d_2$).

Note that we can apply formally the formula to the case $d_1 = 0$ or $d_2 = 0$ (no linear diffusion, just porous-medium type self-diffusion). Although our proof does not apply in such a case (see $({\mathsf{A}}_{2})$), we conjecture that this formula is indeed the correct one.

Second, we consider cross-taxis systems with logistic growth, namely systems of the form (1.3), where (3.1) holds, $\mathbf{H} = \mathbf{0}$ and

It turns out that for such a system, we recover exactly the same formula as in the case of constant $\mathbf{D}$: the sign of $c_\infty$ is that of $\alpha^2 d_1-rd_2$. The values of $\gamma_1$ and $\gamma_2$ have no effect. Hence "Disunity is strength" again, whatever the strength or the sense (attraction or repulsion) of the cross-taxis.

This conclusion is in sharp contrast with the "Fortune favors the bold" conclusion suggested numerically by Potts and Petrovskii in ^[1]. The contrast is not contradictory and is explained by the fact that their simulations take finite values of $k$ whereas we focus on the limit $k\to+\infty$, where the effect of the aggressive taxis becomes negligible due to spatial segregation.

Let us end this discussion by relating this work to the wide literature on mathematical models for the evolution of dispersal in nature (we refer for instance to [44,Chapter 11] and references therein). Adopting such a viewpoint, our result tends to show that, for a species trying to survive a strong competitor, the formation by means of mutations of an aggressive phenotype – in the cross-taxis sense of Potts and Petrovskii –, or more generally of a phenotype whose dispersal strategy accounts for the competitor, should actually not help, and therefore such a mutant should not be selected. This might seem counter-intuitive at first, yet it can be explained heuristically at the individual scale: the infinite competition limit means that as soon as two individuals of adversary populations meet, both die, instantaneously. Since no one will ever survive such an encounter, even for the tiniest amount of time, it is therefore useless to try to learn how to deal with these encounters. As a matter of fact, according to the model, the fittest mutations in such a situation are those that improve the diffusion of the species, be it linear diffusion or nonlinear self-diffusion. This is of course in sharp contrast with the well-known "Unity is strength"-type result in spatially heterogeneous environments without strong competitor proved by Dockery et al. ^[45] and this might lead to evolutionary traps, as explained by the first author in [10,Section 3.5].

A.   The fully nonlinear bistable scalar equation with piecewise-continuous diffusion and advection rates

In this appendix, we sketch briefly the proof of the following theorem that confirms that the functions $d$ and $h$ can be defined arbitrarily at $0$. This theorem extends the main result of Malaguti–Marcelli–Matucci ^[33].

Theorem A.1. Let $U_\pm\in\mathbb{R}$ such that $U_- < 0 < U_+$ and let

1. $d:[U_-, U_+]\to\mathbb{R}$ be continuously differentiable and positive in $[U_-, U_+]\backslash\left\{ 0 \right\}$ with positive limits at $0^\pm$;

2. $h:[U_-, U_+]\to\mathbb{R}$ be continuous in $[U_-, U_+]\backslash\left\{ 0 \right\}$ with limits at $0^\pm$;

3. $g:[U_-, U_+]\to\mathbb{R}$ be continuous with $g(U_-) = g(0) = g(U_+) = 0$ and $g < 0$ in $(U_-, 0)$ and $g > 0$ in $(0, U_+)$.

Let $c_\star^\pm$ be the minimal wave speed of nonincreasing classical solutions $(z, c)$ of

with limits $0$ at $+\infty$ and $U_\pm$ at $-\infty$.

Then, if $-c_\star^- < c_\star^+$, the equation (A.1) supplemented with the constraints

1. $z$ admits $U_+$ and $U_-$ as limits at $-\infty$ and $+\infty$ respectively;

2. $z$ is nonincreasing;

3. $z$ is continuous;

admits a unique (up to shifts) weak solution $(z, c)$, and its wave speed $c$ satisfies $-c_\star^- < c < c_\star^+$.

Conversely, if $-c_\star^-\geq c_\star^+$, no such solution exists.

Proof. The existence of the wave, its monotonicity, its continuity and its limits when $-c_\star^- < c_\star^+$ directly follow from a standard regularization of the functions $d$ and $h$, from a locally uniform $L^2$ estimate on the regularized profile derivative (see ^[4] or Section 3.2.9 above) and from the continuity with respect to $d$ and $h$ of the minimal wave speed for monostable equations ^[34]. When passing to the limit, the nontriviality of the limit $z$ has to be verified, as in the main proof of the paper. In order to do so, a normalization $z(0) = \frac12 U_\pm$ depending on the limiting wave speed can be used, as in the main proof of this paper. Note that at this point, we have $-c_\star^-\leq c\leq c_\star^+$ but not the strict inequalities.

In the sequel, we will need the continuity of $d(z)z'$. Although it is not assumed a priori, it can be established by integrations by parts, exactly as in the main proof of this paper. In fact, our proof actually shows that any monotonic continuous traveling wave weak solution necessarily satisfies $d(z)z'\in \mathscr{C}(\mathbb{R})$.

The uniqueness (up to shifts) can be established by contradiction, assuming that there are two different nonincreasing continuous waves $(z_1, c_1)$ and $(z_2, c_2)$ with, for instance, $c_1\leq c_2$. Then we have two different positive semi-waves $(z_1^+, c_1)$ and $(z_2^+, c_2)$ or two different negative semi-waves $(-z_1^-, c_1)$ and $(-z_2^-, c_2)$. The positive semi-waves are solutions of

and the negative semi-waves are solutions of

For both sub-problems, the functions $d$ and $h$ are continuous, so that the uniqueness result for semi-waves [33,Lemma 10] implies directly that $c_1 < c_2$, and then the comparison principle [33,Lemma 10] implies

so that the continuity of either $d(z_1)z_1'$ or $d(z_2)z_2'$ is contradicted:

The strict inequalities $-c_\star^- < c < c_\star^+$ are obtained with the same argument (the uniqueness result [33,Lemma 10] does not distinguish semi-waves and regular traveling waves, so that the two cannot coexist).

The nonexistence when $-c_\star^-\geq c_\star^+$ follows similarly from [33,Lemma 10].

Acknowledgments

This work was supported by a public grant as part of the Investissement d'avenir project, reference ANR-11-LABX-0056-LMH, LabEx LMH

Conflict of interest

The authors declare there is no conflicts of interest.