Oscillatory solutions and smoothing of a higher-order p-Laplacian operator

1.   Introduction

In recent years, the search for high-precision numerical solutions of differential equations has been the focus of scholars' research ^[1,2,3]. The non-locality and memory of fractional calculus make it better to describe complex practical problems; so, many scholars have done a lot of research on the problem and applied it to various practical mathematical physics problems ^{[4,5,6,7,8,9]}. Since obtaining analytical solutions of fractional differential equations is a challenging task, numerical methods for solving fractional differential equations have drawn extensive attention. At present, a series of effective numerical methods have been developed for solving fractional differential equations, such as the finite difference method ^[10,11], the finite element method ^[12,13], the spectral method ^[14,15], and the meshfree methods (MFMs) ^[20,21,22]. In ^[16], it was introduced the finite difference method to deal with time and space problems. A first-order finite difference (L1) of the time discretization scheme was presented by Langlands and Henry ^[17]. Lin et al. ^[18] introduced an improved numerical method that uses a finite difference scheme for time discretization and the Legendre spectral method for space discretization. Deng ^[19] studied the finite element method (FEM) of fractional Fokker-Planck equation. In recent years, MFMs have become increasingly popular in solving practical engineering problems by reducing the dependence on grids ^[20,21,22]. Recently, Li et al. ^[23] proposed a new meshless numerical method called the finite integral method (FIM) to approximate one-dimensional problems. The FIM of Hadamard fractional derivative has received extensive attention ^[24]. Li et al. ^[25] proved that the FIM has high stability, efficiency, and accuracy when solving multi-dimensional problems.

Deep learning has grown in popularity as a numerical technique for solving integer-order partial differential equations. Numerous models based on data-driven deep neural networks (DNNs) have been proposed for partial differential equations ^{[26,27,28,29,30,31,32]}, which only utilize information from observed data. Wang et al. ^[33] combined the residual neural network with the data-driven method to solve the high-dimensional problem efficiently. Yohai et al. ^[34] introduced a data-driven discretization scheme that uses neural networks to estimate spatial derivatives and perform end-to-end optimization of spatial derivatives. However, data-driven networks are unable to solve the issue with only physical constraints since they need a large amount of labeled data. Given the limitations of data-driven networks, one kind of neural network incorporating physical information has been developed. The networks have demonstrated powerful capabilities in solving partial differential equations and have received extensive attention ^{[35,36,37,38,39,40]}. At present, neural network technologies for solving classical partial differential equations are developing and showing promising results in practical applications ^{[41,42,43,44,45,46,47,48]}. Lin and Chen ^[49] proposed two physics-informed neural network (PINN) schemes based on the Miura transform. They introduced Miura transform constraints into neural networks to solve nonlinear partial differential equations and achieve unsupervised learning. Pu and Chen ^[50] obtained the data-driven vector local waves of the Manakov system with initial and boundary conditions by improving the output function and the number of physical constraints of the physical information neural network and using the local adaptive activation function of neurons and the slope recovery term. Because the automatic differentiation function used in the PINNs cannot be implemented for solving fractional-order problems, the construction of a stable and efficient neural network for solving fractional-order partial differential equations has become a hot research topic in deep learning. Fractional PINNs (fPINNs) ^[51] used the L1 scheme to discretize the time-fractional derivative. Rostami ^[52] implemented a series expansion as a substitute solution, enabling more accurate resolutions of high-order linear fractional partial differential equations (FPDEs). Wang et al. ^[53] combined fractional-order physical information with the nonlinear function of neural networks to improve the modeling and solving effect of temporal fractional-order phase-field models.

The classical first-order finite difference (L1) scheme for discretizing the fractional derivative exhibited good stability and numerical accuracy. However, due to its low convergence order, it may require more grid nodes to obtain the same numerical precision as higher-order difference schemes. The piecewise quadratic interpolation (PQI) in the sense of the Hadamard finite partial integral proposed by Li et al. ^[54] has higher convergence, which can improve the precision of the predicted solutions and enhance the efficiency of the model.

In this paper, the fractional derivative of time is discretized using PQI rather than L1 as in fPINN. The higher-order discretization scheme causes the residual loss of the governing equation to decrease rapidly, resulting in a more accurate solution. In order to address the gradient imbalance of different loss terms in PINN and fPINN, the adaptive learning rate is proposed in the loss function, which can effectively keep the network from failing in the local optimal solution and significantly enhance its trainability, convergence, and accuracy. Furthermore, a new composite activation function is designed, greatly improving the precision of the destruction solution.

The rest of the paper is organized as follows. In Section 2, the precise format of the fractional differential equation is given, including the governing equation, initial condition, and boundary conditions. In Section 3, the techniques used to construct the proposed adaptive-fPINN-PQI framework are introduced in detail, including the formula of PQI discretization scheme, the principle and formula of the adaptive learning rate, the architecture of the network, and the components of the composite activation function. In Section 4, intensive numerical examples are conducted to demonstrate the excellent performance in accuracy and efficiency of the adaptive-fPINN-PQI. Some conclusions about the adaptive-fPINN-PQI are drawn in Section 5.

2.   Time-fractional equation

In this paper, we consider the following form of time-fractional partial differential equation:

where ${}_0^CD_t^\alpha u\left({\mathbb{X}, t} \right)$ is the fractional derivative of $u\left({\mathbb{X}, t} \right)$ with respect to time t under the Caputo definition, $\alpha$ is the order of the derivative, $\alpha \in \left[{0, 1} \right]$. $L$ represents a differential operator.

The initial condition can be written as

where ${g_1}(\mathbb{X})$ is a given function of the space.

The boundary condition can be expressed in detail as follows

where $\partial \Omega$ is the boundary of $\Omega$ and ${g_2}(\mathbb{X})$ is given for the well-posed time-fractional partial differential equations.

3.   Methodology

Physics-informed neural networks (PINNs) ^[35] incorporate the partial difference equations into the loss function as a penalty term, enabling the network to learn the hidden information in the physical equations. However, for partial difference equations, any order derivative of space and time can be easily derived using automatic differentiation of networks, whereas the fractional derivative is not feasible in calculation. Therefore, a variety of difference schemes are tried in PINNs to approximate the time-fractional differential operators.

3.1.   Time discretization

The fractional derivative is defined in Caputo sense by ^[58]

where Γ represents the Gamma function and α is the time-fractional derivative.

The interval [0, T] is divided uniformly into nodes 0 = t₀ < t₁ < t₂ < ... < t_2s < t_2s+1 < ... < ${t_{2{N_T}}} = T$, in which s and N_T denote position integer. When t = t_2s, according to the first-order finite difference method in the sense of the Caputo fractional derivative, the fractional derivative can be evaluated as follows:

where ${f_i}$ represents $f({t_i})$, $\Delta t$ is the size of time step, and

For time dependent $\hat f(\mathbb{X}, {t_{2s}}) \in {\mathbb{R}^d}$, Eq (3.2) can be further written as:

where ${\bar \psi _{k, 2s}}$ is evaluated using

In the piecewise quadratic form, the Riemann-Liouville fractional derivative ^[58] is first used

and in the sense of Hadamard finite-part integral, the fractional-order integral discretization scheme within the interval [a, b] can be defined ^[55]

in which ${R}_{\gamma -1}(t, a)$ is evaluated using

$\int$ is the Hadamard finite-part integral and is the maximum operator. In Hadamard finite-part integral sense, the Riemann-Liouville fractional derivative in Eq (3.1) becomes ^[55]:

Based on the PQI polynomial on Eq (3.2), we have

where $|R_2^{2s}| \leqslant C\Delta {t^{3 - \alpha }}\mathop {\max }\limits_{0 < t < 1} |{\dot {\hat f}^{(3)}}(\mathbb{X}, {t_{2s}})|$, ${\dot {\hat f}^{(3)}}$ is the third derivative, and C is a finite constant. The weights ${\nu _{k, 2s}}$, k = 0, 1, 2, ..., 2s, s = 1, 2, ..., N_T have the form of

where

in which ${W_i}(k)$ and ${V_i}(k, \alpha)$ are evaluated separately using

When T is set as 1, we have ${t_{2s}} = \frac{{2s}}{{2{N_T}}} = \frac{s}{{{N_T}}}$. The Riemann-Liouville fractional derivative is transformed into the fractional derivative in Caputo sense.

where

3.2.   The adaptive learning rate

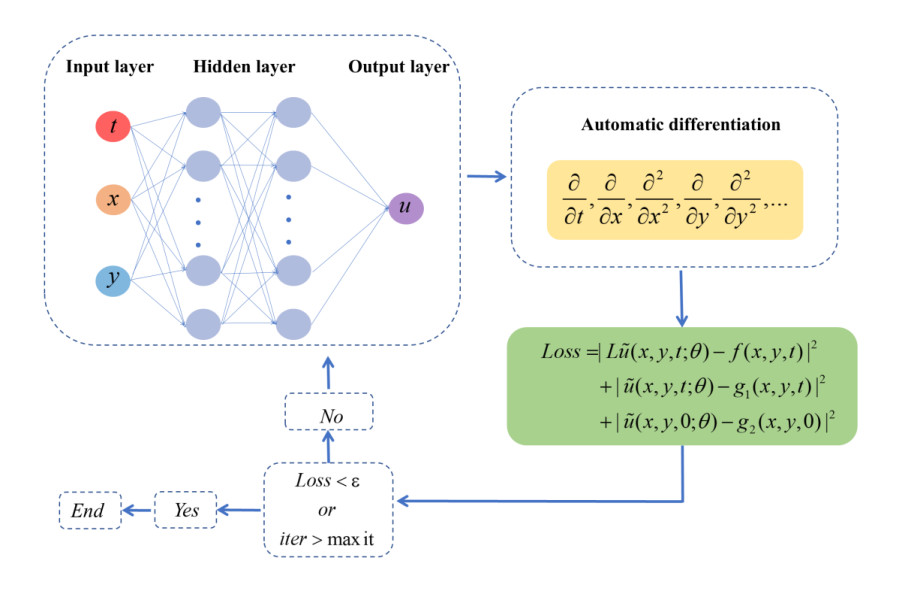
In our work, the time-fractional differential operators are approximated using the PQI discrete form, which is then integrated into the loss function of fPINNs ^[51], whose network structure is shown in Figure 2.

The PQI scheme is used to discretize the fractional derivative, which can be written as:

where $\tilde \nu$ can be calculated using Eq (3.9).

Then, by substituting Eq (3.10) into Eq (2.1), we obtain

Hence, the loss function is defined as the mean-squared error (MSE) of the residual loss term, boundary loss term, and initial loss term.

where λ_b and λ_i represent the adaptive learning rate of the boundary loss term and the initial loss term, respectively, and θ is the network parameters including the weights and biases, which are updated and iterated using the gradient descent method:

where η is the learning rate, ${\nabla _\theta }{L_r}(\theta), {\nabla _\theta }{L_{{u_i}}}(\theta), {\nabla _\theta }{L_{{u_b}}}(\theta)$ denotes the gradient value of the residual loss term, boundary loss term, and initial loss item.

The coefficients of different loss terms for both standard PINNs and fPINNs are often fixed at 1, as shown in Figures 1 and 2. However, due to the gradient imbalance of different loss terms, the network easily falls into the local optimum because it pays too much attention to the boundary condition, initial condition, or governing equation. To illustrate the issue, we conduct a two-dimensional time-fractional diffusion equation given in Example 2 as an example, which is solved by the fPINNs. The loss function of the network is shown in Figure 3(a), where the loss value of the initial loss term decreases greatly, while the loss values of the boundary loss and residual loss terms remain steady, which results in sluggish convergence or deviation from the optimal solution due to the fixed learning rate.

Hence, we introduce an adaptive weight parameter to mitigate the gradient imbalance between ${\nabla _\theta }{L_r}(\theta)$, ${\nabla _\theta }{L_{{u_i}}}(\theta)$ and ${\nabla _\theta }{L_{{u_b}}}(\theta)$, which is defined as

and

where $\overline {|{\nabla _\theta }{L_r}(\theta)|}, \, \; \overline {|{\nabla _\theta }{L_{{u_i}}}(\theta)|}$ and $\overline {|{\nabla _\theta }{L_{{u_b}}}(\theta)|}$ denote the gradient mean of residual loss term, boundary loss term, and initial loss term with respect to parameters θ, respectively. When ${\lambda _{{u_i}}} = \frac{{\max |{\nabla _\theta }{L_r}(\theta)|}}{{\overline {|{\nabla _\theta }{L_{{u_i}}}(\theta)|} }}$ and ${\lambda _{{u_b}}} = \frac{{\max |{\nabla _\theta }{L_r}(\theta)|}}{{\overline {|{\nabla _\theta }{L_{{u_b}}}(\theta)|} }}$, it is more conducive to training.

Dynamic weights are assigned to the boundary loss term and initial loss term adaptively according to gradient statistics, so they can alleviate the imbalance gradient of these terms to ensure that the network pays attention to all the loss terms in backpropagation. We introduce the idea of adaptive learning rate into fPINNs and apply it to solve the 2D time-fractional diffusion equation, as shown in Figure 3(b). Through the comparison between Figure 3(a), (b), it is evident that the loss value of the boundary loss item decreases obviously due to the adaptive learning rate.

3.3.   The composite activation function

Tanh activation function is widely used by neural networks to solve partial differential equations, and its effectiveness has been proved in many experiments. In the experiments of this paper, we find that the swish activation function also has excellent performance in solving partial differential equations. Using Example 2 of 2D time-fractional diffusion equation as an example, a different activation function is imposed in the neural network, whose results are recorded in Table 1 and Figure 4. Swish activation function has more accuracy than the other three activation functions, the second being tanh(x).

Considering the excellent performance of swish activation function, we combine it with a novel triangular activation function proposed by authors in ^[56], which is defined as follows

where $m\in \left(\text{0}, \text{1}\right)$ is used to adjust the output range. Through numerous numerical examples, m = 0.5 has proven to be the most effective.

The well-known Fourier series expansion is that any periodic function can be decomposed into a combination of simple sin and cos functions with different frequencies and amplitudes. Therefore, the neural network $\Im (x)$ can be considered as a function of a series of triangular function expansion and combination, namely

${B_n}(x; \theta)$ represents triangular functions that served as the activation function for the first hidden layer, and $a(x; \theta)$ represents a set of Fourier coefficients derived from the remaining hidden layers. For the neural network, the simpler the learning content, the better the learning impact. The novel triangular activation function simplifies a complex function to facilitate machine learning by functioning as the Fourier transform.

We create a composite activation function by combining the newly proposed triangular activation function with the typical activation function, allowing the benefits of different activation functions to be fully utilized. It is evident from the results in Table 1 that tanh and swish perform better than the others. Therefore, the composite activation function employs the proposed triangular activation function in the first hidden layer and tanh activation function or swish activation function in the remaining hidden layers.

In this activation function setting, the 2D time-fractional diffusion equation is also conducted to compare the efficiency of the composite function activation along with the single triangular activation function. Each group of experiments was calculated 10 times in a 3-200-200-200-200-200-200-1 neural network. The number of iterations for each operation was 60, 000 times. The experimental results come from the average of 10 test results, which are shown in Table 2. The best combination is the triangular activation function and the swish activation function, which is chosen for the following numerical examples.

3.4.   The architecture of adaptive-fPINN-PQI

ResNet structure ^[57], shown in Figure 5, can efficiently resolve the problem of gradient disappearance in the traditional fully connected neural network (DNN) used in PINNs. In this paper, the ResNet block replaces DNN beginning with the second hidden layer to guarantee the backpropagation efficiently.

In conclusion, an adaptive-fPINN-PQI algorithm is put forward that makes use of PQI scheme and the composite activation function, together with the Resnet blocks, whose principle is shown in Figure 6 and flowchart is shown in Algorithm 1.

4.   Numerical examples and results

In this section, intensive time-fractional diffusion equations and time-fractional AC equations are conducted to verify the effectiveness of adaptive-fPINN-PQI. In order to evaluate the performance of our method, we consider the absolute error $||{\mathbf{\tilde u}}{\text{ - }}{\mathbf{u}}|{|_1}$, and the relative error is expressed as $\frac{{||{\mathbf{\tilde u}}{\text{ - }}{\mathbf{u}}|{|_2}}}{{||{\mathbf{u}}|{|_2}}}$, where ${\mathbf{\tilde u}}$ and ${\mathbf{u}}$ denote the approximated and the exact solutions, respectively.

All numerical experiments in this paper are carried out on AMD Ryzen 9 5900HS with Radeon Graphics 3.30 GHz, RTX3060, memory 16.0 GB, and Windows 11 system. TensorFlow (version 2.13.0) is applied for programming utilizing its automatic distinguishing property, and the Adam algorithm is used to optimize the loss function. Xavier is employed for the initialization. The learning rate, the number of hidden layers, the number of neurons, and the number of iterations of the neural network are fixed at 1×10⁻³, 5200, and 6×10⁴, respectively. In the numerical examples, we will compare the results of the proposed adaptive-fPINN-PQI with other models. To objectively quantify the accuracy and stability of the neural networks, each model is calculated 10 times and the mean of the errors is then obtained. The models involved in all numerical studies are presented in the following.

•fPINN^[51]: fPINNs are an improvement of PINNs, using the mathematical discrete method of fractional derivatives to make up for the technical problem that PINNs cannot calculate fractional derivatives by automatic differentiation. The loss function in the fPINNs consists of residual loss, boundary loss, and initial loss, in which their weights are set at 1. The fractional derivative is discretized using the first-order finite difference scheme. Tanh is used as the activation function.

•adaptive-fPINN: This model introduces Resnet structure and assigns dynamic weights to different loss terms in the loss function according to the gradient statistics to alleviate the gradient imbalance. The activation function is also changed from a single tanh to a coincidence activation function. The first layer of this composite activation function is a triangular activation function ($0.5(\sin x + \cos x)$), and the remaining layers are swish functions. The other settings are the same as the fPINN model.

•fPINN-PQI: In this model, the PQI is introduced for the time-fractional derivative. The activation function uses the same composite activation function as the adaptive fPINN. The rest of the configuration is the same as the fPINN model.

•adaptive-fPINN-PQI: Compared with the adaptive-fPINN model, the only adjustment of this model is that the PQI scheme replaces the L1 scheme as the discretization method of the time-fractional derivative.

4.1.   Time-fractional diffusion equations

where $\Delta$ represents the Laplacian operator, $\Omega = {\left[{0, 1} \right]^d}$, $d = 1, 2, 3$ and $\partial \Omega$ is the boundary of $\Omega$, T is set as 1.

4.1.1.   Example 1. 1D time-fractional diffusion equation

Consider a 1D time-fractional diffusion equation having the form of Eq (4.1) with the fabricated analytical solution $u(x, t) = {t^4}({x^2} - x)$. We can derive the forcing term formula with the form:

First, Table 3 examines the relative errors of the solutions obtained by different neural networks under different α with the time interval of 0.01. It is obviously shown that 1) in general, the proposed adaptive model produces more accurate results than other counterparts using the same settings; 2) when α is 0.8, the accuracy of the networks using PQI scheme is higher than that of the networks using L1 scheme whether adaptive learning rate is employed or not; and 3) when α is 0.2, the accuracy of the L1 networks is superior to that of the PQI networks.

Figure 7(a) displays the distributions of the solutions obtained by the fPINN, adaptive-fPINN, fPINN-PQI, and the proposed adaptive-fPINN-PQI when α is 0.8, $\Delta t$ is 0.01, and T is 1. It is clearly found that the predicted solutions of the networks utilizing the PQI discretization format accurately are in better agreement with the exact solution compared to the L1 discretization format. Figure 7(b) is the box diagram of the relative errors of these predicted solutions, which further shows the performance of these neural networks. It is obvious that the new model clearly outperforms both in terms of convergence and accuracy.

Then, the evolution process of the loss function in adaptive-fPINN-PQI, as well as those of the other models, is analyzed in Figure 8. When comparing Figure 8(a), (c), it is not difficult to find that the residual loss under the PQI discrete scheme decreases significantly, which is probably reduced by three orders of magnitude. This phenomenon is consistent with the theory of the higher order difference property of the PQI scheme, which provides effective experimental evidence and theoretical basis for the higher accuracy of our model. In addition, the initial loss term in adaptive-fPINN has a clear decreasing trend due to the prominent advantage of adaptive learning rate, observed in Figure 8(a), (b).

4.1.2.   Example 2. 2D time-fractional diffusion equation

Consider a 2D time-fractional diffusion equation defined in Eq (4.1) with the fabricated solution $u(x, y, t) = {t^4}({x^2} - x)({y^2} - y)$. The forcing term formula can be deduced as follows:

First, the solution error obtained using the proposed neural frame, together with those of the other three models for the 2D time-fractional diffusion equation, is listed in Table 4. It is seen that the adaptive-fPINN-PQI model stands out clearly, where the PQI discrete format also has a significant impact on the solution accuracy for this problem.

To more intuitively reflect the performance of each model, the abstract point-wise error distributions of the four models are plotted in Figure 9. We can observe that the abstract point-wise error of the proposed network is the smallest among the four networks. In the problem domain, the proposed adaptive-fPINN-PQI agrees well with the exact solution, and its abstract error is clearly controlled below 10⁻⁷ in contrast to the other models, which perform poorly and have large errors distributed throughout the region. On the boundary of the problem domain, the abstract error of our model is still controlled in 10⁻⁶, despite the fact that its accuracy has decreased, whereas those of some other models even approach 10⁻⁴.

We also investigated the convergence performance of four models in Figure 10. The maximum and minimum values from the 10 experiments are represented by the shadow boundaries, while the average is represented by the solid line. It demonstrates that the accuracy of adaptive-fPINN-PQI is better than that of the other models. After 30, 000 iterations, the shadow width of these models gradually decreases, indicating that the network prediction is more and more stable.

Finally, the effectiveness of the newly proposed composite activation function is discussed for the 2D time-fractional diffusion equation. Figure 11 plots the relative error of adaptive-fPINN-PQI utilizing various activation functions. In comparison to the two traditional activation functions, tanh and swish, the proposed composite triangular activation function has a significant impact on enhancing the calculation accuracy. Although the result using the suggested composite activation function exhibits some fluctuation in error, the maximum error remains one or two orders smaller than its counterparts, and the fluctuation becomes less pronounced as the number of iterations increases.

4.1.3.   Example 3. 3D time-fractional diffusion equation

Consider a 3D time-fractional diffusion equation defined in Eq (4.1) with the fabricated exact solution $u(x, {\text{y}}, z, t) = {t^4}({x^2} - x)({y^2} - y)({z^2} - z)$ and the forcing term can be written as follows:

Table 5 presents the relative error of the adaptive-fPINN-PQI for the 3D time-fractional diffusion equation defined above, in comparison with the other three models. Among these neural frameworks, adaptive-fPINN-PQI turns out to be the most accurate, proving once more how well the proposed model performs in terms of precision.

Next, Figure 12 displays the distributions of the abstract errors obtained using the four models with α fixed at 0.8. A graph shows that the accuracy of the adaptive-fPINN-PQI model surpasses that of the competition models. Positions where the accuracy of these learning models is poor have one thing in common: the error is concentrated around the boundary, which is consistent with the way numerical computations work. However, the suggested approach is still effective in reducing the boundary error and narrowing the error range.

To investigate the learning capability of adaptive-fPINN-PQI, we plot its loss function against the number of iterations in Figure 13, along with those of the other models. Generally, all four algorithms demonstrate excellent learning efficiency when forecasting the solution of the 3D time-fractional diffusion equation. When compared to L1 and PQI schemes, it is clear that the neural network using PQI significantly reduces the residual loss. Besides, the adaptive learning rate obviously balances the gradient differences of various loss terms, which come from the narrowed shadow width in Figure 13(b), (d).

Furthermore, we conducted a comparative analysis of the activation function for the 3D time-fractional diffusion equation, which is displayed in Figure 14. Among various activation functions, we noted that our composite activation functions exhibited superior convergence and stability. Especially after 5000 iterations, the conclusion becomes clearer.

4.2.   Time-fractional AC equation

where $\Delta$ represents the Laplacian operator, $\Omega = {\left[{0, 1} \right]^d}$, $d = 1, 2$ and $\partial \Omega$ is the boundary of $\Omega$, besides we fix $\varepsilon = 1, {\rm T} = 1$.

4.2.1.   Example 1. 1D time-fractional AC equation

Consider the 1D time-fractional AC equation having the form of Eq (4.5) with the fabricated exact solution $u(x, t) = (1 + {t^2})\sin (2\pi x)$ and the forcing term

A comparative investigation on the accuracy of four neural models solving the 1D time-fractional AC equation is summarized in Table 6. We observed that the accuracy of adaptive-fPINN-PQI and fPINN-PQI is one to two orders of magnitude higher than the accuracy of fPINN and adaptive-fPINN, which is attributed to the higher-order discrete format. Additionally, the adaptive learning rate in loss function causes an order of magnitude increase in the precision of adaptive-fPINN-PQI.

The accuracy and stability of the prediction solutions of the four deep learning networks are examined in Figure 15, where the distribution of the solutions is plotted in Figure 15(a) and its box diagram is plotted in Figure 15(b). In terms of precision, the adaptive-fPINN-PQI model exhibits the best agreement with the exact solution, followed by fPINN-PQI, and fPINN and adaptive-fPINN perform worse. It can be observed from the box diagram that the adaptive-fPINN-PQI model has the shortest box length among its competitors, indicating that the proposed network is the most stable.

Experiments are then carried out for the 1D time-fractional AC equation to verify the effectiveness of the composite activation function proposed in our study. The results are presented in Figure 16, which shows that the composite activation function offers superior prediction accuracy, better convergence, and greater stability than the other competitors.

4.2.2.   Example 2. 2D time-fractional AC equation

Consider a 2D time-fractional AC equation having the form of Eq (4.5) with the fabricated exact solution $u(x, t) = (1 + {t^2})\sin (2\pi x)\sin (2\pi y)$, the force term $f(x, y, {t_i})$ can be obtained:

The relative errors of the different neural networks' solutions are summarized in Table 7. It shows clearly that adaptive-fPINN-PQI produces much more accurate solutions, which are one or two orders of magnitude higher than other methods.

Then, the distributions of the predicated solutions are plotted in Figure 17 to further validate the performance of our neural network. In terms of the error in accuracy and distribution, the solution of adaptive-fPINN-PQI is the best, followed closely by that of adaptive-fPINN.

Figure 18 shows the trend of the loss values during the training process of four neural networks. We can find that the PQI discrete scheme has a significant effect on reducing the residual loss terms. In addition, the PQI format accelerates the convergence of the loss function compared to the format of L1, allowing the neural network to learn the governing equation and boundary information more thoroughly, thereby improving the predictive accuracy.

A shadow graph of the relative error of 10 experimental results versus the number of iterations for the 2D fractional AC equation is depicted in Figure 19. The suggested adaptive-fPINN-PQI model outperforms the other three models regardless of α value. The PQI discrete scheme overcomes the issue in which the residual loss term does not decrease, and the adaptive learning rate balances the gradient of different loss terms, resulting in the high precision of adaptive-fPINN-PQI.

5.   Conclusions

In this paper, an adaptive-fPINN-PQI network is built for solving time-fractional partial differential equations. The adaptive learning rate balances the interaction of different loss terms in order to solve the local optimal problem in the classical PINN and fPINN. The L1 scheme in fPINN is replaced by the higher-order scheme of PQI in our neural network, substantially reducing the residual loss term. Additionally, a composite function made up of the triangular activation function and swish activation function is more efficient than the tanh function. The numerical examples of time-fractional diffusion equations and time-fractional AC equations lead to the following conclusions:

● The proposed neural network outperforms fPINN in terms of precision, with a potential improvement of 1-2 orders of magnitude.

● The accuracy of the prediction solutions remains steady with the increase of the dimension of the problems.

● Adaptive-fPINN-PQI performs effectively with various time-fractional partial differential equations.

However, the model proposed in this paper is not as effective as the traditional fPINN model for the diffusion problem when the α value is small, while this issue does not arise for the phase-field problem. Therefore, it is the common goal of researchers to find a model with wider applicability and higher accuracy.

In future work, we will further research the fractional derivatives under different definitions, especially to solve the Hadamard-type fractional problems. A breakthrough for fractional-order problems is to find a higher-order convergent discrete format, which is a challenge for many mathematical researchers. In addition, developing a more widely applicable machine learning model for solving fractional-order problems is the focus of our future work.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

In this paper, the work was supported by the National Youth Science Foundation of China (Grant No. 12102283) and the Youth Science Research Foundation of Shanxi Province (Grant No. 20210302124159).

Competing Interests

No potential conflict of interest was reported by the authors.