1.
Introduction
All graphs considered in this paper are finite, simple and undirected. For a graph G, we use V(G),E(G), Δ(G), and δ(G) to denote its vertex set, edge set, maximum degree, and minimum degree, respectively. A plane graph is a planar graph with a given planar drawing on the Euclidean plane. If G is a plane graph, let F(G) denote the set of faces in G. We say that two cycles (or faces) are adjacent if they share at least one edge. In particular, when they share exactly one edge and two vertices, they are said to be normally adjacent. Two cycles (or faces) are intersecting if they share at least one vertex.
The vertex arboricity, denoted by a(G), of a graph G is the minimum number of subsets into which V(G) can be partitioned so that each subset induces a forest. Obviously, a(G)=1 if and only if G itself is a forest. In 1968, Chartrand, Kronk and Wall [2] first introduced the vertex arboricity of a graph and proved that a(G)≤⌈Δ(G)+12⌉ for any graph G and a(G)≤3 for any planar graph G. It is known that there exist infinitely many planar graphs G such that a(G)=3. In 1989, Hakimi and Schmeichel [6] provided a characterization by showing that a plane graph G has a(G)=2 if and only if G∗, the dual of G, contains a connected Eulerian spanning subgraph. In 2008, Raspaud and Wang [10] conjectured that every planar graph G without adjacent 3-cycles has a(G)≤2. To attack this conjecture, Chen, Raspaud and Wang [3] confirmed a weak version, i.e., every planar graph G without intersecting 3-cycles has a(G)≤2. Some sufficient conditions for a planar graph G to have a(G)≤2 have been obtained in [5,7,10,13].
A graph G is said to be L-forested-colorable if for any color list L={L(v)∣v∈V(G)}, one can choose a color for each vertex v from its list L(v) so that the subgraph induced by every color class is a forest. The list vertex arboricity al(G) is the minimum number of integer k such that G is L-forested-colorable with |L(v)|≥k for each v∈V(G). Obviously, a(G)≤al(G) for any graph G. In 2009, Borodin and Ivanova [1] proved that al(G)≤2 if G is a planar graph without 4-cycles adjacent to 3-cycles. This result has been recently extended by Chen, Huang and Wang [4] to a toroidal graph without 4-cycles adjacent to 3-cycles. In 2020, Wang, Huang and Chen [9] proved that every planar graph G without intersecting 5-cycles has al(G)≤2. The list vertex arboricity of toroidal graphs has also been extensively investigated, see [8,11,14].
In this paper, we prove the following result:
Theorem 1. If G is a planar graph without 5-cycles intersecting with 6-cycles, then al(G)≤2.
We first introduce a few concepts and terminology used in the paper. Let G be a plane graph. For x∈V(G)∪F(G), let dG(x), or simply d(x), denote the degree of x in G. A vertex of degree k (resp., at least k, at most k) is called a k-vertex (resp., k+-vertex, k−-vertex). Similarly, we can define a k-face, k+-face and k−-face. For a k-vertex v∈V(G), we usually use v0,v1,…,vk−1 to denote the neighbors of v in G in a clockwise order, and let fi denote the incident face of v that contains vvi,vvi+1 as two boundary edges for i=0,1,…,k−1, where indices are taken modulo k. For a face f∈F(G), we use b(f) to denote the boundary walk of f and write f=[v1v2⋯vn] if v1,v2,…,vn are the vertices of b(f) in a clockwise order. Let V(f)=V(b(f)). Moreover, the face adjacent to f with e=vivi+1 as a common boundary edge is simply denoted by fvivi+1. For v∈V(G), let Fi(v) (or Fi+(v)) denote the set of i-faces (or i+-faces) incident to v. Moreover, let mi(v)=|Fi(v)| and mi+(v)=|Fi+(v)|. A k-vertex v is called a (d0,d1,…,dk−1)- vertex if d(fi)=di for i=0,2,…,k−1. A cycle C in a plane graph G is called separating if both its interior and exterior contain at least one vertex of G.
This paper is organized as follows: In section 2 we give the proof of Theorem 1. Initially, we explore structural properties of a minimal counterexample. Then we use the discharging technique to contradict the existence of such a graph. Finally, in Section 3 we conclude with conjectures.
2.
Proof of Theorem 1
We prove Theorem 1 by contradiction. Suppose that G is a minimal counterexample to the Theorem 1, i.e., G is a planar graph satisfying the following conditions:
(ⅰ) without 5-cycles intersecting with 6-cycles;
(ⅱ) al(G)>2; and
(ⅲ) having as few as possible vertices.
Let L be a list assignment of V(G) such that every v∈V(G) has |L(v)|=2. If G contains a vertex v of degree at most 3, let H=G−v. By the minimality of G, H admits an L-forested-coloring π. Based on π, we may color v with a color in L(v) which appears at most once in its neighbors such that π is extended to G, which is a contradiction. Hence suppose that δ(G)≥4.
2.1. Structural properties of G
As given in [9], the following lemma still holds for the current graph G:
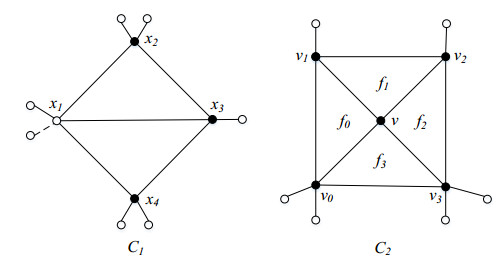
Lemma 1. G contains no a 4-cycle C=x1x2x3x4x1 with a chord x1x3 such that dG(x1)≤5 and dG(xi)=4 for i=2,3,4, as shown in the configuration C1 of Figure 1.
For S⊂V(G), let G[S] be a subgraph of G induced on S and let π be an L-forested-coloring of G[S]. Note that by definition every color class of π induces a forest in G. We call π a partial L-forested-coloring of G. For a vertex u∈V(G)∖S and a color c∈L(u), we use τL(c,u) to denote the number of times that c appears in the colored neighbors of u in G. Set
Vertex u is said to be free with respect to (L,π) if π can be extended into a partial L-forested-coloring of G by coloring u with a color c∈L(u) such that τL(c,u)=τL(u).
Lemma 2. ([12]) Let u∈V(G)∖S be a 4-vertex. If at least one of the following conditions holds, then u is free.
(1) At least one of neighbors of u is uncolored;
(2) At least three colors appear in the neighbors of u;
(3) Some color appears at least three times in the neighbors of u.
Lemma 3. G does not contain a internal 4-vertex v incident to four 3-faces such that v1,v2 are internal 4-vertices and v0,v3 are internal 5-vertices, as shown in the configuration C2 of Figure 1.
Proof. Suppose that G contains such a 4-vertex v. By symmetry, we have to discuss the following cases.
Case 1. v0v2∉G.
Let v′0,v0″ be the neighbors of v_0 other than v, v_1, v_3 ; v_3', v_3'' be the neighbors of v_3 other that v, v_0, v_2 ; v_1' be the neighbor of v_1 other than v, v_0, v_2 ; v_2' be the neighbor of v_2 other than v, v_1, v_3 . Consider the graph H = G-\{v, v_0, v_1, v_2, v_3\} . By the minimality of G , H has an L -forested-coloring \pi . Define a sublist L' of colors as follows:
L'(v_i) = L(v_i)\setminus \{\pi(v'_i), \pi(v''_i)\} for i = 0, 3 .
It is easy to see that |L'(v_i)|\ge 0 for i = 0, 3 . Moreover, if \pi(v'_i) = \pi(v''_i) , or \pi(v'_i)\ne \pi(v''_i) and L(v_i)\ne \{\pi(v'_i), \pi(v''_i)\} , then |L'(v_i)|\ge 1 . Let S = \{x \in \{v_0, v_3\} \ |\ |L'(x)|\ge 1\} . Obviously, 0\le |S|\le 2 . We are going to extend \pi to G , which leads to a contradiction.
Firstly, we give each v_i a color, i = 0, 1, 2, 3 . For i = 1, 2 , since |L(v_i)|\geq 2 and v_i has only one neighbor which is colored, there exists a color a_i\in L(v_i)\setminus\pi(v_i') that we use to color v_i with \alpha_i . Suppose that i\in\{0, 3\} . If v_i\in S , then we color the vertex v_i with a color b_i\in L'(v_i) . Otherwise, color v_i with the color \pi(v_i') . We have to discuss the following cases.
Case 1.1 |S|\geq 1 .
By symmetry, assume that |L'(v_0)|\ge 1 and a_0 \in L'(v_0) . Let \pi(v_1) = a_1 , \pi(v_2) = a_2 , and \pi(v_3) = a_3 .
Case 1.1.1. a_0\neq a_3 .
Suppose that \{a_1, a_2\}\neq\{a_0, a_3\} . Then v is free by Lemma 2 and \pi can be extended to G , a contradiction. Otherwise, \{a_1, a_2\} = \{a_0, a_3\} . If a_1 = a_0 and a_2 = a_3 , then we recolor v_2 with a color in L(v_2)\backslash \{a_2\} and color v with a color in L(v)\backslash \{a_0\} . If a_1 = a_3 and a_2 = a_0 , then we color v with a color in L(v) .
Case 1.1.2. a_0 = a_3 .
If a_1\neq a_2 , then v is free by Lemma 2 and \pi can be extended to G , a contradiction. If a_1 = a_2 = a_0 , then recolor v_1 with a color in L(v_1)\backslash \{a_0\} , and color v with a color in L(v)\backslash \{a_0\} . Otherwise, a_1 = a_2\neq a_0 , then we recolor v_2 with a color in L(v_2)\backslash \{a_2\} and color v with a color in L(v)\backslash \{a_0\} . Now if G does not contain monochromatic cycle, then we get an L -forested-coloring of G , a contradiction. Otherwise, G contains a monochromatic cycle v_2v_3\cdots v_2'v_2 , then |L'(v_3)| = 0 , L(v_3) = \{\pi(v_3'), \pi(v_3'')\} and \pi(v_3')\neq \pi(v_3'') . Recoloring v_3 with a color in L(v_3)\backslash \{a_3\} , we extend \pi to G , a contradiction.
Case 1.2. |S| = 0 .
Without loss of generality, let \pi(v_i) = a_i , i = 0, 1, 2, 3 .
Case 1.2.1. a_0\neq a_3 .
Suppose that \{a_1, a_2\}\neq\{a_0, a_3\} . Then v is free by Lemma 2 and \pi can be extended to G , a contradiction. Otherwise, \{a_1, a_2\} = \{a_0, a_3\} . If a_1 = a_0 and a_2 = a_3 , then we recolor v_0 with the color \pi(v_0'') , and color v with a color in L(v)\setminus \{a_3\} . If there is no monochromatic cycle in G , then \pi is extended to G , a contradiction. Otherwise, if G contains a monochromatic cycle v_0v_3\cdots v_0''v_0 , then color v_3 with the color \pi(v_3'') . If a_1 = a_3 and a_2 = a_0 , then we color v with a color in L(v) .
Case 1.2.2. a_0 = a_3 .
Recolor v_0 with the color \pi(v_0'') , and then the proof can be given as in Case 1.2.1.
Case 2. v_0v_2\in G .
Let v'_0 be the neighbors of v_0 other than v, v_1, v_2, v_3 ; v_3', v_3'' be the neighbors of v_3 other that v, v_0, v_2 ; v_1' be the neighbor of v_1 other than v, v_0, v_2 .
Consider the graph H = G-\{v, v_0, v_1, v_2, v_3\} . By the minimality of G , H has an L -forested-coloring \pi . Define a sublist L'(v_3) = L(v_3)\setminus \{\pi(v'_3), \pi(v''_3)\} .
Firstly, we give each v_i a color, i = 0, 1, 2, 3 . For i = 0, 1 , since |L(v_i)|\geq 2 and v_i has only one neighbor which is colored, there exists a color a_i\in L(v_i)\setminus\{\pi(v_i')\} that we use to color v_i with a_i . We color the vertex v_2 with a color a_2\in L(v_2)\setminus\{a_0\} . If L'(v_3)\ge 1 , then we color the vertex v_3 with a color a_3\in L'(v_3) . Otherwise, color v_3 with the color \pi(v_3') .
Case 2.1. a_0\neq a_3 .
Suppose that \{a_1, a_2\}\neq\{a_0, a_3\} . Then v is free by Lemma 2 and \pi can be extended to G , a contradiction. Otherwise, \{a_1, a_2\} = \{a_0, a_3\} . Thus, a_0 = a_1 and a_2 = a_3 . We recolor v_1 with a color in L(v_1)\backslash \{a_0\} and color v with a color in L(v)\backslash \{a_3\} .
Case 2.2. a_0 = a_3 .
If a_1\neq a_2 , then v is free by Lemma 2 and \pi can be extended to G , a contradiction. If a_1 = a_2 , then recolor v_1 with a color in L(v_1)\backslash \{a_2\} , and color v with a color in L(v)\backslash \{a_0\} .
This completes the proof of Lemma 3 .
2.2. The discharging technique
To obtain a contradiction by applying discharging technique, we define a new graph H from G as follows: If there is no separating 3-cycle in G , let H = G ; otherwise, choose a separating 3-cycle T with the least internal vertices, and let H = G[V^0(T)\cup V(T)] , where V^0(T) is the set of internal vertices of T . Let V^0(H) = V^0(T) , which are called the set of internal vertices in H . Let f^\Delta denote the outer face of H , and let the set of interior faces of H be F^0(H) = F(H)\setminus \{f^\Delta\} . For each vertex v\in V^0(H) , it holds obviously that d_H(v) = d_G(v) . Since G is connected, so is H . In the following, we will contradict the existence of subgraph H and therefore of G , by using the discharging technique. Using Euler's formula |V(H)|-|E(H)|+|F(H)| = 2 , we can deduce the following identity.
Define an initial weight w on vertices and faces of H by w(v) = 2d_H(v)-6 if v\in V(H) and w(f) = d_H(f)-6 if f\in F(H) . It follows from (2.1) that the total sum of weights is equal to -12 . In what follows, we will design some discharging rules and redistribute weights accordingly. Once the discharging is finished, a new weight function w' is produced. However, the total sum of weights is kept fixed during the discharging process. Nevertheless, we can show that the sum of w'(x) is at least -11.6 for all x\in V(H)\cup F(H) . This leads to the following obvious contradiction
and hence the theorem follows.
For a 3-face f\in F(G) , we say that it is bad if V(f) contains three internal 4 -vertices; weak if V(f) contains two internal 4 -vertices and one 5^+ -vertex, or two internal 4 -vertices with |V(f)\cap V(T)| = 1 ; and good otherwise.
Observation 1. Let f', f''\in F^0(H) with d_H(f') = 3 and d_H(f'') = 4 . If f' is normally adjacent to f'' , then b(f')\cup b(f'') contains a 5-cycle.
Let C_5 \bowtie C_6 denote a configuration that a vertex lies in a 5-cycle and a 6-cycle at the same time.
Observation 2. Let f', f''\in F^0(H) with d_H(f') = 3 and d_H(f'') = 5 . If f' is normally adjacent to f'' , then b(f')\cup b(f'') contains a configuration C_5 \bowtie C_6 .
Proof. Suppose that f'' = [x_1x_2x_3x_4x_5] and f' = [x_1x_2x_6] . Since f'' is a 5-face, x_1, x_2, \ldots, x_5 are mutually distinct. Since f' and f'' are normally adjacent, it follows that x_6\notin V(f'') and hence a 6-cycle x_1x_6x_2x_3x_4x_5x_1 is found. Thus, b(f')\cup b(f'') has a configuration C_5 \bowtie C_6 at the vertex x_1 .
Claim 1. If v\in V^0(H) is a 5^+ -vertex, then m_3(v)\leq \lfloor \frac {3d_H(v)}{4} \rfloor .
Proof. Since v is an internal vertex, all the faces incident to v are internal faces. It is easy to check that if v is incident to four consecutive 3-faces, then G will contain a configuration C_5 \bowtie C_6 . This shows that m_3(v)\leq \lfloor \frac {3d_H(v)}{4} \rfloor .
Claim 2. If v\in V^0(H) is incident to two 3 -faces f_i, f_{i+1} , then d_H(f_j)\ne 4, 5 for each j\in \{i-1, i+2\} .
Proof. Without loss of generality, assume that i = 1 .
\bullet d_H(f_{3}) = 4 .
Suppose that f_3 = [vv_3uv_4] . If u, v_1, v_2 are mutually distinct, then a 5-cycle vv_2v_3uv_4v and a 6-cycle vv_1v_2v_3uv_4v are found. Thus, b(f_1)\cup b(f_2) \cup b(f_3) has a configuration C_5 \bowtie C_6 at the vertex v , a contradiction. If v_2 = u , then a separating 3-cycle vv_2v_4v with fewer internal vertices than T appears, contradicting the choice of T . If v_1 = u , then a separating 3-cycle vv_1v_3v with fewer internal vertices than T appears, contradicting the choice of T .
\bullet d_H(f_{3}) = 5 .
Suppose that f_3 = [vv_3u_1u_2v_4] . By Observation 2, f_2, f_3 are not normally adjacent, thus v_2 = u_1 or v_2 = u_2 . If v_2 = u_1 , then v_3 is a 2 -vertex and v is a vertex on T , a contradiction. If v_2 = u_2 , then a separating 3-cycle vv_2v_4v with fewer internal vertices than T appears, contradicting the choice of T .
Claim 3. Let v\in V^0(H) with d_H(v)\ge 4 . If d_H(f_i) = d_H(f_{i+1}) = d_H(f_{i+2}) = 3 , then d_H(f_{i-1}), d_H(f_{i+3}) \ge 7 .
Proof. Without loss of generality, assume that i = 1 . By Claim 1, d_H(f_{0})\neq 3 . By Claim 2, d_H(f_{0})\neq 4, 5 . If d_H(f_{0}) = 6 , a 5-cycle vv_1v_2v_3v_4v and a 6-cycle f_0 are found. Thus, b(f_0)\cup b(f_1) \cup b(f_2)\cup b(f_3) has a configuration C_5 \bowtie C_6 at the vertex v , a contradiction.
Claim 4. If v\in V^0(H) is incident to two 3 -faces f_i, f_{i+2} , then d_H(f_{i+1})\ne 4, 5 .
Proof. Without loss of generality, assume that i = 1 .
\bullet d_H(f_{2}) = 4 .
Suppose that f_2 = [vv_2uv_3] . If u, v_1, v_4 are mutually distinct, then a 5-cycle vv_1v_2uv_3v and a 6-cycle vv_1v_2uv_3v_4v are found. Thus, b(f_1)\cup b(f_2) \cup b(f_3) has a configuration C_5 \bowtie C_6 at the vertex v , a contradiction. If v_1 = u , then a separating 3-cycle vv_1v_3v with fewer internal vertices than T appears, contradicting the choice of T . If v_4 = u , then a separating 3-cycle vv_2v_4v with fewer internal vertices than T appears, contradicting the choice of T .
\bullet d_H(f_{2}) = 5 .
Suppose that f_2 = [vv_2u_1u_2v_3] . By Observation 2, f_1, f_2 are not normally adjacent and f_2, f_3 are not normally adjacent, thus v_1 = u_1 and v_4 = u_2 . In this case, v_2 and v_3 are both 2-vertices and they are stand on different 3-faces, a contradiction.
Our discharging rules are defined as follows:
(R0) Let v\in V(T) . We carry out the following three subrules (R0.1), (R0.2) and (R0.3):
(R0.1) v sends 0.5 to each incident 4-face, and 0.2 each incident 5-face.
(R0.2) If d_H(v)\geq5 , then v sends 2 to each incident internal 3 -face. Otherwise, assume that 3\leq d_H(v)\leq4 . If m_3(v) = d_H(v) , then v sends 1.5 to each incident internal 3 -face. If m_3(v)\leq d_H(v)-1 , then v sends 2 to each incident internal 3 -face.
(R0.3) If f = [vx_1x_2x_3] is a 4-face, then v sends 0.1 to x_2 through the face f .
(R1) Every 4-face gets 0.5 from each of its incident internal vertices.
(R2) Every 5-face gets 0.2 from each of its incident internal vertices.
(R3) Let v\in V^0(H) with m_3(v)\ge 1 .
(R3.1) Suppose that d_H(v) = 4 .
\bullet Assume that m_3(v) = 4 . If v is incident with a bad 3-face and a good 3-face, then v sends 1 to bad 3-face, 0 to good 3-face and 0.5 to each of its incident weak 3-faces. Otherwise, v sends 0.5 to each of its incident 3-faces.
\bullet Assume that m_3(v) = 3 . If v is incident with a bad 3-face, then v sends 1 to bad 3-face, and 0.5 to each of its other incident 3-faces. If v is incident with at least one good 3-face, then v sends 0.5 to good 3-face, and 0.75 to each of its incident weak 3-faces. Otherwise, v sends 0.5 to each of its incident weak 3-faces.
\bullet If m_3(v)\le 2 , then v sends 1 to each of its incident 3-faces.
(R3.2) Suppose that d_H(v) = 5 .
\bullet If d_H(f_i) = 3 for i = 0, 1, 2 , and d_H(f_3), d_H(f_4)\ge7 , then v sends 1.25 to each of f_0, f_1, f_2 .
\bullet If d_H(f_i) = 3 for i = 0, 1, 3 , and d_H(f_2), d_H(f_4)\ge6 , then v sends 1.25 to each of f_0, f_1 and 1.5 to f_3 .
\bullet For other cases, v sends 1.5 to each of its incident 3-faces.
(R3.3) If d_H(v)\ge 6 , then v sends 1.5 to each of its incident 3-faces.
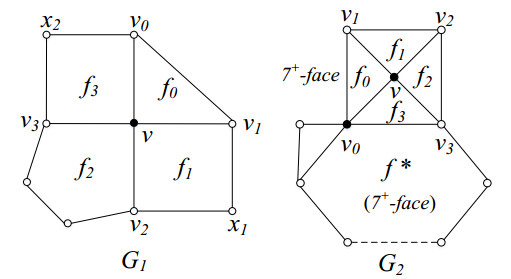
(R4) Assume that v\in V^0(H) is a (3, 4, 5, 4) -vertex with f_1 = [vv_1x_1v_2] and f_3 = [vv_3x_2v_0] , as shown in the configuration G_1 of Figure 2. Then each of x_1 and x_2 send 0.1 to v .
(R5) Assume that v\in V^0(H) is an internal (3, 3, 3, 3) -vertex and v_0 is an internal (3, 3, 7^+, 3, 7^+) -vertex. Let f^* , other than f_3 , denote the incident face of the edge v_0v_3 . Such configuration G_2 is depicted Figure 2.
(1) If v_1, v_2 are internal 4 -vertices and v_3 is an internal 6^+ -vertex, then f^* sends 0.25 to f_3 .
(2) If v_3 is an internal 4 -vertex, then f^* send 0.25 to f_3 .
If v is a k -vertex incident with m 3-faces, then v is called a k_m -vertex. If a k -vertex v sends the weight a to an incident 3-face f , then v is called a k^a -vertex for f . A k_m^a -vertex for a 3-face f is a k_m -vertex that sends the weight a to f .
For x, y \in V (H)\cup F(H) , let \tau (x \rightarrow y) denote the amount of weights transferred from x to y according to the rules (R0)-(R5).
Observation 3. Let v be an internal 4^+ -vertex incident to an internal 3-face f . Then
\rm (1) \tau(v\to f)\in \{1, 0.75, 0.5, 0\} if d_H(v) = 4 ;
\rm (2) \tau(v\to f)\in \{1.25, 1.5\} if d_H(v) = 5 ;
\rm (3) \tau(v\to f) = 1.5 if d_H(v)\ge 6 .
Claim 5. Suppose that f = [x_1x_2x_3] is an internal 3 -face. Let s denote the total number of 4^{0.75} -vertices, 4^{0.5} -vertices and 4^0 -vertices which are adjacent to f . Then s \leq 1 .
Proof. Suppose that s \geq2 . By the discharging rules, if x_i is a 4^{0.75} -vertex, 4^{0.5} -vertex or 4^0 -vertex, then x_i is an internal 4_3 -vertex or 4_4 -vertex. We consider the following possibilities by symmetry.
\bullet At least one of x_1 , x_2 is a 4_3 -vertex in V^0(H) .
If f^{x_1x_2} and f^{x_1x_3} are 3-faces, then neither x_2 nor x_3 is an internal 4_3 -vertex or 4_4 -vertex, for otherwise H will contain a separating 3-cycle with fewer internal vertices than T or a configuration C_5 \bowtie C_6 at the vertex x_1 , a contradiction. The case in which f^{x_1x_2} = [x_1x_2w] and f^{x_1w} = [x_1wy] are 3-faces can be similarly discussed, where y and w are the neighbors of x_1 other than x_2 and x_3 .
\bullet Both x_1 and x_2 are internal 4_4 -vertices.
In this case, H contains a separating 3-cycle with fewer internal vertices than T or a configuration C_5 \bowtie C_6 at the vertex x_1 , also a contradiction.
The above discussion implies that s \leq 1 .
Lemma 4. w'(f)\ge 0 for each f\in F^0(H) .
Proof. Let f\in F^0(H) . Clearly, d_H(f)\ge 3 .
Case 1. Suppose that d_H(f) = 3 and f = [x_1x_2x_3] .
Then w(f) = -3 . Since f is an internal face of H , we can derive that |V(f)\cap V(T)|\leq2 .
Case 1.1. |V(f)\cap V(T)| = 2 .
Then f is a good 3-face. By (R0), f receives 1.5 or 2 from each of its two vertices of T . Hence w'(f)\ge -3+1.5\times 2 = 0 .
Case 1.2. |V(f)\cap V(T)| = 1 .
Without loss of generality, let x_1\in V(T) . We distinguish cases depending on whether x_2 and x_3 are internal 4 -vertices or internal 5^+ -vertices. Assume that both x_2 and x_3 are internal 4 -vertices. Then f is a weak 3 -face. Rule (R3.1) assures that 4 -vertices always send non-zero weight to weak faces. Hence by Observation 3, x_2 and x_3 send either 0.5 or 0.75 or 1 to f . Now, by Claim 5, at most one of x_2 and x_3 is an 4^{0.5} -vertex or 4^{0.75} -vertex. Equivalently at least one of them is a 4^1 -vertex. Thus, w'(f)\ge -3+1.5+1+0.5 = 0 by (R0) and (R3). Assume that x_2 is a internal 4 -vertex and x_3 is a internal 5^+ -vertex. If x_2 is not a 4^0 -vertex, then w'(f)\ge -3+1.5+1.25+0.5 = 0.25 by (R0) and (R3). Otherwise, x_2 is a 4^0 -vertex. By (R3.1), x_2 is a 4_4 -vertex. If d_H(x_1) = 3 , then |V(f)\cap V(T)| = 2 , a contradiction. If d_H(x_1)\ge4 , then f^{x_1x_3} is a 4^+ -face and m_3(x_1)\le d_H(x_1)-1 , otherwise it will produce a 3 -vertex in v^0(H) , or a separating 3 -cycle with fewer internal vertices than T or a configuration C_5 \bowtie C_6 at the vertex x_1 , a contradiction. Thus f gets 2 from x_1 . Therefore, w'(f)\ge -3+2+1.25 = 0.25 by (R0) and (R3). Assume that both x_2 and x_3 are 5^+ -vertices, then w'(f)\ge -3+1.5+1.25\times2 = 1 by (R0) and (R3).
Case 1.3. |V(f)\cap V(T)| = 0 .
Let d_H(x_1) \leq d_H(x_2) \leq d_H(x_3) .
\bullet Assume that d_H(x_1)\geq5 , then f gets at least 1.25 from each of x_1, x_2, x_3 by Observation 3. Thus w'(f)\geq -3+1.25\times 3 = 0.75 .
\bullet Assume that d_H(x_1) = 4, d_H(x_2)\geq5 , then f gets at least 1.25 from each of x_2, x_3 by (R3.2) and (R3.3). If x_1 is not a 4^0 -vertex, then f gets at least 0.5 from x_1 by (R3.1). Hence, w'(f)\geq -3+0.5+1.25\times 2 = 0 . Otherwise, x_1 is a 4^0 -vertex, then x_1 is a internal 4_4 -vertex and x_1 is incident with a bad 3-face by (R3.1). By Lemma 1 and Lemma 3, x_2 or x_3 is a internal 6^+ -vertex, say x_2 , and f gets 1.5 from x_2 by (R3.3). If x_3 is a internal 6^+ -vertex, or a internal 5-vertex with m_3(x_3) = 2 , then f gets 1.5 from x_3 by (R3.2) and (R3.3). Thus, w'(f)\geq -3+1.5\times 2 = 0 . Otherwise, x_3 is a internal 5-vertex with m_3(x_3) = 3 . If x_3 is a internal (3, 3, 3, 6^+, 6^+) -vertex, a (3, 3, 6, 3, 6^+) -vertex, or a (3, 3, 6^+, 3, 6) -vertex, it will contain a configuration C_5 \bowtie C_6 at the vertex x_3 , a contradiction. If x_3 is a internal (3, 3, 7^+, 3, 7^+) -vertex, it is the construction G_2 and f gets 0.25 from the 7^+ -face f^{x_2x_3} by (R5). Thus, w'(f)\geq -3+1.5+1.25+0.25 = 0 by (R3.2) and (R3.3).
\bullet Assume that d_H(x_1) = d_H(x_2) = 4 and d_H(x_3)\geq5 . By definition, f is a weak 3-face and f gets at least 0.5 from each of x_1, x_2 by (R3.1). By Claim 5, at least one of x_1 and x_2 is a 4^1 -vertex. Without loss of generality, assume that x_2 is a 4^1 -vertex. If x_1 is a 4^1 -vertex or a 4^{0.75} -vertex, then w'(f)\geq -3+1+0.75+1.25 = 0 by (R3). Otherwise, x_1 is a 4^{0.5} -vertex. If x_3 is a internal 6^+ -vertex or a 5^{1.5} -vertex, then w'(f)\geq -3+1+1.5+0.5 = 0 by (R3). Therefore, x_3 is a internal 5-vertex with m_3(x_3) = 3 . By Lemma 1 and the definition of good 3-face, we can derive that x_1 is incident with a good 3-face. If x_1 is a internal 4_3 -vertex, then f gets 0.75 from x_1 by (R3.1), a contradiction. Otherwise, x_1 is a internal 4_4 -vertex. If x_3 is a (3, 3, 3, 6^+, 6^+) -vertex, (3, 3, 6, 3, 6^+) -vertex or (3, 3, 6^+, 3, 6) -vertex, it will contain a configuration C_5 \bowtie C_6 at the vertex x_3 , which is a contradiction. If x_3 is a (3, 3, 7^+, 3, 7^+) -vertex, it is the construction G_2 and f gets 0.25 from the 7^+ -face f^{x_2x_3} by (R5). Thus, w'(f)\geq -3+1+0.5+1.25+0.25 = 0 by (R3).
\bullet Assume that d_H(x_1) = d_H(x_2) = d_H(x_3) = 4 .
By definition, f is a bad 3-face and f gets 1 from each of x_1, x_2, x_3 by (R3). Thus, w'(f)\geq -3+1\times3 = 0 .
Case 2. 4\leq d_H(f)\leq 6 .
(1) If d_H(f) = 4 , then w'(f) = -2+0.5\times4 = 0 by (R0) and (R1).
(2) If d_H(f) = 5 , then w'(f) = -1+0.2\times5 = 0 by (R0) and (R2).
(3) If d_H(f) = 6 , then w'(f) = 0 .
Next, if f = [v_1v_2v_3 \cdots v_n] is a 7^+ -face, v_iv_{i+1} is in the configuration G_2 , [v_iv_{i+1}x] is a 3-face and x is a 4_4 -vertex, then we say that f is adjacent to a configuration G_2 by v_iv_{i+1} . Let t denote the number of the configuration G_2 which f is adjacent to.
Claim 6. Suppose that f is a 7^+ -face in H , then t \leq \lfloor\frac{2d_H(f)}{3}\rfloor .
Proof. Let f = [v_1v_2v_3 \cdots v_n] be a 7^+ -face in H .
If f is adjacent to a configuration G_2 by v_iv_{i+1} , then v_i or v_{i+1} is a internal (3, 3, 7^+, 3, 7^+) -vertex. By symmetry, let v_i be a internal (3, 3, 7^+, 3, 7^+) -vertex. If f is adjacent to another G_2 by edge v_{i-1}v_i , then v_i would be a (3, 3, 3, 3, 7^+) -vertex, contradicting the definition of G_2 . Hence, if f is adjacent to a G_2 by edge v_iv_{i+1} at least one of v_{i-1}v_i or v_{i+1}v_{i+2} is not adjacent to G_2 . It means that the three consecutive edges on f are adjacent to at most two G_2 configurations. Consequently, t\leq \lfloor\frac{2d_H(f)}{3}\rfloor .
Case 3. d_H(f)\geq7 .
Suppose that d_H(f) = 7. By Claim 6, t\leq \lfloor\frac{2d_H(f)}{3}\rfloor = 4 , then w'(f)\ge 7-6-0.25\times 4 = 0 by (R5). Suppose that d_H(f)\geq8 , then w'(f)\ge d_H(f)-6-0.25\times \lfloor\frac{2d_H(f)}{3}\rfloor\geq\frac{5}{6}d_H(f)-6\geq0 by (R5).
This completes the proof of Lemma 4 .
Lemma 5. w'_H(v)\ge 0 for each v\in V^0(H) .
Proof. Since v is a vertex of G and \delta(G)\geq 4 , it follows that d_H(v) = d_G(v)\ge 4 . We have six cases to consider.
Case 1. d_H(v) = 4 .
Case 1.1. Suppose that v is x_1 (or x_2 ) in the configuration G_1 .
In the configuration G_1 , we can derive that m_5^+(v)\ge2 and m_3(v)\le1 , otherwise it will produce a separating 3-cycle with fewer internal vertices than T or a configuration C_5 \bowtie C_6 , a contradiction. Hence, w'(v)\geq 2-0.5-0.1-0.2\times 2-1 = 0 .
Case 1.2. Suppose that v is not x_1 (or x_2 ) in the construction G_1 .
\bullet Assume that m_3(v) = 0 , then w'(v)\geq 2-0.5\times 4 = 0 by (R1) and (R2).
\bullet Assume that m_3(v) = 1 . If m_4(v)+m_5(v)\leq 2 , then w'(v)\geq 2-1-0.5\times2 = 0 by (R1), (R2) and (R3.1). Suppose that m_4(v)+m_5(v) = 3 . If m_5(v)\geq2 , then w'(v)\geq 2-1-0.5-0.2\times2 = 0.1 by (R1), (R2) and (R3.1). Suppose that m_5(v) = 1 and m_4(v) = 2 . If v is a (4, 3, 5, 4) -vertex, then it will produce a separating 3-cycle with fewer internal vertices than T or a configuration C_5 \bowtie C_6 at the vertex v , a contradiction. If v is a (4, 3, 4, 5) -vertex, then it is the configuration G_1 . Thus, w'(v)\geq 2-1-0.5\times2-0.2+0.1\times2 = 0 by (R1), (R2), (R3.1) and (R4). If m_4(v) = 3 , then it will produce a separating 3-cycle or a configuration C_5 \bowtie C_6 , a contradiction.
\bullet Assume that m_3(v) = 2 . If d_H(f_0) = d_H(f_1) = 3 , then d_H(f_2)\geq 6 and d_H(f_3)\geq6 by Claim 2. Thus, w'(v)\geq 2-1\times2 = 0 by (R3.1). If d_H(f_0) = d_H(f_2) = 3 , then d_H(f_1)\geq 6 and d_H(f_3)\geq6 by Claim 4. Thus, w'(v)\geq 2-1\times2 = 0 by (R3.1).
\bullet Assume that m_3(v) = 3 . Suppose that d_H(f_0) = d_H(f_1) = d_H(f_2) = 3 , then d_H(f_3)\geq 7 by Claim 3. By Lemma 1, at least one of v_0, v_1, v_2, v_3 is an internal 5^+ -vertex or belongs to V(T) . If v_0 or v_3 is an internal 5^+ -vertex or belongs to V(T) , say v_0 , then one of v_1, v_2, v_3 is an internal 5^+ -vertex or belongs to V(T) by Lemma 1 and v is incident with at most one bad 3-face. If v_1 or v_2 is an internal 5^+ -vertex or belongs to V(T) , then v is incident with at most one bad 3-face. Thus, w'(v)\geq 2-1-0.5\times2 = 0 , or w'(v)\geq 2-0.5-0.75\times2 = 0 , or w'(v)\geq 2- 0.5\times3 = 0.5 by (R3.1).
\bullet Assume that m_3(v) = 4 . If v is not incident with any bad 3-face, then w'(v)\geq 2-0.5\times4 = 0 (R3.1). Otherwise, v is incident with bad 3-faces. By Lemma 1, at least two of v_0, v_1, v_2, v_3 are internal 5^+ -vertices or belong to V(T) , it means that v is incident with one bad 3-face, one good 3-face and two weak 3-faces. Thus, w'(v)\geq 2-1-0.5\times2 = 0 by (R3.1).
Case 2. d_H(v) = 5 .
Note that w(v) = 4 . By Claim 1, m_3(v)\le\lfloor\frac 34d_H(v)\rfloor = 3 . If m_{6^+}(v) \geq 3 , then w'(v)\geq 4-1.5\times2 = 0 . Assume that m_{6^+}(v)\leq2 . If m_3(v) = 0 , then w'(v)\geq 4-0.5\times5-0.1\times5 = 1 by (R1)-(R4). If m_3(v) = 1 , then w'(v)\geq 4-1.5-0.5\times 4-0.1\times 4 = 0.1 by (R1)-(R4). Suppose that m_3(v) = 2 . If d_H(f_0) = d_H(f_1) = 3 , then d_H(f_2)\geq 6 and d_H(f_4)\geq6 by Claim 2. Thus, w'(v)\geq 4-1.5\times2-0.5-0.1 = 0.4 by (R1)-(R4). If d_H(f_0) = d_H(f_2) = 3 , then d_H(f_1)\geq 6 by Claim 4. If d_H(f_3) = d_H(f_4) = 4 , it will produce a separating 3-cycle with fewer internal vertices than T or a configuration C_5 \bowtie C_6 at the vertex v , a contradiction. Thus w'(v)\geq 4-1.5\times2-0.5-0.1-0.2 = 0.2 by (R1)-(R4).
Suppose that m_3(v) = 3 . If d_H(f_0) = d_H(f_1) = d_H(f_2) = 3 , then d(f_3)\geq 7 and d(f_4)\geq7 by Claim 3 . Thus w'(v)\geq 4-1.25\times3 = 0.25 by (R3.2). If d_H(f_0) = d_H(f_1) = d_H(f_3) = 3 , then d_H(f_2)\geq 6 and d_H(f_4)\geq6 by Claim 2 . Thus, w'(v)\geq 4-1.25\times2-1.5 = 0 by (R3.2).
Case 3. d_H(v) = 6 .
Note that w(v) = 6 . By Claim 1, m_3(v)\le\lfloor\frac 34d_H(v)\rfloor = 4 . If m_{6^+}(v) \geq 2 , then w'(v)\geq 6-1.5\times4 = 0 by (R3.3).
Suppose that m_{6^+}(v) \leq 1 . If m_3(v)\leq 2 , then w'(v)\geq 6-1.5 \times 2-0.5\times4-0.1\times4 = 0.6 by (R1)-(R4). Assume that m_3(v) = 3 . If d_H(f_0) = d_H(f_1) = d_H(f_2) = 3 , then d_H(f_3)\geq 7 and d_H(f_5)\geq7 by Claim 3, a contradiction. If d_H(f_0) = d_H(f_1) = d_H(f_3) = 3 , then d_H(f_2)\geq 6 and d_H(f_5)\geq6 by Claim 2, a contradiction. If d_H(f_0) = d_H(f_2) = d_H(f_4) = 3 , then d_H(f_1)\geq 6 , d_H(f_3)\geq6 and d_H(f_5)\geq6 by Claim 4. Assume that m_3(v) = 4 . If d_H(f_0) = d_H(f_1) = d_H(f_2) = d_H(f_4) = 3 , then d_H(f_3)\geq 7 and d_H(f_5)\geq7 by Claim 3, a contradiction. If d_H(f_0) = d_H(f_1) = d_H(f_3) = d_H(f_4) = 3 , then d_H(f_2)\geq 6 and d_H(f_5)\geq6 by Claim 2, a contradiction.
Case 4. d_H(v) = 7 .
Note that w(v) = 8 . By Claim 1, m_3(v)\le\lfloor\frac 34d_H(v)\rfloor = 5 . If m_{6^+}(v) \geq 2 , then w'(v)\geq 8-1.5\times5 = 0.5 by (R3.3). Suppose that m_{6^+}(v) \leq 1 . If m_3(v)\leq 4 , then w'(v)\geq 8-1.5 \times 4-0.5\times3-0.1\times3 = 0.2 by (R1)-(R4). Assume that m_3(v) = 5 . If d_H(f_0) = d_H(f_1) = d_H(f_2) = 3 , then d_H(f_3)\geq 7 and d_H(f_6)\geq7 by Claim 3, a contradiction. If d_H(f_0) = d_H(f_1) = 3 , then d_H(f_2)\geq 6 and d_H(f_6)\geq6 by Claim 2, a contradiction.
Case 5. d_H(v) = 8 .
Note that w(v) = 10 . By Claim 1, m_3(v)\le\lfloor\frac 34d_H(v)\rfloor = 6 . If m_{6^+}(v) \geq 2 , then w'(v)\geq 10-1.5\times6 = 1 by (R3.3). Suppose that m_{6^+}(v) \leq 1 . If m_3(v)\leq 5 , then w'(v)\geq 10-1.5 \times 5-0.5\times3-0.1\times3 = 0.7 by (R1)-(R4). Assume that m_3(v) = 6 . If d_H(f_0) = d_H(f_1) = d_H(f_2) = 3 , then d_H(f_3)\geq 7 and d_H(f_7)\geq7 by Claim 3, a contradiction. If d_H(f_0) = d_H(f_1) = 3 , then d_H(f_2)\geq 6 and d_H(f_7)\geq6 by Claim 2, a contradiction.
Case 6. d_H(v)\geq 9 .
We have the following estimation:
This completes the proof of Lemma 5.
Lemma 6. w'(f^\Delta)+\Sigma_{x\in V(T)}w'(x)\geq -11.6 .
Proof. By (R0), w'(f^\Delta)\geq 3-6 = -3 . Let v \in V(T) . First assume that d_H(v) = 2 . Note that v is not be incident with any 3 -face or 4 -face for otherwise we can find another separating 3 -cycle with fewer internal vertices than T , which is impossible. Consequently, w'(v)\geq 2\times2-6-0.2 = -2.2 by (R0). Next assume that d_H(v) = 3 . If m_3(v) = 3 , then w'(v)\geq 2\times3-6-1.5\times2 = -3 by (R0). Otherwise, w'(v)\geq 2\times3-6-2-0.6 = -2.6 by (R0). Now assume that d_H(v) = 4 . If m_3(v) = 4 , then w'(v)\geq 2\times4-6-1.5\times3 = -2.5 by (R0). Otherwise, w'(v)\geq 2\times4-6-2\times2-0.6 = -2.6 by (R0). Finally assume that d_H(v)\geq 5 . It follows that m_3(v)\leq d_H(v)-1 , otherwise a configuration C_5 \bowtie C_6 at the vertex v will be found. Thus, w'(v)\geq 2\times d_H(v)-6-2\times (d_H(v)-2)-0.6 = -2.6 by (R0).
If f^\Delta is incident with a vertex that is not a 3_3 -vertex, then w'(f^\Delta)+\Sigma_{x\in V(T)}w'(x)\geq -3-3-3-2.6 = -11.6 . Otherwise there is an internal 3 -vertex, which is impossible.
Recall that the sum of the initial weights of vertices and faces of H equals -12 . From Lemma 4-6, the corresponding sum of the new weights satisfies \Sigma_{x\in V^0(H)\cup F^0(H)}w'(x) + w'(f^\Delta)+\Sigma_{x\in V(T)}w'(x)\geq -11.6 . Since the total weight of H has been preserved during the discharging process, this is a contradiction to our initial assumptions that G , the minimal counterexample to Theorem 1, exists. This completes the proof of Theorem 1.
3.
Conjectures
In this paper, we show that the list vertex arboricity of every planar graph without a 5-cycle intersecting with a 6-cycle is at most 2. This implies directly that if G is a planar graph without 5-cycles or without 6-cycles, then a_l(G)\le 2 . We like to conclude this paper by raising the following conjectures:
Conjecture 1. Every planar graph G without intersecting 4 -cycles has a_l(G)\le 2 .
Conjecture 2. If G is a planar graph without a vertex lying on all cycles of length from 3 to 7 , then a_l(G)\le 2 .
Acknowledgments
The authors would like to thank the anonymous referees for their valuable comments and suggestions, which led to considerable improvement of the article.
The research is supported by the Natural Science Foundation of China (Grant No. 12031018).
Conflict of interest
The authors declare that they have no competing interests.









 DownLoad:
DownLoad: