Non-self-centrality number of some molecular graphs

1.   Introduction

Let ${\mathscr{G}}$ be a connected graph with vertex set ${\mathscr{V}(\mathscr{G})}$ and edge set ${\mathscr{E}(\mathscr{G})}$. Two adjacent vertices $w, z\in {\mathscr{V}(\mathscr{G})}$ are denoted by $wz$ (or $zw$). The order (resp. size) of ${\mathscr{G}}$ is $|{\mathscr{V}(\mathscr{G})}|$ (resp. $|{\mathscr{E}(\mathscr{G})}|$). The distance between $w$ and $z$ in ${\mathscr{G}}$ is the length of a shortest path connecting $w$ and $z$ and is denoted by $d_{{\mathscr{G}}}(w, z)$. For a vertex $w\in {\mathscr{V}(\mathscr{G})}$, its eccentricity is defined as $e_{{\mathscr{G}}}(w) = \max\{d_{{\mathscr{G}}}(w, z)\mid z\in{ \mathscr{V}(\mathscr{G})}\}$. For convenience, we can denote the eccentricity of $w\in{\mathscr{G}}$ by $e(w)$ if no ambiguity occurs. Furthermore, the minimum eccentricity over all the vertices of a graph ${\mathscr{G}}$ is called its radius of ${\mathscr{G}}$ denoted by $r({\mathscr{G}})$. Similarly, the maximum eccentricity over all the vertices of a graph ${\mathscr{G}}$ is called diameter of ${\mathscr{G}}$ denoted by $d({\mathscr{G}})$. A vertex $w\in {\mathscr{V}(\mathscr{G})}$ is said to be diametrical (resp. central) vertex of ${\mathscr{G}}$ if $e(w) = d({\mathscr{G}})$ (resp. $e(w) = r({\mathscr{G}})$). Moreover, the periphery $P({\mathscr{G}})$ of a graph ${\mathscr{G}}$ is defined as

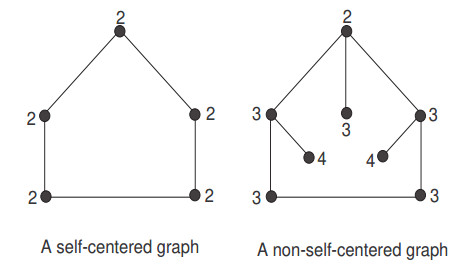
Whereas, center of a graph ${\mathscr{G}}$ is the subgraph induced by the central vertices of ${\mathscr{G}}$. The neighborhood ${\mathscr{N}}_{{\mathscr{G}}}(w)$ of a vertex $w\in {\mathscr{V}(\mathscr{G})}$ is defined as ${\mathscr{N}}_{{\mathscr{G}}}(w) = \{z\in {\mathscr{V}(\mathscr{G})}\mid wz\in {\mathscr{E}(\mathscr{G})}\}$. The degree $\deg(w)$ of a vertex $w$ in ${\mathscr{G}}$ is the number $|{\mathscr{N}_{\mathscr{G}}}(w)|$. A connected graph is called self-centered if the eccentricities of all the vertices are equal; otherwise, ${\mathscr{G}}$ is called a non-self-centered graph, shown in Figure 1.

A molecular graph ${\mathscr{G}}$ represents a chemical compound. A topological index is a numerical parameter of a molecular graph ${\mathscr{G}}$ which characterizes the properties of ${\mathscr{G}}$. Topological indices can be divided into many classes; some of them are degree-based, eccentricity-based, and distance-degree-based indices.

Recently, Xu et al. ^[7] introduced a new graphic invariant for indicating the non-self centrality of the graph more efficiently. This invariant was named as non-self centrality number (henceforth, NSC) of a graph ${\mathscr{G}}$, which is given by

where sum is over all vertex pair of vertices of a graph ${\mathscr{G}}$. For non-self-centered graph ${\mathscr{G}}$, the formula (1.1) was further simplified using the eccentricity sequence of the graph. If the eccentricity $e_{i}$ appears $l_{i}\geq1$ times in ${\mathscr{G}}$ we write, $e_{i}^{l_{i}}$ in short. Let us assume that $e_{1} > e_{2} > \dots > e_{k}$ be the distinct eccentricities of ${\mathscr{G}}$ with $l_{1}, l_{2}, ..., l_{k}$ be their respective multiplicities. Then the eccentricity sequence is $\zeta({\mathscr{G}}) = \{e_{1}^{l_{1}}, e_{2}^{l_{2}}, \dots, e_{k}^{l_{k}}\}$. Therefore, the NSC number of ${\mathscr{G}}$ can be written as

We refer ^[4] to the readers for some more results on NSC number. By graph structure, we can easily calculate the eccentricities of its vertices. When the eccentricities of vertices of a graph are known, the eccentricity sequence can easily be obtained. Therefore, we will write directly the eccentricity sequences of graphs in this paper.

Ashrafi et al. ^[3] computed the eccentric-connectivity index of $TUC_{4}C_{8}$ nanotubes and nanotori. Also Kwun et al. ^[5] computed M-polynomials and topological indices like Zagreb indices of V-phenylenic nanotubes and nanotori. For further details, we refer ^[1,2,6]. Heretofore, NSC number is considered for finite family of graphs ^[7,4]. It motivates us to consider NSC number of infinite family of graphs. In this paper, we calculate NSC number of $TUC_{4}C_{8}$ and $V$-phenylenic nanotubes.

2.   $V$-phenylenic nanotubes

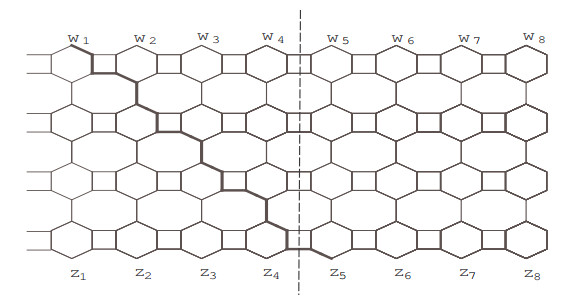
Here we compute the non-self centrality number of $V$-phenylenic nanotubes. An infinite structure of $V$-phenylenic nanotubes and nanotori is made by alternating $C_{4}$, $C_{6}$ and $C_{8}$ cycles. The arrangement of $C_{4}$, $C_{6}$ and $C_{8}$ cycles in $V$-phenylenic structure is such that $C_{4}$ ring is attached to two $C_{6}$ rings and also each $C_{4}$ is attached to two $C_{8}$ rings. We will denote the $V$-phenylenic nanotubes by $G[h, f]$, where $f$ and $h$ are the number of columns and rows, respectively, as shown in the Figures 2 and 3. Consider

and

Then $|X| = 2h$ and $|Y| = 6hf-2h.$ From the structure of $G[h, f]$, we notice that there are two types of edges given by

and

It is easy to see that $|\mathscr{E}_{1}| = 4h$ and $|\mathscr{E}_{2}| = h(9f-5)$. Hence, $|\mathscr{E}| = |\mathscr{E}_{1}|+|\mathscr{E}_{2}| = h(9f-1)$ is the number of total edges in $G[h, f]$.

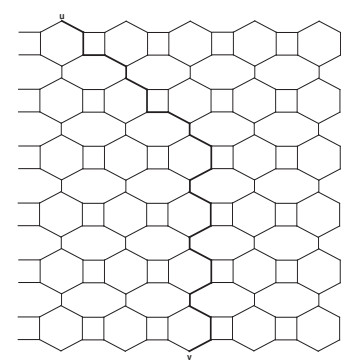
Before moving to the main results, it is important to know that structure of $V$-phenylenic nanotube is symmetric and hence it can be divided into two halves as shown in Figure 2. Whereas, we can also divide the structure into two different classes depending on $h$ and $f$. When $h < 2f$ we get a vertical structure shown in Figure 3, while we obtain a horizontal structure for $h > 2f$. Now let us begin with the following result:

Lemma 1. For $f\geq2$ the diameter of $G[h, f]$ is

Proof. Let $w_{i}$ and $z_{j}$, $1\leq i, j\leq h$, be the peripheral vertices in $G[h, f]$, as shown in Figure 2. We can partition $\mathscr{E}(G[h, f])$ into three classes; horizontal, oblique and vertical edges. Now if $h\leq 2f$ and $h$ is an even integer then, to find the diameter we have to find the path's length that connects two vertices of $X$. Let $w_{i}$ be the vertex with an eccentric vertex $z_{j}$ in $G[h, f]$, shown in Figure 2. For $j < \big(\frac{h}{2}+i\big)$, length of a shortest $w_{i}, z_{j}$-path contains $2f$ oblique, $(2f-1)$ vertical and $j-1$ horizontal edges. Therefore,

Similarly, for $j = \big(\frac{h}{2}+i\big)$, the length of a shortest $w_{i}, z_{j}$-path contains exactly $2f-1$ vertical, $2f$ oblique and $\frac{h}{2}$ horizontal edges. Therefore,

Now for $j > \big(\frac{h}{2}+i\big)$, the length of the shortest $w_{i}, z_{j}$-path contains $2f$ oblique, $(2f-1)$ vertical and $h-j$ horizontal edges. Therefore,

From the above discussion and Figure 2, it is observed that $d_{G[h, f]}(w_{i}, z_{j}) = \frac{h}{2}+4f-1$ is the maximum distance. Therefore, $d(G[h, f]) = \frac{h}{2}+4f-1$.

Similarly, in case of odd $h$, we choose $w_{i}$ and $z_{j}$, where $z_{j}\in X\cup Y$, such that $d_{G[h, f]}(w_{i}, z_{j})$ is maximum. We need $2f$ oblique edges, $2f-1$ vertical edges and $\frac{h-1}{2}$ horizontal edges to connect $w_{i}$ and $z_{j}$. Hence, the diameter is given by $d(G[h, f]) = \frac{h-3}{2}+4f$. In similar manner, we can find the diameter of $G[h, f]$ when $h < 2f$.

Theorem 2. For $f\geq 2$, we have

Proof. We discuss five possible cases:

Case 1: $h > 2f-1$ and $h$ is even.

Here we have

Using formula (1.2), the NSC number of $G[h, f]$ is given by

After simplification, we get

Case 2: $h > 2f-1$ and $h$ is odd.

In this case, we have

Using (1.2), the NSC number of $T[h, f]$ is given by

Case 3: $h\in\{2f-2, 2f-1\}$.

The eccentricity sequence of $G[h, f]$ in this case is given by

Using formula (1.2), the NSC number of $G[h, f]$ is given by

After simplification, we obtain:

Case 4: $h < 2f-2$ and $f$ is even.

In this case, for $G[h, f]$ we have

Using formula (1.2), the NSC number of $G[h, f]$ is given by

After simplification we get

Case 5: $h < 2f-2$ and $f$ is odd.

In this case, the eccentricity sequence of $G[h, f]$ is given by

By formula (1.2), the NSC number of $G[h, f]$ is given by

Simplifying above, we obtain

This completes the proof.

Remark. For $V$-phenylenic nanotori, the graph become self-centered. Therefore non-self-centrality number of $V$-phenylenic nanotori is zero.

3.   $TUC_{4}C_{8}$ nanotubes

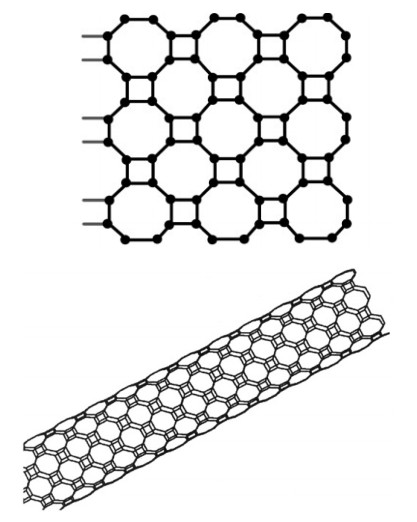
In this section, we compute the non-self centrality number of $TUC_{4}C_{8}$ nanotubes. In the structure of $TUC_{4}C_{8}$ nanotube, every $C_{4}$ cycle is adjacent to four $C_{8}$ cycles. We will denote $TUC_{4}C_{8}$ nanotube by $G[u, v]$, where $s$ is the number of octagons in a fixed row and $t$ denotes the sum of $C_{4}$ and $C_{8}$ cycles in a fixed column (see Figure 4).

Consider

Then $|X| = 4s\rm{\space and \space} |Y| = 4st.$ Also

Remark. The graph $G[s, t]$ becomes self-centered for $t = 1$. Therefore the non-self-centrality number of $G[s, 1]$ is zero.

Theorem 3. Assume that $s \geq 2$ and $t$ is an odd integer. Then the NSC number of $TUC_{4}C_{8}$ nanotube is given by

Proof. The eccentricity sequence of $G[s, t]$ is given by

Using formula (1.2) the NSC of $G[s, t]$ is given by

This completes the proof.

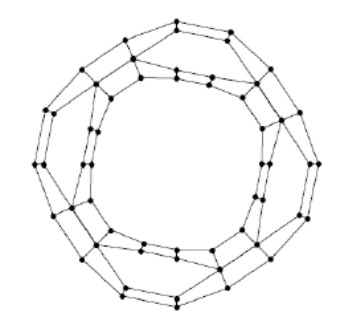
Remark. The graph of $TUC_{4}C_{8}$ nanotori, shown in Figure 5, is self-centered. Therefore non-self-centrality number of nanotori is zero.

4.   Conclusions

In this paper, we computed general formulas for the non-self-centrality number of V-Phenylenic and $TUC_{4}C_{8}(R)$ nanotubes. For future study, we can calculate the non-self-centrality number of other molecular structures such as $\alpha$-Boron nanotubes, some layer structures and dendrimers.

Conflict of interest

The authors have no conflict of interest to declare.