Dynamical behaviors of a vector-borne diseases model with two time delays on bipartite networks

1.   Introduction

In history, vector-borne diseases such as malaria, yellow fever, plague, Lyme disease and dengue fever caused a large number of human diseases and deaths. In the early to mid-20th world, people controlled most of the vector-borne diseases through measures such as improving sanitation and reducing the number of vectors. However, over the past four decades, due to climate change and other reasons, many vector-borne infectious diseases that have been "eliminated" have shown a resurgence ^[1]. According to statistics, nearly half of the world's population has been infected with at least one vector-borne pathogen ^[2]. Considering that vector-borne infectious diseases pose a huge threat to human health and social economy, it is urgent to study the characteristics of their transmission and how to prevent and control them.

Mathematical models of vector-borne diseases play an important role in understanding and studying epidemiological characteristics and transmission laws. In 1911, Ross-Macdonald first established a model of malaria disease, which used differential equations to describe mosquitoes and humans ^[3], and his study methods laid the foundation for subsequent research. In recent years, many research results in this area have continuously emerged. For example, Traoré ^[4] proposed a vector-borne disease model with human and vectors immigration, which considered the influence of long-distance migration of wind-borne vector and the influence of human migration. Nyang'inja et al. ^[5] and Abiodun et al. ^[6] investigated the impact of vaccination and climate change on the vector-borne disease, respectively.

It is worth noting that above researches for vector-borne diseases were based on the assumption that the contact between humans and vectors is uniformly homogeneous. In fact, real networks underlying disease transmission are highly heterogeneous ^[7,8,9]. Similarly, due to the heterogeneity of the population and the distribution of vectors in different regions, the contact between humans and vectors is also heterogeneous ^[10,11,12]. To study this spreading characteristic, many researchers have been studying vector-borne diseases model on bipartite networks. Yang et al. ^[13] studied a modified susceptible–infected–susceptible model with an infective medium on bipartite networks, and compared it with the standard SIS model. Wang et al. ^[14] established a modified SIS model with an infective vector on complex networks, which included not only transmission through the vectors, but also transmission through direct contact between people. Wang et al. ^[15] proposed a more concise method to investigate the global dynamics of a mean-field vector-borne diseases model on bipartite networks. It is worth noting that in 2020, Zhang ^[16] established the following malaria disease model on bipartite networks,

where $y_k$ and $x_l$ represent the relative density of infected humans with degree $k$ and infected mosquitoes with degree $l$ respectively, $\Theta_{y} = \frac{\sum_{k = 1}^{n} k p(k) y_{k} N}{\sum_{k = 1}^{n} k p(k) N}$ and $\Theta_{x} = \frac{\sum_{l = 1}^{m} l q(l) x_{l} V}{\sum_{l = 1}^{m} l q(l) V}$ represent the probabilities rate that any link points to an infected human and an infected mosquito respectively, $\langle k\rangle_{y}$ is the average degree of humans, $\gamma$ is recovery rate of humans, $\mu$ represents mortality rate of mosquitoes, $a$ is the biting rate on humans by a single mosquito, $b$ and $c$ represent probabilities of infected bites that produce an infected human and an infected mosquito respectively, $N$ and $V$ are the total number of human population and mosquito population respectively. According to the description of the parameters, $\frac{a b V}{N\langle k\rangle_{y}}$ can be regarded as the linear transmission rate from infected mosquitoes to susceptible humans, and $ac$ represents the linear transmission rate from infected humans to susceptible mosquitoes. The author obtained the basic reproduction number $R_0$ and studied dynamical behaviors of the above model.

Most of researches for vector-borne disease model on bipartite networks only consider the two states of humans and vector populations: susceptibility and infected. In reality, many vector-borne diseases have incubation periods in both vectors and humans. For malaria ^[17], during the incubation period of mosquitoes, there are no sporozoites in the salivary glands of the "infected" mosquitoes, and the disease cannot be transmitted to humans through bites. Similarity, during the incubation period of humans, the malaria parasites lie dormant in the liver or there are not enough malaria gametocytes in the human blood. At this time, mosquito cannot take up the gametocytes by sucking up blood and become infected. Furthermore, due to the incubation period of different forms of parasites, the feedback dynamics from mosquito to human to mosquito has a considerable time delay. The prolonged delayed onset of the disease brings huge risks to the prevention and control of the disease ^[18]. However, there are few researches about vector-borne disease model on bipartite networks with time delay ^[19].

Based on Zhang's work ^[16], to study the impact of the incubation periods of humans and mosquitoes, we construct a novel vector-borne diseases model with two time delays on bipartite networks. In this paper, we will study the effect of the incubation periods on the basic reproduction number and the dynamical behaviors of the novel model.

The remaining parts of this paper are organized as follows: The vector-borne diseases model with two time delays on bipartite networks is presented in Section 2. The dynamical behaviors of the model are discussed in Section 3. Numerical simulations are offered to demonstrate the main results in Section 4. The conclusion is given in Section 5.

2.   Model

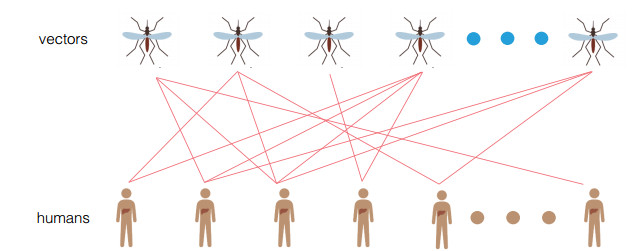
We suppose the contact patterns between humans and vectors form the bipartite network. The edge between a human and a vector represents contacts between the human and the vector. Since the adding and removal nodes and edges only take a small proportion in the network and will slightly change the structure of the network ^[20], we assume the human birth rate is equal to the human mortality rate, denoted by $d$, and the birth rate of vectors is equal to the mortality rate of vectors, denoted by $\mu$. Thus, the total number of human population is a constant $N$, and the total number vector population is also a constant $V$. Therefore, we construct the bipartite network between humans and vectors, as shown in Figure 1.

Let $p(k)$ $(k = 1, 2, ..., n)$ and $q(l)$ $(l = 1, 2, ..., h)$ represent the human degree distribution and vector degree distribution respectively, which can reflect contact patterns between humans and vectors. $n$ and $h$ are the maximum number of vectors contacted by humans and the maximum number of humans contacted by vectors respectively. $N_k = Np(k)$ are the human groups in which each human contacts with $k$ vectors. $V_l = V q(l)$ are the vector groups in which each vector contacts with $l$ humans. Suppose the degree of each human and each vector is time invariant. Human population are divided into four categories: susceptible, exposed (infected but unable to to spread disease when in contact with susceptible vectors), infected (infected and able to spread disease when in contact with susceptible vectors) and recovered (recovered and acquired full immunity). Vector population are divided into three categories: susceptible, exposed (infected but unable to to spread disease when in contact with susceptible humans), infected (infected and able to spread disease when in contact with susceptible humans). Then, $S_k(t)$, $E_k(t)$, $I_k(t)$ and $R_k(t)$ represent the relative density of susceptible, exposed, infected and recovered humans with degree $k$ $(k = 1, 2, ..., n)$ at time $t$ respectively. $S_l^m(t)$, $E_l^m(t)$ and $I_l^m(t)$ represent the relative density of susceptible, exposed and infected vectors with degree $l$ $(l = 1, 2, ..., h)$ at time $t$ respectively.

In order to reflect the impact of incubation periods in disease transmission. Let $\tau$ and $\omega$ represent the disease incubation period of humans and the disease incubation period of vectors respectively. That is, the exposed human becomes an infected human after $\tau$, and the exposed vector becomes an infected vector after $\omega$. Thus we can establish the following vector-borne diseases model with two delays on bipartite networks:

in which the descriptions of parameters $\gamma$, $a$, $b$ and $c$ are consistent with the system (1.1). $\langle k\rangle_{k} = \sum_{k = 1}^{n}kp(k)$ and $\langle l\rangle_{l} = \sum_{l = 1}^{h}l q(k)$ are average degree of humans and vectors respectively. Therefore, $N\langle k\rangle_{k}$ is the total number of edges of humans, furthermore, we obtain $\frac{a b V}{N\langle k\rangle_{k}}$ represents the infection probability of each edge from infected humans to susceptible vectors, and $ac$ represents the infection probability of each edge from infected vectors to susceptible humans. $\Theta(t)$ and $\Theta(t)^m$ are the probability rate that any link points to an infected human and an infected vector respectively, and

where $\varphi(k)$ and $\psi(l)$ are infectious of occupied edges which can transmit the disease from the infected human with degree $k$ and the infected vector with degree $l$, respectively. There are many forms of $\varphi(k)$. The simple forms are $\varphi(k) = Ck$ ^[21] ($0 < C\leq1$), which represent the infectivity of each node is proportional to its degree, and $\varphi(k) = A$^[21] ($A$ is a positive constant), which represents each node generate $A$ contacts. The more suitable form is nonlinear infectivity $\varphi(k) = \mathrm{a} k^{\mathrm{c}} /\left(1+\mathrm{b} k^{\mathrm{c}}\right)$^[22] ($0\leq\mathrm{c}\leq1$, $\mathrm{a} > 0$, $\mathrm{b}\geq0$), which can be divided into different cases: when $\mathrm{c} = 1$ and $\mathrm{b} = 0$, $\varphi(k) = \mathrm{a}k$; when $\mathrm{c} = 0$, $\varphi(k) = \mathrm{a}/(1+\mathrm{b})$; when $\mathrm{b}\neq0$, $\varphi(k) = \mathrm{a} k^{\mathrm{c}} /\left(1+\mathrm{b} k^{\mathrm{c}}\right)$ is monotonically increasing with $k$, and it has an upper bound, $\lim_{k\rightarrow +\infty}\varphi(k) = \mathrm{a}/\mathrm{b}$, which means that the infectivity of the node reaches the maximum. The form of $\psi(l)$ is similarly to the form of $\varphi(k)$. For clarity, we introduce the description of the parameters in Table 1 and the disease transmission diagram in Figure 2.

It is clearly that the normalization condition of system (2.1) is

where $\phi = (\phi_{1}^{1}(\eta), ..., \phi_{1}^{n}(\eta), \phi_{2}^{1}(\eta), ..., \phi_{2}^{n}(\eta), \phi_{3}^{1}(\eta), ..., \phi_{3}^{n}(\eta), \phi_{4}^{1}(\eta), ..., \phi_{4}^{n}(\eta), \phi_{5}^{1}(\eta), ..., \phi_{5}^{h}(\eta), \phi_{6}^{1}(\eta), ..., \phi_{6}^{h}(\eta), \\ \phi_{7}^{1}(\eta), ..., \phi_{7}^{h}(\eta))\in {\bf{C}}([-T, 0], {\bf{R}}_{+}^{4n+3h})$ are non-negative continuous on interval $[-T, 0]$. ${\bf{C}}([-T, 0], {\bf{R}}_{+}^{4n+3h})$ denotes the Banach space of continuous functions mapping the interval $[-T, 0]$ into ${\bf{R}}_{+}^{4n+3h}$, and it equipped with the norm

where $|\phi(\eta)| = \sup_{-T\leq\eta\leq0}|\phi(\eta)|$. We can prove through the fundamental theory of functional differential equations ^[23] that system (2.1) has a unique solution satisfying the initial condition (2.3).

3.   Dynamics

Note that the second and sixth equations of system (2.1) can be further transformed into the following integral equations.

Thus, in order to study the dynamical behaviors of system (2.1), we only need to study the following system:

Now, we mainly analyze system (3.1).

Theorem 3.1. If any solution $(S_1(t), ..., S_n(t), I_1(t), ..., I_n(t), R_1(t), ..., R_n(t), S_1^m(t), ..., S_h^m(t), I_1^m(t), ..., I_h^m(t))$ of system (3.1) satisfies the initial condition (2.3), then all solutions of system (3.1) are non-negative for $t > 0$.

Proof. Firstly, we prove $S_k(t) > 0$ for $t > 0$. Suppose it is not true, there would be at time $T$ such that $S_k(t) = 0$. From the first equation of (3.1),

This means that there is a positive constant $\epsilon$ such that $S_k(t) < 0$ when $t\in(T-\epsilon, T)$. This leads to a contradiction, i.e., $S_k(t)$ is always positive. Similarly, $S_l^m(t)$ has the same conclusion.

Secondly, we consider $I_k(t)$ and $I_l^m(t)$. From the second and forth equations of (3.1),

and

It is easy to see that $I_k(t)$ and $I_l^m(t)$ are non-negative.

Finally, from the third equation of (3.1),

Therefore, this completes the proof.

From Theorem 3.1 and the normalization condition (2.2), the following set $\Omega$ is the positive invariant for system (3.1),

Now, we consider that dynamics of system (3.1) on the region $\Omega$.

Theorem 3.2. Denote

where $\langle k \varphi(k)\rangle_k = \sum_{k = 1}^{n}k \varphi(k)p(k)$, $\langle k\rangle_k = \sum_{k = 1}^{n}kp(k)$, $\langle l\psi(l)\rangle_l = \sum_{l = 1}^{h}l\psi(l)q(l)$ and $\langle l\rangle_l = \sum_{l = 1}^{h}lq(l)$. Then, we have the following assertions.

(1) System (3.1) always has a disease-free equilibrium $E^0$, where

(2) System (3.1) has a endemic equilibrium $E^*$ when $R_0 > 1$, where

Proof. Obviously, system (3.1) always has a disease-free equilibrium

Then, we suppose that system (3.1) has a endemic equilibrium

and $E^*$ satisfies the following equations

where

By a simple calculation,

From (3.4) and (3.3), we obtain

Substitute $(\Theta^m)^*$ into $\Theta^*$,

Obviously, $\Theta^* = 0$ is a solution of equation (3.5), i.e., system (3.1) always has a disease-free equilibrium $E^0$. Then, we take $\Theta^* > 0$ to ensure equation (3.5) has a nontrivial solution. Taking the derivative of $F(\Theta^*)$, we get

Denote

Since $\dot{F_1}(\Theta^*) < 0$ and $\dot{F_2}(\Theta^*) > 0$,

Thus, equation (3.5) has a nontrivial solution if and only if

Therefore, we define the basic reproduction number

Based on the above analysis, when $R_0 > 1$, system (3.1) has a endemic equilibrium $E^*$.

Remark 3.1. Zhang has obtained the basic reproduction number from the model in Ref. ^[16] formed

In our work, when $\varphi(k) = k$ and $\psi(l) = l$, the basic reproduction number $R_0$ of system (3.1) becomes

Comparing the two basic reproduction numbers, we find that

That is, the influence of time delays causes a change in the basic reproduction number, and $R_0$ decreases as time delays increase.

Theorem 3.3. If $R_0 < 1$, the disease-free equilibrium $E^0$ of system (3.1) is globally asymptotically stable for $\tau\geq0$ and $\omega\geq0$.

Proof. Denote the following Lyapunov function

where

Taking the derivative of $V(t)$ along the solution of system (3.1), we obtain

Note that $0\leq S_k(t)\leq1$ and $0\leq S_l^m(t)\leq1$,

Thus, $R_0 < 1$ follows that $\frac{\mathrm{d}V(t)}{\mathrm{d}t}\mid_{(3.1)}\leq0.$ Simultaneously, $\frac{\mathrm{d}V(t)}{\mathrm{d}t}\mid_{(3.1)} = 0$ if and only if $I_k(t) = 0.$ From (3.1), we have $\lim _{t \rightarrow +\infty} S_{k}(t) = 1$, $\lim _{t \rightarrow +\infty} R_{k}(t) = 0$, $\lim _{t \rightarrow +\infty} S_{l}^m(t) = 1$ and $\lim _{t \rightarrow +\infty} I_{l}^m(t) = 0$. According to the LaSalle Invariance Principle ^[24], we conclude that $E^0$ is globally asymptotically stable when $R_0 < 1$.

Theorem 3.4. If $R_0 > 1$, the endemic equilibrium $E^*$ of system (3.1) is globally asymptotically stable for $\tau\geq0$ and $\omega\geq0$.

Proof. Define the following Lyapunov function

where

in which

It is obviously that $W_x(t)\geq 0$ for $x(t) > 0$, and $W_x(t) = 0$ if and only if $x(t) = x^*$.

From the first equation of (3.2), we get $d = \frac{abVk}{N\langle k \rangle_k}S_k^*(\Theta^m)^*+dS_k^*.$ Differentiating $W_{S_k}(t)$ along the solution of (3.1), we obtain

From the second equation of (3.2),

Differentiating $W_{\Theta}(t)$ along the solution of (3.1), we have

Moreover,

Combining (3.13), (3.14) and (3.15), we obtain

where $G(x) = x-1-\ln x$.

Through the above similar deduction process, calculate the derivative of $V_2(t)$ along solution of (3.1)

Combining (3.16) and (3.17),

Note $G(x) = x-1-\ln x\geq0$ for all $x > 0$ and $G(x) = 0$ if and only if $x = 1$. Thus, $\frac{\mathrm{d}V(t)}{\mathrm{d}t}\mid_{(3.1)}\leq0$, and $\frac{\mathrm{d}V(t)}{\mathrm{d}t}\mid_{(3.1)} = 0$ if and only if $S_{k}(t) = S_{k}(t-\tau) = S_k^*$, $S_l^m(t) = S_l^m(t-\omega) = (S_l^m)^*$, $\Theta(t) = \Theta(t-\tau) = \Theta^*$ and $\Theta^m(t) = \Theta^m(t-\omega) = (\Theta^m)^*$. According to (3.1), we obtain $\lim _{t \rightarrow +\infty} I_k(t) = I_k^*$, $\lim _{t \rightarrow +\infty} R_k(t) = R_k^*$ and $\lim _{t \rightarrow +\infty} I_l^m(t) = (I_l^m)^*$. By the LaSalle Invariance Principle ^[24], the endemic equilibrium $E^*$ of system (3.1) is globally asymptotically stable when $R_0 > 1$.

4.   Simulations

In this section, we present some numerical simulations to verify the correctness of our main results, discuss the impact of the incubation periods on transmission scale and reveal the influence of network structure on the basic reproduction number $R_0$.

Since the model (2.1) is suitable for malaria, the vector population is mainly mosquito population, and we select the following parameter values based on the pioneers' research. The biting rate on human by a vector $a$ is about 0.193 to 0.421 per day ^[25]. The probability of being bitten by an infected human is equal to the probability of being bitten by an infected vector, i.e., $b = c = 0.5$ ^[26]. The recovered rate of human $\gamma$ is about 0.01 to 0.05 per day ^[26]. The mortality rate of vectors $\mu$ is about 0.006 to 0.1588 per day ^[25]. According to the World Health Organization, the average life expectancy of Africans in 2019 is 56.4 years ^[27]. Since most malaria outbreaks occur in Africa ^[28], wo choose the mortality rate of humans $d = 1/(56.4\times 365)\approx0.000048$ per day. Similar to the assumption in Ref. ^[15], the total number of human population is $N = 10^9$ and the total number of vector population is $V = 7.0\times 10^8$. The disease incubation period of humans $\tau$ is about 10 to 100 days ^[26], and the disease incubation period of vectors $\omega$ is about 6 to 19 days ^[25]. For clarity, the parameter values are listed in Table 2.

Assume that the bipartite network is a finite network. The degree of humans and degree of vectors in the network are $k = 1, 2, ..., n$ and $l = 1, 2, ..., h$, respectively. The power-law distribution of the human population and vector population are $p(k) = C_1k^{-\alpha_1}$ and $q(l) = C_2l^{-\alpha_2}$ respectively, where $\alpha_1\in [2, 3), \alpha_2\in [2, 3)$, and $C_1$, $C_2$ are both positive constants satisfying $\sum_{k = 1}^n C_1p(k) = \sum_{l = 1}^h C_2q(l) = 1$. The nonlinear infectivity $\varphi(k)$ and $\psi(l)$ have the same form, and $\varphi(k) = \mathrm{a} k^{\mathrm{c}} /\left(1+\mathrm{b} k^{\mathrm{c}}\right)$, $\psi(l) = \mathrm{a} l^{\mathrm{c}} /\left(1+\mathrm{b} l^{\mathrm{c}}\right)$, in which $\mathrm{a} = 0.5, \ \mathrm{c} = 0.75, \ \mathrm{b} = 0.02$. Denote $I(t)$ is the average density of the infected humans at time $t$, and $I^m(t)$ is the average density of the infected vectors at time $t$,

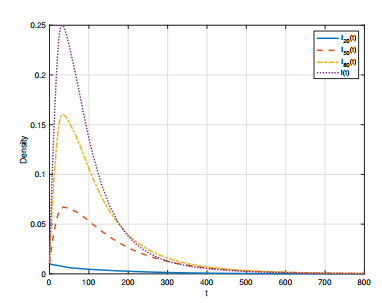
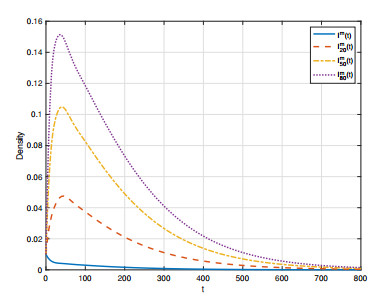
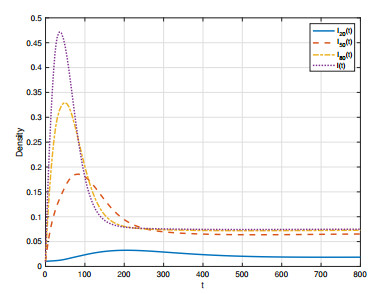
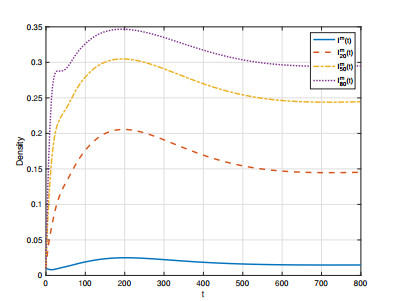
First, we perform some numerical simulations to illustrate our theoretical results. We choose the initial values are $I_k(0) = 0.01, k = 1, ..., 100$ and $I_l^m(0) = 0.01, l = 1, ..., 100$. Let $a$ vary, the other parameters are $\mu = 0.08$, $\gamma = 0.04$, $\tau = 20$, $\omega = 10$ and $\alpha_1 = \alpha_2 = 2.8$. When $a = 0.2$, the basic reproduction number $R_0\approx0.8370 < 1$. Figure 3 shows the time evolution of $I(t)$, $I_{20}(t)$, $I_{50}(t)$, $I_{80}(t)$, and Figure 4 shows the time evolution of $I^m(t)$, $I^m_{20}(t)$, $I^m_{50}(t)$, $I^m_{80}(t)$. We find that the infected humans and vectors are both tend to zero, i.e., the infection eventually disappears, which is consistent with Theorem 3.3. When $a = 0.4$, the basic reproduction number $R_0\approx3.3482 > 1$. From Figure 5 and Figure 6, the infected humans and vectors are all converge to positive constants as $t \rightarrow +\infty$, which is consistent with Theorem 3.4.

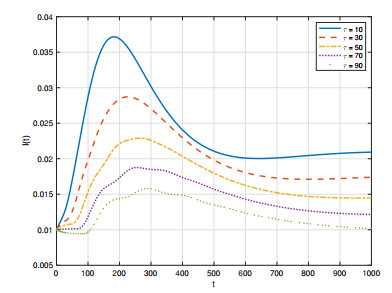
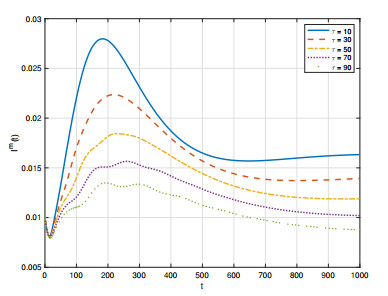
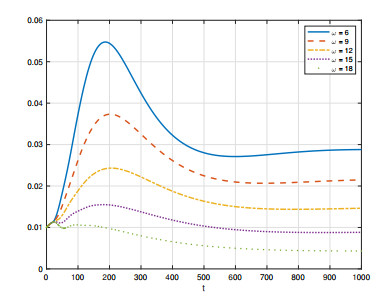
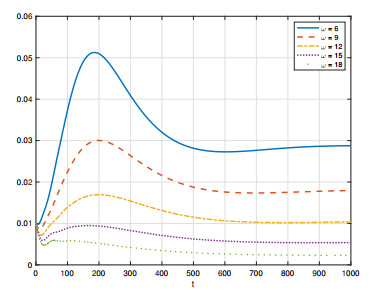
Next, we focus on the influence of the two time delays on the scale of disease spread. Let $\tau$ and $\omega$ change separately, the other parameters are fixed as $a = 0.4$, $\mu = 0.08$, $\gamma = 0.04$ and $\alpha_1 = \alpha_2 = 2.8$. Figure 7 and Figure 8 demonstrate that as $\tau$ increases, both $I(t)$ and $I^m(t)$ decrease. We also find that as $\omega$ increases, both $I(t)$ and $I^m(t)$ decrease in Figure 9 and Figure 10. Moreover, Figure 11 shows the influence of $\tau$ and $\omega$ to the basic reproduction number $R_0$. It can be seen that $R_0$ decreases as $\tau$ and $\omega$ increase, which is consistent with Remark 3.1. From these phenomena, we obtain that the larger the two delays, the slower and less widely the spread of disease.

Last, we concentrate on the relationship between the basic reproduction number $R_0$ and the network structure. Since the contact bipartite network has two states, it is reasonable to consider the human population structure and the vector population structure, respectively. We discuss the impact of the following three cases: the heterogeneity of network, the maximum degree of node and the average degree of node.

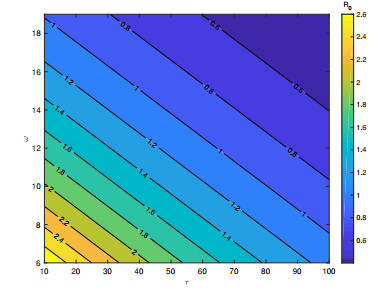
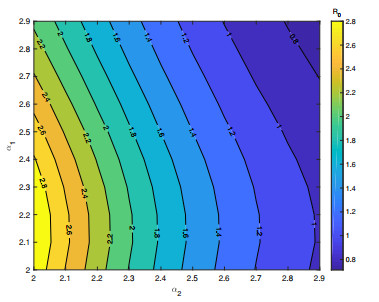
Case 1: The power-law distribution index can reflect the heterogeneity of the network. Let the power-law index of humans $\alpha_1$ and vectors $\alpha_2$ change separately, the other parameters are $a = 0.2$, $\mu = 0.08$, $\gamma = 0.04$, $\tau = 20$, $\omega = 10$ $k = 1, ..., 100,$ and $l = 1, ..., 100$. Figure 12 shows $R_0$ decreases as $\alpha_1$ and $\alpha_2$ increase. That is, the smaller the heterogeneity transmission between humans and vectors, the more difficult it is to control the disease.

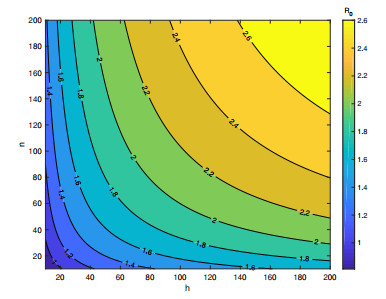
Case 2: Since the range of nodes degree are $k = 1, 2, ..., n$ and $l = 1, 2, ..., h$, let $n$ and $h$ change separately, and the other parameters are $\alpha_1 = \alpha_2 = 2.5$, $a = 0.25$, $\mu = 0.08$, $\gamma = 0.04$, $\tau = 20$ and $\omega = 10$. Figure 13 shows $R_0$ increases as $n$ and $h$ increase, and the rate of increase of $R_0$ continues to slow down. In other words, the larger the maximum number of contacts between humans and vectors, the more difficult it is to control the disease, but the impact continues to decrease.

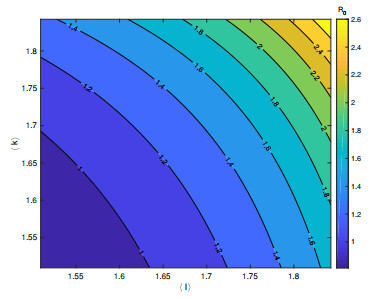
Case 3: The average degree of the node represents the average number of connections of the node in network. We use the range of the node degree control the change of the average degree. Let the average degree of humans $\langle k \rangle$ and vectors $\langle l \rangle$ change separately, the other parameters are the other parameters are $\alpha_1 = \alpha_2 = 2.5$, $a = 0.25$, $\mu = 0.08$, $\gamma = 0.04$, $\tau = 20$ and $\omega = 10$. Figure 14 shows $R_0$ increases as $\langle k \rangle$ and $\langle l \rangle$ increase. That is, the more the average number of contacts between humans and vectors, the harder it is to control the disease.

From above three phenomena, we conclude that the network structure has a great influence on the basic reproduction number, and the vector population structure has a greater impact on disease transmission than the human population structure. In other words, controlling the vector population can effectively curb the spread of vector-borne diseases.

5.   Conclusion

Due to the connection between humans and vectors in vector-borne diseases is heterogeneous ^[12], in this paper, we concentrate on the impact of incubation periods of humans and vectors on diseases transmission and propose a novel vector-borne diseases model with two time delays on bipartite networks.

For this delayed model, we identify the formula of the basic reproduction number $R_0$ which depends on the two time delays. By constructing appropriate Lyapunov functions, we prove that when $R_0 < 1$, the disease-free equilibrium $E ^ 0$ is globally asymptotically stable; when $R_0 > 1$, the endemic equilibrium $E ^ *$ is globally asymptotically stable.

Based on the pioneers' researches on real data, we present numerical simulations to verify the correctness of our results and discuss the impact of the incubation periods. The results show the incubation periods of humans and vectors can constrain the diseases transmission. That is, the longer the incubation periods, the slower and less widely the spread of diseases. Moreover, we reveal the influence of the structure of bipartite network on the basic reproduction number. It is shown the power-law distribution index of networks is negatively correlated with the basic reproduction number, and the maximum degree and average degree of node are positive correlated with it. We also find that compared with the human population structure in bipartite network, the vector population structure has a greater impact on disease transmission.

These results can help us understand the dynamics of vector-borne diseases on bipartite networks, and the analysis of the incubation periods and the network structure could provide a reference for taking measures to control vector-borne diseases.

Acknowledgments

The authors thank the anonymous reviewers for carefully reading the manuscript and for making important suggestions and comments, thereby improving their manuscript. This research was supported by Hebei Provincial Natural Science Foundation of China under Grant No. A2016506002.

Conflict of interest

The authors declare that they have no conflict of interest.