The many behaviors of deformable active droplets

1.   Introduction

Suspensions of active particles in viscous fluids have been extensively studied and the mechanisms that give rise to the dramatic instabilities that occur in these fluids have been sought and sometimes characterized ^[1,2,3,4]. The behavior of these fluids in confined geometries is less well understood than in bulk, but basic phenomena have been explained, including the generation of vortical flows and edge currents in suspensions of motile pushers ^[5,6,7,8], the appearance of globally aligned states and traffic jams in dilute suspensions of fore-aft asymmetric swimmers ^[7], and the transition from roiling to stable flows in toroidal and racetrack geometries ^[9,10]. Such suspensions of microscopic particles that exert stresses on the surrounding fluid are commonly called "active fluids". The emergent macroscopic behavior of these fluids, which depends on the details of those microscopic particles, has been the topic of intense theoretical and experimental study over the past decade.

Although various active fluid models simulated within drops or membranes have been used as simplified mimics for crawling cells ^[11,12], especially in the thin-film geometry ^{[13,14,15,16,17]}, the basic behavior and instabilities of model active fluids confined within deforming geometries has not been fully categorized. Simulations of droplets containing active gels or liquid crystals have revealed undulatory instabilities ^[18], as well as swimming, meandering, and rotational behaviors ^[19,20,21], while linear stability analysis has identified critical activity parameters in certain geometries ^[22]. The kind of comprehensive theory required to allow parameter selection and guide experimentation, such as that developed for rigid squirmers ^[23,24,25], is still nascent.

In this work, we examine the behavior of droplets confining semi-dilute suspensions of non-motile extensile or contractile active particles. This suspension is assumed to be immiscible with an outer fluid, and confined to two dimensions, a geometry similar to several other previous studies ^[20,21]. We characterize the linear stability of such drops near an isotropic steady state to azimuthal perturbations of the nematic field. For active fluids whose microscopic constituents are extensile dipoles^*, we show that the behavior is dominated by a few low wavenumber modes, which correspond to several of the previously revealed states: an axisymmetric rotating configuration (a rotor), a motile, ballistic swimming configuration (a swimmer), and a nonmotile ellipsoidal droplet that drives an extensional flow along its axis of elongation and internal nematic alignment (an extensor). We present a detailed overview of how parameter changes alter which of these modes (or what mixture of modes) is preferred by the system. We then present the results of nonlinear simulations, when only one mode is unstable. Such droplets, initialized with low-wavenumber random perturbations, are robustly attracted to steady states qualitatively similar to the unstable eigenmodes predicted by the linear theory. When multiple modes are unstable the behavior of the droplet is more complex, and simulations reveal nontrivial time dependent trajectories, including previously observed states, such as the zigzagger and washing machine observed in ^[20], as well as other states, including wanderers, with behavior reminiscent of run-and-tumble dynamics, as well as drops with apparently chaotic behavior. We finally examine contractile fluids, which have subtly different linear stablity properties, and give rise to other novel behaviors, including swimmers with a time-dependent velocity, which we term pulsators.

^*For brevity we will refer to active fluids driven by extensile dipoles or contractile dipoles as extensile fluids and contractile fluids, respectively.

The model active fluid that we use is derived with clear assumptions and identifiable parameters that can be related, in principle, to control parameters for several widely used experimental systems, including suspensions of tripartite rods ^[26], or suspensions composed of microtubules, depletent molecules, and molecular motors ^[27,28]. These systems are well characterized, with parameters that can be tuned by adjusting ATP and depletent concentrations ^[29], or in real time by adjusting the intensity of incident light ^[30]. The results presented here provide guidance for constructing experimental systems constructed of multiple (or many) interacting active droplets, each with a rich set of accessible behaviors.

This paper is organized as follows. In Section 2 we outline a previously developed coarse-grained model for a suspension of active nematic particles ^[20], and provide an appropriate formulation for the problem studied here: an active suspension confined within a droplet. In Section 3, we show that axisymmetric configurations do not drive exterior flows when the only source of frictional dissipation is the coupling to the fluid surrounding the droplet. When a bottom drag is added a counter-rotating boundary layer appears, and an exterior flow is driven, as shown in 9. In Section 4 we analyze the linear stability of the system to azimuthal perturbations of the dipolar tensor, identifying in the extensile case three dominant modes of instability corresponding to states that we term rotors, swimmers, and extensors. In Section 5, we analyze the nonlinear dynamics for parameter sets where only one of these modes is unstable, and show that the nonlinear behavior is robustly predicted by the linear theory. We then examine active drops whose parameters yield multiple unstable modes, and show how these give rise to more complex behaviors, first for extensile fluids, in Section 6, and then for contractile fluids, in Section 7. Finally in Section 8 we conclude and discuss possible future directions.

2.   Formulation

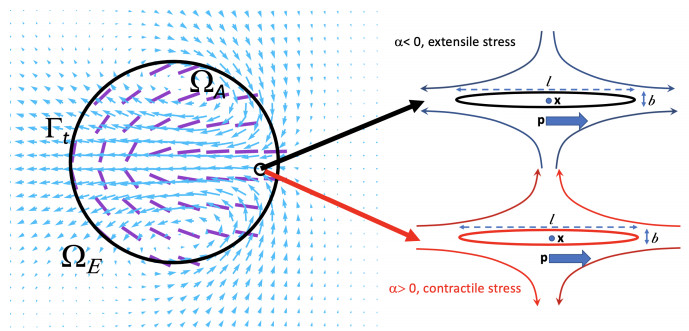
We consider a drop of active fluid immersed in a Newtonian viscous fluid, as illustrated in Figure 1. The 'active fluid' is a suspension of elongated, immotile yet mobile microscopic particles that exert dipolar stresses upon the surrounding fluid. These stresses arise from axisymmetric active extensional or contractile flows along their axis of elongation; See Figure 1. These active dipoles are confined to the domain $\Omega_A(t)$ by a deformable boundary $\Gamma_t$ which supports a surface tension. The number density of active dipoles at time $t$ with position ${\bf x}$ and orientation vector ${\bf p}$ ($|{\bf p}| = 1$; along the elongation axis) is given by $\Psi({\bf x}, {\bf p}, t)$. Its zeroth, second, and fourth orientational moments, defined respectively by the following integrals over the surface of the unit ${\bf p}$-sphere ^[31]:

arise naturally in our theory. Here $\phi$ is particle concentration, ${\bf D}$ is the unnormalized tensor order parameter, while ${\bf Q} = {\bf D}/\phi$ is the nematic tensor order parameter. For brevity, we will refer to ${\bf D}$ as the "dipolar tensor"; this tensor provides a local measure of how aligned the microscopic particles within the suspension are. In a system made dimensionless as in ^[32]†, the distribution function $\Psi$ satisfies the Fokker-Planck equation with associated conformational fluxes:

^†The system is made adimensional by rescaling on the lengthscale $b/\nu$, the characteristic velocity scale $|u_0|$ of active axial flows, and the stress scale $\mu|u_0|\nu/b$; see Table 1 for a description of parameters.

where $d_R$ and $d_T$ are non-dimensional rotational and translational diffusion coefficients. Particle alignment via steric interactions are modeled via a phenomenological Maier-Saupe theory ^[33] which introduces an effective parameter $\zeta$. The coarse-grained velocity ${\bf u}$ and pressure field $\Pi$, satisfy the Stokes equations

driven by an extra stress

This stress is composed of an active stress, $\alpha{\bf D}$, that arises due to the extensile or contractile stresses the microscopic particles exert on the fluid; constraint stress $\beta{\bf S}:{\bf E}$, arising due to particle rigidity; and steric stress $2\zeta\beta\left({\bf D}\cdot{\bf D} - {\bf S}:{\bf D}\right)$ arising due to particle-particle collisions. The activity parameter $\alpha$ is negative for extensile particles and positive for contractile particles. The constraint and steric stresses are both proportional to $\beta$, the effective volume fraction of the microscopic particles. This parameter is often taken to be $0$, giving the dilute limit, e.g., in ^[34]. Finally, ${\bf E} = (\nabla{\bf u} +{\nabla{\bf u} }^\intercal)/2$ is the symmetric strain-rate tensor. The relationship between the non-dimensional parameters $\alpha$, $\beta$, $\zeta$, $d_R$, and $d_T$, and physical parameters describing the properties of the fluid and its embedded microstructure, are given in detail in ^[32], and summarized in Tables 1 and 2.

Working with the full kinetic theory is computationally expensive, even in two spatial dimensions as $\Psi$ depends upon three independent variables (two spatial, and one orientational) plus time. Instead, we find an evolution equation for the second-moment tensor ${\bf D}$ by integrating ${{{\bf{pp}}}}$ against Eq (2.2a) over the unit ${{{\bf{p}}}}$-sphere, and making use of the conformational fluxes Eqs (2.2b) and (2.2c) ^[32] to find:

Here $d$ is the dimension of the system ($d = 2$ throughout this paper) and $\overset{\triangledown}{\bf D}$ denotes the upper-convected derivative:

with $(\nabla{\bf u})_{ij} = \partial_{x_j}{\bf u} _i$. It is a feature of this system that if $\phi$ is initially uniform it will remain so, and we will make this assumption henceforth (indeed, for nonmotile dipole suspensions, unlike motile ones, concentration fluctuations are damped ^[32]). The fact that the fourth moment tensor ${\bf S}$ arises in this necessitates a closure assumption. Here we use the Bingham closure ^[35,36], in which ${\bf S}$ is replaced by ${\bf{S}}_{B}$, defined as:

with $\Psi_B$ the Bingham distribution. This distribution takes the functional form $\Psi_B({{{\bf{x}}}}, t) = A({{{\bf{x}}}}, t)e^{B({{{\bf{x}}}}, t):{{{\bf{p}}}}{\bf p} }$, where the constant $A$ and the symmetric tensor $B$ are determined by enforcing that the zeroth and second orientational moments of $\Psi_B({{{\bf{x}}}}, t)$ are $\phi$ and ${\bf D} ({{{\bf{x}}}}, t)$, respectively.

The bulk flow and stability properties of such an active suspension are well understood (^[2,32] and references therein). In this work, we consider the dynamics of immiscible droplets of such an active fluid in an infinite bath of another viscous, Newtonian fluid as shown in Figure 1. For this enlarged system, the equations in each domain are:

where the active domain is denoted by $\Omega_A(t)$ and the complementary exterior domain is $\Omega_E(t)$. Throughout this paper, we consider the simplest case where there is no viscosity contrast between the interior and exterior fluids, except in Figure 3(a) and the associated discussion in Section 4.1. Continuity of velocity and stress balance at the drop interface gives rise to the boundary conditions

where $Ca = \mu |u_0|/\gamma_0$ is the capillary number with $\gamma_0$ the surface tension coefficient, $\kappa$ is the local curvature of $\Gamma_t$, and ${\bf n}$ is the outward unit normal. Some special cases, such as ata planar interface ^[22,37] or when the inner and outer fluids are miscible ^[38]) have been previously analyzed. The left-hand side of Eq (2.9b) gives the jump in the total stress across $\Gamma_t$, and $[\sigma_ \text{tot}]$ is given explicitly as:

where $f\big|_E$ and $f\big|_A$ denote exterior and interior (active) limits, respectively. The droplet interface $\Gamma_t$ moves with the local fluid velocity, i.e., $d {\bf X}/dt = {\bf u}\left({\bf X}\right)$ for ${\bf X}\in \Gamma_t$. A boundary condition for ${\bf D}$ can be derived by requiring that the active particle number inside the drop is conserved ($\frac{d}{dt}\int_{\Omega_A(t)}\phi({{{\bf{x}}}}, t)\, d{{{\bf{x}}}} = 0$), leading to ${\bf n} \cdot\nabla{\bf D} = 0$.

A uniform, isotropically arranged suspension within a circular droplet, having ${\bf u} = {\bf{0}}$ and $\Psi = 1/2\pi$, is easily verified to be a steady-state solution to the equations in two spatial dimensions ($\Psi = 1/4\pi$ in three spatial dimensions). For this steady state, $\phi = 1$ and ${\bf D} = \mathbb{I}/d$.

Finally, visualization of the dipolar tensor ${\bf D}$ can be challenging, especially when the nematic field is nearly isotropic. It is useful to define a scalar nematic order parameter as $2\lambda-1$, where $\lambda$ is the largest eigenvalue of ${\bf D}$. When the suspension is isotropic, this order parameter is $0$, when sharply aligned, it is 1. The dipolar tensor field ${\bf D}$ can be effectively visualized by plotting bars that align with the direction of maximal alignment (given by the eigenvector corresponding to the maximal eigenvalue), overlaid by a pseudocolor plot whose colors are determined by the scalar nematic order parameter.

3.   Behavior of rotationally symmetric drops

In two dimensions, when ${\bf D}$ and ${\bf u}$ are rotationally symmetric, active drops drive no external flow. This surprising fact can easily be verified. In the interior of the drop, momentum balance reduces to:

which has a solution $2E_{r\theta}+\sigma_{r\theta}\propto r^{-2}$. Because the stress has to be regular at the origin $r = 0$, we conclude that

To satisfy far field boundary conditions, the exterior flow must be of the form ${\bf u} = (A/r){\bf e}_\theta$, with an associated strain rate tensor $E_{r\theta} = -A/r^2$. Since tangential stresses must balance on $\Gamma_t$ (see Equation (2.9b)), we conclude that $A = 0$, and thus the exterior flow is quiescent. Note that this does not imply that the velocity ${\bf u}$ inside the droplet is zero. This is verified by nonlinear simulations, see Section 5, where the interior flow fields and dipolar tensor at steady-state are also shown.

In experiments, it has been found that bacteria inside a viscous drop induce a rotational flow both inside and outside the drop ^[8]. Although the details differ-in that experiment the underlying activity is induced by swimmers, rather than immotile dipoles-we show in 9 that friction due to the vertical confinement can give rise to both a exterior rotational flow and a counter-rotating boundary layer, as observed in ^[5,6,8].

4.   Linear stability of the isotropic state

A two-dimensional circular drop (of unperturbed radius 1) has a no-flow isotropic equilibrium with ${\bf u} _0 = {\bf{0}}$, $\Psi_0 = 1/2\pi$, ${\bf D}_0 = \mathbb{I}/2$, and $\left({\bf S}_0\right)_{ijkl} = \left(\delta_{ik}\delta_{jl}+\delta_{il}\delta_{jk}+\delta_{ij}\delta_{kl}\right)/8$. Letting the perturbed dipolar tensor, fourth-moment tensor, velocity field, and interface radius be given by ${\bf D} = {\bf D}_0 + \epsilon\bar{\bf D}$, ${\bf S} = {\bf S}_0 + \epsilon\bar{\bf S}$, ${\bf u} = {\bf u} _0+\epsilon\bar{\bf u}$, and $r(\theta) = 1+\epsilon\bar h(\theta)$, respectively, and plugging these perturbed variables into Eqs (2.3), (2.4), and (2.5) yields the following linearized evolution equations for the perturbation variables $\bar{\bf D}$ and $\bar h$:

once quadratic and higher order terms in $\epsilon$ are dropped. Here ${\bf e}_r$ is the unit radial vector and $\bar{\bf u}$ is slaved to $\bar{\bf D}$:

The terms proportional to $\beta$ in Eq (4.3) arise due to the constraint stresses and differ in constants from the linearized system in ^[32] due to the different spatial dimensionality of the respective systems. Since the dipolar tensor must be symmetric and with unit trace, the perturbation $\bar{\bf D}$ must satisfy $\sum_i \bar D_{ii} = 0$ and $\bar D_{ij} = \bar D_{ji}$. The last term on the right hand side of Eq (4.3) is the only contribution which arises due to $\bar{\bf S}$, and is rewritten in terms of $\bar{\bf D}$ via the closure-independent identity $\nabla\cdot\left(\bar{\bf S}:{\bf D}_0\right) = \nabla\cdot{\bar {\bf D}}/2$. For the remainder of the discussion of the linearized problem, we will drop the explicit bar notation for the perturbations.

Together with the associated boundary conditions for ${\bf u}$ and ${\bf D}$, Eqs (4.1)–(4.3) are converted to an eigenvalue problem by assuming that the perturbations are separable with a time dependence of $e^{\lambda t}$, where the real part of the eigenvalue $\lambda$ corresponds to the growth rate. To proceed we expand the dipolar tensor ${\bf D}$ and the streamfunction $\psi$ in Fourier series in the azimuthal angle $\theta$. For a non-negative integer $m$ the $m$th mode of the streamfunction $\psi$ is explicitly denoted as

The exterior Stokes flow is also expanded in the Fourier series ^[39], and the coefficients for each mode can be expressed in terms of the stream function, its gradient, and ${\bf D}$ evaluated on the boundary.

When $m = 0$, the velocity field is rotational, and the general solution to the eigenvalue problem associated with Eqs (4.1)–(4.3) is:

where $J_i$ is the $i$th Bessel function of the first kind. The vanishing tangential velocity at the boundary of an axisymmetric drop (see § 3) is used to derive the general solution of $\psi_0$ in Eq (4.7). Satisfying the remaining boundary condition that ${\bf e}_r\cdot\nabla{\bf D} = 0$ requires that $J_1(r_0) = J_3(r_0)$, which has multiple solutions that can be computed numerically. The smallest such solution $r_0$ corresponds to the largest eigenvalue $\lambda$, which is given explicitly by

For general non-zero values of $m$, the linear system is solved numerically by first extending the $r$ interval from $r\in[0, 1]$ to $r\in[-1, 1]$ and choosing the Chebyshev collocation points to remove the singularity at $r = 0$. Boundary conditions are enforced using tau-correction ^[40] and parity conditions ^[41] are used to filter for physically admissible eigenvector/eigenvalue pairs.

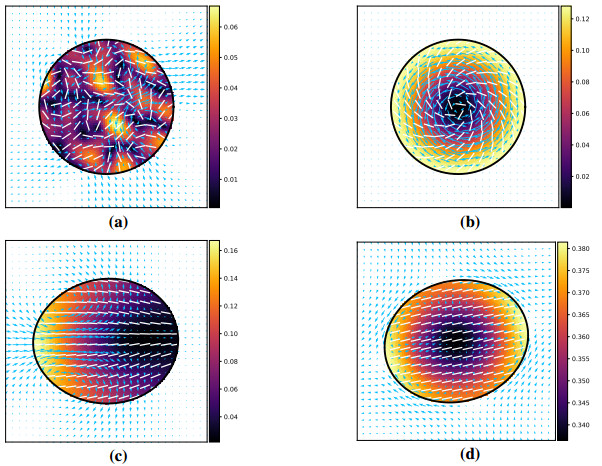
The choice to expand ${\bf D}$ and $\psi$ in Fourier series in the azimuthal angle is not arbitrary: the associated modes correspond to simple behaviors of the active droplet system. To demonstrate this, we choose one set of parameters: $\alpha = -4$, $\beta = 0.2$, $\zeta = 0.1$, $d_T = 0.1$, $d_R = 0.1$, and $Ca = 1$. In Figure 2, we show the flow field constructed from the eigenfunctions for the $m = 0$, $m = 1$, and $m = 2$ modes (panels (a), (b), and (c), respectively). For the $m = 0$ mode (the rotor), the interior flow is axisymmetric and the exterior flow is quiescent, consistent with the proof in 3 (as is must be). For the $m = 1$ mode (the swimmer), the drop translates at a constant velocity, and the interior flow is dipolar in the co-moving frame. For the $m = 2$ mode (the extensor), the drop is stationary, with an interior quadrupolar flow corresponding to an exterior extensional flow coaligned with the axis of nematic alignment.

4.1.   Extensile systems ($\alpha < 0$)

We first examine the behavior of drops that confine an extensile active fluid (i.e., $\alpha < 0$)^‡. Changes in parameter values can alter not just the linear growth rates of different angular modes, but which of those modes are dominant. To illustrate these effects, we examine the growth rates as a function of angular wave number $m$ for several choices of parameters in Figure 3. In panel (a), we alter the viscosity contrast $\overline\mu$, holding all other parameters fixed. The most unstable mode switches from $m = 0$ when the viscosity contrast is neutral ($\overline\mu = 1$) to $m = 1$ when the viscosity contrast is lowered to $\overline\mu = 0.005$ (that is, the solvent viscosity inside the drop is two hundred times more viscous than the viscosity of the exterior fluid). We note that in all other results presented throughout this paper, $\overline\mu$ will be fixed to $1$. In panel (b), we alter the capillary number, again holding all other parameters fixed. When $Ca = 0.1$, the surface tension is high (surface tension is given by $Ca^{-1}$), and the $m = 0, \ 1$, and $2$ modes have nearly equal growth rates. When the surface tension is decreased so that $Ca = 1$, the extensor mode ($m = 2$) becomes dominant over the $m = 0$ and $m = 1$ modes. This result is physically intuitive: the flows created by the extensor mode generate surface deformation (see Figure 2c), thus this mode is damped relative to the other modes as the surface tension (capillary number) is increased (decreased).

^‡Note that this does not imply that the behavior of the drop is extensile, although it may be: the flow fields shown in Figure 2 all correspond to a droplet that confines an extensile fluid, yet only the flow field associated with the $m = 2$ mode is extensile.

As we will show in Sections 5 and 6, the mixture of dominant linear modes is predictive of the full nonlinear behavior of droplets. As this non-dimensional system has seven parameters ($\alpha$, $\beta$, $\zeta$, $d_T$, $d_R$, $Ca$, and $\overline\mu$), a full parameter sweep, while computationally feasible, is impossible to present. Instead, we focus on understanding how the behavior changes as a function of several important parameters. In Section 4.1.1, we vary the activity parameter $\alpha$ and the Maier-Saupe parameter $\zeta$ that governs how strongly the microstructure aligns itself in the absence of flow, and in Section 4.1.2, we examine the behavior as the rotational and translational diffusion $d_R$ and $d_T$ are varied.

4.1.1.   Distribution of unstable modes in the $(\alpha, \zeta)$ plane

Analysis of the behavior of this system is complicated by the fact that for many parameter choices, multiple linear modes are unstable. This leads to rich behaviors, as we shall see in Section 6, when we examine the behavior of the full nonlinear system in such mixed-mode regimes, yet it makes extracting information from the linear theory complicated. The simplest analysis is to examine the dominant mode, i.e., the linearly unstable mode that is largest.

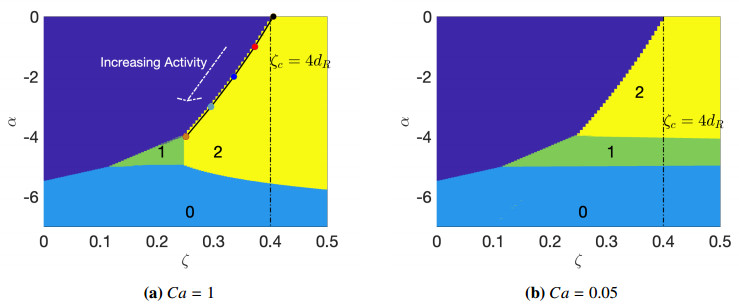
Figure 4 shows the dominant mode, as a function of $\alpha$ and $\zeta$, when $d_T = d_R = 0.1$ and $\beta = 1$, for two different capillary numbers: $Ca = 1$ in panel (a), and $Ca = 0.05$ in panel (b). The isotropic homogeneous steady base state is linearly stable in the purple region (at the top left of both panels). The dash-dotted line shows the critical value of $\zeta_c = 4d_R$ that corresponds to the isotropic-nematic transition of the homogeneous base state in a bulk fluid. The isotropic state is stable when $\zeta/d_R < 4$; a nematically aligned state is stable when $\zeta/d_R > 4$, see ^[32]. Regions of the phase space where the growth rate associated with the $m = 0$ (rotor) mode is positive and larger than the growth rate associated with any other mode are shown in blue, regions defined analogously for the $m = 1$ (swimmer) and $m = 2$ (extensor) modes are shown in green and yellow, respectively.

The nematic field associated with the extensor mode is typically well aligned, with a large scalar order parameter, similar to the nematic state in bulk fluids when $\zeta/d_R > 4$. It is thus unsurprising that this mode is dominant in the region where $\alpha$ is relatively small and $\zeta$ is sufficiently large to destabilize the isotropic state, i.e., the upper right corner in both panels. In fact, when $\alpha = 0$, the stability boundary in these drops agrees exactly with the bulk theory. As the extensile activity level increases ($\alpha$ becomes more negative), flow-driven alignment provides an additional mechanism for instability, and the boundary that delineates dominance of the extensor mode shifts left. Continuing to increase the activity level leads to an instability in the aligned nematic field (see Section 5), typically with the appearance of a defect which breaks symmetry and leads to the dominance of the $m = 1$ (swimmer) mode. As activity is further increased, a stable, symmetric defect located at the center of the drop is most preferential, and the $m = 0$ (rotor) mode becomes dominant. The boundary that separates where the region where the homogeneous state is stable and those regions where only the $m = 0$ and $m = 1$ modes are unstable is unaffected by the {c}apillary number, as these modes do not deform the interface. Instead, the primary affect of decreasing $Ca$ (increasing the surface tension) is to desensitize the modal distribution to $\zeta$.

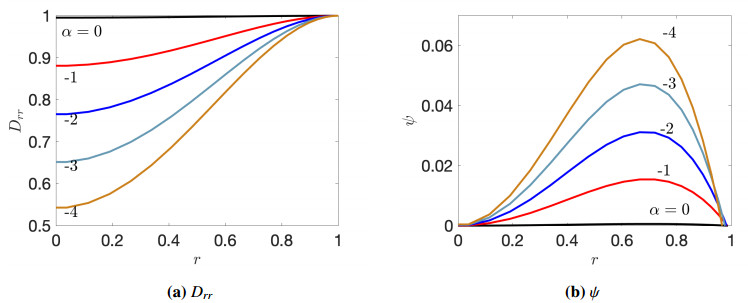
Figure 5 shows how the eigenfunctions depend on the level of activity ($\alpha$) and nematic parameter ($\zeta$) along the thin line with symbols in Figure 4(a) that separates the region where the homogeneous state is stable and the region where the extensor mode is unstable and dominant. The growth rate is $\approx0.012$ at each location marked with a colored circle, all of which lie just inside the region where the extensor mode is dominant. The eigenfunctions are scaled so that the maximum of $D_{rr}$ is unity for different parameters. The perturbation to $D_{rr}$, along with its corresponding streamfunction, are shown in Figure 5(a) and (b), respectively. The magnitude of the streamfunction increases with the activity level, as expected, since the active stress scales with $\alpha$. As the active flows strengthen, so too does the corresponding spatial inhomogeneity in the nematic field $D_{rr}$.

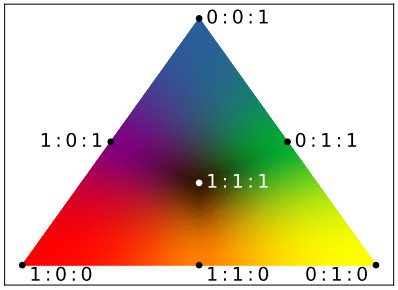
The analysis presented thus far looks only at which mode is most dominant. While useful, this doesn't tell the whole story: information regarding the relative importance of modes when more than one mode is active is lost. We now introduce a way to visualize the mixture of active modes for a given set of parameters. We first observe that in Figure 4, there are only four regions: those dominated by the rotor, swimmer, and extensor modes, and the region where no mode is unstable. In fact, this is the case for all parameter values that we have examined (but it is not true for contractile systems, where there are regions in which the $m = 3$ mode is dominant, see 4.2). First, define the growth rate associated with a given mode to be $r_k$, for $k = 0$, $1$, and $2$, and define $\overline r$ to be the maximum over $k$, i.e.. $\overline r = \max\{r_0, r_1, r_2, \ldots\}$. When $\overline r > 0$, we may then define $s_k = r_k/\overline r$. We then let $s_0$, $s_1$, and $s_2$ define the channels in a red/yellow/blue colorspace, respectively. Points in the parameter space with only the rotor ($m = 0$) mode unstable appear purely red, points with only the swimmer ($m = 1$) mode unstable appear purely yellow, and points with only the extensor ($m = 2$) mode unstable appear purely blue. Points with mixed active modes are represented by intermediate colors, accordingly. Points where the homogeneous state is stable are shown in white. A reference triangle is shown in Figure 6 which can be used to help interperet these visualizations.

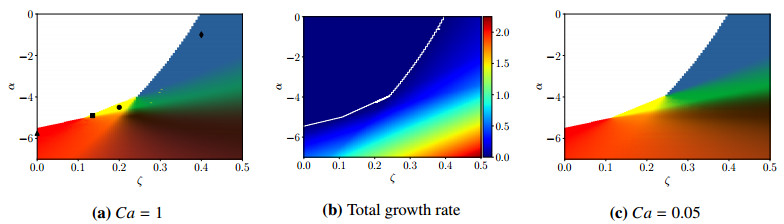
In panels (a) and (c) of Figure 7, we show the same plots as in Figure 4, but in the color scheme as described above and shown in the reference triangle in Figure 6. As is clear now, it is relatively rare for only one mode to be active, with these "pure" modes clustered near the stability boundary. As the system moves further away from the region of stability, multiple modes tend to mix, with the rotor mode predominant when the fluid is highly active and the extensor mode predominant when the fluid is less active and when the microstructure tends to self-align even in the absence of flow (large $\zeta$). When both $\alpha$ and $\zeta$ are large, all three modes are active^§ (and relatively equally mixed), which results in complex dynamics, as we shall see in Section 6. Reducing the capillary number (increasing the surface tension) should damp the extensor mode, and indeed leads to mixtures of active modes which are more heavily weighted to the rotor and swimmer modes across the phase space. In panel (b), we show the total growth rate across the first three modes (i.e., $\sum_{k = 0}^2 r_k$) associated with the phase space shown in panel (a). Near the stability boundary where pure modes arise, growth rates are typically far lower than in the regions where mixed modes arise.

^§Indeed, higher-order modes than the $m = 0$, $m = 1$, and $m = 2$ modes may also be active, although these never dominate the dynamics.

4.1.2.   Distribution of dominant unstable modes in $(d_R, d_T)$ plane

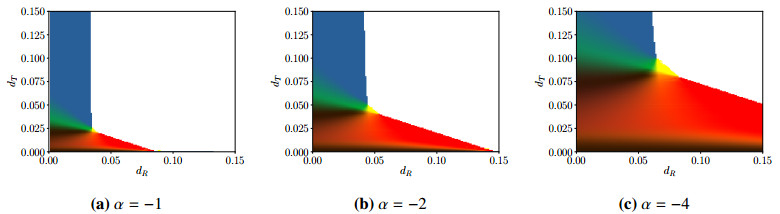
We now examine the effect of both spatial and rotational diffusivity on the stability of the system. Figure 8 shows how the mixture of unstable modes changes as a function of $d_R$ and $d_T$, for three different values of the activity parameter $\alpha$, with $\alpha = -1$, $-2$, and $-4$ in panels (a), (b), and (c) respectively. In all panels, $\beta = 0.2$, $\zeta = 0.1$, and $Ca = 1$. As expected, increasing the activity parameter $\alpha$ destabilizes the system across the board, but perhaps surprisingly, the mixture of dominant modes shifts across the $(d_R, d_T)$ plane with little change in its shape or composition. Again, the region where pure modes dominate lies near the stability boundary, while mixed modes persist away from the boundary. The rotor mode dominates when translational diffusion is small but rotational diffusion is large, and the extensor mode dominates the opposite limit, when translational diffusion is large and rotational diffusion is small. The swimmer mode again dominates in only a small region of parameter space, where the translational and rotational diffusivities are similar in scale. When both diffusion coefficients are small, multiple modes of the system are active, with the exact balance dependent on the ratio of $d_R$ to $d_T$.

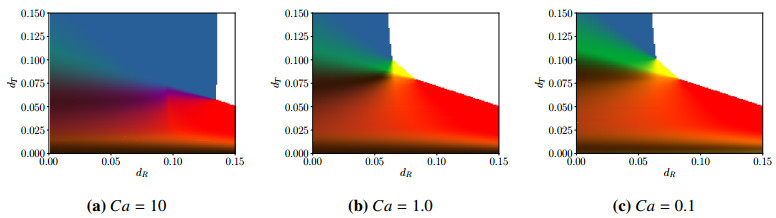
Results in Figure 8 are for a fixed capillary number $Ca = 1$, with the activity parameter $\alpha$ varying across panels. In Figure 9, we hold the activity parameter constant at $\alpha = -4$, and show how the distribution of unstable modes changes as the surface tension is varied: in panel (a), $Ca = 10$, in panel (b) $Ca = 1$, and in panel (c) $Ca = 0.01$. Recall that the capillary number $Ca$ is inversely proportional to the surface tension, so that the surface tension in panel (c) is 1000 times higher than the surface tension in panel (a). In all panels, $\beta = 0.2$ and $\zeta = 0.1$. Since $\zeta = 0.1$, the isotropic to nematic transition in the bulk fluid occurs when $d_R\leq \zeta/4 = 0.025$. As the activity level is strong, we see that the extensor state persists to higher values of $d_R$, significantly so when the surface tension is weak. As the surface tension is increased, the extensor mode is damped, with reduction of the blue hue across much of the plane. In particular, the portion of the plane where the swimmer mode dominates (or where the swimmer and extensor mode are well mixed) increases in size. Little change occurs outside of the region where $d_T$ is large and $d_R$ is small, as the extensor mode is irrelevant regardless of the surface tension.

4.2.   Contractile system $\alpha > 0$

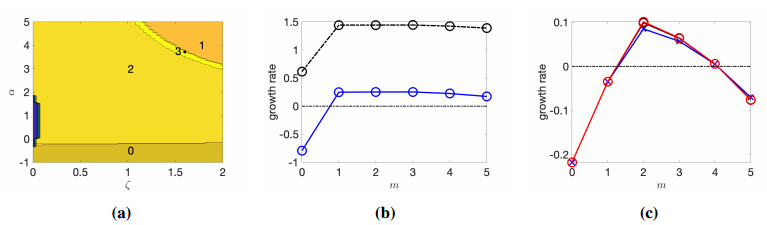
We now examine the linear stability of the isotropic state in the contractile case where $\alpha > 0$. In figure 10(a) we show the dominant mode over the ($\zeta$, $\alpha$) plane for $\beta = 0.1$, $d_T = 0.005$, $d_R = 0.01$, and $Ca = 0.1$. Unlike the extensile system, where only the $m = 0$, $1$, and $2$ modes dominate over the ranges of parameters we have investigated, we find that the $m = 3$ mode can be the most unstable mode in a contractile system, albeit in a relatively small region of the phase space. Figure 10(b) shows two parameter combinations where the $m = 3$ mode is most unstable; the black dash-dotted curve corresponds to the black dot in panel (a).

Figure 10(c) shows the effect of surface tension on the growth rate when $\alpha = 1.0$, $\beta = 0.1$, $\zeta = 0.2$, $d_T = 0.01$ and $d_R = 0.02$. As expected, the growth rate for the $m = 0$ and $m = 1$ modes does not depend on $Ca$, since they do not perturb the interface. As surface tension increases ($Ca$ decreases from $Ca = 1$ to $Ca = 0.1$ and $Ca = 0.01$), the growth rate at $m = 2, 3, 4$ increases slightly. The direction of the dependence between the growth rate for modes $m\geq2$ and the capillary number is opposite to that which exists for the extensile system, where the growth rate decreases with decreasing $Ca$ for $m\ge 2$.

5.   Nonlinear dynamics of pure modes in an extensile drop

In this section we examine the behavior of the full non-linear system for "pure-mode" extensile droplets, that is, for droplets with parameter combinations for which the linear theory predicts that only one azimuthal mode is unstable. Parameter sets are selected from Figure 7(a) by choosing values of $\alpha$ and $\zeta$ that lie within regions where one of the modes is clearly dominant (the solidly red, yellow, and blue regions, for rotor, swimmer, and extensor modes, respectively), and each parameter location is marked on Figure 7(a). To be precise, we let $\beta = 0.2$, $d_R = 0.1$, $d_T = 0.1$, and $Ca = 1.0$, and vary $\alpha$ and $\beta$: for $m = 0$, $\alpha = -1.0$, $\zeta = 0.0$, marked with a $\blacktriangle$; for $m = 1$, $\alpha = -4.5$, $\zeta = 0.2$, marked with a ●; and for $m = 2$, $\alpha = -1.0$, $\zeta = 0.4$, marked with a $\blacklozenge$. The linear growth rates predicted for these sets of parameters are shown in Figure 11. For all simulations, the initial configuration at $t = 0$ is the same small, low wave-number perturbation of the homogeneous state, shown in panel (a) of Figure 12. The steady-state for each droplet is shown in Figure 12(b–d). The blue arrows indicate the velocity field. The white bars inside the drop denote the orientation of the dipole field. The contours are for the scalar order parameter, the difference between the maximum and minimum of the two eigenvalues of ${\bf D}$. Defined as such, the scalar order parameter is between zero and one. A topological defect is associated with scalar order parameter equal (or close) to zero, where there is not a well-defined dipolar orientation.

The rotor, with only the $m = 0$ mode unstable, shown in panel (b), has nematic and flow fields qualitatively similar to those predicted by the linear theory for $m = 0$ instabilities (see Figure 2)^¶. As in the linear eigenmode, the boundary remains perfectly circular, and the exterior fluid is quiescent up to numerical discretization error (see Section 4). The swimmer, with only the $m = 1$ mode unstable, shown in panel (c), drives an interior dipolar flow, and indeed translates at a constant velocity through the fluid. Because the initial data is random, so is the ultimate swimming direction. Note that this swimmer does not have an interior defect, unlike the eigenfunction shown in Figure 2. This is typical of swimmers whose $m = 2$ mode is less strongly damped, which tend to be elongated along their swimming axis. Changing the parameters slightly to $\alpha = -4.9$ and $\zeta = 0.135$ yields a swimmer with subtly different behavior. This parameter set is marked on Figure 7(a) with a $\blacksquare$, and the linear growth rates are shown as the dashed yellow curve in Figure 11. When swimmers' $m = 2$ modes are more strongly damped, as this one is, interior defects are typical, and the swimmer acquires a teardrop shape, wider along its leading than its trailing edge. Finally, the extensor, with only the $m = 2$ mode unstable, shown in panel (d), drives a quadrupolar flow in its interior, and a far-field dipolar flow that is extensile along the drops axis of elongation, as suggested by the linear theory. Boundary deformation is pronounced, and becoming more so if $\alpha$ is increased, although increasing $\alpha$ sufficiently, while holding all other parameters fixed, will also excite the $m = 1$ mode.

^¶Note that the parameters used for the simulations shown in Figure 12 are not the same as those that were used when computing the eigenfunctions shown in Figure 2. Nevertheless, $m = 0$, $m = 1$, and $m = 2$ modes are typically similar in nature.

For each of the pure-mode droplets, the qualitative steady-state behavior is predicted by the linear theory, even when initial data is random. Although exceptions exist close to the boundaries that delineate pure-mode regions from regions where multiple modes are active, parameter combinations that yield only one unstable mode typically act as robust attractors to steady, nonlinear states whose qualitative behavior is a rotator, swimmer, or extensor, for parameters whose unstable mode is $m = 0$, $m = 1$, and $m = 2$, respectively.

6.   Nonlinear dynamics of mixed modes in an extensile drop ($\alpha < 0$)

Although parameter regimes with pure modes do exist, they are somewhat atypical and dominate the dynamics only near the stability boundary. Farther from this boundary, multiple modes are typically active, and the dynamics of the nonlinear system are more complicated, with behavior that cannot be so simply classified as in Section 5. In this section, we catalogue some of the many behaviors that can emerge when multiple modes are active. We first examine in detail particular combinations of modes: in Section 6.1, the case where the swimmer and extensor modes dominate; in Section 6.2 the case where the rotor and extensor modes dominate; and in Section 6.3 the case where the rotor and swimmer modes dominate.

To further aid in understanding the droplet behavior, we define two additional quantities. The first of these is the drop deformation number, which characterizes how deformed the boundary is, and is defined as $d = (L-S)/(L+S)$, where $L$ and $S$ are the longest and shortest distances, respectively, between the drop boundary $\Gamma_t$ and the droplet center $|\Gamma_t|^{-1}\int_{\Gamma_t}{\bf X}(s)\, ds$. The second is the absolute Fourier amplitude $|P_m|$ of the vorticity, where $P_m = \widehat{\omega}_m$, the discrete Fourier transform of the interior limit of the fluid vorticity evaluated at the boundary. This quantity is used to characterize the internal behavior of the droplet as a function of time, and for the linear eigenstates (such as those shown in Figure 2), $|P_m|$ is nonzero only for the associated eigenmode.

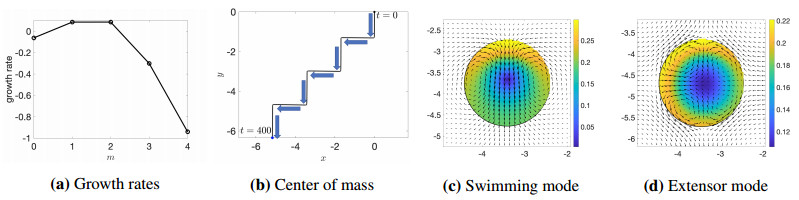
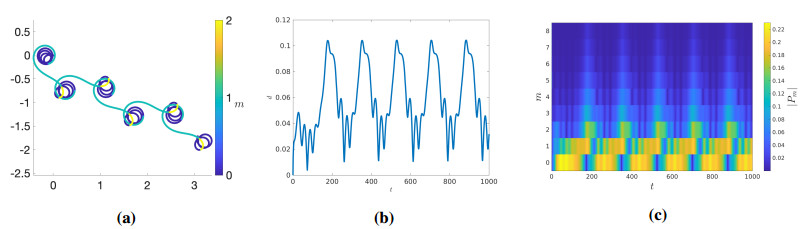
6.1.   Zigzaggers: $m=1$ and $m=2$

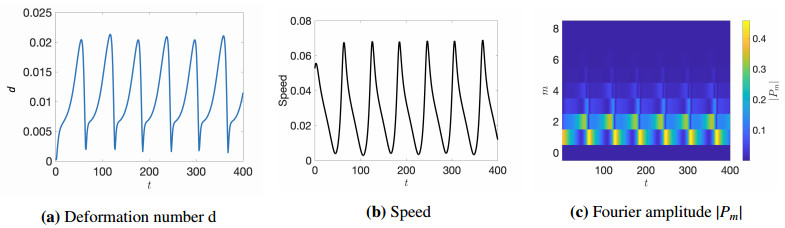
To examine the nonlinear coupling between multiple unstable modes we simulate the long-time dynamics of a drop that the linear theory predicts will have only the azimuthal modes $m = 1$ and $m = 2$ unstable, with parameter values $(\alpha, \beta, \zeta, d_T, d_R, Ca) = (-4, 1, 0.56, 0.1, 0.16, 0.1)$). The linear growth rates of the associated eigenfunctions are plotted in Figure 13(a) as a function of the azimuthal wavenumber $m$. For this set of parameters the growth rates of the two unstable $m = 1$ and $m = 2$ modes are very nearly identical. For initial conditions, we choose the $m = 1$ eigenfunction, seeded as a small perturbation to the isotropic case. The position of the center of mass of the droplet is shown in Figure 13(b). As this perturbation grows, the drop begins to swim in a constant direction, much as the $m = 1$ drop discussed in Section 5. Initially, this motion is in the $-\hat y$ direction, dictated by the initial condition. The scalar order parameter and associated flow field associated with this configuration are shown in Figure 13(c). As time progresses, the drop slows, and stops, elongating along the axis it was once swimming along, and appears qualitatively similar to the pure $m = 2$ mode droplet shown in Figure 12(d), but with pronounced asymmetry; see Figure 13(d). As the droplet continues to elongate, a defect appears, and the droplet transitions back toward the $m = 1$ state with motion now in the $-\hat x$ direction. This swim-elongate-turn-swim pattern continues indefinitely.

The drop deformation number and center of mass speed are shown in Figure 14(a) and (b), and show a periodic behavior. The seeded $m = 1$ mode induces a translational mode, with motion that slows as the $m = 2$ mode begins to dominate. When the drop deformation reaches its peak, the drop speed reaches a minimum and we observe that the $m = 2$ mode is maximized in the absolute Fourier amplitude ($|P_m|$) of the fluid vorticity along the interface, shown in Figure 13(c). As the drop comes to a nearly full stop, the $m = 1$ mode begins to grow again and the drop moves in the orthogonal direction as shown in Figure 14(c). Initializing the simulation with a small, low-wavenumber perturbation to ${\bf D}$ (as in Figure 12(a)), with the resultant direction of the zigzag pattern in a random direction.

Such meandering behavior of an active drop is also reported by Gao & Li ^[20] (red curve in their Figure 4(a)), although the underlying mechanisms for such dynamics are not reported. We propose that this state appears when the $m = 1$ and $m = 2$ modes are the only linearly unstable modes (or at least, are highly dominant among unstable modes), and the meandering behavior is driven by the periodic transitioning between these two modes.

6.2.   Washing machines: $m=0$ and $m=2$

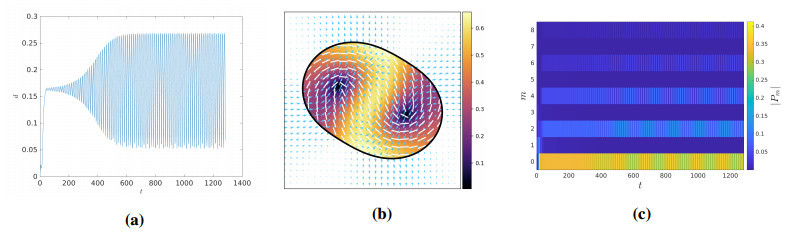
Gao and Li also reported a rotating active drop with two topological defects that circle around each other, inducing a vortical flow inside the drop ^[20]. These drops do not translate as they rotate and deform (wobble), much like an unbalanced washing machine during its spin-cycle, and we will henceforth refer to these kinds of droplets as washing machines. As the primary behavior of such a drop is rotational, but with an elliptical boundary deformation and well-aligned structure reminiscent of extensors, we expect we may find such a mode by locating regions where the $m = 0$ and $m = 2$ modes are most dominant. No such state exists when the drop is small and the capillary number is small, as in Figure 8(a). As the capillary number or droplet size increase, such states appear, see for example purple regions in Figure 9(a). Here we let $\alpha = -2.4$, $\beta = 0.2$, $\zeta = 0.123$, $d_T = d_R = 0.05$, $Ca = 1$, but with a larger drop radius: $r = 1.75$. At these parameter values, the drop initially attempts to form a steady rotor, but the central defect splits into two defects that circle around each other, as shown in Figure 15(b), at $t = 200$. This configuration induces an internal vortical flow, and drives rotation of the droplet. Although the droplet behavior is primarily rotational, the exterior flow is not quiescent, as it is for pure rotors. Shortly after the defect splits, the boundary is nearly stable, even as the defects orbit each other. As time progresses, the droplet undergoes successive cycles of increasing and decreasing deformation, shown in Figure 15(a). As the droplet elongates, its rotation rate begins to increase, and then as the rotation further increases, the elongation relaxes, repeating in sequence as can be seen in the modal decomposition shown in Figure 15(c).

When $r = 1$ and the fluid parameters are $\alpha = -5.5$, $\beta = 1$, $\zeta = 1.5$, $d_T = 0.11$, $d_R = 0.08$ and $Ca = 1$, many azimuthal modes are unstable, with the $m = 2$ mode the most unstable, as shown in Figure 16. Simulations with these parameter values that are initialized with random initial data do not tend towards washing machine behavior. However, when initialized from the $m = 0$ eigenmode, the washing-machine dynamics develop. In this case the droplet tends towards a steady conformation, with a boundary deformation that is independent of time, as shown in Figure 16(b). After $t\approx 60$, the drop remains in this quasi-steady state, rotating at a constant angular velocity as the internal defects orbit each other. Although the $m = 1$ and $m = 2$ modes both have higher growth rates than the $m = 0$ mode, the modal decomposition shown in Figure 16(c) clearly shows the $m = 0$ mode dominating, with some power in the $m = 2$ (and higher harmonics), but none in the $m = 1$ mode. Although this does state does not appear robustly at these parameters, it illustrates how in this complex system, certain preparations or perturbations may lead to quasi-stable nonlinear dynamics not immediately apparent from analyzing the linear theory.

6.3.   Wanderers: $m=0$ and $m=1$

Flagellated bacteria, such as Escherichia coli, conduct random walks via a run-and-tumble mechanism ^[42]: they 'run' in relatively straight lines when their flagella are bundled together, and 'tumble', randomly reorienting their bodies and the consequent direction of their next run, when their flagella rotate separately. Here, we ask if we can mimic these dynamics by having droplets that transition between the $m = 0$ mode, where they reorient themselves (i.e., 'tumble') and the $m = 1$ mode, where they swim ballistically (i.e., 'run').

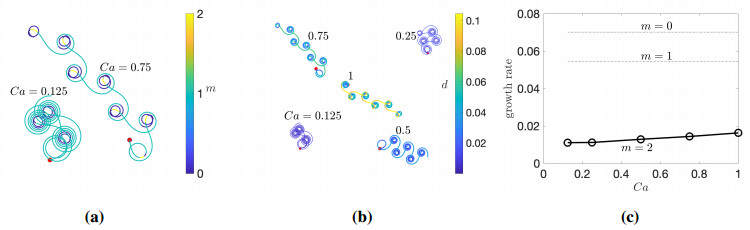
To explore this, we first choose parameters for which the rotor and swimmer modes dominate the linear behavior: $\alpha = -2.6$, $\beta = 0.2$, $\zeta = 0.1$, $d_R = 0.05$, $d_T = 0.05$, and $Ca = 1$. The linear growth rates are shown in Figure 18(c); although the extensor mode is unstable, the rotor and swimmer modes have substantially larger growth rates. Figure 17(a) shows the trajectory of the droplet center color-coded by dominant mode – that is, the value of $m$ that maximizes $|P_m|$. The drop periodically transitions between a tumbling behavior, where it primarily rotates with small center-of mass motion, similar to the $m = 0$ rotor, and a running behavior, where it moves nearly ballistically, before again tumbling. The droplet deformation as a function of time is shown in Figure 17(b). During the tumbling phase, where the droplet is dominated by the rotor mode, the drop deformation number is small. As the drop transitions to the swimmer mode, the deformation grows, and the drop briefly becomes dominated by the extensor mode as it transitions from the run phase back to the tumbling phase. Such alternating dynamics between running and tumbling shown in Figure 17(a) correlate with the oscillation in deformation shown in panel (b) and the magnitude of the vorticity spectra along the interface shown in panel (c), where we clearly observe a particular repetition of dominant modes: $0\rightarrow 1\rightarrow 2 \rightarrow 0\rightarrow 1 \rightarrow 2$, etc.

Since the drop deformation number increases as the drop transitions into the run mode, we hypothesize that we can control the relative importance of the run vs. the tumble states by varying the capillary number. In Figure 18, we show the trajectories from several different simulations, at all the same parameter values as for the simulation shown in Figure 17. Panel (a) shows close-up trajectories for two different cases, colored by the dominant mode, while panel (b) shows trajectories for a wider set of cases, colored by the deformation. When the capillary number is smallest, the drop deformation stays small, runs are short, and the drop never transitions, even briefly, into the extensor mode. As the capillary number is increased, drop deformation also increases, and the drop spends a greater percentage of time in the run phase before tumbling. Panel (c) shows the growth rates at each different capillary number. The growth rates for the rotor and swimmer modes, shown as dashed horizontal lines, are unaffected by the capillary number since these modes do not deform the surface at linear order. As the capillary number is increased, the growth rate for the extensor mode increases significantly, by {47}% from $Ca = 0.125$ to $Ca = 1$, although it stays significantly smaller than either the rotor or swimmer modes.

The type of motion observed here is not run-and-tumble, but rather a deterministic analog, producing a motion closer to the zigzagger (albeit through a different mechanism) than the more familiar chaotic trajectories of run-and-tumble swimmers, in which randomness occurs due both to a non-deterministic tumbling process as well as variations in the length of runs. One possible source of randomness could come from thermal fluctuations in the underlying active particles, which could lead to variations in the tumbling rate (and hence run direction), as well as run length and velocity. The methods used throughout this paper do not lend themselves to studying this. Instead, we search parameters near to the run-and-tumble state shown in Figure 17 to find parameter combinations that yield seemingly chaotic behavior. One such parameter combination is $\alpha = -2.9$, $\zeta = 0.12$, $\beta = 0.2$, $d_R = 0.05$, $d_T = 0.05$, and $Ca = 1.0$. The center of mass trajectory is shown in Figure 19. For this simulation, the direction of the swimmer following tumbles is no longer deterministic, but the run length is constant, or nearly so (in contrast to traditional run-and-tumble dynamics).

6.4.   Nonlinear behavior over the $(\alpha, \zeta)$ plane

Having isolated a rich (but certainly non-exhaustive) set of behaviors that an extensile active drop can take, we now sweep over the ($\alpha$, $\zeta$) plane and classify the qualitative behavior for full nonlinear simulations across a wide range of parameters. Here $\beta = 0.2$, $d_R = 0.05$, $d_T = 0.05$, and $Ca = 1.0$, and the initial data is a small-amplitude and low wave-number perturbation to the isotropic steady state. The results of this sweep are shown in Figure 20, where white and red markers indicating the behavior of the nonlinear simulation are superimposed over the predictions made by the linear theory. In the lower left corner, where $\alpha$ is large and $\zeta$ is small, the $m = 0$ mode is predicted to dominate the modal distribution, and simulations converge to steady state rotors, qualitatively similar to the drop shown in Figure 12(b). As $\zeta$ is increased, $m = 1$ modes mix with the $m = 0$ modes, and the steady rotors transition to wanderers (denoted with solid circles), qualitatively similar to the drops explored in Section 6.3 which have run-and-tumble like dynamics. In the upper right corner, where $\alpha$ is small and $\zeta$ is large, the extensional $m = 2$ mode dominates, and simulations converge to steady extensors, denoted with open ellipses. As the activity level is increased, the droplets instead converge to zigzaggers, qualitatively similar to the behavior of drops examined in Section 6.1. When the activity is moderate and $\zeta$ is large, all modes mix equally (in the darkest region of the phase space). Here we observe dynamics that are qualitatively similar to wanderers, but whose behavior appears to be chaotic, rather than periodic or quasiperiodic, denoted with red squares.

6.5.   Design principles for extensile droplets

Combining the results of our linear theory and nonlinear simulations leads to relatively simple set of design principles for constructing active extensile droplets with a desired qualitative behavior. The easiest droplets to produce are pure rotors or pure extensors. Pure rotors are found at high activity ($\alpha$), low alignment $(\zeta)$, where rotational ($d_R)$ diffusion is large and translational diffusion $(d_T)$ is low. Pure extensors are found in the opposite regime: low $\alpha$, high $\zeta$, low $d_R$, and high $d_T$. Swimmer modes are found when these parameters are all moderate, but care is required to locate parameter regimes that yield steady ballistic swimmers. Drops with higher surface tension yield larger regions where these swimmers can be found, while drops with lower surface tension are more dominated the rotor and extensor modes. Mixed-mode swimmers, whether they are zigzaggers (when rotor and extensor modes mix) or wanderers (when rotor and swimmer modes mix) are found across much of the phase space, and parameters which yield specific mixtures can be predicted directly from the linear theory.

7.   Nonlinear dynamics in a contractile drop ($\alpha > 0$)

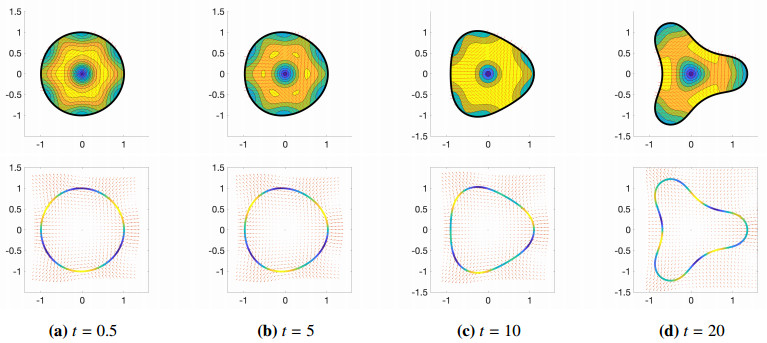
In Section 4.2 we analyzed the linear stability of azimuthal perturbations to the homogeneous, isotropic steady state for contractile drops ($\alpha > 0)$, and showed that the $m = 3$ mode can be the dominant unstable mode. It may be possible that this can occur for extensile systems, although we have not observed such a case over the parameter ranges that we have explored. The dynamics of such a droplet, with $\alpha = 4.8$, $\beta = 0.1$, $\zeta = 0.5$, $d_T = 0.01$, $d_R = 0.005$ and $Ca = 1$ are shown in Figure 21. The growth rates associated with this set of parameters, as a function of azimuthal wavenumber $m$, are shown as the blue curve in Figure 10(b); many modes are unstable, with the $m = 1$, $2$, and $3$ modes nearly equally mixed and the growth rate associated with the $m = 3$ mode the largest. The initial condition for the dipolar tensor is the uniform isotropic state with a small perturbation given by the $m = 3$ eigenmode. The drop quickly develops a topological defect at its center where the scalar order parameter is nearly zero. As time progresses the drop deforms into a three-lobed shape with flow aligned orthogonal to the dipolar orientation inside each lobe as shown in Figure 21.

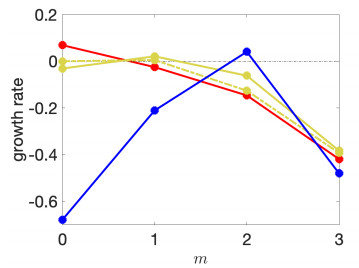
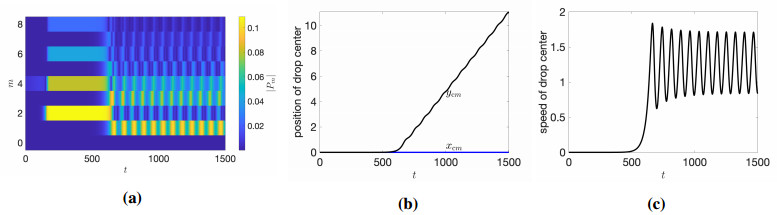
In Section 6, we saw that when extensile drops which had multiple unstable modes were seeded with initial data that was a small perturbation to the isotropic steady state, whether random or given by an eigenmode that is not the fast growing mode, the drop typically exhibits complex, time-dependent dynamics due to the nonlinear coupling between the different unstable modes. This is true of contractile droplets, as well. A novel behavior that we have not observed in an extensile drop is a pulsating swimmer, or pulsator, which occurs when $\alpha = 1$, $\beta = 0.1$, $\zeta = 0.2$, $d_T = 0.01$, $d_R = 0.02$ and $Ca = 1$. The growth rates for this system are shown as the blue solid curve in Figure 10(c). Only the $m = 2$, $m = 3$, and $m = 4$ modes are unstable, with the $m = 2$ and $m = 3$ modes having by far the largest growth rates. The initial condition for the dipolar tensor is an isotropic tensor, with a small perturbation given by the $m = 4$ eigenmode. The contractile drop shape initially evolves towards an ellipse that corresponds to the most unstable ($m = 2$) mode. In Figure 22(a) we show the spectrum of the boundary vorticity as a function of time, which is dominated by the $m = 2$ (and other even modes) from $t\sim 50$ to $t\sim 600$.

At $t\approx600$, odd modes begin to grow, and thereafter the spectrum alternates periodically in time between even and odd modes, with significant energy in the $m = 1$ mode (despite the fact that this mode is not linearly unstable). As with extensile droplets, the $m = 1$ mode is characterized by translation of the drop, and indeed the drop begins to swim along the $y$-axis after the onset of this oscillation. The position of the center of mass of the drop is shown in Figure 22(b), and the drop speed is shown in (c). After translational motion begins, the swimming speed oscillates steadily as a function of time, and the drop pulses forward as it moves.

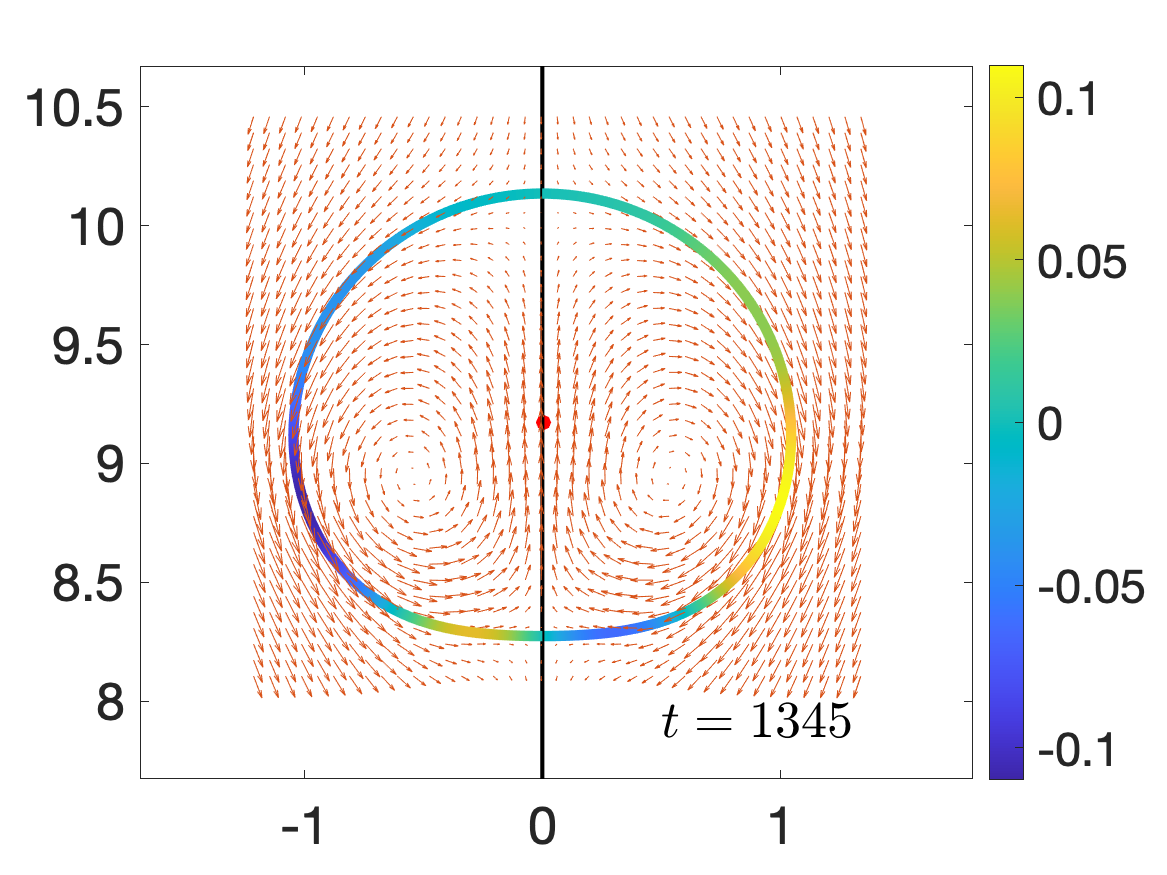
In Figure 23(a), we show the flow field in the co-moving frame of the drop center at $t = 1345$, when a pair of defects are found inside the drop. The drop boundary is color-coded by the vorticity on the drop surface. The thin black curve is the drop center trajectory over time, and the red dot denotes the drop center at $t = 1345$. The exterior flow is closest to that of a neutral squirmer, rather than a pusher or puller ^[43,44]. During the oscillation we also find periodic birth and death of a pair defects (where the scalar order parameter is nearly zero) as shown in Figure 23(b), where we use grey bars to denote the time intervals when a pair of defects are found inside the drop. We observe that the defect activity is nearly anti-correlated with the swimmer $m = 1$ mode, which correlates well with the swimming speed (solid red curve).

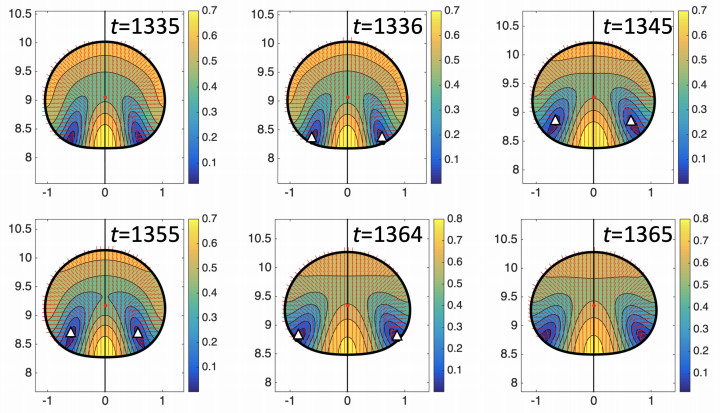
The details of the cyclic dynamics are further illustrated in Figure 24, where we show the contours of the scalar order parameter over-plotted by the direction of the largest eigenvector of ${\bf D}$ at six different times as labeled. At $t = 1335$ there is no defect inside the drop. At $t = 1336$ we observe two defects are created spontaneously near the boundary in the rear as the drop swims up. As time progresses (up to $t\sim 1355$) the two defects move towards the drop center (denoted by the red dot), with the drop shape elongating more in the vertical direction. During this time the drop speed decreases and the drop elongation along the propulsion direction is reduced. After $t\sim 1355$ the two defects move back towards the drop interface and then disappear at $t = 1365$. Such oscillation continues for the remainder rof the simulation.

8.   Concluding remarks

In this work we closely examine the dynamics of a model active droplet. Using a combination of linear modeling and nonlinear simulations, we categorize a rich set of behaviors these droplets can exhibit. At linear order, droplets containing suspensions of immotile (but mobile) active dipoles are largely dominated by three simple modes: rotors, swimmers, and extensors. Although parameter combinations where single modes dominate the dynamics exist, multiple modes can be active. We explore some of these possibilities, finding states which include wanderers, zigzaggers, washing machines, and pulsators, a few of which have been previously observed in silico ^[20]. We show how the often complex, time-dependent dynamics can be generally predicted from linear theory, and use modal decomposition of the boundary vorticity to dissect how the coupling of different linear modes drives the droplet dynamics. The model we use has seven physical parameters, and a full exploration of the phase space is impractical. Instead, we focus on several key parameters, and provide a relatively simple set of heuristics to aid in finding parameter combinations that lead to particular droplet behaviors.

The physical parameters that govern the dynamics of an active gel of bundled microtubules can be tuned by adjusting ATP and depletant concentrations ^[29], and the activity can be altered by adjusting the intensity of incident light ^[30]. Our results suggest that if such active fluids are confined in drops, these known mechanisms for parameter control are sufficient to allow the generation of droplets with multiple different behaviors from the same experimental system. Although the details of our analysis depend on the active fluid model that we have used, we suspect that the fundamental conclusions do not: droplets of active fluid will exhibit a multitude of behaviors, and which behavior dominates the dynamics will be set by tuning the physical parameters that govern the bulk properties of the active fluid and the interfacial properties.

Acknowledgments

The authors acknowledge useful discussions with Tony Gao, Petia Vlahovska, Kela Lushi, and Reza Farhadifar. MJS acknowledges support by the National Science Foundation under awards DMR-1420073 (NYU MRSEC), DMS-1620331, and DMR-2004469. YNY acknowledges support from NSF (DMS 1614863) and Flatiron Institute, part of Simons Foundation.

Conflict of interest

There is no conflict of interest between authors.

Appendix A.   Supplementary material on the effect of bottom drag on the axisymmetric case

Here we examine the effect of bottom drag on the exterior flow generated by an axisymmetric active droplet. Such a bottom drag may arise due to confinement in one direction (e.g., along the axis orthogonal to the plane in which the droplet is located). In this case, the resultant flow is well approximated by a depth-averaged two-dimensional flow in the $(x, y)$ plane with a bottom friction $k$. This kind of vertical confinement effect has been previously incorporated in modeling droplets of bacteria immersed in oil ^[8].

Outside the active droplet the governing equations are

Inside the active droplet, the governing equations are the same (see Section 2) but for the equation that determines the fluid velocity:

with $\sigma$ defined as before, see Section 2. In the axisymmetric case, the exterior fluid flow ${\bf U} = U_{\theta}(r) e_{\theta}$ satisfies the equation

which has the solution $U_\theta = c_1K_1(\sqrt{k/\mu}r)$, where $K_1$ is the modified Bessel function of order $1$. The coefficient $c_1$ needs to be determined by the interface condition at $\Gamma_t$.

Inside the active droplet, the governing equation for $u_{\theta}$ is

When the bottom friction $k\neq 0$ this equation is not integrable and we cannot proceed using the trick used in Section 3 to obtain the result in Eq (3.2). Instead, we will proceed as we did for nonzero $m$ in the main text, discretizing and computing the flow and dipolar fields numerically. The linear equations for $u_{\theta}$ and $D_{r\theta}$ are

The boundary conditions at the drop interface ($r = 1$) are that $u_\theta = U_\theta$ and

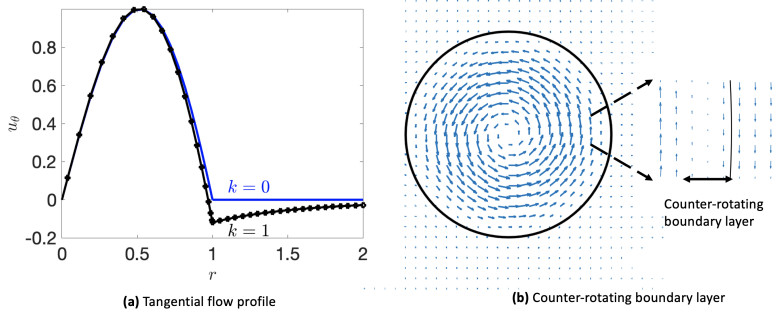
As in the main text, we numerically compute the eigenvalues and eigenvectors to the associated eigenvalue problem. The flow field associated with the leading eigenvector is shown in Figure 25, when the parameters of the system are $k = 1$, $\alpha = -2.212$, $\beta = 0.6$, $\zeta = 1.5$, $d_T = 0.05$, and $d_R = 0.05$. Panel (a) shows $u_{\theta}$ in black, along with the solution without bottom drag (shown in blue). The linear solutions have been scaled so that the magnitude of $u_{\theta}$ is unity for both curves. In the absence of bottom drag the tangential velocity $u_{\theta} = 0$ at $r = 1$, and the exterior flow is zero. However, when bottom drag is present the tangential flow changes sign close to the drop boundary, when $r$ is slightly less than $1$. The azimuthal velocity is non-zero and negative (that is, counter-rotating relative to the azimuthal flow in most of the interior of the droplet) at the interface. Panel (b) shows the velocity field inside the droplet, with a close-up near the boundary to make clear the thin counter-rotating boundary layer. Notice that the exterior rotational flow driven by the droplet is counter-rotating relative to the motion in most of the droplet.