Homogenisation of high-contrast brittle materials

1.   Introduction

In this note we analyse the large-scale behaviour of high-contrast composite materials which can undergo fracture. In a variational setting, the microscopic behaviour of high-contrast composites is typically described by means of scale-dependent energy functionals with "degenerate" integrands. For brittle materials the scale-dependent energies are of the general form

where $\varepsilon > 0$ describes both the composite-microstructure and the degeneracy of the mechanical properties of the material (cf. (1.3)). In (1.1) the variable $u \colon \Omega \subset {\mathbb R}^n \to {\mathbb R}$ belongs to $SBV(\Omega)$, the space of special functions of bounded variation in $\Omega$. In this simplified scalar setting, $u$ represents an anti-plane displacement and $\Omega$ is the cross-section of an infinite cylindrical body. Being $u$ an $SBV$-function, discontinuities are allowed and the discontinuity set of $u$, denoted by $S_u$, models the cracks in the material. The deformation gradient $Du$ can be decomposed into the sum of a bulk part $\nabla u \, dx$ and a surface part $(u^+-u^-)\nu_u\mathcal H^{n-1}\llcorner{S_u}$, where $\nabla u$ denotes the approximate gradient of $u$, $u^+$ and $u^-$ the traces of $u$ on both sides of $S_u$, and $\nu_u$ denotes the (generalised) normal to $S_u$. The volume term in $\mathcal F_ \varepsilon$ represents the elastic energy stored in the unfractured part of the material, whereas the surface term in $\mathcal F_ \varepsilon$ accounts for the presence of cracks. According to the Griffith criterion, in brittle materials, already for the smallest crack-amplitude, there is no interaction between the two lips of the crack, so that the corresponding fracture energy does not depend on $[u] = u^+-u^-$.

For finite-contrast brittle materials, the limit behaviour of energies of type (1.1) is by-now well-understood and the corresponding theory provides a rigorous micro-to-macro upscaling for brittle fracture. In fact, if $f_ \varepsilon$ and $g_ \varepsilon$ satisfy (mild regularity assumptions and) standard growth and coercivity conditions of type

for every $\varepsilon > 0$, $x, \xi \in {\mathbb R}^n$, $\nu \in {\mathbb S}^{n-1}$, for some $p > 1$, and $0 < c_1\leq c_2 < +\infty$, $0 < c_3\leq c_4 < +\infty$, then in ^[18] Giacomini and Ponsiglione showed, among other, that the limit behaviour of $\mathcal F_ \varepsilon$ is captured by a scale-independent free-discontinuity functional of the same type as $\mathcal F_ \varepsilon$; i.e.,

with $f_0$ and $g_0$ also satisfying (1.2). Under these assumptions, Giacomini and Ponsiglione also showed that volume and surface energy decouple in the limit, so that the energy density $f_0$ is not affected by the presence of the surface term in $\mathcal F_ \varepsilon$, whereas the surface energy density $g_0$ is not affected by the volume term in $\mathcal F_ \varepsilon$. In a recent work, Cagnetti, Dal Maso, Scardia and Zeppieri ^[12] generalised the asymptotic analysis carried out in ^[18] and devised (nearly optimal) sufficient conditions which ensure a macroscopic bulk-surface energy decoupling for a wide class of finite-contrast vectorial free-discontinuity functionals which may also depend on $[u]$. The class of periodic free-discontinuity functionals originally analysed by Braides, Defranceschi and Vitali ^[9] satisfy the sufficient conditions provided in ^[12]. Moreover, random free-discontinuity functionals with stationary finite-contrast integrands can be also seen as a special instance of those treated in ^[12], as shown by Cagnetti, Dal Maso, Scardia and Zeppieri in ^[13]. Therefore, a volume-surface interaction can be ruled out for a large class of finite-contrast free-discontinuity functionals. In this setting, in particular, microscopic brittle energies always converge to macroscopic brittle energies. However, the general theory established in ^[9,12,13,18] is not well-suited for studying the large-scale behaviour of those brittle composites whose different constituents have very different mechanical properties from one another. Indeed, in this case the integrands $f_ \varepsilon$ and $g_ \varepsilon$ in (1.1) may exhibit a so-called high-contrast behaviour and satisfy (1.2) only in a subset $\Omega_ \varepsilon$ of $\Omega$.

In the last decade there has been an ever increasing interest in the study of high-contrast free-discontinuity functionals and in the derivation of their effective properties. In particular, the case where (at least) one of the conditions in (1.2) is violated in "many small" periodically distributed regions inside $\Omega$ has been considered (see, e.g., ^{[3,4,5,6,11,14,16,17,19,20,21]}). Depending on the type of degeneracy of $f_ \varepsilon$ and $g_ \varepsilon$, nonstandard limit effects have been also observed. These nonstandard effects are typical of the high-contrast setting and arise from a nontrivial volume-surface limit interaction, which cannot be excluded in this degenerate setting. In fact, in the two companion papers ^[4,16], Barchiesi, Dal Maso and Zeppieri show that when only $g_ \varepsilon$ is degenerate, already for very simple free-discontinuity functionals of Mumford-Shah type, a bulk-surface interaction cannot be ruled out. Namely, a volume-surface coupling can be observed when homogenising a material made of "many" purely brittle inclusions periodically distributed in a connected unbreakable structure, whose fracture-resistance is assumed to be infinite. This coupling produces a homogeneous material whose overall behaviour is of ductile (or cohesive) type; in other words, the homogenised surface energy explicitly depends on $[u]$. A similar phenomenon is also observed by Barchiesi, Lazzaroni and Zeppieri ^[6] who show that a ductile behaviour can be seen as the macroscopic effect of a nontrivial volume-surface interaction in the homogenisation of two purely brittle materials with a high-contrast bulk energy. Moreover, in the recent work ^[19] Pellet, Scardia and Zeppieri prove, instead, that nonstandard constitutive laws may arise when homogenising two purely brittle materials with a high-contrast surface energy. The functionals analysed in ^[6] and ^[19] are both of type

where the elastic modulus $a_ \varepsilon$ and the fracture resistance (or fracture thoughness) $b_ \varepsilon$ are $Q$-periodic functions and in the unit periodicity cell $Q: = (-1/2, 1/2)^n$ are defined as

with $\alpha_ \varepsilon, \beta_ \varepsilon \in [0, 1]$, $r\in (0, 1)$, and $Q_r: = (-r/2, r/2)^n$. Since $\alpha_ \varepsilon, \beta_ \varepsilon$ are not bounded away from zero, the functions $a_ \varepsilon$ and $b_ \varepsilon$ can be degenerate. In their turn, the integrands $f_ \varepsilon(y, \xi) = a_ \varepsilon(y)|\xi|^2$ and $g_ \varepsilon(y, \nu) = b_ \varepsilon(y)$ in (1.3) will not satisfy, in general, the coercivity conditions in (1.2).

The limit case $\alpha_ \varepsilon = \beta _ \varepsilon = 0$ corresponds to the case of periodically perforated brittle materials studied by Cagnetti and Scardia ^[14] and by Focardi, Gelli, and Ponsiglione ^[17] (see also Barchiesi and Focardi ^[5] for more general free-discontinuity functionals). In spite of the strong degeneracy of the coefficients $a_ \varepsilon$ and $b_ \varepsilon$, which in this case are equal to zero in a "large" portion of $\Omega$, in this case it can be proven that the functionals $\mathcal F^{0, 0}_ \varepsilon$ exhibit a limit behaviour which is qualitatively similar to that of free-discontinuity functionals with coercive integrands. Namely, in this case bulk and surface terms do not interact in the limit.

The aim of this note is to show that, contrary to the coercive case, where general homogenisation results can be proven to describe the limit behaviour of a large class of free-discontinuity functionals, in the non-coercive setting, already for special functionals of type (1.3), a unified homogenisation theory cannot be established. In fact, the limit behaviour of $\mathcal F^{\alpha_ \varepsilon, \beta_ \varepsilon}_ \varepsilon$ is highly sensitive both to the choice of the parameters $\alpha_ \varepsilon$ and $\beta _ \varepsilon$ and to their vanishing rate compared to the period of the microstructure $\varepsilon$.

This note is divided into two main parts and organised as follows. In first part we will deal with sequences of general free-discontinuity functionals of type (1.1) whose coefficients $f_ \varepsilon$ and $g_ \varepsilon$ are "weakly coercive" or "degenerate"; i.e., they satisfy the lower bounds in (1.2) only in a set $\Omega_ \varepsilon$ which is obtained removing from $\Omega$ many small periodically distributed connected regions. We will use the localisation method of $\Gamma$-convergence ^[8,15] to prove that these kind of functionals are (pre)compact. That is, up to subsequences, they always $\Gamma$-converge to a free-discontinuity functional of type

Moreover, the limit integrands $f$ and $g$ are non-degenerate and satisfy coercivity conditions of type (1.2) for some positive constants $\hat c_1, \hat c_3$ which are strictly smaller than $c_1, c_3$, respectively. In this part of the analysis a pivotal role is played by an extension result for $SBV$-functions defined in periodically perforated domains, proved by Cagnetti and Scardia ^[14] (see also the later variant in ^[5]).

In the second part of this note we will specialise the general theory to some prototypical and yet relevant model cases. Namely, we will briefly review the case of perforated (or porous) brittle materials studied by Cagnetti and Scardia ^[14] and by Focardi, Gelli and Ponsiglione ^[17] (see also ^[5]), the case of high-contrast brittle materials with soft inclusions treated by Barchiesi, Lazzaroni and Zeppieri in ^[6], and eventually the case of high-contrast brittle materials with weak inclusions analysed by Pellet, Scardia and Zeppieri in ^[19]. In particular we will show that the choice of the integrands $f_ \varepsilon$ and $g_ \varepsilon$ in (1.1) strongly affects the form of the $\Gamma$-limit which can give rise to macroscopic models accounting for damage as well as to models accounting for cohesive fracture.

2.   Part Ⅰ: A compactness result for high-contrast free-discontinuity functionals

In this part we will use the localisation method of $\Gamma$-convergence ^[8,15] to prove a convergence result for a general class of free-discontinuity functionals of brittle type, with degenerate coefficients.

In the choice of the convergence to compute the $\Gamma$-limit, a crucial role will be played by an extension result for $SBV$-functions defined in periodically perforated domains due to Cagnetti and Scardia [14,Theorem 1.3] and by a later variant due to Barchiesi and Focardi [5,Theorem 1].

2.1.   Notation and setting of the problem

We list below a few notation which will be used throughout the paper.

● $\Omega \subset {\mathbb R}^n$ denotes an open and bounded set with Lipschitz boundary. The set $\mathcal{A} (\Omega)$ denotes the collection of all open subsets of $\Omega$;

● $Q$ denotes the open unit cube of ${\mathbb R}^n$ centred at the the origin, whereas for $x\in {\mathbb R}^n$ and $r > 0$ we set $Q_r(x): = rQ+x$;

● for $\nu\in {\mathbb S}^{n-1}$ we denote with $Q^\nu$ the open unit cube of ${\mathbb R}^n$ centred at the the origin, with one face orthogonal to $\nu$ and for $x\in {\mathbb R}^n$ and $r > 0$ we set $Q^\nu_r(x): = r Q^\nu +x$;

● for $x\in {\mathbb R}^n$ and $\nu\in {\mathbb S}^{n-1}$ we denote by $\Pi^\nu(x)$ the hyperplane through $x$ and perpendicular to $\nu$; i.e., $\Pi^\nu(x): = \{y\in {\mathbb R}^n \colon (y-x) \cdot \nu = 0\}$. If $x = 0$ we simply write $\Pi^\nu$;

● For $u\in L^1(\Omega)$ and $m > 0$ the function $u^m$ denotes the truncated function of $u$ at level $m$; i.e., $u^m: = (u \wedge m) \vee (-m)$;

● For $\xi\in {\mathbb R}^n$ we denote by $u_\xi$ the linear function with gradient equal to $\xi$; i.e., $u_\xi(x): = \xi \cdot x$, for every $x\in {\mathbb R}^n$;

● For $x\in {\mathbb R}^n$, $t\in {\mathbb R}$, and $\nu \in {\mathbb S}^{n-1}$ we denote with $u_x^{\nu, t}$ the piecewise constant function taking values $0, t$ and jumping across the hyperplane $\Pi^\nu(x)$; i.e.,

The functional setting we are going to consider in this note is that of $SBV$, the space of special functions of bounded variation. We recall here only the definition of the spaces which are relevant for our analysis and we refer the reader to ^[2] for a comprehensive treatment on the subject. We set

Here $S_{u}$ denotes the approximate discontinuity set of $u$, $\nu_{u}$ is the generalised normal to $S_{u}$, $u^{+}$ and $u^{-}$ are the traces of $u$ on both sides of $S_{u}$. In this paper we work with the following vector subspace of $SBV(\Omega)$

where $p > 1$. We consider also the larger space of generalised special functions of bounded variation in $\Omega$,

as well as

We consider also

it is known (see [2,Theorem 4.23]) that every $u$ in $SBV^{\mathrm{pc}}(\Omega)\cap L^\infty(\Omega)$ is piecewise constant in the sense of [2,Definition 4.21], namely there exists a Caccioppoli partition $(E_i)$ of $\Omega$ such that $u$ is constant $\mathcal{L}^n$-a.e. in each set $E_i$. Moreover, we set

For $u, w \in L^1(U)$, in what follows, by "$u = w$ near $\partial U$" we mean that there exists a neighbourhood $V$ of $\partial U$ in ${\mathbb R}^n$ such that $u = w$ $\mathcal{L}^n$-a.e. in $V \cap U$. Let $f_k \colon {\mathbb R}^n \times {\mathbb R}^n \to [0, +\infty)$ be Carathéodory functions such that

(H1) there exist $p > 1$ and $0 < c_1\leq c_2 < +\infty$ such that for every $(x, \xi)\in {\mathbb R}^n\times {\mathbb R}^n$ and for every $k\in {\mathbb N}$

(H2) $f_k(x, 0) = 0$ for every $x\in {\mathbb R}^n$ and for every $k\in {\mathbb N}$.

Let moreover $g_k\colon {\mathbb R}^n\times {\mathbb S}^{n-1} \to (0, +\infty)$ be Borel functions such that

(H3) there exist $0 < c_3\leq c_4 < +\infty$ such that for every $(x, \nu)\in {\mathbb R}^n\times {\mathbb S}^{n-1}$ and every $k\in {\mathbb N}$

(H4) $g_k(x, \nu) = g_k(x, -\nu)$, for every $(x, \nu)\in {\mathbb R}^n\times {\mathbb S}^{n-1}$ and every $k\in {\mathbb N}$.

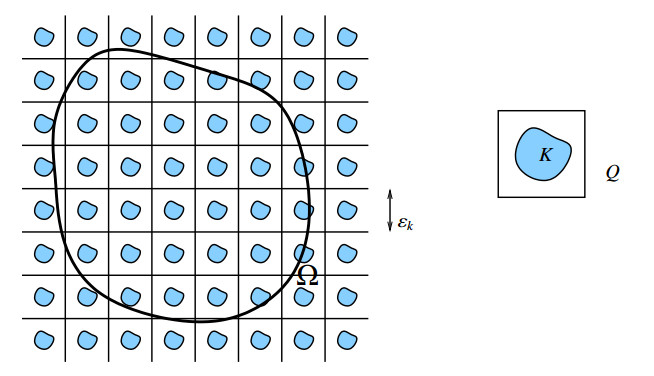
Let $\Omega\subset {\mathbb R}^n$ be open bounded and with Lipschitz boundary and let $K\subset Q$ be compact and such that $Q\setminus K$ has a Lipschitz boundary. We define

the set $E$ is open, connected, $Q$-periodic, and has a Lipschitz boundary. Let $\varepsilon_k$ be a sequence of positive numbers such that $\varepsilon_k \searrow 0$ as $k\to +\infty$ and denote by $\Omega_k$ the $\varepsilon_k Q$-periodic set defined as $\Omega_k: = \Omega \cap \varepsilon_k E$ (see Figure 1).

Let moreover $\alpha_ k, \beta _ k \in [0, 1]$ and consider the sequence of functionals ${\mathcal F}_k \colon L^1(\Omega) \longrightarrow [0, +\infty]$ defined as

We observe that thanks to assumption (H2) the functionals ${\mathcal F}_k$ decrease by truncation, wherease they do not satisfy the standard coercivity conditions required, e.g., in ^[9,12,18] since the coefficients $\alpha_ k, \beta _ k$ are not bounded away from zero.

2.2.   Equi-coercivity and choice of the convergence

Due to the possible degeneracy of the coefficients $\alpha_ k$ and $\beta _ k$, the functionals ${\mathcal F}_k$ are not, in general, equi-coercive with respect to the strong $L^1(\Omega)$-convergence. Similarly as in ^[5,11,17,19], in what follows we give a notion of convergence on $L^1(\Omega)$ which is weaker that the $L^1(\Omega)$-convergence and ensures the equi-coercivity of the functionals ${\mathcal F}_k$. This will be done by appealing to [5,Theorem 1]. For the readers' convenience we recall here a slightly simplified version of this result which is useful for our purposes.

Theorem 2.1 (cf. Theorem 1 in ^[5]). Let $(u_k)\subset SBV^p(\Omega_k)$ be such that

Then, there exist $(\tilde u_k)\subset SBV^p(\Omega)$, with $\tilde u_k = u_k$ a.e. in $\Omega_k$, and a function $u\in GSBV^p(\Omega)\cap L^p(\Omega)$ such that (up to subsequences) $\tilde u_k \to u$ in $L^1(\Omega)$.

If moreover $\sup_k\|u_k\|_{L^\infty(\Omega_k)} < +\infty$ then $u\in SBV^p(\Omega)\cap L^\infty(\Omega)$ and $\tilde u_k \to u$ in $L^p(\Omega)$.

Let $(u_k)\subset L^1(\Omega)$ be a sequence satisfying

Then, clearly $(u_k) \subset SBV^p(\Omega_k)$; moreover in view of (H1) and (H3) the sequence $(u_k)$ satisfies the uniform bound (2.4). Therefore invoking Theorem 2.1 immediately yields the existence of a function $u\in GSBV^p(\Omega)\cap L^p(\Omega)$ and a sequence $(\tilde u_k) \subset SBV^p(\Omega)$ with $\tilde u_k = u_k$ a.e. in $\Omega_k$, such that (up to subsequences not relabelled) $\tilde u_k \to u$ in $L^1(\Omega)$.

This observation motivates the choice of the following notion of convergence on $L^1(\Omega)$.

Definition 2.2 (Convergence). Let $(u_k)$ be a sequence in $L^1(\Omega)$. We say that $(u_k)$ converges to a function $u\in L^1(\Omega)$, and we write $u_k \leadsto u$, if there exists a sequence $(\tilde u_k) \subset L^1(\Omega)$ such that $\tilde u_k = u_k$ a.e. in $\Omega_k$, and $\tilde u_k$ converges to $u$ in $L^1(\Omega)$.

Remark 2.3 (Uniqueness of the limit). We observe that since $C(K): = \mathcal L^n(Q \setminus K) > 0$, then the limit in the sense of Definition 2.2 is well-defined. Indeed, assume that $u_k \leadsto u_1$ and $u_k \leadsto u_2$. Then by definition there exist $(\tilde u_{1, k}), (\tilde u_{2, k})\subset L^1(\Omega)$ such that $\tilde u_{1, k} = \tilde u_{2, k} = u_k$ in $\Omega_k$ and $\tilde u_{1, k} \to u_1$ and $\tilde u_{2, k} \to u_2$ in $L^1(\Omega)$. Therefore

where the last inequality follows by the Riemann-Lebesgue Theorem applied to the $\varepsilon_kQ$-periodic function $\chi_{ \Omega_k}$. Then, since $C(K) > 0$ we necessarily have $u_1 = u_2$ a.e. in $\Omega$.

We notice moreover that the convergence $u_k \leadsto u$ readily implies

Remark 2.4 (Convergence of truncated functions). Let $(u_k)\subset L^1(\Omega)$ be such that $u_k \leadsto u$ for some $u\in L^1(\Omega)$. Let $m\in {\mathbb N}$ and denote by $(u_k^m)$ the sequence of truncated functions of $u_k$ at level $m$, then $u_k^m \leadsto u^m$ where $u^m$ denotes the truncated function of $u$ at level $m$. Indeed, set $v_k: = (\tilde u_k)^m$, then $v_k = u_k^m$ a.e. in $\Omega_k$, moreover since $\tilde u_k \to u$ in $L^1(\Omega)$ then $(\tilde u_k)^m \to u^m$ in $L^1(\Omega)$, and actually in any $L^p(\Omega)$.

In what follows we study the $\Gamma$-convergence of the functionals ${\mathcal F}_k$ with respect to the convergence as in Definition 2.2. To this end we give the following sequential notion of $\Gamma$-convergence.

Definition 2.5 (Sequential $\Gamma$-convergence). Let ${\mathcal F}_k, {\mathcal F} \colon L^1(\Omega) \longrightarrow [0, +\infty]$; we say that the functionals ${\mathcal F}_ \varepsilon$ -converge to ${\mathcal F}$ with respect to the convergence as in Definition 2.2 if for every $u\in L^1(\Omega)$ the two following conditions are satisfied:

$(i)$ (Ansatz-free lower bound) For every $(u_k)\subset L^1(\Omega)$ with $u_k \leadsto u$ we have

$(ii)$ (Existence of a recovery sequence) There exists $(\bar u_k) \subset L^1(\Omega)$ with $\bar u_k \leadsto u$ such that

Remark 2.6. It is standard to show that ${\mathcal F}$ is lower semicontinuous with respect to the convergence as in Definition 2.2 and hence with respect to the strong $L^1(\Omega)$-convergence.

For every $u\in L^1(\Omega)$ we consider the functionals

and

It is easy to show that the infima in (2.5) and (2.6) are actually attained.

In what follows we also use the compact notation

It is immediate to see that Definition 2.5 is equivalent to ${\mathcal F}' = {\mathcal F}" = {\mathcal F}$ in $L^1(\Omega)$.

Remark 2.7 (The case $\alpha_ k, \beta _ k = 0$). In the case of porous brittle materials ^[5,14,17], which corresponds to the parameter choice $\alpha_ k, \beta _ k = 0$, the $\Gamma$-convergence of the functionals ${\mathcal F}_k$ can be equivalently studied with respect to the strong $L^1(\Omega)$-convergence. Indeed, in this case a sequence $(u_k)$ with equibounded energy can be replaced by the $L^1(\Omega)$-converging sequence $(\tilde u_k)$ given by Theorem 2.1, without changing the energy.

The following proposition shows that the domain of the $\Gamma$-limit of ${\mathcal F}_k$ (if it exists) is $GSBV^p(\Omega)$.

Proposition 2.8 (Domain of the $\Gamma$-limit). Let ${\mathcal F}'$ and ${\mathcal F}"$ be as in (2.7); then

Proof. We first show that $GSBV^p(\Omega)\subset {\rm dom}\, {\mathcal F}"$. By the growth conditions (2.1) and (2.2) we have ${\mathcal F}_k(u) \leq \mathcal G(u)$ where

The functional $\mathcal G$ is lower semicontinuous with respect to the strong $L^1(\Omega)$-convergence, hence we have

Since the convergence in Definition 2.2 is weaker than the $L^1(\Omega)$-convergence we then have ${\mathcal F}"\leq \mathcal G$, and thus the desired inclusion.

We now prove that ${\rm dom}\, {\mathcal F}' \subset GSBV^p(\Omega)$. To this end, let $u\in {\rm dom}\, {\mathcal F}'$ then there exists $(u_k)\subset L^1(\Omega)$ with $u_k \leadsto u$ such that $\liminf_{k} {\mathcal F}_k(u_k) = {\mathcal F}(u) < +\infty$. Then, up to subsequences (not relabelled) we have $\sup_k {\mathcal F}(u_k) < +\infty$, thus in particular $(u_k)\subset SBV^p(\Omega)$.

Let $m\in {\mathbb N}$ and let $u_k^m$ be the truncated function of $u_k$ at level $m$; then $(u_k^m)\subset SBV^p(\Omega)\cap L^\infty(\Omega)$. Since the functionals ${\mathcal F}_k$ decrease by truncation, for every fixed $m\in {\mathbb N}$ it also holds $\sup_k {\mathcal F}_k(u_k^m) < +\infty$. Therefore, for $m\in {\mathbb N}$ fixed we can appeal to Theorem 2.1 to deduce the existence of a sequence $(v_k)\subset L^1(\Omega)$ such that $v_k = u_k^m$ a.e. in $\Omega_k$ and of a function $v\in SBV^p(\Omega)$ such that up to subsequence (not relabelled) $v_k \to v$ in $L^1(\Omega)$. Since $u_k \leadsto u$ we have

therefore $v = u^m$ a.e. in $\Omega$. Eventually, the arbitrariness of $m\in {\mathbb N}$ yields $u \in GSBV^p(\Omega)$.

2.3.   $\Gamma$-convergence and integral representation

In this section we show that, up to subsequences, the functionals ${\mathcal F}_k$ $\Gamma$-converge to a free-discontinuity functional of the form

for some $f_\infty$ and $g_\infty$. Moreover, we show that, despite the degeneracy of the coefficients $\alpha_ k, \beta _ k$, the limit integrands $f_\infty$ and $g_\infty$ satisfy standard coercivity conditions similar to (2.1) and (2.2), respectively.

If not otherwise specified, in what follows the $\Gamma$-convergence of the functionals ${\mathcal F}_k$ is always understood in the sense of Definition 2.5.

To prove the existence of a $\Gamma$-convergent subsequence of ${\mathcal F}_k$ we make use of the so-called localisation method ^[8,15] which we adapt to the sequential notion of $\Gamma$-convergence as in Definition 2.5.

We start by localising the functionals ${\mathcal F}_{k}$; that is we consider ${\mathcal F}_k: L^1(\Omega)\times \mathcal{A}(\Omega)\longrightarrow [0, +\infty]$ defined as

where $U_k: = U \cap \varepsilon_k E$.

We also define the localised versions of (2.5) and (2.6); i.e., for every $U\in \mathcal{A}(\Omega)$ we consider the functionals defined as

Remark 2.9 (Properties of ${\mathcal F}', {\mathcal F}"$). It is easy to show that ${\mathcal F}'$ and ${\mathcal F}"$ are lower semicontinuous with respect to the convergence in Definition 2.2, local, and that they decrease by truncation. Moreover, as set functions they are both increasing, whereas ${\mathcal F}'$ is also superadditive.

Remark 2.10 (On assumption (H2)). If we drop assumption (H2) the functionals ${\mathcal F}_k$ will not decrease by truncation, but rather satisfy

If $\alpha_ k$ is infinitesimal, the inequality in (2.11) implies

(and analogously for ${\mathcal F}"$). In fact, by definition of $\Gamma$-liminf there exists a sequence $(u_k)\subset L^1(\Omega)$ such that $u_k \leadsto u$ and ${\mathcal F}'(u, U) = \liminf_{k\to +\infty} {\mathcal F}_k(u_k, U)$. Then if $u_k^m$ is the truncated function of $u_k$ at level $m$, by (2.11) we get

where $\tilde u_k$ is as in Definition 2.2 and thus $\tilde u_k \to u$ in $L^1(\Omega)$. Therefore, taking the liminf as $k \to +\infty$ gives

hence (2.12) follows by the definition of $\Gamma$-liminf, taking into account that $u_k^m \leadsto u^m$, and by the Chebyshev inequality. Therefore, (2.12) ensures that ${\mathcal F}'$ "almost" decreases by truncation up to an error which becomes small for $m$ large. Inequality (2.12) is then enough to to carry out the $\Gamma$-convergence analysis below (cf. ^[12]). Hence, if $\alpha_ k$ is infinitesimal assumption (H2) can be dropped.

However, if the sequence $\alpha_ k$ is uniformly bounded from below, we have no control on the term $\alpha_ k\, c_2 \mathcal L^n (U \setminus U_k \cap \{|u_k| \geq m\})$, therefore from (2.11) we cannot infer (2.12). Since with we want to study the $\Gamma$ convergence of ${\mathcal F}_k$ for any choices of $\alpha_ k\in [0, 1]$, assumption (H2) is actually necessary.

In general the set functions ${\mathcal F}'(u, \cdot)$ and ${\mathcal F}"(u, \cdot)$ are not inner regular. Then we consider their inner regular envelopes defined as:

and

Remark 2.11 (Properties of ${\mathcal F}'_-, {\mathcal F}"_-$). The functionals ${ {\mathcal F}}'_-$ and ${ {\mathcal F}}"_-$ are lower semicontinuous with respect to the convergence in Definition 2.2 [15,Remark 15.10], local [15,Remark 15.25], and it is immediate to check that they decrease by truncation. Furthermore, as set functions, they are both increasing and ${\mathcal F}'_-$ is superadditive [15,Remark 15.10].

The following compactness result is the analogue of [15,Theorem 16.9], when the sequential notion of $\Gamma$-convergence in Definition 2.5 is considered. We omit its proof since it is standard.

Proposition 2.12 (Compactness by $\Gamma$-convergence). Let ${\mathcal F}_k$ be the localised functionals as in (2.9). Then there exists a subsequence $({\mathcal F}_{k_j})\subset ({\mathcal F}_k)$ such that the corresponding functionals ${\mathcal F}'$ and ${\mathcal F}"$ defined in (2.10) satisfy ${\mathcal F}'_- = {\mathcal F}"_-$.

We now set

In what follows we show that actually ${\mathcal F}$ coincides with the $\Gamma$-limit of the subsequence $({\mathcal F}_{k_j})$. To this end we start noticing that by monotonicity we always have ${\mathcal F}"_- = {\mathcal F}'_-\leq {\mathcal F}'\leq {\mathcal F}"$. Therefore, if we show that ${\mathcal F}" = {\mathcal F}"_-$; i.e., that ${\mathcal F}"$ is inner regular, we immediately get ${\mathcal F}' = {\mathcal F}" = {\mathcal F}$ and therefore that ${\mathcal F}_{k_j}(\cdot, U)$ $\Gamma$ $-converges to$ {\mathcal F}(\cdot, U) $for every$ U\in A(\Omega) $, as desired.

A crucial preliminary result needed to prove the inner-regularity of ${\mathcal F}"$ is the so-called fundamental estimate, which has to hold uniformly in $k$. Since the $\Gamma$-limit is computed with respect to the convergence in Definition 2.2, the fundamental estimate we need is non-standard. Namely, we have to prove that the error in the fundamental estimate tends to zero when $u_k \leadsto u$. This is achieved by first showing that the error goes like $\|u_k-u\|_{L^p(\Omega_k)}$ and then by resorting to a truncation argument.

We notice that an analogous estimate for degenerate functionals defined in Sobolev spaces can be found in [10,Proposition 3.3]. Whereas in the $SBV$-setting, for functionals of Mumford-Shah type with degenerate surface energy it can be found in the recent [19,Lemma 4.4].

Following ^[10] we start showing how to construct suitable cut-off functions which are constant in $\bigcup_{i\in {\mathbb Z}^n} \varepsilon_k (K+i)$. To this end let $\delta > 0$ be small enough so that the set $K_\delta: = \{x\in {\mathbb R}^n \colon {\rm dist}(x, K) < \delta\}$ satisfies $K_{\delta}\subset \subset Q$. Let $\psi\in C_0^\infty(Q)$ be a cut-off function between $K$ and $K_{\delta}$ (that is $0\leq \psi\leq 1$, $\psi \equiv 1$ on $K$, and ${\rm spt}\, \psi\subset K_{\delta}$) such that $|\nabla \psi|\leq \frac{2}{\eta}$.

For $k\in {\mathbb N}$ and $i\in {\mathbb Z}^n$, we define the operator $R_{i}^{k} : W_{ \rm{loc}}^{1, \infty}(\mathbb{R}^{n}) \rightarrow W_{ \rm{loc}}^{1, \infty}(\mathbb{R}^{n})$ as

By definition we have that

while $R_{i}^k$ is constant in $\varepsilon_k K+\varepsilon_k i$, namely we have

Finally, we consider the operator $\mathcal R^{k} : W_{ \rm{loc}}^{1, \infty}(\mathbb{R}^{n}) \rightarrow W_{ \rm{loc}}^{1, \infty}(\mathbb{R}^{n})$ defined as

Let $U\subset {\mathbb R}^n$ be open and bounded and let $\phi \in W^{1, \infty}(U)$ then $\nabla \mathcal R^k (\phi)$ is uniformly bounded in $k$. More precisely, we have

where $d$ denotes the diameter of $K_\delta$. In fact,

and

In the next proposition we make use of the operator $\mathcal R^k$ to construct cut-off functions whose gradient vanishes in ${\mathbb R}^n \setminus \varepsilon_k E$; these cut-off functions are then used to prove the desired fundamental estimate.

Proposition 2.13 (Fundamental estimate). For every $\eta > 0$, and for every $U'$, $U"$, $V \in \mathcal{A}(\Omega)$, with $U'\subset\subset U"$, there exist two constants $M(\eta) > 0$ and $k_\eta \in {\mathbb N}$ satisfying the following property: For every $k > k_\eta$, for every $u \in L^{1}(\Omega)$ with $u \in SBV^{p}(U")$, and for every $v \in L^{1}(\Omega)$ with $v \in SBV^{p}(V)$, there exists a function $\varphi \in {C}_{0}^{\infty}(\Omega)$ with $\varphi = 1$ in a neighbourhood of $U'$, ${\rm spt}\, \varphi \subset U"$ and $0 \leq \varphi \leq 1$ such that

where $S: = (U"\setminus U') \cap V$.

Proof. Let $U', U", V\in \mathcal A(\Omega)$ be as in the statement. Let $\eta > 0$ be fixed and choose $N \in {\mathbb N}$ in a way such that

Let moreover $U\in \mathcal A(\Omega)$ be such that $U' \subset \subset U \subset \subset U"$ and consider the open sets

where

We notice that by definition of $U_l$ we have that

For every $j = 0, \ldots, N-1$ let $\phi_j$ be a cut-off function between $U_{3j+1}$ and $U_{3j+2}$ with $|\nabla \phi_j| < 4N$.

Let $k_\eta \in {\mathbb N}$ be such that

where $d: = {\rm diam}(K_\delta) < \sqrt{2}$.

If $i\in {\mathbb Z}^n$ is such that $(\varepsilon_k K+ \varepsilon_k i)\cap U_l \neq \emptyset$ for every $k > k_\eta$, then thanks to (2.17)–(2.18) we can deduce that $(\varepsilon_k K+ \varepsilon_k i)\cap ({\mathbb R}^n \setminus U_{l+1}) = \emptyset$. Therefore the functions $\varphi_j: = \mathcal R^k (\phi_j)$ are cut-off functions between the sets $U_{3j}$ and $U_{3(j+1)}$, for every $j = 0, \ldots, N-1$ (where we have set $U_0: = U'$).

Now let $u \in SBV^{p}(U")$ and $v \in SBV^{p}(V)$; for every $j = 0, \ldots, N-1$ fixed we have

We set

and estimate the term ${\mathcal F}_{k}(w_j, S_j)$. We clearly have

By construction $\nabla \varphi_j = 0$ in ${\mathbb R}^n \setminus \varepsilon_k E$, therefore appealing to (2.1) and (2.2) we deduce

Moreover, again invoking (2.1) and (2.2), in $\varepsilon_k E$ we have

Since $|\nabla \phi_j|\leq 4N$, combining the definition of $\varphi_j$ with (2.14) gives

In view of (2.19), by gathering (2.20)–(2.22) we then obtain for every $j = 0, \ldots, N-1$

where

Therefore there exists $j^\ast \in \{0, \ldots, N-1\}$ such that

Finally the thesis follows from (2.16) by choosing $\varphi_{j^\ast}$ as a cut-off function and setting $S: = (U"\setminus U') \cap V$.

Thanks to the fundamental estimate Proposition 2.13 we are now able to prove the following abstract $\Gamma$-convergence result for the sequence of localised functionals ${\mathcal F}_{k_j}(\cdot, U)$.

Theorem 2.14 (Abstract $\Gamma$-convergence and properties of the $\Gamma$-limit). Let ${\mathcal F}$ be as in (2.13), then:

$a.$ (locality and lower semicontinuity) for every $U\in \mathcal{A}(\Omega)$, the functional ${\mathcal F}(\cdot, U)$ is local and lower semicontinuous with respect to the $L^1(\Omega)$-convergence;

$b.$ (measure property) for every $u\in GSBV^p(\Omega)$, the set function ${\mathcal F}(u, \cdot)$ is the restriction to $\mathcal{A}(\Omega)$ of a Radon measure on $\Omega$;

$c.$ ($\Gamma$-convergence) for every $U\in \mathcal{A}(\Omega)$ it holds ${\mathcal F} (\cdot, U) = {\mathcal F}'(\cdot, U) = {\mathcal F}"(\cdot, U)\; \mathit{\text{on $GSBV^p(\Omega)$; }}$

$d.$ (translational invariance in $u$) for every $u \in L^{1}(\Omega)$ and $U \in \mathcal{A}(\Omega)$ there holds ${\mathcal F} (u+s, U) = {\mathcal F} (u, U)$ for every $s \in \mathbb{R}$.

Proof. Since the $L^1(\Omega)$-convergence implies the convergence in the sense of Definition 2.2, property 1 immediately follows from Remark 2.11. In view of Remark 2.11, property 2 follows by the De Giorgi and Letta criterion (see, e.g., [15,Theorem 14.23]) once we show that for every $u\in GSBV^p(\Omega)$ the set function ${\mathcal F}(u, \cdot)$ is subadditive. In its turn, the subadditivity of ${\mathcal F}(u, \cdot)$ follows from Proposition 2.13. Since in our setting this proof is not entirely standard, we discuss it in detail for the readers' convenience.

We start observing that on $GSBV^p(\Omega)$ the functional ${\mathcal F}$ satisfies the following limsup-type inequality: For every $u\in GSBV^p(\Omega)$ and for every $U, U'\in \mathcal{A}(\Omega)$ with $U'\subset\subset U$, there exists a sequence $(u_j)\subset GSBV^p(U')\cap L^1(\Omega)$ with $u_j\leadsto u$ such that

(see, e.g., [15,Proposition 16.4 and Remark 16.5] also recalling that the infimum in the definition of ${\mathcal F}"$ is actually attained).

Now let $U, V\in \mathcal{A}(\Omega)$ and let $u\in GSBV^p(\Omega)\cap L^\infty(\Omega)$. Fix any $U'\subset\subset U$, $V'\subset\subset V$, $U', V'\in \mathcal{A}(\Omega)$. Choose an open set $U"$ such that $U'\subset\subset U"\subset\subset U$ and two sequences $(u_j)\subset GSBV^p(U")\cap L^1(\Omega)$ and $(v_j)\subset GSBV^p(V')\cap L^1(\Omega)$, with $u_j\leadsto u$ and $v_j\leadsto u$ such that

Since the functionals ${\mathcal F}_k$ decrease by truncation, we can additionally assume that $\|u_j\|_{L^\infty(\Omega)}, \|v_j\|_{L^\infty(\Omega)}\leq \|u\|_{L^\infty(\Omega)}$; clearly,

Let $\eta > 0$ be fixed and arbitrary. The fundamental estimate Proposition 2.13 provides us with constants $M(\eta) > 0$ and $j_\eta \in {\mathbb N}$ and with a sequence $(\varphi_j)$ of cut-off functions between $U'$ and $U"$ such that

for every $j\geq j_\eta$. Hence appealing to (2.23), to the convergence $\varphi_j u_j+(1-\varphi_j)v_j\leadsto u$, and to the obvious inequality ${\mathcal F} \leq {\mathcal F}'$, by taking the limit as $j\to+\infty$, we get

Now letting $\eta\to 0$, and then $U'\nearrow U$, $V'\nearrow V$ in view of the inner-regularity of ${\mathcal F}$ we get

hence the subadditivity of ${\mathcal F}(u, \cdot)$ for $u\in GSBV^p(\Omega)\cap L^\infty(\Omega)$.

Now let $u\in GSBV^p(\Omega)$ and, for every $m\in {\mathbb N}$, set $u^m: = (u\wedge m)\vee (-m)$. Then, since ${\mathcal F}$ decreases by truncation (2.25) immediately gives

Then, taking the limit as $m \to +\infty$, in view of the convergence $u^m \to u$ in $L^1(\Omega)$ and the lower semicontinuity of ${\mathcal F}$ we obtain

and thus the subadditivity of ${\mathcal F}(u, \cdot)$ for every $u\in GSBV^p(\Omega)$.

The proof of property 3 is achieved by showing that ${\mathcal F}"$ is inner-regular. Indeed, this is equivalent to ${\mathcal F}" = {\mathcal F}"_-$, which by definition of ${\mathcal F}$ implies ${\mathcal F}"\leq {\mathcal F}\leq {\mathcal F}'$. Since clearly ${\mathcal F}'\leq {\mathcal F}"$, we actually deduce that ${\mathcal F}$ is the $\Gamma$-limit of ${\mathcal F}_{k_j}$.

The inner regularity of ${\mathcal F}"$ follows from the fundamental estimate Proposition 2.13. To see this, for every $U\in \mathcal{A}(\Omega)$ let $\mathcal G(\cdot, U)$ be the localised version of the functional $\mathcal G$ defined in (2.8); i.e.,

Now fix $W\in \mathcal{A}(\Omega)$ and $u\in GSBV^p(\Omega)$; since $\mathcal G(u, \cdot)$ is the restriction to $\mathcal{A}(\Omega)$ of a Radon measure, for every $\eta > 0$ there exists a compact set $\widetilde W\subset W$ such that and $MS(u, W\setminus \widetilde W) < \eta$.

Now choose $U, U'\in \mathcal{A}(\Omega)$ satisfying $\widetilde W\subset U'\subset \subset U \subset \subset W$ and set $V: = W\setminus \widetilde W$. Recalling that ${\mathcal F}"(u, \cdot)$ is increasing, appealing to Proposition 2.13 easily gives

Recalling that ${\mathcal F}"\leq \mathcal G$, by taking the sup on $U \subset \subset W$ we get

Hence, by the arbitrariness of $\eta > 0$ we get ${\mathcal F}"(u, W) \leq {\mathcal F}"_-(u, W)$ for every $W\in \mathcal{A}(\Omega)$ and every $u\in GSBV^p(\Omega)$. Since the opposite inequality is always satisfied, we readily deduce the inner regularity of ${\mathcal F}"(u, \cdot)$, as desired.

Eventually, the proof of property 4 is standard and follows as in, e.g., [9,Lemma 3.7].

In the following theorem we show that the $\Gamma$-limit ${\mathcal F}$ can be represented in an integral form as a free-discontinuity functional. Moreover, thanks to [5,Theorem 4] the functional ${\mathcal F}$ turns out to be non-degenerate, unlike the functionals ${\mathcal F}_k$.

Theorem 2.15 (Integral representation of the $\Gamma$-limit). Let ${\mathcal F}$ be as in Theorem 2.14. Then, there exist a Carathéodory function $f_\infty \colon {\mathbb R}^n \times {\mathbb R}^n\to [0, +\infty)$ and a Borel function $g_\infty \colon {\mathbb R}^n \times {\mathbb S}^{n-1}\to (0, +\infty)$ such that

for every $u\in GSBV^p(\Omega)$ and every $U\in \mathcal{A}(\Omega)$.

Furthermore, the function $f_\infty \colon {\mathbb R}^n \times {\mathbb R}^n\to [0, +\infty)$ satisfies the following properties:

i) (convexity in $\xi$) for a.e. $x\in {\mathbb R}^n$, $f_\infty(x, \cdot)$ is convex;

ii) ($p$ growth and coercivity) there exists $\tilde c_1 > 0$ such that for a.e. $x\in {\mathbb R}^n$ and for every $\xi\in {\mathbb R}^n$ it holds

where $c_2$ is as in (2.1).

The function $g_\infty \colon {\mathbb R}^n \times {\mathbb R} \times {\mathbb S}^{n-1} \to [0, +\infty)$ satisfies the following properties:

iii) (monotonicity in $t$ and symmetry) for a.e. $x\in {\mathbb R}^n$ and for every $\nu\in {\mathbb S}^{n-1}$, $g_\infty (x, \cdot, \nu)$ is nondecreasing on $(0, +\infty)$ and satisfies the symmetry condition $g_\infty(x, -t, -\nu) = g_\infty(x, t, \nu)$ for every $t\in {\mathbb R}$;

iv) (subadditivity in $t$) for a.e. $x\in {\mathbb R}^n$ and for every $\nu\in {\mathbb S}^{n-1}$

for every $t_1, t_2\in {\mathbb R}$;

v) (convexity in $\nu$) for a.e. $x\in {\mathbb R}^n$ and for every $t\in {\mathbb R}$, the $1$-homogeneous extension of $g_\infty(x, t, \cdot)$ to ${\mathbb R}^n$ is convex. Equivalently, for a.e. $x\in {\mathbb R}^n$ and for every $t\in {\mathbb R}$ the function $g_\infty$ satisfies

for every $\nu, \nu_1, \nu_2\in {\mathbb S}^{n-1}$, $\lambda_1, \lambda_2\geq 0$ such that $\lambda_1 \nu_1+\lambda_2 \nu_2 = \nu$;

vi) (bounds) there exists $\tilde c_3 > 0$ such that for a.e. $x\in {\mathbb R}^n$, for every $t\in {\mathbb R}$, and every $\nu\in {\mathbb S}^{n-1}$ it holds

where $c_4$ is as in (2.2).

Proof. Let $\mathcal E_k: L^1(\Omega)\times \mathcal{A}(\Omega)\longrightarrow [0, +\infty]$ be the functionals defined as

with $c_1$ and $c_3$ as in (2.1) and (2.2), respectively. Appealing to [5,Theorem 4] and also noticing that the $L^p$-convergence in the statement can be equivalently replaced by the convergence in Definition 2.2, we deduce that $\mathcal E_{k}(\cdot, U)$ $\Gamma$-converges to $\mathcal E(\cdot, U)$ for every $U\in \mathcal{A}(\Omega)$, where

with $\hat f$ and $\hat g$ as in [5,Theorem 4] formulas (40) and (41), respectively. Moreover $\hat f$ and $\hat g$ satisfy

for some $\tilde c_1, \tilde c_3 > 0$. Then, since $\mathcal E_k \leq {\mathcal F}_k$, we may deduce that for every $u\in SBV^p(\Omega)$ and every $U\in \mathcal{A}(\Omega)$ we have

We recall that for every $u\in SBV^p(\Omega)$ and every $U\in \mathcal{A}(\Omega)$ we also have

where $\mathcal G$ is as in (2.26).

Now let $\sigma > 0$ and for every $u\in SBV^p(\Omega)$ and $U\in \mathcal{A}(\Omega)$ set

For every fixed $\sigma > 0$ the functional ${\mathcal F}^\sigma$ satisfies properties 1, 2, and 4 in Theorem 2.14. Moreover, in view of (2.31)–(2.32) it holds

Therefore, we can invoke the integral representation result [7,Theorem 1] to deduce that for every $u\in SBV^p(\Omega)$ and every $U\in \mathcal{A}(\Omega)$ we have

where $f^\sigma_\infty$ and $g^\sigma_\infty$ are given by the following derivation formulas

and

By (2.33) and (2.34) the sequences $(f^\sigma_\infty)_{\sigma > 0}$ and $(g^\sigma_\infty)_{\sigma > 0}$ are decreasing as $\sigma$ decreases, therefore by setting $f_\infty: = \lim_{\sigma\to0^+}f_\infty^\sigma$ and $g_\infty: = \lim_{\sigma\to0^+}g_\infty^\sigma$, by the pointwise convergence of $({\mathcal F}^\sigma)_{\sigma > 0}$ to ${\mathcal F}$ and the Monotone Convergence Theorem, we get

for every $u\in SBV^p(\Omega)$ and $U\in \mathcal{A}(\Omega)$. Eventually, a standard truncation and continuity argument allows to extend this integral representation to the whole space $GSBV^p(\Omega)$ and thus to get exactly (2.27).

The measurability properties of $f_\infty$ and $g_\infty$ follow from the derivation formulas (2.33) and (2.34), arguing as in the appendix of ^[12]. The convexity of $f_\infty$ in $\xi$, the subadditivity of $g_\infty$ in $t$, and the convexity in $\nu$ of its $1$-homogeneous extension are immediate consequences of the $L^1(\Omega)$-lower semicontinuity of ${\mathcal F}$.

To show that $f_\infty$ and $g_\infty$ satisfy, respectively, the lower bounds as in $ii)$ and $vi)$ we argue as follows. Set

and for every $x\in {\mathbb R}^n$ and $\xi\in {\mathbb R}^n$ define

while for every $x\in {\mathbb R}^n$, $t\in {\mathbb R}$, and $\nu\in {\mathbb S}^{n-1}$ set

Since $\Phi^\sigma \leq {\mathcal F}^\sigma$ on $SBV^p(\Omega)$ we clearly have both $\phi^\sigma \leq f_\infty^\sigma$ and $\psi^\sigma \leq g_\infty^\sigma$. We now show that $\phi^\sigma(x, \xi) = \tilde c_1 |\xi|^p$ for every $x\in {\mathbb R}^n$ and every $\xi\in {\mathbb R}^n$ and $\psi^\sigma(x, t, \nu) = \tilde c_3 +\sigma t$. To do so we notice that by the homogeneity in $x$ of $\Phi^\sigma$, we have both $\phi^\sigma(x, \xi) = \phi^\sigma(0, \xi)$ for every $x\in {\mathbb R}^n$ and every $\xi\in {\mathbb R}^n$ and $\psi^\sigma(x, t, \nu) = \psi^\sigma(0, t, \nu)$. We can now apply the integral representation result [7,Theorem 1] to $\Phi^\sigma$ so that choosing $u = u_\xi$ and $U = Q$ we obtain

while choosing $u = u^{t, \nu}_0$ and $U = Q^\nu$ we obtain

and hence the desired equalities. Therefore we deduce

which immediately gives the lower bound of $f_\infty$; moreover there holds

hence, taking the inf on $\sigma > 0$ yields the the lower bound on $g_\infty$.

The upper bound in $ii)$ immediately follows from (2.33) and the obvious inquality ${\mathcal F}^\sigma(u_\xi, Q_\rho(x)) \leq \rho^n c_2(1+|\xi|^p)$, while the upper bound in $vi)$ follows from (2.34) and

which holds true for every $\sigma > 0$ and hence also in the limit as $\sigma \to 0^+$.

Finally, the monotonicity in $t$ and the symmetry of $g_\infty$ easily follow from (2.34).

Theorem 2.16 ($\Gamma$-convergence). Let ${\mathcal F}_k$ be the functionals defined in (2.3). Then, there exists a subsequence $k_j \to +\infty$ such that $({\mathcal F}_{k_j})$ $\Gamma$-converges to the functional ${\mathcal F}$ given by (2.27), for some Carathéodory function $f_\infty \colon {\mathbb R}^n \times {\mathbb R}^n\to [0, +\infty)$ and some Borel function $g_\infty \colon {\mathbb R}^n \times {\mathbb S}^{n-1}\to (0, +\infty)$ satisfying properties $(i)-(vi)$ as in Theorem 2.15.

Proof. The proof is an immediate consequence of Theorem 2.14 and Theorem 2.15.

Corollary 2.17 ($\Gamma$-convergence of porous brittle materials). Let $\alpha_ k = \beta _ k = 0$ and let ${\mathcal F}_k$ be the corresponding functionals given by (2.3). Then, there exists a subsequence $k_j \to +\infty$ such that $({\mathcal F}_{k_j})$ $\Gamma$-converges with respect to the $L^1(\Omega)$-convergence to the functional ${\mathcal F}$ given by (2.27), for some Carathéodory function $f_\infty \colon {\mathbb R}^n \times {\mathbb R}^n\to [0, +\infty)$ and some Borel function $g_\infty \colon {\mathbb R}^n \times {\mathbb S}^{n-1}\to (0, +\infty)$ satisfying properties $(i)-(vi)$ as in Theorem 2.15.

Proof. Since the $L^1(\Omega)$-convergence implies the convergence in Definition 2.2, the proof of the liminf inequality is immediate from Theorem 2.16. Now let $u\in GSBV^p(\Omega)$, then by Theorem 2.16 there exists $(u_j)\subset L^1(\Omega)$ such that $u_j \leadsto u$ and $\lim_j {\mathcal F}_{k_j}(u_j) = {\mathcal F}(u)$. In view of Definition 2.2 this means that there exists a sequence $(\tilde u_j) \subset L^1(\Omega)$ such that $\tilde u_j = u_j$ a.e. in $\Omega_{k_j}$ and $\tilde u_j \to u$ in $L^1(\Omega)$. Then, since the choice $\alpha _{k_j} = \beta _{k_j} = 0$ implies the equality ${\mathcal F}_{k_j}(\tilde u_j) = {\mathcal F}_{k_j}(u_j)$, the sequence $(\tilde u_j)$ is the desired recovery sequence.

2.4.   Convergence of minimisation problems

On account of the $\Gamma$-convergence result Theorem 2.14 in this section we establish a convergence result for minimisation problems associated to a suitable perturbation of the functionals ${\mathcal F}_k$. To this end, let $h\in L^\infty(\Omega)$ and for every $k$ set

By a standard truncation argument it is immediate to show that

Proposition 2.18. Let ${\mathcal F} = \Gamma\hbox{-}\lim_{j} {\mathcal F}_{k_j}$ and let $(u_j) \subset SBV^p(\Omega)$ be such that

Then, up to subsequences (not relabelled), $u_j$ converges in the sense of Definition 2.2 to a function $\bar u \in SBV^p(\Omega)\cap L^\infty(\Omega)$ which solves

where $C(K): = \mathcal L^n(Q\setminus K)$. Moreover it holds $M_{j} \to M$, as $j\to +\infty$.

Proof. Let $(u_j)\subset SBV^p(\Omega)$ be as in (2.36). Then, in view of (2.35), (H1), and (H3) we have

Therefore Theorem 2.1 yields the existence of a function $\bar u\in SBV^p(\Omega)\cap L^\infty(\Omega)$ and of a sequence $(\tilde u_j) \subset SBV^p(\Omega)$ with $\tilde u_j = u_j$ a.e. in $\Omega_{k_j}$ such that (up to subsequences) $\tilde u_j \to \bar u$ in $L^p(\Omega)$, moreover $\|\bar u\|_{L^\infty(\Omega)}\leq \|h\|_{L^\infty(\Omega)}$. We have

thus by Theorem 2.14 we get

Therefore, by definition of $u_j$ we obtain

Now let $w\in SBV^p(\Omega)\cap L^\infty(\Omega)$ be an arbitrary function such that $\|w\|_{L^\infty(\Omega)}\leq \|h\|_{L^\infty(\Omega)}$. Again appealing to Theorem 2.14 we can find $(w_j) \subset L^1(\Omega)$ such that $w_j \leadsto w$ and $\lim_{j} {\mathcal F}_j(w_j) = {\mathcal F}(w)$. Now let $\tilde w_j$ be as in Definition 2.2, let $m: = \|h\|_{L^\infty(\Omega)}$ and denote with $(\tilde w_j^m)$ the sequence of truncated functions of $(\tilde w_j)$ at level $m$. We clearly have $\tilde w^m_j = w^m_j$ a.e. in $\Omega_{k_j}$ and $\tilde w^m_j \to w$ in $L^p(\Omega)$. Hence

Moreover, since $\limsup_{j} {\mathcal F}_j(w^m_j) \leq {\mathcal F}(w)$, we immediately deduce

Finally, by gathering (2.37) and (2.38) we obtain

hence by the arbitrariness of $w$ we deduce that $\bar u$ is a minimiser for ${\mathcal F}+C(K)\|\cdot -h\|^p_{L^p(\Omega)}$. Finally, taking $w = \bar u$ also implies $M_j \to M$. Since moreover this limit does not depend on the subsequence, the convergence holds true for the whole $(M_j)$.

3.   Part Ⅱ: Examples

In this section we restrict the analysis to the case of $\varepsilon_k$-periodic integrands $f_k$ and $g_k$. That is, we consider the functionals ${\mathcal F}_k^{\alpha_ k, \beta _ k} \colon L^1(\Omega)\longrightarrow [0, +\infty]$ defined as

where $f$ and $g$ are $Q$-periodic in the first variable and satisfy (H1)–(H2) and (H3)–(H4), respectively.

With the help of some specific examples, which correspond to some specific choices of $f$, $g$, and $\Omega_k$, we show that the $\Gamma$-limit of ${\mathcal F}_k^{\alpha_ k, \beta _ k}$ is highly sensitive both to the choice of the coefficients $\alpha_ k$, $\beta _ k$ and to the asymptotic behaviour of $\alpha_ k$, $\beta _ k$ compared to the period of the microstructure $\varepsilon_k$. The examples we are going to discuss are taken from Barchiesi and Focardi ^[5] (see also Cagnetti and Scardia ^[14] and Focardi, Gelli and Ponsiglione ^[17]), from Barchiesi, Lazzaroni and Zeppieri ^[6], and from Pellet, Scardia and Zeppieri ^[19]. For the corresponding proofs we refer the reader to the aforementioned papers.

3.1.   Periodic brittle porous materials

In this subsection we consider the limit case $\alpha_ k = \beta _ k = 0$; i.e., we consider the functionals

Loosely speaking, in this case the soft or weak inclusions in the material are replaced by perforations ^[5,14,17].

Theorem 3.1 (Homogenisation of periodic porous brittle materials). Let ${\mathcal F}_k^{0, 0}$ be the functionals as in (3.2). Then $({\mathcal F}_k^{0, 0})$ $\Gamma$-converges both with respect to the convergence in Definition 2.2 and with respect to the $L^1(\Omega)$-convergence to the functional ${\mathcal F}^0$ which is finite on $GSBV^p(\Omega)$ and given by

where $f^0$ and $g^0$ are, respectively, given by the following homogenisation formulas

for every $\xi \in {\mathbb R}^n$, whereas

for every $\nu \in {\mathbb S}^{n-1}$.

Proof. Theorem 2.16 and Corollary 2.17 yield the existence of a subsequence $k_j \to +\infty$ such that the corresponding functionals ${\mathcal F}_{k_j}^{0, 0}$ $\Gamma$-converge to ${\mathcal F}$ as in (2.27), both with respect to the convergence in Definition 2.2 and to the $L^1(\Omega)$-convergence. Then, the homogenisation formulas (3.4) and (3.5) together with the identity ${\mathcal F} = {\mathcal F}^0$ follow from [5,Theorem 4]. Finally, since (3.4) and (3.5) are subsequence-independent, invoking the Urysohn property [15,Proposition 8.3] readily implies the $\Gamma$-convergence of the whole sequence $({\mathcal F}_k^{0, 0})$ to ${\mathcal F}^0$.

The following result is an immediate consequence of Theorem 3.1 and of an adaptation of the Cagnetti and Scardia extension result [14,Theorem 1.3] to the case of a general exponent $p > 1$.

Corollary 3.2. Let $\alpha_ k, \beta _ k \to 0$ and let ${\mathcal F}_k^{\alpha_ k, \beta _ k}$ be the corresponding functionals as in (2.3). Then, the sequence $({\mathcal F}_k^{\alpha_ k, \beta _ k})$ $\Gamma$-converges to the functional ${\mathcal F}^0$ given by (3.3).

Proof. By Theorem 2.16 (up to subsequences not relabelled) the functionals ${\mathcal F}^{\alpha_ k, \beta _ k}_k$ $\Gamma$-converge to ${\mathcal F}$. Since ${\mathcal F}_k^{0, 0} \leq {\mathcal F}_k^{\alpha_ k, \beta _ k}$ by Theorem 3.1 we immediately get ${\mathcal F}^0\leq {\mathcal F}$.

We now prove the converse inequality. To this end let $u\in SBV^p(\Omega) \cap L^\infty(\Omega)$ and let $(u_k) \subset SBV^p(\Omega_k)$ be a recovery sequence for ${\mathcal F}_k^{0, 0}$. That is $u_k \leadsto u$ and $\lim_k {\mathcal F}_k^{0, 0}(u_k) = {\mathcal F}(u)$. Since the functionals ${\mathcal F}_k^{0, 0}$ decrease by truncation it is not restrictive to assume that $\|u_k\|_{L^\infty(\Omega)}\leq \|u\|_{L^\infty(\Omega)}$. Starting from $(u_k)$ we now want to construct a sequence $(v_k)$ which both satisfies $v_k \to u$ in $L^1(\Omega)$ and $\lim_k {\mathcal F}_k^{\alpha_ k, \beta _ k}(v_k) = {\mathcal F}^0(u)$. To this end, we start noticing that the bounds (2.1) and (2.2) readily imply

For every fixed $k$ let $v_k: = T^k u_k \in SBV^p(\Omega)$ be the extended function of $u_k$ to $\Omega$ whose existence is given by [14,Theorem 1.3]; i.e., $v_k$ is such that $v_k = u_k$ a.e. in $\Omega_k$, $\|u_k\|_{L^\infty(\Omega)}\leq \|u\|_{L^\infty(\Omega)}$, and

for some $C > 0$ independent of $k$. By definition of $v_k$, also invoking the Ambrosio compactness Theorem, it is immediate to check that $v_k \to u$ in $L^1(\Omega)$.

By (3.7) we get that

where (3.8) is infinitesimal thanks to (3.6), since $\max\{\alpha_ k, \beta _ k\}\to 0$ as $k\to +\infty$. Thus eventually

hence $(v_k)$ is the desired sequence. Therefore, by the $\Gamma$-convergence of ${\mathcal F}_k^{\alpha_ k, \beta _ k}$ to ${\mathcal F}$ we can deduce that for every $u\in SBV^p(\Omega)\cap L^\infty(\Omega)$ it holds ${\mathcal F}(u)\leq {\mathcal F}^0(u)$.

Now let $u\in GSBV^p(\Omega)$ and denote with $u^m$ its truncated function at level $m > 0$. We clearly have ${\mathcal F}(u^m)\leq {\mathcal F}^0(u^m)\leq {\mathcal F}^0(u)$, hence the desired inequality follows by the $L^1(\Omega)$ convergence $u^m$ to $u$ and by the lower semicontinuity of ${\mathcal F}$.

The following remarks are in order.

Remark 3.3. In view of Remark 2.10, both in Theorem 3.1 and in Corollary 3.2 assumption (H2) on $f$ can be dropped.

Remark 3.4 (On $f^0$). The homogenised volume energy density $f^0$ given by (3.4) is the same as that obtained by Acerbi, Chiadó-Piat, Dal Maso and Percivale ^[1] in the case of elastic perforated materials. Moreover, it is easy to check that if $f$ is $p$-homogeneous then the corresponding $f^0$ given by (3.4) is also $p$-homogeneous.

Remark 3.5 (Energy decoupling). In spite of the strong degeneracy of the integrands in (3.2) (resp. in (3.1)), which in this case are identically equal to zero (resp. both infinitesimal) in the $\varepsilon_k$-periodic set $\Omega\setminus \Omega_k$, Theorem 3.1 (resp. Corollary 3.2) shows that the functionals ${\mathcal F}_k^{0, 0}$ (resp. ${\mathcal F}_k^{\alpha_ k, \beta _ k}$) exhibit a limit behaviour which is qualitatively similar to that of free-discontinuity functionals with coercive integrands ^[9,13,18]. Namely, in the homogenised limit there is no interaction between bulk and surface term. As a consequence the homogenised surface energy density $g^0$ does not depend on $t$, and therefore the $\Gamma$-limit is of brittle type.

3.2.   Periodic brittle high-contrast materials

In this section we show that if only one of the coefficients $\alpha_ k$ and $\beta _ k$ is infinitesimal (while the other stays uniformly bounded from below), then the asymptotic behaviour of the functionals ${\mathcal F}^{\alpha_ k, \beta _ k}_k$ can be very different from that of ${\mathcal F}^{0, 0}_k$ (or of ${\mathcal F}^{\alpha_ k\to 0, \beta _ k\to 0}_k$). In particular, we show that in this case a volume-surface energy coupling cannot be excluded in general. To do so we exhibit coefficients $\alpha_ k, \beta _ k$, integrands $f, g$ and a geometry for the periodic set $E$ which give rise to the desired limit coupling. This is done by resorting to the analysis of Barchiesi, Lazzaroni and Zeppieri ^[6] and Pellet, Scardia and Zeppieri ^[19], which is briefly reviewed in Subsection 3.2.1 and Subsection 3.2.2, respectively.

The functionals analysed in ^[6] and ^[19] are both of Mumford-Shah type and can be written in the form

where $a_k, b_k \colon {\mathbb R}^n \to [0, 1]$ are $Q$-periodic functions and in the periodicity cell $Q$ are defined as

with $r\in (0, 1)$. From (3.9)–(3.10) we infer that in this case $f = f(\xi) = |\xi|^2$, $g\equiv 1$, and $\Omega_k = \Omega \cap \varepsilon_k E$ with $E = {\mathbb R}^n \setminus \bigcup_{i\in {\mathbb Z}^n} (\overline Q_r+i)$.

Remark 3.6 (Mumford-Shah functional in perforated domains). The choice $\alpha_ k = \beta _ k = 0$ corresponds to the Mumford-Shah functionals in perforated domain. The functional $\mathcal{MS}^{0, 0}_k$ is a special instance of (3.2) and its homogenised limit is treated in ^[14,17] for general sets $E$. In this case the homogenised integrands (3.4) and (3.5) reduce, respectively, to

for every $\xi \in {\mathbb R}^n$, and to

for every $\nu \in {\mathbb S}^{n-1}$. From (3.11) and (3.12) it is easy to check that $f^0(\xi) = A^0 \xi \cdot \xi$, for some $A^0 \in {\mathbb R}^{n\times n}$ which satisfies $\tilde c_1 I \leq A^0 \leq I$, in the sense of quadratic forms (cf. (2.28)). Hence, $f^0$ is a positive quadratic form. Moreover, it holds $g^0(e_i) = 1-r^{n-1}$, for every $i = 1, \ldots, n$.

3.2.1.   Soft inclusions

We consider the case $\alpha_ k \to 0$ and $\beta _ k = 1$ which models the situation where the periodic set $\Omega \setminus \Omega_k$ is occupied by a brittle material with a very small elastic modulus. For this reason, we refer to the set $\Omega \setminus \Omega_k$ as the set of soft inclusions. With this choice the functionals in (3.9) become

In ^[6] Barchiesi, Lazzaroni and Zeppieri showed that the asymptotic behaviour of $\mathcal{MS}^{\alpha_k, 1}_k$ heavily depends on the mutual vanishing rate of $\alpha_ k$ and $\varepsilon_k$; that is, it depends on the parameter

For the proof of Theorem 3.7 below we refer the reader to [6,Theorems 1,4,and Remark 6].

Theorem 3.7 (Homogenisation of periodic brittle materials with soft inclusions). Let $\mathcal{MS}_k^{\alpha_ k, 1}$ be the functionals defined in (3.13) and let $\ell\in [0, +\infty]$ be as in (3.14). Then, up to subsequences not relabelled, $(\mathcal{MS}_k^{\alpha_ k, 1})$ $\Gamma$-converges to the functional ${\mathcal F}^\ell$ which is finite on $GSBV^2(\Omega)$ and given by

where $f^0$ is as in (3.11) and for every $t\in {\mathbb R}$, $\nu\in {\mathbb S}^{n-1}$

Moreover for every $\ell \in (0, +\infty)$ it holds

for every $t > 0$, $i = 1, \dots, n$, and for some $c_\ell, \hat c_\ell > 0$, with $\lim_{\ell \to 0+}c_\ell = \lim_{\ell \to 0+}\hat c_\ell = 0$.

Remark 3.8. The following remarks are in order.

$(i)$ As far as the homogenised volume energy is concerned, the soft inclusions are (energetically) equivalent to the perforations in the material.

$(ii)$ For $\ell = 0$, which corresponds to $\alpha_ k \ll \varepsilon_k$, the functionals $\mathcal{MS}_k^{\alpha_ k, 1}$ are equivalent to the functionals $\mathcal{MS}_k^{0, 0}$, in the sense of $\Gamma$-convergence.

$(iii)$ For $\ell\in (0, +\infty)$ the bounds in (3.16) imply that, along the coordinate directions, $g^\ell$ depends on $t$. Moreover it becomes constant (and equal to $1$) above a certain threshold $t_0 > 0$; i.e., $g^\ell$ is of cohesive type. Being the microscopic energies $\mathcal{MS}_k^{\alpha_ k, 1}$ of brittle type, the cohesive behaviour of $g^\ell$ can only be explained as the result of a non trivial bulk-surface coupling by homogenisation. This interaction is particularly apparent from the upper-bound construction in ^[6] which we briefly illustrate here in the case $n = 2$.

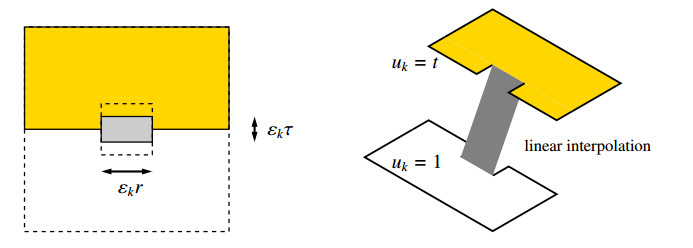
For $i = 1, 2$ we have $g^\ell(t, e_i) = {\mathcal F}^\ell(u_{0}^{e_i, t}, Q)$, moreover it is immediate to check that $g^\ell(t, e_1) = g^\ell(t, e_2)$. Clearly $g^\ell(t, e_2)\leq 1$ for every $t > 0$. Then, to get the upper bound in (3.16) it suffices to show that $g^\ell(t, e_2)\leq g^0(e_2)+\hat c_\ell t$ for some $\hat c_\ell > 0$. Let $R\subset Q \subset {\mathbb R}^2$ be the open rectangle defined as

with $\tau \in (0, r)$ to be determined. Set

and let $(u_k)\subset SBV^2(Q)$ be the sequence of functions defined as

(see Figure 2). We clearly have $u_k\rightarrow u_{0}^{e_2, t}$ in $L^1(Q)$; moreover

therefore

Hence, by optimising on $\tau$ we get

thus the desired estimate follows with $\hat c_\ell = 2\sqrt{2 \ell}$, by recalling that $g^0(e_2) = 1-r$.

Loosely speaking, the construction as above shows that, the cost of an elastic deformation of the soft inclusions is of the same order of the energy spent to create a microscopic crack. Since the former depends linearly on $t$ (while the latter is constant in $t$) for small values of $t$, to approximate a macroscopic crack it can be convenient to combine microscopic deformations of the soft inclusions (with high gradients) and microscopic jumps.

$(iv)$ Even if not immediately apparent from the homogenisation formulas, a volume-surface interaction takes place for $\ell = 0$, as well. Indeed, in this case $g^\ell = g^0$ whereas in $\mathcal{MS}^{\alpha_ k, 1}_k$ the surface energy density is identically equal to one. In this case in fact, the cost of an elastic deformation of the soft inclusions is negligible (cf. (3.17) for $\ell = 0$) so that to approximate a macroscopic crack it is never convenient to introduce microscopic cracks inside the soft material. On the contrary, in the regime $\ell = +\infty$, which corresponds to $\alpha_ k\gg \varepsilon_k$, there is a complete volume-surface decoupling, as in the coercive case.

3.2.2.   Weak inclusions

We consider the case $\alpha_ k = 1$ and $\alpha_ k \to 0$ which models the situation where the periodic set $\Omega \setminus \Omega_k$ is occupied by a brittle material with a very small fracture resistance. For this reason, we refer to the set $\Omega \setminus \Omega_k$ as the set of weak inclusions. With this choice the functionals in (3.9) become

In ^[19] Pellet, Scardia and Zeppieri showed that the asymptotic behaviour of $\mathcal{MS}^{1, \beta _ k}_k$ heavily depends on the mutual vanishing rate of $\beta _ k$ and $\varepsilon_k$, that is on the parameter

For the proof of Theorem 3.9 below we refer the reader to ^[19].

Theorem 3.9 (Homogenisation of periodic brittle materials with weak inclusions). Let $\mathcal{MS}_k^{1, \beta _ k}$ be the functionals defined in (3.18) and let $\ell'\in[0, +\infty]$ be as in (3.19). Then, up to subsequences not relabelled, $(\mathcal{MS}_k^{1, \beta _ k})$ $\Gamma$-converges to the functional ${\mathcal F}^{\ell'}$ which is finite on $GSBV^2(\Omega)$ and given by

where $g^0$ is as in (3.12) and for every $\xi\in {\mathbb R}^n$

Moreover for every $\ell' \in (0, +\infty)$ it holds

for every $\xi\in {\mathbb R}^n$ and for some $C > 0$.

Remark 3.10 The following remarks are in order.

$(i)$ As far as the homogenised surface energy is concerned, the weak inclusions are (energetically) equivalent to the perforations in the material.

$(ii)$ For $\ell' = 0$, which corresponds to $\beta _ k \ll \varepsilon_k$, the functionals $\mathcal{MS}_k^{1, \beta _ k}$ are equivalent to the functionals $\mathcal{MS}_k^{0, 0}$, in the sense of $\Gamma$-convergence. Indeed, "removing the weak inclusions from the material" has an infinitesimal cost of order $\beta _ k/ \varepsilon_k$ given by the perimeter of the weak inclusions (proportional to $\beta _ k \varepsilon_k^{n-1}$) multiplied by $\varepsilon_k^{-n}$ (the number of $\varepsilon_k$-cells contained in $\Omega$). In this case a volume-surface energy coupling takes place since the elastic energy can be lowered by introducing cracks in the materials.

$(iii)$ For $\ell'\in (0, +\infty)$ the bounds in (3.21) hold true (see [19,Lemma 6.1]). The bound from below is immediate and it is a consequence of the trivial bound $\mathcal{MS}_k^{0, 0}\leq \mathcal{MS}_k^{1, \beta _ k}$. The bound from above shows that for large deformations; i.e., for large $|\xi|$, to approximate a macroscopic elastic deformation is energetically favourable to mix elastic deformations and jumps in the weak inclusions. Moreover, (3.21) implies that for $|\xi|$ large it holds $f^{\ell'}(\xi) < |\xi|^2$. The latter shows that a stiffness degradation occurs in the homogenised limit, and that the macroscopic energy ${\mathcal F}^{\ell'}$ describes a damaged material (the same being true for $\ell = 0$).

$(iv)$ The bounds in (3.21) combined with an easy scaling argument show that in the regime $\ell'\in(0, +\infty)$ the homogenised volume energy density $f^{\ell'}$ is not $2$-homogeneous. Indeed, assume by contradiction that this is not the case and let $\lambda \neq 0$. Taking into account that $f^0$ is $2$-homogeneous (see Remark 3.4), we can replace in (3.21) $\xi$ with $\lambda \xi$ and divide by $\lambda^2$ to get

Therefore by letting $|\lambda| \to +\infty$ we get $f^{\ell'}\equiv f^0$ which leads to a contradiction in view of [19,Proposition 6.10].

$(v)$ In the regime $\ell' = +\infty$, which corresponds to $\beta _ k\gg \varepsilon_k$, there is a complete volume-surface decoupling, as in the coercive case. Loosely speaking, in this case the fracture resistance of the weak inclusions is not small enough to make cracks energetically more convenient than (or at least comparable to) elastic deformations.

Acknowledgments

This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under the Germany's Excellence Strategy EXC 2044-390685587, Mathematics Münster: Dynamics–Geometry–Structure.

Conflict of interest

The author declares no conflict of interest.