Linearization and computation for large-strain visco-elasticity

1.   Introduction

In-time-semidiscretized problems of nonlinear visco-elasticity in Kelvin-Voigt rheology lead to a sequence of minimization problems where a current solution depends on the previous one. More precisely, starting from an initial condition $y^0$ we must find for $k = 1, \ldots T/\tau$

where $\tau > 0$ is a time step, $T$ is a final time, $W$ is an elastic energy density and $D$ is a dissipation due to viscosity. However, physically acceptable dissipation functions are not (Morrey) quasiconvex ^[1]. As we are interested in the limit for $\tau\to 0$, the problem (1.1) does not necessarily have a minimizer since, for small $\tau$, the non-quasiconvexity of $D$ cannot be compensated for by any convexity of $W$. This suggests microstructure formation due to rapidly oscillating deformation gradients, which, however, is not observed in reality. The aim of this work is to explore this discrepancy.

Due to dissipative effects, we expect $y^k$ to be found in a small neighborhood of $y^{k-1}$. Thus, the minimization in (1.1) should be local. For that reason, we linearize the energy functional in (1.1) in the spirit of ^[7]. Thus, we obtain a quadratic energy contribution that stems from the dissipation and stress of the elastic energy. The resulting functional is not coercive, but, in spite of this, minimizers exist, as we show.

We perform numerical experiments by comparing the original nonlinear scheme in (1.1) with our linearized scheme for small time steps that show very good quantitative agreement. Moreover, both schemes satisfy an energy balance.

2.   Modeling of nonlinear visco-elasticity

If we neglect inertial effects, the deformation $y:[0, T]\times \Omega\to {\mathbb R}^d$ of a nonlinear viscoelastic material in Kelvin-Voigt rheology obeys the following system of equations

Here, $[0, T]$ is a process time interval, $\Omega\subset {\mathbb R}^d$ ($d = 2$ or $d = 3$) is a smooth bounded domain representing the reference configuration, $\Gamma_D\cup\Gamma_N$ is a disjoint partition of $\partial\Omega$ such that $\Gamma_D$ has a positive $(d-1)$-dimensional Hausdorff measure. In addition, $f:[0, T]\times\Omega\to {\mathbb R}^d$ is a density of body forces and $g:[0, T]\times\Gamma_N\to {\mathbb R}^d$ is a density of surface forces. We also impose boundary data $y_D : [0, T]\times \Gamma_D \to {\mathbb R}^d$ and an initial condition $y^0: \Omega \to {\mathbb R}^d$.

The properties of the material are described by the stored energy density $W: {\mathbb R}^{d\times d}\to [0, \infty]$, where its gradient represents the first Piola-Kirchhoff stress tensor, and by a (pseudo)potential of dissipative forces $R: {\mathbb R}^{d \times d} \times {\mathbb R}^{d \times d} \to [0, \infty)$.

The stress tensor ${S}(F, \dot F): = \partial_{\dot F} R(F, \dot F)$ has its origin in the viscous dissipative mechanisms of the material. Naturally, we require $R(F, \dot F)\ge R(F, 0) = 0$. The viscous stress tensor must comply with the time-continuous frame-indifference principle, meaning that for all $F, \dot{F}\in {\mathbb R}^{d\times d}$

with some $\tilde {S} : {\mathbb R}^{d \times d}_{{\mathop{{\text{sym}}}}} \times {\mathbb R}^{d \times d}_{{\mathop{{\text{sym}}}}} \to {\mathbb R}^{d \times d}_{{\mathop{{\text{sym}}}}}$ where $C = F^{\top} F$ and $\dot{C} = \dot{F}^{\top} F + F^{\top} \dot{F}$. This condition constrains $R$ so that (see ^[1,2,12])

for some non-negative function $\tilde R$ such that $\tilde R(C, 0) = 0$. In other words, $R$ must depend on the right Cauchy-Green strain tensor $C$ and its time derivative $\dot C$. On the other hand, this property makes the analysis of (2.1) very difficult. To our knowledge, the existence of a solution has not been established so far. If the stored energy is enriched by the second gradient of deformation, the existence results are available in various settings; see ^[8,11] in three dimensions and ^[3,12] in one dimension.

In any case, a standard approach to obtain solutions for such evolution problems is to introduce an implicit time discretization. For simplicity, we will assume that $y_D$ is constant in time in the sequel. Let $\tau > 0$ be a time step such that $T/\tau\in {\mathbb N}$. Given an initial condition $y^0_\tau$, for $k = 1, \ldots, T/\tau$, we now want to find $y_\tau^k$ such that

that is, $y_\tau^k$ should solve a discretized version of (2.1). In the following, we summarize our setting and the basic assumptions used to treat this incremental time minimization problem.

Stored elastic energy and body forces: We assume that the stored elastic energy $W: {\mathbb R}^{d \times d} \to [0, \infty]$ has the following properties:

We introduce the nonlinear elastic energy $\phi^k_\tau: W^{1, p}(\Omega; {\mathbb R}^d) \to [0, \infty]$ by

for $y: W^{1, p}(\Omega; {\mathbb R}^d) \to {\mathbb R}^d$. In what follows, we assume that $\phi^k_\tau:W^{1, p}(\Omega; {\mathbb R}^d)\to {\mathbb R}\cup\{+\infty\}$ is sequentially weakly lower semicontinuous.

Dissipation potential and viscous stress: Consider a time-dependent deformation $y: [0, T] \times \Omega \to {\mathbb R}^d$. Viscosity is not only related to strain $\nabla y(t, x)$, but also to strain rate $\nabla \dot y(t, x)$ and can be expressed in terms of dissipation potential $R(\nabla y, \nabla \dot y)$. An admissible potential has to satisfy the frame indifference in the sense (see ^[1,12])

for all $F \in {\mathrm{GL}}_+(d)$ and $\dot{F} \in {\mathbb R}^{d \times d}$, where

Following the discussion in [12,Section 2.2], from the point of view of modeling, it is much more convenient to postulate the existence of a (smooth) global distance $D: {\mathrm{GL}}_+(d) \times {\mathrm{GL}}_+(d) \to [0, \infty)$ that satisfies $D(F, F) = 0$ for all $F \in {\mathrm{GL}}_+(d)$. From this distance, an associated dissipation potential $R$ can be calculated by

for $F \in {\mathrm{GL}}_+(d)$, $\dot{F} \in {\mathbb R}^{d \times d}$. Above, the fourth-order tensor $\partial^2_{F_1^2} D^2(F_1, F_2)$ denotes the Hessian of $D^2$ in the direction of $F_1$ at $(F_1, F_2)$.

For the sake of simplicity, in the present work we use

where $C_i = F_i^\top F_i$ for $i = 1, 2$ and $|A|^2 = \operatorname{tr}(A^\top A)$. In this case, a direct computation yields

For justification of this choice for $D$ and for further examples of admissible dissipation distances, we refer the reader to [12,Section 2.3].

Now, the solutions to (2.3) can formally be written as solutions of the following sequence of problems:

The non-quasiconvexity of $F\mapsto D(F, G)$ for a given $G$, see ^[6], would suggest that an energy-minimizing microstructure is formed in the viscous relaxation of materials. However, such a microstructure has not been observed in experiments. Thus, we propose that, in such a viscous evolution, the energy landscape is only explored in a small neighborhood of the current state, instead of the global minimization suggested by (2.9). Therefore, our approach is to minimize in each time step a problem that is linearized around $y^{k-1}_{\tau}$ in a suitable sense.

3.   Linear visco-elasticity

To motivate our linearization approach for this implicit time-discretization problem, we first consider the case of (already) linearized visco-elasticity. Here, we simply recover the original evolution equations, which (neglecting any forces) are given by the linear Kelvin-Voigt visco-elasticity problem

Here $\mathbb{C}$ and $\mathbb{D}$ are positive definite fourth-order tensors of elasticity and viscosity coefficients, respectively. Note that in this linearized setting, we work with a displacement field $u$ instead of the deformation $y$.

The variational formulation for the linear counterpart of (2.3) reads: For a given $u^{k-1}_{\tau}\in W^{1, 2}(\Omega; {\mathbb R}^d)$ with $u^{k-1}_\tau = u_D$ on $\Gamma_D$, find the minimizer $u^{k}_{\tau}$ of

under the constraints $u\in W^{1, 2}(\Omega; {\mathbb R}^d)$ and $u = u_D$ on $\Gamma_D$. Since the functional is quadratic and convex in $\nabla u$, the minimizer exists in fact and is unique. It is clear that this iterative minimization scheme, in the limit of small time steps $\tau$, leads to a solution of (3.1).

Our idea is to reformulate the minimization problem to (3.2) in terms of minimizing an increase in displacement. More precisely, we write $u = u_\tau^{k-1} + \tau z$ and minimize

or, equivalently, after subtracting the constant first term and rescaling by $\frac{1}{\tau}$, minimize

under the constraints $z \in W^{1, 2}(\Omega; {\mathbb R}^d)$ and $z = 0$ on $\Gamma_D$. We observe that the second term is dominated by the third for small $\tau$. Therefore, we minimize

instead. This problem admits a unique minimizer $z$ that solves the associated Euler-Lagrange equation

Then $u^k_\tau = u_\tau^{k-1} + \tau z$ fulfills

We note that this is an explicit Euler time step for the original evolution equation (3.1), where the standard minimization of movement results in the implicit scheme

Note that we obtained this solution from the linearized functional (3.5) and not from (3.4). This suggests that we can write a minimization problem in the velocity $z$ for the dissipated power and still obtain a reasonable time-stepping scheme for linearized Kelvin-Voigt visco-elasticity.

Emboldened by this result for the linearized problem, for which existence of solutions is of course already well known, we attempt to treat the fully non-linear case.

4.   The limit for the nonlinear visco-elastic minimization problem

We now consider again the fully nonlinear implicit time-stepping problem for visco-elasticity.

4.1.   Linearization of the minimization problem

Neglecting forces, we start with the (ill-posed) time-step problem of finding $y_\tau^{k}$ minimizing the problem

This minimization problem can be restricted to include appropriate boundary conditions. Let us, as in the linear case, see (3.3), rewrite this problem in terms of minimizing increments. By substituting $y_\tau^{k} = y_\tau^{k-1} + \tau z_\tau^{k}$, we arrive at the problem of finding $z_\tau^{k}$ as a minimizer of

We notice that for small $\tau$ the terms that are linear in $\tau$ play the crucial role in the minimization. Therefore, let us for a suitable $y : \Omega \to {\mathbb R}^{d}$ and any $\tau > 0$ define a singularly perturbed functional

Notice that the functionals in (4.2) and ${\cal F}_{y_\tau^{k-1}, \tau}$ of (4.3) are equivalent with respect to minimization. Since $\tau$ is small, let us explore the limit $\lim_{\tau \to 0} {\cal F}_{y, \tau}$ for a fixed $y$. We begin with some pointwise assessments of the density of the functional (4.3). Therefore, for simplicity, we write $Y : = \nabla y$ and $Z : = \nabla z$ and assume $\det Y \ge c > 0$ and $|Y|, |Z| \le M < \infty$.

Since $W$ is smooth, it holds

for some $\xi \in [0, \tau]$. Thus, the first two terms in (4.3) can be rewritten as

For the third term, we have (considering $D(F, G) = | F^{\top} F - G^{\top} G |$)

We note that terms containing $\tau$ become negligible since we have a uniform upper bound on admissible $|Y|$ and $|Z|$.

Then

with the remainder satisfying

for some $C = C_{c, M} > 0$. Therefore, if $y, z \in W^{1, \infty}(\Omega; {\mathbb R}^{d})$ and $\det \nabla y \ge c > 0$, we obtain the pointwise convergence

This immediately leads to the following approximation result.

Lemma 4.1. Let $y \in W^{1, \infty}(\Omega; {\mathbb R}^{d})$ with $\det \nabla y \ge c > 0$. On the set $\{ z \in W^{1, \infty}(\Omega; {\mathbb R}^{d}) : \| \nabla z \|_{ L^{\infty} } \le M \}$, the functional ${\mathcal F}_{y, \tau}$ defined in (4.3) can be uniformly approximated by

so that

where $C$ depends only on $\Omega$, $\| \nabla y \|_{ L^{\infty} }$, $c$, $M$, and $W$.

Hence, the solution to the visco-elastic evolution problem should be well approximated by

for small $\hat{\tau}$, with $z$ calculated as the minimizer of (4.7) (with $y = y^{k-1}$) in each time step. The heuristic interpretation of this method is that we derived a linearized functional (depending on given state) whose minimizer is the velocity in the evolution problem corresponding to the state. Equation (4.8) then is nothing but a forward Euler time step with this velocity.

4.2.   Existence of minimizers

Let us explore the properties of the functional in (4.7). In the following, restricting ourselves to the physically relevant case $d = 3$, we fix $y \in C^{2}(\overline{\Omega}; {\mathbb R}^{3})$ so that $\inf_{x \in \Omega} \det \nabla y > 0$.

We immediately notice that the quadratic form in the energy (4.7) is not fully coercive, as $2 | {\mathop{{\text{sym}}}}((\nabla y)^{\top} \nabla z) |^{2} = 0$ for any skew-symmetric $(\nabla y)^{\top} \nabla z$. This is in a sense similar to the problem of linearized elasticity. It appears that the presence of the first term $\partial_F W(\nabla y) : \nabla z$ means that ${\mathcal F}_y$ is not bounded from below for directions $\nabla z$ where linearized dissipation vanishes. However, this is not the case since the second Piola-Kirchhoff stress tensor $(\nabla y)^{-1} \partial_F W(\nabla y)$ is always symmetric.

For the sake of clarity, let us denote the energy density by

If $Y^{-1} \partial_F W(Y)$ is symmetric, for any $Z \in {\mathbb R}^{3 \times 3}$ it holds

Therefore,

Therefore, the minimum of $f_{Y}$ is $- \frac{1}{8} | Y^{-1} \partial_F W(Y) |^{2}$ and is achieved at $Z$ for which it holds that ${\mathop{{\text{sym}}}}(Y^{\top} Z) = - \frac{1}{4} Y^{-1} \partial_F W(Y)$, i.e., the set of minimizers is $- \frac{1}{4} (Y Y^{\top})^{-1} \partial_F W(Y) + Y^{-\top} {\mathrm{Skew}}(3)$. Moreover, we have

Therefore, the density $f_{Y}$ and, consequently, the functional ${\mathcal F}_y$ are bounded from below.

Now we consider the lack of coercivity since the functional depends only on ${\mathop{{\text{sym}}}}((\nabla y)^{\top} \nabla z)$. Here, we rely mainly on the results in ^[13]. Let us start by determining the subspace

First, we notice

From Lemma 4.1 in ^[13] follows a higher regularity, namely $z \in C^{2}(\overline{\Omega}; {\mathbb R}^{3})$ and $\nabla z (\nabla y)^{-1} \in C^{1, 1/2}(\overline{\Omega}; {\mathbb R}^{3 \times 3})$. In Corollary 3.10 in ^[13] it was shown that if we have matrix fields $A, B \in C^{1}(\overline{\Omega}; {\mathbb R}^{3 \times 3})$ such that $A$ is skew-symmetric and $B = \nabla \psi$, then

For $z \in \mathcal{N}_{y}$ the matrix field $A = \nabla z (\nabla y)^{-1}$ is skew-symmetric. If we take $B = \nabla y$, all assumptions are fulfilled, since

Therefore, $A$ is constant and therefore $\nabla z = A \nabla y$. Consequently, $z = a + A y$ for some vector $a \in {\mathbb R}^{3}$. Equivalently, $z = a + \omega \times y$ for some vectors $a, \omega \in {\mathbb R}^{3}$. Thus, we have shown

It is a 6-dimensional subspace.

Theorem 4.2. For a given $y\in C^{2}(\overline{\Omega}; {\mathbb R}^{3})$ with $\det \nabla y > 0$, let us consider the functional

(a) ${\mathcal F}_{y}$ admits a unique minimizer on any subspace $H \subset W^{1, 2}(\Omega; {\mathbb R}^{3})$ with $H \cap \mathcal{N}_{y} = \{ 0 \}$. This includes the case $H = \{ z \in W^{1, 2}(\Omega; {\mathbb R}^{3}) : z|_{\Gamma_{D}} = 0 \}$ for some smooth $\Gamma_{D} \subset \partial \Omega$ with $\mathcal{H}^{2}(\Gamma_{D}) > 0$.

(b) On the whole $W^{1, 2}(\Omega; {\mathbb R}^{3})$ minimizers exist and are unique up to an addition of elements from $\mathcal{N}_{y}$.

The proof will rely on generalized Korn's second inequality. For the proof, see Corollaries 4.6, 4.7, and Section 5 in ^[13].

Lemma 4.3 (Generalized Korn's second inequality).Let $\Omega \subset {\mathbb R}^{3}$ be a Lipschitz domain, and $y\in C^{1}(\overline{\Omega}; {\mathbb R}^{3})$ with $\det \nabla y > 0$. Then

is a norm on $W^{1, 2}(\Omega; {\mathbb R}^{3})$ that is equivalent to $\|\cdot\|_{W^{1, 2}(\Omega)}$.

Generalizing the standard Korn's inequality, one proves that for any subspace $H \subset W^{1, 2}(\Omega; {\mathbb R}^{3})$ with $H \cap {\mathrm{Skew}}(3) y = \{0\}$ there exists a constant $C$ such that for every $z \in H$

Proof of Theorem 4.2. First, consider a subspace $H$ with $H \cap \mathcal{N}_{y} = \{ 0 \}$. The functional ${\mathcal F}_y$ is strictly convex on $H$. This can be easily seen since, for a given $Y \in {\mathbb R}^{3 \times 3}$, the function is

is a composition of a linear function $Z \mapsto {\mathop{{\text{sym}}}}(Y^{\top} Z)$ and a strictly convex function $X \mapsto Y^{-1} \partial_F W(Y) : X + 2 |X|^2$. Moreover, as

there is a unique minimizer $z_{H}$ on $H$. We refer to [13,Theorem 4.3] for the proof that (a) applies to $\{ z \in W^{1, 2}(\Omega) : z|_{\Gamma_{D}} = 0 \}$, that is, $\{ z \in W^{1, 2}(\Omega) : z|_{\Gamma_{D}} = 0 \} \cap \mathcal{N}_{y} = \{0\}$.

For the whole space case, let $H = \mathcal{N}_{y}^{\perp}$ be the orthogonal complement of $\mathcal{N}_{y}$ in $W^{1, 2}(\Omega; {\mathbb R}^{3})$. By (a), there is a unique minimizer $z_{\mathcal{N}_{y}^{\perp}}$ on $\mathcal{N}_{y}^{\perp}$. Therefore, ${\mathcal F}_y$ admits a minimizer in $W^{1, 2}(\Omega; {\mathbb R}^{3})$, and the set of all minimizers reads

Remark 4.4. Since by (2.8)

the Euler-Lagrange equation for the functional ${\mathcal F}_y$ is

or

Let us return to (4.8) and suppose that $z$ is a minimizer of ${\mathcal F}_{y^{k-1}}$. By plugging $z = (y^{k} - y^{k-1})/\tau$ in (4.12), we arrive at

Since this is a simple time discretization of the original evolution equation (2.1a), we conjecture that our linearization method yields a solution of the original nonlinear visco-elastic problem. The convergence study below already suggests that the energy-dissipation equality is satisfied by our method.

5.   Numerical results

We now consider a numerical implementation of the time-step method given in (4.8), where the velocity $z$ is computed in each time step minimizing (4.7). For simplicity, we denote the time-step size here again by $\tau$. Our implementation is based on finite elements, so we approximate

with a vector $\mathbf{y}^{k-1}$ of degrees of freedom and finite element basis functions $\phi_j$. In each time step we thus solve a linear system of the form

where the symmetric system matrix is given by

corresponding to the linearization of a nonlinear dissipation potential $D(F, G) = c|F^\top F - G^\top G|$. Compared to the previous discussion, we introduce a scaling parameter $c > 0$. The vector on the right-hand side is

The linear system is solved using the sparse direct Cholesky solver CHOLMOD ^[5] after a small shift of $K$ (which, without boundary conditions, is only positive semidefinite) by $\delta M$ (with finite element mass matrix $M$) to ensure positive definiteness. In all numerical experiments below, the value of $\delta$ has been fixed at $1\cdot 10^{-8}$.

Finally we compute

and iterate this procedure. The finite element system can be endowed with appropriate boundary conditions, body forces, and surface tractions in the usual way. In the following we use the Neo-Hookean material model

with Lamé parameters $\mu$ and $\lambda$. All 3d simulations are performed using P2 finite elements on a tetrahedral mesh.

Experiment 1: a visco-elastic plate. In ^[8] a rigorous thin-plate limit for nonlinear visco-elastic materials was derived in the Föppl–von Kármán-scaling regime. Numerical experiments for thin-plate equations were performed in ^[9] combining Bogner-Fox-Schmit (BFS) finite elements ^[4,14] for out-of-plane deformation $v\colon \omega \to {\mathbb R}$ and Q1 elements for in-plane deformation $u\colon \omega\to {\mathbb R}^2$ in the plate domain $\omega = (-1, 1)^2\subset {\mathbb R}^2$. We use this setting as a first test case for our method, computing the visco-elastic relaxation of an initially deformed plate with clamped boundary conditions. As an initial condition, we choose

The thin-plate model minimizes the energy $\phi(u, v) +\frac{1}{2\tau}\mathcal{D}^2((u_{n-1}, v_{n-1}), (u, v)),$ where the von Kármán energy functional $\phi$ is defined as

and the global dissipation distance $\mathcal{D}$ as

respectively. As $Q^2_W$ and $Q^2_D$ we take the limiting Föppl–von Kármán plate material, i.e.,

for every symmetric $G\in {\mathbb R}^{2\times 2}_{\rm sym}$. The constants $\lambda, \mu$ are the Lamé constants from (5.3) and $c > 0$ is the same viscosity parameter as in (5.1).

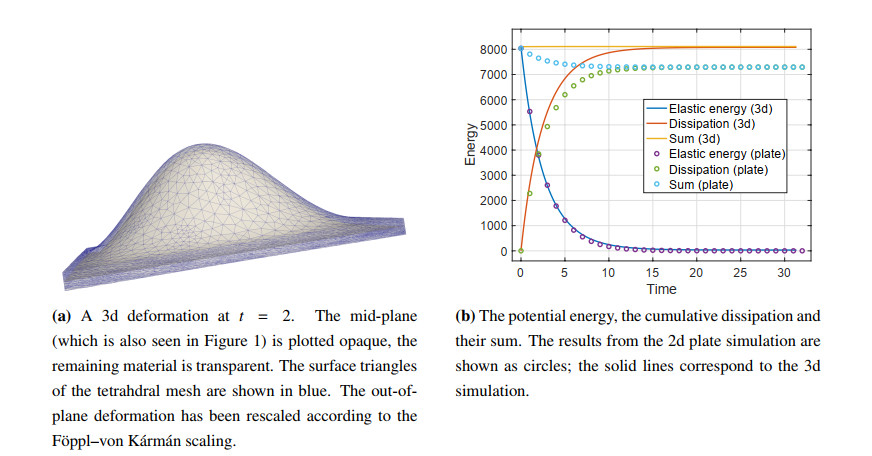
We then compare the solution of the thin-plate model with a full three-dimensional simulation using the algorithm from the beginning of Section 5 developed in this article, applied to a 3d plate with thickness $h$ in a reference domain $\omega \times (-\frac{1}{2}, \frac{1}{2})$ and $x_3$ derivative rescaled by $\frac{1}{h}$. The initial configuration is given as the respective element of the recovery sequence for $v$, $u$ above, as detailed in [10,Section 6.2], yielding approximately the same starting energy as the thin-plate limit. The simulation was performed using 201,514 tetrahedra resulting in 818,538 degrees of freedom. The wall time to full relaxation at $t\approx 30$ was approximately 6 days on 8 cores of an Intel Xeon Gold 6230.

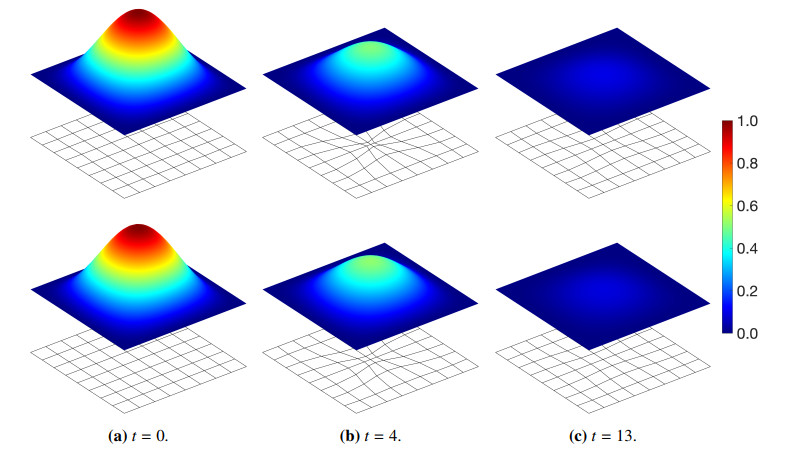
The parameters of this experiment are $\mu = \lambda = 1.0\cdot 10^3$, $c = 3.0\cdot 10^3$ and $h = 0.1$. The time-step size for the plate simulation was $\tau_ \text{plate} = 1$, for the 3d simulation it was $\tau_ \text{3d} = 0.01$. A comparison of midplane deformation in the 3d simulation with the limiting plate model is shown in Figure 1. Figure 2 shows the 3d deformation at a $t = 2$, as well as a comparison of the energy and cumulative dissipation of the plate model and the 3d simulation (see also the convergence study below). One can clearly see that our model and the plate limit yield very similar results, as one would expect. We also point out the near perfect adherence to energy-dissipation equality by the 3d simulations using the method developed here.

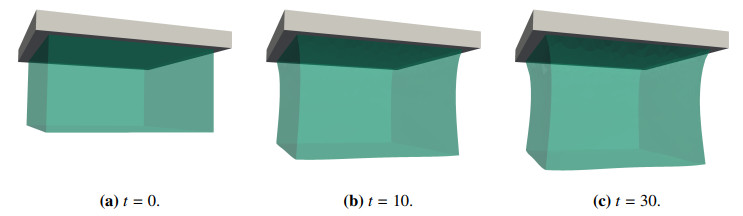
Experiment 2: Jello. We simulate the viscous evolution of a rectangular block of a material attached at the top under the influence of a gravitational body force. The jello has a reference configuration that occupies a domain $\Omega = (-1, 1) \times (-1, 1) \times (-\frac{1}{2}, \frac{1}{2})$ and an initial condition $y(x) = x$. A Dirichlet boundary condition fixes $y|_{\{x_3 = \frac{1}{2}\}} = x$ for all time. The energy is a sum of the Neo-Hookean energy in (5.3) and $-\int_\Omega f y_3 \, \mathrm{d}x$. The parameters in this simulation are $\mu = 1.0\cdot 10^3$, $\lambda = 1.5\cdot 10^3$, $f = -2.0 \cdot 10^3$, $c = 3.0\cdot 10^3$, and $\tau = 0.01$. Again, we see nearly perfect adherence to the energy-dissipation balance in this simulation. The number of degrees of freedom and the running time are the same as for Experiment 1 above. The results are illustrated in Figure 3.

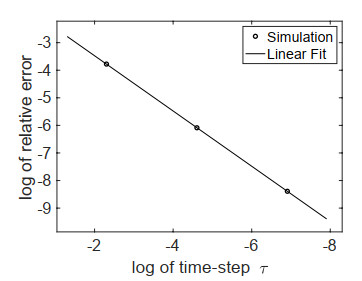
Convergence study. We performed a simple study testing the relative error in the energy-dissipation equality according to the time-step size $\tau$. In the reference domain $\Omega = (-1, 1)^3$, we choose an initial condition

and perform the linearized time-stepping scheme in (5.2) until final time $T = 1$, i.e., up to step $K_\tau = \frac{1}{\tau}$ for time steps $\tau \in \{0.1, 0.01, 0.001\}$. Finally, we compute the relative error in the energy-dissipation equality with the nonlinear dissipation distance, i.e., we compute

The simulation was performed using the parameters $\mu = 1.0\cdot 10^3$, $\lambda = 1.5\cdot 10^3$, $c = 3.0\cdot 10^3$, no body force and stress-free boundary conditions on a domain discretized using 147 342 P2 finite elements. From Figure 4 one can clearly obtain that $e_\tau = \mathcal{O}(\tau)$. The same scaling is also obtained using coarser discretizations with 71,369 and 33,216 P2 finite elements. We thus conclude that our linearized time-stepping scheme recovers the correct energy-dissipation equality for nonlinear Kelvin-Voigt visco-elasticity.

Acknowledgements

PD and MJ are grateful for the hospitality afforded by The Institute of Information Theory and Automation of the Czech Academy of Sciences. MJ and MK acknowledge the support from the University of Freiburg during their stays there. PD acknowledges support by the state of Baden-Württemberg through bwHPC and from the DFG via project 441523275 in SPP 2256. MK and JV were supported by the GAČR project 21-06569K and by the MŠMT ČR project 8J21AT001 Model Reduction and Optimal Control in Thermomechanics. MK also thanks the ESI Vienna for its hospitality during his stay in January-February 2022.

Conflict of interest

The authors declare no conflict of interest.