The incidence of pulmonary tuberculosis in patients with anthracosis

1.   Introduction

Nowadays, due to the development of nanotechnology, new materials called nanocomposites have attracted the attention of scientific communities. Nanocomposite materials are made of two or more constituent materials having significantly different optical, plasmonic, catalytic, biological, physical, and chemical properties ^[1,2,3], that, when combined, produce a material with a characteristic different from the individual components. In a composite material, one of the constituents is a continuous matrix which is called a host matrix while the others dispersed in the host matrix are called inclusions or fillers.

Among the nanoinclusions, core-shell nanoparticles (CSNPs) that consists of two or more nanomaterials by using encapsulation process are widely employed to obtain a new material with combined and/or other unique properties neither shown by the components ^[4,5,6]. This new or unique properties mainly arise from the interaction of plasmonic shell materials with the electromagnetic field, which is greatly intensified by a phenomenon known as the surface plasmon resonance (SPR) and the interaction of plasmon of the metallic shell with plasmon/exciton/plariton of the inner material ^[7,8]. The plasmonic properties of the composite strongly depend on the geometry, size, composition, and dielectric function (DF) of the host matrix ^[7,9,10]. The shell material has a protective effect on the inner material; such as dissolution, corrosion, enhancement of the structural stability, and can also impart its plasmonic, catalytic, magnetic, and optical properties and functions to the inner material.

Recently, noble metal nanoparticles (NPs) (like Ag, Au, Cu, Pt) have attracted the attention of the researchers due to their unique catalytic, electronic, plasmonic and optical properties ^[11] as well as their high chemical stability, bio-affinity, strong absorption of light from visible to infrared (IR) regions ^[1,12,13], which are dominated by the localized surface plasmon resonance (SPR) ^[14]. In addition to these properties, the potential applications of noble metal NPs are preferable as coating material.

As stated above, CSNPs have unique/new properties and such unique, useful and tailorable properties have also advanced CSNPs as a very important class of emerging nanocomposites for a wide range of applications in, for instance, catalysis, biomedical, energy/data storage, solar cell, antibacterial, renewable energy, photonics, electronics ^{[15,16,17,18,19,20,21,22,23]}. With all these advantages, core-shell nanostructures (CSNSs) have been broadly investigated experimentally and/or theoretically ^[4,24,25] by many research groups in the past decade and applied to a wide variety of fields. CSNPs can be assembled from metals, semiconductors, dielectrics or organic/inorganic materials; one used as a core and another or the same material used as a shell ^[7,21,26,27].

In this paper, the authors studied the effect of core size/shape on the plasmonic properties of spherical ZnO@Au core-shell nanostructures embedded in passive host matrix, with highly tunable plasmonic response of the composites. The shell metal, i.e., Au NP, has been investigated most extensively because of its high catalytic, universal biocompatibility, optical sensitivity, facile preparation, resistance to oxidation, and surface plasmon resonance (SPR) band that can absorb and scatter visible light relative to other noble metals ^[28]. ZnO NP is wurtzite zinc oxide wich has wide band gap (3.37 eV), high exciton binding energy (~60 meV) at room temperature, and high dielectric constant ^[29,30,31], and it is reliable material for visible and near-UV applications ^[29,30]. ZnO NP has attracted extensive attention due to its potential applications in laser diodes, solar cells, field-emission displays, light emitting diodes, optoelectronics devices, photovoltaic cells, gas sensors, photo-catalysis, ultraviolet lasers ^[32,33,34]. ZnO nanoparticles have been experimentally synthesized for various applications with different morphologies; like rod shape ^{[34,35,36,37]}, flower like shape ^[38,39,40], spherical shape ^{[34,35,41,42]}, ellipsoidal shape ^{[42,43,44,45,46]}, tube like structure ^[47], and plate/sheet like shape ^[34,48]. Due to this noble properties, different morphologies, and noble applications of ZnO and Au NPs, core-shell combination of them is a desirable way to generate new/unique properties and enhanced applications. Indeed, ZnO@Au CSNSs have been investigated for various applications ^{[28,29,30,31,32,33,34,49,50]} and display improved properties. In the present work, the plasmonic resonance of ZnO@Au CSNSs is shown to be tuned from visible region to infrared spectral regions. To the best of our knowledge, the plasmonic response of spherical ZnO@Au CSNSs by varying the core shape and size for a fixed composite size embedded in the passive host-matrix of MgF₂ is not reported yet. The authors choice MgF₂ as a host matrix, which is good transparent over a wide range of wavelengths and used to optical coating. MgF₂ is low refractive index, high band gap energy, antireflective, stable, and light polarizer material, which is a promising candidate for the desired optical performance and future investigation ^{[51,52,53,54]}.

In this work, mainly the absorption cross-section and local field enhancement factor (LFEF) of noble metal Au-coated ZnO nano-composite with the diameter of composite of 20 nm is systematically studied by optimizing the size and shape of the ZnO core. For the nanocomposites which have the size < 40 nm, the quasistatic limit is an appropriate method to study the plasmonic response and the dipolar mode resonance is more enhanced than the other higher-order multipoles.

The paper is organized as follows: in Section 2, we will discuss the basic idea of nanoinclusion with a representative model by using electrostatic approximation. Section 3, describes the plasmonic response of spherical core-shell nanostructures: absorption cross-section and local field enhancement factor by optimizing the parameters. Finally, the main result of the work is summarized in Section 4.

2.   Theoretical model and calculation

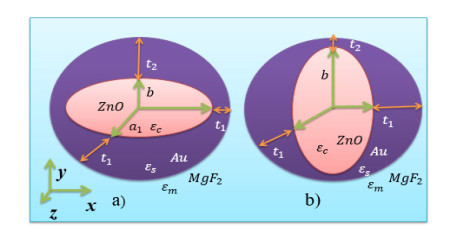
The plasmonic properties of two-layered core-shell nanoparticles consisting of a core and shell can be successfully described within the framework of classical electrodynamics of continuous media. Consider an array of spherical core-shell nanoparticle consisting of a semiconductor core (ZnO) of dielectric function (DF) $ {\epsilon }_{\mathit{c}} $, and a metallic shell (Au) of DF ${\varepsilon _s}$ embedded in a non-absorptive (passive) host matrix having a real DF ${\varepsilon _m}$, as shown in Figure 1, i.e., cross-sectional view of the composite. As shown in the figure, the composite is spherical shape with fixed radius 10 $ nm $ (i.e., $ b+{t}_{2} = {a}_{1}+{t}_{1} = {a}_{2}+{t}_{1} = 10nm $), however, the core is oblate Figure 1a and prolate Figure 1b with semi-principal axes $ {a}_{1} $, $ {a}_{2} $, and $ b $. The thickness of the Au-shell is not homogeneous due to the alignment of ZnO core nanoparticles: (i) $ {t}_{2}>{t}_{1} $, $ {a}_{1} = {a}_{2}>b $ for oblate core and (ii) $ {t}_{2} < {t}_{1} $, $ {a}_{1} = {a}_{2} < b $ for prolate core.

Figure 1.  (Color online) The cross-sectional view of spherical CSNSs embedded in the dielectrics host medium of MgF₂: oblate core (a) and prolate core (b).

DownLoad: Full-Size Img PowerPoint

When the system is irradiated (placed in) with an electromagnetic field, assumed to be polarized along $ xy- $ plane (along $ b $, see Figure 1), the applied filed causes the polarization of the system. As explain in Eq 1, the effective polarizability $ {\alpha }_{i} $ of the system depends on the dielectrics function of the constituents, which can be expressed as ^[55]:

where $ V $ is the volume of the core-shell nanocomposite, $ f $ is the fraction of the total volume occupied by the core (or core concentration); $ {L}_{i}^{s} $ and $ {L}_{i}^{c} $, are the depolarization factors of the composite (core + shell) and core, respectively, and the subscripts $ i = 1, 2, 3 $ refer to the longitudinal ($ i = 1 $) and transverse modes ($ i = 2, 3 $). The other parameters in Eq 1 are given from Eq 2 to 4 as

The polarization factor of the spherical shape is $ {L}_{1} = {L}_{2} = {L}_{3} = 1/3 $, while the polarization factors of the spheroidal shapes (oblate and prolate) depend on the ellipticity ($ e $). For the spheroidal prolate core, the polarization factors along the $ b $, $ {a}_{1} $, and $ {a}_{2} $ axes, respectively, are given by Eqs 5 and 6 ^[56]:

where the ellipticity of the prolate core is given by Eq 7

Similarly, the corresponding depolarization factors for the oblate spheroidal core are given by Eqs 8 and 9 ^[57]:

where the ellipticity of the oblate core is given by Eq 10

The aspect ratios (ARs) of the prolate and oblate core ZnO nanoparticles are defined by $ AR = b/{a}_{1} $ and $ AR = {a}_{1}/b $, respectively.

In the quasistatic limit, the extinction cross-section $ {\sigma }_{ecs} $ of the ensembles (systems) have the form of Eq 11:

where $ {\sigma }_{acs} $ and $ {\sigma }_{scs} $ are the absorption and scattering cross-sections defined by Eqs 12 and 13, rspectively

where $ k $ is a parameter which depends on the wavelength ($ \lambda $) of the incident light (see Eq 14). That is,

The local electric field inside the composites can be enhanced due to the difference between the dielectric properties of the two materials ZnO/Au and Au/MgF₂ as well as the surface plasmon resonance of the Au-shell. The local field enhancement factor ($ F $) is defined as the ratio of the intensities of the electric field around the composite to the applied electric field. The square of the local field enhancement factor (LFEF) ($ {\left|F\right|}^{2} $) of the nanocomposite is expressed as Eq 15 ^[58]:

where $ E $ is the electric field inside the composite, $ {E}_{0} $ is the applied electric field, and $ r $ is the radius of the composite.

3.   Numerical result and discussion

For the dimension of composite less than the wavelength of the incident light, the quasistatic approach is appropriate for the calculation of the polarizability and then the absorption cross-section and local field enhancement factor. For small size composite, the incident electric field may be regarded as being spatially uniform over the extent of the particle; so that the particle can be replaced by an oscillating dipole and this is referred to as the quasistatic approximation. In this study, the observed spectra of the two-layered spheroidal core of spherical core-shell nanostructures extends from the visible to the infrared (IR) spectral region, i.e., between 400-1300 nm. In this type of composite nanostructure, four plasmonic resonances are observed, two resonances corresponding to the two interfaces (ZnO/Au and Au/MgF₂) and the other two resonances corresponding to the two oscillating modes ^[55,58,59].

Below, we theoretically investigated the effect of the core material's size and shape on the plasmonic response of ZnO@Au core-shell composite nanostructures. For numerical calculations, we considered a system that consists of spherical nanocomposite ZnO@Au with spheroidal core ZnO dispersed in MgF₂ host of DF $ {\epsilon }_{m} = 1.98 $. In the frequency domain of interest, we assumed that the DF of the ZnO core to be a real constant that is independent of frequency ($ {\epsilon }_{c} = 8.5 $) ^[31]. In addition, the DF of the Au-shell is chosen to be of the Drude form as written in Eq 16.

where $ {\epsilon }_{\infty } = 9.84 $ is the phenomenological parameter describing the contribution of bound electrons to the polarizability, $ {\omega }_{p} = 9.01eV $ is the bulk plasmon frequency, and $ \gamma = 0.072eV $ is the damping constant of the bulk material ^[9].

3.1.   Absorption cross-section

Among the parameters which affect the plasmonic properties of nanocomposites are the size and shape of the core material. Here, we investigated the plasmonic response of spherical core-shell nanostructures by optimizing the core shape to oblate-prolate-spherical and also its size for a fixed composite size.

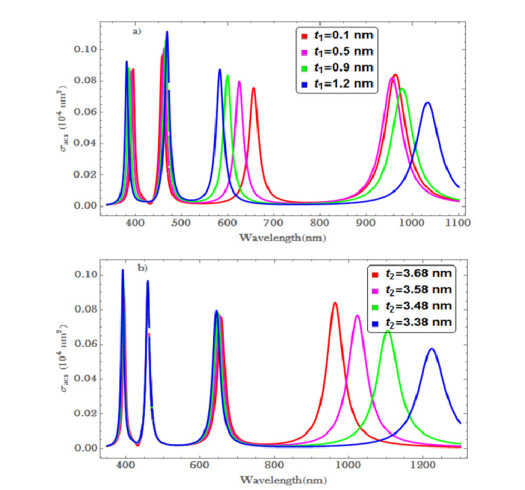
Absorption cross-sections of the oblate core spherical core-shell nanostructure as a function of wavelength are depicted in Figure 2, for non-uniform Au-shell material distribution. In addition to core shape and size, the non-uniform distribution of the coating material on the surface of the inner material also affects the palsmonic response of the composite. Figure 2a, shows the simulated $ {\sigma }_{acs} $ spectra of the oblate core spherical CSNSs when the $ AR $ values are 1.57, 1.50, 1.44, 1.39 corresponding to the core concentrations ($ f $) of 61.94%, 57.04%, 52.94%, 48.94%, respectively. The parameters are derived by removing some portion of core ZnO from $ x- $ and $ z- $ direction, while the $ y- $ direction is kept constant. The first two resonance peaks (located between 340-500 $ nm $) correspond to the surface plasmon resonances of the Au-shell at the inner and outer interfaces. The peaks of these two resonances are found to increase as well as blue- and red-shifted, respectively, with a decrease of the core concentration. The third and fourth set of resonance peaks (around 600 nm and 1000 nm, respectively) are due to the polarization of charges along the principal axes of the spheroid core ZnO. In particular, the third resonance peaks are associated with the transverse plasmon mode (TM), while the fourth peaks correspond to the longitudinal mode (LM). The peaks of the TM mode are increased and blue-shifted when the core's aspect ratio is decreased. However, the peaks of the LM mode decrease and are red-shifted with a decrease of the core's aspect ratio.

Figure 2.  (Color online) The absorption cross-sections for oblate core ZnO spherical ZnO@Au CSNS; (a) $ {t}_{2} $ = 3.68 nm, $ AR $ = 1.57, 1.50, 1.44, 1.39 and (b) $ {t}_{1} $ = 0.1 nm, $ AR $ = 1.57, 1.54, 1.52, 1.50.

DownLoad: Full-Size Img PowerPoint

Here, in order to compare the plasmonic response of different size of oblate core by keeping $ {t}_{1} = 0.1nm $ remain the same, the absorption cross-section of the composite is depicted in Figure 2b. Here, the size of core is changed by increasing the core thickness along the $ y- $ direction (or along $ b $ dimension); i.e., by decreasing $ {t}_{2} $. Due to this, the aspect ratio of the core are changed to 1.57, 1.54, 1.52, 1.50, and correspondingly the concentrations of the ZnO core are 61.94%, 62.94%, 63.90%, 64.88%. Accordingly, two resonances are observed associated with the interfaces of the metallic shell: the first resonances corresponding to the inner interface and the second resonances associated with the outer interface. The peaks of these two resonances are increased without shifting. The remaining third and fourth resonances, associated with the transverse and longitudinal plasmon resonance, respectively, are the same as that obtained in Figure 2a; but, the third peaks resonance slightly shifted and the fourth resonance peaks are more shifted to higher wavelength. When the electromagnetic wave interacts with the composite, positive and negative charges are generated; the induced charges move and are collected on the surface of the inner and outer materials. The interaction that arises due to the separation of these positive and negative charges is more pronounced when the size of the core becomes bigger or the shell thickness is decreased. Due to this, the resonance peaks associated with the inner interface are more enhanced than the other resonance peaks, as shown in the figure.

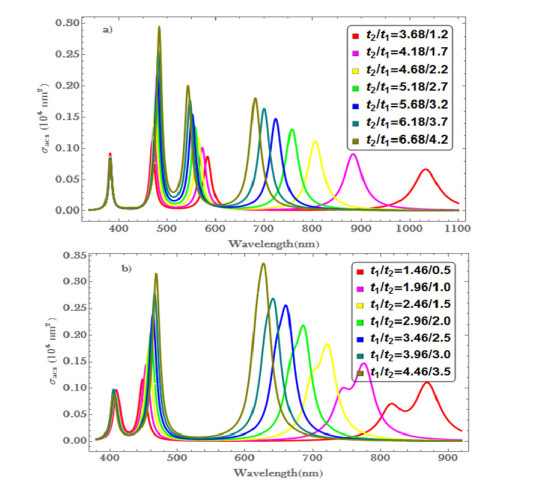
The plasmonic response of ZnO@Au CSNSs is also varied by changing the oblate core to a prolate shaped core. The absorption cross-section of the CSNSs with prolate core materials is depicted in Figure 3, for a fixed size of nano-composites. As shown in the Figure 3a, the absorption cross-section of the system with prolate core is investigated by removing some portion from $ y- $ axis, so that the aspect ratios of the ZnO NPs are 1.31, 1.26, 1.19, 1.13 with the corresponding concentrations being 56.28%, 54.01%, 51.17%, 48.32%, respectively. From the figure, it is seen that when the concentrations of the ZnO NPs are increased, all peaks of the plasmon resonances are increased except the first resonances which are associated with the inner interface of the shell. Moreover, both the TM and LM peaks of resonances are increased and blue-shifted. Note that the dipolar modes are accompanied by higher-order multipoles modes, such as the fifth peaks (indicated by arrow head) associated with quadrapole appear between the peaks of the inner and outer interface's resonances. These fifth resonances are more enhanced for higher aspect ratios, as shown in both Figure 3a, b.

Figure 3.  (Color online) The absorption cross-sections for prolate core ZnO spherical ZnO@Au CSNS; (a) $ {t}_{1} $ = 2.46 nm, $ AR $ = 1.31, 1.26, 1.19, 1.13 and (b) $ {t}_{2} $ = 0.1 nm, $ AR $ = 1.31, 1.23, 1.16, 1.10.

DownLoad: Full-Size Img PowerPoint

As shown in Figure 3b, when $ {t}_{1} $ is decreased from 2.46 to 0.96 nm with the concentration of ZnO being 56.28%, 64.00%, 72.20%, 80.90%; i.e., the core material becomes spherical and the shell becomes thinner, the first two resonance peaks are increased and shift towards each other, whereas the peaks of the TM and LM resonances are decreased and red-shifted. The resonance with high tunability of nanocomposite from near UV to near IR spectral regions is used for biomedical application ^[60].

Furthermore, to see the effect of shell thickness on the optical response of the ZnO@Au CSNSs, we investigated both systems by fixing the core size while increasing the shell thicknesses. Accordingly, in the numerical analysis the size of the composites is changed from 10 to 13 nm (with a range of 0.5 nm) without changing the shape and size of the core material. Figure 4 shows the absorption cross-section as a function of the incident wavelength for different shell thickness. For the two morphologies (i.e., ZnO@Au CSNSs with oblate and prolate cores are depicted in Figure 4a, b, respectively), the optical responses are almost the same. Except for the first resonances, all plasmonic resonance peaks are enhanced, when the thickness ($ {t}_{1} $ and $ {t}_{2} $ are increased with the range 0.5 nm) is increased or when the concentration of ZnO is decreased. The corresponding concentration of the ZnO NP is summarized in Table 1. The plasmonic resonance associated with the interface of the host medium and shell materials is highly enhanced accompanied with red-shifts, whereas the resonance peaks associated with the transverse and longitudinal modes are enhanced and blue-shifted. As shown in Figure 4b, the third resonance peaks corresponding to the TM are becoming diminished which is dominated by the resonance of the LM.

Figure 4.  (Color online) The absorption cross-sections for a fixed core size of ZnO@Au core-shell nanostructures; for (a) oblate with b/$ {a}_{1} $ /$ {a}_{2} $ = 6.32/8.8/8.8 nm and (b) prolate with $ {a}_{1} $ /$ {a}_{2} $ /b = 8.54/8.54/9.5 nm.

DownLoad: Full-Size Img PowerPoint

Table 1.  The concentration of ZnO for the increment of $ {t}_{1} $ and $ {t}_{2} $, simultaneously.

Shape	Concentration (%)
Oblate	48.94	42.28	36.77	32.18	28.32	25.06	22.28
Prolate	69.29	59.85	52.06	45.56	40.10	35.47	31.54

---

 | Show Table

DownLoad: CSV

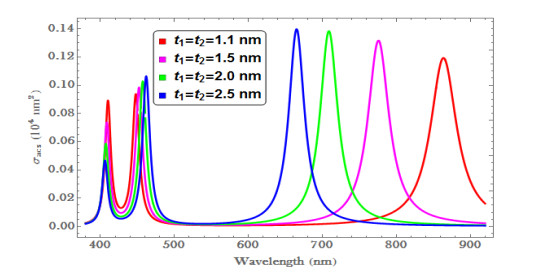
In addition to the oblate and prolate core spherical ZnO@Au CSNSs, the plasmonic properties of the spherical core is also studied for the same size of nanocomposite. As shown in Figure 5, the plasmonic response of the spherical shape with different size: the first plasmonic peaks associated with the inner interface are decreased without shifting; while the second peaks associated with the outer interface are increased and red-shifted. For the spherical core nano-composite, the charge distribution on each surface is the same; in the special case, due to the separation of positive and negative charges on surface of the core and shell, respectively, or vice versa, the third resonances are observed. The peaks of these resonances are increased with a decrease of the core concentration or an increase of the shell thickness.

Figure 5.  (Color online) The absorption cross-sections of spherical core ZnO@Au core-shell nanostructures for different shell thicknesses (with $ {t}_{1} = {t}_{2} = 1.1, 1.5, 2.0, 2.5nm $). The corresponding concentrations of the core ZnO NPs are 70.41%, 61.41%, 51.20%, 42.19%, respectively.

DownLoad: Full-Size Img PowerPoint

3.2.   Local field enhancement factor

When an electric field is applied to the core-shell structure, charges are induced which resides on the core's surface as well as the surface of the shell material. This separation of negative and positive charges on the surfaces results in the generation of internal electric field. The electric field in the composite is the superposition of the applied field in the composite and the generated electric field. The electric field in the composite is much larger than the local electric field. The enhancement of electric field in the composite depends on the shape as well as the size of the core materials or the separation distance of holes and electrons.

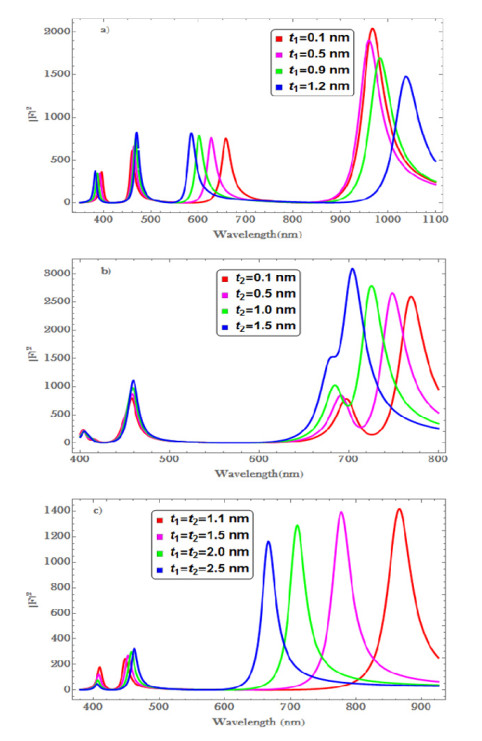
The local field enhancement factor for oblate, prolate, and spherical shaped CSNSs having different sizes is depicted in Figure 6. For the oblate core ZnO@Au CSNSs, as the thickness is increased the local field enhancement factor is enhanced and shifted apart for the first and second set of resonances (see Figure 6a). Similar to that in Figure 2a, with an increase of thickness the peaks of the TM resonances increase and blue-shifted, while the peaks of the LM resonances decrease and red-shifted. As shown in the Figure 6b, the first resonances decrease, whereas the second resonances increase without shifting. However, the peaks of the TM and LM resonances are seen to increase and blue-shifted when the concentration of the core is decreased.

Figure 6.  (Color online) Local filed enhancement factor for different core shape and size; (a) oblate core, (b) prolate core, and (c) spherical core. The other parameters are similar to that used in Figure 2a, Figure 3a, and Figure 5, respectively, for (a), (b), and (c).

DownLoad: Full-Size Img PowerPoint

Figure 6c illustrates the local field enhancement factor of spherical ZnO@Au core-shell nanostructure with spherical core. The first peaks of resonance decrease, whereas the second peaks of resonance increase and shifted to higher wavelengths when the core concentration is decreased. The third peaks of resonance associated with induced charge separation are seen to decrease with a decrease in core concentration. It is worth noting that as the shell thickness is increased (i.e., charge separation distance is increased), the electric field developed in the composite is decreased.

Generally, these results are directly or indirectly related to the interaction of the plasmons of the metallic shell with the polaritons of the core material. In particular, when the size of the core material is becoming bigger for the same size of nanocomposite, the interaction between the plasmons and polaritons gets stronger and vice versa.

4.   Conclusions

In this work, we studied the effect of shape and size of the core material on the plasmonic response of two-layered spherical ZnO@Au core-shell nanostructures embedded in the passive host-matrices of MgF₂ using the method of quasistatic approximation. In particular, the absorption cross-section and local field enhancement factor (LFEF) of the nanocomposites of fixed radius ($ r = 10nm $) are investigated as a function of the wavelength of the incident light. For both the prolate and oblate core spherical ZnO@Au CSNSs, the absorption cross-sections as well as the enhancement factor possess four plasmonic resonances with peaks extending from the visible to infrared spectral regions. The first and second peaks of the resonances are associated with the inner and outer interfaces of Au-shell; i.e., ZnO/Au and Au/MgF₂ interfaces, whereas the third and fourth peaks of the resonances are associated with the transverse and longitudinal modes of resonances, respectively. The peaks position, enhancement of the resonances, and shifting of resonance peaks depend on the shape and size of the ZnO core, the shell distribution on the inner material, and shell thickness. Note that the results obtained show that the two-layered spherical ZnO@Au CSNSs, which are composed of a semiconductor core of ZnO coated by thin Au NPs exhibit high tunable optical responses that extends from the visible to infrared spectral regions, and hence can be ideal candidates for enhancing biological, solar-cell, catalysis, renewable energy, and energy storage applications.

Acknowledgements

This work is supported financially by the Addis Ababa University and Adama Science and Technology University

Conflicts of interests

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analysis, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.