1. Introduction

Vector-borne diseases such as malaria, dengue, schistomiasis, Chagas disease, and yellow fever are illnesses that are transmitted by vectors, which include mosquitos, ticks, and fleas. They account for over 17% of all infectious diseases and are great threat to the health of human and animal. Every year there are more than 1 billion cases and over 1 million deaths from vector-borne diseases.

Mathematical modeling has been successfully used to better understand the mechanisms underlying vector-borne disease spread and to provide efficient control strategies. The Ross-Macdonald model on vector-borne diseases was described by ordinary differential equations [14, 19, 20]. Macdonald [14] established a threshold condition on the invasion and persistence of infection, which is determined by the basic reproduction number (defined as the average number of secondary cases produced by an index case during its infectious period). Most of the existing vector-borne disease models, especially those on malaria that investigate complications arising from host superinfection, immunity, and other factors, are based on this fundamental model [3, 5, 8, 12, 18, 21, 23, 24]. In particular, Lashari and Zaman [12] considered the following vector-borne disease model with horizontal transmission in the host population,

$\label{A1.1} \left\{ \begin{array}{rcl} \frac{dS_h(t)}{dt}= &\lambda_h-\mu_hS_h-\beta_1S_hI_h-\beta_2S_hI_v, \\ \frac{dE_h(t)}{dt}= &\beta_1S_hI_h+\beta_2S_hI_v-(\alpha_h+\mu_h)E_h, \\ \frac{dI_h(t)}{dt}= &\alpha_hE_h-(\mu_h+\delta_h+\gamma_h)I_h, \\ \frac{dR_h(t)}{dt}= &\gamma_hI_h-\mu_hR_h, \\ \frac{dS_v(t)}{dt}= &\lambda_v-kS_vI_h-\mu_vS_v, \\ \frac{dE_v(t)}{dt}= &kS_vI_h-(\alpha_v+\mu_v)E_v, \\ \frac{dI_v(t)}{dt}= &\alpha_vE_v-(\mu_v+\delta_v)I_v, \end{array} \right.$

(1)

where $S_h$, $E_h$, $I_h$, and $R_h$ denote the susceptible, exposed, infectious, and recovered epidemiological classes in the host, respectively, while $S_v$, $E_v$, and $I_v$ denote the susceptible, exposed, and infectious epidemiological classes in the vector, respectively. There is no recovered class for the vector (mosquitos) because no infected mosquito can recover from the infection. The biological meanings of the parameters in (1) are summarized in Table 1.

It is well known that the infectivity varies during the infectious period and hence the time passed since being infected, called infection age, affects the number of secondary infections. In recent years, epidemic models with infection age have been extensively studied. For works on vector-borne diseases, not much has been done [10, 13, 17, 25], where only the host has infection age. In [10], an SI(host)SI(vector) model is proposed, which incorporated horizontal transmission. Under additional condition besides the basic reproduction ratio $\mathcal{R}_0<1$, it is shown that the disease-free steady state is globally asymptotically stable. Moreover, only the local stability of the endemic steady state is discussed. In [13], Lou and Zhao considered a periodic SEIRS(host)SEI(vector) model with standard incidence. It is shown that there exists at least one positive periodic state and that the disease persists when the basic reproduction ratio $\mathcal{R}_0>1$ while the disease will die out if $\mathcal{R}_0<1$. One of the models in [25] is an SIR(host)SI(vector) model with constant vector population and a threshold dynamics characterized by the basic reproduction number is obtained.

The purpose of this paper is to modify (1) by introducing infection age into the host and study the dynamics of the resulted model. The remaining part of this paper is organized as follows. In the next section, we introduce the model and state some preliminary results on solutions. Then, in Section 3, we study the existence of equilibria and their local stability. Section 4 is the main part of this paper, where we establish a threshold dynamics with the approach of Lyapunov functional. The threshold dynamics is characterized only by the basic reproduction number. Here, to obtain the stability of the infected equilibrium, we need the existence of a global attractor and the uniformly strong persistence. The theoretical results are illustrated with numerical simulations in Section 5. The paper concludes with a brief summary.

---

2. The model and preliminary results

Our model is based on model (1). To build it, we further subdivide the infectious host according to the infection age $a$. Let $i_h(t, a)$ be the density of infectious hosts at time $t$ with infection age $a$. Then $\int_{a_1}^{a_2}i_h(t, a)da$ is the number of infectious hosts with infection ages between $a_1$ and $a_2$ at time $t$ and the total number of infectious hosts at time $t$ is $I_h(t) = \int_{0}^{\infty}i_h(t, a)da$. We assume that the infectivity of infectious hosts, the biting rate of an infectious host by a susceptible vector, disease-induced death rate of infectious hosts, and the recovery rate of infectious hosts all depend on the infection age $a$ and denote them by $\beta_1(a)$, $k(a)$, $\delta_h(a)$, and $\gamma(a)$, respectively. Then the rate of horizontal transmission of the disease from infectious hosts to susceptible hosts is $\int_{0}^{\infty}\beta_1(a)i_h(t, a)da$ and the force of infection of the host to susceptible vectors is $\int_{0}^{\infty}k(a)i_h(t, a)da$. Since the recovered hosts have permanent immunity, there is no need to consider the evolution of $R_h$ in time. Based on our assumptions and model (1), the vector-borne disease model with infection age in host to be studied in this paper is as follows,

$\label{A2.2} \left\{ \begin{array}{l} \frac{dS_h(t)}{dt} = \lambda_h-S_h(t)\int_0^{\infty}\beta_1(a)i_h(t, a)da-\beta_2S_h(t)I_v(t)-\mu_hS_h(t), \\ \frac{dE_h(t)}{dt} = S_h(t)\int_0^{\infty}\beta_1(a)i_h(t, a)da+\beta_2S_h(t)I_v(t)-(\alpha_h+\mu_h)E_h(t), \\ \frac{\partial i_h(t, a)}{\partial t}+\frac{\partial i_h(t, a)}{\partial a} = -\delta(a)i_h(t, a), \\ \frac{dS_v(t)}{dt} = \lambda_v-\int_0^{\infty}k(a)S_v(t)i_h(t, a)da-\mu_vS_v(t), \\ \frac{dE_v(t)}{dt} = \int_0^{\infty}k(a)S_v(t)i_h(t, a)da-(\alpha_v+\mu_v)E_v(t), \\ \frac{dI_v(t)}{dt} = \alpha_vE_v(t)-\mu_vI_v(t), \\ i_h(t, 0) = \alpha_hE_h(t), t>0, \\ S_h(0) = S_{h0}\in R_+, \ \ E_h(0) = E_{h0}\in R_+, \ \ i_h(0, \cdot) = i_{h0}\in L_+^1(0, \infty), \\ S_v(0) = S_{v0}\in R_+, \ \ E_v(0) = E_{v0}\in R_+, \ \ I_v(0) = I_{v0}\in R_+, \end{array} \right.$

(2)

where $\delta(a) = \mu_h+\delta_h(a)+\gamma(a)$, $R_+ = [0, \infty)$, and $L_+^1(0, \infty)$ is the nonnegative cone of $L^1(0, \infty)$.

To continue our discussion, in the sequel, we assume that $k(\cdot)\in L_+^{\infty}(0, \infty)\setminus \{0\}$ and $\beta_1(\cdot), \ \gamma(\cdot)\in L_+^{\infty}(0, \infty)$, where $L_+^{\infty}(0, \infty)$ is the nonnegative cone of $L^{\infty}(0, \infty)$. Clearly, $\delta(a)\ge \mu_h$ for $a\in R_+$. For (2), there should be an inherent relationship between the initial value and the boundary value for the partial differential equation, that is, $i_h(0, 0) = i_{h0}(0)$. Therefore, we always assume that the initial values satisfy $\alpha_h E_{h0} = i_{h0}(0)$.

Note that the partial differential equation in (2) is a linear transport equation with decay. With integration along the characteristic line $t-a = \text{const.}$, one can solve

$\left\{ \begin{array}{l} \frac{\partial i_h(t, a)}{\partial t}+\frac{\partial i_h(t, a)}{\partial a} =-\delta(a)i_h(t, a) \\ i_h(t, 0) = \alpha_hE_h(t), ~~~~t\geq 0 \end{array} \right.$

to get

$i_h(t, a) = \left\{ \begin{array}{ll} \sigma(a) \alpha_h E_h(t-a)&\mbox{if $t>a\geq 0$, } \\ \frac{\sigma(a)}{\sigma(a-t)}i_h(0, a-t) \quad&\mbox{if $ a\geq t>0$, } \end{array} \right.$

where $\sigma(a) = \exp(-\int_0^a\delta(s)ds)$ represents the probability that an infectious host survives to infection age $a$. Then we obtain the following equivalent system of integro-differential equations to (2),

$\begin{equation}\label{A2.3} \left\{ \begin{array}{l} \frac{dS_h(t)}{dt} = \lambda_h-S_h(t)\int_0^{\infty}\beta_1(a)i_h(t, a)da-\beta_2S_h(t)I_v(t)-\mu_hS_h(t), \\ \frac{dE_h(t)}{dt} = S_h(t)\int_0^{\infty}\beta_1(a)i_h(t, a)da+\beta_2S_h(t)I_v(t)-(\alpha_h+\mu_h)E_h(t), \\ i_h(t, a) = \sigma(a)\alpha_hE_h(t-a){\bf 1}_{t>a}+\frac{\sigma(a)}{\sigma(a-t)}i_h(0, a-t){\bf 1}_{a>t}, \\ \frac{dS_v(t)}{dt} = \lambda_v-\int_0^{\infty}k(a)S_v(t)i_h(t, a)da-\mu_vS_v(t), \\ \frac{dE_v(t)}{dt} = \int_0^{\infty}k(a)S_v(t)i_h(t, a)da-(\alpha_v+\mu_v)E_v(t), \\ \frac{dI_v(t)}{dt} = \alpha_vE_v(t)-\mu_vI_v(t), \end{array} \right. \end{equation}$

(3)

where

${\bf 1}_{t>a} = \left\{ \begin{array}{ll} 1 &\mbox{if $t>a\geq 0$} \\ 0 \quad&\mbox{if $a\geq t\geq 0$} \end{array} \right.\quad \mbox{and}\quad {\bf 1}_{a>t} = \left\{ \begin{array}{ll} 0\quad &\mbox{if $t>a\geq 0$, } \\ 1&\mbox{if $a\geq t\geq 0$.} \end{array} \right.$

Let

$X_+ = R_+^2 \times L_+^1(0, \infty)\times R_+^3,$

which is the nonnegative cone of the Banach space $X = R^2\times L^1(0, \infty)\times R^3$ equipped with norm $\|\cdot\|$ defined by

$\|x\| = |x_1|+|x_2|+\|x_3\|_1+|x_4|+|x_5|+|x_6|$

for $x = (x_1, x_2, x_3, x_4, x_5, x_6)\in X$. With a reasonable modification of the proofs of Theorem 2.1 and Lemma 2.2 in Browne and Pilyugin [1], we can prove the existence and nonnegativeness of solutions to (3) and hence to (2).

Theorem 2.1. For any $x\in X_+$, system (2) has a unique solution on $R_+$, which depends continuously on the initial value and time. Moreover, $(S_h(t), E_h(t), i_h(t, \cdot), S_v(t), E_v(t), I_v(t))\in X_+$ for $t\in R_+$.

In fact, every solution is bounded. On the one hand, let

$N_h(t) = S_h(t)+E_h(t)+\int_0^{\infty}i_h(t, a)da.$

Then we have $\frac {dN_h(t)}{dt}\le \lambda_h-\mu_h N_h(t)$ and hence $\limsup_{t\to\infty}N_h(t)\le \lambda_h/\mu_h$. On the other hand, let

$N_v(t) = S_v(t)+E_v(t)+I_v(t).$

Then $\frac{dN_v(t)}{dt} = \lambda_v-\mu_v N_v(t)$, which implies that $\lim_{t\to\infty} N_v(t) = \lambda_v/\mu_v$. Denote

$\Omega = \left \{(S_h, E_h, i_h, S_v, E_v, I_v)\in X_+ \left \vert \begin {array}{ll} S_h+E_h+\|i_h\|_1\le \frac{\lambda_h}{\mu_h}, \\ S_v+E_v+I_v = \frac{\lambda_v}{\mu_v} \end {array} \right. \right \}.$

Then we have shown that $\Omega$ is an attracting set for (2). Moreover, one can easily see that $\Omega$ is also a positively invariant set for (2).

---

3. The existence of equilibria and their local stability

In this section, we study the local dynamics of (2). We first consider the existence of equilibria. It turns out that this only depends on the basic reproduction number $R_0$, which is defined as

$R_0 = \frac{\lambda_h[\xi\alpha_h(\alpha_v+\mu_v)\mu_v^2+\beta_2\lambda_v\alpha_v\eta \alpha_h]}{\mu_h\mu_v^2(\alpha_h+\mu_h)(\alpha_v+\mu_v)},$

where $\eta = \int_0^{\infty}k(a)\sigma(a)da$ and $\xi = \int_0^{\infty}\beta_1(a)\sigma(a)da$.

Clearly, (2) always has the infection-free equilibrium $E^0 = (S_h^0, 0, 0, S_v^0, 0, 0)\in\Omega$, where $S_h^0 = \lambda_h/\mu_h, S_v^0 = \lambda_v/\mu_v$. Let $E^* = (S_h^*, E_h^*, i_h^*, S_v^*, E_v^*, I_v^*)$ be an equilibrium. Then we have

$\begin{align} \left\{ \begin{array}{l} \lambda_h-\mu_hS_h^*-\beta_2S_h^*I_v^* -S_h^* \int_0^{\infty}\beta_1(a)i_h^* (a)da = 0, \\ S_h^* \int_0^{\infty}\beta_1(a)i_h^*(a)da+\beta_2S_h^* I_v^* = (\alpha_h+\mu_h)E_h^*, \\ \frac{di_h^* (a)}{da} = -\delta(a)i_h^*(a), \\ i_h^* (0) = \alpha_h E_h^*, \\ \lambda_v-\int_0^{\infty}k(a)S_v^*i_h^* (a)da-\mu_v S_v^* = 0, \\ \int_0^{\infty}k(a)S_v^*i_h^* (a)da = (\alpha_v+\mu_v)E_v^*, \\ \alpha_v E_v^* = \mu_v I_v^*. \end{array} \right. \end{align}$

(4)

It is easy to see that an equilibrium other than $E^0$ must be infected, that is, all components are positive. For an infected equilibrium, it is not difficult to deduce from (4) that

$\begin{eqnarray} S_h^*= &\frac {\lambda_h-(\alpha_h+\mu_h)E_h^*}{\mu_h}, \nonumber \\ i_h^*(a)= &\alpha_h \sigma(a) E_h^*, \nonumber \\ S_v^*= &\frac{\lambda_v}{\mu_v+\eta\alpha_h E^*_h}, \label {eqnEq} \\ E_v^*= &\frac{\lambda_v\eta\alpha_h E_h^*}{(\alpha_v+\mu_v)(\mu_v+\eta\alpha_h E_h^*)}, \nonumber \\ I_v^*= &\frac{\lambda_v\alpha_v\eta\alpha_h E_h^*}{\mu_v(\alpha_v+\mu_v)(\mu_v+\eta\alpha_h E_h^*)}, \nonumber \end{eqnarray}$

(5)

where $E_h^*$ is a positive zero of $H$ with

$\begin{align} H(x) = &\lambda_h [\xi\alpha_h(\alpha_v+\mu_v)(\mu_v+\eta\alpha_h x)\mu_v+\beta_2\alpha_v\lambda_v\eta\alpha_h] \\ & -\mu_v\mu_h(\alpha_h+\mu_h)(\alpha_v+\mu_v)(\mu_v+\eta\alpha_h x) \\ & -\beta_2\alpha_v\lambda_v\eta\alpha_h x(\alpha_h+\mu_h) \\ & -(\alpha_h+\mu_h)(\alpha_v+\mu_v)\mu_v\xi\alpha_h x(\mu_v+\eta\alpha_h x). \end{align}$

(6)

Theorem 3.1. (i) Suppose $R_0\le 1$. Then (2) only has the infection-free equilibrium $E^0$.

(ii) Suppose $R_0>1$. Then, besides $E^0$, (2) also has a unique infected equilibrium $E^* = (S_h^*, E_h^*, i_h^*, S_v^*, E_v^*, I_v^*)$, where $E_h^*$ is the unique positive zero of $H$ defined by (6) and the other components are determined by (5).

Proof. (ⅰ) Since $R_0\le 1$, we have $\lambda_h \xi\alpha_h\le \mu_h (\alpha_h+\mu_h)$. Note that $H$ is a quadratic function with negative coefficient for $x^2$. Moreover, the coefficient of $x$ in $H(x)$ is

$\begin {eqnarray*} && \lambda_h \xi \alpha_h(\alpha_v+\mu_v)\eta \alpha_h \mu_v -\mu_v\mu_h (\alpha_h+\mu_h)(\alpha_v+\mu_v)\eta \alpha_h \\ & & -\beta_2\alpha_v\lambda_v \eta \alpha_h (\alpha_h+\mu_h)-(\alpha_h+\mu_h)(\alpha_v+\mu_v)\mu_v \xi\alpha_h \mu_v \\ & < & \mu_h(\alpha_h+\mu_h)(\alpha_v+\mu_v)\eta \alpha_h \mu_v -\mu_v\mu_h (\alpha_h+\mu_h)(\alpha_v+\mu_v)\eta \alpha_h \\ & =& 0 \end {eqnarray*}$

and $H(0) = \mu_h \mu_v^2(\alpha_h+\mu_h)(\alpha_v+\mu_v)(R_0-1)\le 0$. It follows that $H(x)$ has no positive zeros and hence there is no infected equilibrium.

(ⅱ) Now, since $R_0>1$, we have $H(0) = \mu_h \mu_v^2(\alpha_h+\mu_h)(\alpha_v+\mu_v)(R_0-1)>0$. Then $H(x)$ has a unique positive zero since $H(x)$ is a quadratic polynomial with negative coefficient for $x^2$. Therefore, there is a unique infected equilibrium as described in the statement. This completes the proof.

Now, we study the stability of the equilibria by linearization. For more detail, see Iannelli [9].

Theorem 3.2. (i) The infection-free equilibrium $E^0$ of (2) is locally asymptotically stable if $R_0<1$ and it is unstable if $R_0>1$.

(ii) If $R_0>1$, then the infected equilibrium $E^{\ast}$ of (2) is locally asymptotically stable.

Proof. (ⅰ) The characteristic equation at $E^0$ is

$\begin {eqnarray*} 0 & = & F(\tau) \\ & \stackrel{\Delta}{=}& (\tau+\alpha_h+\mu_h)(\tau+\mu_v)(\tau+\alpha_v+\mu_v) \\ && -\alpha_hS_h^0\left[(\tau+\mu_v)(\tau+\alpha_v+\mu_v)\int_0^{\infty}\beta_1(a) \sigma(a)e^{-\tau a}da \right. \\ && \left. +\beta_2\alpha_vS_v^0\int_0^{\infty}k(a)\sigma(a)e^{-\tau a}da\right]. \end {eqnarray*}$

First, assume $R_0>1$. Then $F(0) = \mu_v(\alpha_h+\mu_h)(\alpha_v+\mu_v)(1-R_0)<0$ and $\lim\limits_{\tau\to \infty}F(\tau) = \infty$. By the Intermediate Value Theorem, $F$ has a positive zero and hence $E^0$ is unstable if $R_0>1$.

Next, assume $R_0<1$. It suffices to show that all zeros of $F$ have negative real parts. If this is not true, then $F$ has a zero $\tau_0$ with ${\text{Re}}(\tau_0)\geq 0$. It follows that

$\begin{eqnarray*} 1= &\mbox{$\frac{|\alpha_hS_h^0\left[(\tau_0+\mu_v)(\tau_0+\alpha_v+\mu_v)\int_0^{\infty}\beta_1(a) \sigma(a)e^{-\tau_0 a}da+\beta_2\alpha_vS_v^0\int_0^{\infty}k(a)\sigma(a)e^{-\tau_0 a}da\right]|}{|(\tau_0+\alpha_h+\mu_h)(\tau_0+\mu_v)(\tau_0+\alpha_v+\mu_v)|}$} \\ \leq& \frac{\alpha_hS_h^0\xi}{\alpha_h+\mu_h}+\frac{\beta_2S_h^0\alpha_h\alpha_vS_v^0\eta}{(\alpha_h+\mu_h)\mu_v(\alpha_v+\mu_v)} \\ = &R_0, \end{eqnarray*}$

which contradicts with $R_0<1$. Therefore, $E^0$ is locally asymptotically stable if $R_0<1$.

(ⅱ) For the infected equilibrium $E^{\ast}$, the associated characteristic equation is,

$\begin{array}{llll} (\tau+A_1)(\tau+\alpha_h+\mu_h)(\tau+\mu_v)(\tau+A_2)(\tau+\alpha_v+\mu_v)\\ -(\tau+\mu_h)\alpha_hS_h^{\ast}\left[(\tau+\mu_v)(\tau+\alpha_v+\mu_v)\int_0^{\infty}\beta_1(a)\sigma(a)e^{-\tau a}da(\tau+A_2)\right.\\ +\left.\beta_2\alpha_vS_v^{\ast}(\tau+\mu_v)\int_0^{\infty}k(a)\sigma(a)e^{-\tau a}da\right] = 0, \end{array}$

(7)

where $A_1 = \mu_h+\beta_2I_v^{\ast}+\int_0^{\infty}\beta_1(a)i_h^{\ast}(a)da$ and $A_2 = \mu_v+\int_0^{\infty}k(a)i_h^{\ast}(a)da$. We claim that (7) has no root with a nonnegative real part. If the claim is not true, then (7) has a root $\hat{\tau}$ with $\text {Re}(\hat{\tau})\geq 0$. On the one hand,

$\begin{align} 1 = &\mbox{$\frac{|(\hat{\tau}+\mu_h)(\hat{\tau}+\mu_v)\alpha_hS_h^{\ast} \left[(\hat{\tau}+\alpha_v+\mu_v)\int_0^{\infty}\beta_1(a)\sigma(a)e^{-\hat{\tau} a}da(\hat{\tau}+A_2) +\beta_2\alpha_vS_v^{\ast}\int_0^{\infty}k(a)\sigma(a)e^{-\hat{\tau} a}da\right]|}{|(\hat{\tau}+A_1)(\hat{\tau}+\alpha_h+\mu_h)(\hat{\tau}+\mu_v)(\hat{\tau}+A_2)(\hat{\tau}+\alpha_v+\mu_v)|}$} \nonumber \\ \leq&\mbox{$\frac{|(\hat{\tau}+\mu_h)\alpha_hS_h^{\ast} \int_0^{\infty}\beta_1(a)\sigma(a)da|}{|(\hat{\tau}+A_1)(\hat{\tau}+\alpha_h+\mu_h)|}$} +\mbox{$\frac{|(\hat{\tau}+\mu_h)(\hat{\tau}+\mu_v)\alpha_h S_h^{\ast}\beta_2\alpha_vS_v^{\ast}\int_0^{\infty}k(a)\sigma(a)da|} {|(\hat{\tau}+A_1)(\hat{\tau}+\alpha_h+\mu_h)(\hat{\tau}+\mu_v)(\hat{\tau}+A_2)(\hat{\tau}+\alpha_v+\mu_v)|}$} \nonumber \\ <&\mbox{$\frac{|\alpha_hS_h^{\ast}\int_0^{\infty}\beta_1(a)\sigma(a)da|}{|(\hat{\tau}+\alpha_h+\mu_h)|}$} +\mbox{$\frac{|\alpha_hS_h^{\ast}\beta_2\alpha_vS_v^{\ast}\int_0^{\infty}k(a)\sigma(a)da|} {|(\hat{\tau}+\alpha_h+\mu_h)(\hat{\tau}+\mu_v)(\hat{\tau}+\alpha_v+\mu_v)|}$} \nonumber \\ \leq& \frac{\alpha_hS_h^\ast\xi}{\alpha_h+\mu_h}+\frac{\alpha_h S_h^\ast\beta_2\alpha_vS_v^\ast\eta}{(\alpha_h+\mu_h)\mu_v(\alpha_v+\mu_v)}. \label {extA} \end{align}$

(8)

On the other hand, it follows from (4) that

$I_v^*=\frac{ \alpha_v}{\mu_v} E_v^* = \frac{\alpha_v}{\mu_v}\frac{\eta S_v^\ast i_h^\ast(0)}{\alpha_v+\mu_v}$

and

$\begin {eqnarray*} i_h^\ast(0) & = & \alpha_hE_h^\ast \\ & = & \alpha_h\cdot\frac{\xi S_h^\ast i_h^\ast(0)}{\alpha_h+\mu_h}+\alpha_h\cdot\frac{\beta_2S_h^\ast I_v^\ast}{\alpha_h+\mu_h} \\ & = & \alpha_h\cdot\frac{\xi S_h^\ast i_h^\ast(0)}{\alpha_h+\mu_h}+\alpha_h\cdot\frac{\beta_2S_h^\ast}{\alpha_h+\mu_h}\cdot\frac{\alpha_v}{\mu_v}\frac{\eta S_v^\ast i_h^\ast(0)}{\alpha_v+\mu_v}. \end {eqnarray*}$

This implies that $\frac{\alpha_hS_h^\ast\xi}{\alpha_h+\mu_h}+\frac{\alpha_h S_h^\ast\beta_2\alpha_vS_v^\ast\eta}{(\alpha_h+\mu_h)\mu_v(\alpha_v+\mu_v)} = 1$, a contradiction with (8). Therefore, the infected equilibrium $E^{\ast}$ of (2) is locally asymptotically stable when $R_0>1$.

---

4. Global stability

We first study the global stability of the infection-free equilibrium $E^0$.

Theorem 4.1. If $R_0<1$, then the infection-free equilibrium $E^0$ of (2) is globally asymptotically stable.

Proof. Define

$\begin {equation} \begin {array}{rcl} \rho_1(a)= &\int_a^{\infty}k(\theta)e^{-\int_a^{\theta}\delta(s)ds}d\theta, \\ \rho_2(a)= &\int_a^{\infty}\beta_1(\theta)e^{-\int_a^{\theta}\delta(s)ds}d\theta. \end {array} \label {extB} \end{equation}$

(9)

Obviously, $\rho_1(0) = \eta$ and $\rho_2(0) = \xi$. Moreover, $\rho_1(a)$ and $\rho_2(a)$ are bounded and satisfy

$\rho_1^{\prime}(a) = \rho_1 (a)\delta(a)-k(a) ~~~~\mbox{and} ~~~~ \rho_2^{\prime}(a) = \rho_2 (a)\delta(a)-\beta_1(a)$

for $a\in R_+$, respectively. Define the Lyapunov functional

$L = L(S_h, E_h, i_h, S_v, E_v, I_v) = L_1+L_2+L_3,$

where

$\begin{align} L_1 = &\frac{1}{S_h^0}\Big(S_h-S_h^0-S_h^0\ln\frac{S_h}{S_h^0}\Big)+\frac{1}{S_h^0}E_h, \\ L_2 = &\frac{\beta_2\alpha_vS_v^0}{(\alpha_v+\mu_v)\mu_v}\int_0^{\infty}\rho_1(a)i_h(t, a)da +\int_0^{\infty}\rho_2(a)i_h(t, a)da, \\ L_3 = &\frac{\beta_2\alpha_v}{(\alpha_v+\mu_v)\mu_v}\Big(S_v-S_v^0-S_v^0\ln\frac{S_v}{S_v^0}\Big)+\frac{\beta_2\alpha_vE_v}{(\alpha_v+\mu_v)\mu_v} +\frac{\beta_2}{\mu_v}I_v. \end{align}$

Clearly, $L(\cdot)$ is non-negative and $L(x) = 0$ if and only if $x = E^0$.

Now, we calculate the time derivatives of $L_1$, $L_2$, and $L_3$ along solutions of (2) one by one. First,

$\begin{align} & \frac{dL_1}{dt} \\ = &\frac{1}{S_h^0}\Big(1-\frac{S_h^0}{S_h}\Big)\Big(\lambda_h-S_h\int_0^{\infty}\beta_1(a)i_h(t, a)da-\beta_2S_hI_v-\mu_hS_h\Big) \\ & +\frac{1}{S_h^0}\Big(S_h\int_0^{\infty}\beta_1(a)i_h(t, a)da+\beta_2S_hI_v-(\alpha_h+\mu_h)E_h\Big) \\ = & \mu_h\Big(1-\frac{S_h^0}{S_h}\Big)\Big(1-\frac{S_h}{S_h^0}\Big) -\Big(1-\frac{S_h^0}{S_h}\Big)\frac{S_h}{S_h^0}\int_0^{\infty}\beta_1(a)i_h(t, a)da \\ &-\beta_2I_v\frac{S_h}{S_h^0}\Big(1-\frac{S_h^0}{S_h}\Big)+\frac{S_h}{S_h^0}\int_0^{\infty}\beta_1(a)i_h(t, a)da \\ &+\beta_2I_v\frac{S_h}{S_h^0}-\frac{\alpha_h+\mu_h}{S_h^0}E_h \\ = &\mu_h\Big(2-\frac{S_h^0}{S_h}-\frac{S_h}{S_h^0}\Big)+\int_0^{\infty}\beta_1(a)i_h(t, a)da +\beta_2I_v-\frac{\alpha_h+\mu_h}{S_h^0}E_h. \end{align}$

Next, applying integration by parts gives

$\begin{align} \frac{dL_2}{dt} = &\frac{\beta_2\alpha_vS_v^0}{(\alpha_v+\mu_v)\mu_v}\int_0^{\infty}\rho_1(a) \Big(-\frac{\partial i_h(t, a)}{\partial a}-\delta(a)i_h(t, a)\Big)da \\ & -\int_0^{\infty}\rho_2(a)\Big(\frac{\partial i_h(t, a)}{\partial a}+\delta(a)i_h(t, a)\Big)da \\ = &\frac{\beta_2\alpha_vS_v^0}{(\alpha_v+\mu_v)\mu_v}\int_0^{\infty}(\rho_1^{\prime}(a)-\rho_1(a)\delta(a))i_h(t, a)da \\ & +\frac{\beta_2\alpha_vS_v^0}{(\alpha_v+\mu_v)\mu_v} \rho_1(0)i_h(t, 0) \\ & +\int_0^{\infty}(\rho_2^{\prime}(a)-\rho_2(a)\delta(a))i_h(t, a)da +\rho_2(0)i_h(t, 0) \\ = &-\frac{\beta_2\alpha_vS_v^0}{(\alpha_v+\mu_v)\mu_v}\int_0^{\infty}k(a)i_h(t, a)da-\int_0^{\infty}\beta_1(a)i_h(t, a)da \\ &+\frac{\beta_2\alpha_vS_v^0}{(\alpha_v+\mu_v)\mu_v}\eta\alpha_hE_h+\xi\alpha_hE_h. \end{align}$

Finally,

$\begin{align} \frac{dL_3}{dt} = &\frac{\beta_2\alpha_v}{(\alpha_v+\mu_v)\mu_v} \Big(1-\frac{S_v^0}{S_v}\Big)\Big(\lambda_v-\int_0^{\infty}k(a)S_vi_h(t, a)da-\mu_vS_v\Big)\\ & +\frac{\beta_2\alpha_v}{(\alpha_v+\mu_v)\mu_v}\Big(\int_0^{\infty}k(a)S_vi_h(t, a)da-(\alpha_v+\mu_v)E_v\Big) \\ &+\frac{\beta_2}{\mu_v}(\alpha_vE_v-\mu_vI_v) \\ = &\frac{\beta_2\alpha_vS_v^0}{\alpha_v+\mu_v} \Big(2-\frac{S_v^0}{S_v}-\frac{S_v}{S_v^0}\Big) \\ & +\frac{\beta_2\alpha_vS_v^0}{(\alpha_v+\mu_v)\mu_v}\int_0^{\infty}k(a)i_h(t, a)da-\beta_2I_v. \end{align}$

Here we have used $\lambda_v = \mu_vS_v^0$.

In summary, we have shown that

$\begin{align} \frac{dL}{dt} = &\frac{dL_1}{dt}+\frac{dL_2}{dt}+\frac{dL_3}{dt} \\ = &\mu_h\Big(2-\frac{S_h^0}{S_h}-\frac{S_h}{S_h^0}\Big) +\frac{\beta_2\alpha_vS_v^0}{\alpha_v+\mu_v}\Big(2-\frac{S_v^0}{S_v}-\frac{S_v}{S_v^0}\Big) \\ & +\Big(\frac{\beta_2\alpha_vS_v^0}{(\alpha_v+\mu_v)\mu_v}\eta\alpha_h+\xi\alpha_h-\frac{\alpha_h+\mu_h}{S_h^0}\Big)E_h \\ = &\mu_h\Big(2-\frac{S_h^0}{S_h}-\frac{S_h}{S_h^0}\Big) +\frac{\beta_2\alpha_vS_v^0}{\alpha_v+\mu_v}\Big(2-\frac{S_v^0}{S_v}-\frac{S_v}{S_v^0}\Big) \\ & +\frac{(\alpha_h+\mu_h)\mu_h}{\lambda_h}(R_0-1)E_h. \end{align}$

It follows that $\frac{dL}{dt}\leq 0$ if $R_0<1$. Furthermore, the equality $\frac{dL}{dt} = 0$ holds if and only if $S_h(t) = S_h^0$, $S_v(t) = S_v^0$, and $E_h(t) = 0$ for $t\in R_+$. It is easy to see that $\{E^0\}$ is the largest invariant set in $\{\frac{dL}{dt} = 0\}$. By the LaSalle invariance principle [11], $E^0$ is globally attractive. This, combined with Theorem 3.2, implies that $E^0$ is globally asymptotically stable.

In order to study the global stability of the infected equilibrium $E^*$, we need the following preparation.

According to Theorem 2.1, there is a continuous solution semiflow of (2), denoted by $\Phi: R_+\times X_+\to X_+$, where

$\Phi(t, x) = (S_h(t), E_h(t), i_h(t, \cdot), S_v(t), E_v(t), I_v(t)) ~~~ \mbox{for $(t, x)\in R_+\times X_+$}$

with $(S_h(t), E_h(t), i_h(t, \cdot), S_v(t), E_v(t), I_v(t))$ being the solution of (2) with the initial value $(S_{h0}, E_{h0}, i_{h0}, S_{v0}, E_{v0}, I_{v0}) = x$. The semiflow $\Phi$ is also written as $\{\Phi(t)\}_{t\in R_+}$.

Define $\rho:X_+\to R_+$ by

$\rho(S_h, E_h, i_h, S_v, E_v, I_v) = S_h\int_0^{\infty}\beta_1(a)i_h(a)da+\beta_2S_hI_v$

for $(S_h, E_h, i_h, S_v, E_v, I_v)\in X_+$. Let

$X_+^0 = \{x\in X_+|\mbox{there exists $t_0\in R_+$ such that $\rho(\Phi(t_0, x))>0$}\}.$

Clearly, if $x\in X_+\setminus X_+^0$ then $\Phi(t, x)\to E^0$ as $t\to\infty$. With the help of Lemma 3.2 of Hale [7] and Theorem 2.3 of Thieme [22], one can obtain the following results with standard arguments (see, for example, Chen et al. [2]).

Theorem 4.2. Suppose $R_0>1$. Then the following statements are true.

(i) There exists a global attractor $\mathcal{A}$ for the solution semiflow $\Phi$ of (2) in $X_+^0$.

(ii) System (2) is uniformly strongly $\rho$-persistent, that is, there exists an $\varepsilon_0>0$ (independent of initial values) such that

$\liminf\limits_{t\to\infty}\rho(\Phi(t, x))>\varepsilon_0 ~~~~~ {for ~x\in X_+^0.}$

Note that the global attractor $\mathcal{A}$ only can contain points with total trajectories through them since it must be invariant. A total trajectory of $\Phi$ is a function $X:R\to X_+$ such that $\Phi(s, X(t)) = X(t+s)$ for all $t\in R$ and all $s\in R_+$. For a total trajectory,

$i_h(t, a) = i_h(t-a)\sigma(a) ~~~~~ \mbox{for all $t\in R$ and $a\in R_+$.}$

The alpha limit of a total trajectory $X(t)$ passing through $X(0) = X_0$ is

$\alpha(X_0) = \cap_{t\le 0}\overline {\cup_{s\le t}\{X(s)\}}\subseteq \mathcal{A}\cap X_+^0.$

Corollary 1. Suppose $R_0>1$. Then there exists an $\varepsilon_0>0$ such that $S_h(t)$, $E_h(t)$, $i_h(t, 0)$, $S_v(t)$, $E_v(t)$, $I_v(t)\ge \varepsilon_0$ for all $t\in R$, where $(S_h(t), E_h(t), i_h(t, \cdot), S_v(t), E_v(t), I_v(t))$ is any total trajectory in $\mathcal{A}$.

Proof. First, since $\Omega$ is attracting and invariant, there exists $T\in R_+$ such that, for $t\ge T$,

$S_h(t), E_h(t), \int_0^{\infty}i_h(t, a)da \le \frac {3\lambda_h}{2\mu_h}$

and

$S_v(t), E_v(t), I_v(t)\le \frac {3\lambda_v}{2\mu_v}.$

Then, for $t\ge T$, it follows from the first equation of (2) that

$\frac{dS_h(t)}{dt} \ge \lambda_h-\left(\mu_h+\frac{3\lambda_h\|\beta_1\|_{\infty}}{2\mu_h}+\frac{3\lambda_v\beta_2}{2\mu_v}\right)S_h(t),$

which implies $\liminf\limits_{t\to\infty}S_h(t)\ge \frac{\lambda_h}{\mu_h+\frac{3\lambda_h\|\beta_1\|_{\infty}}{2\mu_h}+\frac{3\lambda_v\beta_2}{2\mu_v}}\stackrel{\Delta}{ = } \varepsilon_1$. By invariance, $S_h(t)\ge \varepsilon_1$ for $t\in R$. Similarly, $S_v(t)\ge \frac{\lambda _v}{\mu_v+\frac{3\lambda_h \|k\|_{\infty}}{2\mu_h}}\stackrel{\Delta}{ = }\varepsilon_2$ for $t\in R$.

Next, by Theorem 4.2 and invariance, there exists $\varepsilon_3>0$ such that $S_h(t)\int_0^{\infty}\beta_1(a) i_h(t, a)da+\beta_2S_h(t)I_v(t)\ge \varepsilon_3$ for $t\in R$. This, combined with the second equation of (2), gives

$\frac{dE_h(t)}{dt}\ge \varepsilon_3-(\alpha_h+\mu_h)E_h(t) ~~~~~~ \mbox{for $t\in R$.}$

It follows that $\liminf\limits_{t\to\infty}E_h(t)\ge \frac{\varepsilon_3}{\alpha_h+\mu_h}\stackrel{\Delta}{ = } \varepsilon_4$ and hence $E_h(t)\ge \varepsilon_4$ for $t\in R$ by invariance again. Therefore, $i_h(t, 0) = \alpha_hE_h(t)\ge \alpha_h\varepsilon_4\stackrel{\Delta}{ = } \varepsilon_5$ for $t\in R$. Then, for $t\in R$,

$\begin {eqnarray*} \frac{dE_v(t)}{dt}&\ge &\varepsilon_2\int_0^{\infty} k(a)i_h(t-a, 0)\sigma(a)da-(\alpha_v+\mu_v)E_v(t) \\&\ge&\varepsilon_2\varepsilon_5\int_0^{\infty} k(a)\sigma(a)da-(\alpha_v+\mu_v)E_v(t) \\= &\varepsilon_2\varepsilon_5 \eta -(\alpha_v+\mu_v)E_v(t), \end {eqnarray*}$

which implies that $E_v(t)\ge \frac {\varepsilon_2\varepsilon_5\eta}{\alpha_v+\mu_v}\stackrel{\Delta}{ = }\varepsilon_6$ for $t\in R$. Finally, from $\frac{dI_v(t)}{dt}\ge \alpha_v\varepsilon_6-\mu_v I_v(t)$ for $t\in R$, we can similarly get $I_v(t)\ge \frac{\alpha_v\varepsilon_6}{\mu_v}\stackrel{\Delta}{ = } \varepsilon_7$ for $t\in R$.

Letting $\varepsilon_0 = \min\{\varepsilon_1, \varepsilon_2, \varepsilon_4, \varepsilon_5, \varepsilon_6, \varepsilon_7\}$ finishes the proof.

Now, we are ready to establish the global stability of the infected equilibrium $E^*$ with the approach of Lyapunov functionals.

Theorem 4.3. If $R_0>1$, then the infected equilibrium $E^{\ast}$ of (2) is globally asymptotically stable in $X_+^0$.

Proof. By Theorem 3.2, it suffices to show that $\mathcal{A} = \{E^*\}$. To build a Lyapunov functional, we need the function $g:(0, \infty)\ni z\to z-1-\ln z\in R$. Note that $g(z)\ge 0$ for $z\in (0, \infty)$ and $g(z) = 0$ if and only if $z = 1$.

Let $X(t) = (S_h(t), E_h(t), i_h(t, \cdot), S_v(t), E_v(t), I_v(t))$ be a total trajectory in $\mathcal{A}$. Note that all $S_h(t)$, $E_h(t)$, $i_h(t, 0)$, $S_v(t)$, $E_v(t)$, and $I_v(t)$ are bounded above. Moreover, by Corollary 1, they are also bounded away from $0$. Therefore, there exists an $\varepsilon_0>0$ such that $0\le g(z)<\varepsilon_0$ for $z = \frac{S_h(t)}{S_h^*}$, $\frac{E_h(t)}{E_h^*}$, $\frac{i_h(t, 0)}{i_h^*(0)}$, $\frac{S_v(t)}{S_v^*}$, $\frac {E_v(t)}{E_v^*}$, and $\frac{I_v(t)}{I_v^*}$ for all $t\in R$. Noting $\frac {i_h(t, a)}{i_h^*(a)} = \frac {i_h(t-a, 0)}{i_h^*(0)}$, we have $0\le g(\frac{i_h(t, a)}{i_h^*(a)})<\varepsilon_0$ for all $t\in R$ and $a\in R_+$.

Define a Lyapunov functional

$W = W(S_h, E_h, i_h, S_v, E_v, I_v) = W_1+W_2+W_3,$

where

$\begin{align} W_1 = &g\left(\frac{S_h}{S_h^{\ast}}\right) +\frac{E_h^*}{S_h^{\ast}}g\Big( \frac{E_h}{E_h^{\ast}}\Big), \\ W_2 = &\frac{\beta_2I_v^{\ast}}{\eta\alpha_hE_h^{\ast}}\int_0^{\infty}\rho_1(a)i_h^{\ast}(a) g\Big(\frac{i_h(t, a)}{i_h^{\ast}(a)}\Big)da \\ & +\int_0^{\infty}\rho_2(a)i_h^{\ast}(a) g\Big(\frac{i_h(t, a)}{i_h^{\ast}(a)}\Big)da, \\ W_3= &\frac{\beta_2\alpha_v S_v^*}{(\alpha_v+\mu_v)\mu_v}g\Big(\frac{S_v}{S_v^{\ast}}\Big) +\frac{\beta_2\alpha_v E_v^*}{(\alpha_v+\mu_v)\mu_v}g\Big(\frac{E_v}{E_v^{\ast}}\Big) \\ &+\frac{\beta_2 I_v^*}{\mu_v}g\Big(\frac{I_v}{I_v^{\ast}}\Big). \end{align}$

Here $\rho_1$ and $\rho_2$ are those functions defined by (9). Then $W$ is well-defined and is bounded on $X(t)$. In the following, we calculate the time derivative of the components of $W$ along solutions of (2) one by one.

Firstly,

$\begin{align} & \frac{dW_1}{dt} \\ = &\frac{1}{S_h^{\ast}}\Big(1-\frac{S_h^{\ast}}{S_h}\Big) \Big(\lambda_h-S_h\int_0^{\infty}\beta_1(a)i_h(t, a)da-\beta_2S_hI_v-\mu_hS_h\Big) \\ & +\frac{1}{S_h^{\ast}}\Big(1-\frac{E_h^{\ast}}{E_h}\Big) \Big(S_h\int_0^{\infty}\beta_1(a)i_h(t, a)da+\beta_2S_hI_v-(\alpha_h+\mu_h)E_h\Big). \end{align}$

This, combined with

$\begin{align} \lambda_h = &S_h^{\ast}(\xi\alpha_hE_h^{\ast}+\mu_h+\beta_2I_v^{\ast}), \\ \frac{(\alpha_h+\mu_h)E_h^{\ast}}{S_h^{\ast}} = &\xi\alpha_hE_h^{\ast}+\beta_2I_v^{\ast}, \\ \frac{(\alpha_h+\mu_h)E_h}{S_h^{\ast}}= &\xi\alpha_hE_h+\beta_2I_v^{\ast}\frac{E_h}{E_h^{\ast}}, \end{align}$

gives

$\begin{align} \frac{dW_1}{dt} = &\frac{1}{S_h^{\ast}}\Big(1-\frac{S_h^{\ast}}{S_h}\Big) \Big(\mu_hS_h^{\ast}-\mu_hS_h+S_h^{\ast}(\xi\alpha_hE_h^{\ast}+\beta_2I_v^{\ast})\Big) \\ & -\frac{1}{S_h^{\ast}}\Big(1-\frac{S_h^{\ast}}{S_h}\Big)S_h\int_0^{\infty}\beta_1(a)i_h(t, a)da \\ &-\frac{1}{S_h^{\ast}}\Big(1-\frac{S_h^{\ast}}{S_h}\Big)\beta_2S_hI_v +\frac{S_h}{S_h^{\ast}}\int_0^{\infty}\beta_1(a)i_h(t, a)da \\ & -\frac{E_h^{\ast}S_h}{E_hS_h^{\ast}}\int_0^{\infty}\beta_1(a)i_h(t, a)da +\beta_2I_v\frac{S_h}{S_h^{\ast}} \\ & -\beta_2I_v^{\ast}\frac{I_vS_hE_h^{\ast}}{I_v^{\ast}S_h^{\ast}E_h} -\frac{\alpha_h+\mu_h}{S_h^{\ast}}E_h +\frac{\alpha_h+\mu_h}{S_h^{\ast}}E_h^{\ast} \\ = &\mu_h\Big(2-\frac{S_h^{\ast}}{S_h}-\frac{S_h}{S_h^{\ast}}\Big) +(\xi\alpha_hE_h^{\ast}+\beta_2I_v^{\ast})\Big(1-\frac{S_h^{\ast}}{S_h}\Big) \\ & +\int_0^{\infty}\beta_1(a)i_h(t, a)da+\beta_2I_v \\ & -\int_0^{\infty}\beta_1(a)i_h(t, a)\frac{E_h^{\ast}S_h}{E_hS_h^{\ast}}da -\beta_2I_v^{\ast}\frac{I_vS_hE_h^{\ast}}{I_v^{\ast}S_h^{\ast}E_h} \\ & -\xi\alpha_hE_h-\beta_2I_v^{\ast}\frac{E_h}{E_h^{\ast}}+\xi\alpha_hE_h^{\ast}+\beta_2I_v^{\ast}. \end{align}$

Secondly,

$\begin{align} & \frac{dW_2}{dt} \\ = & \frac{\beta_2I_v^{\ast}}{\eta\alpha_hE_h^{\ast}} \int_0^{\infty}\rho_1(a)\Big(1-\frac{i_h^{\ast}(a)}{i_h(t, a)}\Big) \Big(-\frac{\partial i_h(t, a)}{\partial a}-\delta(a)i_h(t, a)\Big)da \\ &+\int_0^{\infty}\rho_2(a)\Big(1-\frac{i_h^{\ast}(a)}{i_h(t, a)}\Big)\Big(-\frac{\partial i_h(t, a)}{\partial a}-\delta(a)i_h(t, a)\Big)da. \end{align}$

Note that $\rho_1(0) = \eta$ and

$i_h^{\ast}(a)\frac{\partial}{\partial a}\Big(g\Big(\frac{i_h(t, a)}{i_h^{\ast}(a)}\Big)\Big) = \Big(1-\frac{i_h^{\ast}(a)}{i_h(t, a)}\Big)\Big(\frac{\partial i_h(t, a)}{\partial a}+\delta(a)i_h(t, a)\Big).$

Then, with integration by parts, we obtain

$\begin{align} & \int_0^{\infty}\rho_1(a)\Big(1-\frac{i_h^{\ast}(a)}{i_h(t, a)}\Big)\Big(\frac{\partial i_h(t, a)}{\partial a}+\delta(a)i_h(t, a)\Big)da \\ = &\int_0^{\infty}\rho_1(a)i_h^{\ast}(a)\frac{\partial}{\partial a}\Big(g\Big(\frac{i_h(t, a)}{i_h^{\ast}(a)}\Big)\Big)da \\ = &\rho_1(a)i_h^{\ast}(a)g\Big(\frac{i_h(t, a)}{i_h^{\ast}(a)}\Big)\Big|_{a = 0}^{a = \infty} \\ & -\int_0^{\infty}g\Big(\frac{i_h(t, a)}{i_h^{\ast}(a)}\Big)(\rho_1^{\prime}(a)i_h^{\ast}(a)+\rho_1(a)i_h^{\ast\prime}(a))da \\ = &\rho_1(a)i_h^{\ast}(a)g\Big(\frac{i_h(t, a)}{i_h^{\ast}(a)}\Big)\Big|_{a = \infty} -\rho_1(0)i_h^{\ast}(0)g\Big(\frac{i_h(t, 0)}{i_h^{\ast}(0)}\Big) \\ & +\int_0^{\infty}k(a)i_h^{\ast}(a)g\Big(\frac{i_h(t, a)}{i_h^{\ast}(a)}\Big)da. \end{align}$

Similarly,

$\begin{align} & \int_0^{\infty}\rho_2(a)\Big(1-\frac{i_h^{\ast}(a)}{i_h(t, a)}\Big)\Big(\frac{\partial i_h(t, a)}{\partial a}+\delta(a)i_h(t, a)\Big)da \\ = &\rho_2(a)i_h^{\ast}(a)g\Big(\frac{i_h(t, a)}{i_h^{\ast}(a)}\Big)\Big|_{a = \infty} -\rho_2(0)i_h^{\ast}(0)g\Big(\frac{i_h(t, 0)}{i_h^{\ast}(0)}\Big) \\ & +\int_0^{\infty}\beta_1(a)i_h^{\ast}(a)g\Big(\frac{i_h(t, a)}{i_h^{\ast}(a)}\Big)da. \end{align}$

Therefore, with the help of $i_h(t, 0) = \alpha_hE_h$ and $i_h^{\ast}(0) = \alpha_hE_h^{\ast}$, we get

$\begin{align} & \frac{dW_2}{dt} \\ = &\beta_2I_v^{\ast}g\Big(\frac{E_h}{E_h^{\ast}}\Big) -\frac{\beta_2I_v^{\ast}}{\eta\alpha_hE_h^{\ast}} \rho_1(a)i_h^{\ast}(a)g\Big(\frac{i_h(t, a)}{i_h^{\ast}(a)}\Big)\Big|_{a = \infty} \\ & -\frac{\beta_2I_v^{\ast}}{\eta\alpha_hE_h^{\ast}}\int_0^{\infty}k(a)i_h^{\ast}(a) g\Big(\frac{i_h(t, a)}{i_h^{\ast}(a)}\Big)da +\xi\alpha_hE_h^{\ast}g\Big(\frac{E_h}{E_h^{\ast}}\Big) \\ & -\rho_2(a)i_h^{\ast}(a)g\Big(\frac{i_h(t, a)}{i_h^{\ast}(a)}\Big)\Big|_{a = \infty} -\int_0^{\infty}\beta_1(a)i_h^{\ast}(a)g\Big(\frac{i_h(t, a)}{i_h^{\ast}(a)}\Big)da. \end{align}$

Finally,

$\begin{align} & \frac{dW_3}{dt} \\ = &\frac{\beta_2I_v^{\ast}}{(\alpha_v+\mu_v)E_v^{\ast}}\Big(1-\frac{S_v^{\ast}}{S_v}\Big) \Big(\lambda_v-\int_0^{\infty}k(a)S_vi_h(t, a)da-\mu_vS_v\Big) \\ & +\frac{\beta_2I_v^{\ast}}{(\alpha_v+\mu_v)E_v^{\ast}}\Big(1-\frac{E_v^{\ast}}{E_v}\Big) \Big(\int_0^{\infty}k(a)S_vi_h(t, a)da- (\alpha_v+\mu_v)E_v\Big) \\ & +\frac{\beta_2}{\mu_v}\Big(1-\frac{I_v^{\ast}}{I_v}\Big)(\alpha_vE_v-\mu_vI_v). \end{align}$

Since

$\begin{align} \lambda_v= &\mu_vS_v^{\ast}+\eta\alpha_hE_h^{\ast}S_v^{\ast}, \\ \eta\alpha_hE_h^{\ast}S_v^{\ast} = &(\alpha_v+\mu_v)E_v^{\ast}, \\ \frac{\beta_2I_v^{\ast}}{(\alpha_v+\mu_v)E_v^{\ast}} = &\frac{\beta_2I_v^{\ast}}{\eta\alpha_hE_h^{\ast}S_v^{\ast}}, \end{align}$

we have

$\begin{align} \frac{dW_3}{dt}= &\frac{\beta_2I_v^{\ast}}{\eta\alpha_hE_h^{\ast}S_v^{\ast}}\Big(1-\frac{S_v^{\ast}}{S_v}\Big)(\mu_vS_v^{\ast}-\mu_vS_v) \\ & +\frac{\beta_2I_v^{\ast}}{\eta\alpha_hE_h^{\ast}S_v^{\ast}}\Big(1-\frac{S_v^{\ast}}{S_v}\Big)\eta\alpha_hE_h^{\ast}S_v^{\ast} \\ & -\frac{\beta_2I_v^{\ast}}{\eta\alpha_hE_h^{\ast}S_v^{\ast}}\Big(1-\frac{S_v^{\ast}}{S_v}\Big)S_v\int_0^{\infty} k(a)i_h(t, a)da \\ & +\frac{\beta_2I_v^{\ast}}{\eta\alpha_hE_h^{\ast}S_v^{\ast}}\Big(1-\frac{E_v^{\ast}}{E_v}\Big)S_v\int_0^{\infty} k(a)i_h(t, a)da \\ & -\beta_2I_v^{\ast}\Big(1-\frac{E_v^{\ast}}{E_v}\Big)\frac{E_v}{E_v^{\ast}}+\beta_2I_v^{\ast}\frac{E_v}{E_v^{\ast}}-\beta_2I_v -\beta_2I_v^{\ast}\frac{I_v^{\ast}E_v}{I_vE_v^{\ast}}+\beta_2I_v^{\ast}\\ = &\frac{\beta_2I_v^{\ast}\mu_v}{\eta\alpha_hE_h^{\ast}}\Big(2-\frac{S_v^{\ast}}{S_v}-\frac{S_v}{S_v^{\ast}}\Big)-\beta_2I_v^{\ast} \Big(\frac{S_v^{\ast}}{S_v}-1\Big) \\ & +\beta_2I_v^{\ast}\int_0^{\infty}k(a)i_h(t, a)da-\frac{\beta_2I_v^{\ast}}{\eta\alpha_hE_h^{\ast}}\frac{E_v^{\ast}S_v}{E_vS_v^{\ast}}\int_0^{\infty}k(a)i_h(t, a)da \\ &+\beta_2I_v^{\ast}-\beta_2I_v-\beta_2I_v^{\ast}\frac{I_v^{\ast}E_v}{I_vE_v^{\ast}}+\beta_2I_v^{\ast}. \end{align}$

To summarize, we have obtained

$\begin {eqnarray*} \frac{dW}{dt}& = & \mu_h\Big(2-\frac{S_h^{\ast}}{S_h}-\frac{S_h}{S_h^{\ast}}\Big) -(\xi\alpha_hE_h^{\ast}+\beta_2I_v^{\ast})\Big(\frac{S_h^{\ast}}{S_h} -1-\ln\frac{S_h^{\ast}}{S_h}\Big) \\ && -\int_0^{\infty}\beta_1(a)i_h^{\ast}(a)\Big(\frac{i_h(t,a)E_h^{\ast}S_h}{i_h^{\ast}(a)E_hS_h^{\ast}} -1-\ln\frac{i_h(t,a)E_h^{\ast}S_h}{i_h^{\ast}(a)E_hS_h^{\ast}}\Big)da \\ && -\beta_2I_v^{\ast}\frac{I_vS_hE_h^{\ast}}{I_v^{\ast}S_h^{\ast}E_h} -(\xi\alpha_hE_h^{\ast}+\beta_2I_v^{\ast})\Big(\frac{E_h}{E_h^{\ast}} -1-\ln\frac{E_h}{E_h^{\ast}}\Big) \\ &&+\beta_2I_v^{\ast}g\Big(\frac{E_h}{E_h^{\ast}}\Big)+\xi\alpha_hE_h^{\ast}g\Big(\frac{E_h}{E_h^{\ast}}\Big) \\ && -\Big(\frac{\beta_2I_v^{\ast}}{\eta\alpha_hE_h^{\ast}}\rho_1(a)+\rho_2(a)\Big)i_h^{\ast}(a)g \Big(\frac{i_h(t,a)}{i_h^{\ast}(a)}\Big)\Big|_{a=\infty} \\ && -\frac{\beta_2I_v^{\ast}}{\eta\alpha_hE_h^{\ast}}\int_0^{\ast}k(a)i_h^{\ast}(a) \Big(\frac{i_h(t,a)E_v^{\ast}S_v}{i_h^{\ast}(a)E_vS_v^{\ast}} -1-\ln\frac{i_h(t,a)E_v^{\ast}S_v}{i_h^{\ast}(a)E_vS_v^{\ast}}\Big)da \\ && +\frac{\beta_2I_v^{\ast}\mu_v}{\eta\alpha_hE_h^{\ast}}\Big(2-\frac{S_v^{\ast}}{S_v}-\frac{S_v}{S_v^{\ast}}\Big) -\beta_2I_v^{\ast}\Big(\frac{S_v^{\ast}}{S_v}-1-\ln\frac{S_v^{\ast}}{S_v}\Big) \\ && -\beta_2I_v^{\ast}\Big(\frac{I_v^{\ast}E_v}{I_vE_v^{\ast}}-1-\ln\frac{I_v^{\ast}E_v}{I_vE_v^{\ast}}\Big)+\beta_2I_v^{\ast} \Big(1+\ln\frac{I_vS_hE_h^{\ast}}{I_v^{\ast}S_h^{\ast}E_h}\Big) \\ & = & \mu_h\Big(2-\frac{S_h^{\ast}}{S_h}-\frac{S_h}{S_h^{\ast}}\Big) -(\xi\alpha_hE_h^{\ast}+\beta_2I_v^{\ast})g\Big(\frac{S_h^{\ast}}{S_h}\Big) \\ && -\int_0^{\infty}\beta_1(a)i_h^{\ast}(a)g\Big(\frac{i_h(t,a)E_h^{\ast}S_h}{i_h^{\ast}(a)E_hS_h^{\ast}} \Big)da-\beta_2I_v^{\ast}g\Big(\frac{I_vS_hE_h^{\ast}}{I_v^{\ast}S_h^{\ast}E_h}\Big) \\ && -\Big(\frac{\beta_2I_v^{\ast}}{\eta\alpha_hE_h^{\ast}}\rho_1(a)+\rho_2(a)\Big)i_h^{\ast}(a)g \Big(\frac{i_h(t,a)}{i_h^{\ast}(a)}\Big)\Big|_{a=\infty} \\ && -\frac{\beta_2I_v^{\ast}}{\eta\alpha_hE_h^{\ast}}\int_0^{\infty}k(a)i_h^{\ast}(a) g\Big(\frac{i_h(t,a)E_v^{\ast}S_v}{i_h^{\ast}(a)E_vS_v^{\ast}} \Big)da \\ && +\frac{\beta_2I_v^{\ast}\mu_v}{\eta\alpha_hE_h^{\ast}} \Big(2-\frac{S_v^{\ast}}{S_v}-\frac{S_v}{S_v^{\ast}}\Big) -\beta_2I_v^{\ast}g\Big(\frac{S_v^{\ast}}{S_v}\Big) -\beta_2I_v^{\ast}g\Big(\frac{I_v^{\ast}E_v}{I_vE_v^{\ast}}\Big) \\ & \le & 0. \end{eqnarray*}$

Therefore, $W$ is nonincreasing. Since $W$ is bounded on $X(\cdot)$, the alpha limit set of $X(\cdot)$ must be contained in the largest invariant subset of $\{\frac{dW}{dt} = 0\}$, which is easily identified to be $\{E^{\ast}\}$. It follows that $W(X(t))\le W(E^*)$ for all $t\in R$. This gives $X(t)\equiv E^*$ and hence $\mathcal{A} = \{E^*\}$, which completes the proof.

---

5. Numerical simulations

In this section, we illustrate the theoretical results obtained in Section 4 with numerical simulations. For this purpose, we take $k(a) = k$. For the form of $\beta_1(a)$, we give some explanation. In general, when the infection age $a$ is relatively small, the age-dependent horizontal transmission rate $\beta_1(a)$ of the disease from the infectious hosts to susceptible hosts is relatively small. With the increase of the infection age, the infection rate also increases and then tends to a constant. When the infection age is very large, the infection rate is reduced to 0 due to the loss of infectivity. Similar explanation can be given for the form of the age-dependent recovery rate $\gamma(a)$. For some more details, we refer readers to [4, 6]. Therefore, we take the following forms for $\beta_1$ and $\gamma$ in the simulations.

$\begin{align} \beta_1(a) = \left\{ \begin{array}{ll} c_1, &0\leq a<10, \\ c_1+c_2(a-10)e^{-0.009(a-25)^2}, &10\leq a<25, \\ c_2, &25\leq a<50, \\ 0, &a\geq 50, \end{array} \right. \end{align}$

and

$\begin{align} \gamma(a) = \left\{\begin{array}{ll} 0, & 0\leq a<10, \\ \frac{c_3}{15}(\arctan 50)(a-10), &10\leq a<25, \\ c_3\arctan(75-a), &25\leq a<50, \\ c_3\arctan(25), &a\geq 50. \end{array} \right. \end{align}$

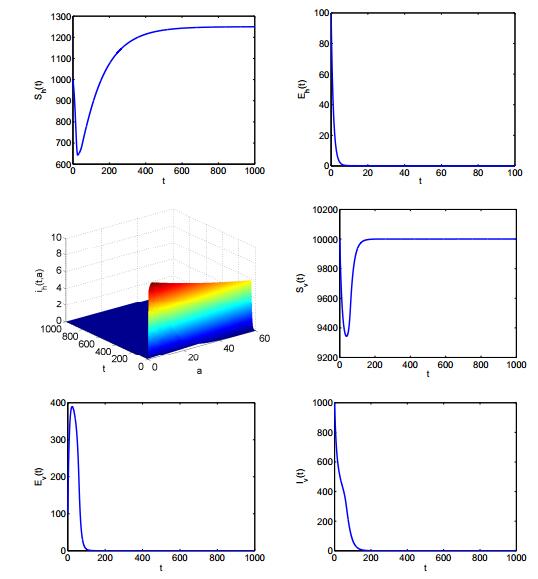
We first set parameters $\lambda_h = 10$, $\lambda_v = 500$, $\mu_h = 0.008$, $\beta_2 = 1.81\times10^{-7}$, $\mu_v = 0.05$, $\alpha_h = 0.833$, $\alpha_v = 0.05$, $k = 4.1665\times10^{-5}$, $c_1 = 0.00003$, $c_2 = 0.00005$, and $c_3 = 5.6\times10^{-6}$, which are chosen from some recent studies [4, 6]. With these parameters, the basic reproductive number is $R_0 = 0.8286<1$. Thus, the infection-free equilibrium $E^0$ is globally asymptotically stable by Theorem 4.1. Fig. 1 shows the time evolution of the solution with the initial value $(1000, 100, 5(a+3)e^{-0.2(a+3)}, 10000, 100, 1000)$.

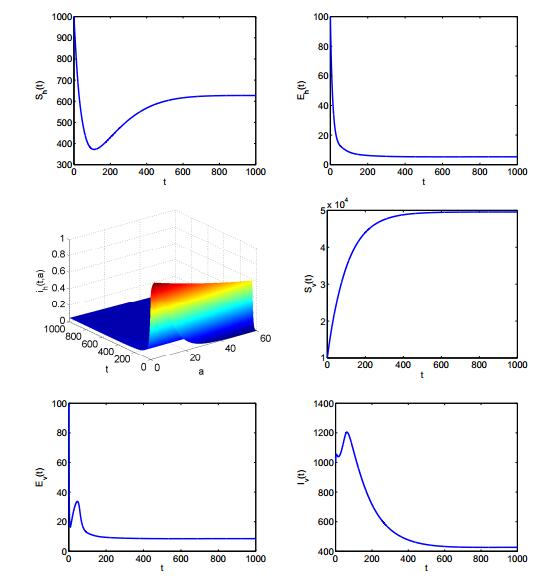
Next, we take another set of parameter values, $\lambda_h = 10$, $\lambda_v = 500$, $\mu_h = 0.008$, $\beta_2 = 1.81\times10^{-6}$, $\mu_v = 0.01$, $\alpha_h = 0.08333$, $\alpha_v = 0.05$, $k = 4.1665\times10^{-5}$, $c_1 = 0.00003$, $c_2 = 0.00005$, and $c_3 = 5.6\times10^{-6}$. In this case, $R_0 = 9.2655>1$. Then Theorem 4.3 tells us that the infected equilibrium $E^{\ast}$ is globally asymptotically stable. Fig. 2 supports this with the time evolution of the solution with the initial value $(1000, 100, 0.5(a+3)e^{-0.2(a+3)}, 10000, 100, 1000)$.

---

6. Conclusion

Infection age is a very important factor in the transmission of infectious diseases such as malaria, TB, and HIV. In this paper, we incorporated infection age into a vector-host epidemic model with direct transmission. In the model, we also took into account the exposed individuals in both human and vector populations. We assumed that the level of contagiousness and the rate of removal (recovery) of infected hosts depend on the infection age. Therefore, our model is described by a system of ordinary differential equations coupled with a partial differential equation, which is very challenging to study because it is an infinitely dimensional system. With the approach of Lyapunov functionals and some recently developed techniques on global analysis in [15, 16], we have established a threshold dynamics completely determined by the basic reproduction number. That is, the infection-free equilibrium is globally asymptotically stable if the basic reproduction number is less than one while the infected equilibrium is globally asymptotically stable if the basic reproduction number is greater than one. Numerical simulations are conducted to illustrate the stability results.

Our result supports the claim that infection age can affect the number of average secondary infections, that is, the effect of infection age is embodied in the expression of the basic reproduction number $R_0$. By appropriate control measures, one can decrease the survival probability to infection age $a$, $\sigma(a)$, the horizontal transmission rate $\beta_1(a)$, and the biting rate $k(a)$. This will decrease the value of $R_0$ and possibly will eliminate the disease. Even if we cannot eliminate the disease, from the expression of the infected equilibrium one can easily show that this will decrease the levels of $E_h^*$, $i_h^*(0)$, $E_v^*$, and $I_v^*$. Because of the globally asymptotical stability of $E^*$, we can keep the infection at a tolerance level.

---

Acknowledgments

X. Wang is supported by the NSFC (No. 11771374), the Nanhu Scholar Program for Young Scholars of Xinyang Normal University, the Program for Science and Technology Innovation Talents in Universities of Henan Province (17HASTIT011). Y. Chen is supported by the NSERC.

---