The functional roles of T-cadherin in mammalian biology

1.   Introduction

Weighted distributions (WDs) provide an approach to deal with model specification and data interpretations problems. They adjust the probabilities of the actual occurrence of events to arrive at a specification of the probabilities when those events are recorded. Reference ^[1] extended the basic ideas of the methods of ascertainment upon the estimation of frequencies in ^[2]. The author defined a unifying concept of the WDs and described several sample conditions that the WDs can model. The usefulness and applications of the WDs in various areas, including medicine, ecology, reliability, and branching processes, can also be seen in ^[3,4,5]. Important findings on the WDs have been reported by several research. For examples, reference ^[6] suggested a weighted x-gamma distribution, reference ^[7] derived a new generalized weighted Weibull distribution, reference ^[8] introduced the weighted exponential-Gompertz distribution, reference ^[9] studied the new weighted inverse Rayleigh distribution, reference ^[10] introduced a weighted version of the generalized inverse Weibull distribution, reference ^[11] proposed a bounded weighted exponential distribution, reference ^[12] derived a new weighted exponential distribution, reference ^[13] proposed a weighted power Lomax distribution, reference ^[14] derived a new generalized weighted exponential distribution, reference ^[15] introduced a new version of the weighted Weibull distribution, reference ^[16] proposed the modified weighted exponential distribution, and reference ^[17] proposed a weighted Nwikpe distribution, reference ^[18] introduced a new version of the double weighted quasi Lindley distribution and reference ^[19] proposed the modified length-biased weighted Lomax distribution.

In contrast, statistical models have the capacity to depict and predict real-world phenomena. Over the past few decades, numerous extended distributions have been extensively utilized in data modeling. Recent progress has been centered on the development of novel distribution families that not only enhance existing distributions but also offer significant versatility in practical data modeling. Engineering, economics, biology, and environmental science are particular examples of this. Regarding this, a number of writers suggested some of the created families of continuous distributions, (see for example ^[20,21,22]). Our interest here is in the same scheme used for the beta-G (B-G) family prepared in ^[23]. The following is the cumulative distribution function (cdf) for the B-G family:

where $G(x)$ is a cdf of a continuous distribution and $r(t)$ is the probability density function (pdf) of the beta distribution. Naturally, any new family can be created by taking another pdf for $r(t)$ with support $[0, 1]$ (see reference ^[23]).

As a matter of fact, few works about the weighted-G family have been proposed in the literature. For example, reference ^[24] studied the weighted exponential-G family, reference ^[25] introduced the weighted exponentiated family, reference ^[26] proposed a weighted general family, and reference ^[27] developed a weighted Topp-Leone-G family.

The primary purpose of this study is to introduce the length-biased truncated Lomax-G (LBTLo-G) family. The following arguments give enough motivation to study it:

$1)$ The LBTLo-G family is very flexible and simple.

$2)$ The LBTLo-G family contains some new distributions.

$3)$ The shapes of the pdfs of the generated distributions can be unimodal, decreasing, bathtub, right-skewed, and symmetric. Also, the hazard rate function (hrf) shapes for these distributions can be increasing, decreasing, U-shaped, upside-down-shaped, or J- shaped.

After emphasizing these important aspects, some statistical and mathematical properties of the newly suggested family are discussed. The maximum likelihood (ML) method of estimation is used to estimate the LBTLo Weibull (LBTLoW) model parameters based on complete and type Ⅱ censoring (T2C).

The variability of the LBTLoW distribution is demonstrated through four authentic data sets. The first data set describes age data on rest times (in minutes) for analgesic patients. The second data set shows the percentage of natural gas reserves in 44 countries in 2020. The third authentic data set listed the top 20 countries by oil reserves. Proven reserves refer to the quantities of petroleum that can be predicted as commercially recoverable from known reservoirs, based on the analysis of geological and engineering data. These estimates are made considering existing economic conditions and are projected from a specific period onwards. The fourth data set displays the top 100 central banks in terms of gold reserves. This gold reserve data, collected from IMF IFS figures, tracks central banks' reported gold purchases and sales as a percentage of their international reserves. The application results show that the LBTLoW distribution can indeed match the data better than other competing distributions.

The following is the structure for this article: Section 2 defines the crucial functions of the LBTLo-G family and provides four special distributions of the family. In Section 3, some statistical properties of the LBTLo-G family are provided. Section 4 deals with the ML estimates (MLEs) of the unknown parameters. A simulation study to examine the theoretical performance of MLEs for the LBTLoW distribution is studied in Section 5. Section 6 presents the applicability and goodness of fit of the proposed models using four real data sets. The paper ends with a few last observations, as may be seen in Section 7.

2.   Construction of the LBTLo-G family

Here, we suggest a new weighted family based on the weighted version of the truncated Lomax distribution, which is called the LBTLo distribution ^[28]. The cdf and pdf of the LBTLo distribution are, respectively, given by

where $\Lambda\left(\alpha \right) = \left[2^{-\alpha } \; \; \left(1+\alpha \right)-1\right]^{-1}.$ For these functions, it is assumed the standard complementary values for $t\le 0$ and $t\ge 1$.

As mentioned in ^[28], the following advantages of the LBTLo distribution are outlined: (ⅰ) It depends on only one parameter; (ⅱ) the pdf has only one maximum point with a relatively sharp peak and a heavy tail; (ⅲ) the hrf has increasing behavior or is N-shaped; and (ⅳ) it outperforms some other competing models in real-world applications to medical data and the percentage of household spending on education out of total household expenditure from the Household Income, Expenditure, and Consumption Survey data for North Sinai Governorate.

In light of these merits, the LBTLo distribution is a great choice to use in various fields. As a consequence, we present a novel generated family that is based on the LBTLo distribution. In order to define the LBTLo-G family, let $G(x; \zeta)$ and $g(x; \zeta)$ be the baseline cdf and pdf, respectively, of a continuous distribution, and $\zeta$ is a vector of parameters. The generalized B-G generator specified in (1.1) and the LBTLo distribution (2.2) are combined to generate the cdf of the LBTLo-G family:

where $\alpha$ is a shape parameter. Therefore, the pdf of the LBTLo-G family is given by

A random variable X with the pdf (2.4) is designated as $X\sim$ LBTLo-G from here on out. The complementary cdf (ccdf), and hrf, are, provided by

We create four new LBTLo-G family sub-distributions in the subsections that follow: LBTLo-inverse exponential, LBTLo-uniform, LBTLo-Weibull, and LBTLo-Kumaraswamy distributions.

2.1.   LBTLo-inverse exponential model

The cdf and pdf of the LBTLo-inverse exponential (LBTLoIE) distribution are obtained from (2.3) and (2.4) for $G\left(x; \beta \right) = e^{-(\beta /x)}, \beta, x > 0,$ as follows:

Further, the hrf is as follows:

2.2.   LBTLo-uniform distribution

The cdf and pdf of the LBTLo-uniform (LBTLoU) distribution are derived from (2.3) and (2.4) by taking $G\left(x; \beta \right) = \beta ^{-1} x, 0 < x < \beta,$ as follows:

Further, the hrf is as follows:

2.3.   LBTLo-Weibull distribution

The cdf and pdf of the LBTLoW distribution are derived from (2.3) and (2.4) taking $G\left(x; \beta, \gamma \right) = 1-e^{-\beta x^{\gamma } }, \, \, x, \beta, \gamma > 0,$ as follows:

Further, the hrf is:

2.4.   LBTLo-Kumaraswamy distribution

The cdf and pdf of the LBTLo- Kumaraswamy (LBTLoKw) distribution are obtained from (2.3) and (2.4) by taking $G(x; \mu, b) = 1-(1-x^{\mu })^{b}, \, \, 0 < x < 1, b, \mu > 0,$ as follows:

Further, the hrf is as follows:

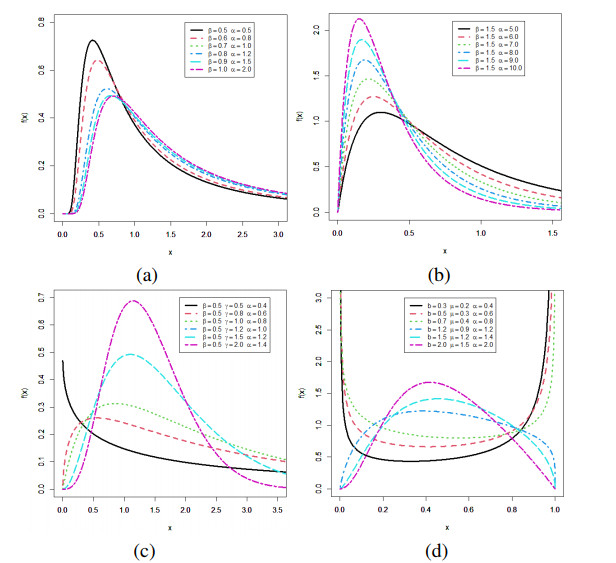
The plots of pdf and hrf for the LBTLoIE, LBTLoU, LBTLoW and LBTLoKw distributions are given in Figures 1 and 2, respectively.

The pdfs of the investigated distributions can have a variety of forms, including right- and left-skewed, bathtub, uni-modal, declining, and symmetric shapes, as shown in Figure 1. The corresponding hrf can take any form, including U, J, reverse J, growing, or decreasing, as seen in Figure 1.

3.   Some statistical properties of LBTLo-G family

In this part, we give some statistical properties of the LBTLo-G family.

3.1.   Important expansion

The LBTLo-G family representations in pdf and cdf format are displayed here. The generalized binomial theorem says that

for $|z| < 1$. Hence, by using (3.1) in (2.4), the pdf of the LBTLo-G family can be written as follows:

where $\vartheta _{i} = \left(-1\right)^{i} \alpha \left(1-\alpha \right)\Lambda\left(\alpha \right)\left(\begin{array}{c} {\alpha +i} \\ {i} \end{array}\right)$. For example, the expansion of pdf of the LBTLoW distribution is derived from (3.2) as follows:

But, in the special case where $b$ is a positive integer, the standard generalized binomial theorem says that

Then using the binomial expansion (3.4) in (3.3), we get

where $\vartheta _{i, \nu } = \beta \gamma \vartheta _{i} \left(-1\right)^{\nu } \left(\begin{array}{c} {i+1} \\ {\nu } \end{array}\right).$ In what follows, an expansion for $F\left(x; \alpha, \zeta \right)^{h}$is derived, for $h$ is an integer, again, the exponential and the binomial expansions are worked out:

Using the binomial expansion (3.4) in (3.6), we get

Using the binomial expansion (3.1), we obtain

By using (3.4) in (3.8), we obtain

where $\varpi _{{d, j, m}} = \sum _{j = 0}^{h}\sum _{m = 0}^{j}\left(-1\right)^{d+m+h-j} \alpha ^{m} \left(\begin{array}{c} {h} \\ {j} \end{array}\right)\left(\begin{array}{c} {j} \\ {m} \end{array}\right) \; \left(\begin{array}{c} {\alpha j+d-1} \\ {d} \end{array}\right)\Lambda\left(\alpha \right)^{h}.$

For example, the expansion of the cdf of the LBTLoW distribution is derived from (3.9), where $G(x, \zeta) = 1-e^{-\beta x^{\gamma } }$, as follows:

By using the binomial expansion (3.4) in the last term of the previous equation, we get

The above representations are of interest to express various important moment measures as series. By truncating the index of summation, we can have a precise approximation with a reasonable computation cost.

3.2.   The Probability Weighted Moments

As a special class of moments, the probability weighted moments (PWMs) have been proposed in ^[29]. This class is used to derive estimates of the parameters and quantiles of distributions expressible in inverse form. Let $X$ be a random variable with pdf and cdf $f(x)$ and $F(x)$, respectively, and $r$ and $q$ be non-negative integers. Then, the $(r, q)^{th}$ PWM of $X$, denoted by ${\pi }_{r, q}$, can be calculated through the following relation:

On this basis, the $(r, q)^{th}$ PMW of $X$ with pdf and cdf of the LBTLo-G family is obtained by substituting (3.2) and (3.9) into (3.11), as follows:

Then, provided that the interchange of the integral and sum is valid, depending on the definitions of $g\left(x; \zeta \right)$ and $G\left(x; \zeta \right)$, we have

where

For example, the $(r, q)^{th}$ of a random variable $X$ that follows the LBTLoW distribution can be obtained by substituting (3.5) and (3.10) into (3.11), and replacing $h$ with $q$. We thus obtain

where $\Gamma \left(.\right)$ stands for gamma function.

3.3.   Moments and incomplete moments

In this part, for any non-negative integer $r$, the $r^{th}$ moment associated with the LBTLo-G family is derived.

Let $X$ be a random variable having the pdf of the LBTLo-G family. Then, the $r^{th}$ moment of $X$ is obtained as follows:

where $\upsilon _{r, i+1}$ is the $(r, i+1)^{th}$ PWM of the baseline distribution. For example, after some developments, the $r^{th}$ moment associated with LBTLoW distribution is given by

Tables 1–3 show the numerical values of the first four moments $\mu '_{1}$, $\mu '_{2}$, $\mu '_{3}$, $\mu '_{4},$ also the numerical values of variance (${\sigma }^{\mathrm{2}}$), coefficient of skewness (CS), coefficient of kurtosis (CK) and coefficient of variation (CV) associated with the LBTLoW and LBTLoIE distribution.

It can be seen from Tables 1–3 that, when the value of $\alpha, \gamma$ increases for a fixed value of $\beta$, the first four moments and ${\sigma }^{\mathrm{2}}$ decrease, while the CS, CK, and CV measures increase. When the value of $\beta$ increases for a fixed value of $\alpha$ and $\gamma$, we observe that the first four moments and $\sigma$ decrease and then increase, while the CS, CK, and CV measures increase. The LBTLoW distribution is skewed to the right by leptokurtic curves.

Furthermore, if $X$ is a random variable having the pdf of the LBTLo-G family, then the $r^{th}$ incomplete moment of $X$ is obtained as follows:

For example, after some developments, the $r^{th}$ incomplete moment associated with the LBTLoW distribution is given by

where $\Gamma \left(., x\right)$ is the lower incomplete gamma function.

3.4.   Some information measures

Here, some uncertainty measures of the LBTLo-G family are derived. Then, these measures are specialized to the LBTLoW distribution. To begin, the Rényi entropy (RE), presented in ^[30], associated with a distribution with pdf $f(x)$, is defined by

A numerical study with integral calculus is possible; here, we focus on a series expansion. In what follows, an expansion for $f\left(x; \alpha, \zeta \right)^{\varepsilon }$ is derived, for $\varepsilon$ is a non-integer (again, the generalized binomial expansion is worked out):

where

Then, the RE associated with the LBTLo-G family is given by

For example, the RE associated with the LBTLoW distribution can be obtained as follows:

The Havrda and Charvát entropy (HaCE) (see ^[31]) associated with a distribution with pdf $f(x)$ is defined by

Hence, the HaCE of the LBTLo-G family is given by

For example, the HaCE of the LBTLoW distribution can be obtained as follows:

The Arimoto entropy (ArE) (see ^[32]) associated with a distribution with pdf $f(x)$ is defined by

Hence, the ArE of the LBTLo-G family is given by

For example, the ArE of the LBTLoW distribution can be obtained as follows:

The Tsallis entropy (TsE) (see ^[33]) associated with a distribution with pdf $f(x)$, is defined by

Hence, the TsE of the LBTLo-G family is obtained as follows:

For example, the TsE of the LBTLoW distribution can be obtained as follows:

Some numerical values for the proposed entropy measures are obtained for the LBTLoW and LBTLoIE distribution in Tables 4 and 5.

We can see from these tables that, as the value of $\varepsilon$ rises, all entropy values decrease, providing more information. For a fixed value of $\beta$, as the values of $\alpha$ and $\gamma$ rise, we infer that all entropy metrics decrease, indicating that there is less fluctuation. Additionally, we deduce that all entropies have less variability as the values of $\alpha$, $\gamma$ and $\beta$ increase. When compared to other measures, the TsE measure values typically have the smallest values.

4.   Maximum likelihood estimates via T2C

Let $x_{(1)} \le x_{(2)} \le \ldots\le x_{(n)}$ be a T2C of size $r$ resulting from a life test on $n$ items whose lifetimes are described by the LBTLo-G family with a given set of parameters $\alpha$ and $\zeta$, see ^{[34,35,36,37]}. The log-likelihood function of $r$ failures and ($n-r$) censored values, is given by

where $A_{r} (\alpha, \zeta) = 1-\Lambda\left(\alpha \right)\left[\left(1+G\left(x_{r}; \zeta \right)\right)^{-\alpha } \left(1+\alpha G\left(x_{r}; \zeta \right)\right)-1\right]$, and we write $x_{(i)} = x_{i}$ for simplified form.

By maximizing the previous likelihood function, the MLEs of unknown parameters are determined. To achieve this, we can first compute the first derivative of the score function $\left(U_{\alpha }, \, U_{\zeta _{k} } \right)$, given as follows:

where

and

By putting $U_{\alpha }$ and $U_{\zeta _{k} }$ equal to zero and solving these equations simultaneously, the MLEs of the LBTLo-G family are found. These equations are not amenable to analytical solution, however they are amenable to numerical solution by iterative techniques utilizing statistical software.

The confidence interval (CI) of the vector of the unknown parameters $\xi = (\alpha, \, \zeta)$ could be obtained from the asymptotic distribution of the MLEs of the parameters as $\left(\hat{\xi }_{MLE} -\xi \right)\to N_{2} \left(0, I^{-1} \left(\hat{\xi }_{MLE} \right)\right),$ where $I\left(\xi \right)$ is the Fisher information matrix. Under particular regularity conditions, the two-sided $100\left(1-v\right)%, 0 < v < 1$, asymptotic CI for the vector of unknown parameters $\xi$ can be acquired in the following ways: $\hat{\xi }_{MLE} \pm z_{{v/ 2} } {}_{} \sqrt{var(\hat{\xi })}$, where $var(\hat{\xi })$ is the element of the main diagonal of the asymptotic variance-covariance matrix $I^{-1} \left(\hat{\xi }_{MLE} \right)$ and $z_{{v/ 2} }$ is the upper ${v^{th} / 2}$ percentile of the standard normal distribution.

5.   Numerical results

This section includes a simulation study to evaluate the performance of the MLEs for the LBTLoW model $(\alpha, \beta, \gamma),$ for complete and T2C. The Mathematica 9 package is used to get the mean squared error (MSE), lower bound (LB) of CI, upper bound (UB) of CI, average length (AL) of 95%, and coverage probability (CP) of 95% of the estimated values of $\alpha$, $\beta$ and $\gamma$. The algorithm is developed in the way described below:

$1)$ From the LBTLoW distribution, 5000 random samples of sizes $n$ = 50,100,150, and 200 are created.

$2)$ Values of the unknown parameters $\left(\alpha, \beta, \gamma \right)$ are selected as Set 1 $= (\alpha = 0.5, \beta = 0.5, \gamma = 0.5)$, Set 2 $= \left(\alpha = 0.7, \beta = 0.5, \gamma = 0.25\right)$, Set 3 $= \left(\alpha = 0.7, \beta = 0.7, \gamma = 0.5\right)$, and Set 4 $= \left(\alpha = 0.6, \beta = 0.3, \gamma = 0.5\right)$.

$3)$ Three levels of censorship are chosen: $r$ = 70%, 80% (T2C), and 100% (complete sample).

$4)$ The MLEs, Biases, and MSEs for all sample sizes and for all selected sets of parameters are computed. Furthermore, the LB, UB, AL, and CP with a confidence level of 0.95 for all sample sizes and for all selected sets of parameters are calculated.

$5)$ Numerical outcomes are reported in Table 6. Based on complete and T2C samples, we can detect the following about the performance of the estimated parameters.

${\rm{A}}.$ For almost all the true values, the MSE of all the estimates decreases as the sample sizes and the censoring level r increase, demonstrating that the various estimates are consistent (see Table 6 and Figure 3).

${\rm{B}}.$ For all true parameter values, the ALs of all the estimates decrease as the sample sizes and the censoring level r increase (see Table 6 and Figure 4).

${\rm{C}}.$ For all true parameter values, the CP of all the estimates increases as the sample sizes and the censoring level r increase (see Table 6).

${\rm{D}}.$ The MSE of the estimate of $\alpha$ at the true value of Set1 yields the lowest values in comparison to the other actual parameter values for all sample sizes (see Table 6 and Figure 5).

${\rm{E}}.$ At all actual values, the MSE of the estimate of $\beta$ produces the largest results for all sample sizes (see Table 6 and Figure 6). Also, it is evident that except for $n = 50$ and 200, the MSE of $\beta$ estimates obtains the smallest values for the actual value of Set1 compared to the other actual sets at the censoring level 70%. At the censoring level 80%, the MSE of $\beta$ estimates gets the smallest values at all sets of parameters except at $n = 50$.

${\rm{F}}.$ The MSE of the estimate of $\gamma$ at the true value of Set2 gets the smallest values in comparison to the other actual parameter values for all sample sizes (see Table 6 and Figure 7).

${\rm{G}}.$ The MSEs, biases, and ALs of $\gamma$ are smaller than the other estimates of $\alpha$ and $\beta$ in almost all of the cases.

${\rm{H}}.$ As $n$ rises, the CI's lengths get shorter.

${\rm{I}}.$ As $n$ increases, parameter estimates grow increasingly accurate, suggesting that they are asymptotically unbiased.

${\rm{J}}.$ For the parameter values examined, the CI's overall performance is fairly strong.

6.   Data analysis

Here, we provide applications to four real data sets to illustrate the importance and potentiality of the LBTLoW distribution. The goodness-of-fit statistics for these distributions and other competitive distributions are compared, and the MLEs of their parameters are provided.

The first real data set ^[38] on the relief times of twenty patients receiving an analgesic is 1.1, 1.4, 3, 1.7, 2.3, 1.4, 1.3, 1.7, 2.2, 1.7, 2.7, 4.1, 1.8, 1.5, 1.9, 1.8, 1.6, 1.2, 1.6, 2.

The second dataset illustrates the proportion of global reserves of natural gas in various countries as of the year 2020. In contrast to other nations, Russia possesses the largest natural gas reserves globally and maintains its position as the leading exporter of natural gas. Iran, on the other hand, ranks second in terms of natural gas reserves worldwide. Qatar, although holding slightly over 13% of the total global natural gas reserves, also plays a significant role in the natural gas market. Lastly, Saudi Arabia possesses the fifth-largest natural gas reserves globally. The electronic address from which it was taken is as follows: https://worldpopulationreview.com/. The data set is reported in Table 7.

The third dataset pertains to the Top 20 Countries with the Largest Oil Reserves, measured in thousand million barrels. Crude oil serves as the predominant fuel source globally and is the primary source of energy on a wide scale. In the year 2020, global oil consumption reached around 88.6 million barrels per day, or 30.1% of the overall primary energy consumption. Venezuela possesses the largest oil reserves globally, over 300 billion barrels in total. Saudi Arabia holds the world's second-largest oil reserves, with 297.5 billion barrels. The United States is the world's leading producer of oil as well as the world's greatest user of oil, necessitating additional imports from dozens of other oil-producing countries. Despite having the world's highest oil production, the United States is only 9th in the world in terms of available oil reserves. It was obtained from the following electronic address: https://worldpopulationreview.com/. The data set is reported in Table 8.

The fourth data set represents the Top 100 central banks that owned the largest gold Reserves (in thousand tons). Because of its safety, liquidity, and return qualities-the three major investment objectives for central banks-gold is an essential component of central bank reserves. As such, they are significant gold holders, accounting for around one-fifth of all gold extracted throughout history. They present gold reserve data derived using IMF IFS figures to help comprehend this sector of the gold market, which records central banks' (and other official institutions, when appropriate) reported purchases and sales of gold as a percentage of their international reserves. It was obtained from the following electronic address: https://www.gold.org/. The data set is reported in Table 9.

The descriptive analysis of all the data sets is reported in Table 10.

These real data sets are utilized to assess the goodness of fit of the LBTLoW distribution. The suggested model is compared with exponentiated transmuted generalized Rayleigh (ETGR) ^[39], beta Weibull (BW) ^[40], transmuted Lindley (T-Li) ^[41], McDonald log-logistic (McLL) ^[42], new modified Weibull (NMW) ^[43], weighted exponentiated inverted Weibull (WEIW) ^[44], transmuted complementary Weibull geometric (TCWG) ^[45], transmuted modified Weibull (TMW) ^[46], exponentiated Kumaraswamy Weibull (EKW) ^[47] and Weibull (W) models.

The maximum likelihood estimators (MLEs) and standard errors (SEs) of the model parameters are computed. In order to assess the distribution models, various criteria are taken into account, including the Akaike information criterion ($A_{IC}$), correct $A_{IC}$ ($C_{AIC}$), Bayesian IC ($B_{IC}$), Hannan-Quinn IC ($H_{QIC}$), Kolmogorov-Smirnov ($K_S$) test, and p-value ($P_V$) test. In contrast, the broader dissemination is associated with reduced values of $A_{IC}$, $C_{AIC}$, $B_{IC}$, $H_{QIC}$, $K_S$, and the highest magnitude of $P_V$. The maximum likelihood estimators (MLEs) of the competitive models, along with their standard errors (SEs) and values of $A_{IC}$, $C_{AIC}$, $B_{IC}$, $H_{QIC}$, $P_V$, and $K_S$ for the suggested data sets, are displayed in Tables 11-18. It has been observed that the LBTLoW distribution, characterized by three parameters, exhibits superior goodness of fit compared to alternative models. This distribution exhibits the lowest values of $A_{IC}$, $C_{AIC}$, $B_{IC}$, $H_{QIC}$, and $K_S$, and the highest value of $P_V$ among the distributions under consideration in this analysis. Furthermore, Figures 8-15 exhibit the graphical representations of the estimated pdf, cdf, ccdf, and probability-probability (PP) plots for the competitive model applied to the given data sets.

From the previous figures, we conclude that the LBTLoW model clearly gives the best overall fit and so may be picked as the most appropriate model for explaining data.

7.   Conclusions

The LBTLo-G family of distributions is explored in this article. The LBTLo-G family of probability distributions has a number of desirable characteristics, including being very flexible and simple, containing a number of new distributions, the ability for the generated distributions' pdfs to be unimodal, decreasing, bathtub-shaped, right-skewed, and symmetric, and the ability for their hrf shapes to be increasing, decreasing, U-shaped, upside-down-shaped, or J-shaped. These include discussion of the characteristics of the LBTLo-G family, including expansion for the density function, moments, incomplete moments, and certain entropy metrics. Estimating the model parameters is done using the ML technique. A simulation study demonstrated that the estimates of the model parameters are not far from their true values. Also, the biases and mean squared errors of estimates based on censored samples are larger than those based on complete samples. As the censoring levels and sample sizes increase, the coverage probability of estimates increases in approximately most cases.

As one distribution of the LBTLo-G family, the real datasets for global reserves of oil, gold, and natural gas were chosen to fit the LBTLoW distribution. The first data set proposed was the lifetime data relating to relief times (in minutes) of patients receiving an analgesic. The second data set provides the percent of global reserves of natural gas for 44 countries. We have considered the third real data analysis of the countries with the largest oil reserves in 20 countries. We consider another real-data analysis of the central bank owning the largest gold reserves in 100 countries. This gold reserve data, compiled using international monetary funds and international financial statistics, tracks central banks' reported purchases and sales of gold as a percentage of their international reserves. The LBTLoW model typically provides superior fits in comparison to certain other alternative models, as shown by real-world data applications.

Use of AI tools declaration

The authors declare that they have not used artificial intelligence tools in the creation of this article.

Acknowledgments

Researchers Supporting Project number (RSPD2023R548), King Saud University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that there are no conflicts of interest.