Modeling and analysis of a stochastic giving-up-smoking model with quit smoking duration

1.   Introduction

The harm of tobacco is one of the most serious public health problems. The World Health Organization has considered the tobacco epidemic in the key control areas of global public health. According to statistics, one person dies of cigarette related diseases every six seconds in the world. With the current trend, the World Health Organization estimates that the number of people will rise to 10 million by 2030, which means one person will die of smoking every three seconds ^[1]. Not only that, smoking behavior may also bring bad guidance to teenagers. In 2018, the prevalence of smoking among people over 15 years old in China was 26.6%, with the prevalence of smoking among men at 50.5% ^[2], and the prevalence of underage smoking in China has been increasing in recent years. The harm of smoking to the human body is inevitable. Basically, smoking can prevent the absorption of vitamin C. Long term smoking can lead to cancer and other diseases. In addition, second-hand smoke can also cause cancer and have adverse effects on the heart. Long term intake of second-hand smoke by pregnant women can also lead to fetal growth retardation, congenital malformations and even abortion. Therefore, tobacco control is particularly necessary.

Tobacco control is the most important measure to prevent disease and death at present. Eliminating the harm of smoking has become a worldwide trend. WHO stressed the importance of legislation in tobacco control measures, strongly advocated health education on tobacco control, advocated a healthy lifestyle and recommended that member states increase tobacco taxes and reduce tobacco consumption ^[3]. Many countries are also strengthening tobacco control through different means, including increasing packaging warnings, increasing the size of warnings, etc. Quitting smoking is a key link to alleviate the harm of smoking. Three days after quitting smoking, nicotine will be basically removed from the body. After quitting smoking for 2 to 3 weeks, lung function will be enhanced. After quitting smoking for 3 to 9 months, the damaged cilia in the lungs will almost be completely repaired. One year after quitting smoking, the probability of coronary heart disease will be 50% lower than that of smokers. Five years after quitting smoking, the probability of stroke will reach the level of non-smokers, and the probability of suffering from other cancers will also be greatly reduced. Therefore, it is particularly necessary to quit smoking. Based on this background, we study a new giving up smoking model.

The development of the research on smoking models is significant. In consideration of the research objects, Castillo-Garsow et al. ^[4] proposed a system including the potential smokers $(P)$, the chain smokers $(S)$ and the permanently quit smokers $(R)$ in 1997. Later, the mathematical model was promoted by Sharomi and Gumel ^[5] in 2008. They introduced a new group of smokers who temporarily quit smoking $(Q_t)$. In the study of Sharomi and Gumel, they proved the local stability of the equilibrium $E ^ *$ by using the Routh-Hurwitz criterion, while the global stability was only speculated by a large number of simulations. Then Lahrouz et al. ^[6] proved that conclusion by constructing a suitable Lyapunov function in 2011. In addition, random noise was included in the deterministic model, and then the deterministic and stochastic stabilities of a class of random smoking models were considered by them. In the same year, Zaman ^[7] proposed a smoking cessation model including the occasional smokers $(L)$ and studied its relevant dynamic behavior such as equilibria in the model, one of which was the smoking-free equilibrium, and the other three were about smoking being present under the assumption that the birth rate was different from the mortality rate. Guerrero et al. ^[8] assumed the population consisted of four types of individuals, non-smokers, normal smokers, excessive smokers and ex-smokers, when they used homotopy analysis method (HAM) to obtain an analytical solution to the model for the spread of the smoking habit in Spain in 2013. In 2015, Sharma et al. ^[9] considered the impact of media factors on the spread of smoking. A mathematical model was proposed to evaluate the impact of media publicity on the prevalence of social smoking. In 2016, the qualitative behavior of a smoking model was studied by Din et al. ^[10] through dividing people into non-smokers, smokers, temporarily quit smokers, permanently quit smokers and people who were associated with illness due to smoking. In 2018, Rahman et al. ^[11] studied an age-structured cigarette smoking model which considered the age of light smokers. They found that smoking had a strong correlation with age. Also, in order to study the optimal control of the problem, Khyar et al. ^[12] and Din et al. ^[13] considered adding two control strategies to the model for analysis, respectively, in 2021. Zhang et al. ^[14] considered a delayed smoking cessation model of relapse in 2022. More relevant analysis about smoking and smoking cessation models can be found in ^{[15,16,17,18,19]}.

As with most epidemic models ^[20,21,22] that describe the form of contact, lots of classical giving-up-smoking models also employ the bilinear incidence rate $\beta PS$ ^[23,24], nonlinear incidence rate $f(P)g(S)$ ^[25,26] between potential smokers $P(t)$ and smokers $S(t)$, square-root incidence functions $\sqrt{PL}$ ^[27,28] or $\beta \frac{2PL}{P+L}$ ^[12] between potential smokers $P(t)$ and light smokers $L(t)$. As we all know, the bilinear incidence rate is assumed to be proportional to the total population in the environment, which is not practical when the population is large. In the real world, the number of potential smokers in contact with smokers is limited in unit time. Thus, the saturated contact rate is more realistic. Hence, in this paper, we choose the saturated incidence rate $\beta \frac{P(t)S(t)}{1+kS(t)}$ between potential smokers $P(t)$ and smokers $S(t)$. Besides, as described in the second paragraph, there is a strong correlation between the quit smoking duration and the level of personal health recovery. Therefore, we consider the quit smoking duration at the first time, and we also notice that some people might not quit smoking completely in the process of formulating the model. In addition, the conclusion of this paper has great practical significance for smoking cessation guidance and treatment of tobacco-related diseases.

We will introduce the arrangement of this article from the following sections. Based on the above descriptions, we formulate a stochastic giving-up-smoking model with age structure in Section 2. In Section 3, we derive the existence and uniqueness of the solution to the model. Section 4 establishes some conditions to prove the extinction of smoking behavior. Section 5 guarantees the sufficient conditions for the persistence of smoking. We prove the sufficient condition for the existence of a unique stationary distribution of the smoking phenomenon in Section 6. We carry out numerical simulations to prove the results in Section 7. A brief discussion is offered in the end.

2.   Model formulation

Drawing on the transmission of virus from infected vectors to susceptible populations in epidemiological models ^[29,30], we also define $\frac{1}{1+kS(t)} \leq \frac{1}{2}$ to describe the saturation caused by the psychological effects of changes in potential smokers when the number of smokers becomes large. We formulate a giving-up-smoking model with quit-smoking duration as

where the total population is divided into four classes: the potential smokers $P(t)$, the smokers $S(t)$, the quitters $Q(t)$ and the removed $R(t)$. $\lambda$, $\mu$, $d$, $\beta$, $h$ and $\alpha$, respectively, denote the recruitment rate of the population, the natural death rate, the mortality rate due to direct or indirect smoking, the effective contact rate between the potential smokers and the smokers, the success rate of quitters and the proportion of quitting smoking. Here, with different smoking cessation deadline, those who successfully quit smoking will enter the removed, while those who show signs of relapse within the smoking cessation deadline will get into the group of potential smokers. Futher, the quitted become the potential smokers with rate $1-h$ due to environmental effect, weak willpower or other factors and turn to the removed with rate $h$ due to strong willpower. $Q(t, \tau)$ denotes the density of quit smokers at time $t$ with quit-smoking duration $\tau$, and $\int_0^{\infty} Q(t, \tau) \mathrm{d} \tau$ denotes the number of quit smokers at time $t$. $b(\tau)$ denotes the emigration rate from quitters, which is a bounded function. Here we assume that $0\leq b(\tau) \leq 1$ and $\int_0^{\infty} b(\tau) \mathrm{d} \tau = \infty$, which guarantees that nobody quits smoking when quit-smoking duration $\tau$ approaches infinity. In other words, the number of quitters tends to zero when quit-smoking duration $\tau$ approaches infinity $\lim_{\tau \rightarrow \infty} Q(t, \tau) = 0$.

The initial conditions are

and the boundary condition is

where

Integrating the third equation in model (2.1) along the characteristic line $t-\tau =$ constant, we obtain that

where

Similar to papers ^[20,22], for $t\geq 0$, we have that

Noticing that

then by setting $\hat{\tau} = \tau-t$, we get

which yields

Thus, (2.3) turns to be

where

Due to the complexity of the social environment, the contact rate between potential smokers and smokers will be affected by environmental factors. We assume that fluctuations in the environment will manifest themselves mainly as fluctuations in the parameter $\beta$, so that $\beta \rightarrow \beta+\sigma \dot{B}(t)$, where $B(t)$ is a standard Brownian motion with intensity $\sigma ^2 > 0$. Reference model (2.1) for other parameters, and we finally establish a stochastic giving-up-smoking model with quit-smoking duration as follows:

The initial condition for system (2.6) takes the form $P(\theta) = \xi_1(\theta), S(\theta) = \xi_2(\theta)$ and $(\xi_1, \xi_2) \in (C(-\infty, 0], R^2_+)$. Without loss of generality, we may assume that $\phi_1(\theta) \leq \phi_1(0)$ and $\phi_2(\theta) \leq \phi_2(0)$ for all $\theta \leq 0$.

3.   Existence and uniqueness of the global solution

We will study the existence and uniqueness of the solution to model (2.6) in this section.

Theorem 3.1. For any initial value $(\xi_1, \xi_2)\in (C(-\infty, 0], R^2_+)$, there exists a unique solution $(P(t), S(t))$ on $R$, which will remain in $\mathbb{R}_{+}^2$ with probability one.

Proof. Because of the locally Lipschitz continuous of coefficients of model (2.6) for any initial solution, there exists a unique positive local solution on $[-\infty, \tau_{e}]$, where $\tau_{e}$ is the explosion time. Let $n_{0} > 1$, be a large integer such that $P(0)$ and $S(0)$ are in the interval $[\frac{1}{n}, n]$. For each integer $n > n_{0}$, to show the solution is global, the stopping time is defined as follows:

Then, $\tau_{n}$ is a nondecreasing function. We define $\lim_{n \rightarrow \infty} \tau_{n} = \tau_{\infty}$, and $\tau_{\infty} \leq \tau_{e}$.

Now, we need to prove $\tau_{\infty} = \infty$ a.s. If this conclusion is not true, then there exist $T > 0$ and $\epsilon \in(0, 1)$ such that $\mathbb{P}\left\{\tau_{\infty} \leq T\right\} \geq \epsilon$. Then, there is an integer $n_{1} > n_{0}$ such that

Let

and we calculate that

Thus

which implies that

Without loss of generality, we can assume that $N(0) \leq \frac{\lambda}{\mu+d}$. Thus, for all $t \geq 0$, it will be studied in the invariant sets $\Omega^* = \{N(t):0 \leq N(t) \leq \frac{\lambda}{\mu+d}\}$.

We define the following function $V$:

Note that $V\big((P(t), S(t) \big)$ is non-negative when $\big((P(t), S(t) \big) \in\mathbb{R}_{+}^2$, and calculating by Itô's formula on system (2.6) leads to

where

Now that

thus (3.7) turns to

Integrating the inequality (3.9) from 0 to $\tau_{n} \wedge T$ yields that

This implies that

Let $\Omega_{n} = \mathbb{P}\left\{\tau_{n} \leq T \right\}$, and then from (3.1), we get that $\mathbb{P}\left\{\Omega_{n} \leq T\right\} \geq \epsilon$, for $n \geq n_{1}$. For all $\omega \in \Omega_{n}$, each component of $(P(\tau_{n} \wedge T), S(\tau_{n} \wedge T))$ equals either $n$ or $\frac{1}{n}$. Consequently, we have that

This will lead to

as $n\to\infty$. Thus, the assertion $\tau_{e} = \infty$ holds almost surely. The proof is complete.

4.   The extinction of smoking

We will talk about the extinction of the smoking behavior in this section.

Theorem 4.1. Let $(P(t), S(t))$ be the solution of model (2.6).

$(i)$ If $\sigma^2\leq \frac{\beta (\mu+d)}{\lambda}$, and

then

$(ii)$ If $\sigma^2\geq \frac{\beta^2 }{2(\mu+d+\alpha)}$, then

Proof. Consider Theorem 3.1 and Eq (3.5). For any $\eta > 0$, there is a constant $T_0$ such that

By making use of Itô's formula on the second equation of model (2.6), we obtain that

Integrating from 0 to $t$ on both sides of (4.3), for any $\epsilon > 0$, we have

Define a function

where $G(x)$ is monotonically increasing for $x \in\left[0, \frac{\beta+\epsilon}{\sigma^2}\right]$ and monotonically decreasing for $x \in\left[\frac{\beta+\epsilon}{\sigma^2}, \infty\right)$. It is easy to obtain that $\frac{\lambda}{\mu+d} \leq \frac{\beta} {\sigma^2}$ from condition $(i) \sigma^2\leq \frac{\beta (\mu+d)}{\lambda}$. Now, we choose a positive $\eta \leq \epsilon$ such that

and thus we have

for all $t\geq T_0$, where $T_0$ is a positive constant number.

Then, for $t\geq T_0$, we get that

We define

which is a local continuous martingale, and $Y_1(0) = 0$. Then for $t\geq T_0$,

According to the large number theorem for martingales ^[31], we obtain that

and thus

Then, it is implied that, for any $\epsilon$ and $\eta$, there is

Thus, when $\widetilde{\mathcal{R}}_0 < 1$, we have

Then, (4.1) is proved completely with condition $(i)$.

Now, we prove (4.2), and note that function $G(x)$ gets its maximum value

at $x = \frac{\beta+\epsilon}{\sigma^2}$. Since

we can get that

By a similar discussion, we can obtain that

When $\epsilon \rightarrow 0$ under the condition $(ii) \sigma^2\geq \frac{\beta^2 }{2(\mu+d+\alpha)}$, we have that

This completes the proof of (4.2).

5.   The permanence of smoking

We will focus on the permanence of the smoking behavior in this section.

Theorem 5.1. Let $\left(P(t), S(t)\right)$ be the solution of model (2.6), and if $\widetilde{\mathcal{R}}_0 > 1$, then

Proof. From model (2.6), we obtain that

and integrating from 0 to $t$ on both sides of (5.2) yields that

Thus,

where

By using Itô's formula, we get that

By integrating (5.4) from 0 to $t$, we have

This inequality can be rewritten as

where

in which $Y_{2}(t)$ is a local continuous martingale with $Y_{2}(0) = 0$. Applying the large number theorem for martingales ^[31], we obtain that

According to (3.5), we have that

Thus, (5.1) is proved completely with condition $\widetilde{\mathcal{R}}_0 > 1$.

6.   Stationary distribution

This section will study the stationary distribution of model (2.6).

Let X(t) be a homogeneous Markov process in $\mathbb{R}^d$ ($\mathbb{R}^d$ denotes a d-dimensional Euclidean space) and be given by following the stochastic differential equation

with its diffusion matrix

Lemma 1. ^[32] The Markov process X(t) has a unique ergodic stationary distribution $\mu(\cdot)$ if there is a bounded domain $\mathbb{D \subset R}^d$ with regular boundary $\Gamma$, and

$(i)$ there exists a positive constant $\widetilde{M}$ such that $\sum_{i, j = 1}^d a_{i j} \xi_i\xi_j \geq \widetilde{M}|\xi|^2, x\in \mathbb{D}, \xi\in \mathbb{R}^d$;

$(ii)$ there exists a nonnegative $C^2$-function $V$ such that $\mathcal{L}V$ is negative for any $\mathbb{R}^d \backslash \mathbb{D}$.

Then,

for all $x\in \mathbb{R}^d$, where $f(\cdot)$ is a function integrable with respect to the measure $\mu$.

Theorem 6.1. If

then model (2.6) admits a unique stationary distribution. Moreover, the stationary distribution is ergodic.

Proof. The diffusion matrix of the stochastic model (2.6) is

Then, there exists a positive constant $\widetilde{M} = \frac{\sigma^2P^2S^2}{(1+kS)^2}$, and we know for any $(P, S)\in \mathbb{\overline{D}}_m$, $\xi = (\xi_i, \xi_j)\in \mathbb{R}_{+}^2$,

where $\mathbb{\overline{ D}}_m = \left[\frac{1}{m}, m\right] \times \left[\frac{1}{m}, m\right]$, and $m > 1$ is a sufficiently large integer. Then, the condition $(i)$ in Lemma 1 holds.

Next, in order to prove the condition $(ii)$, we construct a $C^2$-function $\widetilde{V}$:

where

$\widetilde{N} > 0$ is a sufficiently large constant and satisfies

where

and $\theta > 0$ is a constant satisfying

It is noted that

and $\tilde{V}(P, S)$ is a continuous function. Then, it has a minimum point $(\overline{P}, \overline{S})\in \mathbb{R}^2_+.$

Define a nonnegative $C^2$-function on $V$ as

Applying Itô's formula to $V_1$, we get that

where $\Lambda$ is given by (6.4). In addition,

where B is given by (6.6). From the above discussion, we can derive that

Define $\epsilon$ to be a sufficiently small positive constant. Then, we divide $\mathbb{R}^2_+\backslash \mathbb{D}_\epsilon$ into four domains as follows:

We will show that $\mathcal{L}V(P, S)\leq -1$ on $\mathbb{R}^2_+\backslash \mathbb{D}_\epsilon$ in the above domains.

$Case$ 1. If $(P, S) \in \mathbb{D}_1$, it follows that

where

We take a constant $\epsilon > 0$ small enough such that $-\lambda/\epsilon+F_1 \leq-1$, and then

$Case$ 2. If $(P, S) \in \mathbb{D}_2$, it yields that

where $F_2$ is given by (6.5). We choose a constant $\epsilon > 0$ small enough such that $\widetilde{N}\left(\mu+d+\alpha \right) \epsilon\leq 1$, and therefore

$Case$ 3. If $(P, S) \in \mathbb{D}_3$, we find that

where

We can choose a constant $\epsilon > 0$ small enough such that

Then, it follows that

$Case$ 4. If $(P, S) \in \mathbb{D}_4$, we get that

Hence, from (6.11) to (6.14), we obtain that

Then, the condition $(ii)$ in Lemma 1 holds, and the proof is complete.

7.   Numerical simulations

In this section, some numerical simulations are introduced to verify the main theoretical results of model (2.6).

With the passage of time, people who quit smoking gradually move out. Some people can quit smoking completely and enter the removal group with good results, while others become potential smokers due to poor willpower and other reasons. Obviously, the emigration rate $b(\tau)$ is an increasing function. Here, we let $b(\tau) = \frac{\tau}{1+\tau}$.

By using the discretization method of the differential equation and stochastic differential equation proposed in ^[33,34], the corresponding discretization equations are expressed as follows:

where $E = \int_0^{\infty} \Gamma(\tau) S(t-\tau) \mathrm{d}\tau, \Gamma(\tau) = \alpha b(\tau)\exp \left\{-\int_{0}^{\tau}(b(\nu)+\mu+d) \mathrm{d} \nu \right\}, \zeta_t (t = 1, 2, ...)$ are the Gaussian random variables $N(0, 1)$.

In our application, we fix $\mu = 0.0736$ and $d = 0.0951$ ^[11]. By changing the values of relevant variables, we obtain the dynamic analysis of smoking under different conditions.

First, we let $\lambda = 0.1, \beta = 0.46$ ^[9], $k = 0.9, h = 0.36$, $\alpha = 0.9$ and $\sigma = 0.025$ with $(P(\theta \leq 0), S(\theta \leq 0)) = (P(0), S(0)) = (10, 10)$. It is easy to calculate that

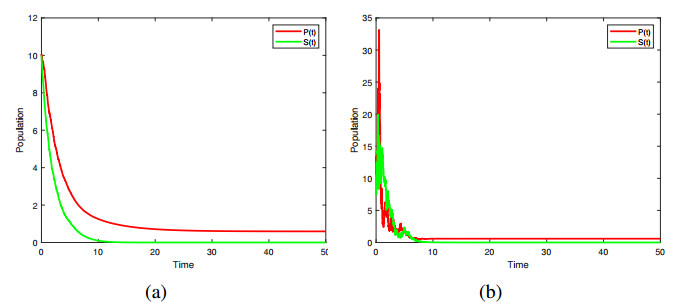
All conditions of $(i)$ of Theorem 4.1 hold. The corresponding densities of the smokers are shown:

which implies the smoking class will disappear. Figure 1(a) shows this result. Further, if we choose $\sigma = 0.89$ and other variables remain unchanged, then $\sigma^2-\frac{\beta^2}{2(\mu+d+\alpha)} = 0.69 > 0$, and $\sigma^2-\frac{\beta (\mu+d)}{\lambda} = 0.016 > 0$, which means the condition $(ii)$ of Theorem 4.1 holds but opposite to condition $(i)$. Also

which implies that the smoking behavior is extinct. Figure 1(b) shows it. Therefore, theoretical results and numerical simulations show that the number of smokers will eventually tend to zero as $t \rightarrow \infty.$

Learning from Figure 1(b), we get that the number of smokers in the early stage may be larger than that of potential smokers, but eventually tends to being extinct. It can improve the speed of smokers tending to be extinct when the value of $\sigma$ increases.

To illustrate the permanence of smoking behavior, we take $\lambda = 100$ and $\sigma = 0.025$ with $(P(\theta \leq 0), S(\theta \leq 0)) = (P(0), S(0)) = (140,140)$. The other parameters are the same as those in Theorem 2. In this case, $\widetilde{\mathcal{R}}_0 = 152.47 > 1$, which satisfies the condition of Theorem 5.1. The smoking behavior is persistent. See Figure 2.

Comparing Figure 1(a) and Figure 2, we find that changing the value of the recruitment rate of the population $\lambda$ will change the dynamic behavior of smoking from an extinct state to a persistent state.

Further, we let $\lambda = 0.8, \sigma = 0.1$, and other data are the same as Theorem 5.1. We can easily calculate $R_0^s = 1.32 > 1$ and $\mu+d-\frac{\sigma^2}{k^2} = 0.16 > 0$. Then, from Theorem 6.1, there exists an ergodic stationary distribution of model (2.6). Figure 3(a), (b) present the ergodic stationary distributions of $P(t)$ and $S(t)$, respectively.

In the following, we study the changes of $P(t)$ and $S(t)$ by respectively changing the values of $\beta$, $\alpha$, $h$ and $\sigma$. Figures 4(a), 5(a), 6(a), 7(a) represent the changes of $P(t)$ and $S(t)$ under the state of extinction as variables change, while Figures 4(b), 5(b), 6(b), 7(b) show the changes under the state of permanence.

Considering that the effective contact rate $\beta$ will be affected by environmental disturbance, we analyze the impact of its change on the populations of potential smokers and smokers. In Figure 4(a), $P_1(t)$ and $S_1(t)$ represent the population when $\beta = 0.88$, while $P_2(t)$ and $S_2(t)$ show the quantity when $\beta = 0.46$. Learned from it, we know that by reducing the effective contact rate $\beta$, the number of smokers will significantly reduce while the quantity of potential smokers is increasing. Figure 4(b) plots the permanence of smoking under the same conditions as Figure 4(a). It follows from Figure 4(b) that smokers will decrease and potential smokers will raise along with the decrease of $\beta$. Also, we find that the quantity gap between $P(t)$ and $S(t)$ becomes larger when $\beta$ decreases in Figure 4(b).

Due to the multifaceted impact of the proportion of quitting smoking $\alpha$, we analyze the changes in the populations under different smoking cessation rates in Figure 5. $P_1(t)$ and $S_1(t)$ denote the populations when $\alpha = 0.36$, while $P_2(t)$ and $S_2(t)$ represent the populations when $\alpha = 0.9$ in Figure 5(a). From it, we can obtain that the smokers are less, while potential smokers become more, when $\alpha$ increases. In Figure 5(b), $P_1(t)$ and $S_1(t)$ denote the population when $\alpha = 0.1$, while $P_2(t)$ and $S_2(t)$ represent the population when $\alpha = 0.9$. As $\alpha$ goes larger, more smokers become potential smokers or removed. It is interesting that the proportions of potential smokers and smokers are different with the change of $\alpha$. The number of smokers is larger than that of potential smokers when the rate of quitting smoking is low. As the rate of quitting smoking increases, the number of smokers will decrease and eventually be lower than that of potential smokers.

In the following, we discuss the effects on $P(t)$ and $S(t)$ when the success rate of quitters $h$ changes. In Figure 6(a), (b), $P_1(t)$ and $S_1(t)$ show the population when $h = 0.1$, while $P_2(t), S_2(t)$ represents the population when $h = 0.9$. From Figure 6(a), we get that the number of smokers naturally decreases with the success rate of quitters increasing. So, there are fewer smokers turning into potential smokers, and then potential smokers also show a downward trend. Similarly, as $h$ increases, the number of smokers and potential smokers in Figure 6(b) will reduce, too.

We choose three sets of white noise data: $(i)\ \sigma_1 = 0.025, (ii)\ \sigma_2 = 0.36$ and $(iii)\ \sigma_3 = 0$ in Figure 7(a). Note that the extinction time would be different for a distinct noise intensity, but smokers will eventually disappear under the condition $\widetilde{\mathcal{R}}_0 < 1$. Besides, we take three sets of white noise data: $(i) \ \sigma_1 = 0.025, (ii) \ \sigma_2 = 0.01$ and $(iii)\ \sigma_3 = 0$ in Figure 7(b). We find that no matter how $\sigma$ changes, it always surrounds $\sigma = 0$, and the fluctuation of population becomes small with the decrease of white noise $\sigma$.

8.   Conclusions

We studied a stochastic giving-up-smoking model considering the quit-smoking duration and saturated incidence rate in this paper, where the quit smoking duration varies with different individuals, and the quit smokers can eventually become the potential smokers or be removed. Further, the effective contact rate $\beta$ between potential smokers and smokers is described by $\beta+\sigma \dot{B}(t)$. We first discussed the existence and uniqueness of the solution of model (2.6) (Theorem 3.1). By adding the analysis of environmental interference, we obtained the threshold $\widetilde{\mathcal{R}}_0$ of extinction (Theorem 4.1) and permanence (Theorem 5.1) of smoking behavior. We conclude that when the white noise is small and satisfies $\widetilde{\mathcal{R}}_0 < 1$, the smoking behavior goes extinct in the long run. Figure 1(a) shows this result. The smokers also disappear when the perturbation becomes large enough, which is illustrated in Figure 1(b). The threshold $\widetilde{\mathcal{R}}_0 < 1$ is sufficient for the persistence of smoking and Figure 2 expresses it. We also derived sufficient conditions $R_0^s > 1$ for the existence and uniqueness of an ergodic stationary distribution (Theorem 6.1) for the positive solution. Figure 3 presents that conclusion by showing the histogram and the probability of potential smokers and smokers for the stochastic model (2.6). Finally, we demonstrated these conclusions by conducting numerical simulations.

There are four key parameters, the effective contact rate $\beta$ between potential smokers and smokers, the proportion of quitting smoking $\alpha$, the success rate of quitters $h$ and the intensity of white noise $\sigma$, that have been emphasized about the extinction and permanence of smoking behavior in our numerical work. Through the analysis of the influence of these variables in Figures 4–7, we can get that the change trends of extinction and persistence affected by variables are the same. In addition, we know by that reducing the effective contact rate $\beta$ between potential smokers and smokers (see Figure 4), increasing the proportion of quitting smoking $\alpha$ (see Figure 5) and strengthening the willpower of quitters to increase the success rate of quitters $h$ (see Figure 6), we can reduce the number of smokers. Therefore, we can take the above measures to reduce the number of smokers in society and create a healthier living environment. Finally, we analyzed the comparison between deterministic and stochastic models in Figure 7 and get that the fluctuation of the population will become large with the increase of white noise $\sigma$.

Because the quit-smoking duration is raised for the first time, the research content is somewhat limited in the text. Still there is much interesting research to do. In our future work, we will continue to discuss a related project, such as adding different control factors to the model to show the application of control factors in tobacco control work, considering the impact of environmental interference on other factors in the model and so on. Therefore there is still a lot of work to be done in the future.

Use of AI tools declaration

The authors declare they have not used artificial intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was supported by the National Natural Science Foundation of China (12271068), the Innovation Development Joint Funds of the Chongqing Natural Science Foundation (CSTB2022NSCQ-LZX0026), Joint Training Base Construction Project for Graduate Students in Chongqing (JDLHPYJD2021016) and Group Building Scientific Innovation Project for universities in Chongqing (CXQT21021).

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.