1.
Introduction
Our goal here is to find reaction networks inducing a given system of polynomial differential equations (or classes of equations with symbolic parameters as coefficients) with as many good properties (e.g., weak reversibility, reversibility, small deficiency, small number of linkage classes or reactions, mass conservation, etc.) as possible.
It has been shown that, under mass action kinetics, a necessary and sufficient condition for realizability is a sign structure in the system of polynomial differential equations [1] (see Lemma 1 below). Once we know that a system can arise from a mass action system, the question still lies: can the system arise from a mass action system with good properties? This is what this present work looks at. There exist similar works outside the realm of mass action kinetics. For example, [2] finds mass action systems that generate the same differential equation as a given S-system or generalized mass action system. The approach allows recent results from Chemical Reaction Network Theory to be applied in Biochemical Systems Theory.
There are several sources of motivation for this problem.
1. Having fitted a system of differential equations to data, one may wonder whether the obtained equations can be interpreted as the mass action type deterministic model of an appropriate reaction network.
2. There is an internal requirement within this branch of science: One should like to know as much as possible about the structure of differential equations that arise from modelling a chemical system.
3. Given a system of polynomial differential equations in any field of pure or applied mathematics, one may wish to have statements on stability or oscillations, similar to those offered by the Horn-Jackson Theorem [3], Zero Deficiency Theorem [3,4,5], Volpert's theorem [6], or the Global Attractor Conjecture, where several cases have been proven [7,8,9,10] *. Then it comes in handy to see that the system of differential equations of interest belongs to a well behaving class.
*A proof in full generality has been proposed in [11].
4. Lastly, results of formal reaction kinetics (to use an expression introduced in [12,13]), e.g., on the existence of stationary points, may offer alternative methods for solving problems in algebraic geometry [14,15]. For instance, one might be able to show the existence of positive roots of a polynomial if the system of polynomial equations is known to be the right hand side of the induced kinetic differential equation of a reversible or weakly reversible reaction network [16].
The structure of our paper is as follows. Section 2 introduces the essential concepts of reaction networks and mass action systems. Section 3 formulates the problem we are interested in, that of realizability of kinetic differential equations. Section 4 treats two special cases: finding realizations for compartmental models (defined later) and reversible networks. Section 5 focuses on the general problem of realizability. We first review existing algorithms available. Then we outline several procedures that modify a reaction network while preserving the system of differential equations, including adding and removing vertices from the reaction graph. Section 6 explores the relation between weakly reversible and complex balanced realizations. Here we work with families of symbolic kinetic differential equations. In Section 7, we prove the geometric meaning of zero deficiency, and discuss when is a realization unique. We also pose several conjectures that may be of interest to the reader. An Appendix contains a very large number of enlightening examples. The present paper intends to be a review of the realizability problem, while containing some new results.
A few remarks on notation and the use of words are in order.
1. The set of vectors in RM with strictly positive coordinates is denoted by RM>0. Also
for any xi>0 and yi≥0. If Y=(y1,y2,…,yN), then
2. We use differential equation to mean a system of ordinary differential equations. In the same vein, we use polynomial to usually mean a system of polynomial equations, i.e. a vector-valued function on RM>0. By monomial we mean a scalar-valued function on RM>0.
3. We say a reaction network induces a differential equation, if we formulate the mass action type differential equation with given reaction rate coefficients, and a differential equation is realized by a reaction network, if the network induces the given differential equation.
2.
Chemical reaction networks and mass action systems
Here we recapitulate some concepts of the mathematical description of reaction networks; for more details, see e.g., [17,18,19].
A reaction network consists of a set of R reaction steps among the chemical species X(1),X(2),…,X(M):
with nonnegative integer stoichiometric coefficients α(m,r), β(m,r). Its induced kinetic differential equation to describe the time evolution of concentrations and assuming mass action type kinetics (and disregarding the change of temperature, pressure and reaction volume) is
The positive number kr is the rate coefficient
† for the r-th reaction.
†Instead of rate constants we use the term rate coefficients, because they do depend on everything (pressure, temperature, volume), except concentrations, although we know that there is a heated argument about this question amongst reaction kineticists, see [20,p. 115].
On the two sides of arrows in (2.1), which represent a reaction step, one has formal linear combinations of the species, called complexes, the left one being the reactant complex, and the right one being the product complex. Associated to each complex is the vector of the coefficients of these linear combinations. By an abuse of notation, we will refer to this vector as a complex. The difference between the product complex and the reactant complex is the reaction vector. These vectors form the columns of the stoichiometric matrix. The stoichiometric space S is the linear span of the reaction vectors, where S=dimS. (This number can also be interpreted as the number of independent reaction steps.) The stoichiometric compatibility class of x0∈RM>0 is the forward-invariant set (x0+S)>:=(x0+S)∩RM>0. The number of complexes is denoted by N.
With sets of reactions and complexes as described above, each reaction network is naturally associated to a directed graph.
Definition 1. The reaction graph (or Feinberg-Horn-Jackson graph) of a given reaction network is a finite directed graph with no self-loops, where the vertices are the complexes of the reaction network, and the edges are precisely the reactions.
The connected components of a reaction graph are also called linkage classes, and L denotes the number of linkage classes in a reaction network. The deficiency of the reaction network is δ:=N−L−S, where N is the number of complexes (i.e., number of nodes in the reaction graph), and S=dimS. The strong components of the reaction graph are also called strong linkage classes. An ergodic component (or strong terminal class) is a strong component with no reaction step such that the reactant complex is in the component while the product complex is outside of it, i.e., an ergodic component is a strongly connected component of the reaction graph. The number of ergodic components will be denoted by T.
Definition 2. A reaction network is reversible if its reaction graph as a relation is symmetric, i.e., i→j is a reaction if and only if j→i is a reaction. It is weakly reversible, if the transitive closure of its reaction graph is symmetric; or if all the reaction arrows are edges of a directed cycle in the reaction graph; or all of its strong components are ergodic.‡
‡Weak reversibility implies T=L, but the converse is false [21].
Definition 3. A reversible reaction network (with rate coefficients kr+, kr− for the r-th pair of reversible reactions)
is detailed balanced at the positive stationary concentration x∗ if for each pair of reversible reactions, the forward step proceeds at the same rate as the backward step; in other words, x∗ is detailed balanced if
The induced kinetic differential equation can be written in many different forms, see e.g., [19,Sec. 6.3]. We introduce the form that will be used frequently below.
For a reaction graph with N complexes, let their associated vectors be columns of the matrix Y:=(y1,y2,…,yN). Implicitly we are imposing an ordering on the set of complexes. For a reaction i→j (from the i-th complex to the j-th complex), assume that the rate coefficient is kji>0. Define the matrix K to be
so that K is a matrix with nonnegative entries, and 0 along the diagonal. Then the column-conserving matrix Ak:=K−diag(K⊤1) is the (weighted) Laplacian of the reaction graph. A matrix with nonnegative off-diagonal entries that is column-conserving is also called Kirchoff.
With these matrices defined and the notation xy:=xy11xy22⋯xyMM for any xi>0, the induced kinetic differential equation (2.2) of the reaction network can be rewritten in the following form:
where xY is the vector of monomials (xy1,xy2,…,xyN)T.
Note that the differential equation (2.3) is completely determined by the complexes (columns of Y) and the connectivity and rate coefficients of the reaction graph (given by Ak).
Definition 4. The reaction system (2.3) is complex balanced at the positive stationary concentration x∗, if all the complexes are destroyed and formed with the same rate at this concentration:
for all n=1,2,…,N. Equivalently, x∗ is complex balanced if Ak(x∗)Y=0.
If one remains within the framework of mass action kinetics – as we do here – then the Deficiency Zero Theorem provides a necessary and sufficient structural condition for complex balancing [3,4,5]:
Theorem 1. A mass action system is complex balanced for all choices of the rate coefficients if and only if it is weakly reversible and its deficiency is zero.
One might notice that in the Deficiency Zero Theorem, it is the mass action system that is described as complex balanced, not one of its stationary concentrations. This is because complex balancing implies a host of good structural and dynamical properties, including:
1. If one of the stationary concentrations is complex balanced, then all stationary concentrations of the system are complex balanced.
2. There is exactly one stationary concentration within every stoichiometric compatibility class.
3. Let x∗ be any complex balanced stationary concentration. The function
defined on Rn>0 is a Lyapunov function, with global minimum at x=x∗.
4. Every positive stationary concentration is locally asymptotically stable within its stoichiometric compatibility class.
5. The set of complex balanced stationary concentrations Zk satisfies the equation lnZk=lnx∗+S⊥.
3.
Formulation of problems
In defining the system of differential equations for a mass action system, note that given a set of reactions and rate coefficients (or equivalently, given a reaction graph and positive weights for each edge), it is straightforward to write down the differential equation. Unfortunately, given a differential equation (satisfying a mild sign condition introduced below), there is in general no unique reaction graph that is associated to it [22].
A natural question arises: given a differential equation, what are the possible reaction graphs that could generate it if we assume mass action kinetics. All the information about a reaction graph is contained inside (Y,Ak).
Definition 5. A realization of a differential equation (2.3) is the pair (Y,Ak), where Y∈ZM×N≥0 and Ak is the weighted Laplacian of a reaction graph. Equivalently, a realization is a Feinberg-Horn-Jackson reaction graph and a positive rate coefficient for each edge. Two different realizations (Y,Ak) and (Y′,A′k) are said to be dynamically equivalent if they give rise to the same differential equation under mass action kinetics.
Dynamical equivalence is written as linear relations in [23]. In other words, the question we are asking in this work is: what are the possible dynamically equivalent realizations (Y,Ak) of a given system of differential equations?
Before searching for dynamically equivalent realizations, we must first ask whether or not a given differential equation can arise from mass action kinetics. In other words, is it even possible to find one realization? We provide a necessary and sufficient condition for realizability in Lemma 1 below.
Assume that we are given a system of differential equations of the form
where Z:=(z1,z2,…,zN), and Y:=(y1,y2,…,yN), and xy:=xy11xy22⋯xyMM for any xi>0.
Definition 6. We say that a system of differential equations (3.1) is kinetic if
A system being kinetic reflects the physical assumption that in order to lose a chemical species via a reaction, that species must participate as a reactant. For example, the system
is not kinetic because the term −xz in ˙y does not involve the variable y.
It turns out that a differential equation can arise from mass action kinetics if and only if it is kinetic in the sense of Definition 6. This has been shown in [1] using a constructive method.
Lemma 1 (Hungarian Lemma). A polynomial system of differential equations of the form (3.1) can be realized by a mass action system if and only if the system of differential equations is kinetic.
One realization (the canonical realization) is the collection of reactions
where em is the m-th vector of the standard basis of RM. Here the product complex vector has nonnegative integer coordinates because of the assumption in (3.2).
Example 1. Given the differential equation
(with k1,k2>0), it is possible to find an inducing reaction network with only two complexes defined by the exponents of the monomials present in the right hand side:
The right hand side contains two monomials, and there exists a realization with two complexes, and is also reversible, and has deficiency zero. This also happens to be the canonical realization.
However, in general, the canonical realization is quite complicated, contains too many complexes and reactions (see Supplementary Example 13). Its main advantage is that it can be automatically constructed and used as a starting point for finding different realizations.
Now we present the set of problems we are interested in (also posed earlier in [24, Section 4.7]).
List of Problems.
1. Given a kinetic differential equation ˙x=Z⋅xY, find Ak such that Y⋅Ak=Z.
2. Find reversible or weakly reversible; complex balanced or detailed balanced; or mass conserving realizations. Determine if such a realization exists.
3. Find realizations with minimal deficiency, with minimal number of reactions, or with minimal number of complexes.
4. Without further restrictions, the question about uniqueness of Ak arises at all levels.
5. In all of the above problems, we may add more columns to Y [25]. For example, if the first problem has no solution, we may consider the following: find ¯Y whose first N columns form precisely Y and find Ak such that ¯Y⋅Ak⋅x¯Y=Z⋅xY. In this case we can also ask what is the minimum number of columns that must be added.
We will answer partially the questions above, especially pertaining to reversible, weakly reversible, complex balanced and detailed balanced realizations. We also consider uniqueness in Section 7 and mass conserving realizations in the Supplementary.
In considering the uniqueness question, the concepts of sparse and dense realizations have been useful [26]. The aim is to find an M×N matrix of nonnegative integer components Y and a Kirchoff matrix Ak giving the product Z=Y⋅Ak. The pair (Y,Ak) is a realization of the matrix Z. Since (Y,Ak) uniquely identifies the reaction graph, when we refer to a subetaaph of the realization, we mean a subetaaph of the reaction graph corresponding to (Y,Ak).
Definition 7. Suppose the set of complexes is fixed, i.e., the matrix Y is given. If the number of zeros in the above setting in Ak is maximal, then a sparse realization has been obtained. If the number of zeros in Ak is minimal then a dense realization has been obtained.
Suppose Z is given and fix the matrix Y, i.e., fix the set of complexes (both the reactant and product complexes) from which we will search for realizations. The following properties of dense and sparse realizations of a given chemical reaction network were proved in [27]:
Theorem 2.
1. The reaction graph of the dense realizations is unique.
2. The reaction graph of any dynamically equivalent realization is a subetaaph of the dense realization.
3. The reaction graph of a system of differential equations is unique if and only if the reaction graph of the dense and sparse realizations are identical.
The above statements hold when the word "realization" is replaced by weakly reversible realization [28]. The above results were extended to the case of constrained realizations, where the rate coefficients fulfil arbitrary polytopic constraints [29]. An important special case of this is when a subset of possible reactions is excluded from the network.
We have seen that the canonical representation may be the sparse realization. Later, we shall give a complete solution to a generalization of part 1 of Problem 3 for the case when the numerical values of the components of the matrices Z and Y are known. We also review results for the solution of the other related problems in Section 5.1.
To date, the problem of finding a realization has used tools and techniques from different mathematical disciplines, ranging from graph theory, combinatorics, linear algebra, to optimization.
4.
Realizations of compartmental models and reversible systems
In this section, we consider two classes of examples: compartmental models and reversible networks. Because of the simpler mathematical structure of compartmental models, the realization problem can be solved even if the rate coefficients are unspecified parameters, i.e., symbolic. Then we will look at an ad hoc method to find reversible realizations.
4.1. Compartmental models
A compartmental system is built using a subset of reactions of the form
It is closed if it only contains reactions of the first type, it is half-open if reactions of the second type are also allowed, and it is open if reactions of the third type may occur. A generalized compartmental system only consists of the reactions
with fixed positive integer numbers y1,y2,…,yN. (It is understood that all the complexes contain a single species, and every species appear in a single complex.) It is closed, if it only contains reactions of the first type, it is half-open if reactions of the second type are also allowed, and it is open, if reactions of the third type also may occur.
First we give a complete, although ineffective solution of the first task of Problem 3 in a slightly modified form. Modification means that the empty complex will be dealt with separately, because in some calculations this implies simplification. First, we need two definitions.
Definition 8. [30,pp. 142,143] A matrix B∈RN×N is a compartmental matrix, if its off-diagonal elements are nonnegative, while its diagonal elements are smaller than or equal to the negative of the corresponding column sums: Bnn≤−∑p≠nBpn. It is a Kirchhoff matrix if it is a compartmental matrix and its diagonal elements are equal to the negative of the corresponding column sums: Bnn=−∑p≠nBpn.
For example, the weighted Laplacian matrix of a reaction graph is Kirchoff.
Let M,N∈N; and suppose the vectors y1,y2,…,yN∈ZM≥0 are arbitrary nonzero vectors. Let us write the reaction network we are interested in, in the form of
Let us introduce the notation (slightly different from the usual)
(Recall that Ak:=K−diag(KT1) is the weighted Laplacian of the reaction network.) Note that knq≥0. Then, the induced kinetic differential equation of the reaction network (4.1)–(4.3) is
Upon denoting Z:=Y(K−diag(K⊤1+u)),b:=Yv one can say that (4.4) is of the form
so that there exists a compartmental matrix B∈RN×N and a nonnegative vector v∈RM≥0 so that
hold. If u=0, then B is a Kirchhoff matrix. (One may call (4.2) outflow, (4.3) inflow, and they are missing if u=0 or v=0, respectively.)
A partial answer to the realization problem follows.
Theorem 3. Suppose that the differential equation
where Y=(y1,y2,…,yN),Z∈RM×N (with M,N∈N) has the property that there exist a compartmental matrix B and a nonnegative vector v∈RM≥0 so that (4.5) holds. Then the equation has a realization of the form (4.1)–(4.3).
Proof. First we prove that the conditions of the theorem imply the differential equation is kinetic. Suppose Zmn<0 for some indices m,n. Then,
and the last sum being nonnegative, ymnBnn should be negative, thus ymn>0.
The components of Y and v are nonnegative, thus the components of b=Yv are nonnegative, as well.
Next, we construct the inducing realization in the following way. Let the reaction rate coefficients of the reaction network (4.1)–(4.3) be defined as follows:
Then simple verification proves the statement. It may happen that a given kinetic differential equation has zero, one or an infinite number of realizations with complexes, or columns of Y, determined by the exponents of its monomials, see Supplementary Examples 11, 12 and 15.
For some nonlinear differential equation s one can provide a zero deficiency realization. Additional conditions may allow to have a realization which is also reversible or weakly reversible. One of the early approaches to this problem was [31,Theorem 9], see also [19,Theorem 11.12] providing a necessary and sufficient condition that a generalized compartmental system induces a given differential equation. If the coefficients of the kinetic polynomial ODEs are known, then a deficiency zero realization can be determined via mixed integer linear programming, if it exists [32]. Moreover, weakly reversible deficiency zero realizations can be determined using simple linear programming [33].
Theorem 4. Let M∈N;Z∈RM×M,Y∈ZM×M≥0,b∈RM≥0. The differential equation
is the induced kinetic differential equation of a
1. closed,
2. half open,
3. open
generalized compartmental system if and only if the following relations hold: all the columns of Y are positive multiples of different elements of the standard basis:
and
1. bm=0;−zmm,zmp,βm:=∑Mp=1zpmyp≥0;zmm=−βmym;
2. bm=0;−zmm,zmp,βm≥0;zmm≤−βmym,∃m:zmm<−βmym;
3. −zmm,zmp,βm≥0;zmm≤−βmym,∃m:bm>0;
respectively, where throughout m,p∈{1,2,…,M},m≠p.
Proof. Necessity is obvious. Instead of direct calculations sufficiency can be learned from the application of Theorem 3, as in this case Y – being diagonal with positive components – is invertible, and its inverse can easily be calculated.
Remark 1.
1. A necessary and sufficient condition of reversibility in the closed case is sign symmetry of the coefficient matrix. Similar conditions can be formulated for the other two cases, as well.
2. Once we have a zero deficiency reversible realization, it is easy to check detailed balancing: only the circuit conditions [34] are to be checked.
4.2. Finding reversible realizations
Let us study reversibility, another relevant property, in more detail, applying different methods——without taking care of the value of deficiency.
An equivalent and useful characterization of the induced kinetic differential equation of reversible reaction networks seems to be missing. What we only have is a heuristic algorithm without the proof that it leads to a reversible realization if there exists one, and the realization is independent from the order of the steps.
Example 2.
1. Consider the polynomial equation
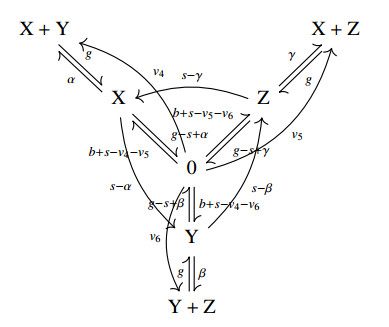
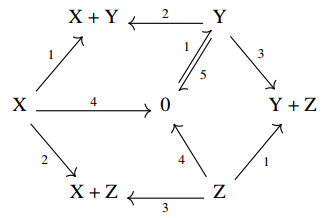
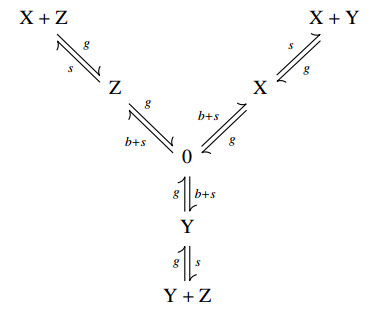
with b,g,s>0 (a transform of the first repressilator model in [14]). The canonical representation of this equation is shown in Figure 1. It is a reversible reaction network with exactly those seven complexes which are given as exponents of the monomials. It consists of a single linkage class and has a three-dimensional stoichiometric space, and it is also a sparse realization. Reversibility allows us to deduce the existence of a positive stationary point by the theorems of [16,35]. In the third part below a more systematic approach to this example will show an infinite number of realizations (not necessarily reversible), actually we shall receive the dense realization.
2. To find a reversible realization one can also use a heuristic: one tries to collect pairs of reactant and product complex vectors. Suppose our goal is to find a reversible reaction network inducing (4.6)–(4.8). Let us rewrite it in the following form
Now we consider the exponent of the monomial as a reactant vector α and the vector with which this monomial has been multiplied, as the reaction vector β−α, then one should have β=(−100)+(101)=(001), thus we need a term where the exponent of the monomial is β, and it is multiplied by a positive constant and α−β. Thus we get:
Repeating steps of this kind we arrive at the decomposition
which again leads to the network in Figure 1.
Conjecture 1. If there exists a reversible realization then the above process (independently from the order of actions) ends and necessarily provides one of them which may or may not depend on the order of steps.
Finally, one can apply Theorem 3 to get all the realizations (with the exponents as complexes only) and choose from them the reversible one(s). Suppose again that the Eqs (4.6)–(4.8) are given, and our goal is to find a reaction network inducing it using Theorem 3. In this case we have
and we have to find a compartmental solution in B of the equation Z=YB, or
which for the coordinates has the following consequences.
and then the equations reduce to
having the solution
implying that
Now the kinetic matrix of the dense realization (without inflow) is
under the conditions that
hold. To have no indices let us introduce α:=u1,β:=u2,γ:=u3. Now consider two cases:
(a) If g≥s, take α, β and γ such that 0≤α,β,γ≤s.
(b) If s≥g, take α, β and γ such that s−g≤α,β,γ≤s.
As to the inflow: the components of the solution v to Yv=b should fulfil
which means that any v defines a solution for which
hold; and then v1:=b+s−v4−v5,v2:=b+s−v5−v6,v3:=b+s−v4−v6.
Summing up, Figure 1 shows a sparse realization, while Figure 2 shows the dense realization. We also obtain the condition of reversibility: α=β=γ=s and v4=v5=v6=0, and that it is exactly the sparse realization which is reversible.
In this example we were lucky to receive a canonical realization with so many nice properties. The reader can easily verify that this is the case with the second three dimensional repressilator model and with the six dimensional one of [14]: the canonical realization is again reversible, and thus assures the existence of a positive stationary point.
Let us emphasize that via a known result in reaction kinetics we were able to assert the existence of a positive solution to a second degree polynomial (in three variables), or to put it another way, we could apply formal reaction kinetics in mathematics.
As to uniqueness of the stationary point: it does not follow from the mentioned theorems. One may try several methods, see e.g., [36]. However, uniqueness of the reversible realization itself does follow (in this special case) from the method based on Theorem 3.
5.
On computing realizations of kinetic equations
In the previous section, we looked at two classes of systems with certain network properties, namely that of (generalized) compartmental models (i.e., complexes consisting of a single species) and that of reversible networks. In this section, we will provide an algorithmic approach to the realizability problem when the coefficients in the ODE are given. To date, there are algorithms based on linear programming (LP) and mixed integer linear programming (MILP) techniques. These are reviewed in Section 5.1.
In the previous section, we only use the complexes that show up as exponents of monomials in the kinetic differential equation. This may not necessarily be the case for more general examples [25]. However, once a set of complexes has been decided on (and must include the exponents of monomials), the algorithms presented below can be used to compute realizations with desirable structural properties.
In Section 5.2, we consider ways to modify an existing realization while preserving dynamical equivalence, including adding to/subtracting from the set of complexes. Finally, we consider cases when a realization with certain properties (e.g., complex balanced) is independent of the choice of the set of complexes.
5.1. Review of algorithms
Qualitative properties can be rewritten in terms of a mixed integer linear programming (MILP) problem [27]. The works [37,38] determine weakly reversible realizations, while [33] provides reversible and detailed balanced realizations. The paper [39] finds detailed balanced subnetworks.
Recall the discussion about possibly enlarging the set of complexes (Problem 5) from Y to ¯Y. We write the dynamical equivalence conditions for finding a realization using linear programming method with this predetermined complex set ¯Y. Note that the columns of Y must also be columns of ¯Y. We want to find a realization of the kinetic differential equation ˙x=Z⋅xY with the complex set ¯Y. In other words, we want to find a Kirchoff matrix Ak such that
We may add columns of 0 to the matrix Z and obtain ¯Z, where the number of columns added is the number of additional columns in ¯Y compared to Y. Then Eq (5.1) becomes
Therefore, kinetic realizability using ¯Y is equivalent to the feasibility of the following convex constraint set
Next, we review algorithms for finding realizations with certain structural properties, namely, reversible, weakly reversible, or complex balancing realizations. In Eqs (5.2)–(5.4) above, the matrices Y and Z do not show up explicitly. Hence, to simplify notation, in what follows below, we let Y denote the complexes to be considered, some of which may not appear explicitly in the differential equation, and Z defines a kinetic differential equation (with possibly columns of 0 so that Z is the same size as Y).
To find a reversible realization, consider the following feasibility problem [40]:
The statement (5.5) is the condition that the reaction step i→j is present if and only if reaction j→i is present. This feasibility problem can be solved in the framework of mixed integer linear programming (MILP).
To find a weakly reversible realization, consider the following feasibility problem [41]:
The inequalities (5.6) ensure that the structure of Ak and A′k are the same, i.e., a reaction is present in one if and only if it is present in the other. Since every weakly reversible network is complex balanced for some choice of parameter (see also Theorem 8), the algorithm searches for a complex balanced A′k (in Eq (5.7)), which shares the network structure we want but bears no relations in terms of the rate coefficients we seek.
In this MILP problem, the decision variables are the off-diagonal entries of Ak and the off-diagonals entries of another Kirchoff matrix A′k, while Z,Y are given matrices, and ε≪1 is a fixed small constant. We will explore the relationship between finding weakly reversible and complex balanced realizations in Section 6. More efficient methods to compute weakly reversible realizations are available; for example, a polynomial time algorithm can be found in [42].
To find a detailed balanced realization, supposed we have the numerical value of one stationary concentration x∗ and consider [33]:
Finally, to find a complex balanced realization, supposed we have the numerical value of one stationary concentration x∗ and consider [33]:
Eqs (5.8), (5.9) are precisely the conditions for the stationary concentration x∗ to be detailed balanced or complex balanced respectively.
5.2. Modifying networks while preserving dynamical equivalence
In this section, we introduce several modifications to an existing realization which preserves dynamical equivalence. These include:
1. positive or convex combinations of realizations,
2. adding new reactions, and
3. eliminating complexes.
This list is non-exhaustive, but we hope that some of the ideas presented in this section will motivate other types of modifications that preserve dynamical equivalences.
5.2.1. Positive and convex combinations of realizations
Suppose we have found several realizations (Y,A1k),(Y,A2k),…,(Y,AIk) to the kinetic differential equation ˙x=Z⋅xY. Then we can easily produce other realizations which may be simpler, or fulfil some further properties [43].
Theorem 5. Suppose that A1k, …, AIk are realizations of a kinetic differential equation, with complex set Y, and let Ak:=∑Ii=1αiAik for some αi>0, i=1,…,I.
1. Ak is a Kirchhoff matrix, and realizes the equation ˙x=(∑iαiY⋅Aik)xY.
2. If ∑Ii=1αi=1, then (Y,Ak) realizes the same kinetic differential equation ˙x=Z⋅xY.
3. If for all i=1,…,I, the matrix Aik defines a reversible realization of some kinetic equation, then Ak defines a reversible realization of some kinetic equation.
4. If for all i=1,…,I, the matrix Aik defines a weakly reversible realization of some kinetic equation, then Ak defines a weakly reversible realization of some kinetic equation.
Proof.
1. Obviously, the off-diagonal terms of Ak are nonnegative. Also the column sums of Ak are conserved. Thus Ak is Kirchoff. We see that
2. This trivially follows from the calculation above.
3. For any p≠q, if [Ak]pq>0, then [Aik]pq>0 for some 1≤i≤I. Since Aik defines a reversible realization, it must be the case that [Aik]qp>0, hence [Ak]qp>0, i.e., Ak defines a reversible realization.
4. The proof is similar to the above. For any p≠q, if [Ak]pq>0, there must be some [Aik]pq>0. Since Aik defines a weakly reversible realization, the reaction q→p must be part of a cycle, i.e., the off-diagonal terms in Aik corresponding to the edges in this cycle are positive, hence those positions in Ak are also positive. In other words, this particular cycle appears in the graph defined by Ak as well.
5.2.2. Adding new reactions to a realization
Now we look at modifying an existing realization by adding new reactions. Suppose that Ak defines a realization with complexes y1,y2,…,yN, and suppose that y is a convex combination of the remaining complexes, i.e., y=∑Nn=1vnyn where vn≥0 for n=1,2,…,N and ∑Nn=1vn=1.
Then we can add the following reactions: for every n such that vn≠0, add a reaction from y to the complex yn, with rate coefficient vn. These reactions together contributes 0 to the differential equation.
We wonder if we can add reactions in the opposite direction, i.e., reactions of the form yn→y. There are cases when it is possible and cases when it is not. While we do not have an answer to this question, we illustrate the complexity using two examples.
Example 3. First we show an example where adding a complex situated in the convex cone of the original complexes seems to be superfluous: its effect on the induced kinetic differential equation can be expressed only using reactions among the original complexes. Consider the system
To add the reaction step 2X→X+Y to get the network
one must borrow from the reactions 2X → 0 and 2X → 2X + 2Y in the sense that
where 0<ε<min.
The example above may lead us to believe that it is always possible to add a reaction from some {\bf{y}}_n on the boundary of the convex hull to some complex {\bf{y}} in the interior of the convex hull of other complexes. The example below illustrates that this is not always the case, and further work is needed to explore when it is possible to add such a reaction.
Example 4. If one takes the system
and tries to add the reaction step 2X → X + Y (note that the new complex X + Y is a convex combination of the old ones), there is no way of choosing the rate coefficients so as to get the induced kinetic differential equation of the extended one.
5.2.3. Eliminating complexes from a realization
Perhaps instead of adding or removing reactions from an existing realization, one may want to add or remove complexes from an existing realization. As noted in [25], it is always possible to add a complex that has not appeared in the current realization, as long as the weighted sum of reaction vectors is {{\bf{0}}} . For example, one can always add the reactions 0 \stackrel{k}{\leftarrow} \mathrm{X} \stackrel{k}{\rightarrow} 2 \mathrm{X} without changing the induced kinetic differential equation. The question lies, then, on when it is possible to eliminate a complex from your realization.
Theorem 6. Suppose that ({\bf{Y}}, {\bf{A}}_{k}) is a realization with N+1 complexes {\bf{y}}_1, \dots, {\bf{y}}_N, {\bf{y}}_{N+1} , where the complex {\bf{y}}_{N+1} participates in at least one reaction as a reactant complex. Suppose that the monomial {\bf{x}}^{ {\bf{y}}_{N+1}} does not appear explicitly in the kinetic differential equation. Then the differential equation can also be realized using only the complexes {\bf{y}}_1, \dots, {\bf{y}}_N .
Proof. We can write the complex matrix and Kirchoff matrix as
where {\bf{u}}, {\bf{v}} \in \mathbb{R}^{N}_{\geq 0} . Then the kinetic differential equation can be written as
Since the complex {\bf{y}}_{N+1} admits some outgoing reactions, we have that \sum_{n = 1}^N {\bf{v}}_n\neq 0 , and, using the fact that the coefficient of {\bf{x}}^{ {\bf{y}}_{N+1}} is zero, we find {\bf{y}}_{N+1} = \frac{1}{\sum_{n = 1}^N {\bf{v}}_n} {\bf{Y}}' {\bf{v}} , and
We conclude that {\bf{y}}_{N+1} is a convex combination of the remaining complexes. More importantly, the Kirchoff matrix {\bf{A}}"_{k} = {\bf{A}}'_{k}+\frac{1}{\sum_{n = 1}^N {\bf{v}}_n} {\bf{v}} {\bf{u}} ^{\top} gives a realization of the same kinetic equation with only the complexes {\bf{y}}_1, \dots, {\bf{y}}_N .
Remark 2. If {\bf{x}}^{ {\bf{y}}} appears explicitly as a term in the kinetic differential equation, then that complex cannot be removed.
After seeing the procedure of eliminating extraneous complexes, one may be tempted to remove all complexes that do not appear as exponents of monomials without ruining desirable properties (e.g., weak reversibility, complex balanced).
Indeed, if one is interested in finding a reversible, or weakly reversible, or detailed balanced, or complex balanced realization, any complex that does not appear in the differential equation (after simplification) can be eliminated from the network [23]:
Theorem 7. A kinetic differential equation \dot{ {\bf{x}}} = \bf{f}({\bf{x}}) has a complex balanced realization if and only if it has a complex balanced realization where the complexes (the columns of {\bf{Y}} ) are precisely the monomials in \bf{f}({\bf{x}}) . Analogous results hold for detailed balanced, weakly reversible, and reversible realizations.
As a consequence, the algorithms described in Section 5.1 can be used to determine whether a given system of kinetic differential equations admits a complex balanced (or detailed balanced, weakly reversible, or reversible) realization. This is a finite calculation as there is no need to compute using different sets of complexes.
6.
Relation between weakly reversible and complex balanced realizations for symbolic kinetic equations
When we discussed the algorithm for computing weakly reversible realizations, the reader may have noticed that we introduced an additional Kirchoff matrix {\bf{A}}_k' that does not appear in the realization ({\bf{Y}}, {\bf{A}}_k) . This reflects the fact that there is a subtle algebraic relation between weak reversibility and complex balancing. In this section, we explore this relationship.
In order to study the possible network structures that can arise from kinetic differential equation to those with unspecified coefficient, we make the following definition:
Definition 9. For a matrix {\bf{Y}} \in {\mathbb{Z}}_{\geq 0}^{M\times N} we say that a sign matrix {\bf{Z}}^\sigma \in \{0, +, -\}^{M \times N} is kinetically compatible with {\bf{Y}} if {\bf{Y}}_{mr} = 0 implies {\bf{Z}}^\sigma_{mr} \in\{ 0, +\} . In such a case, let
where \mathrm{sign}(\cdot) is the componentwise sign function.
For any {\bf{Y}}\in {\mathbb{Z}}_{\geq 0}^{M\times N} and kinetically compatible {\bf{Z}}^\sigma , the set \mathcal{Z}({\bf{Y}}, {\bf{Z}}^\sigma) is an unbounded convex cone in \mathbb{R}^{M\times N} . According to [1], the differential equation \dot{ {\bf{x}}} = {\bf{Z}}\cdot {\bf{x}}^ {\bf{Y}} is kinetic if {\bf{Z}} \in \mathcal{Z}({\bf{Y}}, {\bf{Z}}^\sigma) for any kinetically compatible {\bf{Z}}^\sigma .
Example 5. The Lotka-Volterra equations
(with \alpha, \beta, \gamma, \delta > 0 ) can be written in this framework. Let
where clearly {\bf{Z}}^\sigma is kinetically compatible with {\bf{Y}} . The matrix corresponding to the Lotka-Volterra equations is {\bf{Z}} = \begin{pmatrix} \alpha & -\beta & 0 \\ 0 & \delta & -\gamma \end{pmatrix} , which belongs to the set \mathcal{Z}({\bf{Y}}, {\bf{Z}}^\sigma) .
We defined \mathcal{Z}({\bf{Y}}, {\bf{Z}}^\sigma) in order to study possible behaviours a kinetic differential equation may exhibit for some choice of rate coefficients.
Definition 10. Let {\bf{Z}}^\sigma be kinetically compatible with the matrix {\bf{Y}} . We say that \mathcal{Z}({\bf{Y}}, {\bf{Z}}^\sigma) has the capacity to be complex balanced (or capacity to be weakly reversible) if there exists {\bf{Z}} \in \mathcal{Z}({\bf{Y}}, {\bf{Z}}^\sigma) such that \dot{ {\bf{x}}} = {\bf{Z}} \cdot {\bf{x}}^{ {\bf{Y}}} has a complex balanced (or weakly reversible) realization.
Theorem 8. Let {\bf{Z}}^\sigma be kinetically compatible with the matrix {\bf{Y}} . The set \mathcal{Z}({\bf{Y}}, {\bf{Z}}^\sigma) has the capacity to be complex balanced if and only if it has the capacity to be weakly reversible.
Proof. It is known that complex balancing implies weak reversibility. Suppose there is some {\bf{Z}} \in \mathcal{Z}({\bf{Y}}, {\bf{Z}}^\sigma) with a weakly reversible realization ({\bf{Y}}, {\bf{A}}_k) . Then there is a positive vector {\bf{p}} in the kernel of the Kirchoff matrix {\bf{A}}_k . Fix an arbitrary positive state {\bf{x}}^* . Consider the following scaled Kirchoff matrix
where the division \frac{{\bf{p}}}{({\bf{x}}^*)^{ {\bf{Y}}}} is componentwise. Then
i.e., {\bf{A}}_k' defines a complex balanced realization with stationary concentration {\bf{x}}^* .
7.
On deficiency zero realizations and uniqueness
Recall that the deficiency of a reaction network is the nonnegative integer \delta = N - L - S , where N is the number of complexes, L is the number of linkage classes, and S is the dimension of the stoichiometric subspace \mathcal{S} . A network with lower deficiency tends to have nicer dynamical properties; for example, by the Deficiency Zero Theorem or Deficiency One Theorem. Let us formulate a necessary and sufficient condition on network structure for zero deficiency [17].
We say that the vectors {\bf{y}}_0, {\bf{y}}_1, \dots, {\bf{y}}_N\in \mathbb{R}^M are affinely independent if {\bf{y}}_1- {\bf{y}}_0, \dots, {\bf{y}}_N- {\bf{y}}_0 are linearly independent. Note that in this case {\bf{y}}_0- {\bf{y}}_n, \dots, {\bf{y}}_i - {\bf{y}}_n, \dots, {\bf{y}}_N- {\bf{y}}_n are linearly independent for any n = 1, 2, \dots, N and i \neq n . Also, linearly independent vectors are affinely independent.
Theorem 9. A reaction network is deficiency zero if and only if
1. the complex vectors within each linkage class are affinely independent, and
2. the stoichiometric spaces belonging to the linkage class are linearly independent.
Proof. Consider the \ell -th linkage class. Let N_\ell be the number of complexes in this linkage class, and let \mathcal{S}_\ell be the stoichiometric space belonging to this linkage class. Let \delta_\ell : = N_\ell - 1 - \dim \mathcal{S}_\ell be the deficiency of the \ell -th linkage class. Finally, let \mathcal{S} be the full stoichiometric space.
The deficiency of the entire network can be related to the deficiencies of the linkage classes:
Equality holds if and only if the stoichiometric spaces belonging to the linkage classes \{ \mathcal{S}_\ell\}_{\ell = 1}^L are linearly independent. In this case, \delta = 0 if and only if all \delta_\ell = 0 . Finally, \delta_{\ell} = 0 implies \dim \mathcal{S}_\ell = N_\ell-1 , i.e. the complexes in any given linkage classes are affinely independent.
If we restrict ourselves to weakly reversible realizations, the deficiency \delta is minimized if the set of complexes are precisely the exponents of monomials [23]. Each additional complex that does not appear as exponents of monomials increases the deficiency \delta . It has been shown that any deficiency zero realization with one strong terminal class is unique if the set of complexes is fixed [43]. Combining these two facts, we have the following Proposition.
Proposition 1. Any weakly reversible deficiency zero realization with a single linkage class is unique.
The hypotheses of weakly reversible and deficiency zero in Proposition 1 are required as the following examples illustrate.
Example 6. The reaction networks \mathrm{Y} \stackrel{k}{\leftarrow} 0 \stackrel{k}{\rightarrow} \mathrm{X} and 0 \stackrel{k}{\rightarrow} \mathrm{X}+\mathrm{Y} are two different deficiency zero realizations with one linkage class, although they are not weakly reversible.
Example 7. The reaction network 0 \rightleftharpoons \mathrm{X} \rightleftharpoons 2 \mathrm{X} (with any rate coefficients) and the reaction network
(for wisely chosen rate coefficients) are dynamically equivalent. Both are weakly reversible and with one linkage class, but \delta = 1 .
Example 8. Two dynamically equivalent weakly reversible realizations where one has \delta = 1 are
with all rate coefficients are taken to be 1 .
Nonetheless, Proposition 1 naturally leads us to the following conjecture, for which a proof has been proposed [44]:
Conjecture 2. Any weakly reversible deficiency zero reaction network has a unique realization.
Throughout this work, we have seen over and over again that realizability (more precisely, identifying the network structure) is an underdetermined problem. Is it possible to use this flexibility in network structure to get more out information about a kinetic differential equation?
An idea comes to mind; we will formulate a conjecture following an example.
Example 9. Consider the mass action system
for any rate coefficients k_1 , k_2 , k_3 , k_4 > 0 . This system has a weakly reversible, deficiency zero realization:
The induced kinetic differential equation of both systems is
In particular, the latter mass action system is complex balanced for all choice of rate coefficients. This implies that the kinetic differential equation enjoys all the dynamical properties of complex balanced systems, although we could have been looking at the network that is not weakly reversible.
Conjecture 3. Consider a reaction network \mathcal{N}_1 , and assume that there exists a weakly reversible reaction network \mathcal{N}_2 of deficiency \delta such that any differential equation induced by \mathcal{N}_1 and positive {\bf{k}} values can also be induced by \mathcal{N}_2 and positive \widehat{{{\bf{k}}}} values, and viceversa. Then, the set of rate coefficient values of \mathcal{N}_1 for which \mathcal{N}_1 induces systems that have complex balanced realizations contains an algebraic variety of codimension not larger than \delta .
8.
Discussion
We have been talking about finding realizations (with certain network properties) of kinetic differential equations. Starting with a system of polynomial differential equations (possibly with symbolic parameters), one could try to find a (Feinberg-Horn-Jackson) reaction graph that induces the differential equation under mass action kinetics. After fixing a set of complexes, algorithms exist to find realizations (Section 5.1). Furthermore, conditions on the resulting reaction graph (e.g., weakly reversible, complex balanced, omit certain reactions) can be incorporated into the algorithms.§
§Codes for solving the problems in the paper can be requested from the authors.
We also considered graph operations on the reaction network that will preserve the kinetic differential equation. For example, in certain cases reactions can be added, and complexes can be removed. Our discussion in Section 5.2 is far from complete; it would be interesting to further explore the allowed operations while preserving dynamical equivalence.
In Section 6, we explored the relationship between weakly reversible and complex balanced realizations. Hidden inside the proof of the main theorem in that section is the scaling equation (6.1). We believe there is information hidden about the manifold in parameter space that decides whether or not a kinetic differential equation can be complex balanced.
Finally, in our discussion of deficiency zero realizations and uniqueness, we posed two conjectures. The first is that weakly reversible deficiency zero networks have unique realizations. The latter is more complicated; it asks for what rate coefficients is the reaction network dynamically equivalent to complex balanced.
As the reader can see, a theoretical understanding of the relationships between network structure, the sign structure of the differential equation, and dynamical properties is lacking. We hope to see further studies exploring the realizability problem.
Acknowledgements
The authors started to work on this paper when enjoying the hospitality of the Erwin Schrödinger Institut in Vienna as participants of the meeting Advances in Chemical Reaction Network Theory, 15–19 October, 2018. Gábor Szederkényi and János Tóth thank the support of the National Research, Development, and Innovation Office, Hungary (SNN 125739). Gheorghe Craciun and Polly Y. Yu have been supported by National Science Foundation grant DMS-1816238. Polly Y. Yu also by the Natural Sciences and Engineering Research Council of Canada. Elisa Tonello was supported by the Volkswagen Stiftung (Volkswagen Foundation) under the funding initiative Life? - A fresh scientific approach to the basic principles of life (project ID: 93063). We utilized the detailed comments of the reviewers gratefully.
Conflict of interest
The authors declare there is no conflict of interest.
Supplementary
Examples: Realizations with a minimal number of complexes
Simple examples can be treated directly, without detailed application of Theorem 3.
Example 10. If the differential equation \dot{x} = kx is given (no matter what the sign of k is), then we might try to look for an inducing reaction network consisting of the single complex X and find it impossible, the minimal reason being that one cannot have a reaction network with less than two complexes. The right hand side contains a single monomial, but the realization should contain more than one complex.
Example 11. If the differential equation
is given with k_1, k_2 > 0 , then at least three complexes are needed to realize the equation. How do we prove this?
Two complexes are not enough. With the notations of Theorem 3 we have
As {\bf{Y}} is invertible, {\bf{v}} = {\bf{Y}}^{-1} {\bf{0}} = {\bf{0}} should hold. However, {\bf{Y}} {\bf{B}} = {\bf{B}} = {\bf{Z}} cannot hold, because {\bf{Z}} is not a compartmental matrix.
Three complexes are enough. Consider the realization
It is easy to find a realization with noninteger stoichiometric coefficients:
In the pioneering paper [3] this generalization to nonnegative real coefficients for complexes is allowed, although here we restrict ourselves to nonnegative integer coefficients, which is a common assumption in mass action kinetics.
8.1 More examples
Example 12. Invertibility of the complex matrix {\bf{Y}} is not sufficient to have a realization with the exponents of the monomials as complex vectors, as the following example shows.
implies that
and the (unique) solution to
is
with some negative numbers. We are forced to formulate a problem: Characterize those matrices with nonnegative (integer) components the inverse of which multiplied with a matrix without negative cross effect gives a compartmental matrix. As this problem again requires finding the feasible solutions of a linear programming (more precisely, MIL) problem, there is not too much hope to find an explicit symbolic solution, but at the same time one can have numerical solution(s) using LP-solvers.
Example 13. Consider the polynomial equation
with k_1, k_{-1} > 0 . The canonical representation of this equation is
A reversible realization is
which has N = 2 complexes, L = 1 linkage class and a S = 1 -dimensional stoichiometric space, thus it has a deficiency 0 = N-L-S .
Direct calculation shows that the positive stationary points satisfy
By the Deficiency Zero Theorem [3,4,5] for one linkage class [7,45], we know that within every stoichiometric compatibility class, there is exactly one stationary point, which is globally stable.
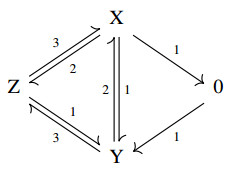
Example 14. The canonical realization of the differential equation
is the irreversible, deficiency three reaction network consisting of a single linkage class of Figure 3. However, it is "obviously" the induced kinetic differential equation of the zero deficiency weakly reversible reaction network in Figure 4. (Here again, the unique positive stationary point can explicitely be determined.)
Let us see a nonlinear example.
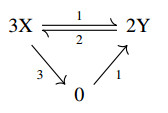
Example 15. The canonical realization of the differential equation
is the irreversible, deficiency 3 reaction network consisting of two linkage classes
However, it is (much less) "obviously" the induced kinetic differential equation of the weakly reversible, zero deficiency reaction network in Figure 5 consisting of a single linkage class. To show this in a formal way, we apply Theorem 3.
With the notations of Theorem 3 we have
As {\bf{Y}} is invertible, {\bf{v}} = {\bf{Y}}^{-1} {\bf{b}} = \left(\begin{array}{c} 0 \\ 1 \end{array}\right) should hold. The unique solution of
under the conditions b_{12}, b_{21}, u_1, u_2\ge0 is calculated with or without the direct use of {\bf{Y}}^{-1} . Thus, the unique reaction network to induce Eq (8.1) (only having the complexes defined by the monomials on the right hand side) is seen in Figure 5.
Example 16. Now we show a network with three complexes inducing a differential equation having two terms on the right hand side. The induced kinetic differential equation of the network
with \alpha_1 < \beta_1 < \beta_2 and
only has two terms on its right hand side of its kinetic differential equation:
No wonder, as the condition (8.2) implies that \beta_1 is a convex combination of \alpha_1 and \beta_2.
Mass conserving realizations
The reaction (2.1) is mass conserving, if there exists a vector \boldsymbol{\varrho}\in {\mathbb{R}}_{ > 0}^M such that for all r = 1, 2, \dots, R
holds. Note that to ensure mass conservation the existence of a positive vector in the left kernel of the span of the range of the right hand side is necessary but not sufficient, [21,p. 89].
Consider again the differential equation
According to the definition (8.3) the existence of a vector \boldsymbol{\varrho}\in {\mathbb{R}}_{ > 0}^M such that
is a necessary condition of mass conservation. However, it is only sufficient with some restrictions.
Theorem 10. If (8.4) has a realization such that the number of linkage classes is equal to the number of ergodic components (terminal strong linkage classes) and there exists a vector \boldsymbol{\varrho}\in {\mathbb{R}}_{ > 0}^M such that (8.5) holds, then this realization is mass conserving.
It is shown in [51] that the same kinetic model may have both mass conserving and non-mass conserving realizations.









 DownLoad:
DownLoad: