Stochastic multiple attribute decision making with Pythagorean hesitant fuzzy set based on regret theory

1.   Introduction

Multi-attribute decision-making (MADM) is interpreted as a process in which decision-makers (DMs) rank the alternatives according to different evaluation attributes and selects the optimal solution. At present, MADM is used in many fields, such as project evaluation ^[1], medical diagnosis ^[2], tertiary hospital management ^[3], financial logistics enterprises performance evaluation ^[4], smart healthcare ^[5], etc. Because of the complexity of the objective decision-making environment and the human cognitive and attentional limitations, the fuzzy and uncertain nature of evaluation information should primarily be considered. Intuitionistic fuzzy sets (IFS) were proposed to present the ambiguity and uncertainty of information based on fuzzy sets ^[6], which consider the degree of membership (MD), the degree of non-membership (NMD), and the degree of hesitancy. However, IFS has some limitations. For example, it can solely describe the case where the sum of MD or NMD is equal to or less than 1. Concerning the problem, Yager ^[7] and Yager and Abbasov ^[8] relaxed the restrictions and presented the concept of the Pythagorean fuzzy set (PFS), which could characterize the situation that the sum of MD or NMD is equal to or greater than 1. Moreover, to characterize the vague phenomenon, Torra ^[9] presented hesitant fuzzy sets (HFS), in which the MD is permitted to contain several probable values. Khan et al. ^[10] introduced the concept of Pythagorean hesitant fuzzy set (PHFS) and discussed some properties of PHFS, which both have the advantages of the above two fuzzy sets and can describe more complex decision-making environments. Since this theory was put forward, many scholars have made in-depth research on this field. Xian et al. ^[11] studied PHFS and proposed some relative arithmetic operators (AOs). Zhang et al. ^[12] extended some general operators regarding the dual hesitant fuzzy linguistic elements; then, an approach to the MADM problem based on the proposed operators was developed. Shakeel et al. ^[13] applied a weighted averaging operator to tackle the MADM problem under the Pythagorean hesitant fuzzy (PHF) environment. Khan et al. ^[14] introduced the Choquet integral and proposed some Pythagorean hesitant fuzzy aggregation operators (PHFAOs) to show the validity and effectiveness of the developed operators. Liang et al. ^[15] constructed a new extension method in the framework of Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) under the PHF environment. Khan et al. ^[16] extended the VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) method for solving the MADM problems with PHFS. Ak and Gul ^[17] studied a PHF MADM method based on TOPSIS and Analytic Hierarchy Process (AHP). Geetha ^[18] extended the ELimination and Choice Expressing Reality (ELECTRE) III method and established the HPF-ELECTRE method with PHFS. Krishankumaar et al. ^[19] introduced a ranking model under a PHFS by evidence theory (ET). Jana and Roy ^[20] presented a linguistic Pythagorean hesitant fuzzy set (LPHFS) by combining a Pythagorean hesitant fuzzy set and a linguistic fuzzy set. To better represent the ambiguity and hesitation of decision-makers (DMs) in the decision-making process, this paper uses PHFS to describe ambiguous information and to avoid the loss of judgment information, and then provides a new interpretation for stochastic multi-attribute decision-making (SMADM) problem to adapt more complex scenario.

The stochastic multi-attribute decision-making problem describes the presence of multiple states in the decision process, where the attribute values are in the form of stochastic variables. Its characteristic is that there are many states in the decision-making process, and it is impossible to determine what state would happen; however, the probability of each natural state can be estimated in advance, and different natural states have different attribute values. Nie et al. ^[21] developed a discrete SMADM method by using the cumulative prospect theory and a generalized Shapley function. Liu et al. ^[22] solved the stochastic multi-attribute group decision-making (SMAGDM) problem through a combination of fuzzy stochastic dominance and the credibility theory, where attribute values are normal discrete fuzzy variables. Qu et al. ^[23] provided an innovative SMADM with dual hesitant fuzzy numbers and unknown attribute weights by integrating group satisfaction and regret theory. To overcome the limitation that it is difficult to discern the domination relationship among certain schemes, Jiang et al. ^[24] put forward a SMADM approach on the basis of almost stochastic dominance rules. Wang et al. ^[25] presented a two-dimension 2-tuple linguistic decision-making method based on stochastic multi-criteria acceptability analysis. Rezaei ^[26] used possibilistic SMADM to rank Iran's biodiesel development policies. Considering the psychological behavior of decision makers, this paper highlights the development of an optimization model and its application to the SMADM problem.

In the decision-making process, DMs are usually affected by psychological behaviors. Bell ^[27], Loomes and Sugden ^[28] presented the concept of regret theory, which was a very obvious psychological factor. Regret theory was originally applied to the choice between two options; however, Quiggin ^[29] extended it to the choice between multiple options. Specifically, in the process of decision making, people usually compare the possible outcomes of chosen alternatives with the possible outcomes of unchosen alternatives. In comparison, if the former is better than the latter, DMs would feel delighted, otherwise, they would feel regret. Thus, it is important to know how to deal with the regret avoidance behavior of DMs and how to choose the most satisfactory alternative. Liu et al. 30] introduced a stochastic decision method by integrating regret theory and group satisfaction degree. Furthermore, Zhu ^[31] described a multi-attribute group decision making (MAGDM) approach utilizing regret theory and evidence theory. Wei and Wang ^[32] integrated the interval-valued HF set and regret theory for solving the stochastic decision-making problem. Tian et al. ^[33] investigated a regret theory under the probabilistic linguistic term (PLT) environment. Jia and Wang ^[34] proposed a probabilistic linguistic PROMETHEE II method which considers the regret psychology of DMs. Ali et al. ^[35] introduced a q-rung positive hesitation fuzzy stochastic method based on regret theory to capture the mental behavior of DMs. Zhu et al. ^[36] explored a three-way multi-attribute decision making method (3W-MADM-R) based on regret theory. Liu et al. ^[37] proposed a MAGDM method based on trust relationship and a data envelopment analysis (DEA) regret cross-efficiency. Since DMs may feel regret if he or she misses the optimal choice, it is necessary to take the DMs' regret as an important evaluation factor in the decision-making process. In this paper, the SMADM problems under the PHF environment would consider the DMs' regret by combining the regret theory.

Based on the above analysis, the main contributions are as follows: 1) Regret theory is applied to quantify the effect of regret aversion on SMADM problems. 2) The PHFS is used to measure the divergence and satisfaction of decision makers according to the overall psychological perception values. 3) The nonlinear programming model is built and applied to SMADM problems with either totally unknown or partially known attribute weights. In this paper, an extended approach is presented to address SMADM, taking the psychological behavior of decision-makers in Pythagorean hesitant fuzzy environment into account. The remainder of this paper is organized as follows: Some relevant basic notions are briefly presented in Section 2. The decision steps of the SMADM method in the PHF environment are provided, which combines the regret theory and the group satisfaction degree in Section 3. A practical case is utilized to demonstrate this approach in Section 4. The feasibility of the presented approach is verified by comparing with four different methods in Section 5. Finally, the conclusion is given.

2.   Preliminaries

2.1.   Pythagorean hesitant fuzzy set

Definition 1 ^[14]. Let $X$ be a fixed set, and ${P}_{H}$ denotes a PHFS in $X$, which satisfies:

where ${\varLambda }_{{P}_{H}}\left(x\right)$ and ${\varGamma }_{{P}_{H}}\left(x\right)$ represent several probable degrees of membership and non-membership. In addition, for all $x\in X$, $\forall {\widehat{h}}_{{P}_{H}}\left(x\right)\in {\varLambda }_{{P}_{H}}\left(x\right)$, $\exists {\widehat{{h}^{{'}}}}_{{P}_{H}}\left(x\right)\in {\varGamma }_{{P}_{H}}\left(x\right)$ such that $0\le {\widehat{h}}_{{P}_{H}}^{2}\left(x\right)+{\widehat{{h}^{{'}}}}_{{P}_{H}}^{2}\left(x\right)\le 1$, and $\forall {\widehat{{h}^{{'}}}}_{{P}_{H}}\left(x\right)\in {\varGamma }_{{P}_{H}}\left(x\right)$, $\exists {\widehat{h}}_{{P}_{H}}\left(x\right)\in {\varLambda }_{{P}_{H}}\left(x\right)$ such that $0\le {\widehat{h}}_{{P}_{H}}^{2}\left(x\right)+{\widehat{{h}^{{'}}}}_{{P}_{H}}^{2}\left(x\right)\le 1$. If ${\varLambda }_{{P}_{H}}\left(x\right)$ and ${\varGamma }_{{P}_{H}}\left(x\right)$ have only one number, the PHFS becomes a PFS. When the degree of non-membership is 0, the PHFS becomes an HFS.

Definition 2 ^[14]. Let ${\widehat{h}}_{1}$ and ${\widehat{h}}_{2}$ be two PHF numbers (PHFNs) on a set $X = \left\{{x}_{1}, {x}_{2}, \cdots, {x}_{n}\right\}$, the distance between ${\widehat{h}}_{1}$ and ${\widehat{h}}_{2}$ is:

where ${\#}{h}_{{\widehat{h}}_{1}}$, ${\#}{h}_{{\widehat{h}}_{2}}$, $\#{{h}^{{'}}}_{{\widehat{h}}_{1}}$, and $\#{{h}^{{'}}}_{{\widehat{h}}_{2}}$ denote the number of elements in ${\varLambda }_{{\widehat{h}}_{1}}$, ${\varLambda }_{{\widehat{h}}_{2}}$, ${\varGamma }_{{\widehat{h}}_{1}}$ and ${\varGamma }_{{\widehat{h}}_{2}}$, respectively.

2.2.   Regret theory

Regret theory is a behavioral decision theory proposed successively by Bell ^[27], Loomes, and Sugden ^[28] in 1982. In regret theory, DMs not only focus on the results obtained during the decision-making process, but also compares the results with them when choosing other options. DMs would feel regret if they do not choose the optimal alternative. Therefore, they pay attention to the expectations of regret and elation when making decisions and try to avoid choosing the alternative that would make them regret.

Definition 3 ^[27]. Let $x$ and $y$ denote the outcomes obtained by choosing solutions $A$ and $B$, respectively; then, the DM's perceived utility with respect to solution $A$ is: $U\left(x, y\right) = v\left(x\right)+R\left(v\left(x\right)-v\left(y\right)\right)$, where $v\left(x\right)$ and $v\left(y\right)$ denote the utility that DM can obtain from the outcome of option $A$ and option $B$, respectively, and $R\left(v\left(x\right)-v\left(y\right)\right)$ denotes the regret-euphoria value. When $R\left(v\left(x\right)-v\left(y\right)\right) > 0$, $R\left(v\left(x\right)-v\left(y\right)\right)$ is the euphoria value, indicating that the DM is pleased with choosing option $A$ and giving up on option $B$. When $R\left(v\left(x\right)-v\left(y\right)\right) < 0$, $R\left(v\left(x\right)-v\left(y\right)\right)$ is the regret value, indicating that the DM regrets choosing option $A$ and gives up on option $B$. Regret theory was originally used for two-option choice problems, which was extended to multiple-option choice problems by Quiggin ^[29].

Suppose ${a}_{i}$ denote the result obtained by the alternative ${A}_{i}$. The regret perception utility of ${A}_{i}$ is $U\left({a}_{i}\right) = u\left({a}_{i}\right)+R\left(u\left({a}_{i}\right)-u\left({a}^{*}\right)\right)$, where ${a}^{*} = \mathrm{m}\mathrm{a}\mathrm{x}\left\{{a}_{i}\left|i = \mathrm{1, 2}, \cdots m\right.\right\}$. $R\left(\text{·}\right)$ is a regret-rejoice function, and it is a monotonically increasing concave function. $R\left(u\left({a}_{i}\right)-u\left({a}^{*}\right)\right)$ represents the regret value generated by choosing option ${A}_{i}$, and $R\left(u\left({a}_{i}\right)-u\left({a}^{*}\right)\right)\le 0$.

3.   Method for SMADM with PHF information

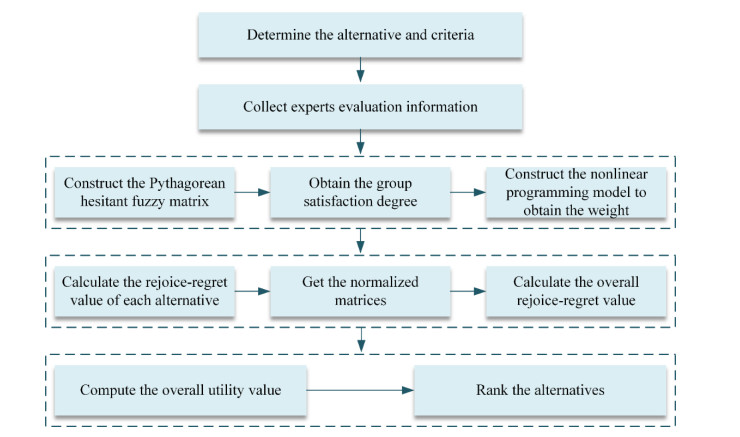
In this section, the SMADM problems under Pythagorean hesitant fuzzy environments is described and then the detailed decision-making steps are given based on the group satisfaction degree of the PHFS and regret theory. A framework was established to further elaborate the following decision-making process in Figure 1.

Assuming that the set of alternatives is $\mathbf{Y} = \left\{{Y}_{1}, {Y}_{2}, \cdots, {Y}_{m}\right\}$, and the set of attributes is $\mathbf{C} = \left\{{C}_{1}, {C}_{2}, \cdots, {C}_{n}\right\}$. The weights of attributes are $\mathbf{W} = {\left({w}_{1}, {w}_{2}, \cdots, {w}_{n}\right)}^{T}$, where $\sum _{j = 1}^{n}{w}_{j} = 1$ and ${w}_{j}\in \left[\mathrm{0, 1}\right]$. Suppose $\mathbf{S} = \left\{{S}_{1}, {S}_{2}, \cdots, {S}_{g}\right\}$ be a set of possible states, and $\mathbf{P} = {\left({p}_{1}, {p}_{2}, \cdots, {p}_{g}\right)}^{T}$ be the probability vector, where $\sum _{t = 1}^{g}{p}_{t} = 1$ and ${p}_{t}\in \left[\mathrm{0, 1}\right]$. The steps of the proposed PHF-SMADM method are listed as follows:

Step 1: Construct the decision-making matrices ${\mathbf{D}}^{t} = {\left({\widehat{h}}_{ij}^{t}\right)}_{m\times n}$ by DMs under different state ${S}_{t}$ to evaluate the alternative ${Y}_{i}$ with the criteria ${C}_{j}$.

Step 2: Obtain the group satisfaction degree $\varphi \left({\widehat{h}}_{ij}^{t}\right)$.

where $d\left({\widehat{h}}_{ij}^{t}, {I}^{+}\right) = \frac{1}{2}\left(\begin{array}{l}\left(\sum _{{i}_{1} = 1}^{\#{h}_{{\widehat{h}}_{ij}^{t}}}\left|{\left({h}_{{\widehat{h}}_{ij}^{t}}\left({x}_{{i}_{1}}\right)\right)}^{2}-1\right|\right)/\#{h}_{{\widehat{h}}_{ij}^{t}}\\ +\left(\sum _{{{i}^{{'}}}_{1} = 1}^{\#{{h}^{{'}}}_{{\widehat{h}}_{ij}^{t}}}\left|{\left({{h}^{{'}}}_{{\widehat{h}}_{ij}^{t}}\left({x}_{{i}_{1}}\right)\right)}^{2}\right|\right)/\#{{h}^{{'}}}_{{\widehat{h}}_{ij}^{t}}\end{array}\right)$ is the distance between the ${\widehat{h}}_{ij}^{t}$ and positive-ideal solution, and $d\left({\widehat{h}}_{ij}^{t}, {I}^{-}\right) = \frac{1}{2}\left(\begin{array}{l}\left(\sum _{{i}_{1} = 1}^{\#{h}_{{\widehat{h}}_{ij}^{t}}}\left|{\left({h}_{{\widehat{h}}_{ij}^{t}}\left({x}_{{i}_{1}}\right)\right)}^{2}\right|\right)/\#{h}_{{\widehat{h}}_{ij}^{t}}\\ +\left(\sum _{{{i}^{{'}}}_{1} = 1}^{\#{{h}^{{'}}}_{{\widehat{h}}_{ij}^{t}}}\left|{\left({{h}^{{'}}}_{{\widehat{h}}_{ij}^{t}}\left({x}_{{i}_{1}}\right)\right)}^{2}-1\right|\right)/\#{{h}^{{'}}}_{{\widehat{h}}_{ij}^{t}}\end{array}\right)$ is the distance between the ${\widehat{h}}_{ij}^{t}$ and the negative-ideal solution ^[38].

Step 3: Construct the nonlinear programming model to obtain the weight $\mathbf{W} = {\left({w}_{1}, {w}_{2}, \cdots, {w}_{n}\right)}^{T}$ of attributes, which is the mathematical method of finding the optimized solution by considering either nonlinear constraints or objective functions.

Step 4: Compute the regret value matrix ${\mathbf{R}}_{j} = {\left({R}_{ikj}\right)}_{m\times m}$ and rejoice value matrix ${\mathbf{G}}_{j} = {\left({G}_{ikj}\right)}_{m\times m}$. During the decision-making process, DMs would compare the results of their own choices with the results that other options may obtain. If they find that choosing other options can obtain better results, they would feel regretful, and conversely, they would feel elated. The DM's perceived a utility of options, which can be obtained by calculating the rejoice and regret values.

Step 5: Get the normalized regret matrix ${\stackrel{-}{\mathbf{R}}}_{j}$ and normalized rejoice matrix ${\stackrel{-}{\mathbf{G}}}_{j}$.

Step 6: Calculate the overall regret value $R\left({Y}_{i}\right)$ and overall rejoice value $G\left({Y}_{i}\right)$ of the alternative ${Y}_{i}$ relative to the other alternatives based on the regret matrix ${\stackrel{-}{\mathbf{R}}}_{j}$ and rejoice matrix ${\stackrel{-}{\mathbf{G}}}_{j}$ :

where $R\left({Y}_{i}\right)\le 0$ represents the degree of alternative ${Y}_{i}$ inferior to other alternatives. The larger the $R\left({Y}_{i}\right)$, the worse the corresponding alternatives becomes. $G\left({Y}_{i}\right)\ge 0$ denotes the degree of alternative ${Y}_{i}$ superior to other alternatives, and the larger $G\left({Y}_{i}\right)$ is, the better the alternatives would be.

Step 7: Compute the overall utility value $F\left({Y}_{i}\right)$ of alternative ${Y}_{i}$, which represents the total psychological perceived value of all DMs for alternative ${Y}_{i}$.

Step 8: Rank the alternatives in accordance with the $F\left({Y}_{i}\right)$. The greater $F\left({Y}_{i}\right)$ represents the superior alternative ${Y}_{i}$.

4.   Illustrative example

To make the approach easier to understand, an actual case about the selection of the air-fighter is adopted ^[39], which is a multiple criteria decision-making analysis to increase the decisive power of air defense and the superior power of defense strategy. Suppose country A plans to buy an air fighter from another country B. Country B would provide country A with the characteristic data of five candidate air fighters. According to each attribute ${C}_{j}\left(j = \text{1, }\text{}\text{2, }\text{}\text{3, }\text{}\text{4}\right)$ under three possible states: fair, poor, and good, with probability $\mathbf{P} = {\left(\text{0.8, }\text{}\text{0.1, }\text{}\text{0.1}\right)}^{T}$, three experts with different backgrounds and knowledge formed an Air Force procurement group, and they are invited to evaluate the alternative ${Y}_{i}\left(i = \text{1, }\text{}\text{2, }\text{}\text{3, }\text{}\text{4, }\text{}\text{5}\right)$.

Step 1: The candidate air fighters are evaluated using the Pythagorean hesitant fuzzy numbers under the above four attributes, and then the decision matrices ${\mathbf{D}}^{t} = {\left({\widehat{h}}_{ij}^{t}\right)}_{5\times 4}\left(t = \text{1, }\text{}\text{2, }\text{}\text{3}\right)$ can be obtained, as shown in Table 1–3.

Step 2: The group satisfaction degree matrix is obtained.

Step 3: The attribute weight $\mathbf{W}\text{}\text{ = }\text{}{\left(\text{0.2522, 0.2741, 0.2047, 0.2690}\right)}^{{T}}$ is calculated by formula (4).

Step 4: The regret value matrix and the rejoicing value matrix are computed, where $\text{α}\text{}\text{ = }\text{}\text{0.3}$ ^[40].

Step 5: The normalized regret matrix and normalized rejoice matrix are obtained, respectively.

Step 6: The overall regret values and rejoicing values of each alternative are calculated.

Step 7: The overall utility value of alternative is obtained.

Step 8: The alternatives are ranked: ${Y}_{\text{4}}\succ {Y}_{\text{5}}\succ {Y}_{\text{2}}\succ {Y}_{\text{3}}\succ {Y}_{\text{1}}$.

From the above discussion, PHFS is a powerful tool to deal with imprecision and hesitation, where a likelihood distribution is built that approximates the likelihood values, though there are several possible values. In addition, decision-making methods based on regret theory are more consistent with the behavior of real decision makers. Considering the psychological characteristics of decision-making, a method to solve the SMADM problem in the Pythagorean hesitant fuzzy environment is proposed.

5.   Comparative analysis

In this section, different methods are applied for solving the SMADM problem under PHF environment.

5.1.   Comparison analysis with TOPSIS method

TOPSIS is a method of ranking a limited number of objects to be evaluated according to their proximity to idealized goals. It is an evaluation of the relative advantages and disadvantages of existing objects and belongs to a purely objective and rational decision-making method. The proposed method considers the influence of a decision maker's regret behavior and the hesitation and ambiguity of decision information in solving the SMADM problem in the PHF environment.

The steps of PHF-TOPSIS method are listed as follows ^[40]:

Step 1: The comprehensive attribute values of alternatives in each state ${S}_{t}$ is calculated based on the decision matrices.

Step 2: The PIS ${Y}^{+}$ and NIS ${Y}^{-}$ are obtained.

Step 3: The revised closeness distances $\zeta \left({Y}_{i}\right) = \frac{D\left({Y}_{I}, {Y}^{-}\right)}{D\left({Y}_{I}, {Y}^{+}\right)+D\left({Y}_{i}, {Y}^{-}\right)}$ are computed.

Step 4: The alternatives are ranked by $\zeta \left({Y}_{i}\right)$, as shown in Table 4.

Obviously, the sorted result is ${Y}_{5}\succ {Y}_{2}\succ {Y}_{4}\succ {Y}_{1}\succ {Y}_{3}$, which is different from that ranked by the proposed method. The differences are focused on the orders between ${Y}_{4}$ and ${Y}_{5}$. The main reason is that the reference points need to be pre-determined in TOPSIS, which would have an impact on the evaluation results. In contrast, the proposed approach does not require artificial reference points. Additionally, by taking account of the influence of the DMs' regret psychology and the hesitation and vagueness of the decision-making information, the proposed method can show great superiority in solving the SMADM problem under the PHF environment.

5.2.   Comparison analysis with the PHFWA

Pythagorean hesitant fuzzy weighted averaging (PHFWA) is applied to decision-making problems in which experts provide their preferences in the Pythagorean hesitant fuzzy environment. The operation cannot reflect the alternatives' overall perception and lacks the subjective will of the decision maker. However, the proposed method considers the bounded rational of decision makers in different natural states.

By the PHFWA operator, the comprehensive attribute values $\text{Φ}\left({Y}_{i}\right) = \sum _{t = 1}^{g}\sum _{j = 1}^{n}{h}_{ij}^{t}{w}_{j}{p}_{t}$ of the alternatives can be obtained under each state ${S}_{t}$. For example,

According to the score function, the scores $S\left({\widehat{h}}_{i}\right)$ of the comprehensive attribute values are calculated:

The ranking order can be obtained as ${Y}_{2}\succ {Y}_{5}\succ {Y}_{1}\succ {Y}_{3}\succ {Y}_{4}$. Compared with the order ${Y}_{4}\succ {Y}_{5}\succ {Y}_{2}\succ {Y}_{3}\succ {Y}_{1}$, the optimal choice is different and the order is also inconsistent. The proposed approach considers the psychological behavior of DMs. From the overall regret values and rejoicing values of each alternative compared to the others, ${Y}_{\text{2}}$ faces more losses and regrets than ${Y}_{\text{4}}$ ($R\left({Y}_{2}\right) = -\text{0.9344} < R\left({Y}_{4}\right) = -\text{0.4656}$). In addition, ${\text{Y}}_{\text{4}}$ faces more rejoicing than ${Y}_{2}$ ($G\left({Y}_{4}\right) = \text{1.4343} > G\left({Y}_{2}\right) = \text{1.1144}$). Therefore, the overall perception of the alternative ${Y}_{4}$ is better than the alternative ${Y}_{2}$.

5.3.   Comparison analysis with VIKOR method

The VIKOR method produces the closest feasible compromise option to the ideal solution by providing the maximum group utility and the minimum individual regret. However, the proposed method significantly reduces the computational burden by applying a regret-happiness function that does not require pairwise comparisons of two alternatives.

According to the decision steps of the VIKOR method with PHFS ^[16], the alternatives are sorted in Table 5. In the table, ${S}$ represents the maximum group utility, ${R}$ represents the minimum individual regret, and the aggregation function ${Q}$ represents the closeness to the ideal solution. The smaller the value of ${S}$, ${R}$, and ${Q}$, the better the solution, and the higher the value of ${Q}$, the better the result.

In addition, $DQ = 1/m-1 = \text{0.25}$, $Q\left({Y}_{2}\right)-Q\left({Y}_{5}\right) = \text{0.3769} > \text{0.25}$, which satisfies $Q\left({Y}_{2}\right)-Q\left({Y}_{5}\right)\ge DQ$. Then, $Q\left({Y}_{1}\right)-Q\left({Y}_{5}\right) = \text{0.5218} > \text{0.25}$, $Q\left({Y}_{3}\right)-Q\left({Y}_{5}\right) = \text{0.6602} > \text{0.25}$, $Q\left({Y}_{4}\right)-Q\left({Y}_{5}\right) = \text{0.8293} > \text{0.25}$ can be obtained. Therefore, the optimal alternative is ${Y}_{\text{5}}$. In practical decision-making, experts may use the different compromise coefficient ${v}$ ^[16]. Additionally, the ranking of alternatives would be affected by the change of ${v}$. Consequently, different values are used to calculate different comprehensive evaluation values, which are shown in Table 6. The sensitivity analysis indicates that ${Y}_{\text{5}}$ is the optimal one, while no alternatives could be a compromise solution.

Under the PHF environment, the ranking order is ${Y}_{5}\succ {Y}_{2}\succ {Y}_{1}\succ {Y}_{3}\succ {Y}_{4}$ by the VIKOR method, while the ranking order is ${Y}_{4}\succ {Y}_{5}\succ {Y}_{2}\succ {Y}_{3}\succ {Y}_{1}$ by the proposed approach. Apparently, the two results are quite different. The alternative ${Y}_{4}$ shows the most obvious change in the order, which is the optimal alternative in our approach, though this is a worse alternative in the VIKOR method. This indicates that regret psychology has a strong influence on decision making results and is an important factor that should be considered when solving SMADM problems.

6.   Conclusions

In this paper, to make the process of decision-making more realistic, an approach of solving the SMADM problem under PHF environment based on regret theory is studied. The features of the presented approach are as follows: 1) Regret psychology is considered to compute the overall psychological perception value of the group in the practical SMADM. 2) Using the satisfaction degree with PHF information, this model is suitable to the situation where the attribute weights are either completely or partly unknown. The proposed approach in this paper has some limitations, which might suggest future research. First, decision makers may prefer to use words to evaluate in a practical sense, such as "good" or "bad". To better express linguistic information, Zadeh proposed a linguistic term set (LTS) ^[41], and then Liu et al. introduced the Fermatean fuzzy linguistic term set (FFLTS) based on FFS and LTS, which can describe the non-membership degree of the evaluation ^[42]. The proposed approach can also be combined with FFLTS to effectively transform linguistic information in different decision-making contexts. Second, classical regret theory only considers static decision at a certain point in time, while regret is a dynamic decision of decision maker within a period of time. Therefore, the application of the dynamic regret theory to SMADM problems would be discussed more deeply in the future. Finally, the proposed approach can be extended to other areas, such as in scheduling, traffic, medicine, etc.

Acknowledgments

The authors would like to thank the anonymous reviewers and editors for their insightful and constructive comments on our paper. This work was supported in part by the Doctoral Project of Chongqing Federation of Social Science Circles (2022NDQN39), the Humanities and Social Sciences Research General Project of Chongqing Education Commission (22SKJD076, 19SKGH051), the Open Topic of Center for International Cooperation and Innovation Development of Digital Economy (P2022-37), the Chongqing Technology Innovation and Application Development Project (Grant No. 2022TIAD-GPX0072), the Chongqing Educational Science Planning Key Project (K22YD206077).

Conflict of interest

The authors declare no conflict of interest regarding the publication of this paper.